1. Introduction
The strontium cation, Sr
2+, in its normal isotopic composition based on natural abundance, is a chemical analog to
90Sr
2+, radioactive strontium-90, a fission byproduct of uranium and plutonium production [
1,
2,
3,
4,
5,
6]. Both uranium and plutonium are part of the nuclear fuel cycle and hence
90Sr is a byproduct of the nuclear fuel cycle, as well as a byproduct of nuclear weapon testing; strontium-90 is a pure beta emitter, as is its daughter product
90Y (half-life 64.2 h) [
6]. Because of its half-life of 29.1 years, strontium-90 is one of the most important radioisotopes in low-level radioactive wastes, given that the half-lives of the other 16 major radioactive isotopes of strontium are shorter than 65 days [
2,
3]. Because of its chemical similarity to calcium,
90Sr can readily replace calcium in the human body; in addition,
90Sr has a tendency to deposit in bone and blood-forming tissue, causing chronic sicknesses, such as leukemia and anemia [
1,
2,
3,
4,
5]. The United States Environmental Protection Agency (EPA) has published a maximum contaminant level (MCL) of 4 millirem per year for photon radioactivity and beta particles from man-made radionuclides in drinking water [
3]. Therefore, the transport of the constituents of nuclear waste resulting from nuclear energy production and Cold War nuclear tests is a major environmental and human health concern at many United States Department of Energy (DOE) sites, such as Hanford, Oak Ridge National Laboratory, Idaho National Laboratory, Nevada National Security Site, and the Savannah River Site [
4,
5,
7,
8,
9,
10,
11,
12].
The transport of metals ions, often regarded as analogs of cationic radionuclides, has been studied extensively [
13,
14,
15,
16,
17]. The effect of pH and other geochemical conditions on metal ion transport has been modeled using reactive transport and surface complexation models both under field [
16] and laboratory conditions [
14,
15]. Specifically, the significant and varying effects of ionic strength on anion and cation sorption on oxide surfaces, as a function of the sorption mechanism, have long been known [
18,
19] and continue to be observed and reported in more recent studies [
13]. However, the majority of these studies involve column experiments under saturated or unsaturated conditions and do not consider the effects of saturation and drying cycles on metal ion mobility.
The work conducted here aimed to explore the dynamics of strontium transport, with an emphasis on the mobilization from porous media after evaporation to dryness. Evaporation is ubiquitous in the unsaturated zone near the ground surface, so liquids entering the environment at the ground surface in dry environments may undergo cycles of evaporation followed by remobilization with rainfall infiltration events. Based on previous work with organic contaminants [
20], it was hypothesized that evaporation/infiltration cycles would be likely to have a substantial impact on the transport of strontium.
Because of the importance of strontium as a component of nuclear waste, a substantial quantity of work has been conducted examining its transport in the environment in both saturated and unsaturated porous media [
4,
6,
8,
9,
10,
21,
22,
23,
24]. Studies have included efforts aimed at understanding how strontium previously immobilized in the subsurface can be released by natural or engineered phenomena (e.g., [
6,
9,
10,
23,
24]); however, little work has examined remobilization of strontium from porous media following evaporation to dryness. Note that as the water evaporates from a porous medium, the concentrations of nonvolatile compounds in porewater increase. This process drives adsorption to solid surfaces and can potentially also lead to surface precipitation once concentrations exceed solubility limits. The work described here was designed to explore how this phenomenon ultimately impacts the dynamics of release following resaturation of porous media. The work included a range of saturated and unsaturated transport experiments designed to explore this phenomenon, as well as an evaluation of the results of the work using a numerical model developed in previous work [
20].
2. Materials and Methods
2.1. Materials
US Silica (Berkeley Springs, WV, USA) F-65 quartz sand was used for all experiments conducted for the work. The quartz sand is a foundry-grade and high-purity sand. Based on X-ray diffraction (XRD) analysis, only trace amounts of meionite, a tectosilicate, could be identified as a separate phase in addition to quartz. No other oxide or hydroxide phases were detectable. The Sauter mean diameter (diameter of a particle with the same volume to surface area ratio as the particle considered) was measured to be 0.215 mm, while 90% of the sand, by mass, had diameters between 0.106 and 0.295 mm. The specific surface area was determined by nitrogen adsorption and the Brunauer, Emmett, and Teller (BET) model using a Micromeritics (Norcross, GA, USA) ASAP 2050 Xtended Pressure Sorption Analyzer, and found to be 0.0519 m²·g−1. The pH of the point of zero net surface charge (pHpzc) of the sand was found to be 2 using an Anton Parr (Ashland, VA, USA) Electrokinetic Analyzer for Solid Surface Analysis: SurPASS 3.
Strontium (Sr) was purchased from Inorganic Ventures (Christiansburg, VA, USA) in the form of a SrCO3 certified reference material (10,000 µg·mL−1 in 1% v/v nitric acid, 99.9937% reported purity), and was diluted as necessary for all experiments. Ionic strength was adjusted in all solutions prepared for the work through addition of sodium nitrate (NaNO3).
2.2. Experimental Procedures
The experiments conducted for this work consisted of saturated breakthrough curves, as well as remobilization elution curves exploring how strontium is released after it has been retained by evaporative drying. The experiments conducted were based on similar systems and procedures described by Normile, Papelis, and Kibbey [
20], adapted for the analysis of strontium.
All experiments were conducted in a cylindrical column measuring 1.91 cm for the inner diameter and 2.54 cm in length, having a total internal volume of 6.72 cm3. The column was made from transparent acrylic. Prior to filling the column, sand was rinsed three times with deionized water to remove fines, and then oven-dried at 110 °C for 24 h. Stainless steel no. 40 mesh screens were used at the top and bottom of the column to support water-wet capillary barrier membranes. Ahlstrom-Munksjö (Leominster, MA, USA) paper filters with a 1.5-µm pore size were used as water-wet capillary barriers to allow water flow while preventing air flow. Membranes were sealed to the column by placing O-rings within a slot machined into the top and bottom of the column.
Experiments were initiated by wet packing approximately 11 g of quartz sand into a column. The typical porosity of the sand column was approximately 0.37. Saturated transport experiments were conducted at a flow rate of 0.50 mL·min−1 (0.47 cm·min−1 porewater velocity) in a horizontal orientation. A pH- and ionic strength-adjusted background solution was pumped through the column for at least 5 pore volumes, removing residual quartz sand fines and stabilizing the column pH. The effluent pH was continuously measured using a Mettler Toledo (Columbus, OH, USA) Seven Excellence pH meter, and deviations from influent pH were small (less than a tenth of a pH unit). Background electrolyte ions were not measured. Especially at the higher ionic strengths, given the nature of the interactions of these major electrolyte ions with the quartz surface, it is not likely that any measurable fraction would be retained by the sand. It should also be noted that, as mentioned earlier, the sand was carefully rinsed three times before the experiments, so that any impurities that could interfere with the ions of interest were removed before the experiments were initiated. A bromide (conservative tracer) breakthrough curve was first obtained, and then a saturated breakthrough experiment was conducted using a solution with the specified strontium concentration, ionic strength, and pH. The effluent pH was monitored throughout each stage of all experiments.
Analysis of strontium concentrations in this and all subsequent experiment stages was conducted through the use of a PerkinElmer (Waltham, MA, USA) SCIEX ELAN DRC-e inductively coupled plasma mass spectrometer (ICP-MS). Effluent samples were collected at fixed intervals and diluted as necessary with a 1% nitric acid solution to a concentration appropriate for strontium determination. A calibration curve, with a correlation coefficient (R2) value of at least 0.999, was generated each time the ICP-MS was operated. Yttrium at 75 µg·L−1 was used as an internal standard. The ICP-MS sampling parameters included speed at 20 rpm, sample flush at 60 s, read delay at 15 s, and wash at 45 s.
Following completion of the saturated breakthrough curve, the column was partially drained to facilitate evaporation. In order to drain the column, the column was placed in a vertical orientation, and the top of the column was linked to a computer-controlled servo-pressure regulator, which was supplied air by an air compressor. The column was drained to approximately 40% saturation in 45 min by applying a ramped pressure input, using the servopressure regulator system described by Chen and Kibbey [
25] and Chen et al. [
26]. The drainage process was monitored by measuring and recording the column mass using a Mettler (Toledo, Columbus, OH, USA) Precision Balance PL602E with a computer interface, and the mass of strontium leaving the column was monitored by collecting samples at regular intervals for analysis by ICP-MS.
Following drainage, the column was opened by removing the top and allowed to evaporate to dryness over 24 h or more. The evaporation process was continuously monitored by recording the column mass as a function of time until no further change in mass could be observed.
Following evaporation, a remobilization elution experiment was conducted. The column was closed and the pH- and ionic strength-adjusted background electrolyte solution was introduced to the dry column. Once the column filled and solution began eluting from the column, samples were collected at fixed intervals and analyzed for the strontium concentration and pH. Flow was continued until the effluent strontium concentration reached the analytical detection limit.
2.3. Finite-Difference Elution Model
To better understand the results of the experiments, a custom-designed finite difference transport model was used. The model was developed in a previous work and is described in detail by Normile, Papelis, and Kibbey [
20]. The purpose of the model is not necessarily to simulate observed elution behavior but rather to examine the extent to which the elution behavior can be predicted from rate-limited desorption, as opposed to dissolution dynamics. The model is based on a standard one-dimensional single-species transport model, Equation (1), with rate-limited adsorption/desorption, Equation (2), capable of simulating saturated transport but also modified to allow simulation of transport during the resaturation process, where a wetting front is advancing into the column:
where
C is the is aqueous concentration (mg·L
−1),
is the porewater velocity (m·s
−1),
is the dispersion coefficient (m
2·s
−1) related to the dispersivity,
, by
,
is the mass of sand in the column, and
is the pore volume of the column.
q is the mass adsorbed to the sand per kg of sand (mg·kg
−1),
krev is the desorption rate constant (s
−1), and
is the distribution coefficient (L·kg
−1) [
20].
Application of the model involves first using it to simulate a saturated breakthrough curve, for the purpose of determining a desorption rate constant (
krev) needed to match the saturated breakthrough curve. The desorption rate constant,
krev, is a first-order parameter that describes rate-limited desorption during transport. For a given
Kd (adsorption distribution constant), a transport curve with a greater
krev exhibits greater deviation from equilibrium transport behavior, i.e., more effects of rate limitation. The
krev parameter is then used to simulate the elution behavior that would be expected from an initially dry column, assuming all transport behavior is the result of rate-limited desorption; deviation from the simulated behavior can be taken as an indicator that rate-limited dissolution is impacting the observed release. The elution model is formulated as an implicit finite-difference model and uses a moving boundary approach (i.e., expansion of the simulated region during the transport simulation) to simulate water movement into the column for resaturation and elution. All parameters, procedures, and solution methods for the model as used in this work were the same as those given by Normile, Papelis, and Kibbey [
20].
3. Results and Discussion
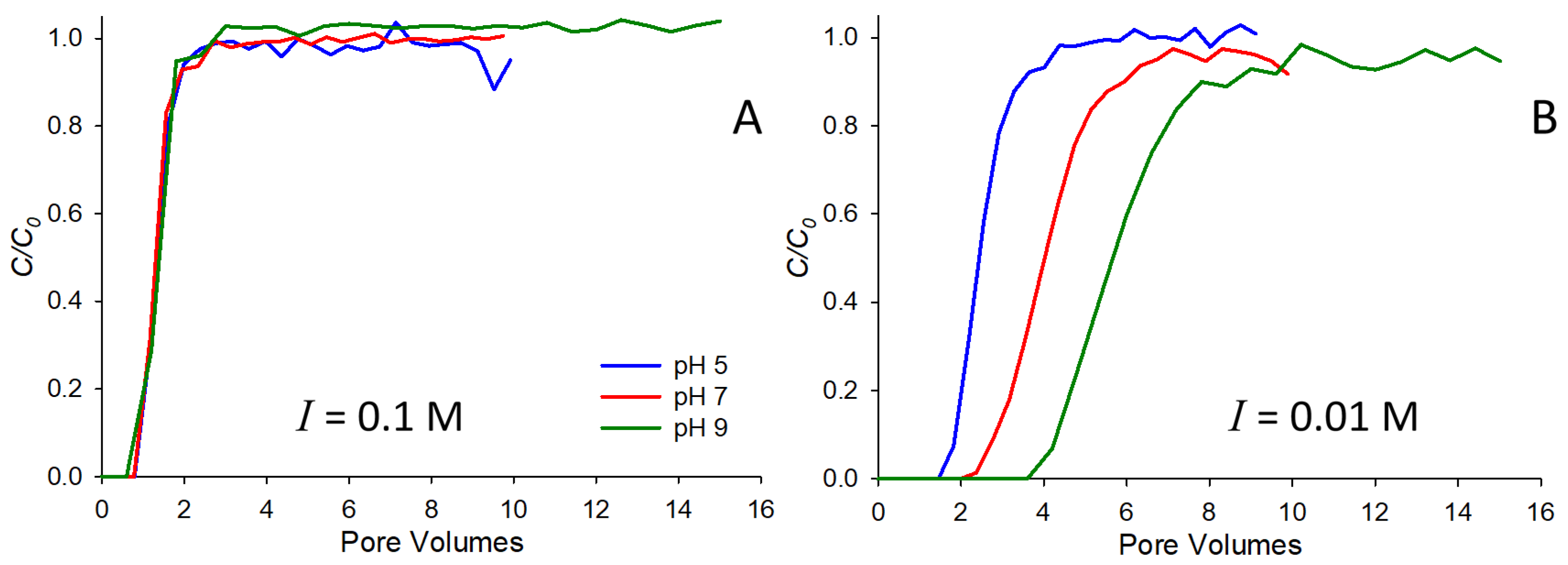
Figure 1 shows saturated breakthrough curves for 10
−4 M strontium at two different ionic strengths, 0.1 (
Figure 1A) and 0.01 M (
Figure 1B) NaNO
3. In each subfigure, breakthrough curves at three pH values are shown. Note that at the higher ionic strength (0.1 M,
Figure 1A), very little retardation is observed at any of the pH values and strontium behaves largely as a conservative tracer. This result is consistent with many previously reported studies of strontium-saturated transport, where authors have observed higher mobility in the presence of higher background electrolytes (e.g., [
4,
6,
9,
23]). The primary reason for the observed behavior is likely competition for sorption sites on the solid surface, with higher concentrations of electrolyte preventing the adsorption of strontium. At the lower ionic strength (0.01 M,
Figure 1B), more substantial retardation is observed, and the behavior is pH dependent, with the greatest retardation occurring at pH 9, and the least at pH 5. Note that this behavior has also been observed by others (e.g., [
4,
6]), and is likely due to the increasingly negative surface charge of the solid as pH increases beyond the pH
pzc (pH 2 for the quartz sand used here), thereby increasingly favoring the sorption of the strontium cation with increasing pH.
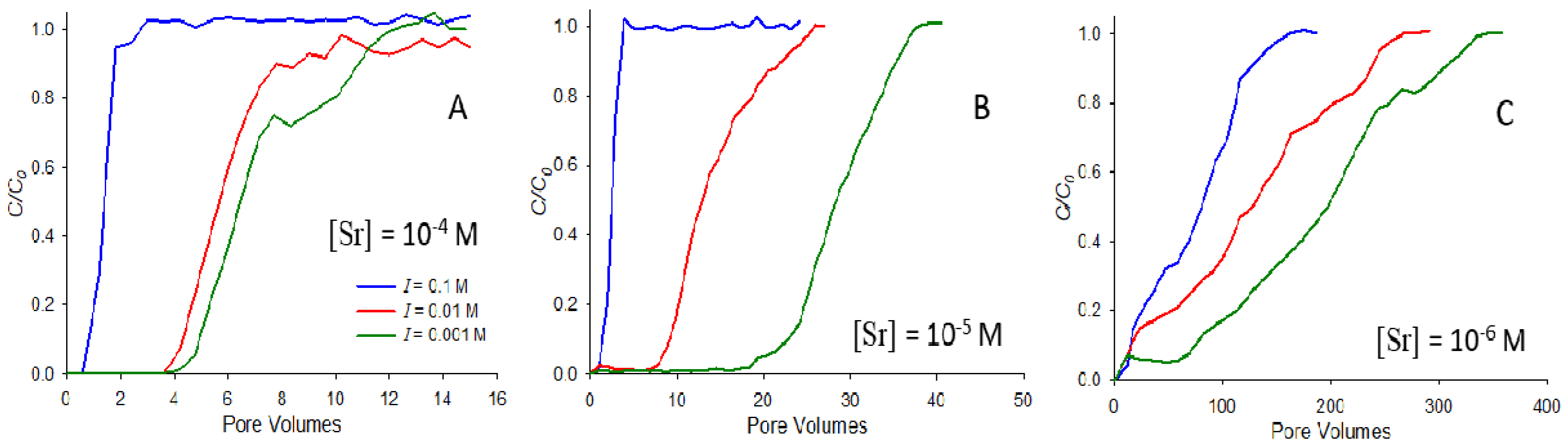
Figure 2 illustrates the effect of the strontium concentration and ionic strength on saturated breakthrough, showing breakthrough curves at pH 9 for strontium concentrations of 10
−4 M (
Figure 2A), 10
−5 M (
Figure 2B), and 10
−6 M (
Figure 2C). In each subfigure, breakthrough curves at three ionic strengths (0.1, 0.01, and 0.001 M NaNO
3) are shown. In each case, the breakthrough of strontium is retarded to the greatest extent in the system with the lowest ionic strength, consistent with the results in
Figure 1. However, the most significant difference between systems is observed between the different concentrations, with strontium at 10
−6 M exhibiting retardation almost two orders of magnitude greater than that at 10
−4 M (note that the horizontal axes of
Figure 2A, B, and C cover different ranges). This result means that strontium exhibits strongly nonlinear adsorption behavior, with the lower concentrations having a substantially stronger adsorption affinity. Others have also observed nonlinear adsorption for strontium, with higher adsorption at lower concentrations (e.g., [
22]).
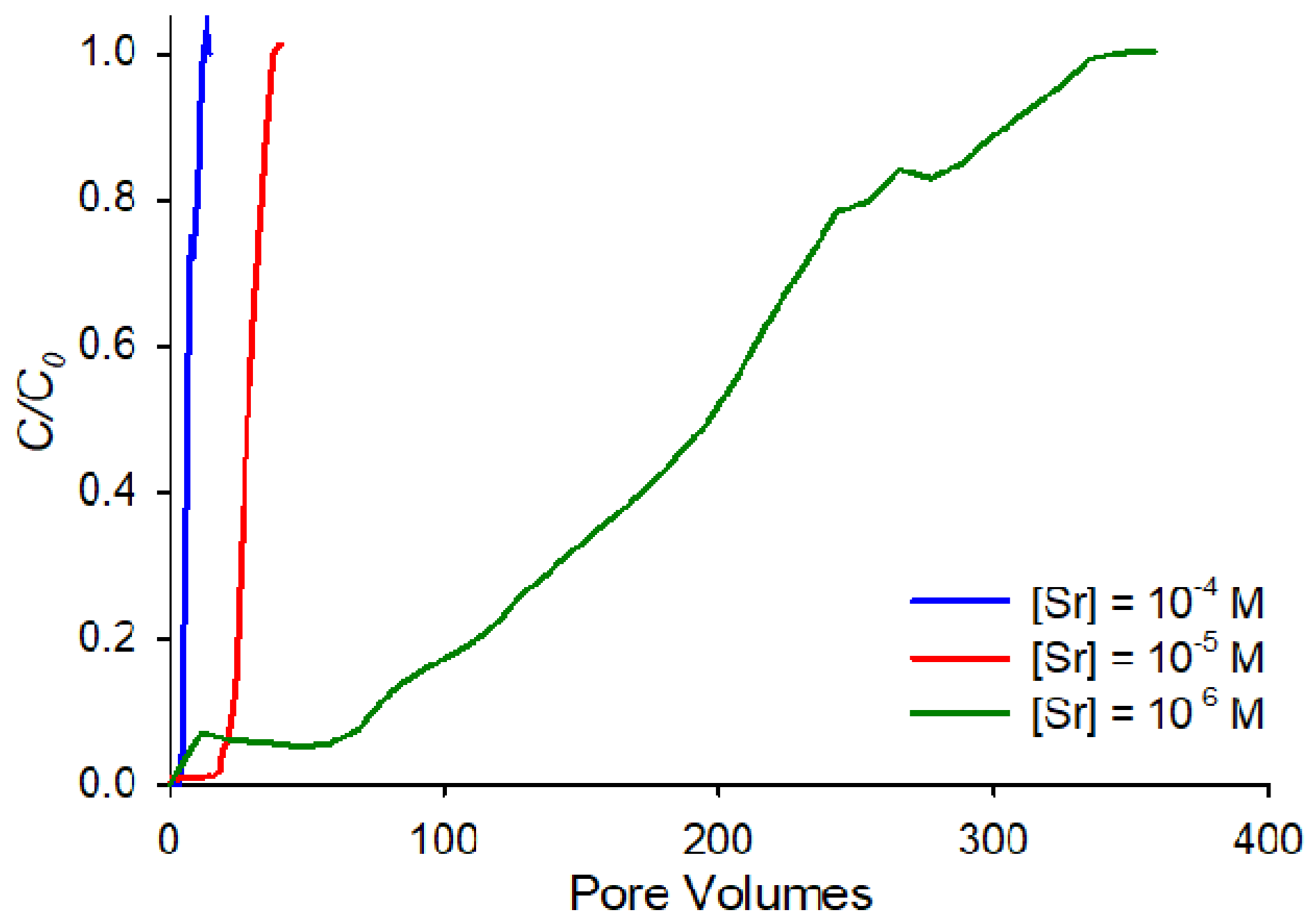
The difference in adsorption affinities as a function of the concentration is even more apparent in
Figure 3, which shows the breakthrough curves at pH 9, and ionic strength of 0.001 M for all three concentrations on the same horizontal axis. The figure highlights the order-of-magnitude differences in affinities between the three concentrations. This behavior can be interpreted in terms of the ratio between the concentration of strontium cations in solution and available sorption sites. Compared to the 10
−6 M strontium concentration, when the strontium concentration is increased by 100-fold to 10
−4 M, similar retardation for the two concentrations could only be observed if strontium sorption were not limited by sorption site availability. If, therefore, at the higher strontium concentrations, the finite number of sorption sites on the sand are exhausted, strontium retardation is expected to fall dramatically.
Retardation coefficients (
Rf) were calculated for all saturated breakthrough curves by integrating to find the area above each
C/C0 vs. pore volume breakthrough curve. The calculated values are shown in
Table 1. Note that the trends in the preceding paragraphs are also apparent in the
Rf values shown in
Table 1.
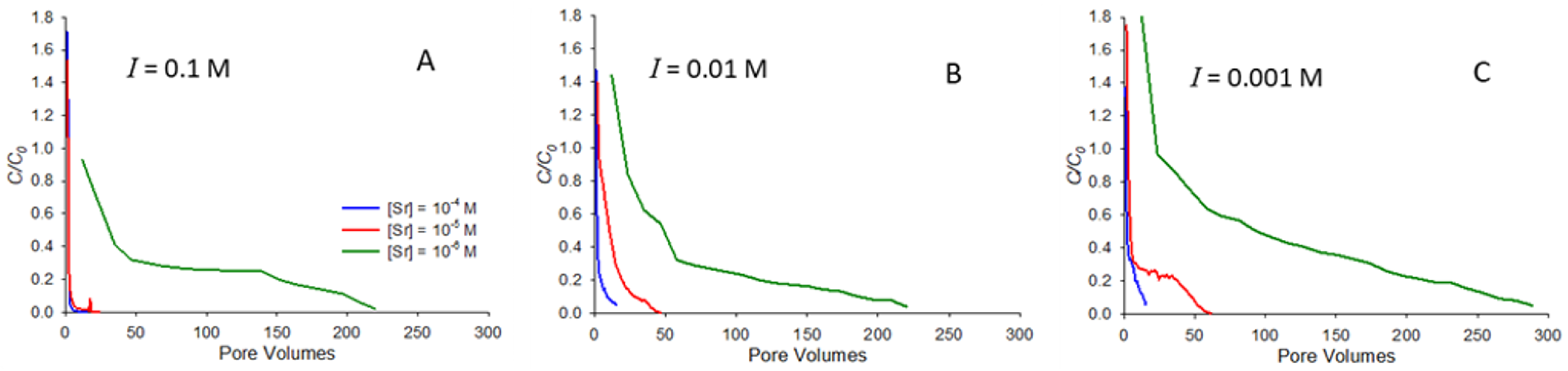
Figure 4 shows the elution curves for the release of strontium following resaturation from an initially dry state. The curves in
Figure 4 all correspond to pH 9 and show elution for ionic strengths of 0.1 (
Figure 4A), 0.01 (
Figure 4B), and 0.001 M (
Figure 4C) NaNO
3. Each curve shows elution from a column following a saturated breakthrough curve at the specified initial concentration, followed by drainage and then evaporation to dryness. Note that pore volumes on the horizontal axes in
Figure 4 correspond to the number of pore volumes elapsed since water began to elute from the column following resaturation.
Several notable features are apparent in
Figure 4. First, it is interesting to note that
C/C0 at the start of most of the elution curves is greater than 1.0. The reason for this is that the process of resaturating the column causes strontium to be dissolved and carried along by the wetting front moving through the column, leading to a concentration magnification at the start of the elution curve as water passes through the column. This behavior was previously reported for a range of organic compounds [
20]. It is also apparent from
Figure 4 that conditions that favor greater retention in saturated transport also correspond to longer elution times. For example, at 0.1 M NaNO
3 ionic strength (
Figure 4A), the two higher concentrations elute almost immediately, consistent with their low saturated retardation factors (
Table 1,
Figure 1A), while the lowest concentration (10
−6 M) system, which exhibits a higher retardation factor (
Table 1), elutes over hundreds of pore volumes.
As with the saturated transport, the most significant factor influencing retention during elution is the concentration, with the lowest initial concentration (10
−6 M) experiments exhibiting the greatest retention in both saturated transport and elution. Furthermore, it is interesting to note that in the systems studied, the number of pore volumes needed for concentrations during elution to approach zero is generally similar to that needed for
C/C0 to approach 1.0 during saturated transport. For example, the 10
−6 M elution curve in
Figure 4C (
I = 0.001 M) exhibits long tailing, but
C/C0 is approaching zero by around 300 pore volumes, while for saturated transport with the same system (
Figure 2C),
C/C0 approaches 1.0 after approximately 350 pore volumes. In contrast, previous work with strongly adsorbing organic solutes found substantially longer tailing in elution curves compared with saturated breakthrough curves [
20].
To further explore the mechanisms underlying the elution behavior observed in
Figure 4, a finite difference elution model developed in a previous work [
20] was used. The model is designed to highlight the extent to which elution results from rate-limited desorption. To apply the model, it must first be fit to saturated breakthrough curves to determine desorption rate constants. The fitting process involves determining an
Rf value by integration of the saturated breakthrough curve (
Table 1), and then using this value to simulate breakthrough while adjusting the desorption rate constant (
krev) to match the observed behavior.
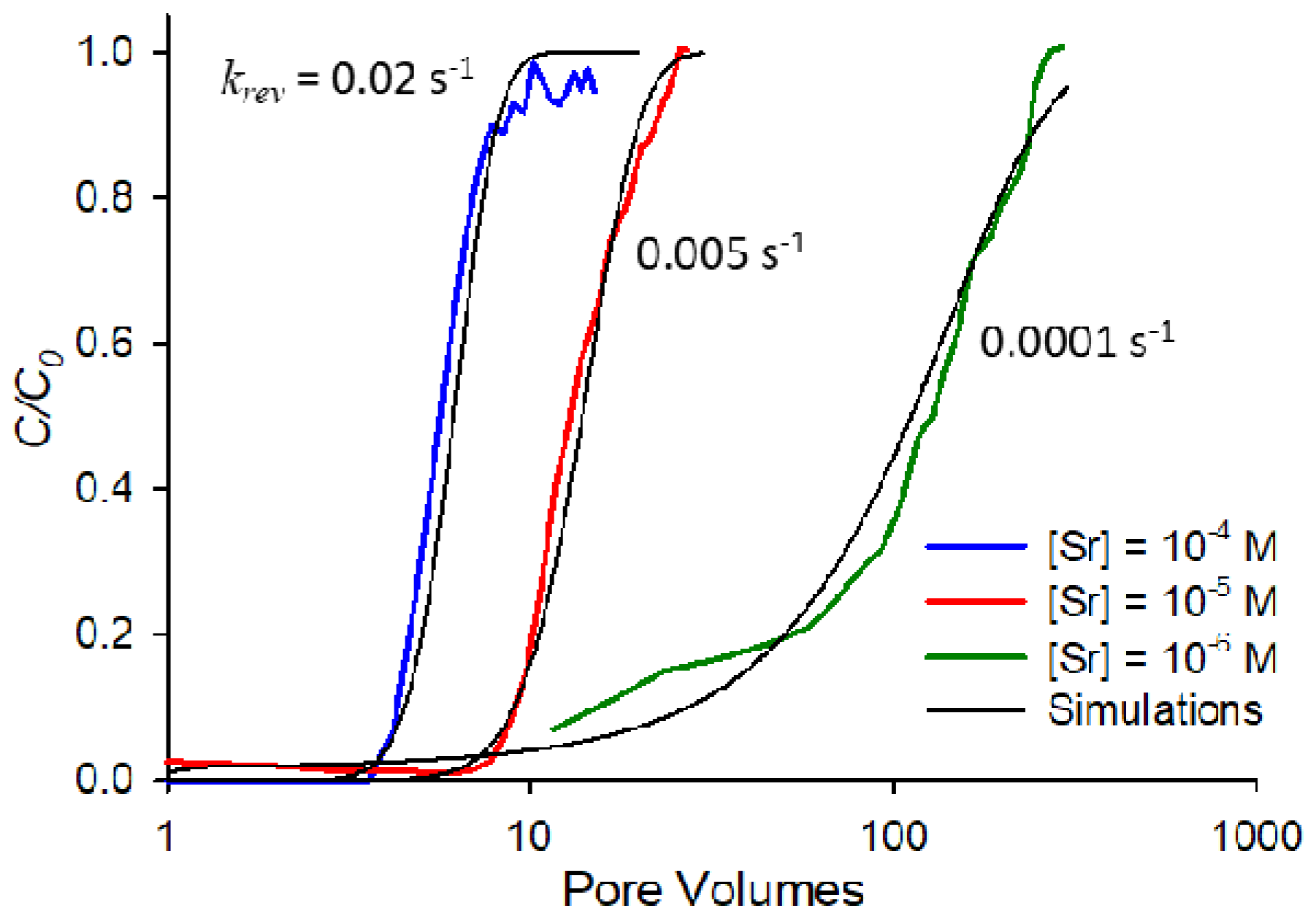
Figure 5 shows the fits for saturated breakthrough curves at the three strontium concentrations (10
−4, 10
−5, and 10
−6 M) at an ionic strength of 0.01 M NaNO
3 and pH 9. Breakthrough curves in
Figure 5 are shown on a semi-log scale for clarity so all three fits can be observed. Of particular note from the results in
Figure 5 is the fact that lower concentrations correspond to significantly lower desorption rate constants, an indication that rate-limited desorption is increasingly important as concentration decreases for this system.
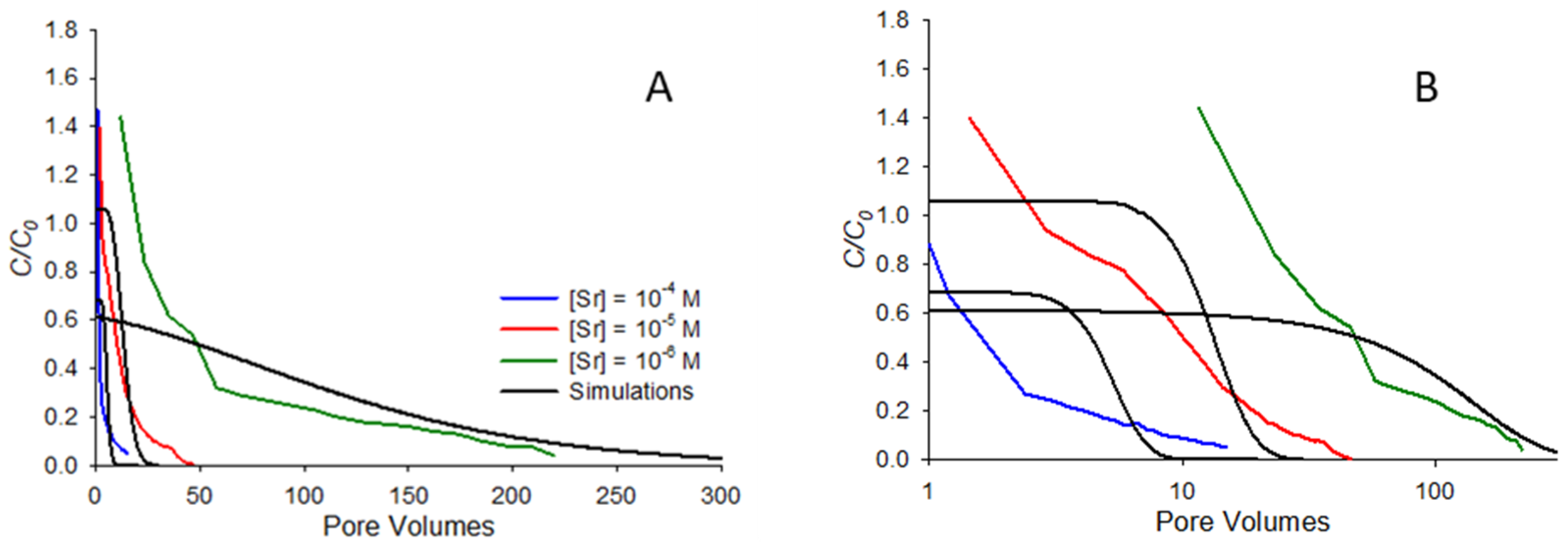
Figure 6 shows comparisons between model-predicted and measured remobilization elution curves for the same systems shown in
Figure 5, with pore volumes shown on linear (
Figure 6A) and semi-log (
Figure 6B) scales. Note from
Figure 6A that the trends predicted by the model generally follow those observed in the elution curves, with more rapid elution observed at the higher concentrations and more gradual elution for the lowest concentration. In particular, the long tailing observed at high pore volumes for the 10
−6 M case is reasonably well-predicted by the model. This is a contrast with previous work with organic compounds [
20], which found that elution curves for more strongly sorbing compounds were not particularly well-predicted by the model. In the organic systems studied in that earlier work, it was observed that the most strongly sorbing compounds did not exhibit particularly low
krev values, yet still exhibited high initial eluting concentrations and long tailing similar to that observed for the 10
−6 M concentration in
Figure 6A. The difference between the model and experiment in that earlier work suggested that rate-limited dissolution was likely important for the high-sorbing organic systems. In this work, at least to a first approximation, rate-limited desorption does appear to capture many of the major features of elution. One notable exception to this is the fact that the model does not capture the high initial
C/C0 values observed in the experiment, a discrepancy most apparent in
Figure 6B, where the semi-log scale accentuates discrepancies at low pore volumes. In general, the model only predicts a high initial
C/C0 for systems that exhibit low sorption affinity (
Rf less than approximately 1.5), so would not be expected for any of the systems in
Figure 6, all of which exhibit
Rf values of 6 or greater. The high initial
C/C0 observed in experiments means that at least some fraction of the strontium released during elution is more mobile than can be predicted from saturated transport behavior alone.