1. Introduction
Risk is usually defined by the association of the terms origin–pathway–target [
1,
2]. The “origin” refers to the identification of polluting agents and contaminant loads associated with the source hazards (
H). The “pathway” is associated with the intrinsic vulnerability (
Y) of an aquifer for contamination. For association among
H and
Y, the authors of [
2] suggested a basic risk (
Rb) to express it by the following:
Rb =
Y ×
H. The “target” is related to the possible consequences of contamination events (socioeconomic and environmental impacts). According to the authors of [
2], the consequence of contamination (
C) is associated with the product of the groundwater reserve (
G) and the quality (
Q) of the groundwater (i.e.,
C =
G ×
Q). Thus, a type of risk known as the value-weighted risk (
R) is calculated by the following equation:
R =
Rb ×
C.However, the commonly used methods to evaluate intrinsic vulnerability, to quantify the hazard degree of a contamination source, to classify the quality, and to estimate the use of groundwater reserves are subjective (shallow or deeper aquifers). Additionally, the lack of available geological, hydro-geochemical, and hydro-geological data is a source of uncertainty that can lead to errors in risks assessments. Therefore, proposing a risk model that can handle these limitations, that is, the subjectivities and uncertainties, is valuable for risk assessment.
1.1. Theoretical Background and Limitations
1.1.1. To Assessment Intrinsic Vulnerability
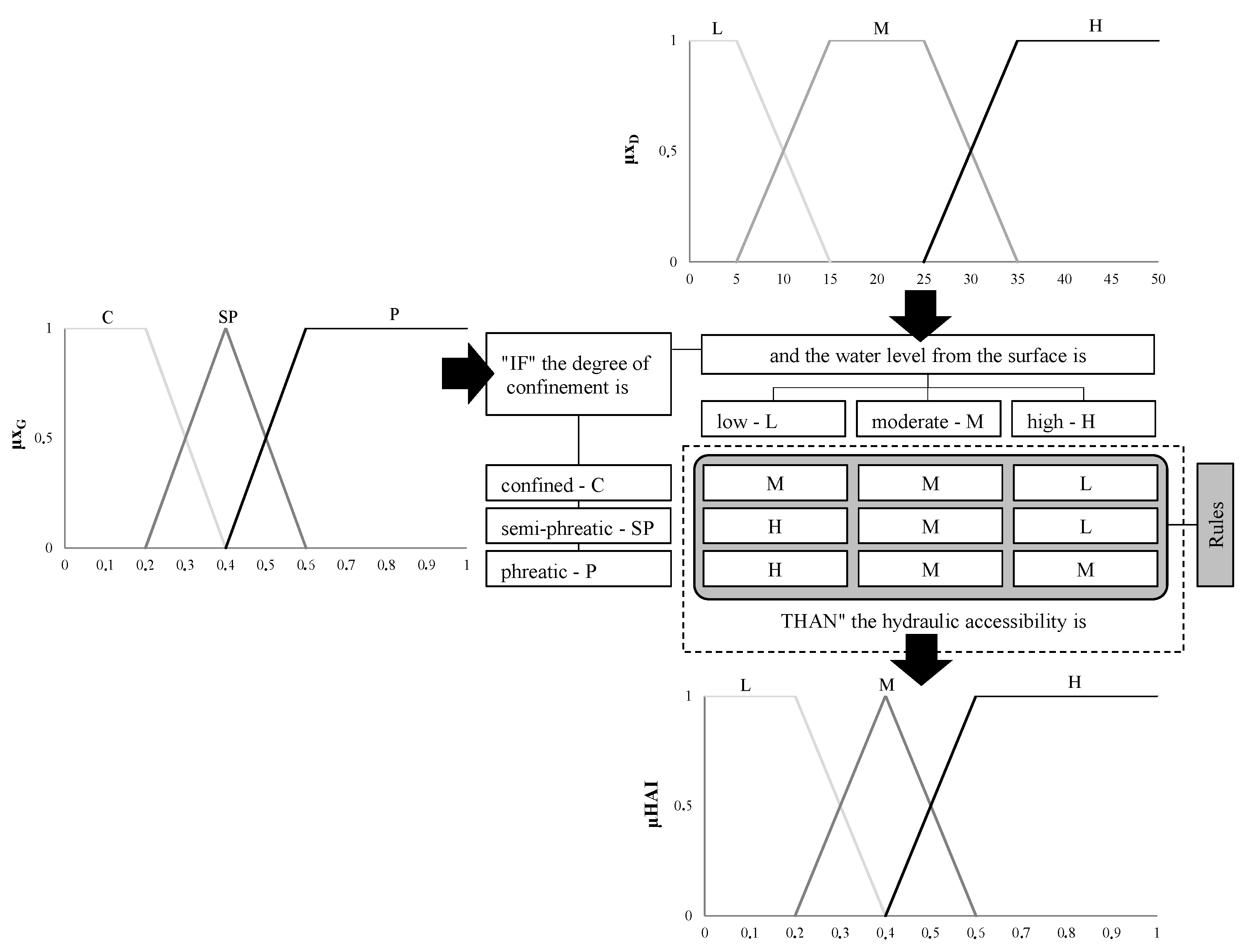
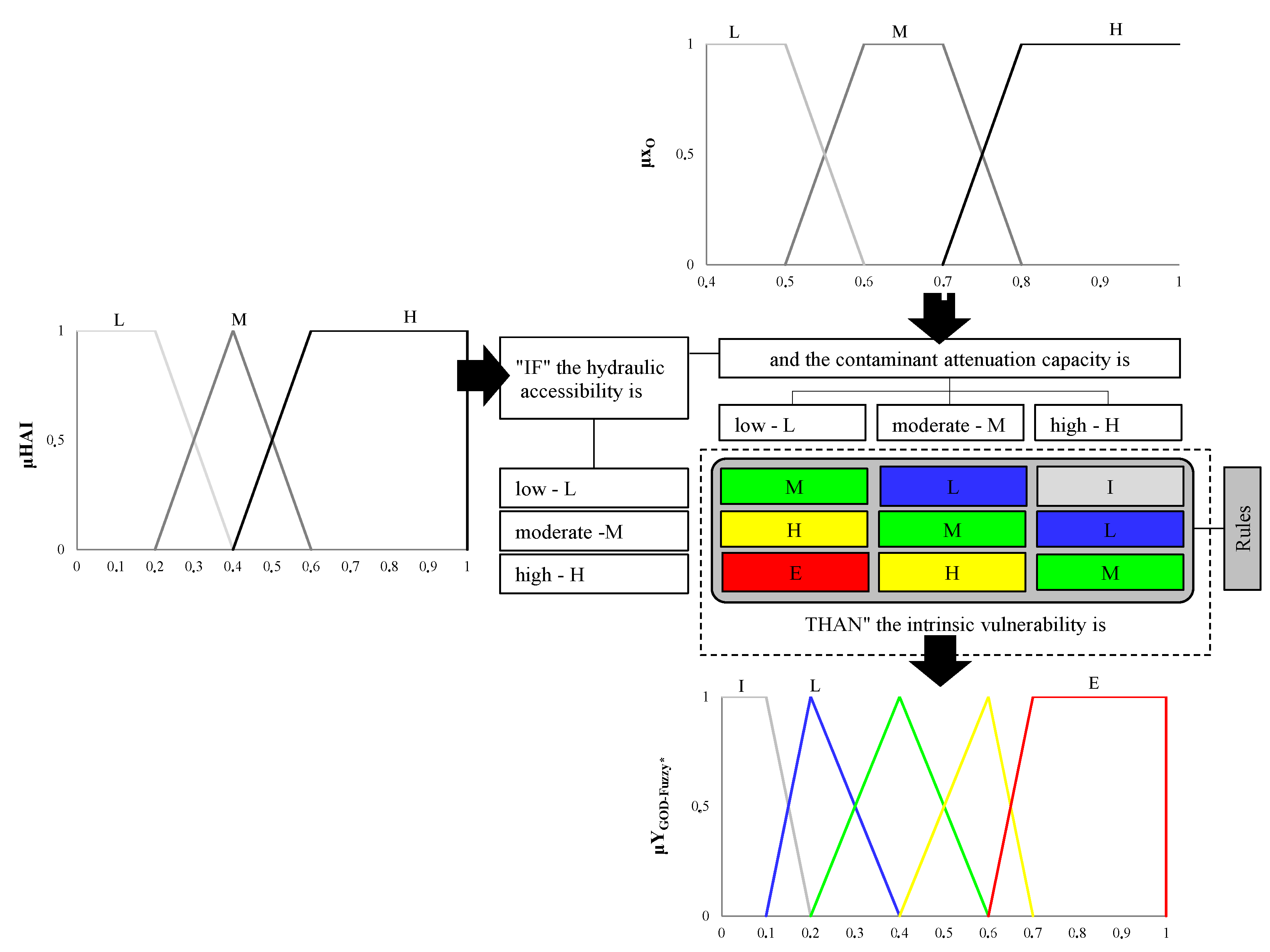
The typical way of assessing vulnerability involves methods structured by a Y-index, which results in the association of input data (X) (x1, x2, ...xi), that is, of hydrogeological parameters. In general, this format imposes subjectivity on the methods, denoting them as conceptual (usual methods seek a simplified interpretation to explain complex interactions that occur in a simultaneous and systemic manner, such as vertical water flow phenomena and contaminant transport, as well as biophysical, chemical, and physical processes) and ambiguous (they define the universal set of X-parameters in imprecise terms, which are used to classify the Y-index into specific degrees of vulnerability).
Although recent work has been developed to overcome the assessment vulnerability limitations [
3], this subjective, conceptual, and ambiguous nature has been circumvented using “intelligent models”, for example, the application of fuzzy models. The works of [
4,
5,
6,
7] applied a multi-criteria fuzzy model to assess vulnerability based on the
X-parameters of the DRASTIC method [
8]. Other works [
9,
10,
11,
12,
13,
14] proposed a fuzzy inference system (FIS) that permits systematic and simultaneous interactions of
X-parameters to evaluate the
Y-index.
Constructing an FIS requires the following three steps: “fuzzification”, inference, and “defuzzification”. The “fuzzification” is defined by attributing linguistic variables to the
X-parameters and to the
Y-index and by selecting a type of membership function (
mf). Although this function can assume many different forms, the usual forms are triangular (
mftri), trapezoidal (
mftrap), and gaussian functions (
mfgau). In the inference, all the applications of one type of FIS to assess the intrinsic vulnerability follow the Mamdani model [
15], as they do in the “defuzzification” using the centroid method [
16]. The FIS was not validated, nor were the performances measured in studies that apply a fuzzy model to assess vulnerability. In these studies, the FIS was only compared to the base-method.
1.1.2. Assessment of the Hazard Degree from Contamination Sources
It is necessary to identify the polluting agents and quantify the contaminant loads. This identification refers to the registration of sources [
17,
18]. The pollutant origin and its surcharge hydraulically (POSH) method, which classifies sources into levels of contaminant load generation, was proposed [
19]. This approach considers the type of activity, contaminant-generating capacity, and associated hydraulic head. Recently, some studies proposed hazard indices (
H), a function of the physico-chemical properties of contaminants [
1,
2,
20,
21,
22]. In general, the studies reviewed that classify the hazard degree are based on the importance of the relationship among physico-chemical properties. Thus, they represent a pattern framing issue with an approach by the multi-criteria method, the objective of which is to classify the hazard degree. However, limitations include the operational difficulty of inserting
n-properties and weighting these properties to quantify the hazard degree.
1.1.3. Assessment of the Natural Groundwater Quality
The Piper diagram is one of the methods proposed to assess the groundwater quality. The Piper diagram is used for the initial hydro-chemical analysis. Diagrams such as the U.S. Salinity Laboratory diagram and the Schoeller–Berkalof diagram classify water quality for use in agriculture or for human consumption, respectively. However, these diagrams do not synthesize information about the water quality and do not find organics or special contaminations as indices.
Thus, the works of [
23,
24,
25] developed methods capable of classifying the groundwater quality with a
Q-index using subjective, conceptual, and ambiguous formulations (the same is justified about limitations of the
Y-index). An FIS may be used to overcome these limitations. Indices are used to classify water quality standards, the parameter weighting of which can be associated with the final intended use (e.g., potable or non-potable water). Thus, adopting a multi-criteria model that manages, in addition to the mentioned limitations, a judgment on the importance between parameters for multiple water use purposes is an asset during this process.
1.1.4. Estimation of the Groundwater Reserves
Although recent work has developed a stochastic assessment of nonpoint source contamination [
26], a similar method was not applied to estimate the probability of use of groundwater reserves. In turn, the various forms of deterministic calculations of the groundwater reserves (
G), the sum of permanent reserves (
GP), and regulating reserves (
GR) [
27,
28] consist of variables with large variability. The authors of [
29] adopted average values for the saturated thickness of aquifers (
b), effective porosity (
ηe), area of occurrence (
A), and water level variation (Δ
h) (during the dry and rainy season), which denote uncertainties that can be overcome using a probabilistic approach.
The probability that the GP reserve will be used can be estimated with the safe use of the GR reserve (and vice-versa). The objective of this study is thus to propose an fuzzy-probabilistic modelling approach for groundwater contamination risk assessment (FPM-risk) for groundwater contamination assessment, and its methodology is described and prescribed below. Its application was conditioned by strategies for the acquisition, identification, and cataloging of geological and hydrogeological data, source characteristics, water physicochemical parameters, and the physical variables of the shallow aquifer.
3. Case Study: Belém Urban Zone
The application of the fuzzy-probabilistic approach was conditioned by data acquisition strategies for a domain that corresponds to the urban zone of Belém city, in the northern region of Brazil, which is an integral part of the metropolitan region of Belém (MRB). In addition to belonging to the hydrogeological province of the Amazon River, which is one of the largest in Brazil with a volume of greater than 30 thousand km³, the selection of this spatial domain is justified by the fact that evidence of hydrocarbon contamination from leaking UFST has been found.
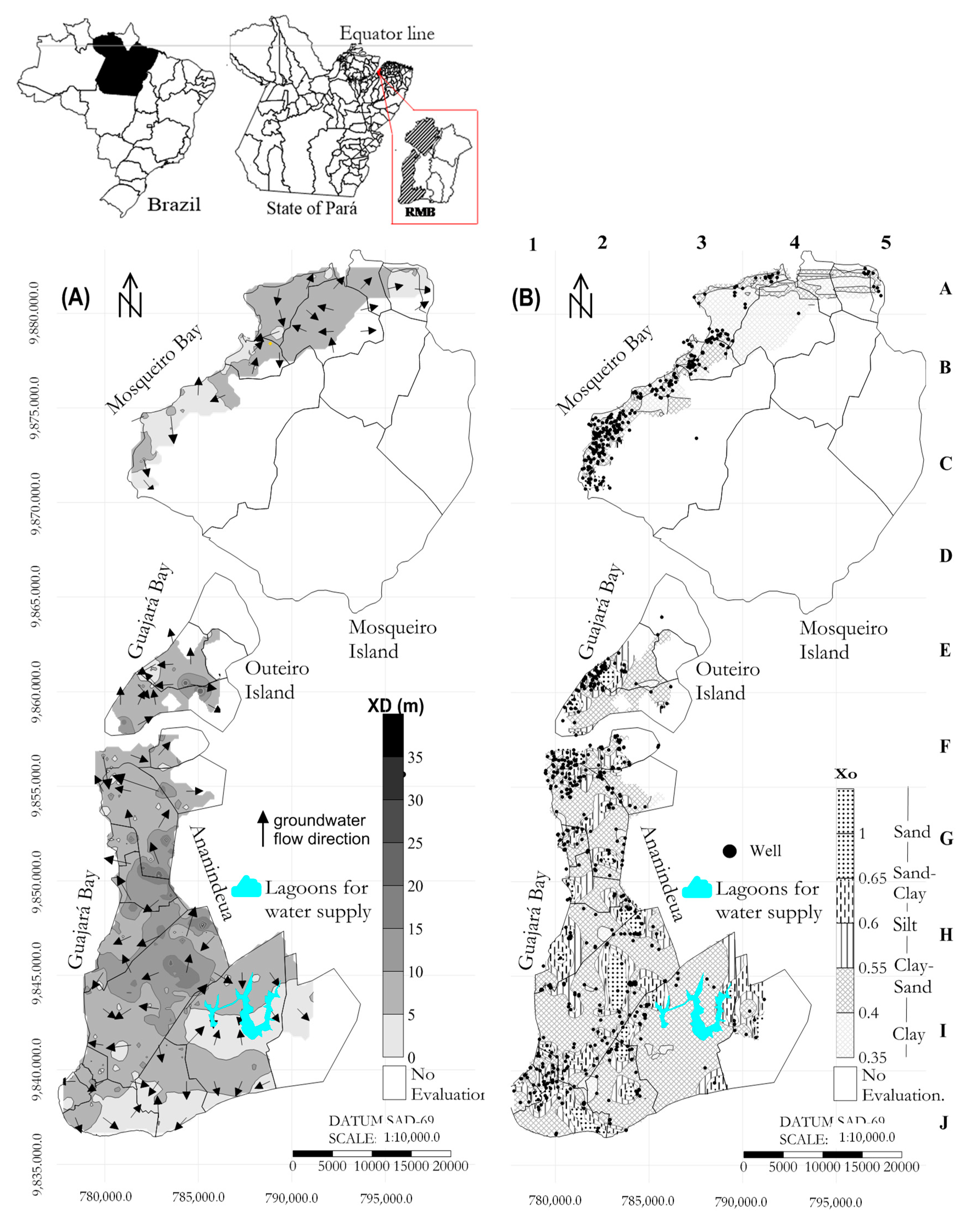
To apply the risk model, the geological and hydrogeological data were initially extracted to evaluate the intrinsic vulnerability. Thus, data were extracted from the Groundwater Information System (
Sistema de Informação de Águas Subterrâneas—SIAGAS), which was generated by the Research and Mineral Resources Company (
Companhia de Pesquisa e Recursos Minerais—CPRM,
Serviço Geológico do Brasil) belonging to the Brazilian Geological Service. A total of 762 data points from wells were catalogued. The information referred to the hydrostatic level and the lithological and construction profiles of the unsaturated zone (to a depth of less than 2 m), the spatial distribution of which is illustrated in
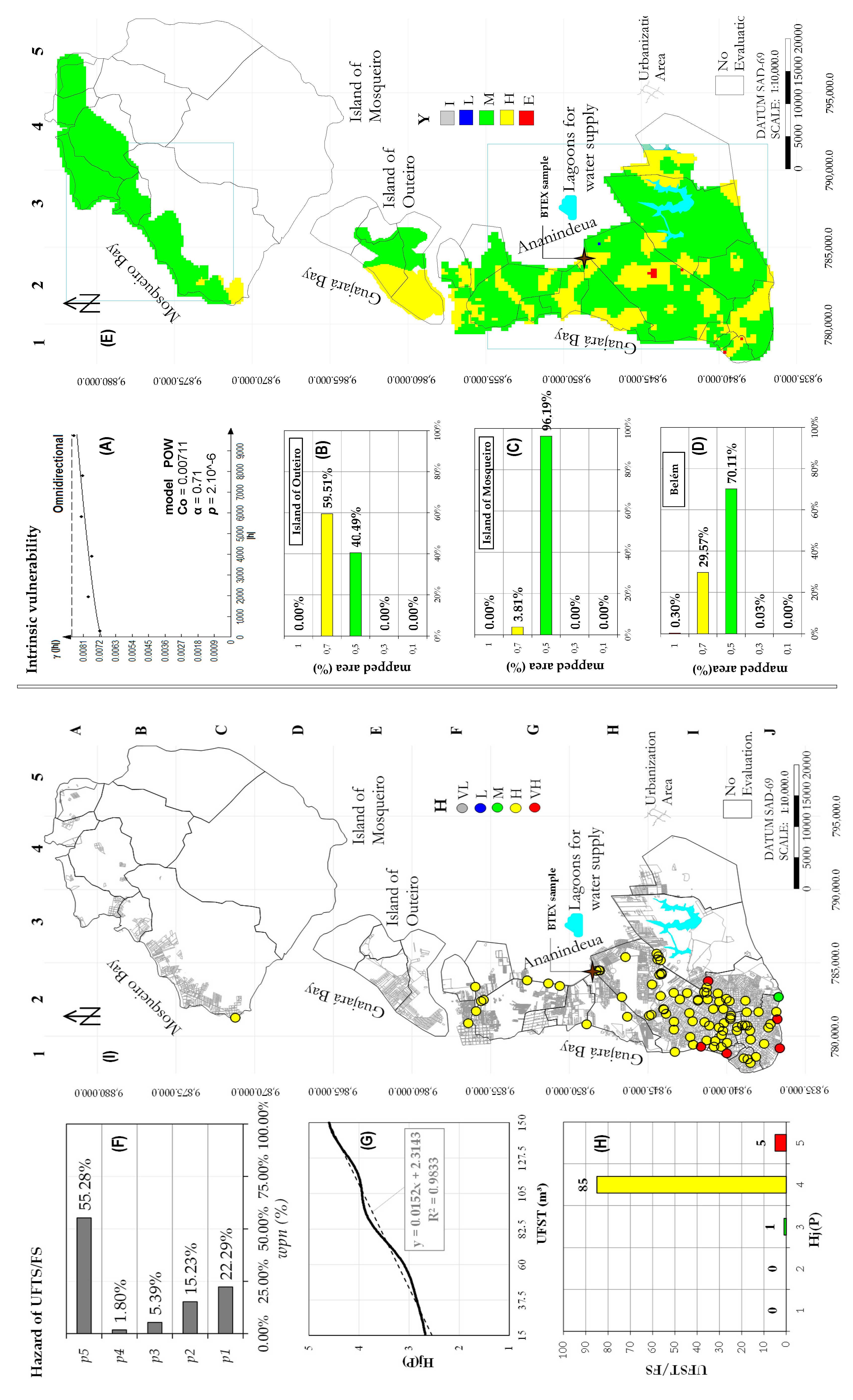
Figure 3A,B.
The vulnerability of the referenced urban zone was measured in shallow aquifers in which a large portion of contamination events began in the most superficial layers of the underground environment. The authors of [
38,
39,
40] discussed the hydrogeological aspects of the metropolitan region of Belém (MRB).
In this vulnerable environment, UFST leaks have already occurred. In northern Brazil, there are currently 2798 registered fuel stations. Their average monthly sales volume as recorded through the end of 2013 was greater than 160 m
3/station. Data from the National Petroleum, Natural Gas, and Biofuel Agency of Brazil (
Agência Nacional do Petróleo, Gás Natural e Biocombustível do Brasil—ANP) show that, in the MRB, there are more than 200 registered fuel stations. In the urban zone of the city of Belém and its islands, there were 91 FS, and their storage capacity is illustrated in
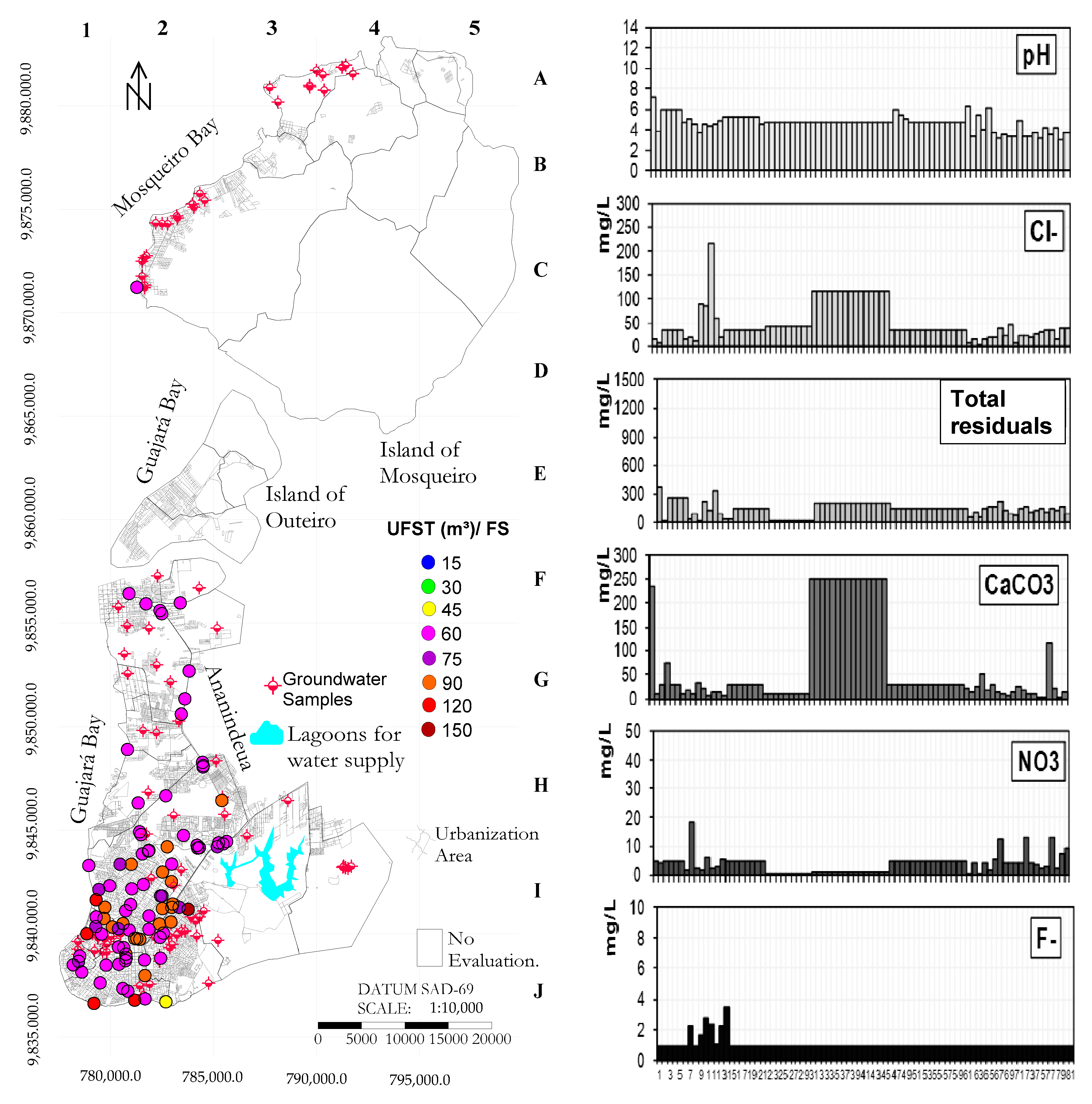
Figure 4. Volumetric data are available on the ANP platform.
With regard to groundwater quality evaluations, recent studies have restricted the analysis to tracers of anthropogenic contamination (e.g., pH, NO
3, and fecal coliforms) [
41,
42,
43]. This information is pertinent because the shallow aquifers are more exposed to contamination than confined aquifers (which are “naturally” protected). However, the natural quality of groundwater evaluated in studies in [
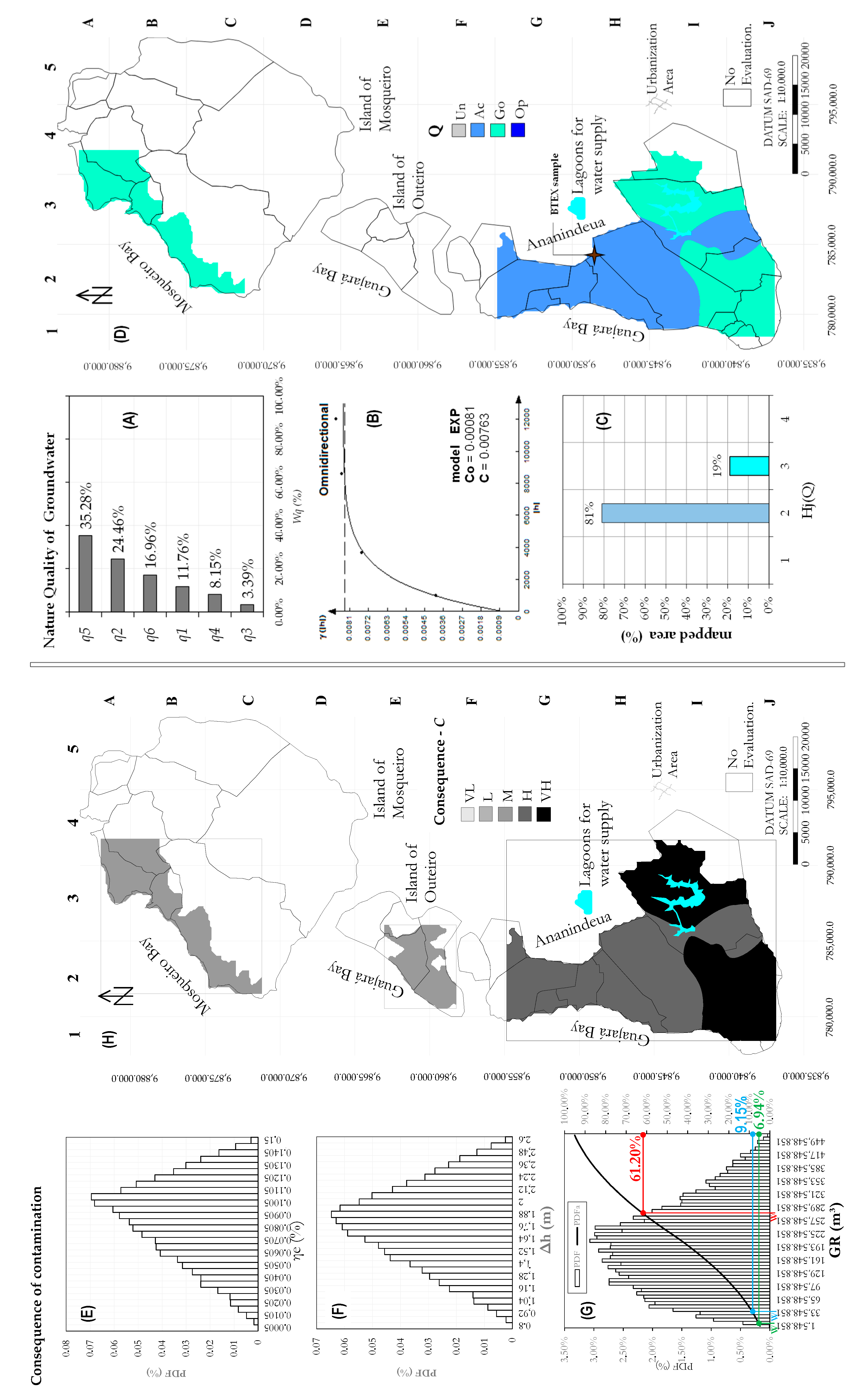
44] showed that, in shallow wells (depths ≤ 50 m), the pH varied from 3.4 to 5.2 and directly corresponded to low levels of electrical conductivity, hardness, and bicarbonate alkalinity, classifying them as chlorinated sodium, sulfated calcium, and sodium bicarbonate when using the Piper diagram.
The samples made available by the authors of [
44] showed the physicochemical parameters that make up the natural quality analyses of groundwater, which can also be tabulated. In turn, 14 data points were inventoried from water analyses of wells (from shallow aquifer) in the urban and periurban zones of the city of Belém and its islands, extracted from the work of [
44]. The authors of [
41] analyzed 20 samples from wells, which captured groundwater from the phreatic aquifer, in June 2002.Nevertheless, data from an experimental water sampling campaign were collected from 13 wells in [
42] from June 2000 to March 2002, and the average values were used. Data catalogued in [
43] were also used, and they were from water collected from 24 wells in the urban and periurban portion of the island of Mosqueiro during two seasons, namely, the dry season in October 2010 and the rainy season in March 2011 (average values were used). Owing to the lack of data from the island of Outeiro, the natural quality of the groundwater there was analyzed as being equal to the portion that corresponds to the urban zone of the island of Mosqueiro.
Figure 4 shows all of the sampling used.
The demand for groundwater was characterized in a study conducted by [
38], which indicated a water quantity of slightly greater than 430,000 m³/day, of which approximately 20% comes from aquifers (around 86 thousand m³/day). The growing urban demand for treated water for industrial and domestic uses combined with the current inefficiency and insufficiency of the water supply network in the urban and periurban zones of Belém and its islands is reflected in the increased capture of groundwater from phreatic wells. A per capita demand of 200 liters/day was adopted, as projected for the year 2033 [
45], considering that 50% of the potable and non-potable demand by the city of Belém comes from wells, that is, for approximately 750,000 inhabitants (the population of the city of Belém is close to 1.5 million inhabitants, according to data in [
46]), the daily volume is close to 150,000 m³ (54.75 million m³/year).
The island zones are dependent on capturing groundwater to supply demand for multiple uses. With an estimated population of close to 50,000 inhabitants, the island of Mosqueiro demands a volume of close to 10,000 m³/day (3.65 million m³/year). For the island of Outeiro, with a population of close to 90,000 inhabitants, the daily demand is close to 18,000 m³ (6.57 million m³/year). Therefore, from these annual demands for potable and non-potable uses, the probability that the GR reserve will be used safely is estimated, without the need to use the GP reserve of the confined aquifers.
5. Conclusions and Recommendations
The groundwater contamination risk assessment method proposed here is a preventive alternative to be considered during the management of groundwater resources, as it overcomes subjectivities and addresses uncertainties in the assessment of intrinsic vulnerability, risk, and water quality and the estimation of groundwater reserve use. The GOD-fuzzy model was proposed to overcome subjective and ambiguous limitations, which are generally associated with the GOD method, and it was used for an intrinsic vulnerability assessment. The GOD-fuzzy model was processed by employing a systematic and simultaneous relationship between “fuzzifier” hydrogeological parameters, which was shown as an alternative with a more preventative nature than the GOD method through an intelligent controller.
For specific hydrogeological configurations, the knowledge base of the GOD-fuzzy model can be readapted such that the interval for the ranges of values for the linguistic variables that defined the fuzzifier of the hydrogeological parameters under consideration can be changed. Thus, the set of rules can also be adjusted, functioning as a type of calibrator for the referenced fuzzy model. In turn, depending on the type of aquifer, other base methods can be used, for example, SINTACS or AVI methods, to measure the fuzzy intrinsic vulnerability.
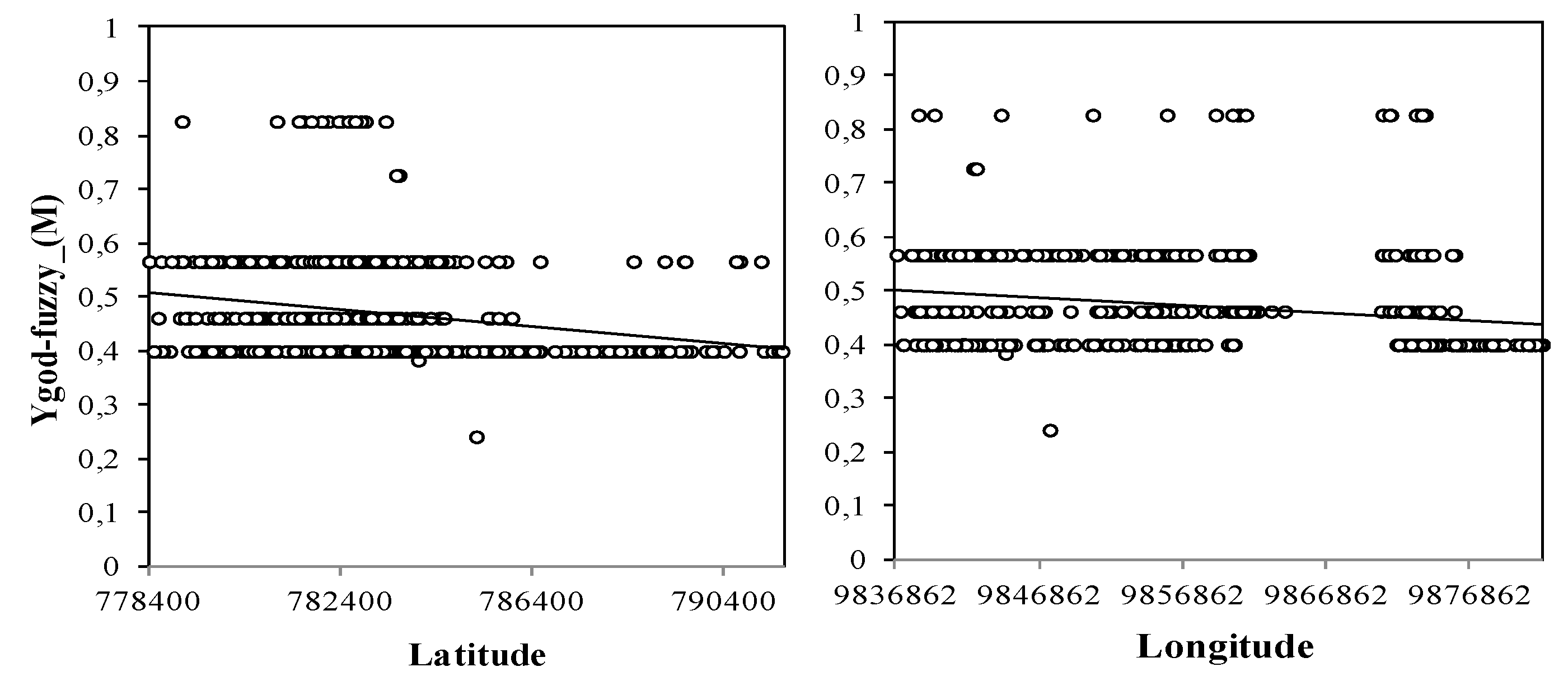
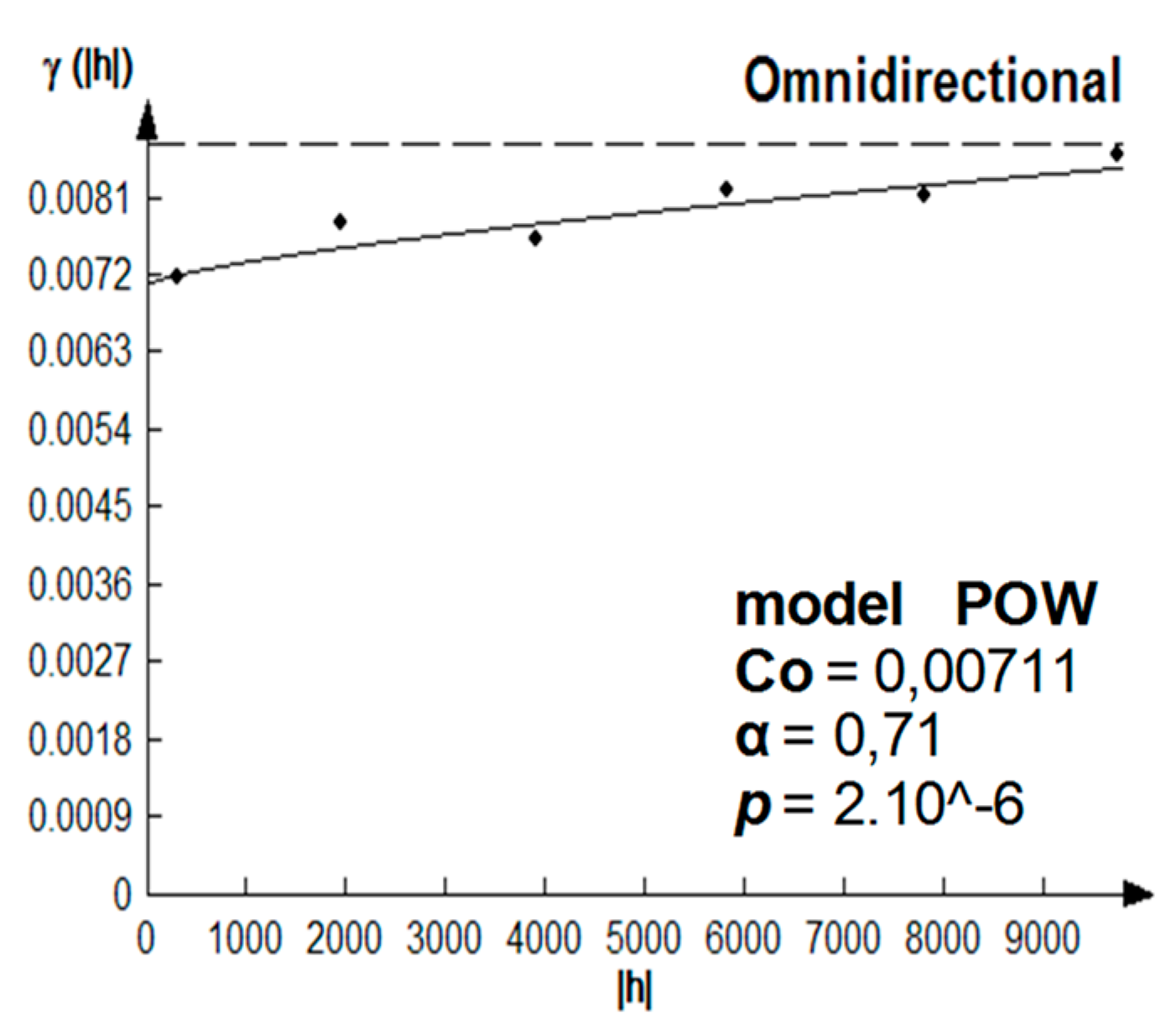
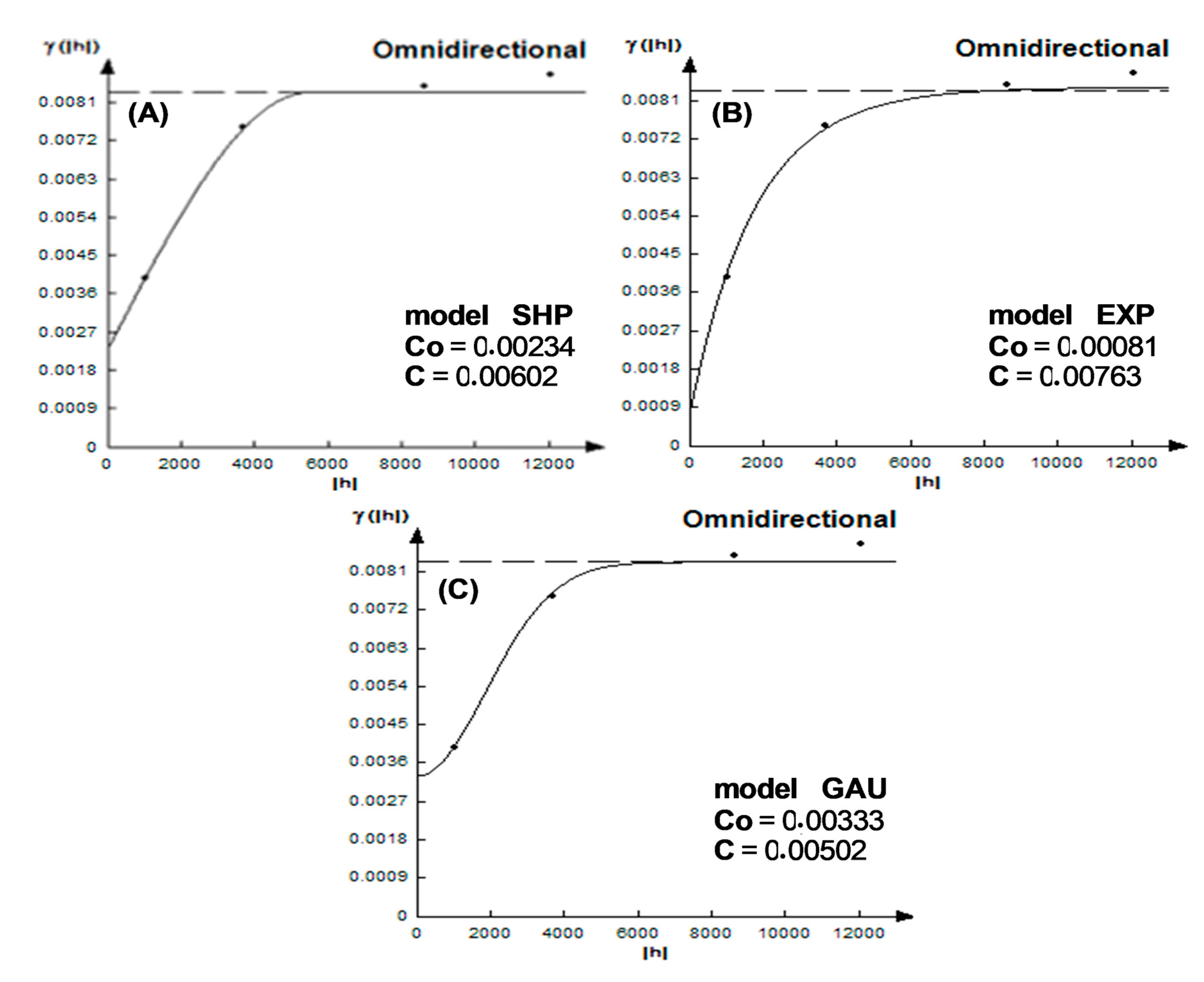
Within the scope of applying the Mamdani-type fuzzy controller, the use of “defuzzifier” methods other than the centroid method used in this study is suggested. The use of other “defuzzifier” methods can cause significant changes in the final results, and consequently, in the intrinsic vulnerability map. Therefore, the YGOD-Fuzzy* index produced by the GOD-fuzzy model was interpolated in the environment within the urban zone of Belém, and the shallow aquifer intrinsic vulnerability map was produced.
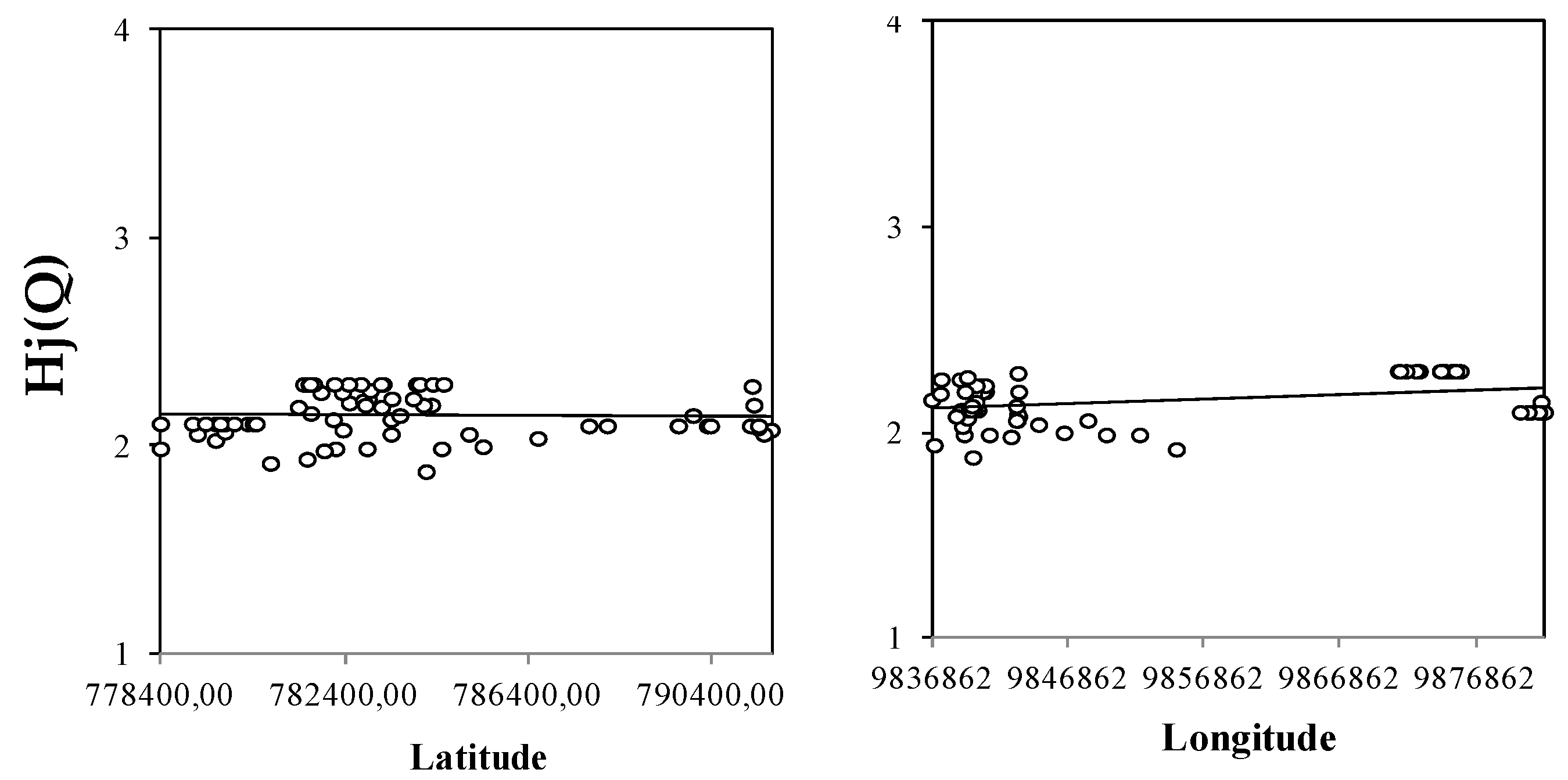
The point sources were located in this environment, namely, fuel stations (associated with the UFST), whose degrees of hazard were quantified with an Hj(P) index generated by a multi-criteria fuzzy pattern recognition model integrated with AHP. The judgment of the importance of the physical and chemical properties (toxicity, degradability, mobility, solubility, and quantity) considered to quantify the degree of hazard can be evaluated. Thus, the classification of a specific degree of hazard can differ from that obtained in this study. Likewise, the inclusion of other properties, for example, the half-life, can lead to hazard classifications different from those obtained in this study. The fuzzy-AHP model designed to classify the hazard is flexible to the point that it performs the following:
adapts to types of patterns established by any regulation;
performs convenient judgments of importance for each type of contamination source, including for scenarios with vehicles;
inserts n physical and chemical contaminant properties.
To quantify the groundwater consequence of contamination, a concept was used that measures the socioeconomic and environmental value of groundwater, which is a function of the association between the degrees of natural water quality and the estimated use of the aquifer reserves. For this purpose, the natural quality of the groundwater for potable uses was classified using a multi-criteria fuzzy-AHP model. This model was configured to classify the natural quality of groundwater from the weighting of the pH, chloride, total residue, hardness, nitrate, and fluorine parameters in the same manner as mentioned previously.
Considering the uncertainties and stochastic nature of the physical variables of an aquifer, a probabilistic proposal was adopted using the MCS method. Thus, the degree of probability of using the GR reserves without activating the GP reserves was estimated. These results can undergo changes if a less conservative concept is adopted, namely, the probability of using the GP reserves while also requiring the GR reserves. For future studies, the inclusion of a stochastic assessment of other physical variables is recommended, as is the use of other algorithms for the generation of pseudo-random numbers, for example, a Latin hypercube.
Finally, using the proposed FPM-risks, strategies can be developed to manage contamination sources to protect underground springs when considering a contamination event in a dense urban environment. The implementation of this model must not be the sole strategy for groundwater protection. Thus, strategies that can be integrated and coordinated with the characteristics of the proposed risk model must be adopted, such as the following:
Imposing compliance with special requirements for handling chemical and toxic substances and persistent wastewater in any industrial zone located in zones of low or moderate vulnerability, which includes the adoption of devices that can prevent and monitor flows;
Widespread weighted risk management must be implemented.
Thus, the fuzzy and probabilistic models proposed for risk assessment permitted the establishment of a connection between groundwater users and decision-makers through the following:
The synthesis and simplification of the hydrogeological conditions by the GOD-fuzzy model;
The quantification of the hazard posed by contamination sources and the classification of the natural groundwater quality for potable uses using the fuzzy-AHP model;
The probabilistic estimation of the use of GR reserves, without using GP reserves;
The generation of thematic maps, in particular.
Although, technically, the risk assessment should be updated regularly because of the dynamic characteristics of hazards from the USFT, the FPM-risks was shown as a tool to be considered for managing groundwater resources. On the order hand, as these models overcome subjectivities and address uncertainties, thereby providing a higher level of accuracy than usual risk methods, a better way for decision making became available. In practice, this study is presented as a strategy to expand the public's consciousness and understanding about the need to protect groundwater.