Remote-Sensing-Based Water Balance for Monitoring of Evapotranspiration and Water Stress of a Mediterranean Oak–Grass Savanna
Abstract
:1. Introduction
2. Materials and Methods
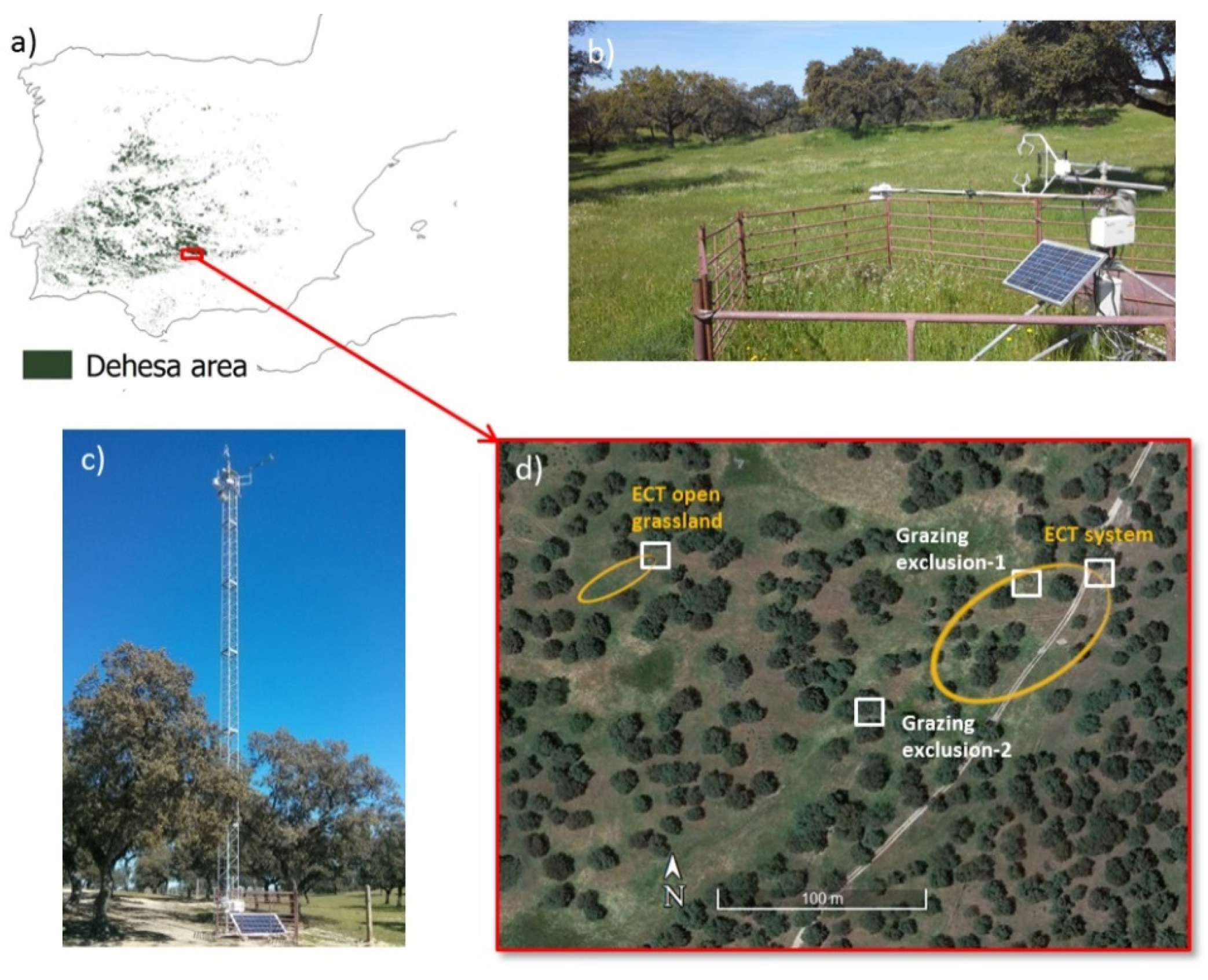
2.1. Study Site
2.2. Ground Validation Measurements
2.3. Remote-Sensing-Based Soil–Water Balance Model
2.4. Tree–Grass Cover Fraction during the Dry Season
2.5. Satellite Remote Sensing Dataset
2.6. Meteorological Information and Soil Properties
2.7. Obtaining Soil and Vegetation Parameters
2.7.1. Tabulated and Measured Soil and Vegetation Parameters
2.7.2. Calibration of Vegetation Parameters
3. Results and Discussion
3.1. Parametrization of the VI-ETo Model over the Dehesa Ecosystem and Open Grassland
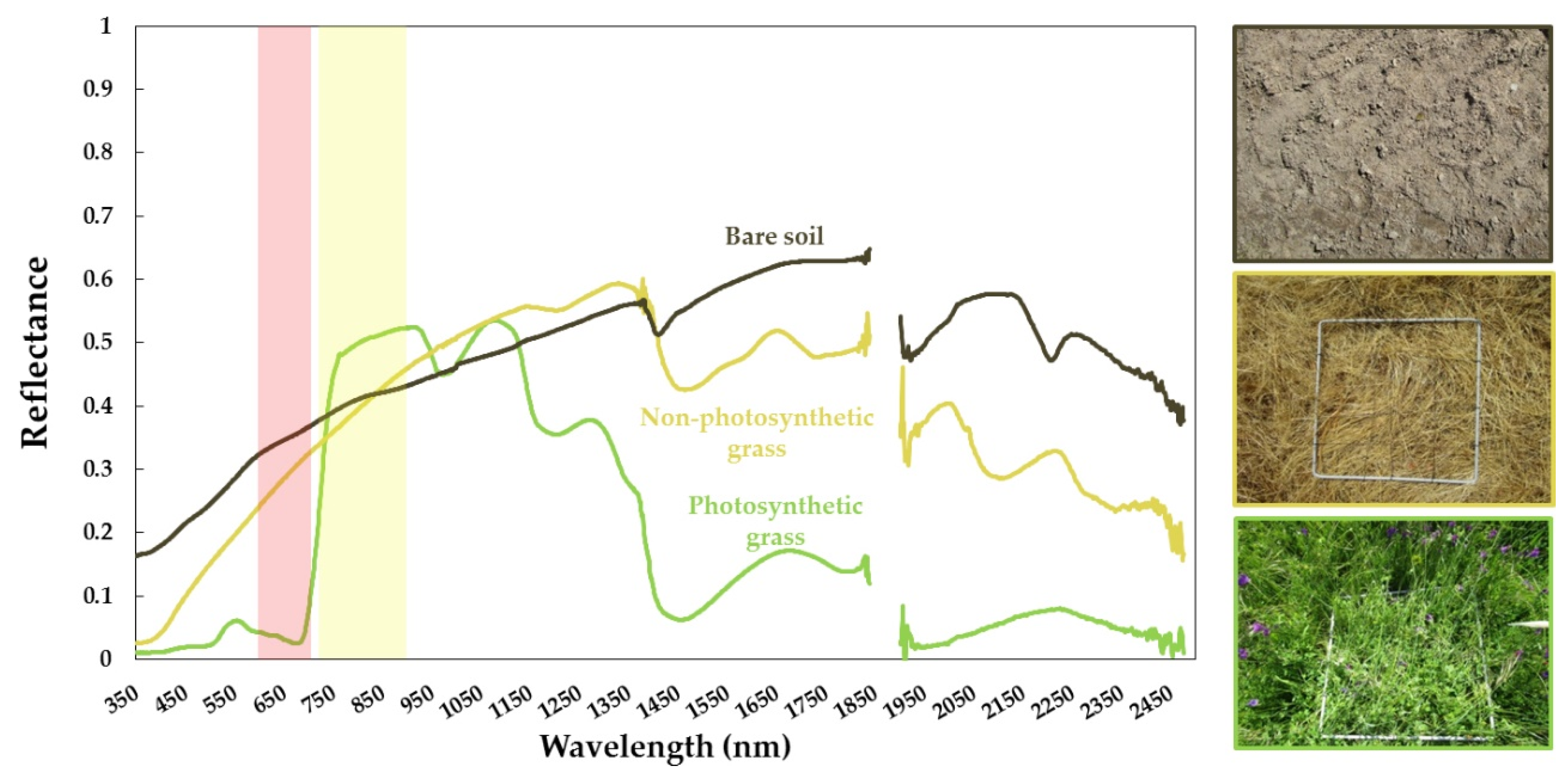
3.2. Dead Grass Impact on ET Estimations during the Dry Season
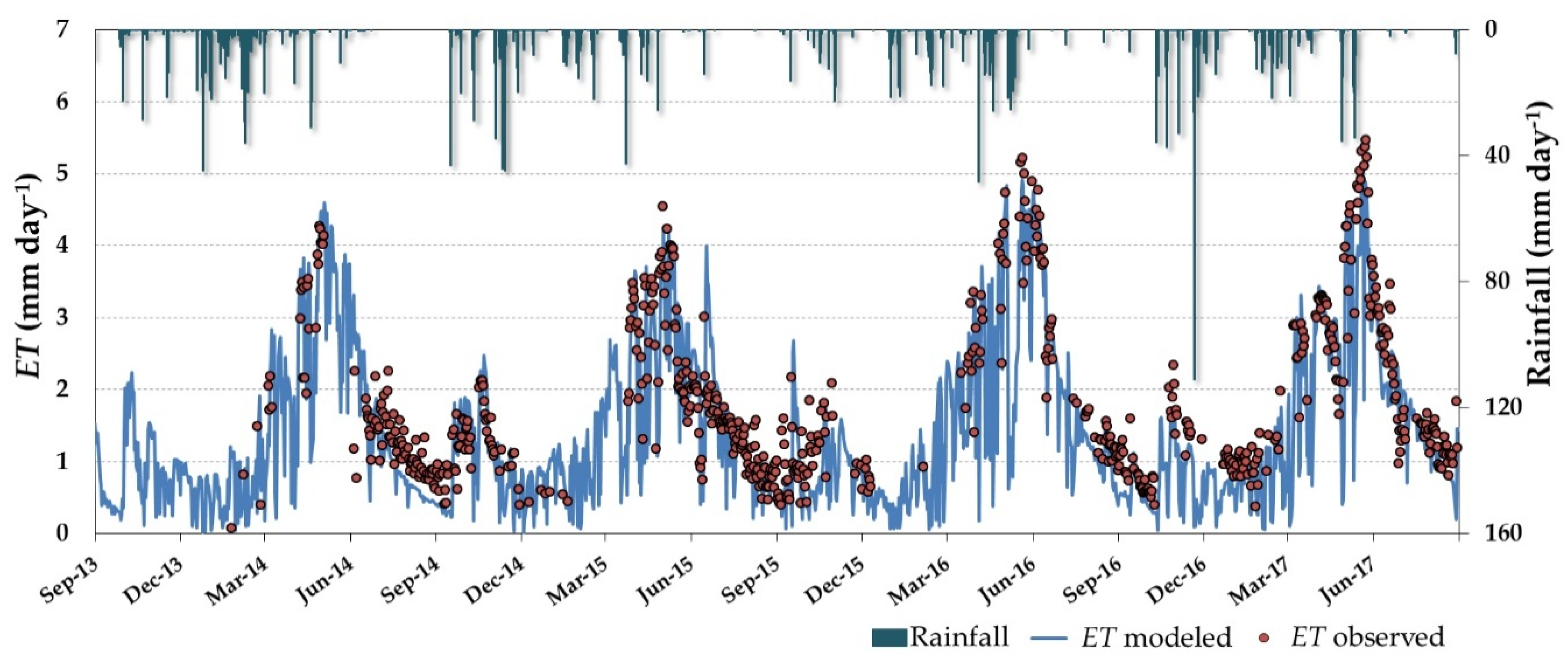
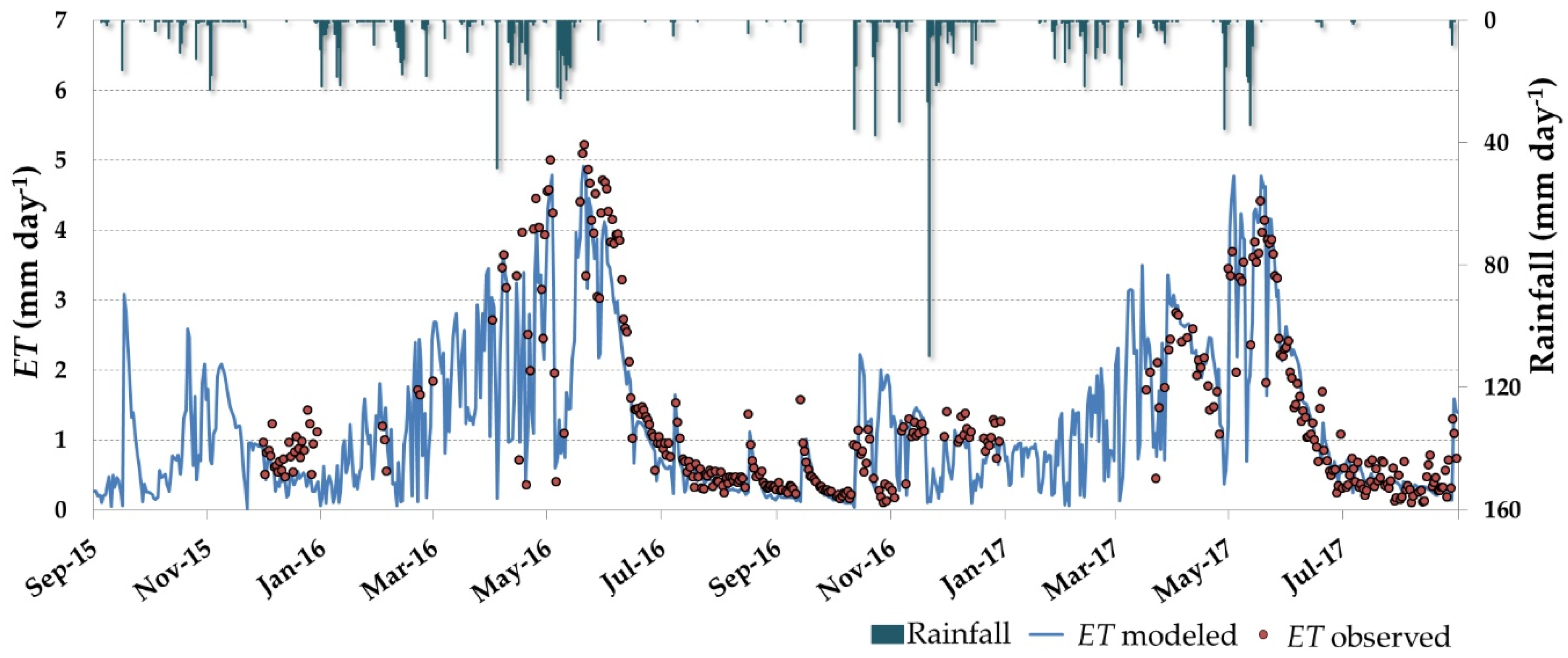
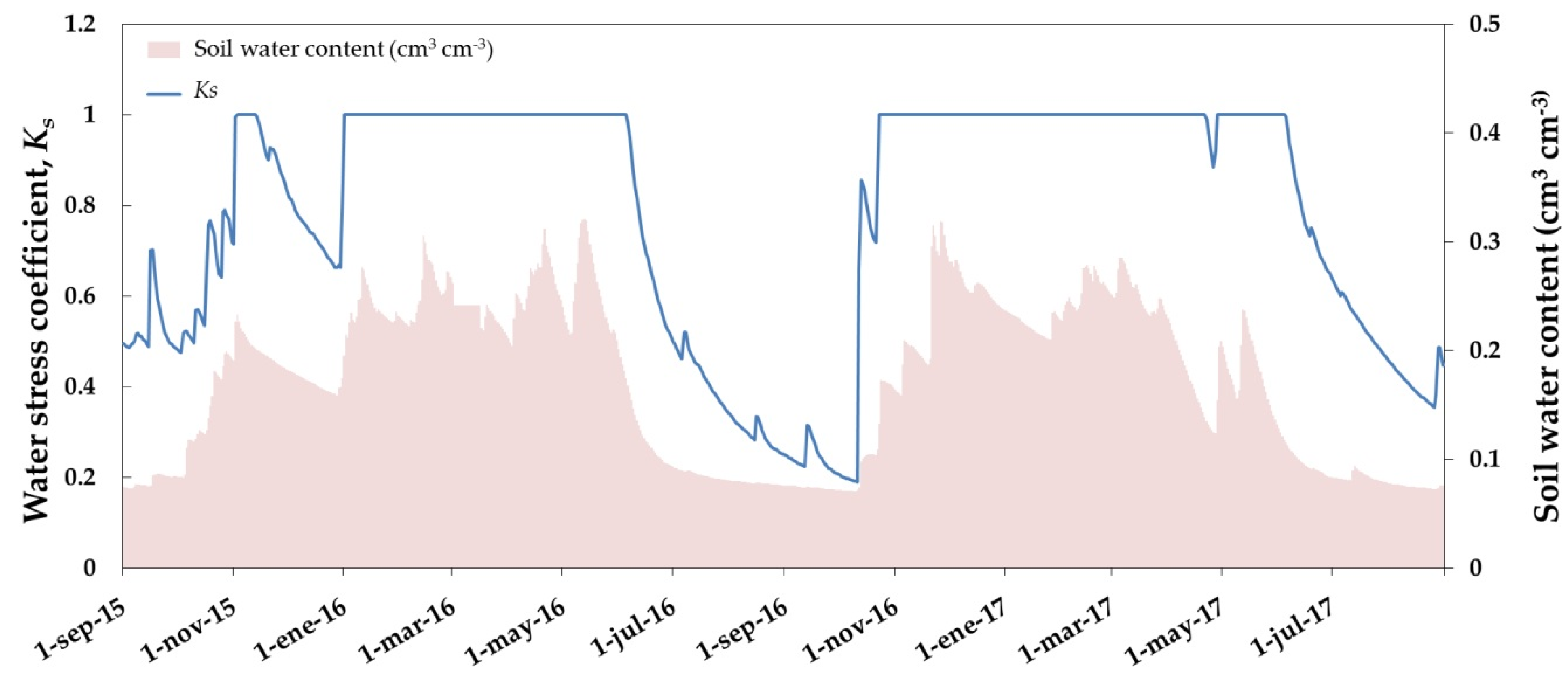
3.3. Daily ET and Water Stress Monitoring over the Dehesa Ecosystem (Tree + Grass)
3.4. Estimation of Evapotranspiration of Grass in Open Areas
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Birot, Y.; Gracia, C.; Palahí, M. Water for Forests and People in the Mediterranean: A Challenging Balance. What Science Can Tell Us; European Forest Institute: Helsinki, Finland, 2011; ISBN 9789525453799. [Google Scholar]
- Milano, M.; Ruelland, D.; Fernandez, S.; Dezetter, A.; Fabre, J.; Servat, E.; Fritsch, J.M.; Ardoin-Bardin, S.; Thivet, G. Current state of Mediterranean water resources and future trends under climatic and anthropogenic changes. Hydrol. Sci. J. 2013, 58, 498–518. [Google Scholar] [CrossRef]
- Baldocchi, D.D.; Xu, L. What limits evaporation from Mediterranean oak woodlands—The supply of moisture in the soil, physiological control by plants or the demand by the atmosphere? Adv. Water Resour. 2007, 30, 2113–2122. [Google Scholar] [CrossRef]
- David, T.S.; Henriques, M.O.; Kurz-Besson, C.; Nunes, J.; Valente, F.; Vaz, M.; Pereira, J.S.; Siegwolf, R.; Chaves, M.M.; Gazarini, L.C.; et al. Water-use strategies in two co-occurring Mediterranean evergreen oaks: Surviving the summer drought. Tree Physiol. 2007, 27, 793–803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moreno, G.; Pulido, F.J. The Functioning, Management and Persistence of Dehesas. Agrofor. Eur. 2008, 10600, 127–160. [Google Scholar] [CrossRef]
- Moreno, G.; Obrador, J.J.; Cubera, E.; Dupraz, C. Fine root distribution in Dehesas of Central-Western Spain. Plant Soil 2005, 277, 153–162. [Google Scholar] [CrossRef]
- Cubera, E.; Morena, G. Effect of single Quercus ilex trees upon spatial and seasonal changes in soil water content in dehesas of central western Spain. Ann. For. Sci. 2007, 64, 355–364. [Google Scholar] [CrossRef] [Green Version]
- Joffre, R.; Rambal, S. How tree cover influences the water balance of Mediterranean rangelands. Ecology 1993, 74, 570–582. [Google Scholar] [CrossRef]
- Gauquelin, T.; Michon, G.; Joffre, R.; Duponnois, R.; Génin, D.; Fady, B.; Bou Dagher-Kharrat, M.; Derridj, A.; Slimani, S.; Badri, W.; et al. Mediterranean forests, land use and climate change: A social-ecological perspective. Reg. Environ. Chang. 2018, 18, 623–636. [Google Scholar] [CrossRef]
- Campos, P.; Huntsinger, L.; Oviedo, J.; Díaz, M.; Starrs, P.; Standiford, R.; Montero, G. Mediterranean Oak Woodland Working Landscapes: Dehesas of Spain and Ranchlands of California; Springer: Berlin, Germany, 2013; ISBN 978-94-007-6706-5. [Google Scholar]
- Plieninger, T.; Rolo, V.; Moreno, G. Large-scale patterns of Quercus ilex, Quercus suber, and Quercus pyrenaica regeneration in central-western Spain. Ecosystems 2010, 13, 644–660. [Google Scholar] [CrossRef]
- Coelho, C.; Ferreira, A.J.D.; Laouina, A.; Hamza, A.; Chaker, M.; Naafa, R.; Regaya, K.; Boulet, A.-K.; Keizer, J.J.; Carvalho, T.M.M. Changes in Land Use and Land Management Practices Affecting Land Degradation within Forest and Grazing Ecosystems in the Western Mediterranean. In Sustainability of Agrosylvopastoral Systems, Dehesas, Montados; Schnabel, S., Ferreira, A., Eds.; Schweizerbart Science Publishers: Stuttgart, Germany, 2004; pp. 137–154. ISBN 978-3-923381-50-0. [Google Scholar]
- Giorgi, F.; Lionello, P. Climate change projections for the Mediterranean region. Glob. Planet. Chang. 2008, 63, 90–104. [Google Scholar] [CrossRef]
- Jacob, D.; Petersen, J.; Eggert, B.; Alias, A.; Christensen, O.B.; Bouwer, L.M.; Braun, A.; Colette, A.; Déqué, M.; Georgievski, G.; et al. EURO-CORDEX: New high-resolution climate change projections for European impact research. Reg. Environ. Chang. 2014, 14, 563–578. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Milano, M.; Ruelland, D.; Fernandez, S.; Dezetter, A.; Ardoin-Bardin, S.; Fabre, J.; Thivet, G.; Servat, E. Assessing the impacts of global changes on the water resources of the Mediterranean basin. IAHS AISH Publ. 2011, 347, 165–172. [Google Scholar]
- Polade, S.D.; Pierce, D.W.; Cayan, D.R.; Gershunov, A.; Dettinger, M.D. The key role of dry days in changing regional climate and precipitation regimes. Sci. Rep. 2014, 4. [Google Scholar] [CrossRef] [Green Version]
- Schleussner, C.F.; Lissner, T.K.; Fischer, E.M.; Wohland, J.; Perrette, M.; Golly, A.; Rogelj, J.; Childers, K.; Schewe, J.; Frieler, K.; et al. Differential climate impacts for policy-relevant limits to global warming: The case of 1.5 °C and 2 °C. Earth Syst. Dyn. 2016, 7, 327–351. [Google Scholar] [CrossRef] [Green Version]
- García-Ruiz, J.M.; López-Moreno, I.I.; Vicente-Serrano, S.M.; Lasanta-Martínez, T.; Beguería, S. Mediterranean water resources in a global change scenario. Earth Sci. Rev. 2011, 105, 121–139. [Google Scholar] [CrossRef] [Green Version]
- Seneviratne, S.I.; Wartenburger, R.; Guillod, B.P.; Hirsch, A.L.; Vogel, M.M.; Brovkin, V.; Van Vuuren, D.P.; Schaller, N.; Boysen, L.; Calvin, K.V.; et al. Climate extremes, land-climate feedbacks and land-use forcing at 1.5°C. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2018, 376. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO; Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Available online: http://www.fao.org/3/x0490e/x0490e00.htm (accessed on 27 November 2019).
- Allen, R.G.; Pereira, L.S.; Smith, M.; Raes, D.; Wright, J.L. FAO-56 dual crop coefficient method for estimating evaporation from soil and application extensions. J. Irrig. Drain. Eng. 2005, 131, 2–13. [Google Scholar] [CrossRef] [Green Version]
- Bausch, W.C. Remote sensing of crop coefficients for improving the irrigation scheduling of corn. Agric. Water Manag. 1995, 27, 55–68. [Google Scholar] [CrossRef]
- Jayanthi, H.; Neale, C.M.U. Seasonal evapotranspiration estimation using canopy reflectance: A case study involving pink beans. IAHS AISH Publ. 2001, 2000, 302–305. [Google Scholar]
- Er-Raki, S.; Chehbouni, A.; Guemouria, N.; Duchemin, B.; Ezzahar, J.; Hadria, R. Combining FAO-56 model and ground-based remote sensing to estimate water consumptions of wheat crops in a semi-arid region. Agric. Water Manag. 2007, 87, 41–54. [Google Scholar] [CrossRef] [Green Version]
- González-Dugo, M.P.; Mateos, L. Spectral vegetation indices for benchmarking water productivity of irrigated cotton and sugarbeet crops. Agric. Water Manag. 2008, 95, 48–58. [Google Scholar] [CrossRef]
- Consoli, S.; Vanella, D. Mapping crop evapotranspiration by integrating vegetation indices into a soil water balance model. Agric. Water Manag. 2014, 143, 71–81. [Google Scholar] [CrossRef]
- Odi-Lara, M.; Campos, I.; Neale, C.M.U.; Ortega-Farías, S.; Poblete-Echeverría, C.; Balbontín, C.; Calera, A. Estimating evapotranspiration of an apple orchard using a remote sensing-based soil water balance. Remote Sens. 2016, 8, 253. [Google Scholar] [CrossRef] [Green Version]
- Glenn, E.P.; Neale, C.M.U.; Hunsaker, D.J.; Nagler, P.L. Vegetation index-based crop coefficients to estimate evapotranspiration by remote sensing in agricultural and natural ecosystems. Hydrol. Process. 2011, 25, 4050–4062. [Google Scholar] [CrossRef]
- Calera, A.; Campos, I.; Osann, A.; D’Urso, G.; Menenti, M. Remote sensing for crop water management: From ET modelling to services for the end users. Sensors 2017, 17, 1104. [Google Scholar] [CrossRef] [Green Version]
- Pôças, I.; Calera, A.; Campos, I.; Cunha, M. Remote sensing for estimating and mapping single and basal crop coefficientes: A review on spectral vegetation indices approaches. Agric. Water Manag. 2020, 233, 106081. [Google Scholar] [CrossRef]
- Glenn, E.P.; Nagler, P.L.; Huete, A.R. Vegetation Index Methods for Estimating Evapotranspiration by Remote Sensing. Surv. Geophys. 2010, 31, 531–555. [Google Scholar] [CrossRef]
- Campos, I.; Villodre, J.; Carrara, A.; Calera, A. Remote sensing-based soil water balance to estimate Mediterranean holm oak savanna (dehesa) evapotranspiration under water stress conditions. J. Hydrol. 2013, 494, 1–9. [Google Scholar] [CrossRef]
- Andreu, A.; Dube, T.; Nieto, H.; Mudau, A.E.; González-Dugo, M.P.; Guzinski, R.; Hülsmann, S. Remote sensing of water use and water stress in the African savanna ecosystem at local scale – Development and validation of a monitoring tool. Phys. Chem. Earth 2019, 112, 154–164. [Google Scholar] [CrossRef]
- Carpintero, E.; Mateos, L.; Andreu, A.; González-Dugo, M.P. Effect of the differences in spectral response of Mediterranean tree canopies on the estimation of evapotranspiration using vegetation index-based crop coefficients. Agric. Water Manag. 2020, 238, 106–201. [Google Scholar] [CrossRef]
- Mateos, L.; González-Dugo, M.P.; Testi, L.; Villalobos, F.J. Monitoring evapotranspiration of irrigated crops using crop coefficients derived from time series of satellite images. I. Method validation. Agric. Water Manag. 2013, 125, 81–91. [Google Scholar] [CrossRef]
- Roberts, D.A.; Smith, M.O.; Adams, J.B. Green vegetation, nonphotosynthetic vegetation, and soils in AVIRIS data. Remote Sens. Environ. 1993, 44, 255–269. [Google Scholar] [CrossRef]
- Xu, D.; Guo, X.; Li, Z.; Yang, X.; Yin, H. Measuring the dead component of mixed grassland with Landsat imagery. Remote Sens. Environ. 2014, 142, 33–43. [Google Scholar] [CrossRef]
- Rivas Martínez, S. Bioclimatología, biogeografía y series de vegetación de Andalucía Occidental. Lagascalia 1988, 15, 91–120. [Google Scholar]
- Melendo, M. Cartografía y Ordenación Vegetal de Sierra Morena: Parque Natural de Las Sierras de Cardeña y Montoro; Universidad de Jaén: Jaén, Spain, 1998. [Google Scholar]
- Román-Sánchez, A.; Vanwalleghem, T.; Peña, A.; Laguna, A.; Giráldez, J.V. Controls on soil carbon storage from topography and vegetation in a rocky, semi-arid landscapes. Geoderma 2018, 311, 159–166. [Google Scholar] [CrossRef]
- Webb, E.K.; Pearman, G.I.; Leuning, R. Correction of flux measurements for density effects due to heat and water vapour transfer. Q. J. R. Meteorol. Soc. 1980, 106, 85–100. [Google Scholar] [CrossRef]
- Andreu, A.; Kustas, W.P.; Polo, M.J.; Carrara, A.; González-Dugo, M.P. Modeling surface energy fluxes over a dehesa (oak savanna) ecosystem using a thermal based two-source energy balance model (TSEB) I. Remote Sens. 2018, 10, 567. [Google Scholar] [CrossRef] [Green Version]
- Mauder, M.; Genzel, S.; Fu, J.; Kiese, R.; Soltani, M.; Steinbrecher, R.; Zeeman, M.; Banerjee, T.; De Roo, F.; Kunstmann, H. Evaluation of energy balance closure adjustment methods by independent evapotranspiration estimates from lysimeters and hydrological simulations. Hydrol. Process. 2018, 32, 39–50. [Google Scholar] [CrossRef]
- Hsieh, C.I.; Katul, G.; Chi, T.W. An approximate analytical model for footprint estimation of scalar fluxes in thermally stratified atmospheric flows. Adv. Water Resour. 2000, 23, 765–772. [Google Scholar] [CrossRef]
- Wright, J.L. New Evapotranspiration Crop Coefficients. J. Irrig. Drain. Div. ASCE 1982, 108, 57–74. [Google Scholar]
- Hunsaker, D.J.; Pinter, P.J.; Barnes, E.M.; Kimball, B.A. Estimating cotton evapotranspiration crop coefficients with a multispectral vegetation index. Irrig. Sci. 2003, 22, 95–104. [Google Scholar] [CrossRef]
- Gonzalez-Piqueras, J.; Calera, A.; Gilabert, M.A.; Cuesta, A.; De la Cruz Tercero, F. Estimation of crop coefficients by means of optimized vegetation indices for corn. Remote Sens. Agric. Ecosyst. Hydrol. V 2004, 5232, 110. [Google Scholar] [CrossRef]
- Hunsaker, D.J.; Pinter, P.J.; Kimball, B.A. Wheat basal crop coefficients determined by normalized difference vegetation index. Irrig. Sci. 2005, 24, 1–14. [Google Scholar] [CrossRef]
- Jayanthi, H.; Neale, C.M.U.; Wright, J.L. Development and validation of canopy reflectance-based crop coefficient for potato. Agric. Water Manag. 2007, 88, 235–246. [Google Scholar] [CrossRef]
- Campos, I.; Neale, C.M.U.; Calera, A.; Balbontín, C.; González-Piqueras, J. Assessing satellite-based basal crop coefficients for irrigated grapes (Vitis vinifera L.). Agric. Water Manag. 2010, 98, 45–54. [Google Scholar] [CrossRef]
- Gonzalez-Dugo, M.P.; Neale, C.M.U.; Mateos, L.; Kustas, W.P.; Prueger, J.H.; Anderson, M.C.; Li, F. A comparison of operational remote sensing-based models for estimating crop evapotranspiration. Agric. For. Meteorol. 2009, 149, 1843–1853. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Anderson, M.C.; Zolin, C.A.; Sentelhas, P.C.; Hain, C.R.; Semmens, K.; Tugrul Yilmaz, M.; Gao, F.; Otkin, J.A.; Tetrault, R. The Evaporative Stress Index as an indicator of agricultural drought in Brazil: An assessment based on crop yield impacts. Remote Sens. Environ. 2016, 174, 82–99. [Google Scholar] [CrossRef]
- Nagler, P.L.; Inoue, Y.; Glenn, E.P.; Russ, A.L.; Daughtry, C.S.T. Cellulose absorption index (CAI) to quantify mixed soil-plant litter scenes. Remote Sens. Environ. 2003, 87, 310–325. [Google Scholar] [CrossRef]
- Aase, J.K.; Tanaka, D.L. Reflectances from Four Wheat Residue Cover Densities as Influenced by Three Soil Backgrounds. Agron. J. 1991, 83, 753–757. [Google Scholar] [CrossRef]
- Nagler, P.L.; Daughtry, C.S.T.; Goward, S.N. Plant litter and soil reflectance. Remote Sens. Environ. 2000, 71, 207–215. [Google Scholar] [CrossRef]
- Mueller-Wilm, U.; Devignot, O.; Pessiot, L. Sen2Core Configuration and User Manual. Ref. S2-PDGS-MPC-L2A- SUM-V2.3 eesa Sentinel 2. Version: 1 November 2017. Available online: https://step.esa.int/thirdparties/sen2cor/2.4.0/Sen2Cor_240_Documenation_PDF/S2-PDGS-MPC-L2A-SUM-V2.4.0.pdf (accessed on 14 October 2019).
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the landsat and MODIS surface reflectance: Predicting daily landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar] [CrossRef]
- Rodríguez, J.; Sotelo, A.; Monge, G.; De la Rosa, D. Sistema de Inferencia Espacial de Propiedades de Los Suelos de Andalucía; Consejería de Agricultura y Pesca: Sevilla, Spain, 2008. [Google Scholar]
- Mbah, C.N. Determining the field capacity, wilting point and available water capacity of some Southeast Nigerian soils using soil saturation from capillary rise. Niger. J. Biotechnol. 2012, 24, 41–47. [Google Scholar]
- Pulido-Fernández, M.; Schnabel, S.; Lavado-Contador, J.F.; Miralles Mellado, I.; Ortega Pérez, R. Soil organic matter of Iberian open woodland rangelands as influenced by vegetation cover and land management. Catena 2013, 109, 13–24. [Google Scholar] [CrossRef]
- Moreno, G.; Cáceres, Y. System report: Iberian Dehesas, Spain; AGFORWARD; Agroforestry for Europe: Plasencia, Spain, 2016. [Google Scholar]
- Canadell, J.; Jackson, R.B.; Ehleringer, J.R.; Mooney, H.A.; Sala, O.E.; Schulze, E.D. Maximum rooting depth of vegetation types at the global scale. Oecologia 1996, 108, 583–595. [Google Scholar] [CrossRef] [PubMed]
- Rolo, V.; López-Díaz, M.L.; Moreno, G. Shrubs affect soil nutrients availability with contrasting consequences for pasture understory and tree overstory production and nutrient status in Mediterranean grazed open woodlands. Nutr. Cycl. Agroecosystems 2012, 93, 89–102. [Google Scholar] [CrossRef]
- Pierret, A.; Maeght, J.L.; Clément, C.; Montoroi, J.P.; Hartmann, C.; Gonkhamdee, S. Understanding deep roots and their functions in ecosystems: An advocacy for more unconventional research. Ann. Bot. 2016, 118, 621–635. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stegman, E.C.; Musick, J.T.; Stewart, J.I. Irrigation water management. In Design and Operation of Farm Irrigation Systems; American Society of Agricultural Engineers: San Jose, MI, USA, 1980; pp. 763–768. ISBN 0-916150-28-3. [Google Scholar]
- Browne, M.W. Cross-Validation Methods. J. Math. Psychol. 2000, 44, 108–132. [Google Scholar] [CrossRef] [Green Version]
- Arlot, S.; Celisse, A. A survey of cross-validation procedures for model selection. Stat. Surv. 2010, 4, 40–79. [Google Scholar] [CrossRef]
- Lee, G.; Kim, W.; Oh, H.; Youn, B.D.; Kim, N.H. Review of statistical model calibration and validation—from the perspective of uncertainty structures. Struct. Multidiscip. Optim. 2019, 60, 1619–1644. [Google Scholar] [CrossRef]
- Schoups, G.; Van De Giesen, N.C.; Savenije, H.H.G. Model complexity control for hydrologic prediction. Water Resour. Res. 2008, 44, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Tegegne, G.; Park, D.K.; Kim, Y.O. Comparison of hydrological models for the assessment of water resources in a data-scarce region, the Upper Blue Nile River Basin. J. Hydrol. Reg. Stud. 2017, 14, 49–66. [Google Scholar] [CrossRef]
- Padilla, F.L.M.; González-Dugo, M.P.; Gavilán, P.; Domínguez, J. Integration of vegetation indices into a water balance model to estimate evapotranspiration of wheat and corn. Hydrol. Earth Syst. Sci. 2011, 15, 1213–1225. [Google Scholar] [CrossRef] [Green Version]
- Cammalleri, C.; Ciraolo, G.; Minacapilli, M.; Rallo, G. Evapotranspiration from an Olive Orchard using Remote Sensing-Based Dual Crop Coefficient Approach. Water Resour. Manag. 2013, 27, 4877–4895. [Google Scholar] [CrossRef]
- Campos, I.; Balbontín, C.; González-Piqueras, J.; González-Dugo, M.P.; Neale, C.M.U.; Calera, A. Combining a water balance model with evapotranspiration measurements to estimate total available soil water in irrigated and rainfed vineyards. Agric. Water Manag. 2016, 165. [Google Scholar] [CrossRef]
- González-Dugo, M.P.; Escuin, S.; Cano, F.; Cifuentes, V.; Padilla, F.L.M.; Tirado, J.L.; Oyonarte, N.; Fernández, P.; Mateos, L. Monitoring evapotranspiration of irrigated crops using crop coefficients derived from time series of satellite images. II. Application on basin scale. Agric. Water Manag. 2013, 125, 92–104. [Google Scholar] [CrossRef]
- Burchard-Levine, V.; Nieto, H.; Riaño, D.; Migliavacca, M.; El-Madany, T.S.; Perez-Priego, O.; Carrara, A.; Martín, M.P. Seasonal adaptation of the thermal-based two-source energy balance model for estimating evapotranspiration in a semiarid tree-grass ecosystem. Remote Sens. 2020, 12, 904. [Google Scholar] [CrossRef] [Green Version]
- Allen, M.F. How Oaks Respond to Water Limitation. In Proceedings of the Seventh California Oak Symposium: Managing Oak Woodlands in a Dynamic World, Albany, CA, USA, 3–6 November 2014; pp. 13–21. [Google Scholar]
- Xu, L.; Baldocchi, D.D.; Tang, J. How soil moisture, rain pulses, and growth alter the response of ecosystem respiration to temperature. Glob. Biogeochem. Cycles 2004, 18. [Google Scholar] [CrossRef]
- Fischer, Z.; Blažka, P. Soil Respiration in Drying of an Organic Soil. Open J. Soil Sci. 2015, 5, 181–192. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Giráldez, P.J.; Pérez-Palazón, M.J.; Polo, M.J.; González-Dugo, M.P. Monitoring grass phenology and hydrological dynamics of an oak-grass savanna ecosystem using sentinel-2 and terrestrial photography. Remote Sens. 2020, 12, 600. [Google Scholar] [CrossRef] [Green Version]





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carpintero, E.; Andreu, A.; Gómez-Giráldez, P.J.; Blázquez, Á.; González-Dugo, M.P. Remote-Sensing-Based Water Balance for Monitoring of Evapotranspiration and Water Stress of a Mediterranean Oak–Grass Savanna. Water 2020, 12, 1418. https://doi.org/10.3390/w12051418
Carpintero E, Andreu A, Gómez-Giráldez PJ, Blázquez Á, González-Dugo MP. Remote-Sensing-Based Water Balance for Monitoring of Evapotranspiration and Water Stress of a Mediterranean Oak–Grass Savanna. Water. 2020; 12(5):1418. https://doi.org/10.3390/w12051418
Chicago/Turabian StyleCarpintero, Elisabet, Ana Andreu, Pedro J. Gómez-Giráldez, Ángel Blázquez, and María P. González-Dugo. 2020. "Remote-Sensing-Based Water Balance for Monitoring of Evapotranspiration and Water Stress of a Mediterranean Oak–Grass Savanna" Water 12, no. 5: 1418. https://doi.org/10.3390/w12051418




