Selection of Hydrological Probability Distributions for Extreme Rainfall Events in the Regions of Colombia
Abstract
1. Introduction
2. Case Study
3. Methodology
3.1. Selection of Rainfall Stations
3.2. Frequency Analysis
- Gumbel distribution
- GEV distribution
- Pearson type III distribution
- Log-Pearson type III distribution
- Normal distribution
3.3. Goodness of Fit Test and Methods of Estimation of Parameters
3.4. Selection of Hydrological Distribution
- For each rainfall stations the mean, maximum and minimum values, and standard deviation of the chi-squared test were computed for the Gumbel-ML, Gumbel-MV, Log-Pearson Type III-SAM, Pearson Type III-ML, Pearson Type III-WM, Normal-ML, GEV-ML and GEV-WM. These eight methods were used because they have adequately fitted the trend of maximum daily precipitation in various publications [22,23]. Based on this analysis, a regional mean value of the chi-squared test for Colombia was calculated based on the number of stations using a weighted mean.
- Estimation of percentage that establishes times where a hydrological distribution reaches the best fits of the trend of maximum daily precipitation records considering the minimum value of the chi-squared test.
4. Analysis of Results
- In all regions of Colombia, the best fits of the chi-squared test were obtained with the GEV probability distribution. The weighted moment method best fits the parameters for this distribution and has an average regional value for Colombia of 5.04. There are other probability distributions that also fit the trend of the data similarly well: GEV with the maximum likelihood method, Gumbel with the weighted moment and maximum likelihood methods and Pearson’s with the method of weighted moments. The Gumbel distribution using the WM method brings a better estimation of maximum daily precipitation for several return periods in comparison with the ML, obtaining a similar result reported in the literature [22].
- In Colombia, the poorest fits were obtained when employing the Pearson type III probability distribution with the maximum likelihood method, where an average value of the chi-square test of 56.57 was obtained, and the log-Pearson type III distribution with the SAM method which had a value of 10.31. This finding is also verified by analyzing the maximum and minimum values and the standard deviation in these probability functions.
- In the Amazonas region, the best fit in the chi-squared test was obtained with the GEV probability distribution and the weighted moment method, with a value of 4.36. This value may have been obtained because few stations were used in the analyses.
5. Conclusions and Recommendations
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| 1107013 | 2102002 | 2120112 | 2120637 | 2312009 | 2602025 | 2618019 |
| 1506001 | 2103003 | 2120113 | 2120639 | 2312012 | 2602503 | 2619010 |
| 1506002 | 2103005 | 2120115 | 2120640 | 2312014 | 2602507 | 2618502 |
| 1506004 | 2103006 | 2120133 | 2120641 | 2312019 | 2603003 | 2618504 |
| 1506005 | 2103008 | 2120134 | 2120644 | 2312024 | 2603005 | 2619009 |
| 1506006 | 2103009 | 2120136 | 2120646 | 2314502 | 2603007 | 2619502 |
| 1506007 | 2103011 | 2120138 | 2120647 | 2319070 | 2603503 | 2620012 |
| 1506008 | 2104001 | 2120141 | 2120652 | 2319511 | 2604026 | 2620507 |
| 1506009 | 2104002 | 2120156 | 2120659 | 2401002 | 2604031 | 2621007 |
| 1506010 | 2104003 | 2120159 | 2123502 | 2401011 | 2604501 | 2621008 |
| 1506011 | 2104004 | 2120166 | 2303502 | 2401015 | 2605006 | 2621009 |
| 1506013 | 2104005 | 2120167 | 2120046 | 2401018 | 2605027 | 2623013 |
| 1506014 | 2104006 | 2120168 | 2120049 | 2401020 | 2605507 | 2701077 |
| 1506015 | 2104007 | 2120169 | 2120139 | 2401021 | 2606003 | 2801020 |
| 1506016 | 2105006 | 2120170 | 2120151 | 2401024 | 2606020 | 2801028 |
| 1506018 | 2105007 | 2120172 | 2120189 | 2401026 | 2606502 | 2801029 |
| 1506020 | 2105014 | 2120173 | 2120691 | 2401027 | 2607011 | 3705001 |
| 4401503 | 2105027 | 2120174 | 2120611 | 2401028 | 2607076 | 3802002 |
| 3509510 | 2105029 | 2120176 | 2305504 | 2401029 | 2607501 | 3212001 |
| 2101005 | 2105502 | 2120177 | 2306014 | 2401030 | 2608007 | 3306001 |
| 2101006 | 2106004 | 2120178 | 2306019 | 2401031 | 2608501 | 4208001 |
| 2101010 | 2106007 | 2120179 | 2306033 | 2401033 | 2609523 | 4704003 |
| 2101011 | 2106008 | 2120180 | 2306034 | 2401035 | 2610030 | 3501006 |
| 2101004 | 2113006 | 2120181 | 2306507 | 2401036 | 2610069 | 3801003 |
| 2101013 | 2116501 | 2120182 | 2306516 | 2401037 | 2610077 | 3705005 |
| 2701507 | 2119022 | 2120183 | 2306517 | 2401038 | 2610079 | 3521001 |
| 2801013 | 2119046 | 2120184 | 2903037 | 2401039 | 2610511 | 3509004 |
| 2621502 | 2103010 | 2120185 | 1401502 | 2401042 | 2610516 | 4701003 |
| 2617026 | 2119026 | 2120186 | 2320503 | 2401043 | 2611004 | 3204002 |
| 2618020 | 2119047 | 2120187 | 2904023 | 2401044 | 2611006 | 4604001 |
| 1506027 | 2119514 | 2120188 | 2904502 | 2401046 | 2611007 | 3207001 |
| 1506504 | 2119515 | 2120190 | 2502516 | 2401049 | 2611011 | 3502006 |
| 1506505 | 2120026 | 2120193 | 2803504 | 2401051 | 2611012 | |
| 1506510 | 2120027 | 2120194 | 2904511 | 2401052 | 2611015 | |
| 1506511 | 2120033 | 2120195 | 1308504 | 2401053 | 2611504 | |
| 1506512 | 2120043 | 2120213 | 1204502 | 2401054 | 2612015 | |
| 1506513 | 2120044 | 2120214 | 2502519 | 2401055 | 2612017 | |
| 1507506 | 2120051 | 2120516 | 2321013 | 2401056 | 2612506 | |
| 1508011 | 2120055 | 2120525 | 2502508 | 2401057 | 2613018 | |
| 1508503 | 2120060 | 2120540 | 1309005 | 2401058 | 2613020 | |
| 2101002 | 2120069 | 2120541 | 1702502 | 2401059 | 2613514 | |
| 2101008 | 2120071 | 2120548 | 1506501 | 2401068 | 2614009 | |
| 2101012 | 2120073 | 2120557 | 1501505 | 2401110 | 2614012 | |
| 2101014 | 2120074 | 2120559 | 2906024 | 2401511 | 2614502 | |
| 2101016 | 2120075 | 2120561 | 2502530 | 2401515 | 2614503 | |
| 2101017 | 2120077 | 2120562 | 1309003 | 2401518 | 2615006 | |
| 2101018 | 2120080 | 2120565 | 2502013 | 2401519 | 2615015 | |
| 2101019 | 2120085 | 2120629 | 2903004 | 2401520 | 2615511 | |
| 2101020 | 2120088 | 2120630 | 1501502 | 2401521 | 2616010 | |
| 2101021 | 2120089 | 2120631 | 2904019 | 2401531 | 2616012 | |
| 2101022 | 2120096 | 2120632 | 2903078 | 2403041 | 2616016 | |
| 2101023 | 2120103 | 2120633 | 2803503 | 2405007 | 2617015 | |
| 2101024 | 2120104 | 2120634 | 1701501 | 2406006 | 2617018 | |
| 2101025 | 2120106 | 2120635 | 2502509 | 2406503 | 2617019 | |
| 2101028 | 2120111 | 2120636 | 2903508 | 2602002 | 2618018 |
References
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: Bogotá, Colombia, 1994. [Google Scholar]
- Frechet, M. Sur la loi de probabilité de l’ecart máximum (On the probability law of máximum values). Ann. de la Soc. Pol. de Math. 1927, 6, 93–116. [Google Scholar]
- Maidment, D. Handbook of Hydrology; Mc Graw-Hill: New York, NY, USA, 1992. [Google Scholar]
- Clarke, R.T.; Dias de Paiva, R.; Bertacchi, C. Comparison of methods for analysis of extremes when records are fragmented: A case study using Amazon basin rainfall data. J. Hydrol. 2009, 368, 26–29. [Google Scholar] [CrossRef]
- Bedient, P.B.; Huber, W.C. Hydrology and Floodplain Analysis. Prentice-Hall: Upper Saddle River, NJ, USA, 2002; pp. 168–224. [Google Scholar]
- Arnaez, J.; Lasanta, T.; Ruiz-Flaño, P.; Ortigosa, L. Factors affecting runoff and erosion under simulated rainfall in Mediterranean vineyards. Soil Tillage Res. 2007, 93, 324–334. [Google Scholar] [CrossRef]
- Gonzalez-Alvarez, A.; Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Ramos, H.M. Effect of the Non-Stationarity of Rainfall Events on the Design of Hydraulic Structures for Runoff Management and Its Applications to a Case Study at Gordo Creek Watershed in Cartagena de Indias. Colomb. Fluids 2018, 3, 27. [Google Scholar] [CrossRef]
- Obeysekera, J.; Salas, J.D. Quantifying the uncertainty of design floods under nonstationary conditions. J. Hydrol. Eng. 2014, 19, 1438–1446. [Google Scholar] [CrossRef]
- Obeysekera, J.; Salas, J.D. Frequency of recurrent extremes under nonstationarity. J. Hydrol. Eng. 2016, 21, 04016005. [Google Scholar] [CrossRef]
- Yang, T.; Shao, Q.; Hao, Z.-C.; Chen, X.; Zhang, Z.; Xu, C.-Y.; Sun, L. Regional frequency analysis and spatio-temporal pattern characterization of rainfall extremes in the Pearl River Basin, China. J. Hydrol. 2009, 380, 386–405. [Google Scholar] [CrossRef]
- Nunn, Dwight. Ingetec, S.A-Empresa de Acueducto y Alcantarillado de Bogotá. In Estimating of Maximum Daily Precipitation of Tributaries of Bogotá River; Ingetec: Bogotá, Colombia, 1968.
- Pathak, C.S. Frequency analysis of rainfall maximums for Central and South Florida, Technical Publication EMA # 390. 2001. Available online: http://my.sfwmd.gov/portal/page/portal/pg_grp_tech_pubs/portlet_tech_pubs/ema-390.pdf (accessed on 12 March 2018).
- Gumbel, E.J. The return period of flood flows. Ann. Math. Stat. 1941, 2, 163–190. [Google Scholar] [CrossRef]
- Weibull, W. A statistical theory of the strength of materials. In Proceedings of the Ingeniors Vetenskaps Akademien (The Royal Swedish Institute for Engineering Research) No. 51, Stockholm, Sweden, 1 Januray 1939; 1939; pp. 5–45. [Google Scholar]
- Grego, J.M.; Yates, P.A. Point and standard error estimation for quantiles of mixed flood distribution. J. Hydrol. 2010, 391, 289–301. [Google Scholar] [CrossRef]
- Koutrouvelisa, I.A.; Canavos, G.C. A comparison of moment-based methods of estimation for thelogPearson type 3 distribution. J. Hydrol. 2000, 234, 71–81. [Google Scholar] [CrossRef]
- Xuewu, J.; Jing, D.; Shen, H.W.; Salas, J.D. Plotting positions for Pearson type-III distribution. J. Hydrol. 2003, 74, 1–29. [Google Scholar] [CrossRef]
- Makkonen, L. Problems in the extreme value analysis. Struct. Saf. 2006, 30, 405–419. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Sulla determinazione empirica di una legge di distribuzione. G. dell’Instituto Ital. degli Attuari 1933, 4, 83–91. [Google Scholar]
- Smirnov, N.V. Estimate of deviation between empirical distribution functions in two independent samples. Bull. Mosc. Univ. 1939, 2, 3–16. [Google Scholar]
- Smirnov, N.V. Table for estimating the goodness of fit of empirical distributions. Ann. Math. Stat. 1948, 19, 279–281. [Google Scholar] [CrossRef]
- Mahdi, S.; Cenac, M. Estimating Parameters of Gumbel Distribution using the Methods of Moments, Probability Weighted Moments and Maximum Likelihood. Rev. de Matemáticas Teoría y Apl. 2005, 12, 151–156. [Google Scholar] [CrossRef]
- Seckin, N.; Yurtal, R.; Haktanir, T.; Dogan, A. Comparison of Probability Weighted Moments and Maximum Likelihood Methods Used in Flood Frequency Analysis for Ceyhan River Basin. Arab. J. Sci. Eng. 2009, 35, 49–69. [Google Scholar]
- Ministerio de Vivienda, Ciudad y Territorio. República de Colombia. Resolution 0330 of 8 June 2017. Available online: http://www.minvivienda.gov.co/ResolucionesAgua/0330%20-%202017.pdf (accessed on 20 March 2020).
- Ministerio de Transporte, Instituto Nacional de Vías. República de Colombia. Manual on Drainage Design for Highways. 2009. Available online: https://www.invias.gov.co/index.php/archivo-y-documentos/documentos-tecnicos/especificaciones-tecnicas/984-manual-de-drenaje-para-carreteras/file (accessed on 20 March 2020).
- Gonzalez-Alvarez, A.; Viloria-Marimón, O.; Coronado-Hernández, O.E.; Vélez-Pereira, A.; Tesfagiorgis, K.; Coronado-Hernández, J. Isohyetal Maps of Daily Maximum Rainfall for Different Return Periods for the Colombian Caribbean Region. Water 2019, 11, 358. [Google Scholar] [CrossRef]
- Krishnamoorthy, K.; Peng, J. Some properties of the exact and score methods for binomial proportion and sample size calculation. Commun. Stat. Simul. Comput. 2007, 36, 1171–1186. [Google Scholar] [CrossRef]
- El Adlouni, S.; Bobée, B. Hydrological Frequency Analysis Using HYFRAN-PLUS Software. User’s Guide available with the software DEMO 2015. Available online: http://www.wrpllc.com/books/HyfranPlus/indexhyfranplus3.html (accessed on 20 March 2020).
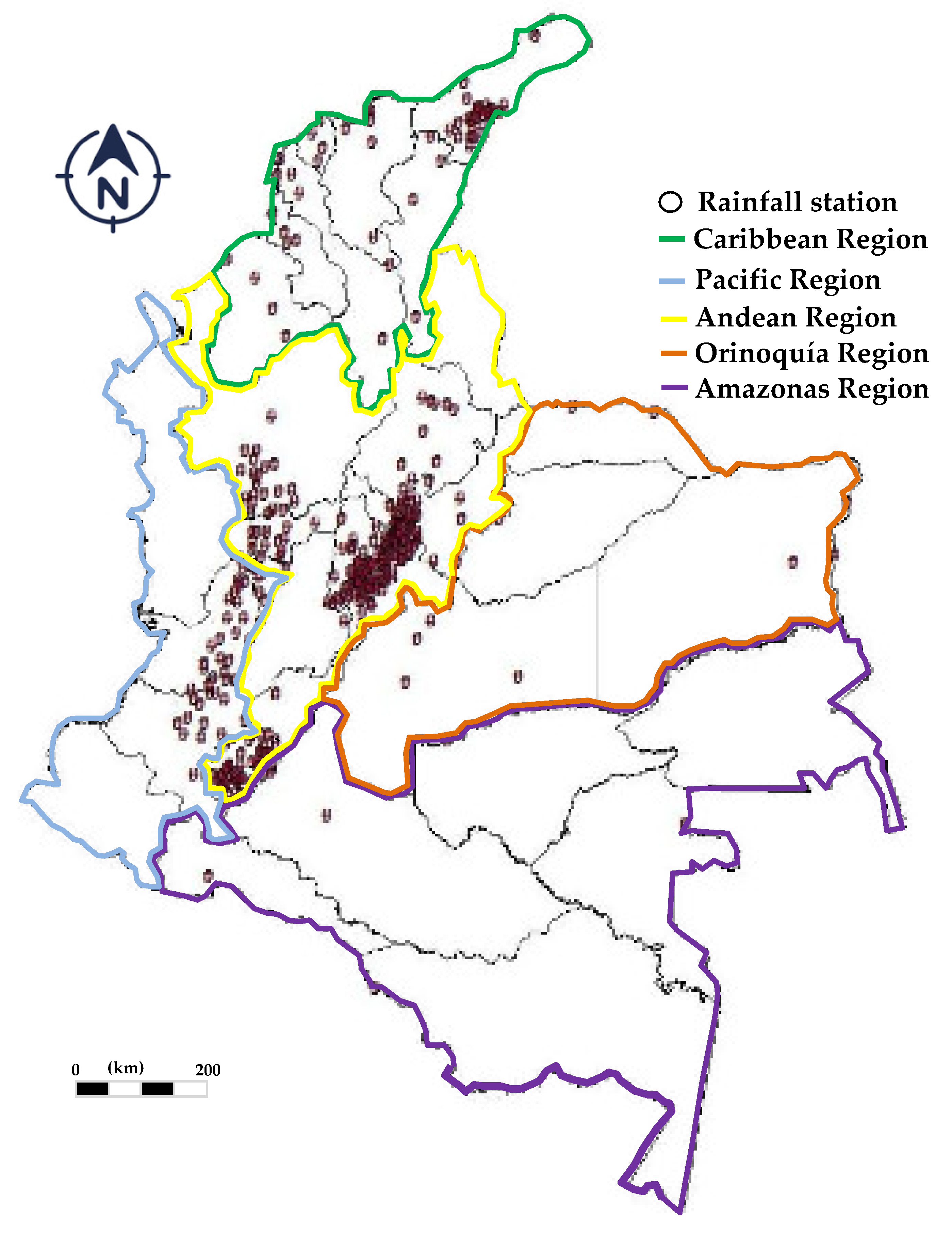
| Region | Number of Rainfall Stations | Percentage of Used Rainfall Stations (%) | Location of Rainfall Stations by Departments of Colombia |
|---|---|---|---|
| Andean | 250 | 69 | Antioquía, Boyacá, Caldas, Cauca, Cundinamarca, Huila, Quindío, Risaralda, Santander, Tolima |
| Caribbean | 59 | 16 | Atlántico, Bolívar, César, Córdoba, Magdalena, San Ándres y Providencia, Sucre |
| Pacific | 37 | 10 | Valle, Cauca |
| Orinoquía | 11 | 3 | Arauca, Vichada, Meta, Casanare |
| Amazonas | 5 | 2 | Vaupés, Putumayo, Guaviare, Amazonas, Caquetá |
| Total | 362 | 100 | N/A |
| Region | Sta. | Probability Distribution | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Gum ML | Gum WM | LP SAM | Pea ML | Pea WM | Nor ML | GEV ML | GEV WM | ||
| Values of the Chi-Squared Test | |||||||||
| Andean | Me | 5.85 | 5.63 | 6.40 | 45.01 | 7.09 | 8.04 | 5.11 | 4.60 |
| Mx | 24.60 | 25.78 | 273.0 | 360.0 | 252.0 | 64.9 | 27.6 | 18.2 | |
| Mn | 0.26 | 0.26 | 0.36 | 0.26 | 0.29 | 0.29 | 0.29 | 0.29 | |
| Sd | 4.30 | 4.13 | 18.55 | 77.43 | 17.89 | 7.63 | 4.05 | 3.52 | |
| Caribbean | Me | 7.72 | 5.64 | 16.81 | 91.57 | 6.34 | 7.41 | 5.41 | 5.18 |
| Mx | 26.12 | 20.61 | 287.0 | 392.0 | 27.22 | 42.5 | 12.9 | 14.8 | |
| Mn | 0.43 | 0.74 | 0.89 | 0.89 | 0.50 | 0.89 | 0.89 | 0.50 | |
| Sd | 5.08 | 3.72 | 50.57 | 111.0 | 4.67 | 6.35 | 3.04 | 3.48 | |
| Pacific | Me | 9.85 | 8.89 | 9.06 | 48.21 | 8.16 | 9.87 | 8.13 | 7.52 |
| Mx | 22.42 | 25.52 | 20.40 | 280.0 | 24.89 | 23.9 | 17.8 | 16.4 | |
| Mn | 1.66 | 1.46 | 0.92 | 0.80 | 0.80 | 2.00 | 0.80 | 1.20 | |
| Sd | 5.25 | 6.00 | 5.19 | 91.97 | 5.47 | 5.97 | 4.44 | 4.26 | |
| Orinoquía | Me | 13.91 | 8.09 | 33.49 | 102.1 | 7.35 | 9.24 | 8.89 | 6.31 |
| Mx | 34.48 | 16.62 | 252.0 | 252.0 | 20.97 | 20.9 | 31.6 | 13.7 | |
| Mn | 4.15 | 2.42 | 2.64 | 4.11 | 3.00 | 3.68 | 1.50 | 1.50 | |
| Sd | 9.06 | 3.99 | 72.82 | 101.1 | 5.31 | 5.60 | 9.03 | 3.83 | |
| Amazonas | Me | 6.64 | 6.32 | 87.14 | 183.0 | 4.93 | 6.70 | 4.37 | 4.36 |
| Mx | 15.50 | 17.62 | 416.0 | 416.0 | 7.50 | 11.7 | 7.00 | 7.50 | |
| Mn | 1.60 | 0.92 | 1.46 | 4.00 | 1.46 | 0.38 | 1.46 | 1.46 | |
| Sd | 5.83 | 6.71 | 183.9 | 171.1 | 2.28 | 4.09 | 2.24 | 2.70 | |
| Regional mean for Colombia based on the number of stations | Me | 6.82 | 6.05 | 10.31 | 56.57 | 7.06 | 8.14 | 5.57 | 5.04 |
| Conventions Sta.: Statistic Me: mean Mx: maximum Mn: minimum Sd: standard deviation | Gum: Gumbel LP: Log-Pearson III Pea: Pearson III Nor: Normal GEV: Generalized extreme value | ML: Maximum likelihood WM: Weighted moments SAM: SAM method | |||||||
| Station | Code | Region | Gum ML | Gum WM | LP SAM | Pea ML | Pea WM | Nor ML | GEV ML | GEV WM |
|---|---|---|---|---|---|---|---|---|---|---|
| Doña Juana | 2120630 | Andean | 2.79 | 1.53 | 1.53 | 1.53 | 1.53 | 3.42 | 1.53 | 1.53 |
| Apto Rafael Núñez | 1401502 | Carribean | 7.71 | 7.71 | 7.43 | 7.43 | 4.57 | 7.14 | 7.14 | 7.71 |
| El Placer | 2610069 | Pacific | 5.51 | 3.87 | 7.56 | 7.97 | 5.92 | 19.87 | 9.21 | 7.56 |
| Santa Rita | 3306001 | Orinoquía | 10 | 7.00 | 5.00 | 168.00 | 5.00 | 5.00 | 7.00 | 5.50 |
| Puerto Asis | 4701003 | Amazonas | 15.5 | 5.46 | 416 | 416 | 5.46 | 6.15 | 5.46 | 5.46 |
| Region | Total Used Rainfall Stations | Reached Percentage of Hydrological Distributions | ||||
|---|---|---|---|---|---|---|
| GEV | Gum | Pea | LP | Nor | ||
| Andean | 250 | 52% | 36% | 31% | 28% | 22% |
| Caribbean | 59 | 44% | 42% | 32% | 20% | 27% |
| Pacific | 37 | 54% | 30% | 43% | 19% | 22% |
| Orinoquía | 11 | 73% | 18% | 36% | 27% | 27% |
| Amazonas | 5 | 40% | 60% | 60% | 20% | 20% |
| Total | 362 | 52% | 36% | 33% | 25% | 23% |
| Region | Total Used Rainfall Stations | GEV and Gum |
|---|---|---|
| Andean | 250 | 74% |
| Caribbean | 59 | 73% |
| Pacific | 37 | 73% |
| Orinoquía | 11 | 82% |
| Amazonas | 5 | 60% |
| Total | 362 | 74% |
| Region | Extreme Values | Return Period | ||||
|---|---|---|---|---|---|---|
| 5 yr. | 10 yr. | 25 yr. | 50 yr. | 100 yr. | ||
| Andean | Min | 37.4 | 39.6 | 41.3 | 42 | 42.6 |
| Max | 147 | 173 | 218 | 259 | 242 | |
| Caribbean | Min | 64.6 | 84.3 | 97.5 | 99.3 | 100 |
| Max | 167 | 199 | 241 | 272 | 306 | |
| Pacific | Min | 35.3 | 40.5 | 47.8 | 53.9 | 60.4 |
| Max | 121 | 135 | 151 | 162 | 172 | |
| Orinoquía | Min | 119 | 131 | 141 | 145 | 149 |
| Max | 145 | 152 | 186 | 220 | 262 | |
| Amazonas | Min | 124 | 134 | 144 | 150 | 154 |
| Max | 139 | 158 | 183 | 200 | 217 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coronado-Hernández, Ó.E.; Merlano-Sabalza, E.; Díaz-Vergara, Z.; Coronado-Hernández, J.R. Selection of Hydrological Probability Distributions for Extreme Rainfall Events in the Regions of Colombia. Water 2020, 12, 1397. https://doi.org/10.3390/w12051397
Coronado-Hernández ÓE, Merlano-Sabalza E, Díaz-Vergara Z, Coronado-Hernández JR. Selection of Hydrological Probability Distributions for Extreme Rainfall Events in the Regions of Colombia. Water. 2020; 12(5):1397. https://doi.org/10.3390/w12051397
Chicago/Turabian StyleCoronado-Hernández, Óscar E., Ernesto Merlano-Sabalza, Zaid Díaz-Vergara, and Jairo R. Coronado-Hernández. 2020. "Selection of Hydrological Probability Distributions for Extreme Rainfall Events in the Regions of Colombia" Water 12, no. 5: 1397. https://doi.org/10.3390/w12051397
APA StyleCoronado-Hernández, Ó. E., Merlano-Sabalza, E., Díaz-Vergara, Z., & Coronado-Hernández, J. R. (2020). Selection of Hydrological Probability Distributions for Extreme Rainfall Events in the Regions of Colombia. Water, 12(5), 1397. https://doi.org/10.3390/w12051397






