A New Parallel Framework of SPH-SWE for Dam Break Simulation Based on OpenMP
Abstract
1. Introduction
2. Methodology
2.1. Governing Equations
2.2. Water Depth Solutions
2.3. Speed Solution
2.4. Time Integration and Boundary Processing
3. SPH-SWE Model Solution Framework
| Algorithm 1. Calculation framework of the SPH-SWEs model. This algorithm is needed to read the particles data (include fluid particles/virtual particles/open boundary particle/riverbed particles). |
| Read parameters Output initial data of the model Mesh riverbed particles and calculate fluid particles and the net water depth Search particles dototal_number_of_timesteps
|
- Calculation of fluid particles in the riverbed;
- Particle search, and calculation of the water depth;
- Calculation of the fluid particle depth and velocity gradient;
- Acceleration and riverbed gradient correction;
- Calculation of velocity and displacement rate.
3.1. Fluid Particle Riverbed Calculation
| Algorithm 2. Computing fluid particle riverbed. |
| 1. Stage 1: , initialize to 0 |
| 2. !$OMP PARALLEL DO PRIVATE(private variable),& |
| 3. !$OMP& SHARED(shared variable), DEFAULT(none), SCHEDULE(static) |
| 4. do total_number_of_fluid particles |
| 5. if particle_i is valid then |
| 6. Calculate particles’ mesh locations based on the riverbed’s mesh |
| 7. ! is used to make shepard correction(CSPM) |
| 8. CALL PURE celij_hb |
| 9. endif |
| 10. enddo |
| 11. !$OMP END PARALEL DO |
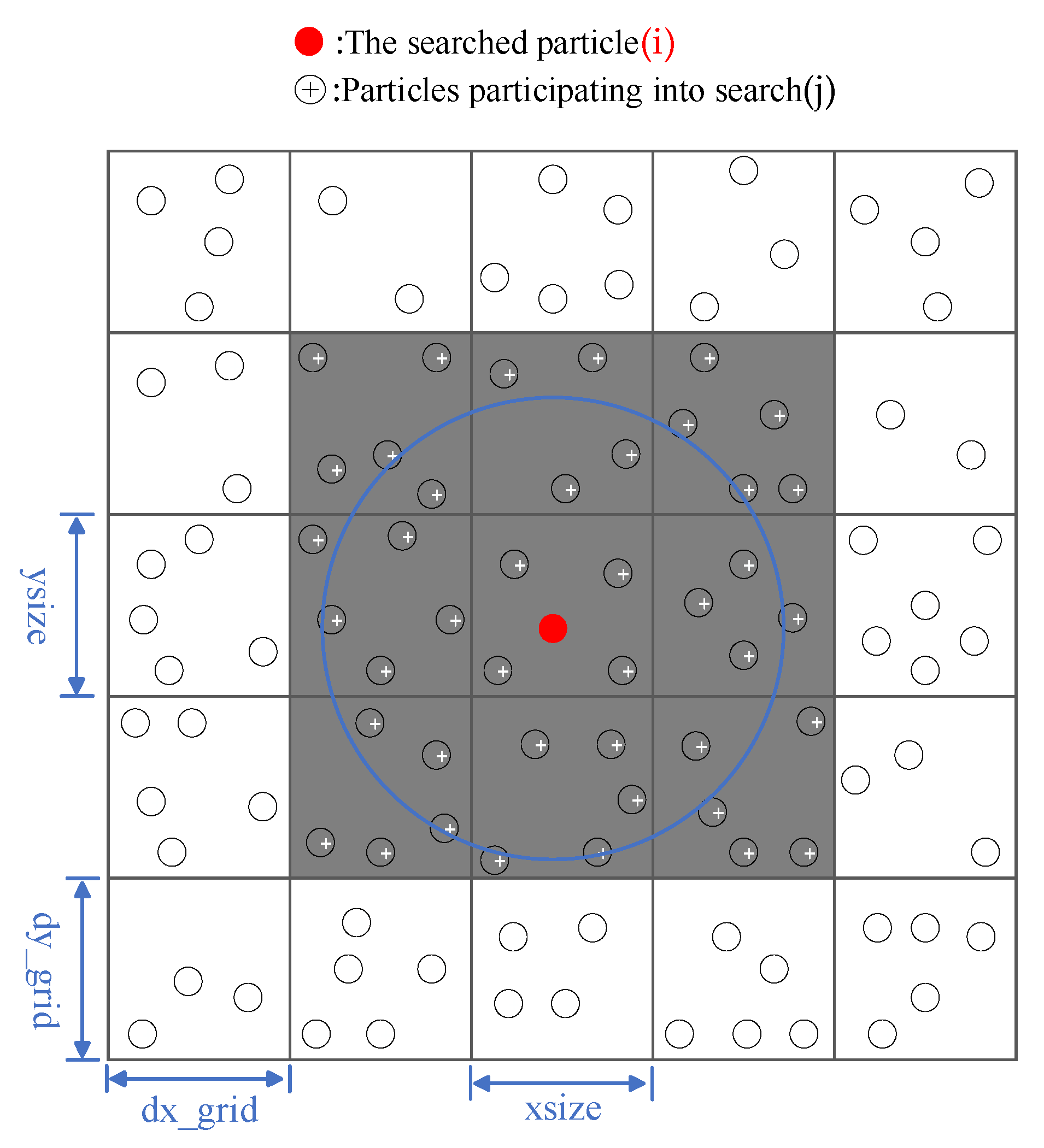
3.2. Particle Search
- Before each time step, the temporary grid position was updated, and each grid was assigned to a unique number; the grid size can be set to a fixed size dx_grid/dy_grid;
- According to the position of the current SPH particles, all the SPH particles were allocated to the temporary mesh space, and the particle chain in the mesh was established;
- According to the range (2hi) of the tight support region of particle i, the search of other meshes (- xsize to xsize, - ysize to ysize) was completed in the tight support region of the mesh, storing the mesh number;
- All the SPH particles i and j in the mesh were searched (icell-xsize to icell + size, jcell-ysize to jcell + ysize) in the tight support domain.
| Algorithm 3: The particle search. Read in the particles data (include fluid particles/virtual parti`cles/open boundary particle/riverbed particles). |
| 1. In each timestep 2. Mesh all particles based on fixed size dx_grid/dy_grid(generally select the maximum smooth length) and particles into nc array 3. ncx/ncy: total number of grids in x/y direction 4. iboxvv/iboxff/iboxob: store the virtual particles, fluid particles and open boundary particles within the affected region into two dimensional arrays 5. !$OMP PARALLEL DO PRIVATE (private variable),SHARED(shared variable),& 6. !$OMP& SHARED(shared variable),DEFAULT(none) 7. do total_number_of_fluid particles 8. if particle_i is valid then 9. Calculate mesh of the particle i:icell/jcell 10. Calculate search mesh range of particle i:xsize/yszie 11. do row -ysize,ysize 12. irow=jcell+1 13. do column -xsize,xsize 14. icolumn=icell+column 15. Calculate number of search grid: gridn 16. gridn=icolumn+(irow-1)*ncx 17. !Search for Virtual particles in the scope of I particle 18. do j nc(grindn,1) 19. if particle_i and particle_j are neighbours then 20. Write particle_j to iboxvv array 21. endif 22. enddo 23. !Search for Fluid particles in the scope of i particle 24. do j nc(grindn,2) 25. if particle_i and particle_j are neighbours then 26. Write particle_j to iboxff array 27. endif 28. enddo 29. !Search for Open boundary particles in the scope of i particle 30. do j nc(grindn,3) 31. if particle_i and particle_j are neighbours then 32. Write particle_j to iboxob array 33. endif 34. enddo 35. enddo 36. enddo 37. endif 38. enddo 39. !$OMP END PARALLEL DO |
3.3. Water Depth Calculation
| Algorithm 4: Water depth calculation. |
| 1. Stage 1: Guess for density and smoothed length 2. !$OMP PARALLEL DO PRIVATE(private variable),& 3. !$OMP& SHARED(shared variable),DEFAULT(none),SCHDULE(static) 4. do total_number_of_fluid particles 5. if particle_i is valid then 6. 1a: 7. 1b: 8. endif 9. enddo 10. !$OMP END PARALLEL DO 11. CALL particle search() %Search particles 12. Stage 2: Calculate depth 13. do while ((maxval(resmax) .gt. Minimum error) .and. (Iterationtimes .lt. max) 14. !$OMP PARALLEL DO PRIVATE(private variable),& 15. !$OMP& SHARED(shared variable),DEFAULT(none),SCHEDULE(static) 16. do total_number_of_fluid particles 17. if particle_i is valid then 18. CALL PURE fluid particle(i,rhop_sum(i),alphap(i)) 19. CALL PURE virtual particle(i,rhop_sum(i),alphap(i)) 20. CALL PURE open boundary particle((i,rhop_sum(i),alphap(i)) 21. %Calculate next step’s water depth and the smooth length 22. 23. 24. 25. 26. endif 27. enddo 28. !$OMP END PARALLEL DO 29. enddo |
3.4. Velocity Calculations
| Algorithm 5: Calculation of fluid particle velocity and water depth gradient. |
| 1. Stage 1: sum_f/alphap/grad_up/grad_vp/grad_dw=0, Initialize to 0 2. !$OMP PARALLEL DO PRIVATE(private variable),& 3. !$OMP& SHARED(shared variable),DEFAULT(none),SCHDULE(static) 4. do total_number_of_fluid particles 5. if particle_i is valid then 6. !First conduct matrix for gradient correction 7. CALL PURE celij_corr(i,sum_f (I,1:4)) 8. CALL PURE celij_alpha(i,alphap(i),grad_dw(i,1:2),grad_up(i,1:2), grad_vp(i,1:2)) 9. CALL PURE celij_alpha_vir(i,alphap(i)) 10. CALL PURE celij_alphap_ob(i,alphap(i),grad_dw(i,1:2),grad_up(i,1:2), grad_vp(i,1:2)) 11. endif 12. enddo 13. !$OMP END PARALLEL DO |
3.5. Calculation of Fluid Particle Acceleration, Riverbed Scouring, Speed, and Displacement
| Algorithm 6: Calculation of acceleration, velocity, and position. The Lagrangian equation of motion for a particle i is d/dt ∂L/(∂v_i )-∂L/(∂x_i )=0, where the Lagrangian functional L is defined in term of kinetic energy K and potential energy π as L = K-π, where π is a function of particles position but not velocity. |
| 1. Stage 1: Calculate 2. !$OMP PARALLEL DO PRIVATE(private variable),& 3. !$OMP& SHARED(shared variable),DEFAULT(none),SCHDULE(static) 4. do total_number_of_fluid particles 5. if particle_i is valid then 6. 1a. use Riemann solution to calculate 7. 1b. use Numerical viscosity to calculate 8. ! ar(i) is used to calculate depth 9. CALL PURE fluid particle(i,ar(i),ay(i),ar(i)) 10. CALL PURE virtual particle(i,ar(i),ay(i),ar(i)) 11. CALL PURE open boundary particle(i,ar(i),ay(i),ar(i)) 12. endif 13. Stage 2: Calculate 14. Stage 3: Calculate 15. Stage 4: Calculate velocity and position of fluid particle 16. enddo 17. !$OMP END PARALLEL DO |
4. Applications
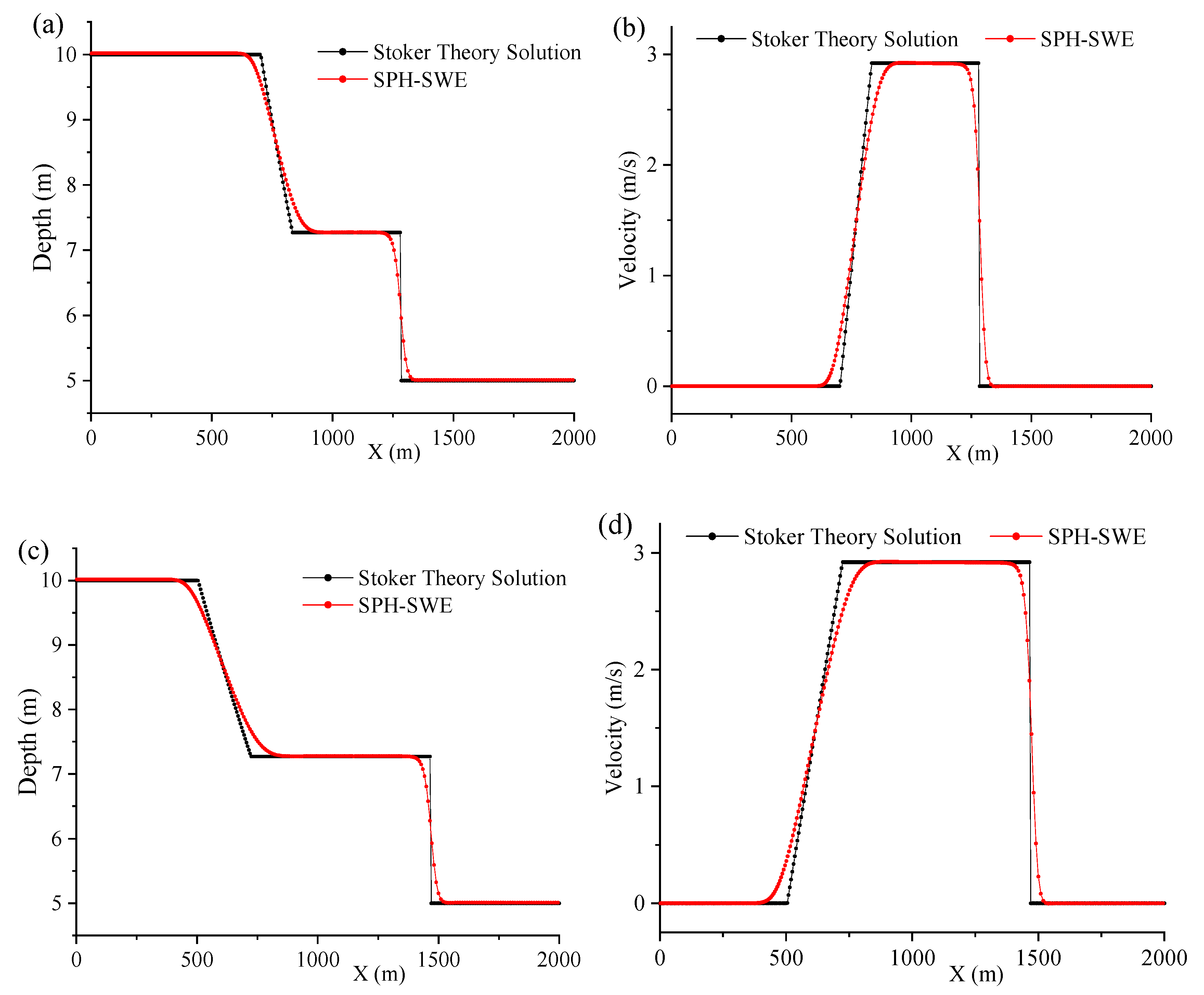
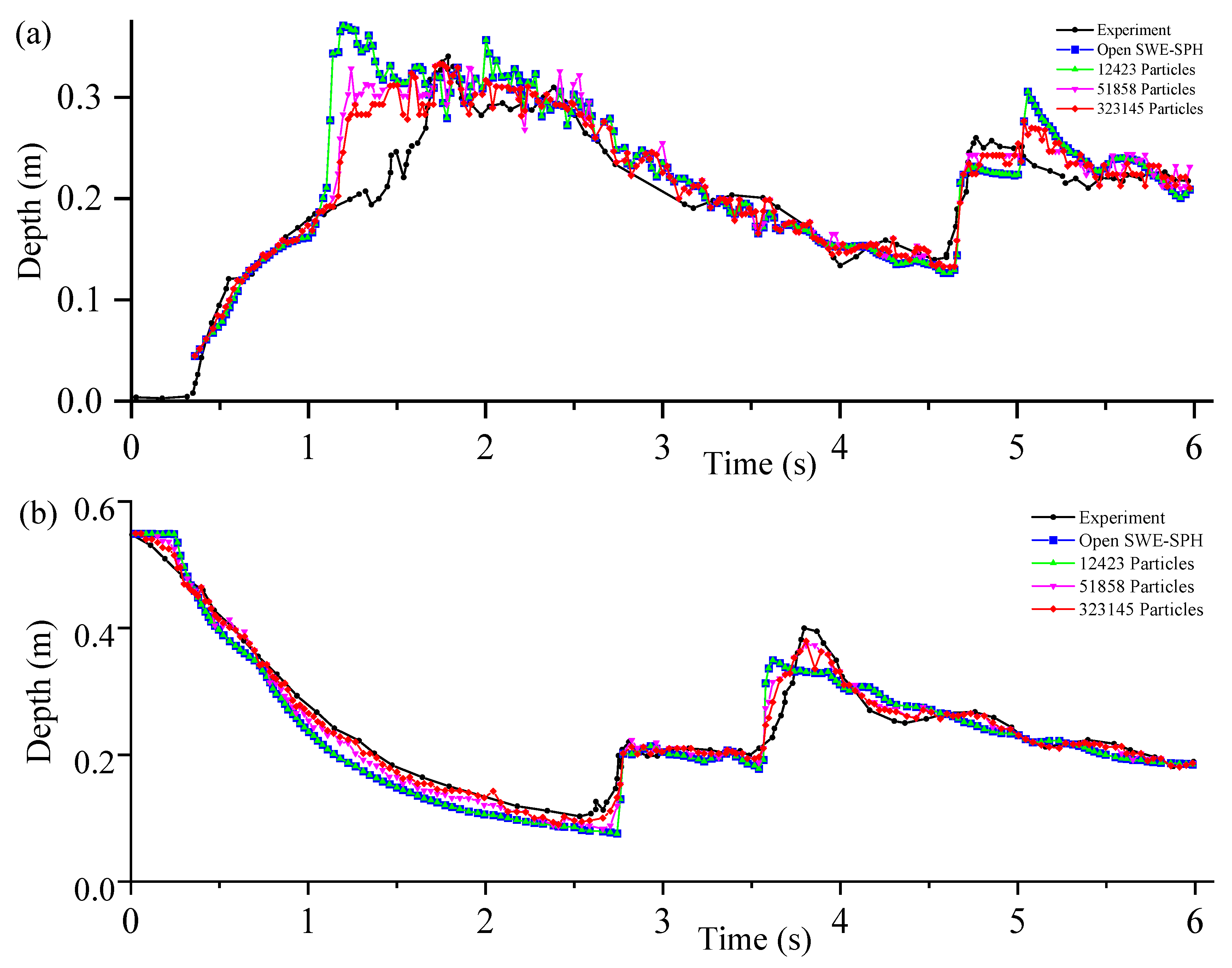
4.1. Validation 1: 2-D Dry Bed Dam Break with Particle Splitting
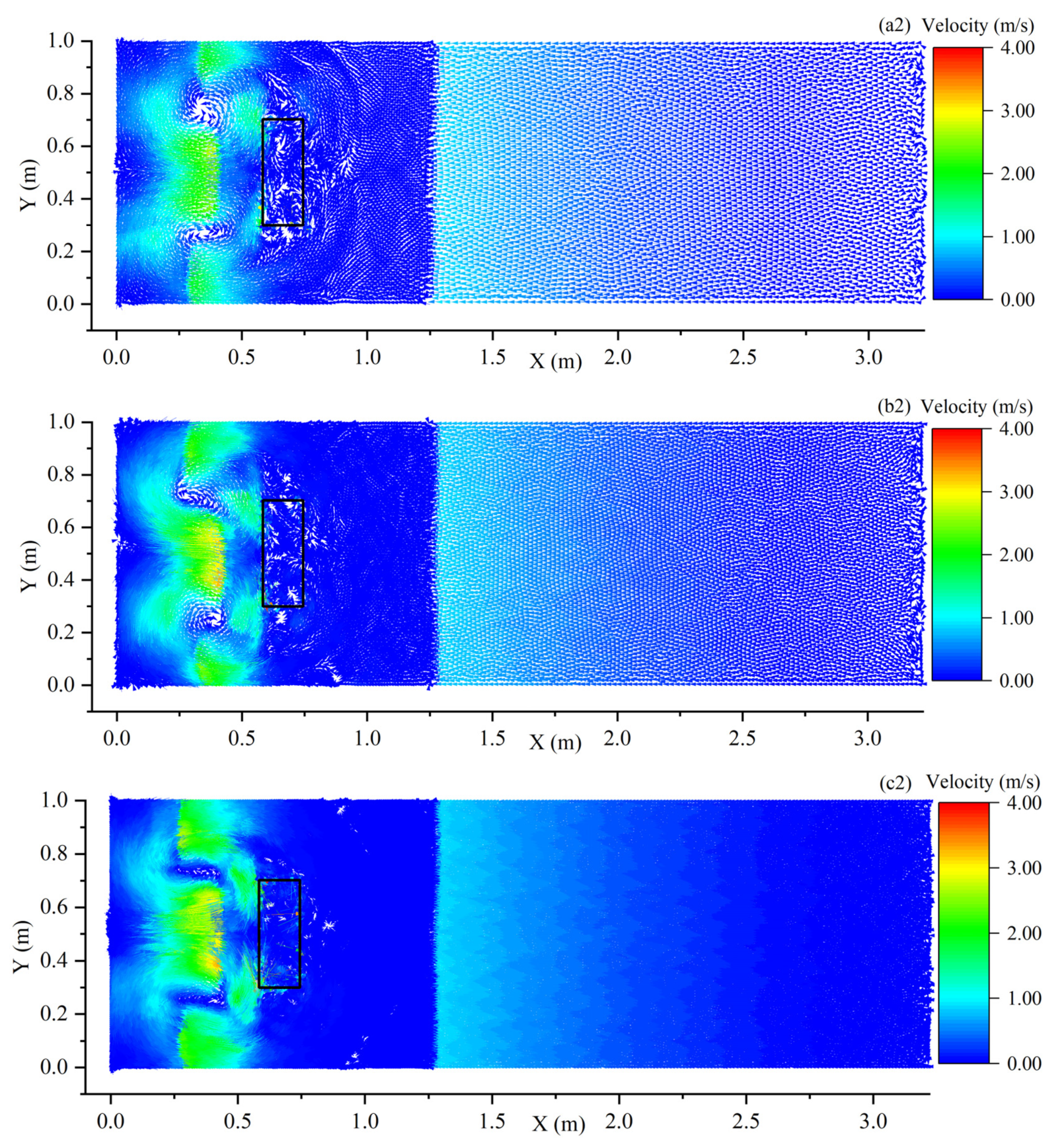
4.2. Validation 2: 2-D Dam Break with A Rectangular Obstacle Located in the Downstream Area
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chang, Y.S.; Chang, T.J. SPH simulations of solute transport in flows with steep velocity and concentration gradients. Water 2017, 9, 132. [Google Scholar] [CrossRef]
- Gu, S.; Zheng, X.; Ren, L.; Xie, H.; Huang, Y.; Wei, J.; Shao, S. SWE-SPHysics simulation of dam break flows at South-Gate Gorges Reservoir. Water 2017, 9, 387. [Google Scholar] [CrossRef]
- Chen, R.; Shao, S.; Liu, X.; Zhou, X. Applications of shallow water SPH model in mountainous rivers. J. Appl. Fluid Mech. 2015, 8, 863–870. [Google Scholar] [CrossRef]
- Peng, X.; Yu, P.; Chen, G.; Xia, M.; Zhang, Y. Development of a Coupled DDA–SPH Method and its Application to Dynamic Simulation of Landslides Involving Solid–Fluid Interaction. Rock Mech. Rock Eng. 2020, 53, 113–131. [Google Scholar] [CrossRef]
- Verbrugghe, T.; Dominguez, J.M.; Altomare, C.; Tafuni, A.; Vacondio, R.; Troch, P.; Kirtenhaus, A. Non-linear wave generation and absorption using open boundaries within DualSPHysics. Comput. Phys. Commun. 2019, 240, 46–59. [Google Scholar] [CrossRef]
- Ni, X.; Feng, W.; Huang, S.; Zhao, X.; Li, X. Hybrid SW-NS SPH models using open boundary conditions for simulation of free-surface flows. Ocean Eng. 2020, 196, 106845. [Google Scholar] [CrossRef]
- Gonzalez-Cao, J.; Altomare, C.; Crespo, A.J.C.; Dominguez, J.M.; Gomez-Gesteira, M.; Kisacik, D. On the accuracy of DualSPHysics to assess violent collisions with coastal structures. Comput. Fluids 2019, 179, 604–612. [Google Scholar] [CrossRef]
- Atif, M.M.; Chi, S.W.; Grossi, E.; Shabana, A. Evaluation of breaking wave effects in liquid sloshing problems: ANCF/SPH comparative study. Nonlinear Dyn. 2019, 97, 45–62. [Google Scholar] [CrossRef]
- Meringolo, D.D.; Marrone, S.; Colagrossi, A.; Liu, Y. A dynamic δ-SPH model: How to get rid of diffusive parameter tuning. Comput. Fluids 2019, 179, 334–355. [Google Scholar] [CrossRef]
- Shu, A.; Wang, S.; Rubinato, M.; Wang, M.; Qin, J.; Zhu, F. Numerical Modeling of Debris Flows Induced by Dam-Break Using the Smoothed Particle Hydrodynamics (SPH) Method. Appl. Sci. 2020, 10, 2954. [Google Scholar] [CrossRef]
- Wu, S.; Rubinato, M.; Gui, Q. SPH Simulation of interior and exterior flow field characteristics of porous media. Water 2020, 12, 918. [Google Scholar] [CrossRef]
- Wang, S.; Shu, A.; Rubinato, M.; Wang, M.; Qin, J. Numerical Simulation of Non-Homogeneous Viscous Debris-Flows based on the Smoothed Particle Hydrodynamics (SPH) Method. Water 2019, 11, 2314. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Hopkins, P. A general class of Lagrangian smoothed particle hydrodynamics methods and implications for fluid mixing problems. Mon. Not. R. Astron. Soc. 2013, 428, 2840–2856. [Google Scholar] [CrossRef]
- Cremonesi, M.; Meduri, S.; Perego, U. Lagrangian-Eulerian enforcement of non-homogeneous boundary conditions in the Particle Finite Element Method. Comput. Part. Mech. 2020, 7, 41–56. [Google Scholar] [CrossRef]
- Sugiyama, K.; Li, S.; Takeuchi, S.; Takagi, S.; Matsumoto, Y. A full Eulerian finite difference approach for solving fluid-structure coupling problems. J. Comput. Phys. 2011, 230, 596–627. [Google Scholar] [CrossRef]
- Miller, G.H.; Colella, P. A conservative three-dimensional Eulerian method for coupled solid-fluid shock capturing. J. Comput. Phys. 2002, 183, 26–82. [Google Scholar] [CrossRef]
- Liu, M.B.; Liu, G.R. Smoothed Particle Hydrodynamics (SPH): An Overview and Recent Developments. Arch. Comput. Methods Eng. 2010, 17, 25–76. [Google Scholar] [CrossRef]
- Liu, G.R.; Liu, M.B. Smoothed Particle Hydrodynamics: A Meshfree Particle Method; World Scientific: Singapore, 2003. [Google Scholar]
- Dalrymple, R.A.; Rogers, B.D. Numerical modeling of water waves with the SPH method. Coast. Eng. 2006, 53, 141–147. [Google Scholar] [CrossRef]
- Huang, C.; Lei, J.M.; Peng, X.Y. A kernel gradient free (KGF) SPH method. Int. J. Numer. Methods Fluids 2015, 78. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Kocharyan, A. SPH simulation of multi-phase flow. Comput. Phys. Commun. 1995, 87, 225–235. [Google Scholar] [CrossRef]
- Chen, A.S.; Djordjevic, S.; Leandro, J. An analysis of the combined consequences of pluvial and fluvial flooding. Water Sci. Technol. 2010, 62, 1491–1498. [Google Scholar] [CrossRef]
- Liang, Q.; Borthwick, A.G.L.; Stelling, G. Simulation of dam and dyke break hydrodynamics on dynamically adaptive quadtree grids. Int. J. Numer. Methods Fluids 2004, 46. [Google Scholar] [CrossRef]
- Chang, T.J.; Kao, H.M.; Chang, K.H.; Hsu, M.H. Numerical simulation of shallow water dam break flows in open channels using smoothed particle hydrodynamics. J. Hydrol. 2011, 408, 78–90. [Google Scholar] [CrossRef]
- Kao, H.M.; Chang, T.J. Numerical modeling of dambreak-induced flood inundation using smoothed particle hydrodynamics. J. Hydrol. 2012, 448–449, 232–244. [Google Scholar] [CrossRef]
- Colagrossi, A.; Landrini, M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics. J. Comput. Phys. 2003, 191, 448–475. [Google Scholar] [CrossRef]
- Yang, F.L.; Zhang, X.F.; Tan, G.M. One and two-dimensional coupled hydrodynamics model for dam break flow. J. Hydrodyn. 2007, 19, 769–775. [Google Scholar] [CrossRef]
- Wang, Z.; Shen, H.T. Lagrangian simulation of one-dimensional dam-break flow. Hydraul. Eng. 1999, 125, 1217–1220. [Google Scholar] [CrossRef]
- Ata, R.; Soulaimani, A. A stabilized SPH method for inviscid shallow water flows. Int. J. Numer. Methods Fluids 2005, 47, 139–159. [Google Scholar] [CrossRef]
- Leffe, M.D.; Touzé, D.L.; Alessandrini, B. SPH Modeling of a shallow-water coastal flows. Hydraul. Res. 2010, 48, 118–125. [Google Scholar] [CrossRef]
- Rodriguez-Paz, M.; Bonet, J. A corrected smooth particle hydrodynamics formulation of the shallow-water equations. Comput. Struct. 2005, 83, 1396–1410. [Google Scholar] [CrossRef]
- Panizzo, A.; Longo, D.; Bellotti, G.; De Girolamo, P. Tsunamis early warning system. Part 3: SPH modeling of nlswe. In Proceedings of the XXX Convegno di Idraulica e Costruzioni Idrauliche, Rome, Italy, 10–15 September 2006. [Google Scholar]
- Vacondio, R.; Rogers, B.D.; Stansby, P.K.; Mignosa, P. A correction for balancing discontinuous bed slopes in two-dimensional smoothed particle hydrodynamics shallow water modeling. Int. J. Numer. Methods Fluids 2013, 71, 850–872. [Google Scholar] [CrossRef]
- Vacondio, R.; Rogers, B.D.; Stansby, P.K.; Mignosa, P. SPH Modeling of Shallow Flow with Open Boundaries for Practical Flood Simulation. J. Hydraul. Eng. 2012, 138, 530–541. [Google Scholar] [CrossRef]
- Vacondio, R.; Rogers, B.D.; Stansby, P.K.; Mignosa, P. Smoothed Particle Hydrodynamics: Approximate zero-consistent 2-D boundary conditions and still shallow water tests. Int. J. Numer. Methods Fluids 2011, 69, 226–253. [Google Scholar] [CrossRef]
- Vacondio, R.; Rogers, B.D.; Stansby, P.K. Accurate particle splitting for SPH in shallow water with shock capturing. Int. J. Numer. Methods Fluids 2012, 69, 1377–1410. [Google Scholar] [CrossRef]
- Skillen, A.; Lind, S.J.; Stansby, P.K.; Rogers, B.D. Incompressible Smoothed Particle Hydrodynamics (SPH) with reduced temporal noise and generalised Fickian smoothing applied to body-water slam and efficient wave-body interaction. Comput. Methods Appl. Mech. Eng. 2013, 265, 163–173. [Google Scholar] [CrossRef]
- Fourtakas, G.; Rogers, B.D.; Laurence, D.R.P. Modelling Sediment resuspension in Industrial tanks using SPH. Houille Blanche 2013, 2, 39–45. [Google Scholar] [CrossRef]
- St-Germain, P.; Nistor, I.; Townsend, R.; Shibayama, T. Smoothed-Particle Hydrodynamics Numerical Modeling of Structures Impacted by Tsunami Bores. J. Waterw. Port Coast. Ocean Eng. 2014, 140, 66–81. [Google Scholar] [CrossRef]
- Cunningham, L.S.; Rogers, B.D.; Pringgana, G. Tsunami wave and structure interaction: An investigation with smoothed-particle hydrodynamics. Proc. Inst. Civ. Eng. Eng. Comput. Mech. 2014, 167, 106–116. [Google Scholar] [CrossRef]
- Aureli, F.; Dazzi, S.; Maranzoni, A.; Mignosa, P.; Vacondio, R. Experimental and numerical evaluation of the force due to the impact of a dam-break wave on a structure. Adv. Water Resour. 2015, 76, 29–42. [Google Scholar] [CrossRef]
- Canelas, R.B.; Domínguez, J.M.; Crespo, A.J.C.; Gómez-Gesteira, M.; Ferreira, R.M.L. A Smooth Particle Hydrodynamics discretization for the modelling of free surface flows and rigid body dynamics. Int. J. Numer. Methods Fluids 2015, 78, 581–593. [Google Scholar] [CrossRef]
- Heller, V.; Bruggemann, M.; Spinneken, J.; Rogers, B.D. Composite modelling of subaerial landslide–tsunamis in different water body geometries and novel insight into slide and wave kinematics. Coast. Eng. 2016, 109, 20–41. [Google Scholar] [CrossRef]
- Fourtakas, G.; Rogers, B.D. Modelling multi-phase liquid-sediment scour and resuspension induced by rapid flows using Smoothed Particle Hydrodynamics (SPH) accelerated with a graphics processing unit (GPU). Adv. Water Resour. 2016, 92, 186–199. [Google Scholar] [CrossRef]
- Mokos, A.; Rogers, B.D.; Stansby, P.K. A multi-phase particle shifting algorithm for SPH simulations of violent hydrodynamics with a large number of particles. J. Hydraul. Res. 2017, 55, 143–162. [Google Scholar] [CrossRef]
- Alshaer, A.W.; Rogers, B.D.; Li, L. Smoothed Particle Hydrodynamics (SPH) modelling of transient heat transfer in pulsed laser ablation of Al and associated free-surface problems. Comput. Mater. Sci. 2017, 127, 161–179. [Google Scholar] [CrossRef]
- Sun, P.N.; Colagrossi, A.; Marrone, S.; Antuono, M.; Zhang, A.M. A consistent approach to particle shifting in the δ-Plus-SPH model. Mech. Eng. 2019, 348, 912–934. [Google Scholar] [CrossRef]
- Sun, P.; Zhang, A.M.; Marrone, S.; Ming, F. An accurate and efficient SPH modeling of the water entry of circular cylinders. Appl. Ocean Res. 2018, 72, 60–75. [Google Scholar] [CrossRef]
- Zheng, X.; Shao, S.; Khayyer, A.; Duan, W.; Ma, Q.; Liao, K. Corrected first-order derivative ISPH in water wave simulations. Coast. Eng. J. 2017, 59. [Google Scholar] [CrossRef]
- Luo, M.; Reeve, D.; Shao, S.; Karunarathna, H.; Lin, P.; Cai, H. Consistent Particle Method simulation of solitary wave impinging on and overtopping a seawall. Eng. Anal. Bound. Elem. 2019, 103, 160–171. [Google Scholar] [CrossRef]
- Ran, Q.; Tong, J.; Shao, S.; Fu, X.; Xu, Y. Incompressible SPH scour model for movable bed dam break flows. Adv. Water Resour. 2015, 82, 39–50. [Google Scholar] [CrossRef]
- Xia, X.; Liang, Q. A GPU-accelerated smoothed particle hydrodynamics (SPH) model for the shallow water equations. Environ. Model. Softw. 2016, 75, 28–43. [Google Scholar] [CrossRef]
- Liang, Q.; Xia, X.; Hou, J. Catchment-scale High-resolution Flash Flood Simulation Using the GPU-based Technology. Procedia Eng. 2016, 154, 975–981. [Google Scholar] [CrossRef]
- Satake, S.I.; Yoshimori, H.; Suzuki, T. Optimazations of a GPU accelerated heat conduction equation by a programming of CUDA Fortran from an analysis of a PTX file. Comput. Phys. Commun. 2012, 183, 2376–2385. [Google Scholar] [CrossRef]
- Yang, C.T.; Huang, C.L.; Lin, C.F. Hybrid CUDA, OpenMP, and MPI parallel programming on multicore GPU clusters. Comput. Phys. Commun. 2011, 182, 266–269. [Google Scholar] [CrossRef]
- Ohshima, S.; Hirasawa, S.; Honda, H. OMPCUDA: OpenMP Execution Framework for CUDA Based on Omni OpenMP Compiler. In Beyond Loop Level Parallelism in OpenMP: Accelerators, Tasking and More; Sato, M., Hanawa, T., Müller, M.S., Chapman, B.M., de Supinski, B.R., Eds.; IWOMP 2010. Lecture Notes in Computer Science, 6132; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Loncar, V.; Young, S.L.E.; Skrbic, S.; Muruganandam, P.; Adhikari, S.; Balaz, A. OpenMP, OpenMP/MPI, and CUDA/MPI C programs for solving the time-dependent dipolar Gross-Pitaevskii equation. Comput. Phys. Commun. 2016, 209, 190–196. [Google Scholar] [CrossRef]
- Bronevetsky, G.; Marques, D.; Pingali, K.; McKee, S.; Rugina, R. Compiler-enhanced incremental checkpointing for OpenMP applications. In Proceedings of the 2009 IEEE International Symposium on Parallel & Distributed Processing, Rome, Italy, 23–29 May 2009; pp. 1–12. [Google Scholar] [CrossRef]
- Dagum, L.; Menon, R. OpenMP: An industry standard API for shared-memory programming. IEEE Comput. Sci. Eng. 1998, 5, 46–55. [Google Scholar] [CrossRef]
- Slabaugh, G.; Boyes, R.; Yang, X. Multicore Image Processing with OpenMP [Applications Corner]. IEEE Signal Process. Mag. 2010, 27, 134–138. [Google Scholar] [CrossRef]
- Chorley, M.J.; Walker, D.W. Performance analysis of a hybrid MPI/OpenMP application on multi-core clusters. J. Comput. Sci. 2010, 1, 168–174. [Google Scholar] [CrossRef]
- Adhianto, L.; Chapman, B. Performance modeling of communication and computation in hybrid MPI and OpenMP applications. Simul. Model. Pract. Theory 2007, 15, 481–491. [Google Scholar] [CrossRef]
- Wright, S.J. Parallel algorithms for banded linear systems. Siam J. Sci. Stat. Comput. 1991, 12, 824–842. [Google Scholar] [CrossRef]
- Jiao, Y.-Y.; Zhao, Q.; Wang, L. A hybrid MPI/OpenMP parallel computing model for spherical discontinuous deformation analysis. Comput. Geotech. 2019, 106, 217–227. [Google Scholar] [CrossRef]
- Przemysław, S. Algorithmic and language-based optimization of Marsa-LFIB4 pseudorandom number generator using OpenMP, OpenACC and CUDA. J. Parallel Distrib. Comput. 2020, 137, 238–245. [Google Scholar]
- Vacondio, R. Shallow Water and Navier-Stokes SPH-Like Numerical Modelling of Rapidly Varying Free-Surface Flows. Ph.D. Thesis, Università degli Studi di Parma, Parma, Italy, 2010. [Google Scholar]
- Vacondio, R.; Rodgers, B.D.; Stansby, P.K.; Mignosa, P. User Guide for the SWE-SPHysics Code. 2013. Available online: https://wiki.manchester.ac.uk/sphysics/images/SWE-SPHysics_v1.0.00.pdf (accessed on 2 April 2020).
- Marion, J.; Thornton, S. Classical Dynamics of Particles and Systems; Harcourt Brace Jovanovich Inc.: San Diego, CA, USA, 1988. [Google Scholar]
- Monaghan, J.J. Smoothed particle hydrodynamics. Rep. Prog. Phys. 2005, 68, 1703–1759. [Google Scholar] [CrossRef]
- Bonet, J.; Lok, T.-S.L. Variational and momentum preservation aspects of Smooth Particle Hydrodynamic formulations. Comput. Methods Appl. Mech. Eng. 1999, 180, 97–115. [Google Scholar] [CrossRef]
- Vila, J.P. On particle weighted methods and smooth particle hydrodynamics. Math. Models Methods Appl. Sci. 1999, 9, 161–209. [Google Scholar] [CrossRef]
- Dinshaw, B.S. Von Neumann stability analysis of smoothed particle hydrodynamics—Suggestions for optimal algorithms. J. Comput. Phys. 1995, 121, 357–372. [Google Scholar]
- Toro, E. Direct Riemann solvers for the time-dependent Euler equations. Shock Waves 1995, 5, 75–80. [Google Scholar] [CrossRef]
- Hernquist, L.; Katz, N. TREESPH: A unification of SPH with the hierarchical tree method. Astrophys. J. Suppl. 1989, 70, 419–446. [Google Scholar] [CrossRef]
- Toro, E. Shock Capturing Methods for Free Surface Shallow Water Flows; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Nikolaos, D.K. A dissipative galerkin scheme for open-channel flow. Hydraul. Eng. 1984, 110, 337–352. [Google Scholar]
- Majda, A.; Osher, S. Numerical viscosity and the entropy condition. Commun. Pure Appl. Math. 1979. [Google Scholar] [CrossRef]
- Stranex, T.; Wheaton, S. A new corrective scheme for SPH. Comput. Methods Appl. Mech. Eng. 2011, 200, 392–402. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Gingold, R.A. Shock simulation by the particle method SPH. J. Comput. Phys. 1983, 52, 374–389. [Google Scholar] [CrossRef]
- Monaghan, J.J. Particle methods for hydrodynamics. Comput. Phys. Rep. 1985, 3, 71–124. [Google Scholar] [CrossRef]
- Chen, F.; Qiang, H.; Gao, W. Coupling of smoothed particle hydrodynamics and finite volume method for two-dimensional spouted beds. Comput. Chem. Eng. 2015, 77, 135–146. [Google Scholar] [CrossRef]
- Kleefsman, K.M.T.; Fekken, G.; Veldman, A.E.P.; Iwanowski, B.; Buchner, B. A volume-of-fluid based simulation method for wave impact problems. J. Comput. Phys. 2005, 206, 363–393. [Google Scholar] [CrossRef]
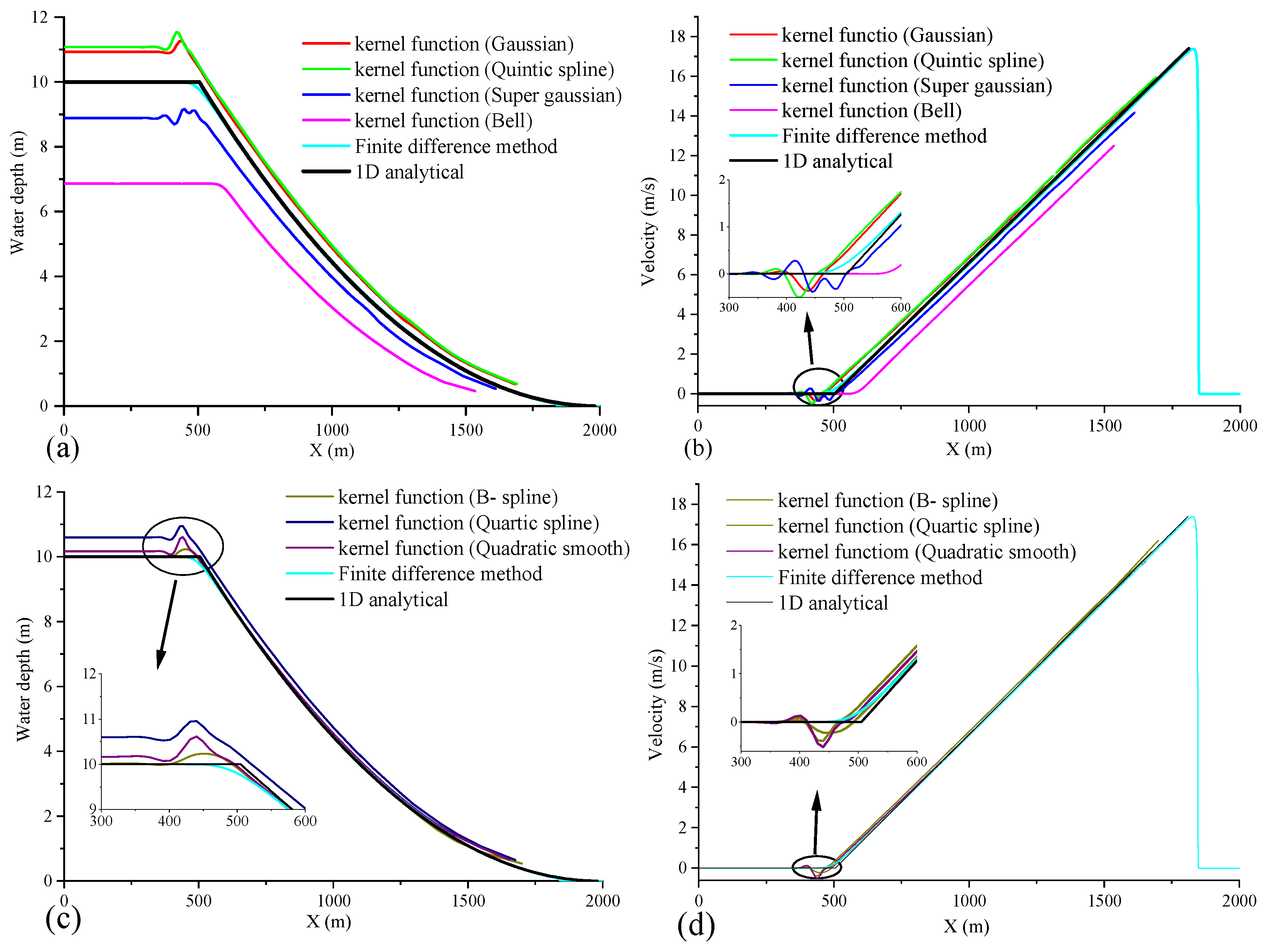
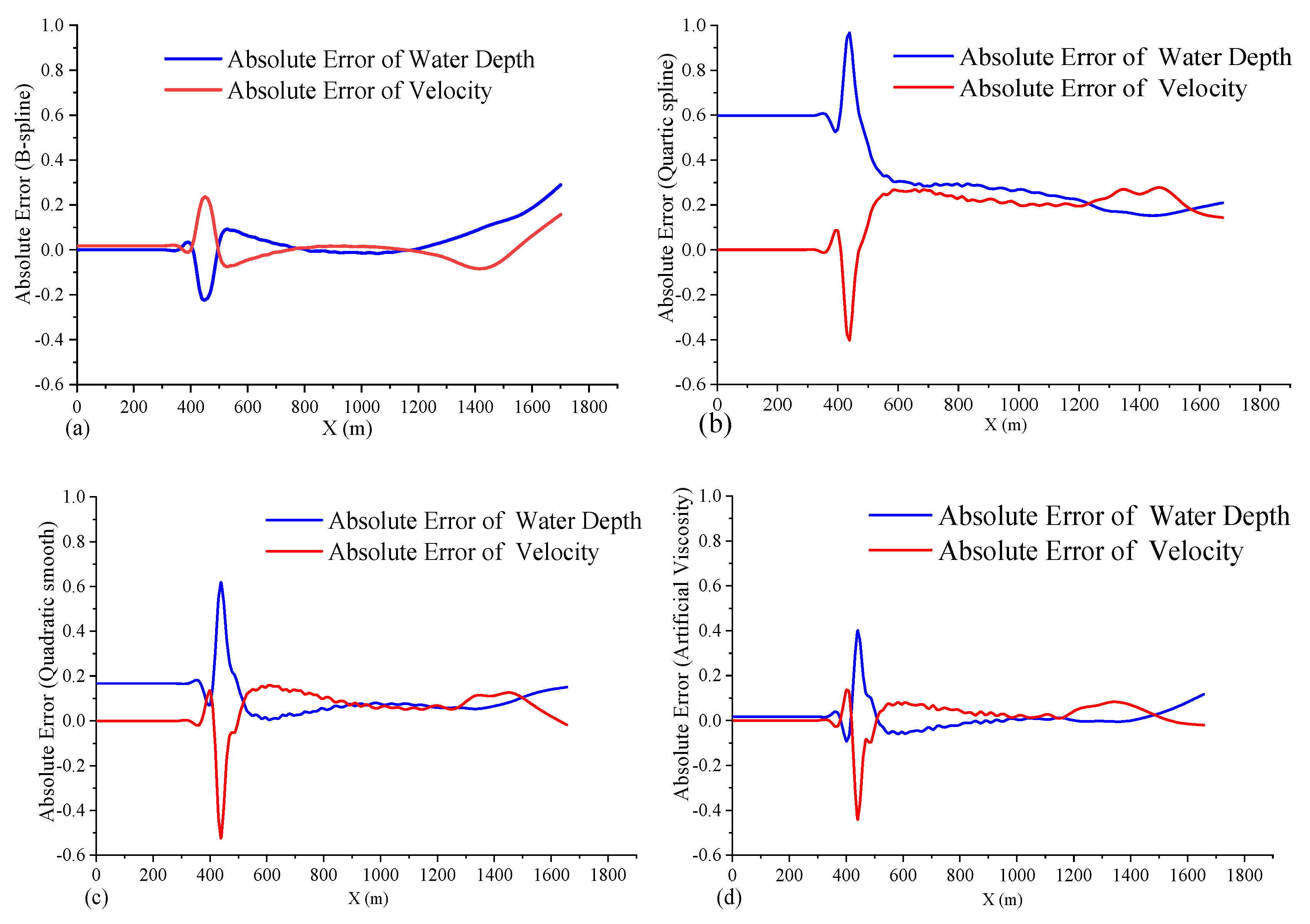
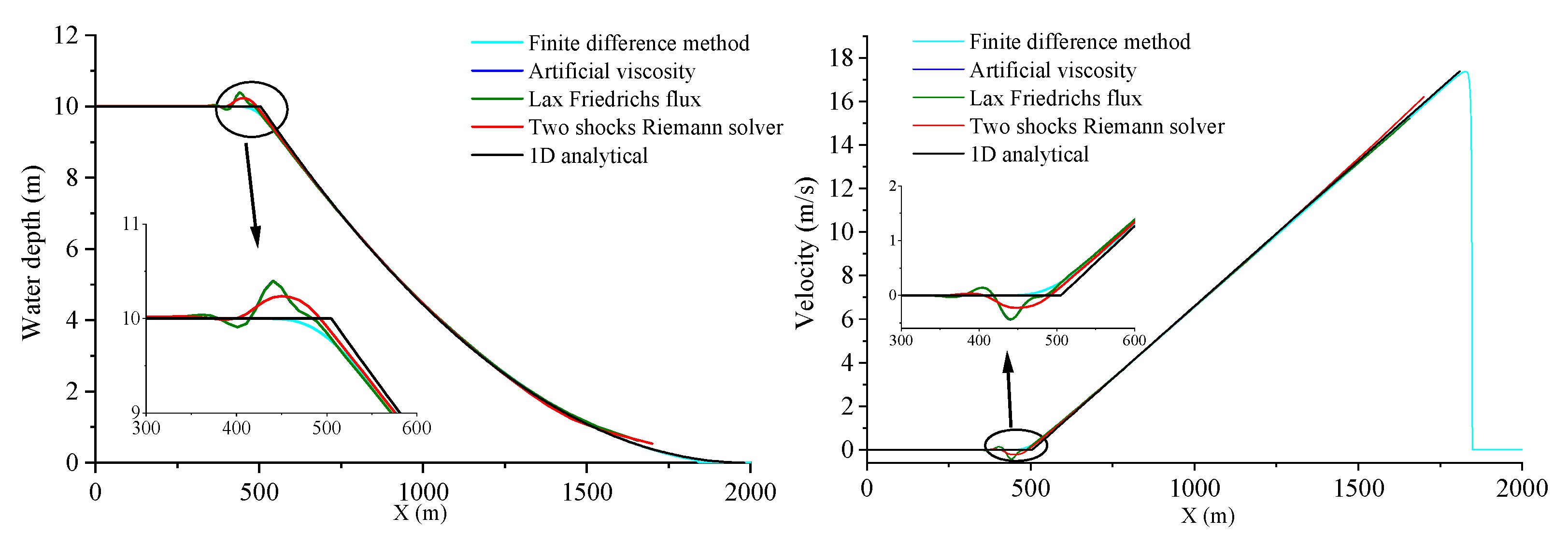

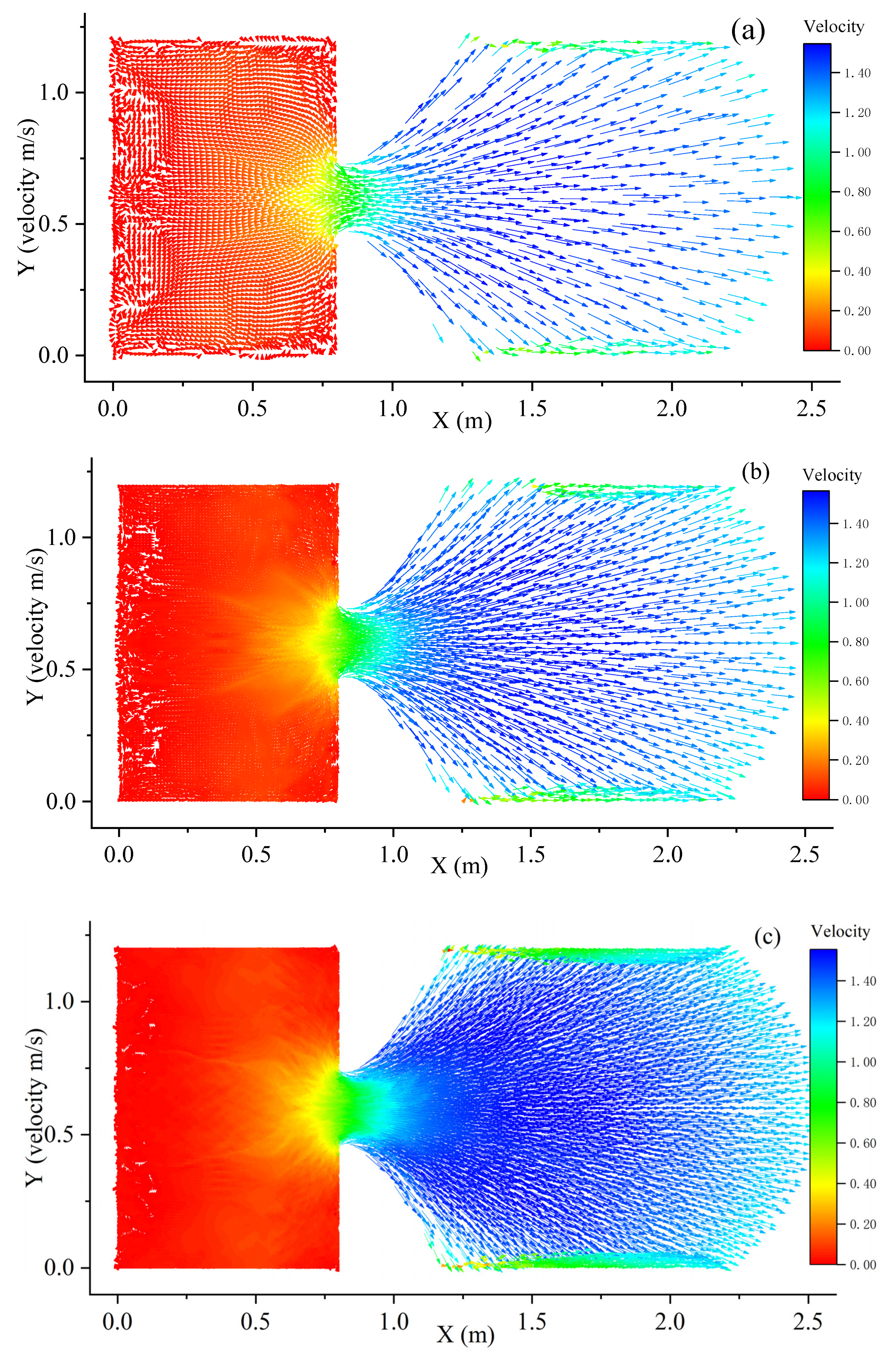
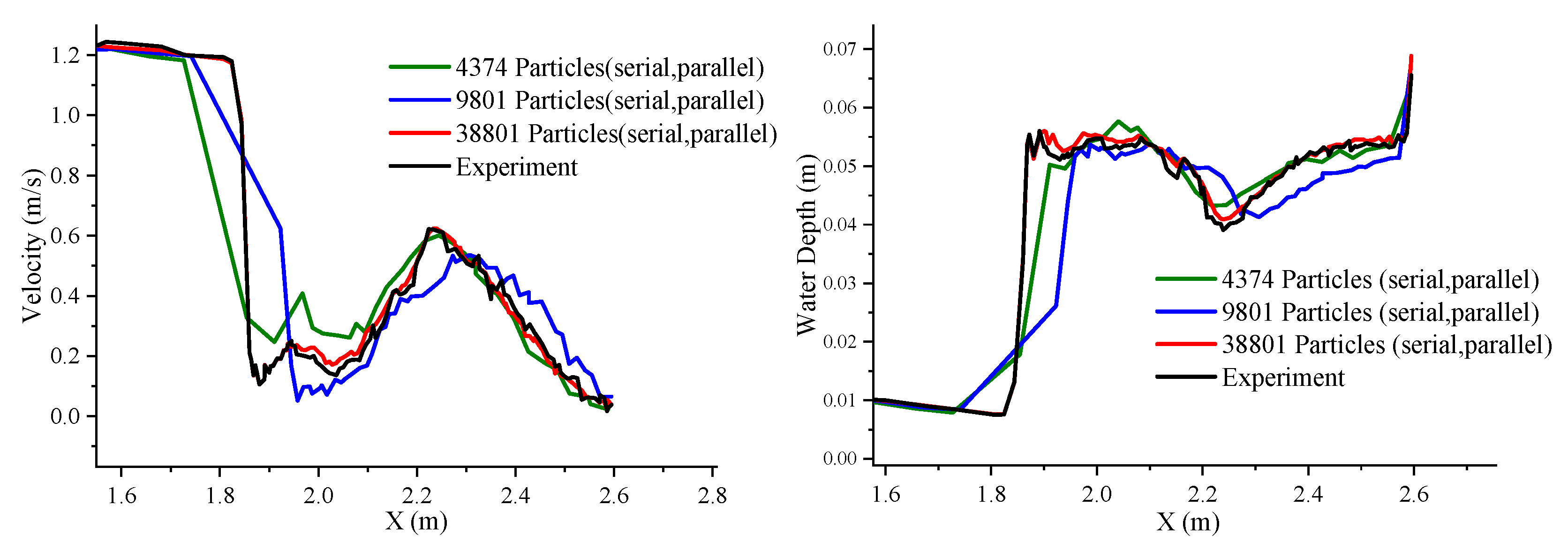
| Parameters | Artificial Viscosity | Lax Friedrichs Flux | Two-Shocks Riemann Solver | |
|---|---|---|---|---|
| Mean Absolute Error | Speed | 0.0617 | 0.0476 | 0.0351 |
| WD | 0.0515 | 0.0482 | 0.0356 | |
| Mean Relative Error | Speed | 0.0718 | 0.0667 | 0.0586 |
| WD | 0.0142 | 0.0089 | 0.0092 | |
| Standard deviation of error | Speed | 0.1042 | 0.0728 | 0.0568 |
| WD | 0.0681 | 0.0633 | 0.0484 |
| Parameters | 30 s | 50 s | |
|---|---|---|---|
| Mean Absolute Error | Speed | 0.0529 | 0.0603 |
| Water Depth | 0.0567 | 0.0613 | |
| Mean Relative Error | Speed | 0.0548 | 0.1037 |
| Water Depth | 0.0075 | 0.0081 | |
| Standard deviation of error | Speed | 0.1543 | 0.1514 |
| Water Depth | 0.1257 | 0.1238 |
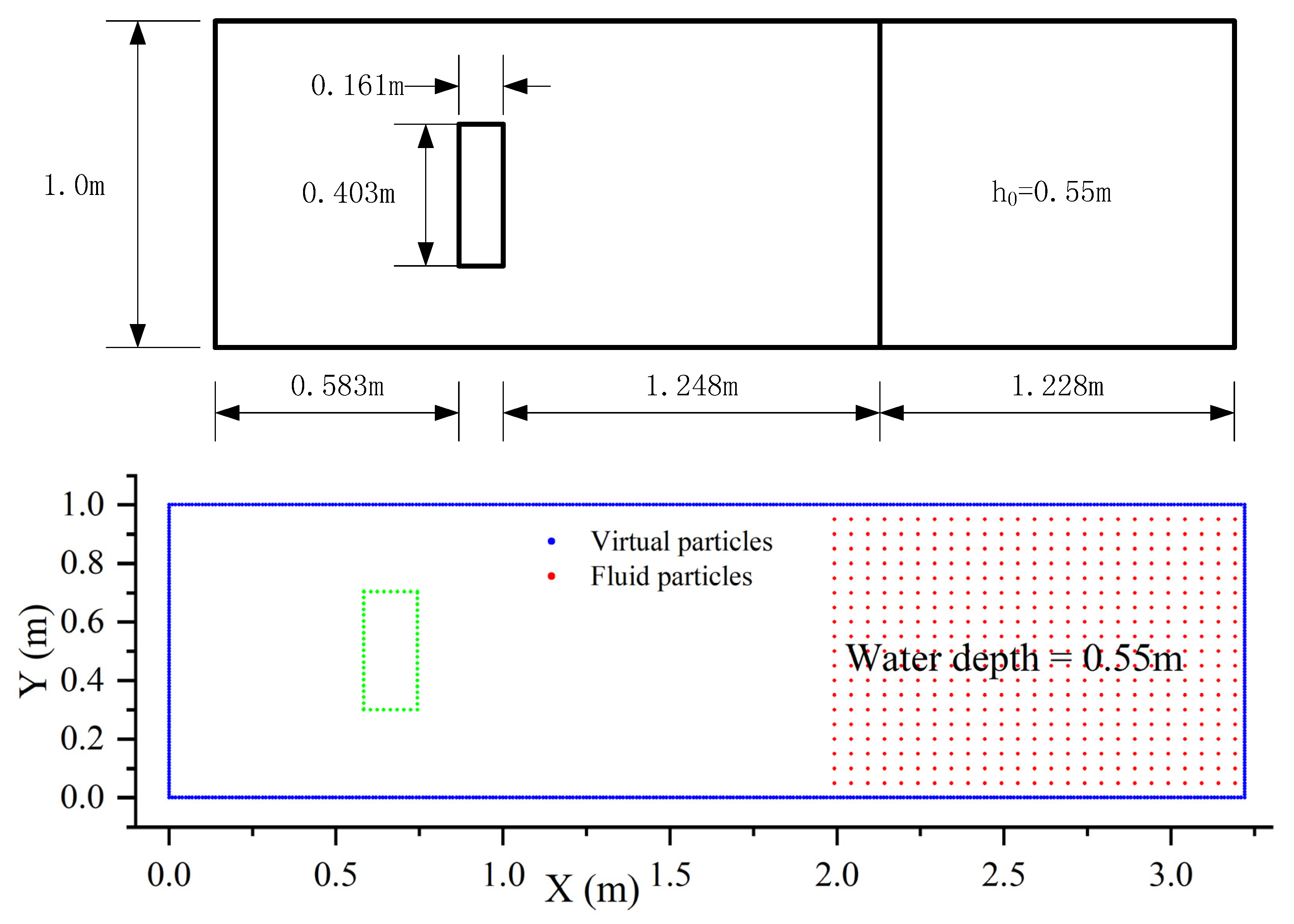
| Case | Number of Fluid Particles | Number of Virtual Particles | Number of Riverbed Particles |
|---|---|---|---|
| Case 1 | 4374 | 1276 | 14,094 |
| Case 2 | 9801 | 3300 | 31,581 |
| Case 3 | 38,801 | 9424 | 125,561 |
| Cases | ||||||
|---|---|---|---|---|---|---|
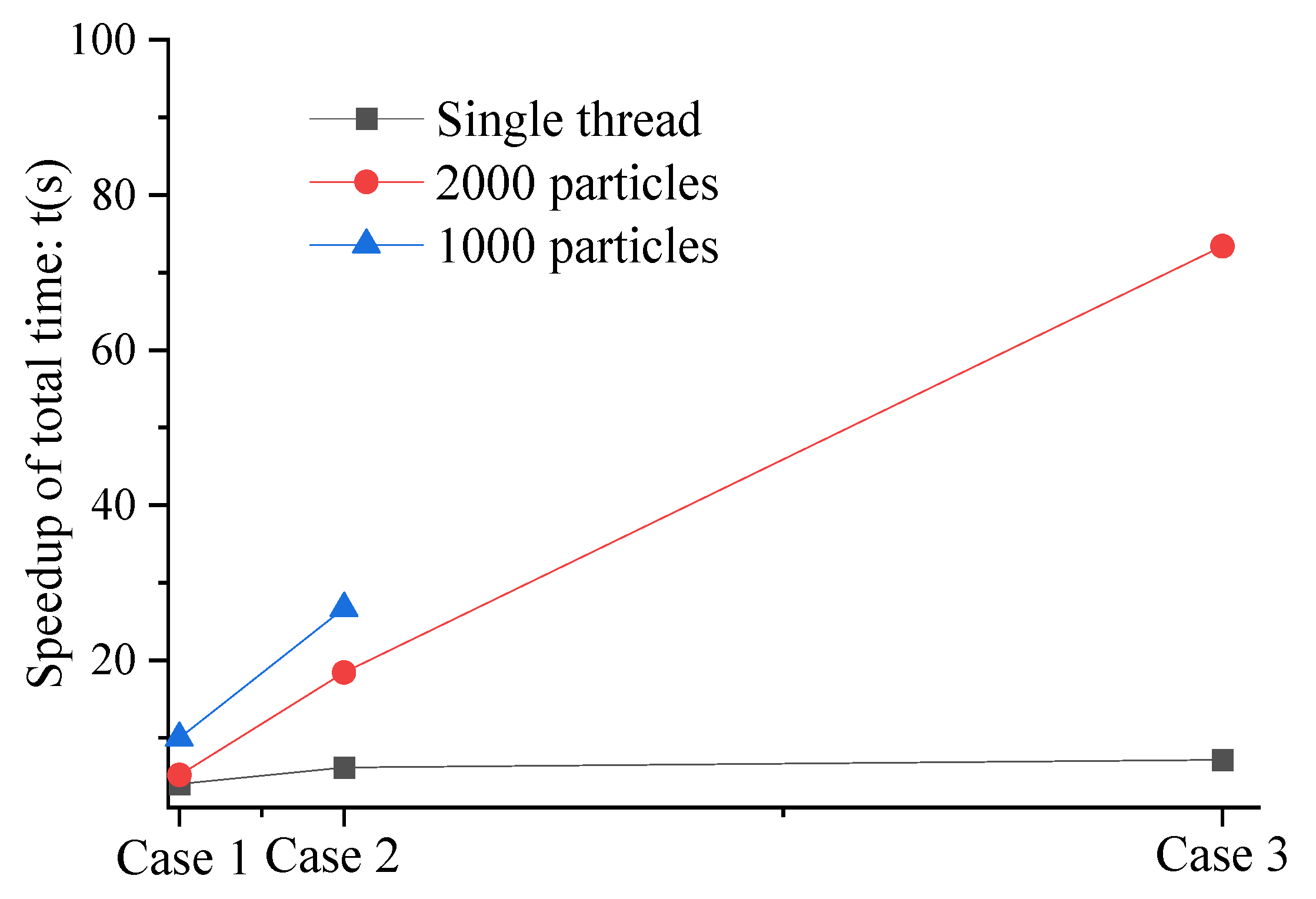
| Open Source Code (Case 1) | N/A | 1040.44 | 213.12 | 1253.56 | 1.0 | |
| Parallel Operation Code | Single Core | 87.47 | 174.95 | 49.99 | 312.41 | 4.01 |
| 2000 | 60.27 | 118.38 | 36.59 | 215.24 | 5.82 | |
| 1000 | 36.43 | 70.34 | 18.84 | 125.61 | 9.98 | |
| Open Source Code (Case 2) | N/A | 5892.29 | 1039.82 | 6932.11 | 1.0 | |
| Parallel Operation Code | Single Core | 338.853 | 643.8207 | 146.8363 | 1129.51 | 6.14 |
| 2000 | 116.8514 | 218.6252 | 41.4634 | 376.94 | 18.39 | |
| 1000 | 75.2985 | 150.597 | 33.7545 | 259.65 | 26.70 | |
| Open Source Code (Case 3) | N/A | 107,218.04 | 16,021.09 | 123,239.13 | 1.0 | |
| Parallel Operation Code | Single Core | 5498.28 | 10,481.09 | 1202.75 | 17,182.12 | 7.17 |
| 2000 | 554.20 | 990.83 | 134.35 | 1679.38 | 73.38 | |
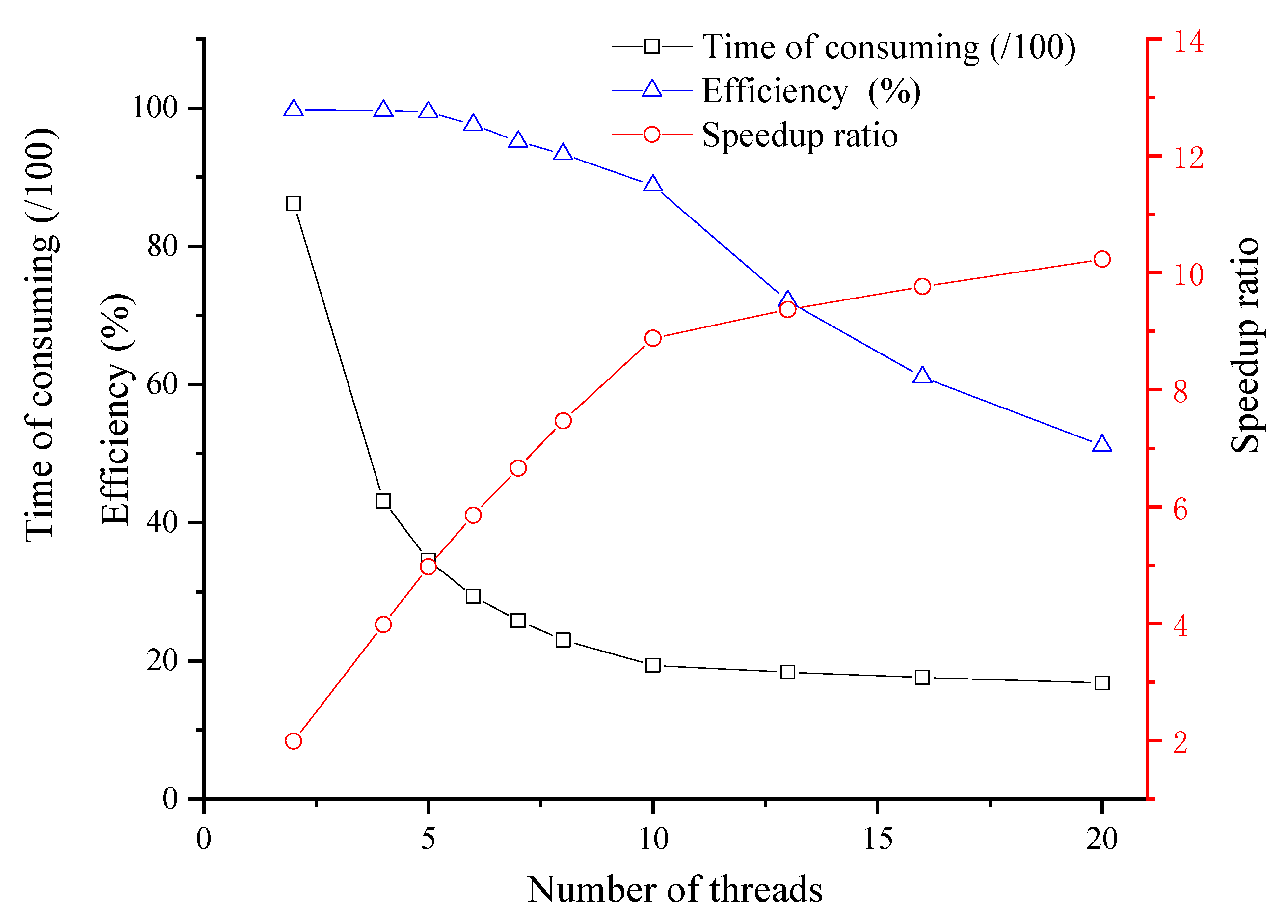
| Number of Single-Thread Particles (pcs) | ||||
|---|---|---|---|---|
| 2000 | 20 | 1679.38 | 10.23 | 51.16 |
| 2500 | 16 | 1759.15 | 9.77 | 61.05 |
| 3000 | 13 | 1833.58 | 9.37 | 72.08 |
| 4000 | 10 | 1935.12 | 8.88 | 88.79 |
| 5000 | 8 | 2300.79 | 7.47 | 93.35 |
| 6000 | 7 | 2579.88 | 6.66 | 95.14 |
| 7000 | 6 | 2934.02 | 5.86 | 97.60 |
| 8000 | 5 | 3455.94 | 4.97 | 99.44 |
| 10,000 | 4 | 4312.39 | 3.98 | 99.61 |
| 20,000 | 2 | 8616.82 | 1.99 | 99.70 |
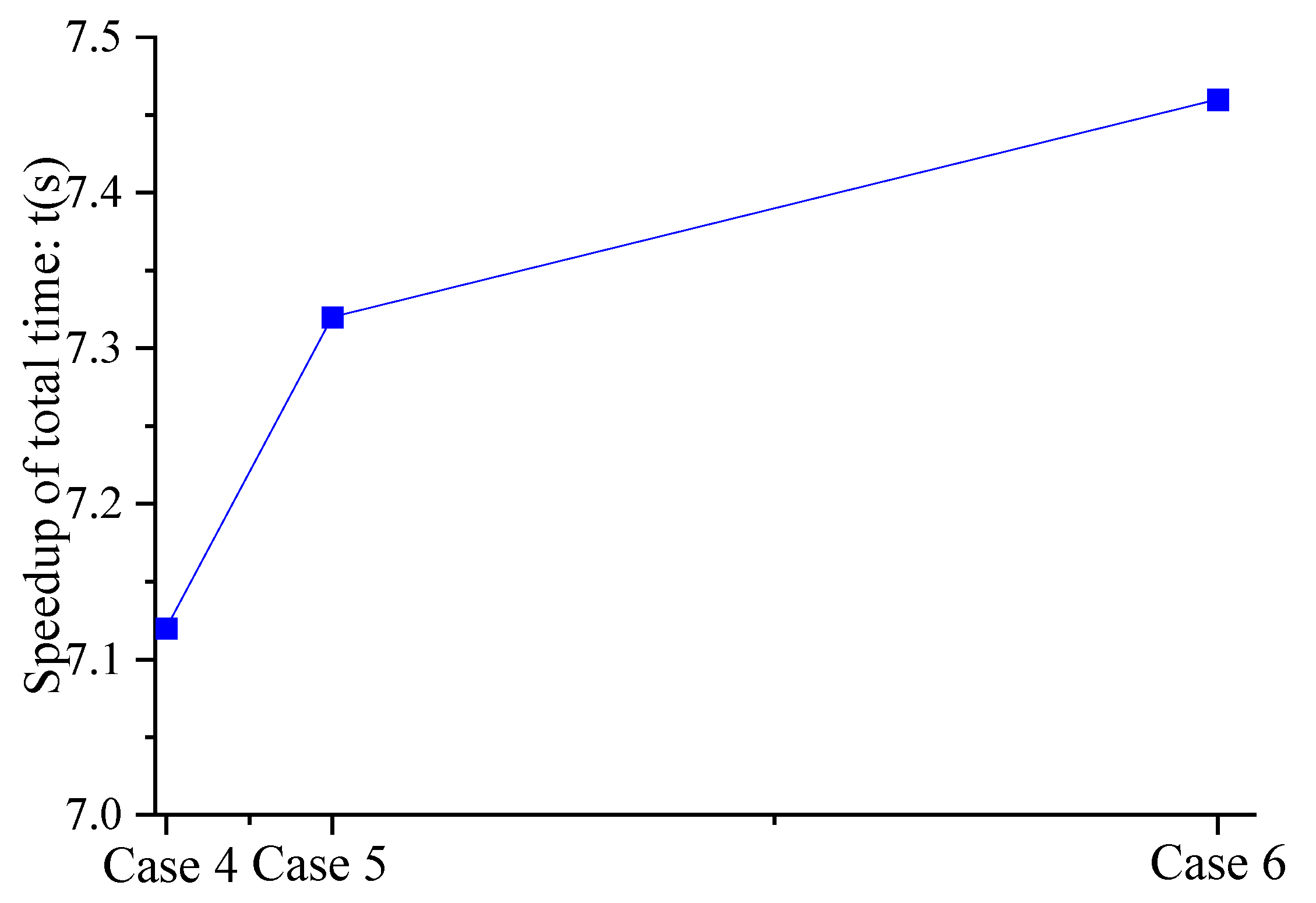
| Case | Particle Spacing | Number of Fluid Particles | Number of Virtual Particles | Number of Riverbed Particles | T8 (s) | T (s) |
|---|---|---|---|---|---|---|
| Case 4 | 0.01 | 12,423 | 4798 | 129,645 | 1511.38 | 7.12 |
| Case 5 | 0.005 | 51,858 | 9582 | 516,889 | 14,538.83 | 7.32 |
| Case 6 | 0.002 | 323,145 | 23,934 | 807,111 | 108,868.42 | 7.46 |
| Cases | R (t) | C (t) | A (t) | T8 (s) | t (s) |
|---|---|---|---|---|---|
| Case 4 | 468.53 | 876.60 | 166.25 | 1511.38 | 7.12 |
| Case 5 | 4216.26 | 8432.52 | 1890.05 | 14,538.83 | 7.32 |
| Case 6 | 34,837.91 | 66,409.72 | 7620.80 | 108,868.42 | 7.46 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Tian, L.; Rubinato, M.; Gu, S.; Yu, T.; Xu, Z.; Cao, P.; Wang, X.; Zhao, Q. A New Parallel Framework of SPH-SWE for Dam Break Simulation Based on OpenMP. Water 2020, 12, 1395. https://doi.org/10.3390/w12051395
Wu Y, Tian L, Rubinato M, Gu S, Yu T, Xu Z, Cao P, Wang X, Zhao Q. A New Parallel Framework of SPH-SWE for Dam Break Simulation Based on OpenMP. Water. 2020; 12(5):1395. https://doi.org/10.3390/w12051395
Chicago/Turabian StyleWu, Yushuai, Lirong Tian, Matteo Rubinato, Shenglong Gu, Teng Yu, Zhongliang Xu, Peng Cao, Xuhao Wang, and Qinxia Zhao. 2020. "A New Parallel Framework of SPH-SWE for Dam Break Simulation Based on OpenMP" Water 12, no. 5: 1395. https://doi.org/10.3390/w12051395
APA StyleWu, Y., Tian, L., Rubinato, M., Gu, S., Yu, T., Xu, Z., Cao, P., Wang, X., & Zhao, Q. (2020). A New Parallel Framework of SPH-SWE for Dam Break Simulation Based on OpenMP. Water, 12(5), 1395. https://doi.org/10.3390/w12051395






