Exploring Spatiotemporal Relations between Soil Moisture, Precipitation, and Streamflow for a Large Set of Watersheds Using Google Earth Engine
Abstract
:1. Introduction
2. Materials and Methods
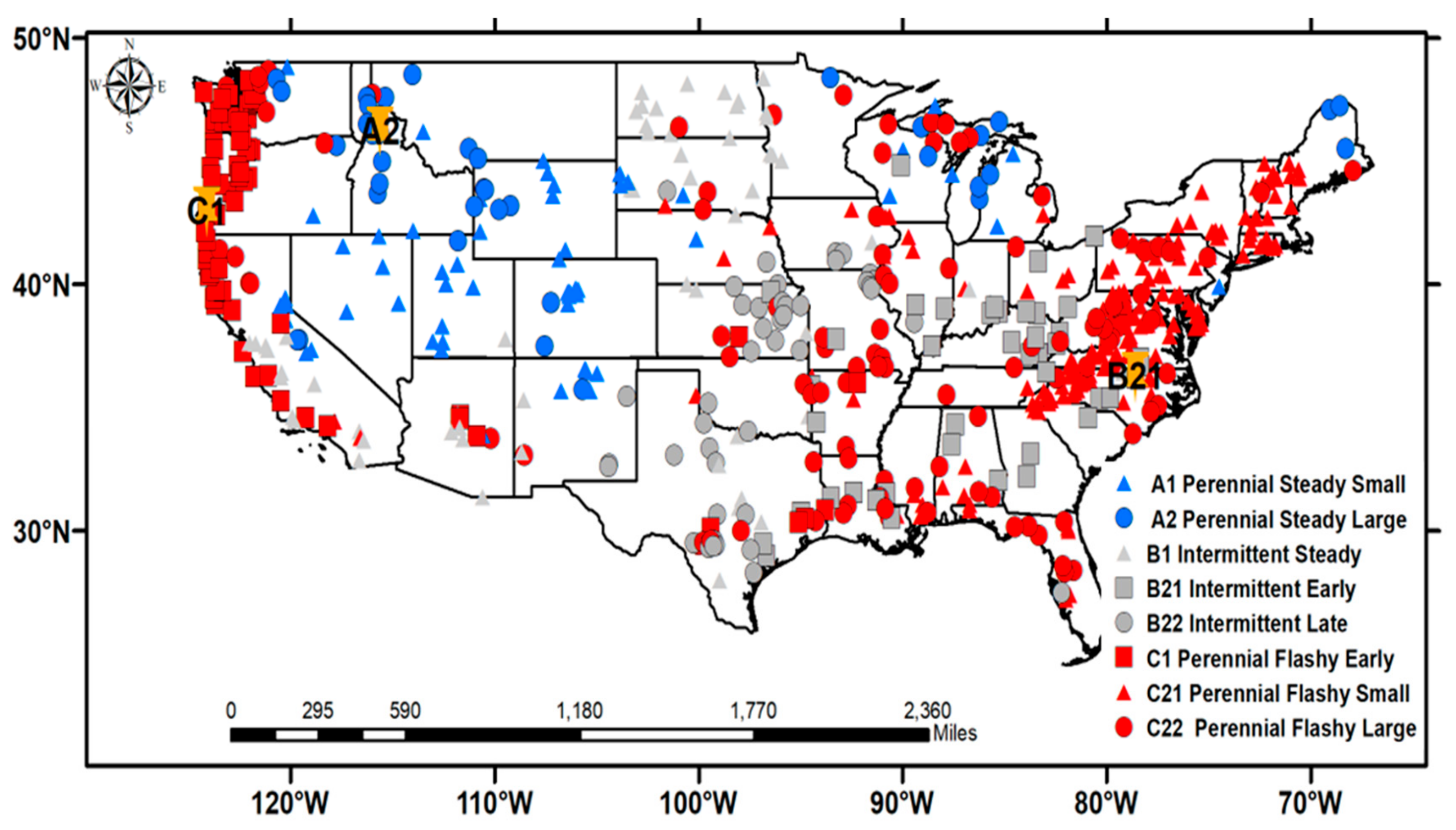
2.1. Study Area and Data Used
2.2. Data Processing
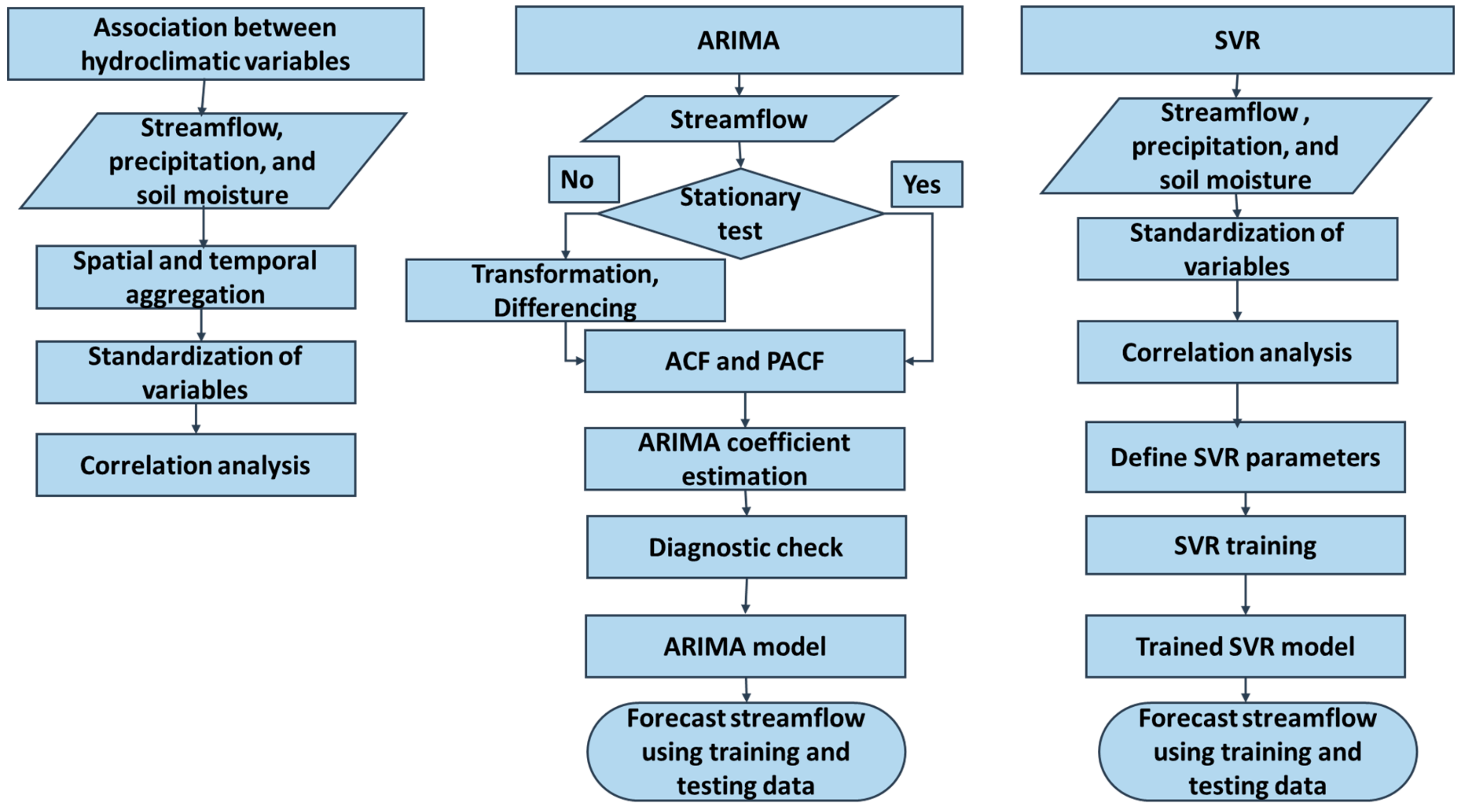
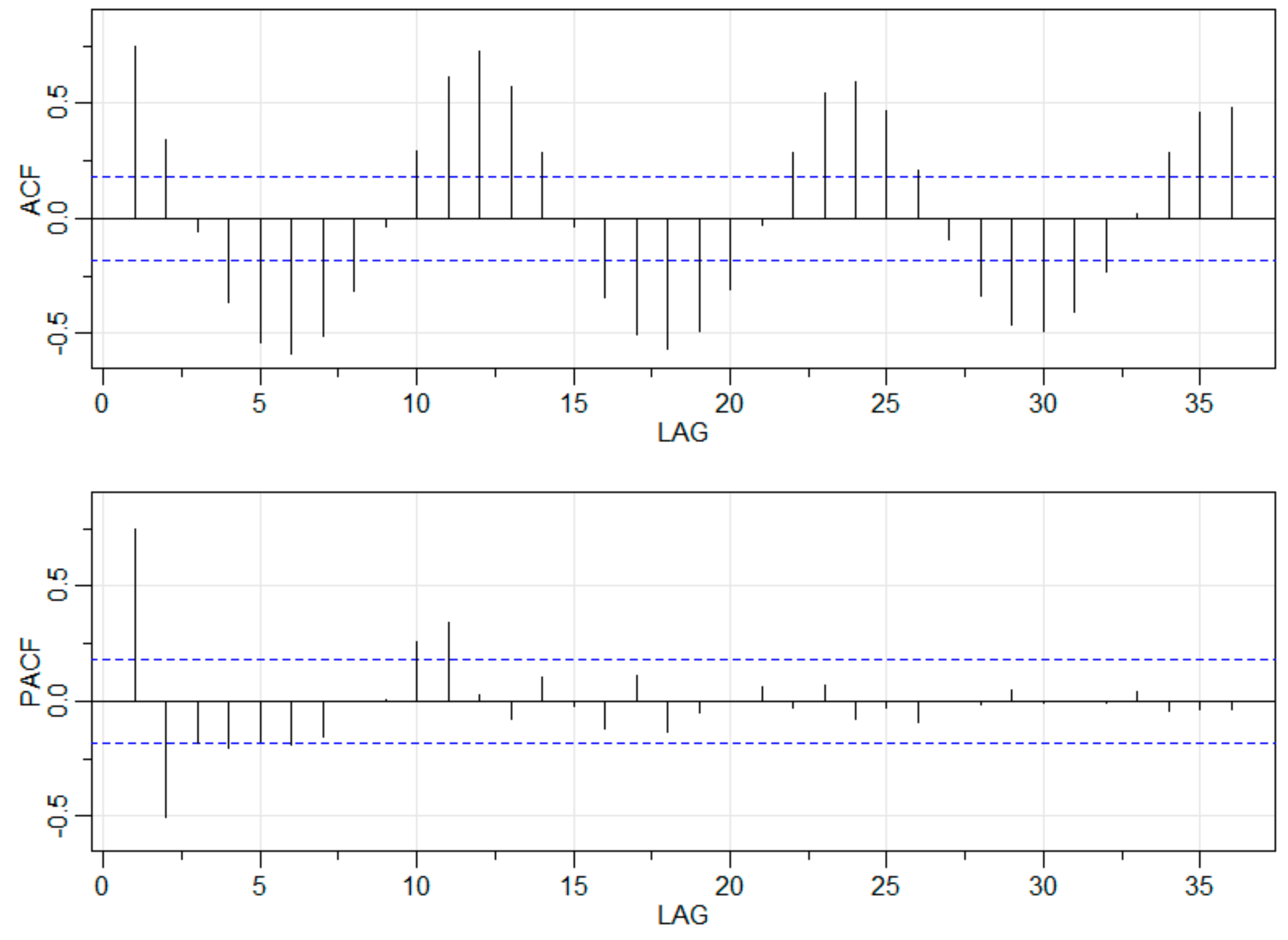
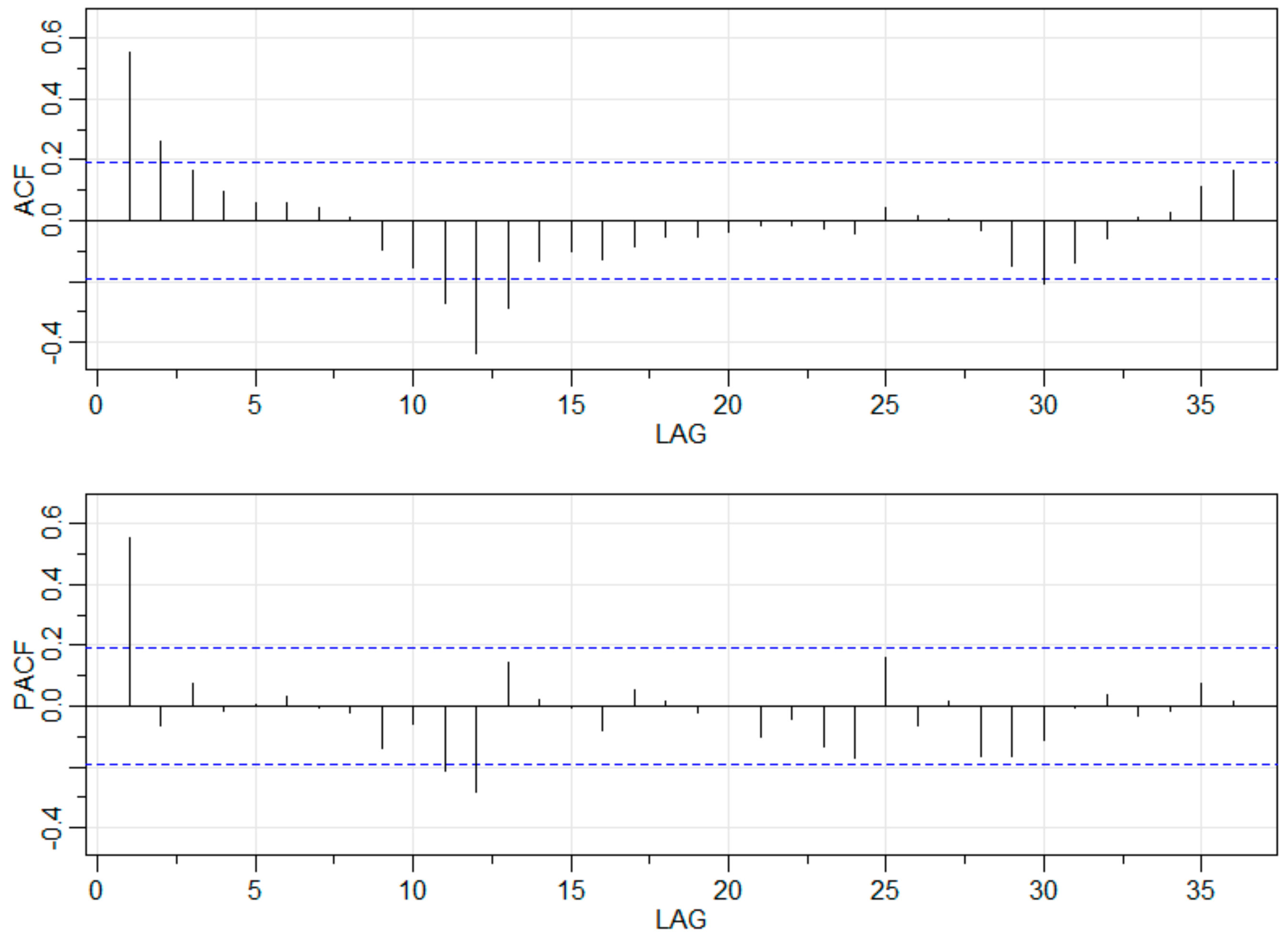
2.3. Development of ARIMA Model
2.4. Development of SVR Model
3. Results
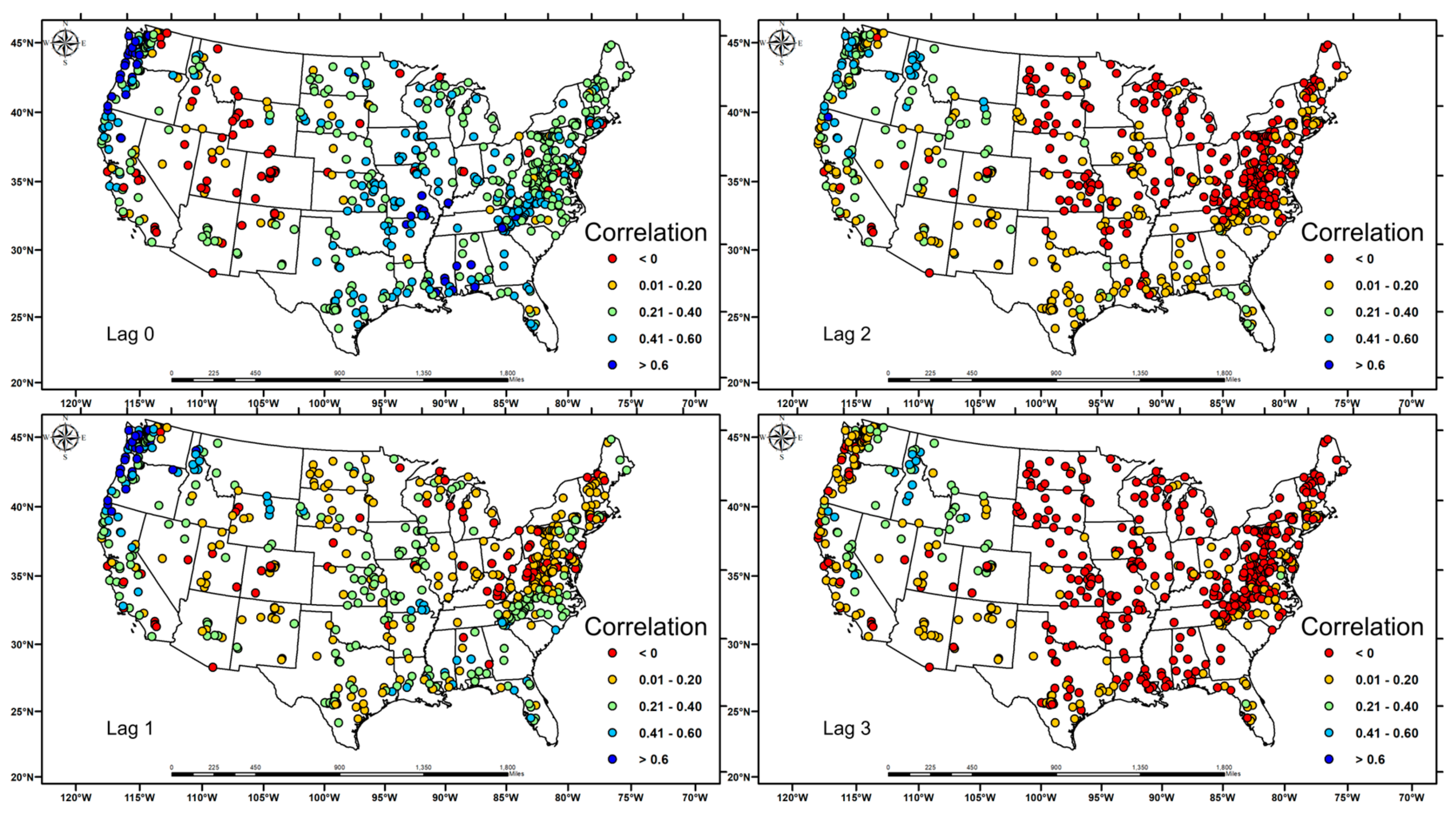
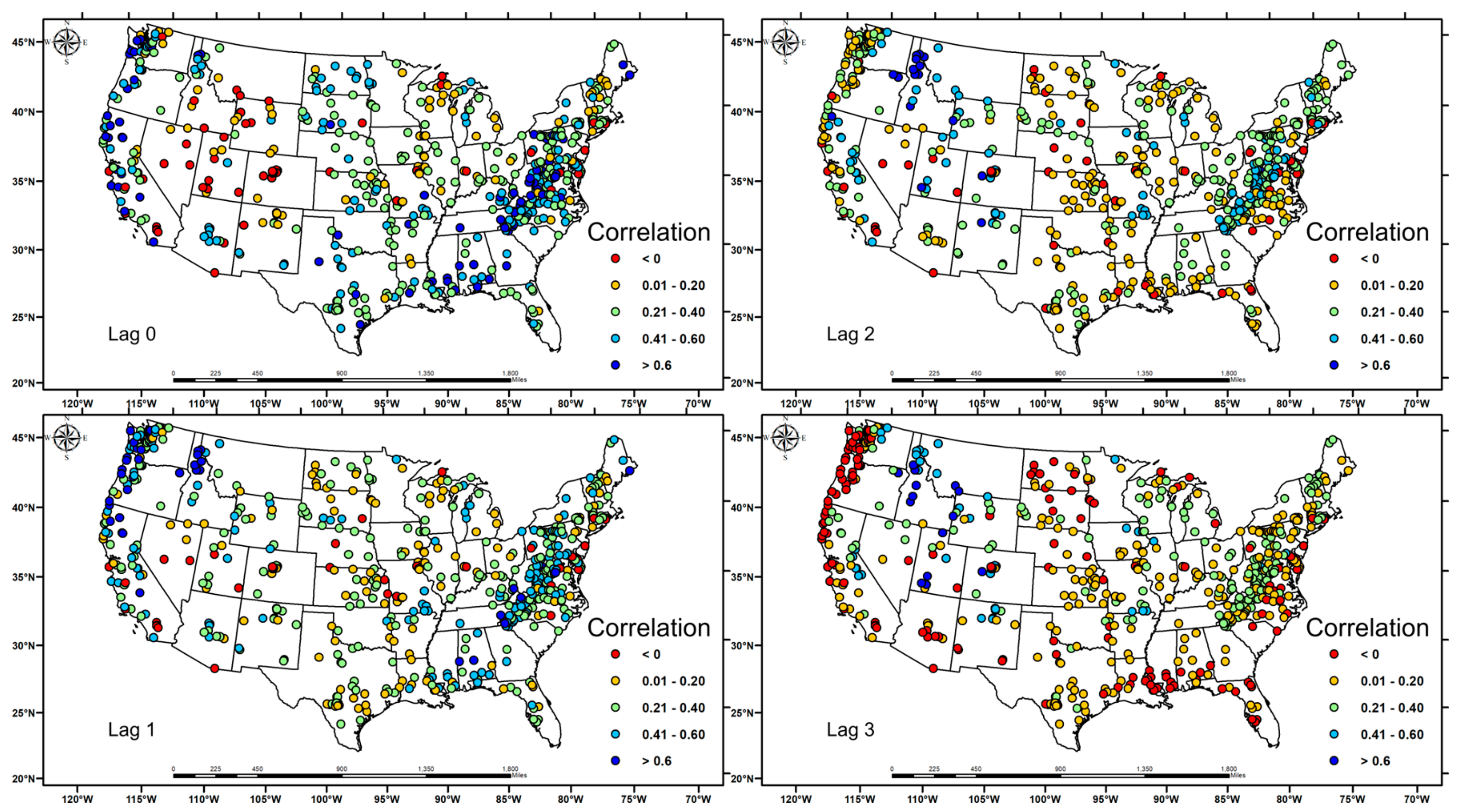
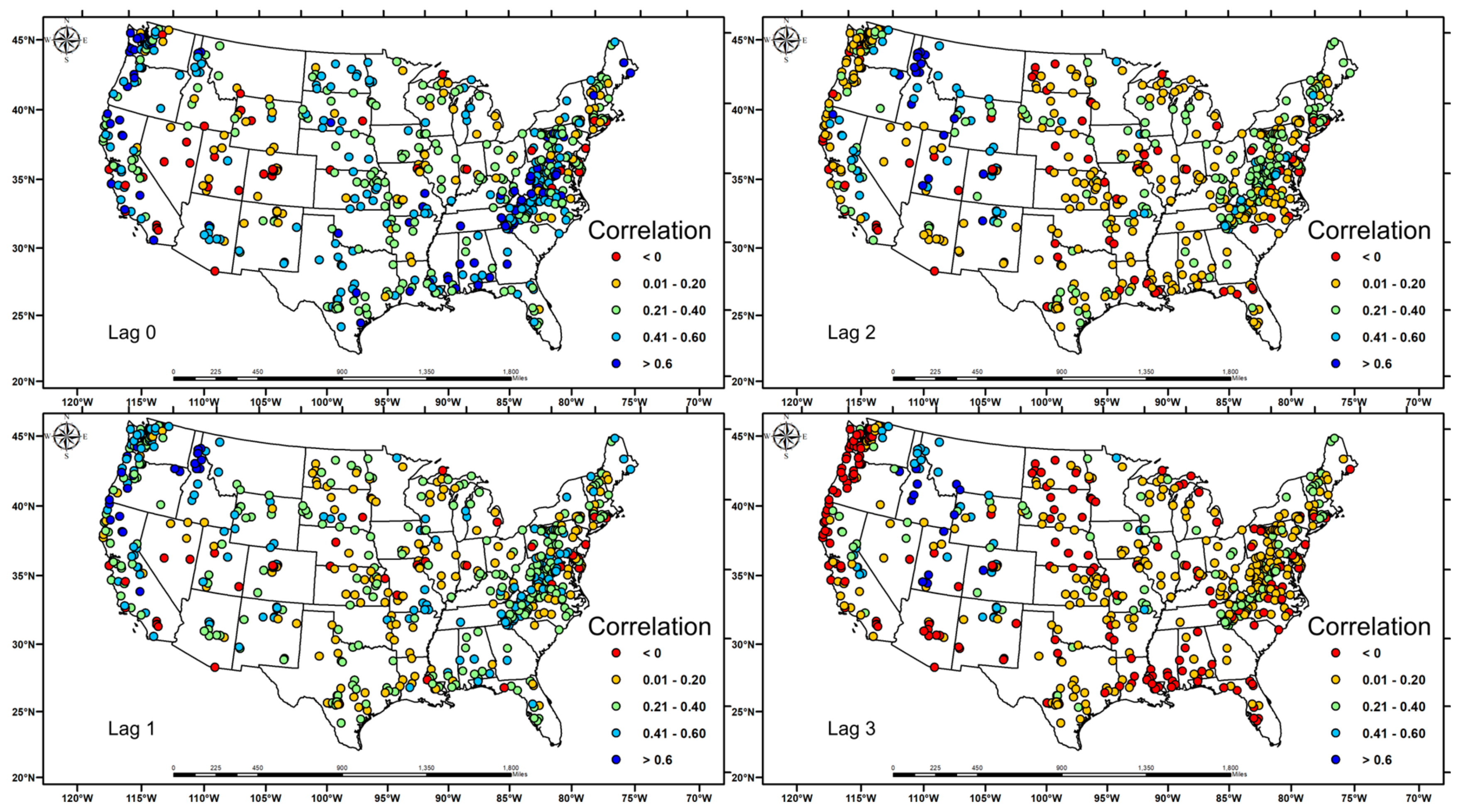
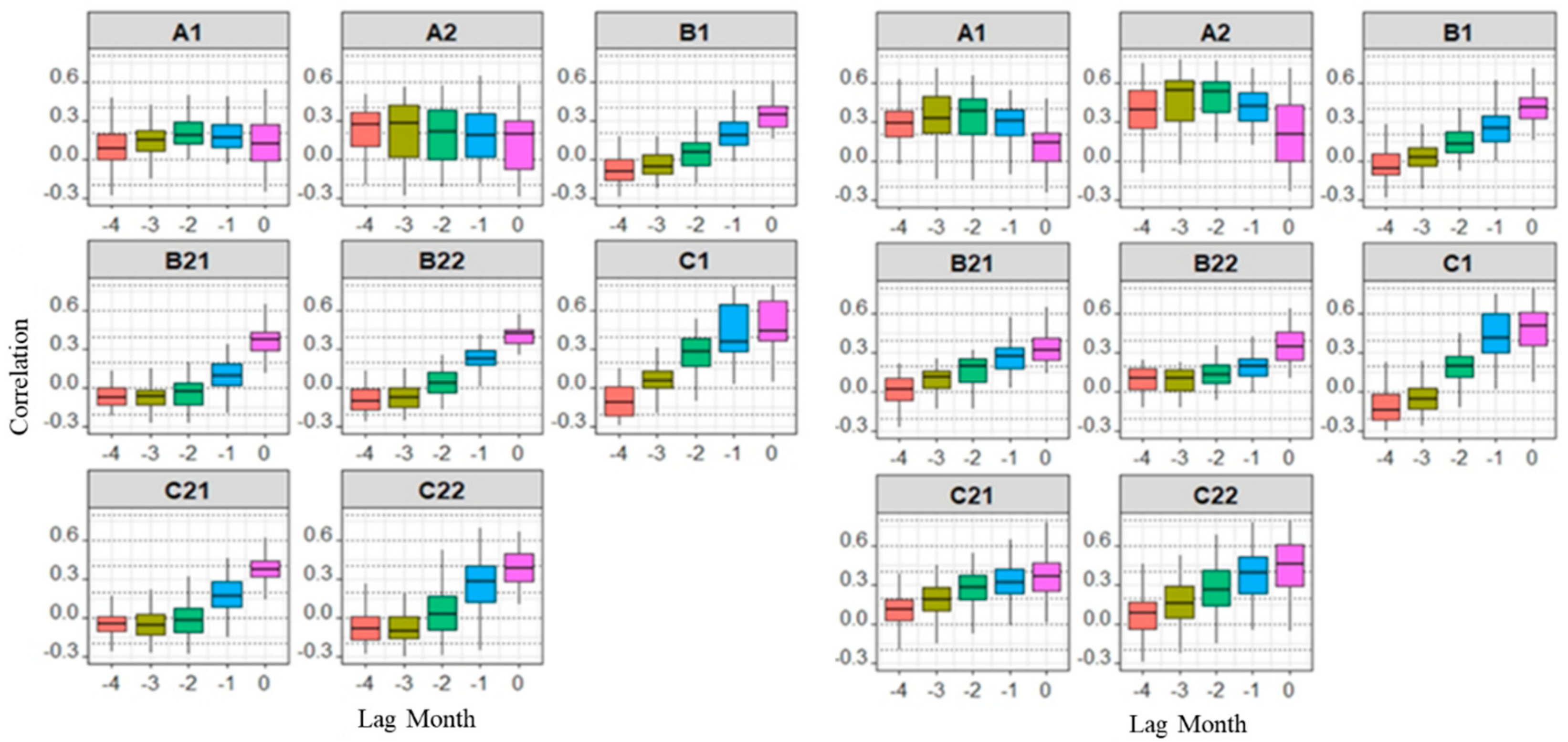
3.1. Relationship between Soil Moisture, Precipitation and Streamflow
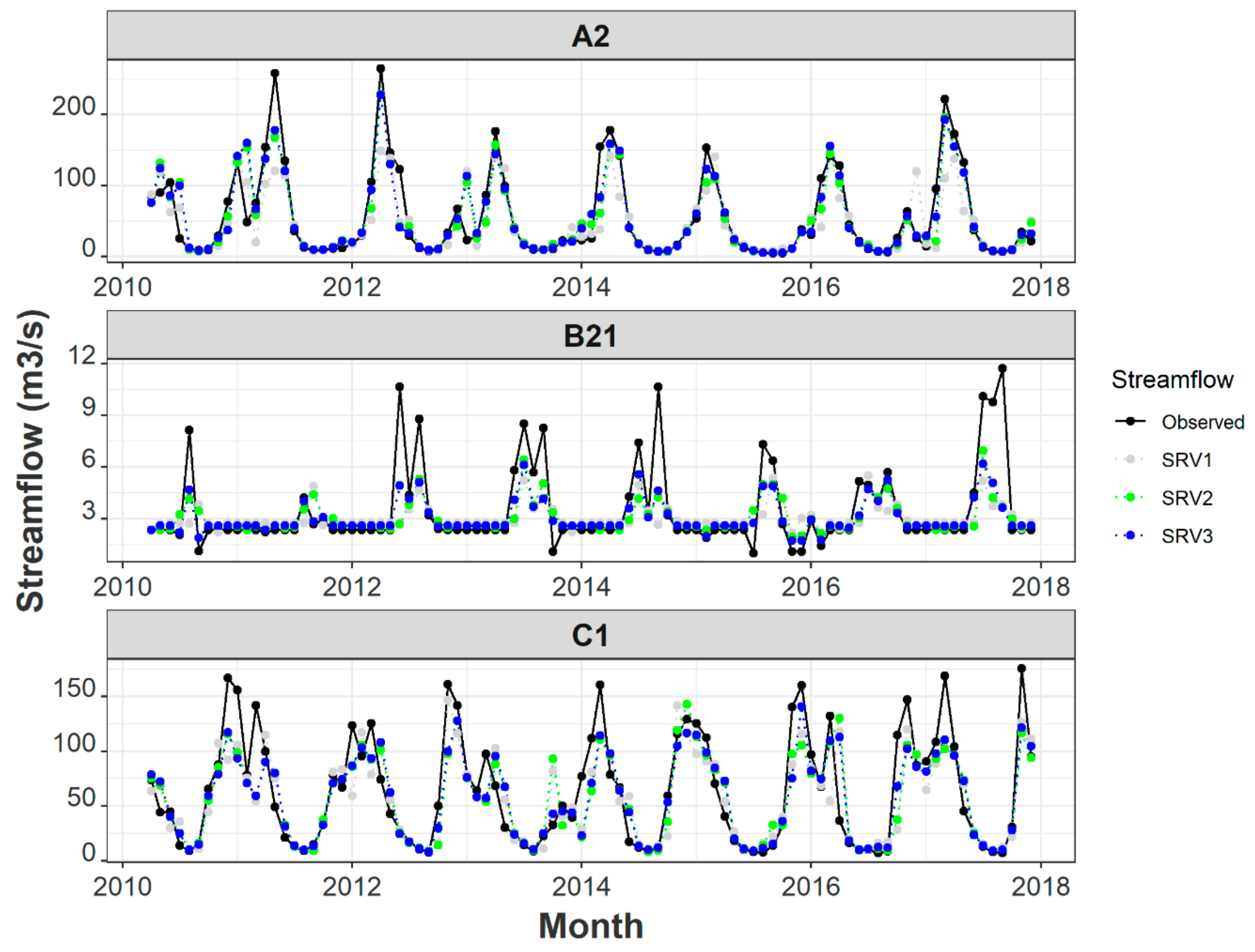
3.2. Streamflow Forecasting
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Lakshmi, V.; Piechota, T.; Narayan, U.; Tang, C. Soil moisture as an indicator of weather extremes. Geophys. Res. Lett. 2004, 31, L11401. [Google Scholar] [CrossRef] [Green Version]
- Meng, L.; Shen, Y. On the Relationship of Soil Moisture and Extreme Temperatures in East China. Earth Interact. 2013, 18, 1–20. [Google Scholar] [CrossRef]
- Nalley, D.; Adamowski, J.; Khalil, B. Using discrete wavelet transforms to analyze trends in streamflow and precipitation in quebec and ontario (1954–2008). J. Hydrol. 2012, 475, 204–228. [Google Scholar] [CrossRef]
- Burn, D.H.; Sharif, M.; Zhang, K. Detection of trends in hydrological extremes for Canadian watersheds. Hydrol. Process. 2010, 24, 1781–1790. [Google Scholar] [CrossRef]
- Zhao, F.; Xu, Z.; Zhang, L.; Zuo, D. Streamflow response to climate variability and human activities in the upper catchment of the yellow river basin. Sci. China Ser. E Technol. Sci. 2009, 52, 3249. [Google Scholar] [CrossRef]
- Hodgkins, G.A.; Dudley, R.W. Historical summer base flow and stormflow trends for New England rivers. Water Resour. Res. 2011, 47, W07528. [Google Scholar] [CrossRef]
- Maurer, E.P.; Lettenmaier, D.P. Predictability of seasonal runoff in the mississippi river basin. J. Geophys. Res. Atmos. 2003, 108, D16. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Shang, S.; Jia, D.; Han, Y.; Sauvage, S.; Sánchez-Pérez, J.-M.; Kuramochi, K.; Hatano, R. Integrated effects of land use and topography on streamflow response to precipitation in an agriculture-forest dominated northern watershed. Water 2018, 10, 633. [Google Scholar] [CrossRef] [Green Version]
- Arenas, A.; Schilling, K.; Niemeier, J.; Weber, L. Evaluating the timing and interdependence of hydrologic processes at the watershed scale based on continuously monitored data. Water 2018, 10, 261. [Google Scholar] [CrossRef] [Green Version]
- Najafi, E.; Devineni, N.; Khanbilvardi, R.M.; Kogan, F. Understanding the Changes in Global Crop Yields through Changes in Climate and Technology. Earth Future 2018, 6, 410–427. [Google Scholar] [CrossRef]
- Mazrooei, A.; Sankarasubramanian, A. Improving monthly streamflow forecasts through assimilation of observed streamflow for rainfall-dominated basins across the CONUS. J. Hydrol. 2019, 575, 704–715. [Google Scholar] [CrossRef]
- Tiwari, M.K.; Chatterjee, C. Development of an accurate and reliable hourly flood forecasting model using wavelet–bootstrap–ANN (WBANN) hybrid approach. J. Hydrol. 2010, 394, 458–470. [Google Scholar] [CrossRef]
- Moeeni, H.; Bonakdari, H. Forecasting monthly inflow with extreme seasonal variation using the hybrid SARIMA-ANN model. Stoch. Environ. Res. Risk Assess. 2017, 31, 1997–2010. [Google Scholar] [CrossRef]
- Moeeni, H.; Bonakdari, H. Impact of Normalization and Input on ARMAX-ANN Model Performance in Suspended Sediment Load Prediction. Water Resour. Manag. 2018, 32, 845–863. [Google Scholar] [CrossRef]
- Liu, S.; Xu, J.; Zhao, J.; Xie, X.; Zhang, W. An innovative method for dynamic update of initial water table in XXT model based on neural network technique. Appl. Soft Comput. 2013, 13, 4185–4193. [Google Scholar] [CrossRef]
- Block, P.J.; Souza Filho, F.A.; Sun, L.; Kwon, H.-H. A Streamflow Forecasting Framework using Multiple Climate and Hydrological Models1. JAWRA J. Am. Water Resour. Assoc. 2009, 45, 828–843. [Google Scholar] [CrossRef]
- Karran, D.J.; Morin, E.; Adamowski, J. Multi-step streamflow forecasting using data-driven non-linear methods in contrasting climate regimes. J. Hydroinformatics 2014, 16, 671–689. [Google Scholar] [CrossRef] [Green Version]
- Moradkhani, H.; Hsu, K.; Gupta, H.V.; Sorooshian, S. Improved streamflow forecasting using self-organizing radial basis function artificial neural networks. J. Hydrol. 2004, 295, 246–262. [Google Scholar] [CrossRef] [Green Version]
- Katimon, A.; Shahid, S.; Mohsenipour, M. Modeling water quality and hydrological variables using ARIMA: A case study of Johor River, Malaysia. Sustain. Water Resour. Manag. 2018, 4, 991–998. [Google Scholar] [CrossRef]
- Moeeni, H.; Bonakdari, H.; Fatemi, S.E. Stochastic model stationarization by eliminating the periodic term and its effect on time series prediction. J. Hydrol. 2017, 547, 348–364. [Google Scholar] [CrossRef]
- Bhuiyan, M.A.E.; Nikolopoulos, E.I.; Anagnostou, E.N.; Quintana-Seguí, P.; Barella-Ortiz, A. A nonparametric statistical technique for combining global precipitation datasets: Development and hydrological evaluation over the Iberian Peninsula. Hydrol. Earth Syst. Sci. 2018, 22, 1371. [Google Scholar] [CrossRef] [Green Version]
- Bhuiyan, M.A.E.; Anagnostou, E.N.; Kirstetter, P. A Nonparametric Statistical Technique for Modeling Overland TMI (2A12) Rainfall Retrieval Error. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1898–1902. [Google Scholar] [CrossRef]
- Rahaman, M.M.; Thakur, B.; Kalra, A.; Ahmad, S. Modeling of GRACE-Derived Groundwater Information in the Colorado River Basin. Hydrology 2019, 6, 19. [Google Scholar] [CrossRef] [Green Version]
- Valipour, M. Long-term runoff study using SARIMA and ARIMA models in the United States. Meteorol. Appl. 2015, 22, 592–598. [Google Scholar] [CrossRef]
- Gharde, K.D.; Kothari, M.; Mahale, D.M. Developed seasonal ARIMA model to forecast streamflow for Savitri basin in Konkan Region of Maharshtra on daily basis. J. Indian Soc. Coastal Agric. Res. 2016, 34, 110–119. [Google Scholar]
- Haltiner, J.P.; Salas, J.D. SHORT-TERM FORECASTING OF SNOWMELT RUNOFF USING ARMAX MODELS1. JAWRA J. Am. Water Resour. Assoc. 1988, 24, 1083–1089. [Google Scholar] [CrossRef]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Abudu, S.; Cui, C.; King, J.P.; Abudukadeer, K. Comparison of performance of statistical models in forecasting monthly streamflow of Kizil River, China. Water Sci. Eng. 2010, 3, 269–281. [Google Scholar] [CrossRef]
- Kalteh, A.M. Monthly river flow forecasting using artificial neural network and support vector regression models coupled with wavelet transform. Comput. Geosci. 2013, 54, 1–8. [Google Scholar] [CrossRef]
- Zealand, C.M.; Burn, D.H.; Simonovic, S.P. Short term streamflow forecasting using artificial neural networks. J. Hydrol. 1999, 214, 32–48. [Google Scholar] [CrossRef] [Green Version]
- Dibike, Y.B.; Solomatine, D.P. River flow forecasting using artificial neural networks. Phys. Chem. Earth Part B Hydrol. Ocean. Atmos. 2001, 26, 1–7. [Google Scholar] [CrossRef]
- Zhang, B.; Govindaraju, R.S. Prediction of watershed runoff using Bayesian concepts and modular neural networks. Water Resour. Res. 2000, 36, 753–762. [Google Scholar] [CrossRef]
- Demirel, M.C.; Venancio, A.; Kahya, E. Flow forecast by SWAT model and ANN in Pracana basin, Portugal. Adv. Eng. Softw. 2009, 40, 467–473. [Google Scholar] [CrossRef]
- Kalra, A.; Ahmad, S. Using oceanic-atmospheric oscillations for long lead time streamflow forecasting. Water Resour. Res. 2009, 45, W03413. [Google Scholar] [CrossRef]
- Yu, P.-S.; Chen, S.-T.; Chang, I.-F. Support vector regression for real-time flood stage forecasting. J. Hydrol. 2006, 328, 704–716. [Google Scholar] [CrossRef]
- Kisi, O. Streamflow forecasting and estimation using least square support vector regression and adaptive neuro-fuzzy embedded fuzzy c-means clustering. Water Resour. Manag. 2015, 29, 5109–5127. [Google Scholar] [CrossRef]
- Jajarmizadeh, M.; Kakaei Lafdani, E.; Harun, S.; Ahmadi, A. Application of SVM and SWAT models for monthly streamflow prediction, a case study in South of Iran. KSCE J. Civ. Eng. 2015, 19, 345–357. [Google Scholar] [CrossRef]
- Anctil, F.; Michel, C.; Perrin, C.; Andréassian, V. A soil moisture index as an auxiliary ANN input for stream flow forecasting. J. Hydrol. 2004, 286, 155–167. [Google Scholar] [CrossRef]
- Oubeidillah, A.; Tootle, G.; Piechota, T. Incorporating Antecedent Soil Moisture into Streamflow Forecasting. Hydrology 2019, 6, 50. [Google Scholar] [CrossRef] [Green Version]
- Dhungel, S.; Tarboton, D.G.; Jin, J.; Hawkins, C.P. Potential effects of climate change on ecologically relevant streamflow regimes. River Res. Appl. 2016, 32, 1827–1840. [Google Scholar] [CrossRef] [Green Version]
- Falcone, J.A.; Carlisle, D.M.; Weber, L.C. Quantifying human disturbance in watersheds: Variable selection and performance of a GIS-based disturbance index for predicting the biological condition of perennial streams. Ecol. Indic. 2010, 10, 264–273. [Google Scholar] [CrossRef]
- Daly, C.; Halbleib, M.; Smith, J.I.; Gibson, W.P.; Doggett, M.K.; Taylor, G.H.; Curtis, J.; Pasteris, P.P. Physiographically sensitive mapping of climatological temperature and precipitation across the conterminous united states. Int. J. Climatol. 2008, 28, 2031–2064. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google earth engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Sazib, N.; Mladenova, I.; Bolten, J. Leveraging the Google Earth Engine for Drought Assessment Using Global Soil Moisture Data. Remote Sens. 2018, 10, 1265. [Google Scholar] [CrossRef] [Green Version]
- Bolten, J.D.; Crow, W.T.; Zhan, X.; Jackson, T.J.; Reynolds, C.A. Evaluating the utility of remotely sensed soil moisture retrievals for operational agricultural drought monitoring. Selected Topics in Applied Earth Observations and Remote Sensing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 57–66. [Google Scholar] [CrossRef] [Green Version]
- Bolten, J.D.; Crow, W.T. Improved prediction of quasi-global vegetation conditions using remotely-sensed surface soil moisture. Geophys. Res. Lett. 2012, 39, 19406. [Google Scholar] [CrossRef] [Green Version]
- Mladenova, I.E.; Bolten, J.D.; Crow, W.T.; Sazibm, N.; Cosh, M.H.; Tucker, C.J.C. Reynolds Evaluating the Operational Application of SMAP for Global Agricultural Drought Monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3387–3397. [Google Scholar] [CrossRef]
- Mladenova, I.E.; Bolten, J.D.; Crow, W.; Sazib, N.; Reynolds, C. Agricultural drought monitoring via the assimilation of SMAP soil moisture retrievals into a global soil water balance model. Front. Big Data 2020, 3, 10. [Google Scholar] [CrossRef] [Green Version]
- Maier, H.R.; Dandy, G.C. Neural networks for the prediction and forecasting of water resources variables: A review of modelling issues and applications. Environ. Model. Softw. 2000, 15, 101–124. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, Y.; Singh, V.P.; Chen, X. The influence of dam and lakes on the Yangtze River streamflow: Long-range correlation and complexity analyses. Hydrol. Process. 2012, 26, 436–444. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C.Y. Applicability of prewhitening to eliminate the influence of serial correlation on the Mann-Kendall test. Water Resour. Res. 2002, 38, 4-1. [Google Scholar] [CrossRef]
- Box, G.E.; Cox, D.R. An analysis of transformations. J. R. Stat. Soc. Ser. B 1964, 26, 211–243. [Google Scholar] [CrossRef]
- Fashae, O.A.; Olusola, A.O.; Ndubuisi, I.; Udomboso, C.G. Comparing ANN and ARIMA model in predicting the discharge of River Opeki from 2010 to 2020. River Res. Appl. 2019, 35, 169–177. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Kisi, O.; Cimen, M. A wavelet-support vector machine conjunction model for monthly streamflow forecasting. J. Hydrol. 2011, 399, 132–140. [Google Scholar] [CrossRef]
- Liong, S.-Y.; Sivapragasam, C. FLOOD STAGE FORECASTING WITH SUPPORT VECTOR MACHINES1. JAWRA J. Am. Water Resour. Assoc. 2002, 38, 173–186. [Google Scholar] [CrossRef]
- Azamathulla, H.M.; Wu, F.-C. Support vector machine approach for longitudinal dispersion coefficients in natural streams. Appl. Soft Comput. 2011, 11, 2902–2905. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Jaafar, O.; Deo, R.C.; Kisi, O.; Adamowski, J.; Quilty, J.; El-Shafie, A. Stream-flow forecasting using extreme learning machines: A case study in a semi-arid region in Iraq. J. Hydrol. 2016, 542, 603–614. [Google Scholar] [CrossRef]
- Sawicz, K.; Wagener, T.; Sivapalan, M.; Troch, P.A.; Carrillo, G. Catchment classification: Empirical analysis of hydrologic similarity based on catchment function in the eastern USA. Hydrol. Earth Syst. Sci. 2011, 15, 2895–2911. [Google Scholar] [CrossRef] [Green Version]
- Mcdonnell, J.; Woods, R. On the Need for Catchment Classification. J. Hydrol. 2004, 299, 2–3. [Google Scholar] [CrossRef]
- Wagener, T.; Sivapalan, M.; Troch, P.; Woods, R. Catchment classification and hydrologic similarity. Geogr. Compass 2007, 1, 901–931. [Google Scholar] [CrossRef]
- Lauzon, N.; Anctil, F.; Petrinovic, J. Characterization of soil moisture conditions at temporal scales from a few days to annual. Hydrol. Process. 2004, 18, 3235–3254. [Google Scholar] [CrossRef]
- Sun, A.Y.; Wang, D.; Xu, X. Monthly streamflow forecasting using Gaussian Process Regression. J. Hydrol. 2014, 511, 72–81. [Google Scholar] [CrossRef]
- Yeh, H.-F.; Hsu, H.-L. Stochastic model for drought forecasting in the southern Taiwan basin. Water 2019, 11, 2041. [Google Scholar] [CrossRef] [Green Version]
- Patil, S.; Stieglitz, M. Controls on hydrologic similarity: Role of nearby gauged catchments for prediction at an ungauged catchment. Hydrol. Earth Syst. Sci. 2012, 16, 551–562. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.L.; Chau, K.W. Rainfall–runoff modeling using artificial neural network coupled with singular spectrum analysis. J. Hydrol. 2011, 399, 394–409. [Google Scholar] [CrossRef] [Green Version]
- Hadi, S.J.; Abba, S.I.; Sammen, S.S.; Salih, S.Q.; Al-Ansari, N.Z.M. Yaseen Non-Linear input variable selection approach integrated with non-tuned data intelligence model for streamflow pattern simulation. IEEE Access 2019, 7, 141533–141548. [Google Scholar] [CrossRef]
- Rezaeianzadeh, M.; Tabari, H.; Arabi Yazdi, A.; Isik, S.; Kalin, L. Flood flow forecasting using ANN, ANFIS and regression models. Neural Comput. Appl. 2014, 25, 25–37. [Google Scholar] [CrossRef]
- Sivapragasam, C.; Vincent, P.; Vasudevan, G. Genetic programming model for forecast of short and noisy data. Hydrol. Process. 2007, 21, 266–272. [Google Scholar] [CrossRef]
- BERG, A.A.; MULROY, K.A. Streamflow predictability in the Saskatchewan/Nelson River basin given macroscale estimates of the initial soil moisture status. Hydrol. Sci. J. 2006, 51, 642–654. [Google Scholar] [CrossRef] [Green Version]
- Harpold, A.A.; Sutcliffe, K.; Clayton, J.; Goodbody, A.; Vazquez, S. Does Including Soil Moisture Observations Improve Operational Streamflow Forecasts in Snow-Dominated Watersheds? JAWRA J. Am. Water Resour. Assoc. 2017, 53, 179–196. [Google Scholar] [CrossRef]
- Chan, S.K.; Bindlish, R.; O’Neill, P.E.; Njoku, E.; Jackson, T.; Colliander, A.; Chen, F.; Burgin, M.; Dunbar, S.; Piepmeier, J. Assessment of the smap passive soil moisture product. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4994–5007. [Google Scholar] [CrossRef]
- Al-Yaari, A.; Wigneron, J.-P.; Ducharne, A.; Kerr, Y.; De Rosnay, P.; De Jeu, R.; Govind, A.; Al Bitar, A.; Albergel, C.; Munoz-Sabater, J. Global-scale evaluation of two satellite-based passive microwave soil moisture datasets (SMOS and AMSR-E) with respect to Land Data Assimilation System estimates. Remote Sens. Environ. 2014, 149, 181–195. [Google Scholar] [CrossRef] [Green Version]


| Watersheds | Shapiro-Wilk Test Results (Median) for Original Streamflow | Shapiro-Wilk Test Results (Median) for Transformed Streamflow | Modified Man-Kendall Test Results(Median) for Original Streamflow |
|---|---|---|---|
| A1 | 1.07 × 10−14 | 0.03 | 0.40 |
| A2 | 6.96 × 10−12 | 0.29 | 0.36 |
| B1 | 1.35 × 10−16 | 0.06 | 0.47 |
| B21 | 7.53 × 10−11 | 0.48 | 0.34 |
| B22 | 3.95 × 10−15 | 0.27 | 0.34 |
| C1 | 1.07 × 10−7 | 0.21 | 0.27 |
| C21 | 8.42 × 10−9 | 0.38 | 0.29 |
| C22 | 7.52 × 10−11 | 0.33 | 0.34 |
| Model | AIC | Model | AIC |
|---|---|---|---|
| ARIMA(1,0,0)(1,1,0) [12] | 124.1372 | ARIMA(1,0,1)(1,1,0) [12] | 124.9614 |
| ARIMA(0,0,1)(0,1,1) [12] | 114.1933 | ARIMA(1,0,1)(1,1,2) [12] | 116.8087 |
| ARIMA(0,0,1)(0,1,0) [12] | 150.2422 | ARIMA(1,0,0)(0,1,1) [12] | 112.348 |
| ARIMA(0,0,1)(1,1,1) [12] | 116.1038 | ARIMA(1,0,0)(0,1,0) [12] | 146.962 |
| ARIMA(0,0,1)(0,1,2) [12] | 116.0554 | ARIMA(1,0,0)(1,1,1) [12] | 114.3932 |
| ARIMA(0,0,1)(1,1,0) [12] | 126.9248 | ARIMA(1,0,0)(0,1,2) [12] | 114.3695 |
| ARIMA(0,0,0)(0,1,1) [12] | 149.5471 | ARIMA(1,0,0)(1,1,2) [12] | 116.5605 |
| ARIMA(1,0,1)(0,1,1) [12] | 112.472 | ARIMA(2,0,0)(0,1,1) [12] | 112.8223 |
| ARIMA(1,0,1)(0,1,0) [12] | 147.5482 | ARIMA(2,0,1)(0,1,1) [12] | 113.9666 |
| ARIMA(1,0,1)(1,1,1) [12] | 114.5846 | ARIMA(2,0,0)(0,1,1) [12] | 112.8223 |
| ARIMA(1,0,1)(0,1,2) [12] | 114.569 | ARIMA(2,0,1)(0,1,1) [12] | 113.9666 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sazib, N.; Bolten, J.; Mladenova, I. Exploring Spatiotemporal Relations between Soil Moisture, Precipitation, and Streamflow for a Large Set of Watersheds Using Google Earth Engine. Water 2020, 12, 1371. https://doi.org/10.3390/w12051371
Sazib N, Bolten J, Mladenova I. Exploring Spatiotemporal Relations between Soil Moisture, Precipitation, and Streamflow for a Large Set of Watersheds Using Google Earth Engine. Water. 2020; 12(5):1371. https://doi.org/10.3390/w12051371
Chicago/Turabian StyleSazib, Nazmus, John Bolten, and Iliana Mladenova. 2020. "Exploring Spatiotemporal Relations between Soil Moisture, Precipitation, and Streamflow for a Large Set of Watersheds Using Google Earth Engine" Water 12, no. 5: 1371. https://doi.org/10.3390/w12051371
APA StyleSazib, N., Bolten, J., & Mladenova, I. (2020). Exploring Spatiotemporal Relations between Soil Moisture, Precipitation, and Streamflow for a Large Set of Watersheds Using Google Earth Engine. Water, 12(5), 1371. https://doi.org/10.3390/w12051371




