Simulating Reservoir Induced Lhasa Streamflow Variability Using ArcSWAT
Abstract
1. Introduction
2. Materials and Methods
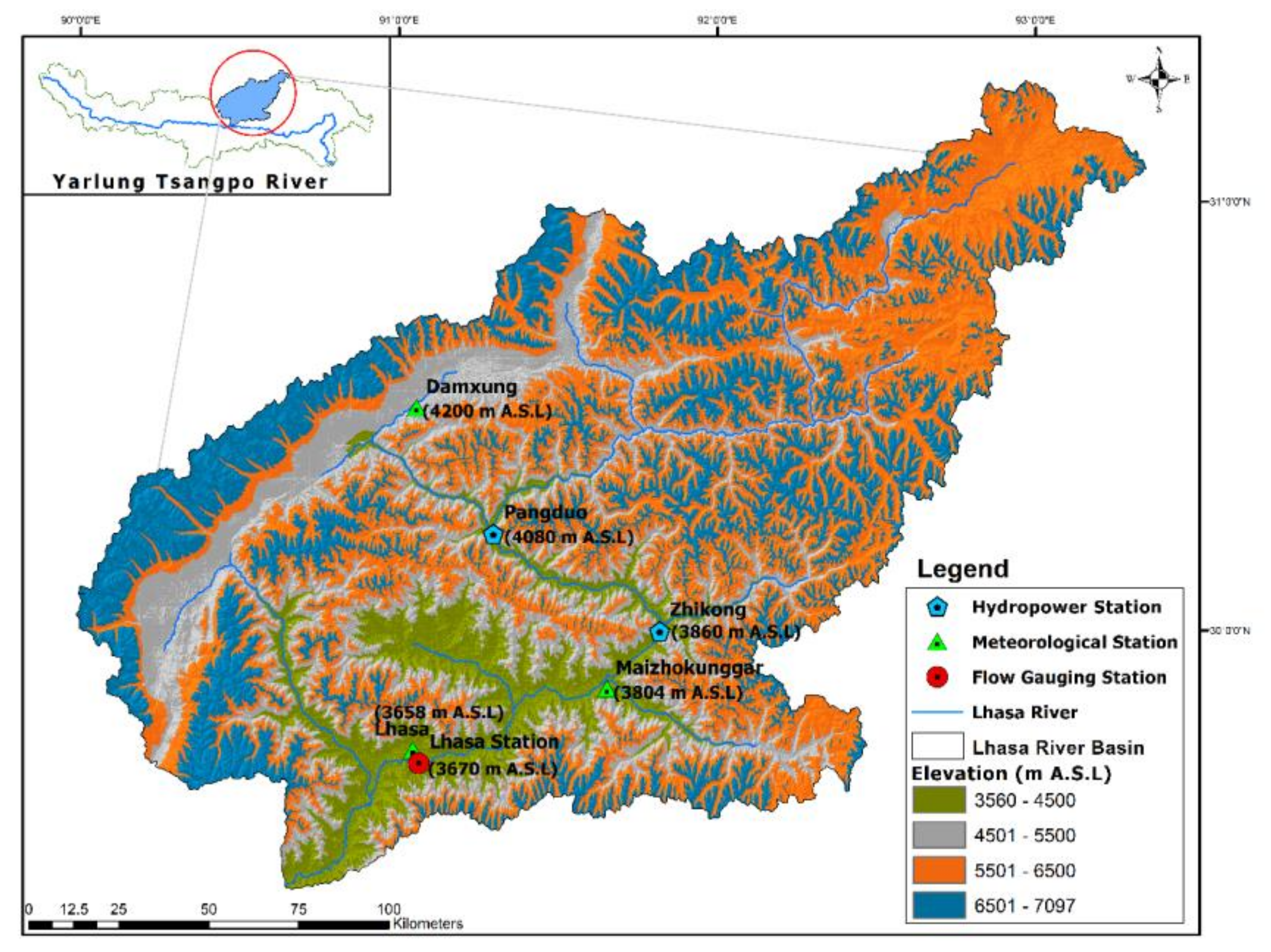
2.1. Study Area
The Pangduo Reservoir
2.2. Research Methodology
2.2.1. Mann–Kendall Trend Analysis on Hydrological Data
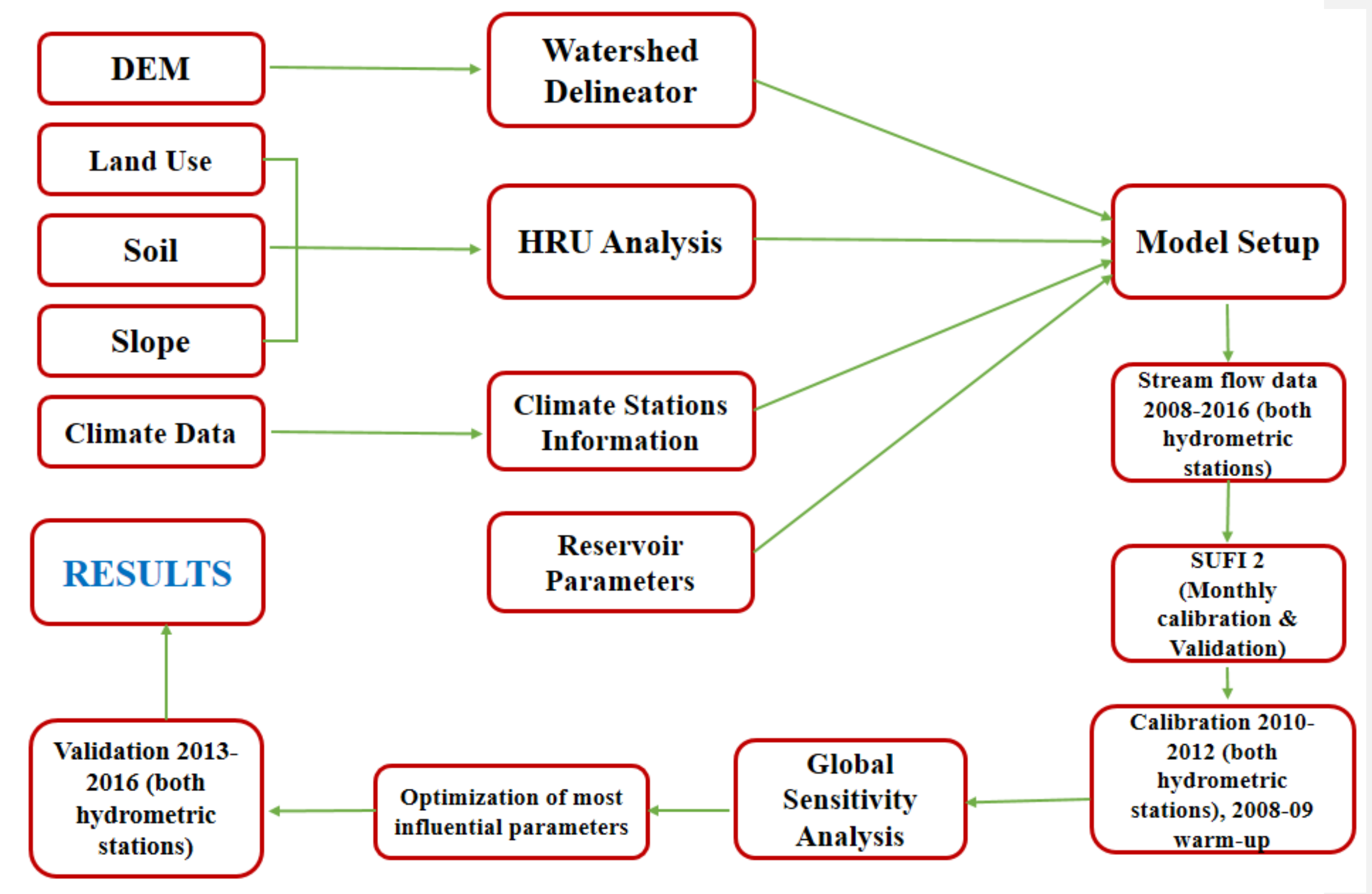
2.2.2. SWAT Model Application
SWAT Model Description
SWAT Model Input Datasets
Soil and Land Use Raster
Hydro-Meteorological Data
Watershed Demarcation
2.2.3. Reservoir Addition to the Model
2.2.4. Model Calibration, Validation and Sensitivity Analysis
2.2.5. Model Evaluation Measures
3. Results
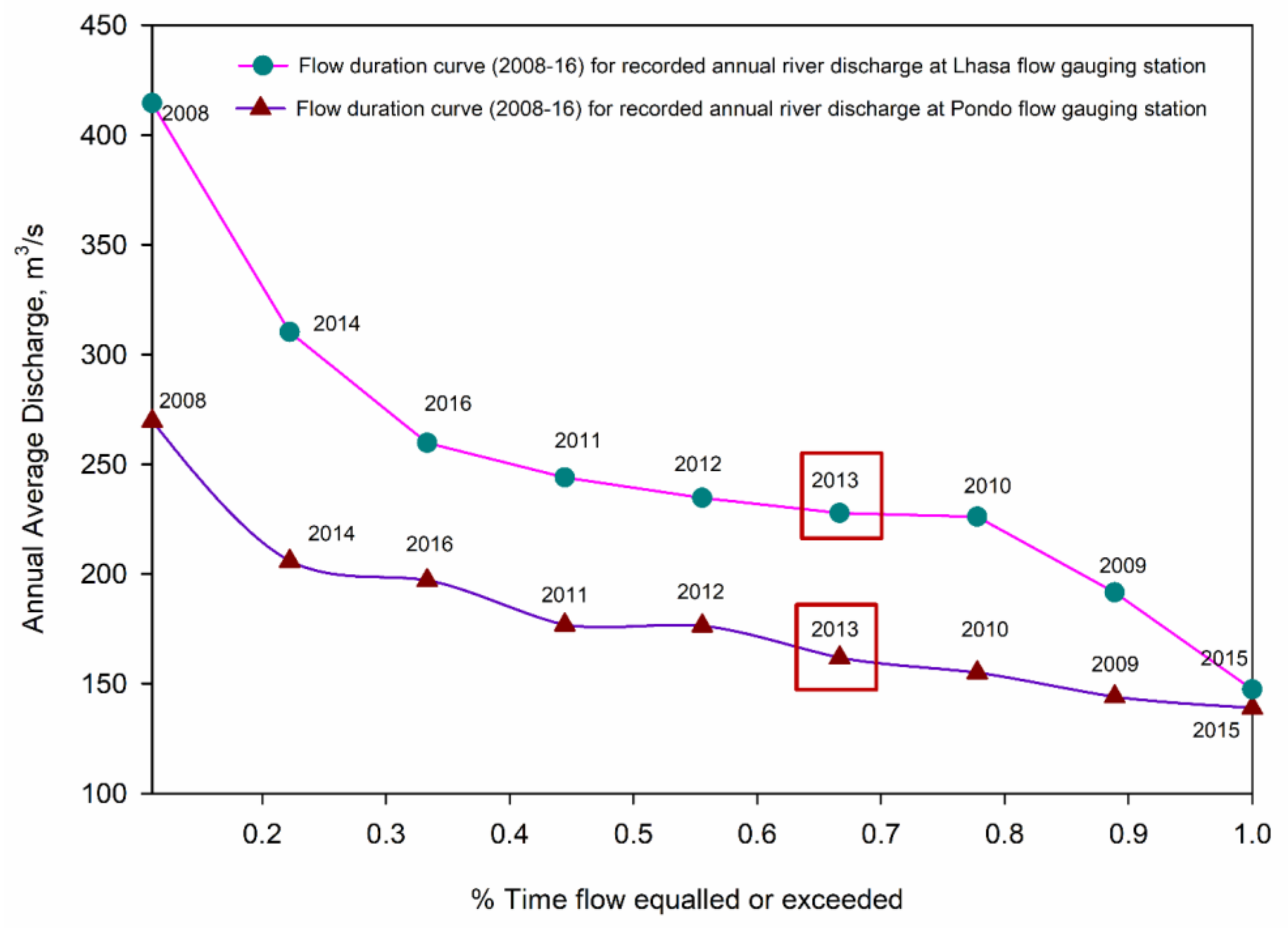
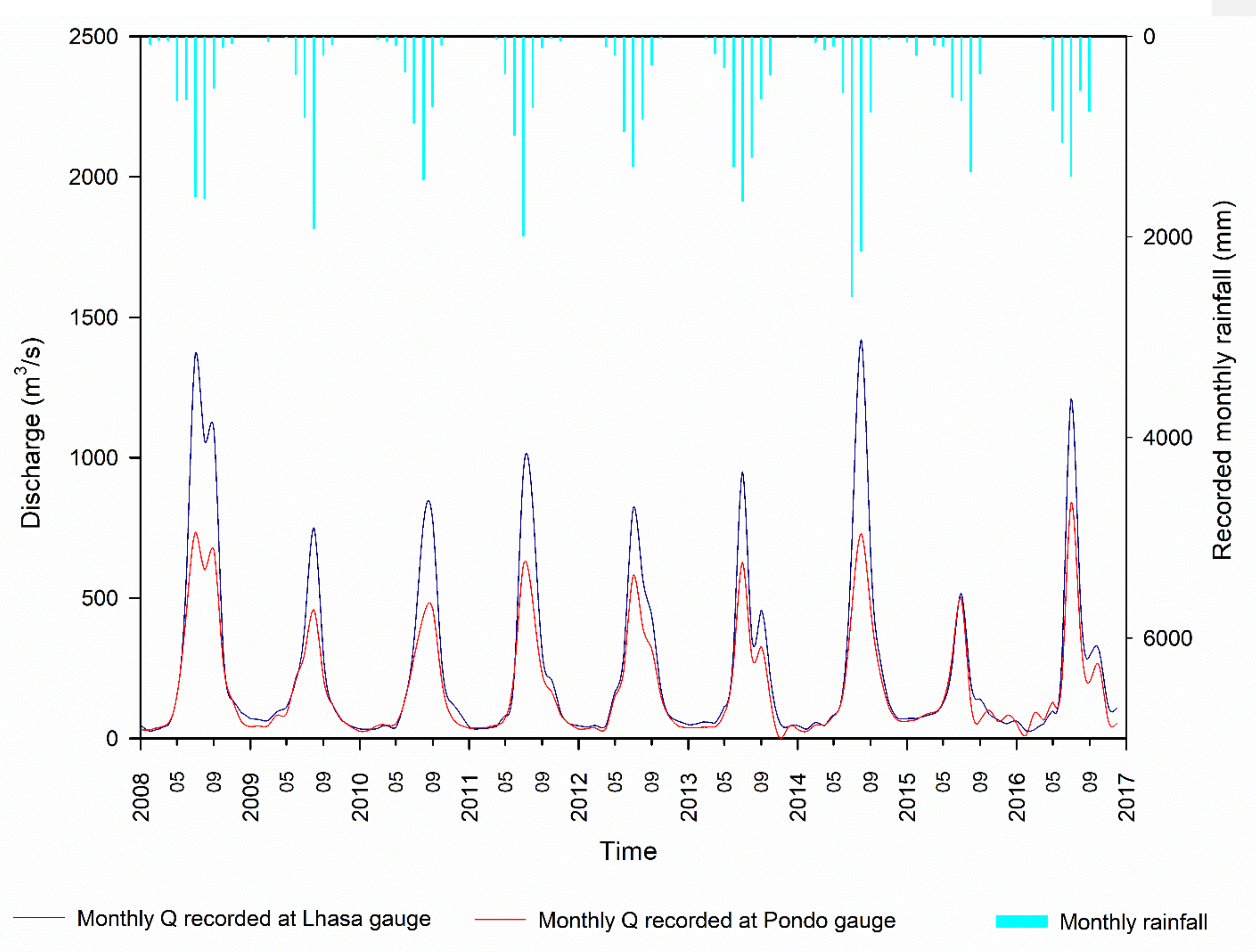
3.1. Hydrological Regime of Lhasa River
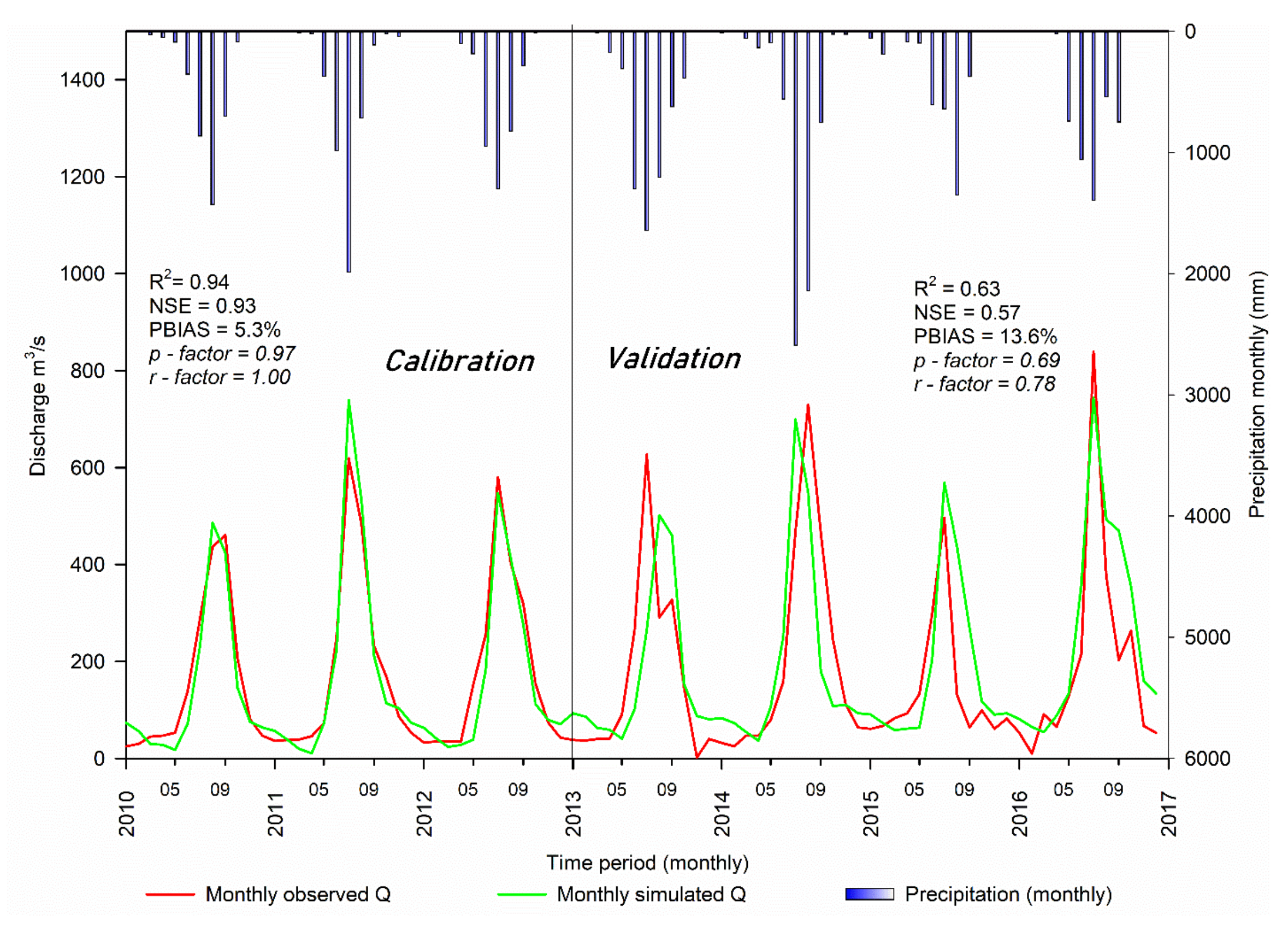
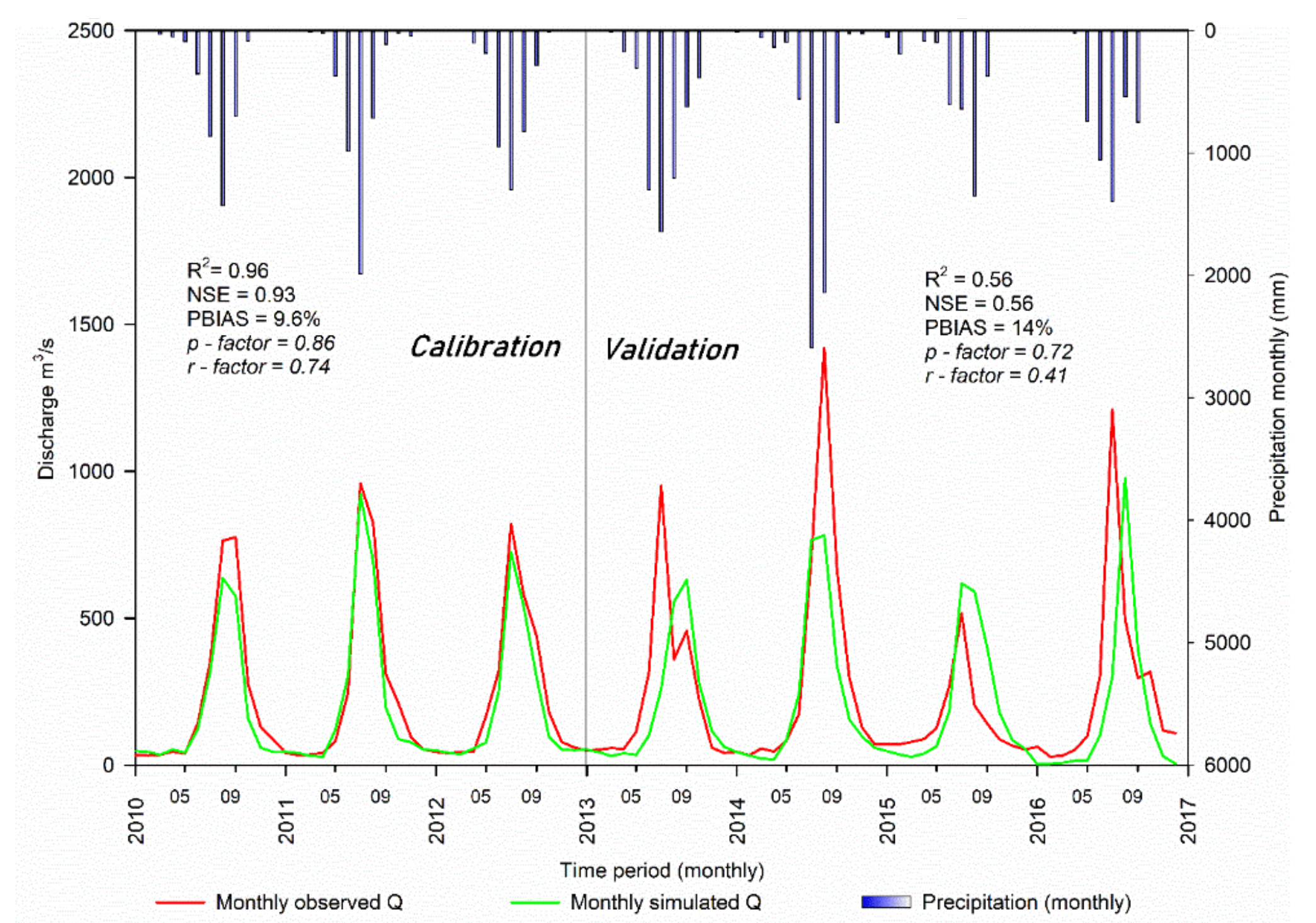
3.2. Lhasa River Flow Calibration, Validation and Parameter Sensitivity Analysis by SWAT
3.2.1. Streamflow Calibration, Validation and Parameter Sensitivity at Pondo Flow Gauge near the Selected Reservoir
3.2.2. Streamflow Calibration, Validation and Parameter Sensitivity at Downstream Lhasa Flow Gauge
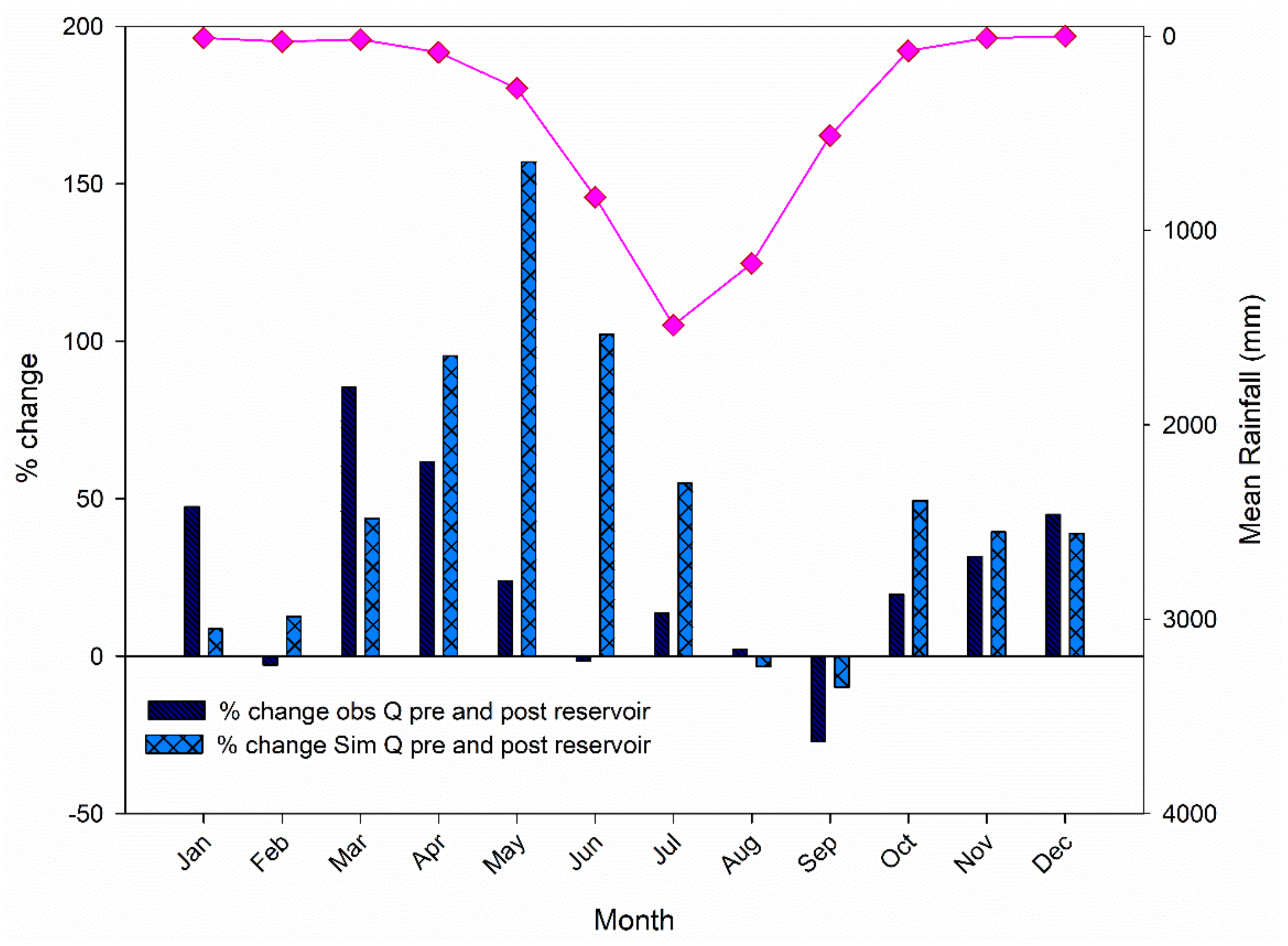
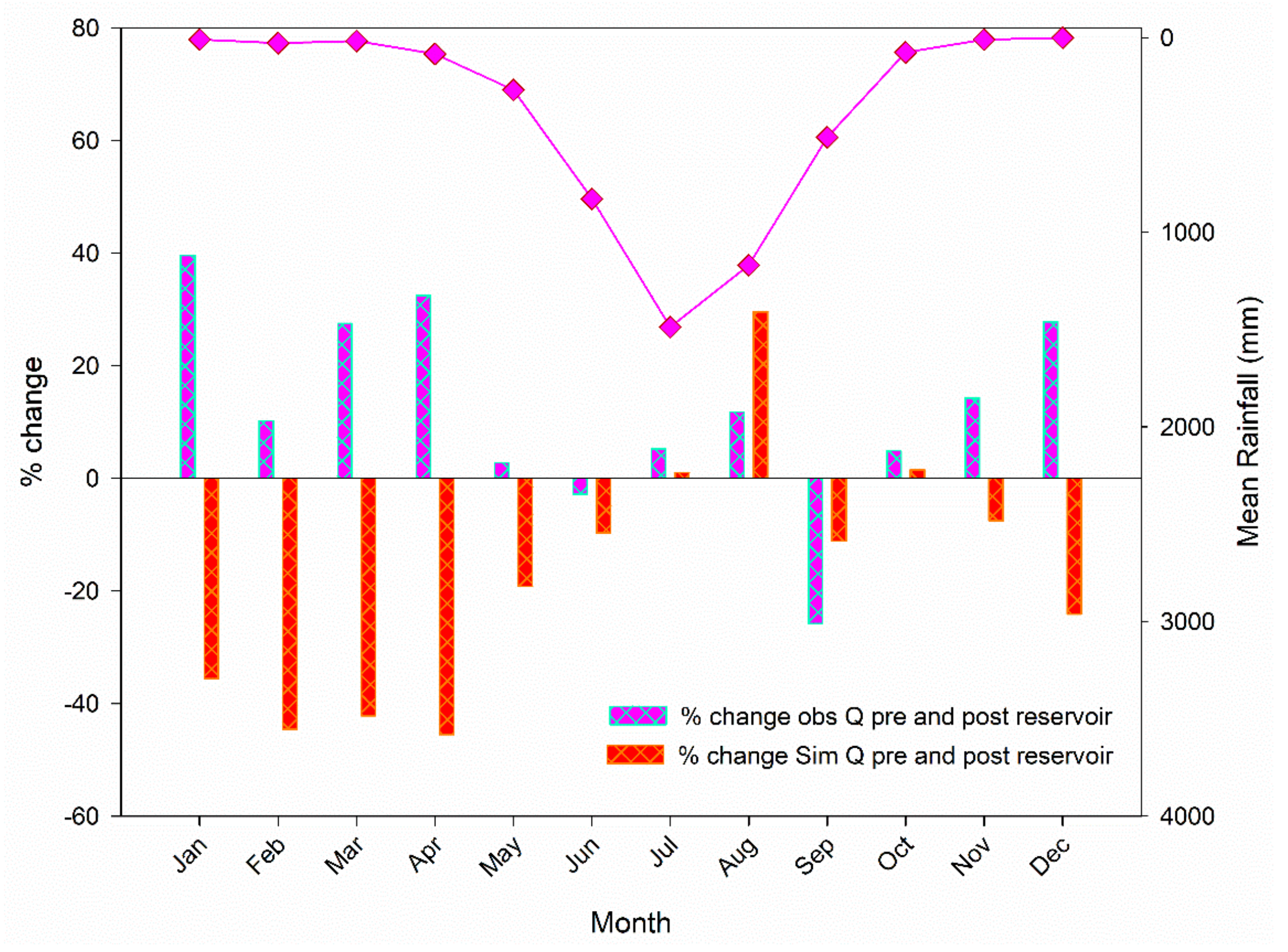
3.3. ArcSWAT Depiction of Change in River Flow Pre and Post Reservoir Operation
3.3.1. Change in Streamflow Upstream the Selected Reservoir
3.3.2. Change in Streamflow Downstream Selected Reservoir
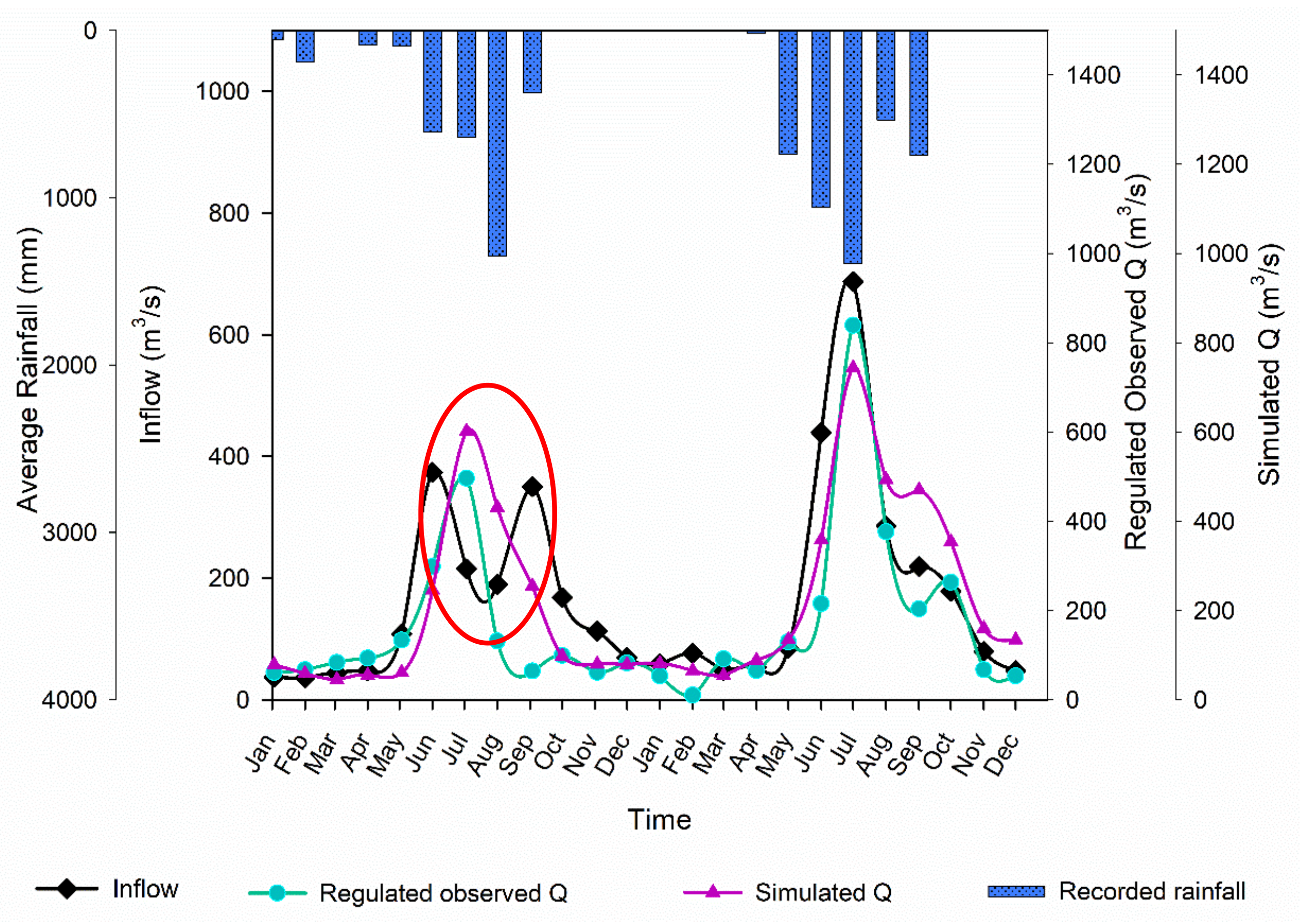
3.4. Inter-Relationship between Water Level and Inflow of Pangduo Reservoir and ArcSWAT Streamflow Simulation (Up and Downstream)
4. Discussion
4.1. Hydrological Institution of Lhasa River Basin and the Resevoir Operation
4.2. About SWAT Simulation of Streamflow at Selected Flow Gauge Sites under Reservoir Influence
4.3. Limitations of the Study
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Naiman, R.J.; Decamps, H.; Pollock, M. The Role of Riparian Corridors in Maintaining Regional Biodiversity. Ecol. Appl. 1993, 3, 209–212. [Google Scholar] [CrossRef]
- Chen, X.; Yan, Y.; Fu, R.; Dou, X.; Zhang, E. Sediment transport from the Yangtze River, China, into the sea over the post-three gorge dam period: A discussion. Quat. Int. 2008, 186, 55–64. [Google Scholar] [CrossRef]
- Rosegrant, M.W.; Cai, X.; Cline, S.A. World Water and Food to 2025: Dealing with Scarcity; International Food Policy Research Institute: Washington, DC, USA, 2002. [Google Scholar]
- Gleick, P.H. China Dams, the World’s Water; Island Press: Washington, DC, USA, 2012. [Google Scholar]
- REN21. Renewables 2014: Global Status Report (Paris: REN21 Secretariat); Technical Report; REN21: Paris, France, 2014; ISBN 978-3-9815934-2-6. [Google Scholar]
- Spänhoff, B. Current status and future prospects of hydropower in Saxony (Germany) compared to trends in Germany, the European Union and the World. Renew. Sustain. Energy Rev. 2014, 30, 518–525. [Google Scholar] [CrossRef]
- Yang, J.; Liu, Q.; Li, X.; Cui, X. Overview of Wind Power in China: Status and Future. Sustainability 2017, 9, 1454. [Google Scholar] [CrossRef]
- Frey, S.K.; Topp, E.; Ball, B.R.; Edwards, M.; Gottschall, N.; Sunohara, M.; Zoski, E.; Lapen, D.R. Tile Drainage Management Influences on Surface-Water and Groundwater Quality following Liquid Manure Application. J. Environ. Qual. 2013, 42, 881–892. [Google Scholar] [CrossRef]
- Condon, L.E.; Maxwell, R.M. Feedbacks between managed irrigation and water availability: Diagnosing temporal and spatial patterns using an integrated hydrologic model. Water Resour. Res. 2014, 50, 2600–2616. [Google Scholar] [CrossRef]
- De Schepper, G.; Therrien, R.; Refsgaard, J.C.; Hansen, A.L. Simulating coupled surface and subsurface water flow in a tile-drained agricultural catchment. J. Hydrol. 2015, 521, 374–388. [Google Scholar] [CrossRef]
- Wu, K.; Xu, Y.J. Evaluation of the applicability of the SWAT model for coastal watersheds in southeastern Louisiana1. JAWRA J. Am. Water Resour. Assoc. 2006, 42, 1247–1260. [Google Scholar] [CrossRef]
- Viviroli, D.; Zappa, M.; Gurtz, J.; Weingartner, R. An introduction to the hydrological modelling system PREVAH and its pre- and post-processing-tools. Environ. Model. Softw. 2009, 24, 1209–1222. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, C.; Qi, W.; Cai, W.; Zhao, X.; Wang, X. Multiple Climate Change Scenarios and Runoff Response in Biliu River. Water 2018, 10, 126. [Google Scholar] [CrossRef]
- Bhuyan, S.J.; Koelliker, J.K.; Marzen, L.J.; Harrington, J.A. An integrated approach for water quality assessment of a Kansas watershed. Environ. Model. Softw. 2003, 18, 473–484. [Google Scholar] [CrossRef]
- Tahir, A.A.; Hakeem, S.A.; Hu, T.; Hayat, H.; Yasir, M. Simulation of snowmelt-runoff under climate change scenarios in a data-scarce mountain environment. Int. J. Digit. Earth 2017, 12, 910–930. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment Part I: Model development 1. JAWRA J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Bärlund, I.; Kirkkala, T.; Malve, O.; Kämäri, J. Assessing SWAT model performance in the evaluation of management actions for the implementation of the Water Framework Directive in a Finnish catchment. Environ. Model. Softw. 2007, 22, 719–724. [Google Scholar] [CrossRef]
- Kaur, R.; Srivastava, R.; Betne, R.; Mishra, K.; Dutta, D. Integration of linear programming and a watershed-scale hydrologic model for proposing an optimized land-use plan and assessing its impact on soil conservation—A case study of the Nagwan watershed in the Hazaribagh district of Jharkhand, India. Int. J. Geogr. Inf. Sci. 2004, 18, 73–98. [Google Scholar] [CrossRef]
- Sun, H.; Cornish, P.S. A catchment-based approach to recharge estimation in the Liverpool Plains, NSW, Australia. Aust. J. Agric. Res. 2006, 57, 309–320. [Google Scholar] [CrossRef]
- Schuol, J.; Abbaspour, K.C. Calibration and uncertainty issues of a hydrological model (SWAT) applied to West Africa. Adv. Geosci. 2006, 9, 137–143. [Google Scholar] [CrossRef]
- Hao, F.-H.; Zhang, X.-S.; Yang, Z.-F. A distributed non-point source pollution model: Calibration and validation in the Yellow River Basin. J. Environ. Sci. (China) 2004, 16, 646–650. [Google Scholar]
- Coerver, H.M.; Rutten, M.M.; Van de Giesen, N.C. Deduction of reservoir operating rules for application in global hydrological models. Hydrol. Earth Syst. Sci. 2018, 22, 831. [Google Scholar] [CrossRef]
- Lu, X.X. Water discharge and sediment flux changes over the past decades in the Lower Mekong River: Possible impacts of the Chinese Dams. Hydrol. Earth Syst. Sci. 2006, 10, 181–195. [Google Scholar] [CrossRef]
- Reeves, J.; Chen, J.; Wang, X.L.L.; Lund, R.; Lu, Q. nA review and comparison of change point detection techniques for climate data. J. Appl. Meteorol. Climatol. 2007, 46, 900–915. [Google Scholar] [CrossRef]
- Cloern, J.E.; Abreu, P.C.; Carstensen, J.; Chauvaud, L.; Elmgren, R.; Grall, J.; Greening, H.; Johansson, J.O.R.; Kahru, M.; Sherwood, E.T.; et al. Human activities andclimate variability drive fast-paced change across the world’ sestuarine-coastal ecosystems. Glob. Chang. Biol. 2016, 22, 513–529. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.S.; Liu, D.F.; Chang, J.X.; Zhang, H.X.; Huang, Q. Impacts of climate change and human activities on run off in Weihe Basin based on Budykohypothesis. IOP Conf. Ser. Earth Env. Sci. 2017, 82, 012063. [Google Scholar] [CrossRef]
- Zhang, A.J.; Zheng, C.M.; Wang, S.; Yao, Y.Y. Analysis of stream flow variations in the Heihe River Basin, northwest China: Trends, abruptchanges, driving factors and ecological influences. J. Hydrol. 2015, 3, 106–124. [Google Scholar] [CrossRef]
- Koch, F.; Prasch, M.; Bach, H.; Mauser, W.; Appel, F.; Weber, M. How Will Hydroelectric Power Generation Develop under Climate Change Scenarios? A Case Study in the Upper Danube Basin. Energies 2011, 4, 1508. [Google Scholar] [CrossRef]
- Stojković, M.; Ilić, A.; Prohaska, S.; Plavšić, J. Multi-temporal analysis of mean annual and seasonal streamflowtrends, including periodicity and multiplenonlinear regression. Water Resour. Manag. 2014, 28, 4319–4335. [Google Scholar] [CrossRef]
- Canuto, N.; Ramos, T.B.; Oliveira, A.R.; Simionesei, L.; Basso, M.; Neves, R. Influence of reservoir management on Guadiana streamflow regime. J. Hydrol. Reg. Stud. 2019, 25, 100628. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.; Yu, Z.; Yao, H.; Li, W.; Zhang, D. Assessing the impact of human regulations on hydrological drought development and recovery based on a ‘simulated-observed’ comparison of the SWAT model. J. Hydrol. 2019, 577, 123990. [Google Scholar] [CrossRef]
- Tu, X.; Wu, H.; Singh, V.P.; Chen, X.; Lin, K.; Xie, Y. Multivariate design of socioeconomic drought and impact of water reservoirs. J. Hydrol. 2018, 566, 192. [Google Scholar] [CrossRef]
- Zhang, Q. Evaluation of ecological instream flow using multiple ecological indicators with consideration of hydrological alterations. J. Hydrol. 2015, 529, 711–722. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, C.; Bai, W.; Zhaofeng, W.; Yanli, T.; Dor, G.Y. Alpine wetlands in the Lhasa River Basin, China. J. Geogr. Sci. 2010, 20, 375–388. [Google Scholar] [CrossRef]
- Kendall, M.; Gibbons, J.D. Rank Correlation Methods. Charles Griffin Book Series, 5th ed.; Oxford University Press: Oxford, UK, 1990; ISBN 978-0195208375. [Google Scholar]
- Arnold, J.G.; Allen, P.M.; Bernhardt, G. A comprehensive surface-groundwater flow model. J. Hydrol. 1993, 142, 47–69. [Google Scholar] [CrossRef]
- Jha, M.K. Evaluating Hydrologic Response of an Agricultural Watershed for Watershed Analysis. Water 2011, 3, 604–617. [Google Scholar] [CrossRef]
- Kannan, N.; White, S.M.; Worrall, F.; Whelan, M.J. Hydrological modelling of a small catchment using SWAT-2000–Ensuring correct flow partitioning for contaminant modelling. J. Hydrol. 2007, 334, 64–72. [Google Scholar] [CrossRef]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The Soil and Water Assessment Tool: Historical Development, Applications, and Future Research Directions. Trans. Asabe 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Douglas-Mankin, K.R.; Srinivasan, R.; Arnold, J.G. Soil and Water Assessment Tool (SWAT) Model: Current Developments and Applications. Trans. Asabe 2010, 53, 1423–1431. [Google Scholar] [CrossRef]
- Tuppad, P.; Douglas-Mankin, K.R.; Lee, T.; Srinivasan, R.; Arnold, J.G. Soil and Water Assessment Tool (SWAT) Hydrologic/Water Quality Model: Extended Capability and Wider Adoption. Trans. ASABE 2011, 54, 1677–1684. [Google Scholar] [CrossRef]
- Van Griensven, A.; Ndomba, P.; Yalew, S.; Kilonzo, F. Critical review of SWAT applications in the upper Nile basin countries. Hydrol. Earth Syst. Sci. 2012, 16, 3371–3381. [Google Scholar] [CrossRef]
- Gassman, P.W.; Sadeghi, A.M.; Srinivasan, R. Applications of the SWAT Model Special Section: Overview and Insights. J. Environ. Qual. 2014, 43, 1–8. [Google Scholar] [CrossRef]
- Krysanova, V.; White, M. Advances in water resources assessment with SWAT—an overview. Hydrol. Sci. J. 2015, 60, 771–783. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation–Version 2009; (TR-406); Texas Water Resources Institute: College Station, TX, USA, 2011. [Google Scholar]
- Khoi, D.N.; Thom, V.T. Parameter uncertainty analysis for simulating streamflow in a river catchment of Vietnam. Glob. Ecol. Conserv. 2015, 4, 538–548. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Yang, J.; Maximov, I.; Siber, R.B.K.; Mieleitner, J.; Zobrist, J.; Srinivasan, R. Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
- Zhao, F.; Wu, Y.; Qiu, L.; Sun, Y.; Sun, L.; Li, Q.; Niu, J.; Wang, G. Parameter Uncertainty Analysis of the SWAT Model in a Mountain-Loess Transitional Watershed on the Chinese Loess Plateau. Water 2018, 10, 690. [Google Scholar] [CrossRef]
- Santhi, C.; Arnold, J.G.; Williams, J.R.; Dugas, W.A.; Srinivasan, R.; Hauck, L.M. Validation of the SWAT model on a large basin with point and nonpoint sources 1. JAWRA J. Am. Water Resour. Assoc. 2001, 37, 1169–1188. [Google Scholar] [CrossRef]
- Mihon, D.; Bacu, V.; Denisa, R.; Teodor, S.; Karim, A.; Elham, R.; Dorian, G. Grid Based Hydrologic Model Calibration and Execution. In Advances in Intelligent Control Systems and Computer Science; Dumitrache, L., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 279–293. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. Asabe 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Gupta Hoshin, V.; Sorooshian, S.; Yapo Patrice, O. Status of Automatic Calibration for Hydrologic Models: Comparison with Multilevel Expert Calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Searcy, J.K. Flow-Duration Curves: Manual of Hydrology: Part 2: Low-Flow Techniques; US Government Printing Office: Washington, DC, USA, 1959.
- Cuo, L.; Li, N.; Liu, Z.; Ding, J.; Liang, L.; Zhang, Y.; Gong, T. Warming and human activities induced changes in the Yarlung Tsangpo basin of the Tibetan plateau and their influences on streamflow. J. Hydrol. Reg. Stud. 2019, 25, 100625. [Google Scholar] [CrossRef]
- Faramarzi, M.; Abbaspour, K.C.; Adamowicz, W.L.; Lu, W.; Fennell, J.; Zehnder, A.J.B.; Goss, G.G. Uncertainty based assessment of dynamic freshwater scarcity in semi-arid watersheds of Alberta, Canada. J. Hydrol. Reg. Stud. 2017, 9, 48–68. [Google Scholar] [CrossRef]
- Tan, M.L.; Gassman, P.W.; Srinivasan, R.; Arnold, J.G.; Yang, X. A Review of SWAT Studies in Southeast Asia: Applications, Challenges and Future Directions. Water 2019, 11, 914. [Google Scholar] [CrossRef]
- Batalla, R.J. Reservoir-induced hydrological changes in the Ebro River basin (NE Spain). J. Hydrol. 2004, 290, 117–136. [Google Scholar] [CrossRef]
- Najjar, R.G.; Pyke, C.R.; Adams, M.B.; Breitburg, D.; Hershner, C.; Kemp, M.; Howarth, R.; Mulholland, R.; Paolisso, M.; Secor, D.; et al. Potential climate-change impacts on the Chesapeake Bay. Estuar. Coast. Shelf Sci. 2010, 86, 1–20. [Google Scholar] [CrossRef]
- Struyf, E.; Van Damme, S.; Meire, P. Possible effects of climate change on estuarine nutrient fluxes: A case study in the highly nutrified Schelde estuary (Belgium, the Netherlands). Estuar. Coast. Shelf Sci. 2004, 60, 649–661. [Google Scholar] [CrossRef][Green Version]
- Tomer, M.D.; Schilling, K.E. A simple approach to distinguish land-use and climate-change effects on watershed hydrology. J. Hydrol. 2009, 376, 24–33. [Google Scholar] [CrossRef]
- Xu, K.; Milliman, J.D.; Xu, H. Temporal trend of precipitation and runoff in major Chinese Rivers since 1951. Glob. Planet. Chang. 2010, 73, 219–232. [Google Scholar] [CrossRef]
- Doyle, M.E.; Saurral, R.I.; Barros, V.R. Trends in the distributions of aggregated monthly precipitation over the La Plata Basin. Int. J. Climatol. 2012, 32, 2149–2162. [Google Scholar] [CrossRef]
- Kustu, M.D.; Fan, Y.; Rodell, M. Possible link between irrigation in the US High Plains and increased summer streamflow in the Midwest. Water Resour. Res. 2011, 47, W03522. [Google Scholar] [CrossRef]
- Fan, J.; Tian, F.; Yang, Y.H.; Han, S.; Qiu, G. Quantifying the magnitude of the impact of climate change and human activities on runoff decline in Mian River Basin, China. Water Sci. Technol. 2010, 62, 783–791. [Google Scholar] [CrossRef]
- Xu, C.Y.; Gong, L.B.; Jiang, T.; Chen, D.; Singh, V.P. Analysis of spatial distribution and temporal trend of reference evapotranspiration in Changjiang (Yangtze River) catchment. J. Hydrol. 2006, 327, 81–93. [Google Scholar] [CrossRef]
- Ye, X.C.; Zhang, Q.; Liu, J.; Li, X.; Xu, C.-Y. Distinguishing the relative impacts of climate change and human activities on variation of streamflow in the Poyang Lake catchment, China. J. Hydrol. 2013, 494, 83–95. [Google Scholar] [CrossRef]
- Li, S.; Xiong, L.H.; Dong, L.H.; Zhang, J. Effects of Three Gorges reservoir on the hydrological droughts at the downstream Yichang station during 2003–2011. Hydrol. Process. 2013, 27, 3981–3993. [Google Scholar] [CrossRef]
- Richter, B.D.; Thomas, G.A. Restoring environmental flows by modifying dam operations. Ecol. Soc. 2007, 12, 12. [Google Scholar] [CrossRef]
- Petts, G.E. Instream-flow science for sustainable river management. J. Am. Water Resour. Assoc. 2009, 45, 1071–1086. [Google Scholar] [CrossRef]
- Yoder, J.; Jonathan, A.; Jennifer, B.; Michael, C.; Joseph, K.; Stephen, J.; Shane, M.K.; McMillan, J.; Yang, Q. Benefit-Cost Analysis of Integrated Water Resource Management: Accounting for Interdependence in the Yakima Basin Integrated Plan. J. Am. Water Resour. Assoc. 2017, 53, 456. [Google Scholar] [CrossRef]
- Tian, P.; Lu, H.; Feng, W.; Guan, Y.; Xue, Y. Large decrease in streamflow and sediment load of Qinghai–Tibetan Plateau driven by future climate change: A case study in Lhasa River Basin. CATENA 2020, 187, 104340, ISSN 0341-8162. [Google Scholar] [CrossRef]
- Tram, V.Q.; Liem, N.D.; Loi, N.K. Assessing Water Availability in PoKo Catchment using SWAT model. Khon Kaen Agric. J. 2014, 42, 74–84. [Google Scholar]
- Anh, N.V.; Fukuda, S.; Hiramatsu, K.; Harada, M. Sensitivity-Based Calibration of the Soil and Water Assessment Tool for Hydrologic Cycle Simulation in the Cong Watershed, Vietnam. Water Env. Res. 2015, 87, 735–750. [Google Scholar] [CrossRef]
- Nguyen, H.Q.; Kappas, M. Modeling Surface Runoff and Evapotranspiration using SWAT and BEACH for a Tropical Watershed in North Vietnam, Compared to MODIS Products. Int. J. Adv. Remote Sens. Gis 2015, 4, 1367–1384. [Google Scholar] [CrossRef]
- Rost, S.; Gerten, D.; Bondeau, A.; Luncht, W.; Rohwer, J.; Schaphoff, S. Agricultural green and blue water consumption and its influence on the global water system. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Hao, Z.; Chen, S.; Li, Z.; Yu, Z.; Shao, Q.; Yuan, F.; Shi, F. Quantitative assessment of the impacts of irrigation on surface water fluxes in the Tarim River, China. Hydrol. Res. 2015, 46, 996–1007. [Google Scholar] [CrossRef]
- Malek, K.; Adam, J.C.; Stöckle, C.O.; Peters, R.T. Climate change reduces water availability for agriculture by decreasing non-evaporative irrigation losses. J. Hydrol. 2018, 561, 444–460. [Google Scholar] [CrossRef]
- Polo, M.J.; Rovira, A.; García-Contreras, D.; Contreras, E.; Millares, A.; Aguilar, C.; Miguel, A.L. Reservoir impacts downstream in highly regulated river basins: The Ebro delta and the Guadalquivir estuary in Spain. Proc. Int. Assoc. Hydrol. Sci. 2016, 373, 45. [Google Scholar] [CrossRef]
- Aeschbach-Hertig, W.; Gleeson, T. Regional strategies for the accelerating global problem of groundwater depletion. Nat. Geosci. 2012, 5, 853. [Google Scholar] [CrossRef]
- Ban, H.G.; Xu, C. Major crop planting methods in the Tibetan Autonomous Region. Agr. Mach. Techonol. Ext. 2016, 9, 26–27. (In Chinese) [Google Scholar]
- Zhuang, Q.S. Investigation of agriculture production in the Tibetan autonomous region. Scient. Res. Rep. Chin. Acad. Agri. Sci. 1959, 23–45. (In Chinese) [Google Scholar]
- Li, D.; Luo, H.; Luo, Y.; Cui, Y.; Li, Y.; Meng, Q. Analysis of irrigation water demand and supply in Lhasa River valley of Tibet. J. Drain. Irrig. Mach. Eng. 2018, 36, 1053–1058. (In Chinese) [Google Scholar]
- AWR-TAR. The Investigation of the Efficiency of Agricultural Irrigation in the Tibetan Autonomous Region; Technical Report; Administration of Water Resources of the Tibetan Autonomous Region: Tibetan, China, 2019. (In Chinese)
- Sridhar, V.; Kang, H.; Ali, S.A. Human-Induced Alterations to Land Use and Climate and Their Responses for Hydrology and Water Management in the Mekong River Basin. Water 2019, 11, 1307. [Google Scholar] [CrossRef]
- Qiu, J.; Yang, Q.; Zhang, X.; Huang, M.; Adam, J.C.; Malek, K. Implications of water management representations for watershed hydrologic modeling in the Yakima River basin. Hydrol. Earth Syst. Sci. 2019, 23, 35–49. [Google Scholar] [CrossRef]
- Lv, M.; Hao, Z.; Lin, Z.; Ma, Z.; Lv, M.; Wang, J. Reservoir operation with feedback in a coupled land surface and hydrologic model: A case study of the Huai River Basin, China. Jawra J. Am. Water Resour. Assoc. 2016, 52, 168–183. [Google Scholar] [CrossRef]
- Zhang, X.; Beeson, P.; Link, R.; Manowitz, D.; Izaurralde, R.C.; Sadeghi, A.; Thomson, A.M.; Sahajpal, R.; Srinivasan, R.; Arnold, J.G. Efficient multi-objective calibration of a computationally intensive hydrologic model with parallel computing software in Python. Environ. Model. Softw. 2013, 46, 208–218. [Google Scholar] [CrossRef]


| Reservoir Specification | Detail |
|---|---|
| total storage capacity of the reservoir (volume of water when the emergency spillway is filled) | 1.23 billion cubic meters |
| adjusted storage capacity (volume of water when the principal spillway is filled) | 811 million cubic meters |
| dead storage capacity | 271 million cubic meters |
| normal water level | 4095 m |
| dead water level | 4066 m |
| restricted water level during the flood | 4093.5 m |
| maximum dam height | 72.30 m |
| elevation of the dam at top | 4100.00 m |
| dam length | 1052 m |
| total installed capacity | 160 MW |
| No. | Parameter | Parameter Description | Method Chosen |
|---|---|---|---|
| 1. | CN2 | Initial SCS curve number for soil condition II | Relative |
| 2. | GW_DELAY | Ground water delay (days) | Replace |
| 3. | GW_REVAP | Ground water “revap” coefficient | Replace |
| 4. | ESCO | Soil evaporation compensation factor | Replace |
| 5. | EPCO | Plant uptake compensation factor | Replace |
| 6. | SOL_BD | Soil bulk density (mg/m3) | Relative |
| 7. | SOL_K | Saturated hydraulic conductivity (mm/h) | Relative |
| 8. | SOL_AWC | Available water capacity of soil layer (mm H2O/mm soil) | Relative |
| 9. | OV_N | Manning’s “n” value for overland flow | Relative |
| Parameter | Range | Fitted Value | Rank | t-stat | p-Value | |
|---|---|---|---|---|---|---|
| Min | Max | |||||
| r__SOL_K | −0.8 | 0.5 | −0.30 | 1 | 2.601 | 0.017 |
| r__SOL_BD | 0 | 1.5 | 0.62 | 2 | 1.606 | 0.123 |
| v__GW_DELAY | 150 | 500 | 167 | 3 | −1.488 | 0.152 |
| r__CN2 | −0.5 | −0.1 | −0.24 | 4 | −1.392 | 0.179 |
| r__SOL_AWC | −0.9 | 0.1 | −0.11 | 5 | 1.246 | 0.226 |
| v__GW_REVAP | 0.5 | 0.9 | 0.77 | 6 | 0.898 | 0.379 |
| v__ESCO | −0.8 | 0.2 | −0.41 | 7 | −0.753 | 0.459 |
| v__EPCO | −0.1 | 0.8 | −0.05 | 8 | −0.287 | 0.776 |
| r__OV_N | −0.3 | 0.5 | 0.03 | 9 | 0.167 | 0.868 |
| Parameter | Range | Fitted Value | Rank | t-stat | p-Value | |
|---|---|---|---|---|---|---|
| Min | Max | |||||
| r__SOL_BD | −1 | 1 | 0.84 | 1 | 24.398 | 0.000 |
| r__SOL_K | −1 | 1 | −0.39 | 2 | 18.243 | 0.000 |
| r__CN2 | −0.25 | −0.01 | −0.20 | 3 | 10.761 | 0.000 |
| v__ESCO | 0.01 | 1 | 0.90 | 4 | 3.420 | 0.000 |
| r__SOL_AWC | −1 | 1 | −0.56 | 5 | −2.300 | 0.021 |
| v__GW_REVAP | 0.02 | 0.1 | 0.06 | 6 | −1.582 | 0.114 |
| v__GW_DELAY | 150 | 500 | 478 | 7 | −1.554 | 0.120 |
| v__EPCO | 0 | 1 | 0.79 | 8 | 0.324 | 0.745 |
| r__OV_N | −1 | 1 | −0.04 | 9 | −0.277 | 0.781 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yasir, M.; Hu, T.; Abdul Hakeem, S. Simulating Reservoir Induced Lhasa Streamflow Variability Using ArcSWAT. Water 2020, 12, 1370. https://doi.org/10.3390/w12051370
Yasir M, Hu T, Abdul Hakeem S. Simulating Reservoir Induced Lhasa Streamflow Variability Using ArcSWAT. Water. 2020; 12(5):1370. https://doi.org/10.3390/w12051370
Chicago/Turabian StyleYasir, Muhammad, Tiesong Hu, and Samreen Abdul Hakeem. 2020. "Simulating Reservoir Induced Lhasa Streamflow Variability Using ArcSWAT" Water 12, no. 5: 1370. https://doi.org/10.3390/w12051370
APA StyleYasir, M., Hu, T., & Abdul Hakeem, S. (2020). Simulating Reservoir Induced Lhasa Streamflow Variability Using ArcSWAT. Water, 12(5), 1370. https://doi.org/10.3390/w12051370







