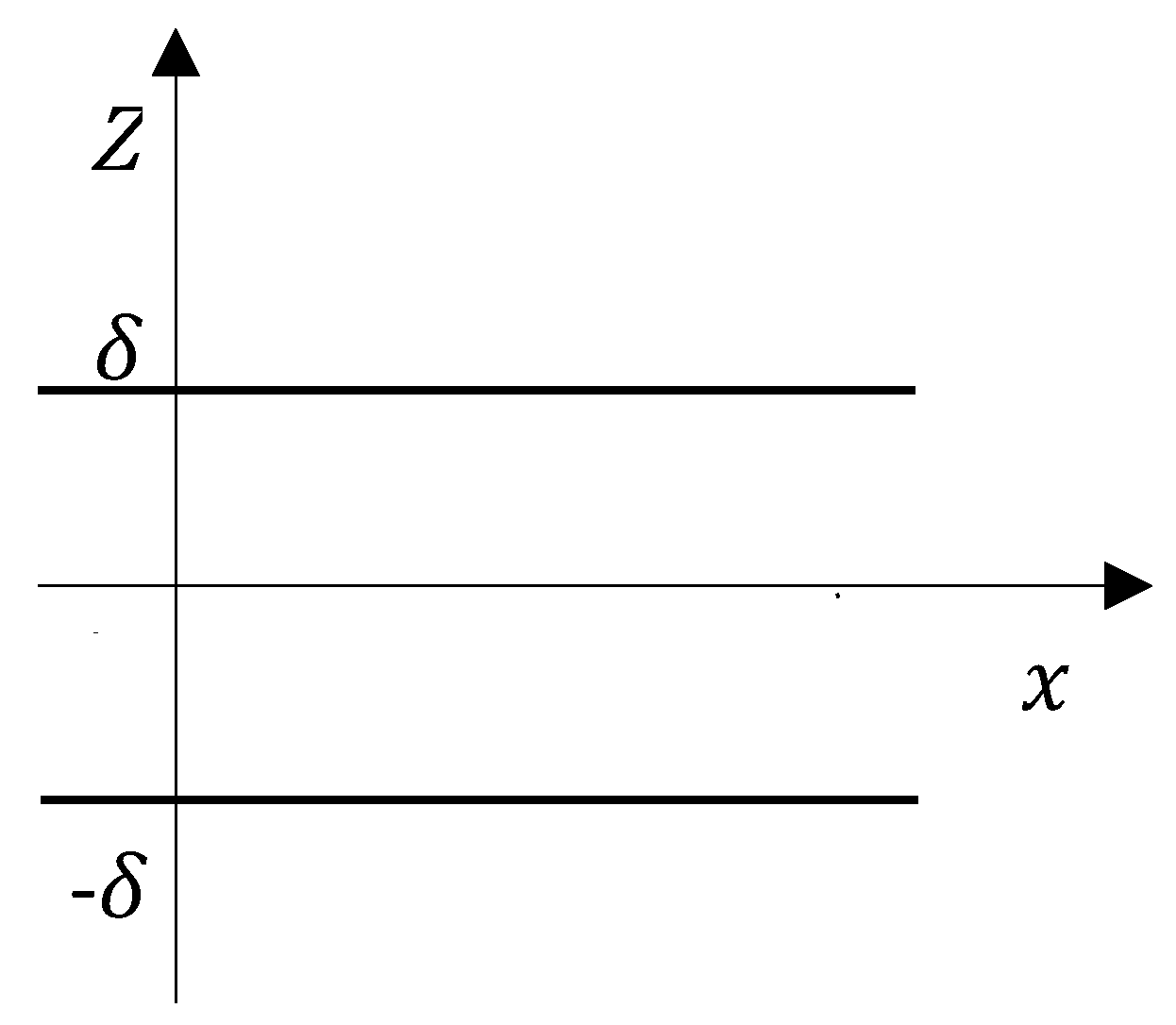1. Introduction
It is well known that the fluid flow within a geological formation takes place mainly through fractures that are often connected to each other to constitute a network. The study of motion through fractures affects many industrial activities, such as exploitation of a basin, oil and gas extraction, contaminant pollution control and hydraulic fracturing. In enhanced oil recovery operations, polymer solutions that exhibit a non-Newtonian shear-thinning behavior are injected [
1].
A literature overview shows that when an oilfield is flooded with a non-Newtonian fluid, the mobility ratio between the displaced fluid and the displacing fluid becomes favorable with respect to flooding with water. Oil displacement tests indicate that water-soluble polymer added to the injection water can recover additional oil from an oilfield. The polymers often used are polyacrylamide or polysaccharide; these substances provide the highest viscosity for an assigned concentration.
The description of the flow in a single fracture has been addressed both analytically and experimentally. With an analytical approach to the problem, and schematizing the rheological behavior of the fluid with a Newtonian one, the cubic law expresses the hydraulic transmissivity as a function of the average fracture opening, assuming that the rough walls can be schematized with two smooth parallel plates [
2]. However, the roughness of natural rock fractures, the variability of the aperture, and the presence of obstructions, complicate the process that deviates from a Poiseuille flow; in [
3], the flow tortuosity and the aperture variation are considered to modify the cubic law to simulate numerically the flow. The experimental work [
4] investigates the influence of geometric characteristics of deformable rough fractures, and the relationships between the hydraulic gradient and the flow rate. Despite the importance of the effects of roughness in fracture flow—as emphasized in the reference work of Zimmerman and Bodvarsson [
5]—the roughness is neglected in the present paper because, for an analytical analysis, the complexity generated by the rheological constitutive law of a non-Newtonian fluid and by the unsteady flow suggests adopting a simplified geometry to solve the problem.
Tsang [
6] and Neuzil [
7] show that the scheme of plane motion gives reliable results if the normal stress is less than ~10 MPa, and if the aperture variation along the flow path is not large.
The plane unsteady flow of a non-Newtonian fluid has been faced by many authors even recently, either for numerical calculation purposes or analytically. Particularly, the motion generated superposing to a constant pressure gradient a small periodical variation has acquired technical and practical uses, because it allows the growth of the mean discharge with a limited increase of power. The non-linearity of the constitutive equation of pseudoplastic fluids makes the variation of the rate of flow during the phase of increase of the pressure gradient exceed the decrease occurring when it falls.
In this paper, the forcing action is given by a constant pressure gradient and a small periodic variation superposed to it.
In the first part, the phenomenon is studied, adopting a constitutive equation given by a logarithmic law (L), which can be considered as a simplified Prandl–Eyring model, and represents, with good approximation, the behavior of pseudoplastic materials (particularly of polymer solution and powder suspensions in Newtonian fluids), in a wide range of shear stress and shear rate. The results will be compared to those obtained by the authors using a Williamson model (W), proposed in [
8] for the same fluid and the same geometry [
9].
The momentum equation is solved using a perturbation method, assuming the amplitude of the pulsatile component of the pressure gradient as a parameter. It is a method widely used to obtain approximated solutions to engineering problems, even if the convergence of the solution is not normally demonstrable.
In particular, the second-order term of the velocity field that gives origin to a variation of the mean discharge will be determined; it will always result positive, thus justifying analytically the intuitive fact that the mean flow rate in a period increases.
2. Problem statement
The plane laminar flow of an incompressible non-Newtonian fluid, in a layer of thickness
, as shown in
Figure 1, is considered, under the action of a small periodic pressure gradient superimposed on a constant one. A sensitivity analysis to test the influence of the roughness would require solving the problem numerically and making a comparison of the results. However, this goes beyond the purpose of this paper, which aims to compare the results provided by using the same fluid with two different models to approximate the experimental points representing the relationship between shear-stress and shear-rate.
The velocity is supposed to have the
direction; taking into account the continuity equation, the equation of motion can be written as
where
is normal to the layer,
is the time,
the pressure,
ρ the fluid density,
the shear stress and
the velocity.
The fluid considered is a pseudoplastic one, and a simple two-parameter model based on a logarithmic law, which is similar to the Prandtl–Eyring model
, can be used:
where
is the shear rate
, and
and
are two rheological parameters.
The flow is symmetric with respect to the
axis, and thus the problem is studied only in the region
where
, and thus
The imposed pressure gradient is
is the constant pressure gradient,
is the amplitude of the periodic perturbation and
its pulsation. Equation (1) becomes
Introducing the following dimensionless quantities
,
,
,
,
,
,
, Equation (5) becomes
Supposing
, the velocity is expanded as a power series in
and thus
Putting
Equation (8) becomes
Taking the logarithm of the two terms and developing the second member in power series, we obtain:
Substituting Equation (11) in (6)
Equating the coefficients of the same order in
, three equations follow:
The velocity
,
and
must satisfy the boundary conditions
and
, where
.
2.1. The Steady Component
Equation (13) has the solution
where
. It must be
and thus
and
which gives a steady rate of flow
2.2. The First-Order Approximation
Writing the solution of Equation (14) in the form
Equation (14) becomes
which has the particular integral
; the solution of Equation (20) can be written as
, where
is the solution of the homogeneous equation
Putting
, where
and recalling that
Equation (21) can be recast in the form
which admits the solution [
10]
where
,
,
and
are the well-known Kelvin function of order 1,
and
are suitable constants to be calculated, imposing the boundary conditions
and
, i.e.,
. The solution of Equation (20) is thus
where
and
The solution of the first-order approximation becomes
2.3. Second-Order Approximation
Equation (15) contains the term
Recalling that for every complex number
it results
, and observing that
, Equation (29) gives
Searching a solution of Equation (30) in the form
allows to write Equation (15) as follows
The steady component
satisfies the equation
and the oscillating one
satisfies the equation
Only the steady component
will be examined, which gives rise to a stationary rate of flow; it results
However,
must satisfy the boundary conditions, and then
. It results
Equation (25), recalling that
and thus
, gives
and then
which can be integrated numerically. The velocity
gives a stationary rate of flow
and integrating by parts, we obtain:
3. A Numerical Example
A literature overview shows that when an oilfield is flooded with a non-Newtonian fluid, the mobility ratio between the displaced fluid and the displacing fluid becomes favorable with respect to flooding with water. Oil displacement tests indicate that water-soluble polymer added to the injection water can recover additional oil from an oilfield. The polymers often used are polyacrylamide or polysaccharide; these substances provide the highest viscosity for an assigned concentration. To show the use of the proposed solution and make a comparison with previous results obtained by the authors, the found results are applied to the particular fluid used in [
9], with the same geometry: a microgel-free xanthan polysaccharide dissolved in saltwater (salinity = 5 g/L NaCl, T = 30 °C). Interpolating, with the least-squares method, the experimental data of the paper of Chauveteau [
11] for a concentration of 800 ppm with the logarithmic model, we obtain
Pa and
s. The density of the solution is
kg/m
3. As in the previous paper [
9], where the same problem is analyzed using the three-parameter Williamson model
, the layer has a half-width
mm, and pressure gradient is
Pa/m; the dimensionless variables and
become
and
. Equation (17) allows to calculate the velocity
, which produces the steady discharge
cm
2/s (W model
cm
2/s); the steady second-order velocity
can be calculated integrating numerically Equation (38), and then
, at frequency
Hz (
Hz)
, produces a discharge
cm
2/s (W model
cm
2/s). The constants
,
,
and
in Equations (26) and (27) become respectively
,
,
and
. Equation (28) allows calculating the first order periodic velocity
. At the layers axis
, i.e.,
, it results
m/s (W model
m/s).
4. Analysis and Discussion
To visualize the results and better understand them, it is useful to refer to the following Figures.
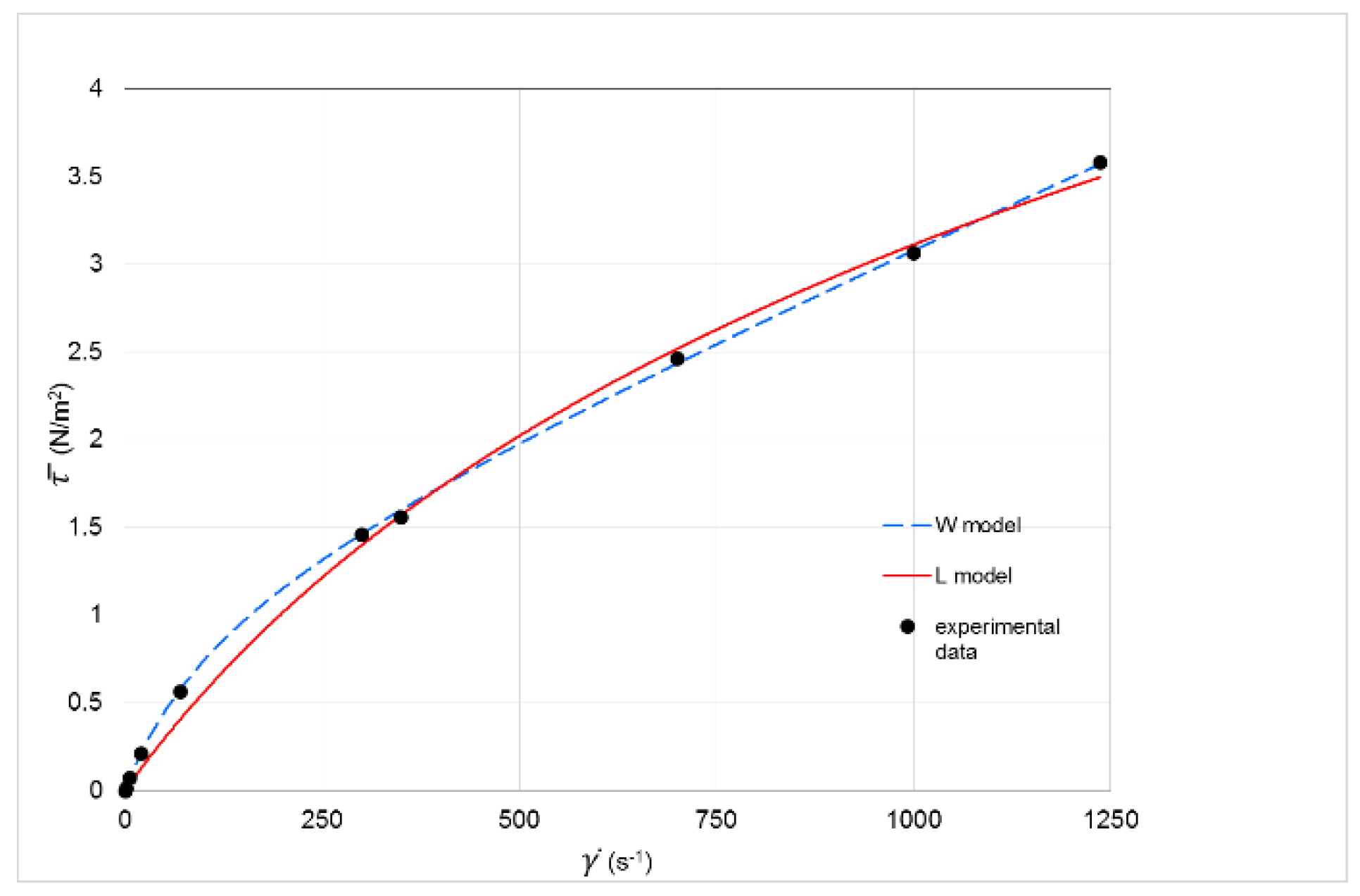
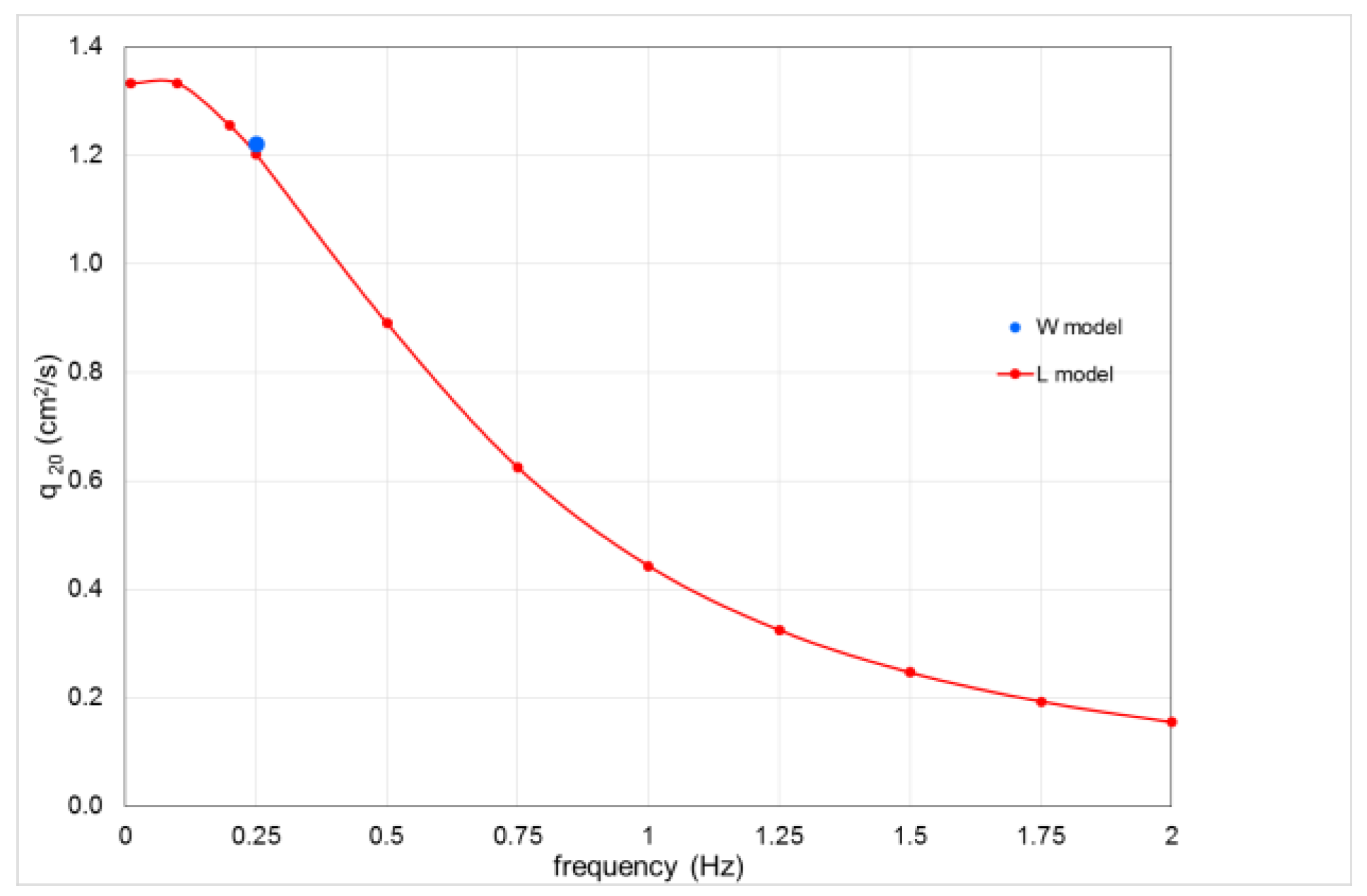
Figure 2 shows the experimental data and the approximating curves for the model of Williamson (W) and the logarithmic model (L); for low values of
, the model L gives minor values for
of the model W, and therefore a higher velocity can be expected at the axis of the layer.
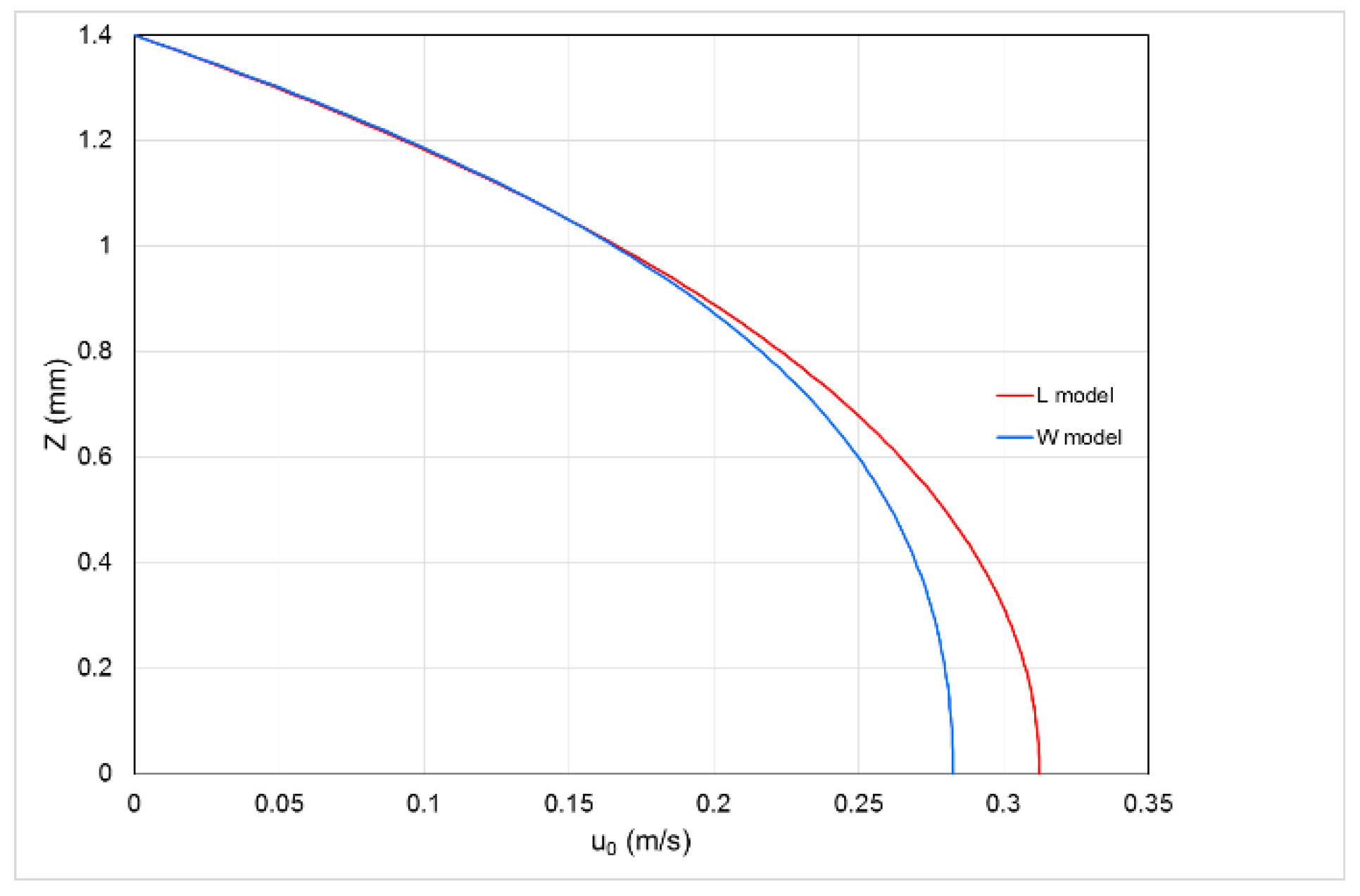
Figure 3 shows the velocity profile in a steady state. As expected, the L model gives rise to a stationary component of the axis velocity greater by about 10% compared to the one given by the model W.
The stationary flow rate, which is the most relevant data, differs in the two cases only by 3%.
Figure 4 shows, as a function of frequency, the first approximation speed evaluated on the axis, for both models. For low frequencies (<1 Hz), the W model gives higher values than the L model, with differences within 10%. It should be noted that the velocity
is less important, because it does not give rise to a flow rate in the period.
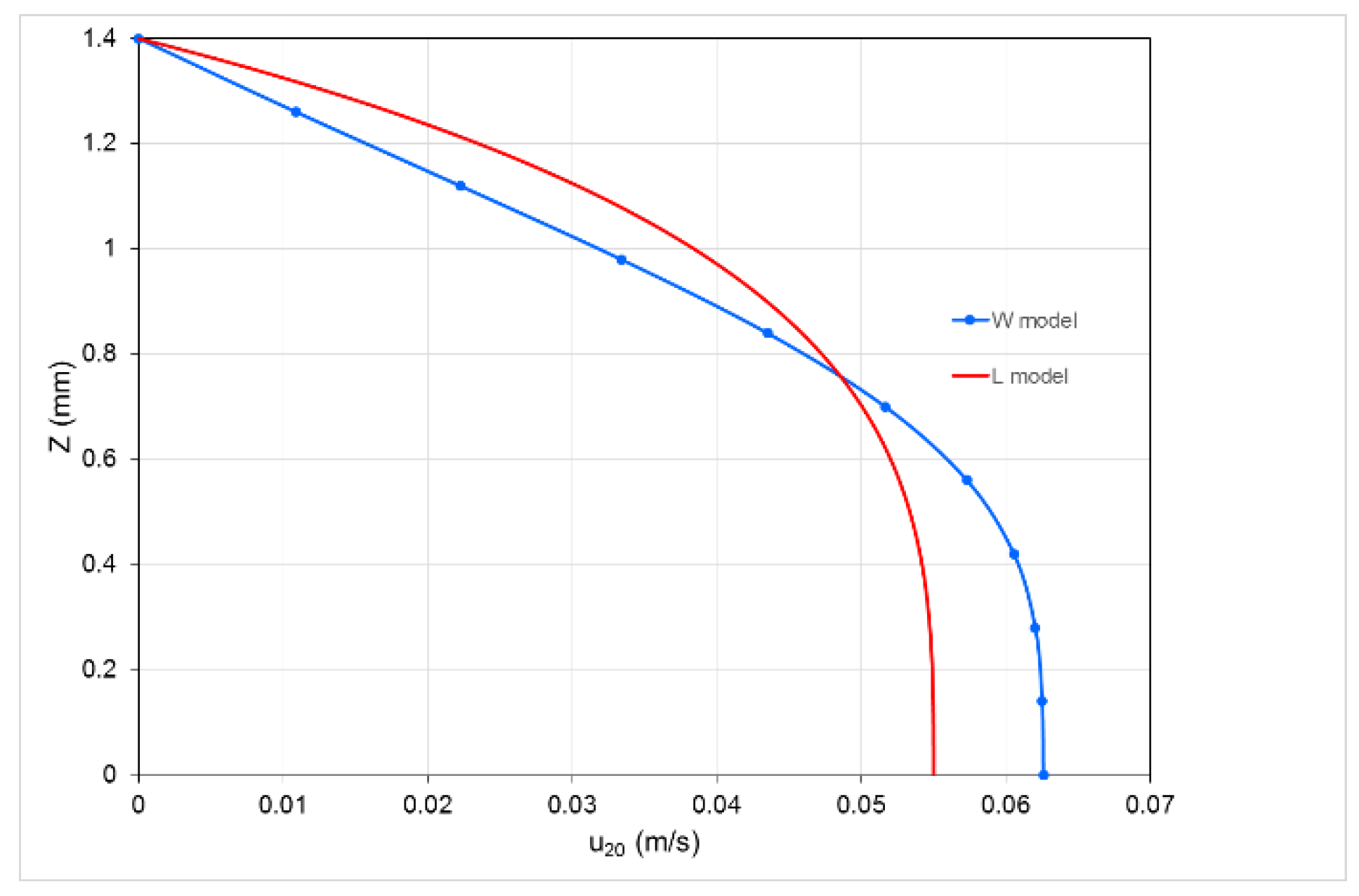
Figure 5 shows the steady component of the second-order approximation velocity
, for a frequency
Hz. Unlike the steady component, in the central part of the layer the W model gives a higher velocity than the L model, while in the zones towards the wall the L model gives a higher velocity. This is due to the great slope of the
curve relative to the W model, compared to that of the L model for low values of
(i.e., near the layers axis, see
Figure 2), which therefore increases the effects of the non-linearity. The opposite happens near the wall, where
is higher and the slope of the
is greater in the L model. The stationary rate of flow
, given by the two models for a frequency
Hz, is practically the same (difference < 2%) as shown in
Figure 6, where the second approximation stationary flow rate, calculated with the L model as a function of frequency, is plotted, together with the value given by the model W for
Hz [
9].
Figure 7 shows the velocity at the axis and at
as a function of time, for
Hz and
, taking into account the components
,
and
:
. As foreseeable by the velocity profiles in
Figure 3, the L model always gives a higher value at
, while for
the differences between the two models are considerably reduced.
From a mathematical point of view, the L model is simpler than the W model; the latter requires the calculation of complex index Bessel functions, while the L model makes use of the Kelvin functions of integer order (0 and 1), which are easily calculable and also tabulated, e.g., in the handbook of Abramowitz and Stegun [
12]. From a fluid mechanics point of view, to judge which of the two models is more suitable it would be necessary to have available experimental data, which the authors however have not been able to find in the literature. Both models do not take into account the roughness of the walls, which probably should produce a decrease in the flow rate. The effect of roughness, however, according to the authors, could be highlighted only by adopting a numerical solution.
5. Conclusions
The velocity field for a pulsatile flow of a non-Newtonian fluid in a rock fracture has been described using an approximate analytical expression. A two-parameter logarithmic model has been chosen to describe the rheological behavior of the fluid. The fracture has been schematized by two parallel smooth plates; this scheme gives reliable results if the normal stress is less than ~10 MPa and if the aperture variation along a flow path is not large. The solution, carried out up to the second order of approximation, is expressed as a power series expansion of the amplitude of the pulsatile component of the pressure gradient. A numerical example is made using the same fluid and the same geometry of a previous work by the authors, in which the fluid was represented with a three-parameter Williamson model in order to compare the results provided by the two models.
From the comparison, there results that the values of the mean flow rate in a period given by two different models are almost identical, even in the case in which the amplitude of the perturbation
ε is a quarter of the steady component. The velocity profiles are quite different; in particular, the velocity near the axis is higher for the L model (with a maximum deviation of 10% on the axis), since the apparent viscosity at low shear rate given by the L model is lower than that provided by the W model, as shown in
Figure 1.
The authors believe that it is essential to have several rheological models to test, because it is not possible to know a priori what will best represent the experimental data. They therefore consider the introduction of this particularly simple rheological model to be justified and useful.