An Improved SCS-CN Method Incorporating Slope, Soil Moisture, and Storm Duration Factors for Runoff Prediction
Abstract
:1. Introduction
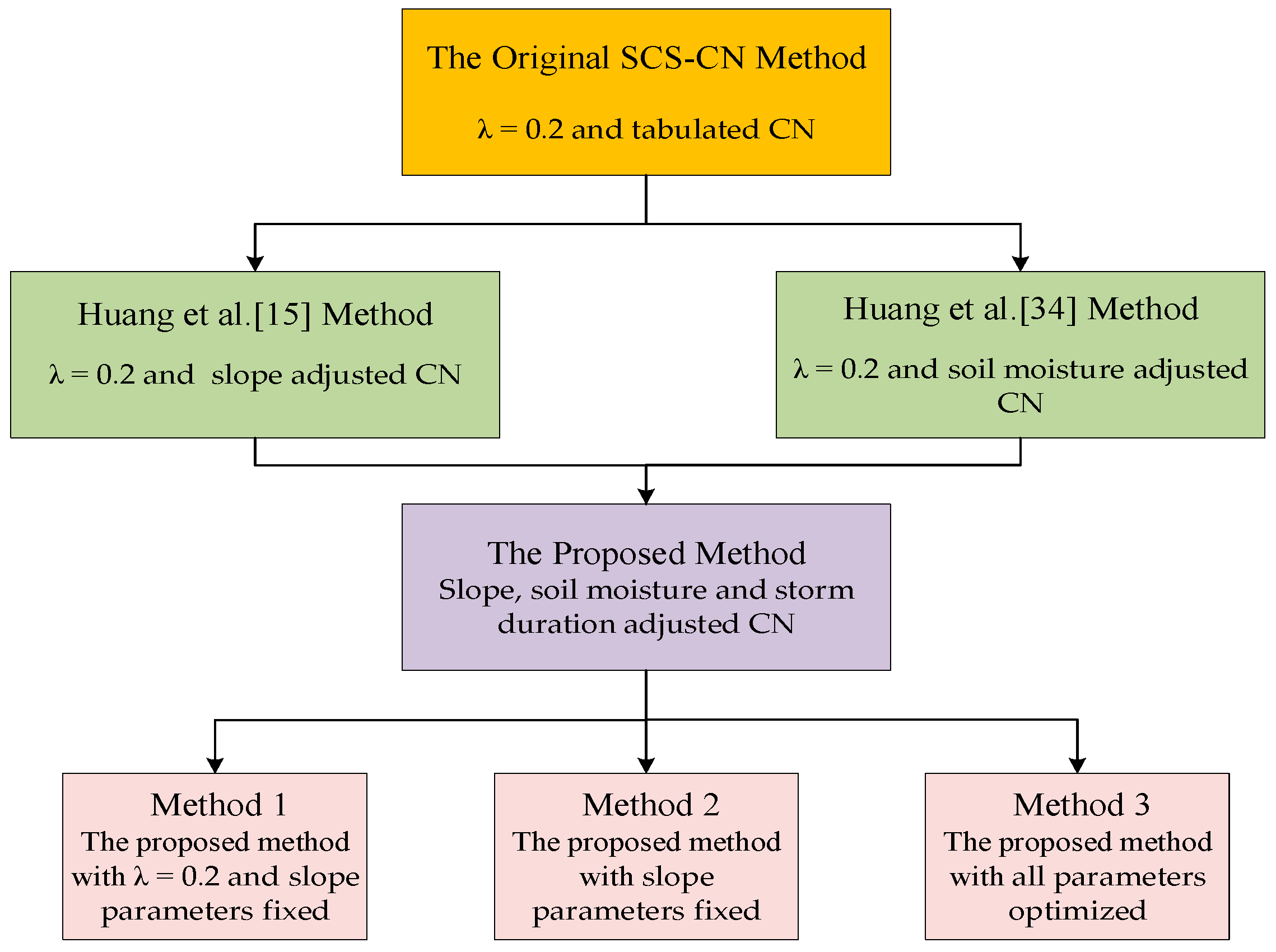
2. Methods
2.1. The Original SCS-CN Method
2.2. The Proposed Method
2.3. Performance of the Methods
3. Study Area and Data
3.1. Study Area
3.2. Data Collection
3.3. Parameter Estimation
4. Results
4.1. Model Calibration and Validation
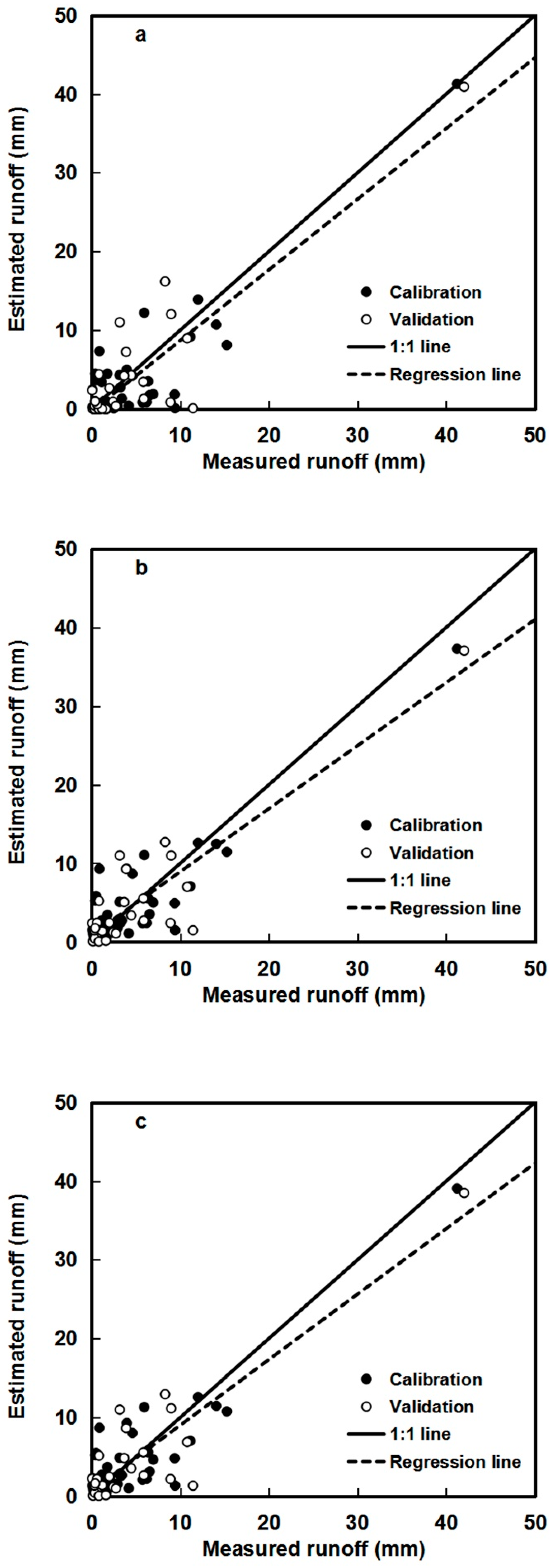
4.1.1. The Original SCS-CN Method
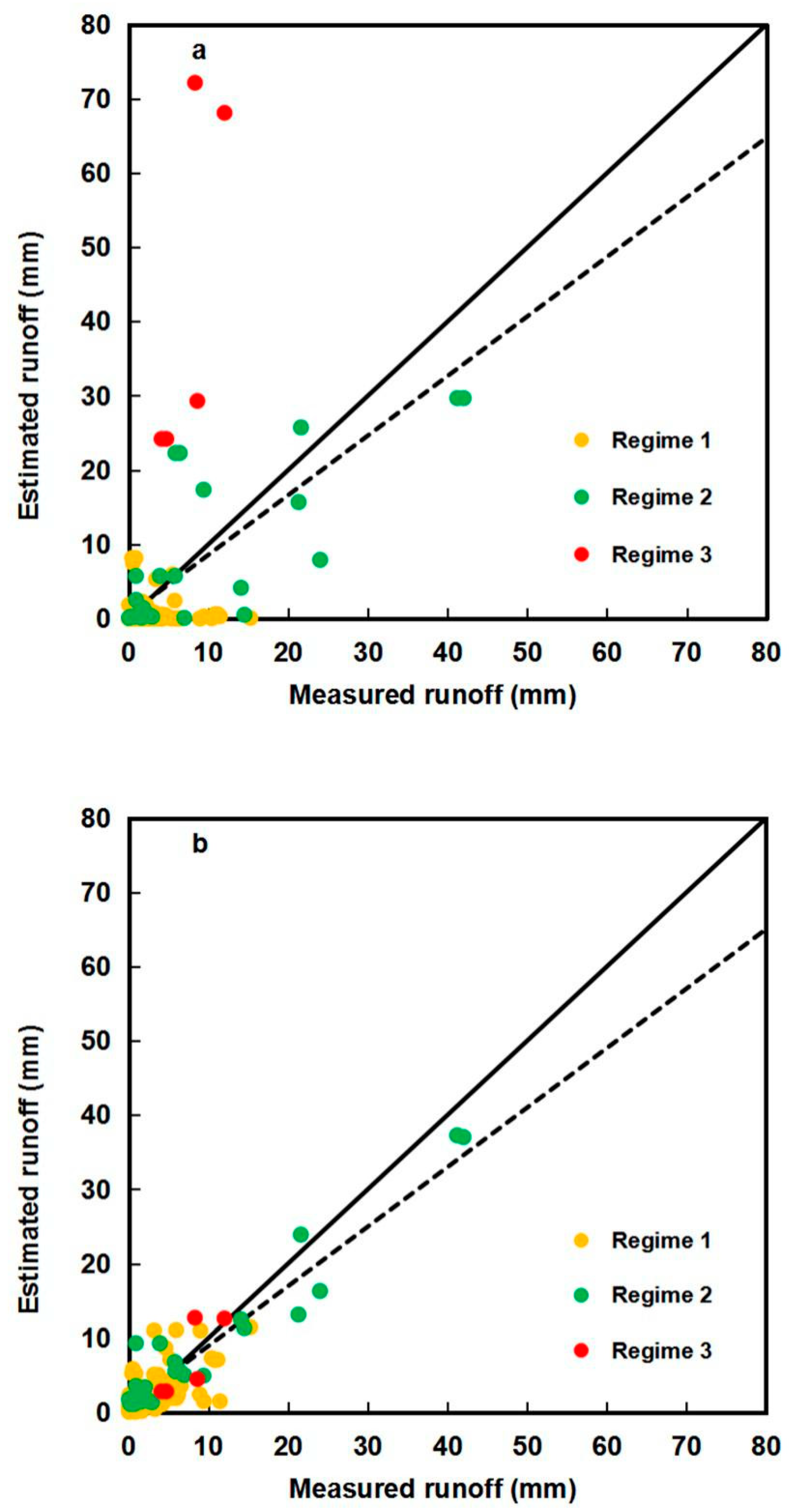
4.1.2. The Huang et al. and Huang et al. Methods
4.1.3. The Proposed Method (Methods 1–3)
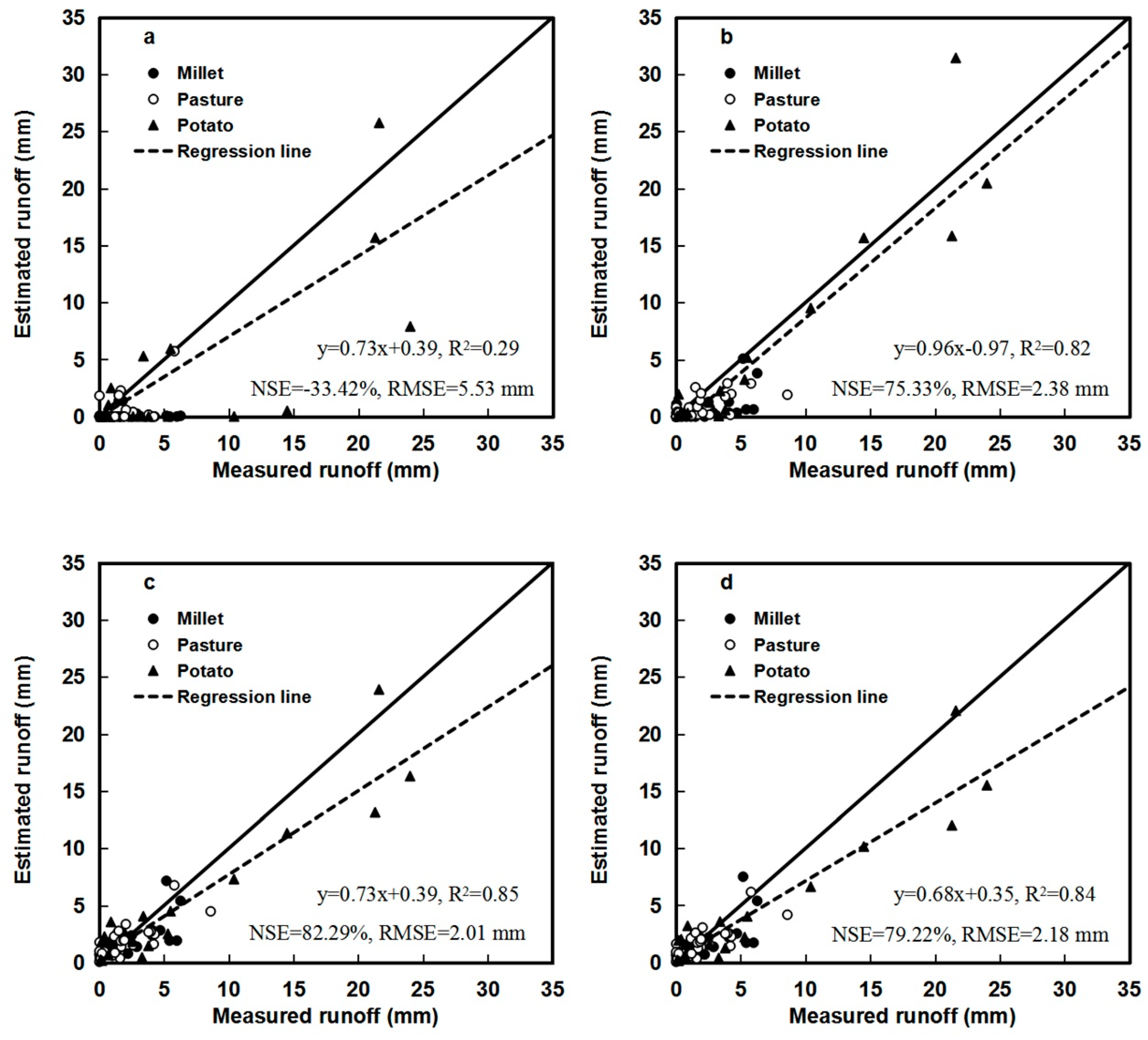
4.2. Model Application
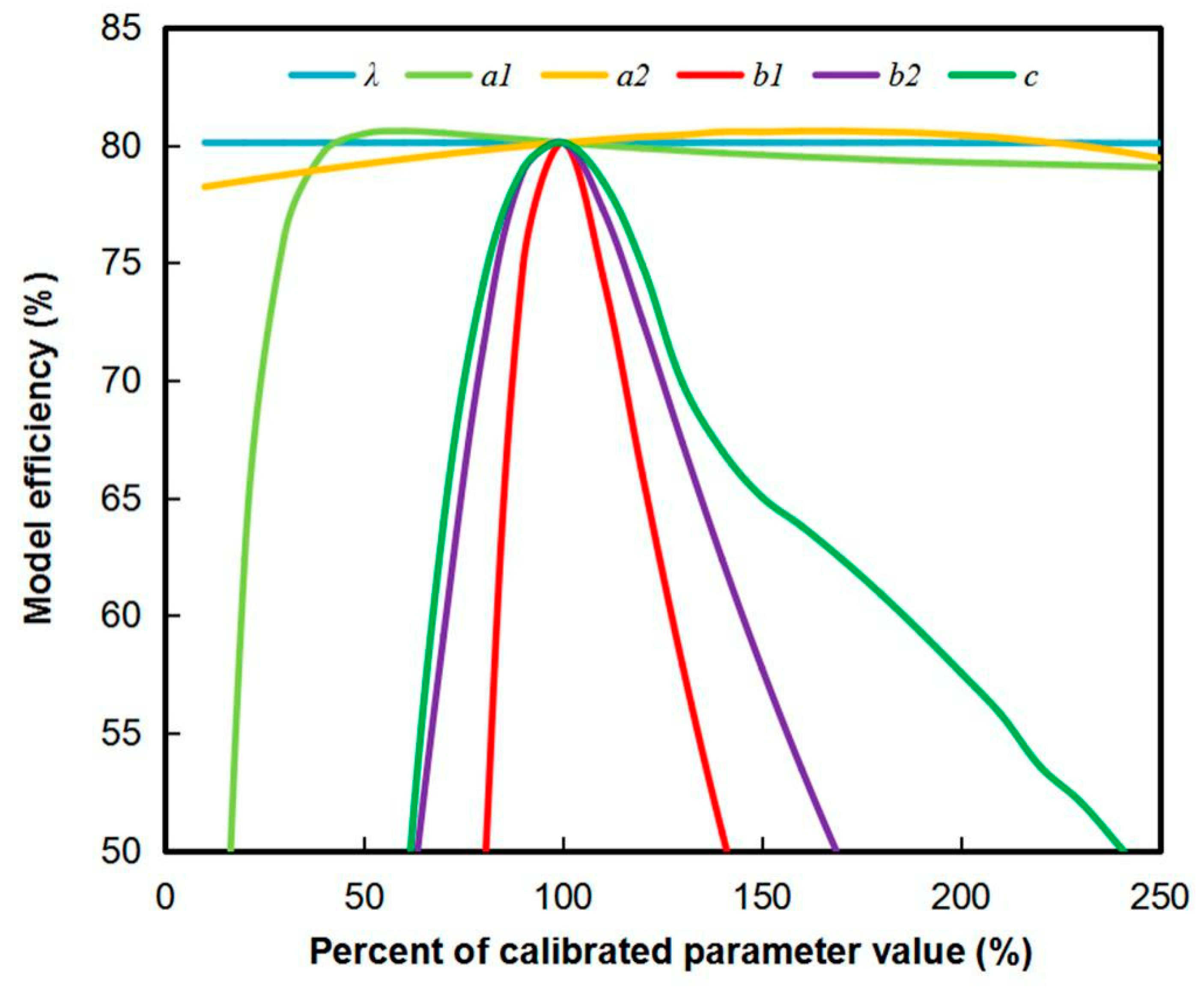
4.3. Sensitivity Analyses
5. Discussion
5.1. The Effect of Rainfall Duration
5.2. The Effect of Slope
5.3. The Effect of Soil Moisture
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data Availability Statement
References
- Shi, Z.H.; Chen, L.D.; Fang, N.F.; Qin, D.F.; Cai, C.F. Research on the SCS-CN initial abstraction ratio using rainfall-runoff event analysis in the Three Gorges Area, China. Catena 2009, 77, 1–7. [Google Scholar] [CrossRef]
- SCS. National Engineering Handbook, Section 4; Soil Conservation Service USDA: Washington, DC, USA, 1972. [Google Scholar]
- Shi, W.H.; Huang, M.B.; Barbour, S.L. Storm-based CSLE that incorporates the estimated runoff for soil loss prediction on the Chinese Loess Plateau. Soil Tillage Res. 2018, 180, 137–147. [Google Scholar] [CrossRef]
- Shi, W.H.; Huang, M.B.; Wu, L.H. Prediction of storm-based nutrient loss incorporating the estimated runoff and soil loss at a slope scale on the Loess Plateau, China. Land Degrad. Dev. 2018, 29, 2899–2910. [Google Scholar] [CrossRef]
- Kaffas, K.; Hrissanthou, V. Estimate of continuous sediment graphs in a basin, using a composite mathematical model. Environ. Process. 2015, 2, 361–378. [Google Scholar] [CrossRef] [Green Version]
- Baginska, B.; Milne-Home, W.; Cornish, P.S. Modelling nutrient transport in Currency Creek, NSW with AnnAGNPS and PEST. Environ. Model. Softw. 2003, 18, 801–808. [Google Scholar] [CrossRef]
- Knisel, W.G. CREAMS: A field-scale model for chemical, runoff and erosion from agricultural management systems. In Conservation Research Report, Volume 26; South East Area, US Department of Agriculture: Washington, DC, USA, 1980. [Google Scholar]
- Sharpley, A.N.; Williams, J.R. EPIC-Erosion/Productivity Impact Calculator: 1. Model Documentation; U.S. Department of Agriculture Technical Bulletin No. 1768; U.S. Government Printing Office: Washington, DC, USA, 1990.
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; Van Griensven, A.; Van Liew, M.W. SWAT: Model use, calibration and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Petroselli, A.; Grimaldi, S. Design hydrograph estimation in small and fully ungauged basins: A preliminary assessment of the EBA4SUB framework. J. Flood Risk Manag. 2018, 11, S197–S210. [Google Scholar] [CrossRef]
- Vojtek, M.; Petroselli, A.; Vojteková, J.; Asgharinia, S. Flood inundation mapping in small and ungauged basins: Sensitivity analysis using the EBA4SUB and HEC-RAS modeling approach. Hydrol. Res. 2019, 50, 1002–1019. [Google Scholar] [CrossRef] [Green Version]
- Ponce, V.M.; Hawkins, R.H. Runoff curve number: Has it reached maturity? J. Hydrol. Eng. ASCE 1996, 1, 11–19. [Google Scholar] [CrossRef]
- Bhuyan, S.J.; Mankin, K.R.; Koelliker, J.K. Watershed-scale AMC selection for hydrologic modeling. Trans. ASABE 2003, 46, 237–244. [Google Scholar] [CrossRef]
- Babu, P.S.; Mishra, S.K. Improved SCS-CN–inspired model. J. Hydrol. Eng. 2012, 17, 1164–1172. [Google Scholar] [CrossRef]
- Huang, M.; Gallichand, J.; Wang, Z.; Goulet, M. A modification to the Soil Conservation Service curve number method for steep slopes in the Loess Plateau of China. Hydrol. Process. 2006, 20, 579–589. [Google Scholar] [CrossRef]
- Grimaldi, S.; Petroselli, A.; Romano, N. Green-Ampt Curve-Number mixed procedure as an empirical tool for rainfall-runoff modelling in small and ungauged basins. Hydrol. Process. 2013, 27, 1253–1264. [Google Scholar] [CrossRef]
- Jain, M.K.; Mishra, S.K.; Babu, P.S.; Venugopal, K.; Singh, V.P. Enhanced runoff curve number model incorporating storm duration and a nonlinear Ia‒S relation. J. Hydrol. Eng. 2006, 11, 631–635. [Google Scholar] [CrossRef]
- Mishra, S.K.; Jain, M.K.; Babu, P.S.; Venugopal, K.; Kaliappan, S. Comparison of AMC-dependent CN-conversion formulae. Water Resour. Manag. 2008, 22, 1409–1420. [Google Scholar] [CrossRef]
- Singh, P.K.; Mishra, S.K.; Berndtsson, R.; Jain, M.K.; Pandey, R.P. Development of a modified SMA based MSCS-CN model for runoff estimation. Water Resour. Manag. 2015, 29, 4111–4127. [Google Scholar] [CrossRef]
- Hawkins, R.H. The importance of accurate curve numbers in the estimation of storm runoff. Water Resour. Bull. 1975, 11, 887–891. [Google Scholar] [CrossRef]
- Hawkins, R.H. Asymptotic determination of runoff curve numbers from data. J. Irrig. Drain. Eng. ASCE 1993, 119, 334. [Google Scholar] [CrossRef]
- Jiao, P.; Xu, D.; Wang, S.; Yu, Y.; Han, S. Improved SCS-CN method based on storage and depletion of antecedent daily precipitation. Water Resour. Manag. 2015, 29, 4753–4765. [Google Scholar] [CrossRef]
- Michel, C.; Andréassian, V.; Perrin, C. Soil conservation service curve number method: How to mend a wrong soil moisture accounting procedure? Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Sahu, R.K.; Mishra, S.K.; Eldho, T.I. An improved AMC-coupled runoff curve number model. Hydrol. Process. 2010, 24, 2834–2839. [Google Scholar] [CrossRef]
- Shi, W.H.; Huang, M.B.; Gongadze, K.; Wu, L.H. A modified SCS-CN method incorporating storm duration and antecedent soil moisture estimation for runoff prediction. Water Resour. Manag. 2017, 31, 1713–1727. [Google Scholar] [CrossRef]
- Petroselli, A.; Grimaldi, S.; Piscopia, R.; Tauro, F. Design hydrograph estimation in small and ungauged basins: A comparative assessment of event based (EBA4SUB) and continuous (COSMO4SUB) modelling approaches. Acta Sci. Pol. Form. Circumiectus 2019, 18, 113–124. [Google Scholar]
- Sahu, R.K.; Mishra, S.K.; Eldho, T.I. Improved storm duration and antecedent moisture condition coupled SCS-CN concept-based model. J. Hydrol. Eng. 2012, 17, 1173–1179. [Google Scholar] [CrossRef]
- Hawkins, R.H. Runoff curve numbers with varying site moisture. J. Irrig. Drain. Div. 1978, 104, 389–398. [Google Scholar] [CrossRef]
- Wood, E.F. An analysis of the effects of parameter uncertainty in deterministic hydrologic models. Water Resour. Res. 1976, 12, 925–932. [Google Scholar] [CrossRef]
- Michele, C.D.; Salvadori, G. On the flood frequency distribution: Analytical formulation and the influence of antecedent soil moisture condition. J. Hydrol. 2002, 262, 245–258. [Google Scholar] [CrossRef]
- Saxton, K.E. User’s Manual for SPAW: A Soil-Plant-Atmosphere Water Model; USDA-ARS: Pullman, WA, USA, 1992. [Google Scholar]
- Koelliker, J.K. User’s Manual of Potential Yield Model Revised (POTYLDR); Kansas State University, Department of Biological and Agricultural Engineering: Manhattan, KS, USA, 1994. [Google Scholar]
- Jacobs, J.M.; Myers, D.A.; Whitfield, B.M. Improved rainfall/runoff estimates using remotely sensed soil moisture. J. Am. Water. Resour. Assoc. 2003, 39, 313–324. [Google Scholar] [CrossRef]
- Huang, M.; Gallichand, J.; Dong, C.; Wang, Z.; Shao, M. Use of soil moisture data and curve number method for estimating runoff in the Loess Plateau of China. Hydrol. Process. 2007, 21, 1471–1481. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.E. River flow forecasting through conceptual models: Part I-A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Risse, L.M.; Nearing, M.A.; Savabi, M.R. Determining the Green-Ampt effective hydraulic conductivity from rainfall-runoff data for the WEEP model. Trans. ASAE 1994, 37, 411–418. [Google Scholar] [CrossRef]
- Liu, B.Y.; Nearing, M.A.; Risse, L.M. Slope gradient effects on soil loss for steep slopes. Trans. ASAE 1994, 37, 1835–1840. [Google Scholar] [CrossRef]
- Kimura, R.; Liu, Y.; Takayama, N.; Zhang, X.; Kamichika, M.; Matsuoka, N. Heat and water balances of the bare soil surface and the potential distribution of vegetation in the Loess Plateau, China. J. Arid Environ. 2005, 63, 439–457. [Google Scholar] [CrossRef]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Ritter, A.; Muñoz-Carpena, R. Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- Baltas, E.A.; Dervos, N.A.; Mimikou, M.A. Technical Note: Determination of the SCS initial abstraction ratio in an experimental watershed in Greece. Hydrol. Earth Syst. Sci. 2007, 11, 1825–1829. [Google Scholar] [CrossRef] [Green Version]
- Walega, A.; Amatya, D.M.; Caldwell, P.; Marion, D.; Panda, S. Assessment of storm direct runoff and peak flow rates using improved SCS-CN models for selected forested watersheds in the Southeastern United States. J. Hydrol. Reg. Stud. 2020, 27, 100645. [Google Scholar] [CrossRef]
- Hong, N. Products and Servicing Solution Teaching Book for SPSS of Windows Statistical; Tsinghua University Press, and Beijing Communication University Press: Beijing, China, 2003; pp. 300–311. [Google Scholar]
- Wei, W.; Chen, L.L.; Fu, B.J.; Huang, Z.L.; Wu, D.P.; Gui, L.D. The effect of land uses and rainfall regimes on runoff and soil erosion in the semi-arid loess hilly area, China. J. Hydrol. 2007, 335, 247–258. [Google Scholar] [CrossRef]
- Fang, H.Y.; Cai, Q.G.; Chen, H.; Li, Q.Y. Effect of rainfall regime and slope on runoff in a gullied loess region on the Loess Plateau in China. Environ. Manag. 2008, 42, 402–411. [Google Scholar] [CrossRef]
- Mishra, S.K.; Pandey, R.P.; Jain, M.K.; Singh, V.P. A rain duration and modified AMC-dependent SCS-CN procedure for long duration rainfall-runoff events. Water Resour. Manag. 2008, 22, 861–876. [Google Scholar] [CrossRef]
- Reaney, S.M.; Bracken, L.J.; Kirkby, M.J. Use of the connectivity of runoff model (CRUM) to investigate the influence of storm characteristics on runoff generation and connectivity in semi-arid areas. Hydrol. Process. 2010, 21, 894–906. [Google Scholar] [CrossRef]
- Evett, S.R.; Dutt, G.R. Length and slope effects on runoff from sodium dispersed, compacted earth microcatchments. Soil Sci. Soc. Am. J. 1985, 49, 734–738. [Google Scholar] [CrossRef]
- Philip, J.R. Hillslope infiltration: Planar slopes. Water Resour. Res. 1991, 27, 109–117. [Google Scholar] [CrossRef]
- Huang, C.H. Empirical analysis of slope and runoff for sediment delivery from interrill areas. Soil Sci. Soc. Am. J. 1995, 59, 982–990. [Google Scholar] [CrossRef]
- Fox, D.M.; Bryan, R.B.; Price, A.G. The influence of slope angle on final infiltration rate for interrill conditions. Geoderma 1997, 80, 181–194. [Google Scholar] [CrossRef]
- Chaplot, V.A.M.; Bissonnais, Y.L. Runoff features for interrill erosion at different rainfall intensities, slope lengths, and gradients in an agricultural loessial hillslope. Soil Sci. Soc. Am. J. 2003, 67, 844–851. [Google Scholar] [CrossRef]
- Koelliker, J.K. Hydrologic design criteria for dams with equal reliability. In Irrigation Systems in the 21st Century; James, L.G., Ed.; ASCE: New York, NY, USA, 1987; pp. 100–107. [Google Scholar]
- Hjelmfelt, A.T.J.; Kramer, K.A.; Burwell, R.E. Curve numbers as random variables. In Proceeding, International Symposium on Rainfall-Runoff Modelling; Singh, V.P., Ed.; Water Resources Publication: Littleton, CO, USA, 1982; pp. 365–373. [Google Scholar]



| Watershed | XDG | CBG | ||||
|---|---|---|---|---|---|---|
| Plot | 1 | 2 | 3 | 1 | 2 | 3 |
| Land use | Grassland | Grassland | Cropland | Grassland | Cropland | Cropland |
| Vegetation | Alfalfa | Sweet clover | Millet | Pasture | Millet | Potato |
| Length (m) | 20 | 20 | 20 | 40 | 20 | 20 |
| Width (m) | 5 | 5 | 5 | 10 | 10 | 10 |
| Slope gradient (°) | 35 | 33 | 15 | 30 | 25 | 22 |
| Soil moisture (%) | 18.54 ± 5.93 | 18.08 ± 5.92 | 19.68 ± 5.89 | 15.82 ± 4.50 | 16.80 ± 5.64 | 16.79 ± 4.30 |
| Rainfall (mm) | 23.59 ± 14.43 | 23.90 ± 22.76 | 25.97 ± 22.08 | 22.31 ± 24.31 | 24.81 ± 28.24 | 23.93 ± 17.88 |
| Runoff (mm) | 4.52 ± 8.54 # | 4.60 ± 7.97 | 4.09 ± 4.52 | 2.07 ± 2.12 | 2.02 ± 1.95 | 6.61 ± 8.16 |
| Strom duration (h) | 4.53 ± 6.08 | 4.88 ± 6.53 | 5.84 ± 6.95 | 4.65 ± 6.74 | 5.82 ± 7.75 | 2.46 ± 2.59 |
| Observation period | 1956–1959 | 1956–1959 | 1954–1959 | 1959–1961 | 1959–1962 | 1964–1965 |
| Model | Parameter | |||||
|---|---|---|---|---|---|---|
| λ | a1 | a2 | b1 | b2 | c | |
| Original SCS-CN | 0.2 | - | - | - | - | - |
| Huang et al. [15] | 0.2 | 323.57 | 15.63 | - | - | - |
| Huang et al. [34] | 0.2 | - | - | 0.01 | 1.12 | - |
| Method 1 | 0.2 | 323.57 | 15.63 | 0.05 | 0.61 | 0.020 |
| Method 2 | 0.001 | 323.57 | 15.63 | 0.13 | 0.31 | 0.035 |
| Method 3 | 0.001 | 213.99 | 25.38 | 0.15 | 0.24 | 0.035 |
| Model | Linear Regression | NSE | RMSE | Performance Rating [40] | ||
|---|---|---|---|---|---|---|
| Slope | Interception | R2 | (%) | (mm) | ||
| Calibration | ||||||
| Original SCS-CN | 0.83 | 0.07 | 0.24 | −118.64 | 9.83 | Unsatisfactory |
| Huang et al. [15] | 0.92 | 0.10 | 0.27 | −133.00 | 10.14 | Unsatisfactory |
| Huang et al. [34] | 0.27 | 0.41 | 0.15 | −9.80 | 6.96 | Unsatisfactory |
| Method 1 | 0.88 | −0.48 | 0.79 | 75.84 | 3.26 | Acceptable |
| Method 2 | 0.80 | 0.95 | 0.80 | 80.58 | 2.94 | Good |
| Method 3 | 0.82 | 0.72 | 0.81 | 80.73 | 2.91 | Good |
| Validation | ||||||
| Original SCS-CN | 0.77 | 1.33 | 0.18 | −182.60 | 13.18 | Unsatisfactory |
| Huang et al. [15] | 0.87 | 1.58 | 0.19 | −229.67 | 14.23 | Unsatisfactory |
| Huang et al. [34] | 0.21 | 1.14 | 0.07 | −32.27 | 9.02 | Unsatisfactory |
| Method 1 | 0.92 | 0.04 | 0.80 | 77.45 | 3.72 | Acceptable |
| Method 2 | 0.81 | 0.87 | 0.81 | 80.44 | 3.46 | Good |
| Method 3 | 0.84 | 0.71 | 0.81 | 81.21 | 3.40 | Good |
| Full data | ||||||
| Original SCS-CN | 0.80 | 0.56 | 0.21 | −148.17 | 11.23 | Unsatisfactory |
| Huang et al. [15] | 0.90 | 0.67 | 0.23 | −177.64 | 11.87 | Unsatisfactory |
| Huang et al. [34] | 0.24 | 0.70 | 0.11 | −20.18 | 7.81 | Unsatisfactory |
| Method 1 | 0.90 | −0.30 | 0.79 | 76.58 | 3.45 | Acceptable |
| Method 2 | 0.80 | 0.92 | 0.81 | 80.50 | 3.15 | Good |
| Method 3 | 0.83 | 0.71 | 0.81 | 80.95 | 3.11 | Good |
| Rainfall Regime | Eigenvalue | Mean | Standard Deviation | Variation Coefficient | Frequency (%) |
|---|---|---|---|---|---|
| Regime 1 | P (mm) | 14.92 | 6.95 | 0.47 | 79.73 |
| D (h) | 2.43 | 2.55 | 1.05 | ||
| Regime 2 | P (mm) | 50.49 | 11.06 | 0.22 | 16.89 |
| D (h) | 12.61 | 7.94 | 0.63 | ||
| Regime 3 | P (mm) | 109.36 | 7.68 | 0.07 | 3.38 |
| D (h) | 22.93 | 1.31 | 0.06 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, W.; Wang, N. An Improved SCS-CN Method Incorporating Slope, Soil Moisture, and Storm Duration Factors for Runoff Prediction. Water 2020, 12, 1335. https://doi.org/10.3390/w12051335
Shi W, Wang N. An Improved SCS-CN Method Incorporating Slope, Soil Moisture, and Storm Duration Factors for Runoff Prediction. Water. 2020; 12(5):1335. https://doi.org/10.3390/w12051335
Chicago/Turabian StyleShi, Wenhai, and Ni Wang. 2020. "An Improved SCS-CN Method Incorporating Slope, Soil Moisture, and Storm Duration Factors for Runoff Prediction" Water 12, no. 5: 1335. https://doi.org/10.3390/w12051335
APA StyleShi, W., & Wang, N. (2020). An Improved SCS-CN Method Incorporating Slope, Soil Moisture, and Storm Duration Factors for Runoff Prediction. Water, 12(5), 1335. https://doi.org/10.3390/w12051335




