Comparison of Local and Global Optimization Methods for Calibration of a 3D Morphodynamic Model of a Curved Channel
Abstract
1. Introduction
2. Methodology
2.1. Experimental Data
2.2. Numerical Model
2.3. Calibration Procedure
2.3.1. Local Optimization Method
2.3.2. Global Optimization Methods
2.3.3. Investigated Parameters
- Roughness height at the bed (ks): For fixed beds, this parameter is typically assumed to be proportional to the representative grain size dn (the diameter where n% of sediment grains are finer) (i.e., Nikoradse’s equivalent grain roughness). For movable beds, however, the roughness caused by bedforms has to be added to the grain roughness, which may increase it with a higher factor than the grain roughness itself. A collection of different equations regarding the roughness height can be found in the literature (e.g., [87]). In this study, despite the dynamic nature of the roughness coefficient due to the formation of bedforms, the roughness height is considered to be uniform along the whole domain, because of the focus on the automatic calibration procedure. The range of this parameter is selected to be between d50 and 10d90.
- Active layer thickness (ALT): This parameter is described as a function of the representative grain diameter and the bedform height as a dynamic value that depends on the sediment properties and the flow conditions. ALT determines the maximum depth of erosion during one time-step in the numerical model. For this study, a constant value of ALT is also chosen, with a range between d50 and 5dmax [88,89].
- The volume fraction of compacted sediments (VFS): This parameter describes the proportion of deposited sediments in the bed compared to the water content, which depends on the bulk density as a function of grain size distribution and packing of sediment depositions. This parameter’s range is adjusted between 40% and 60% in the calibration process.
2.4. Work Structure
3. Results and Discussion
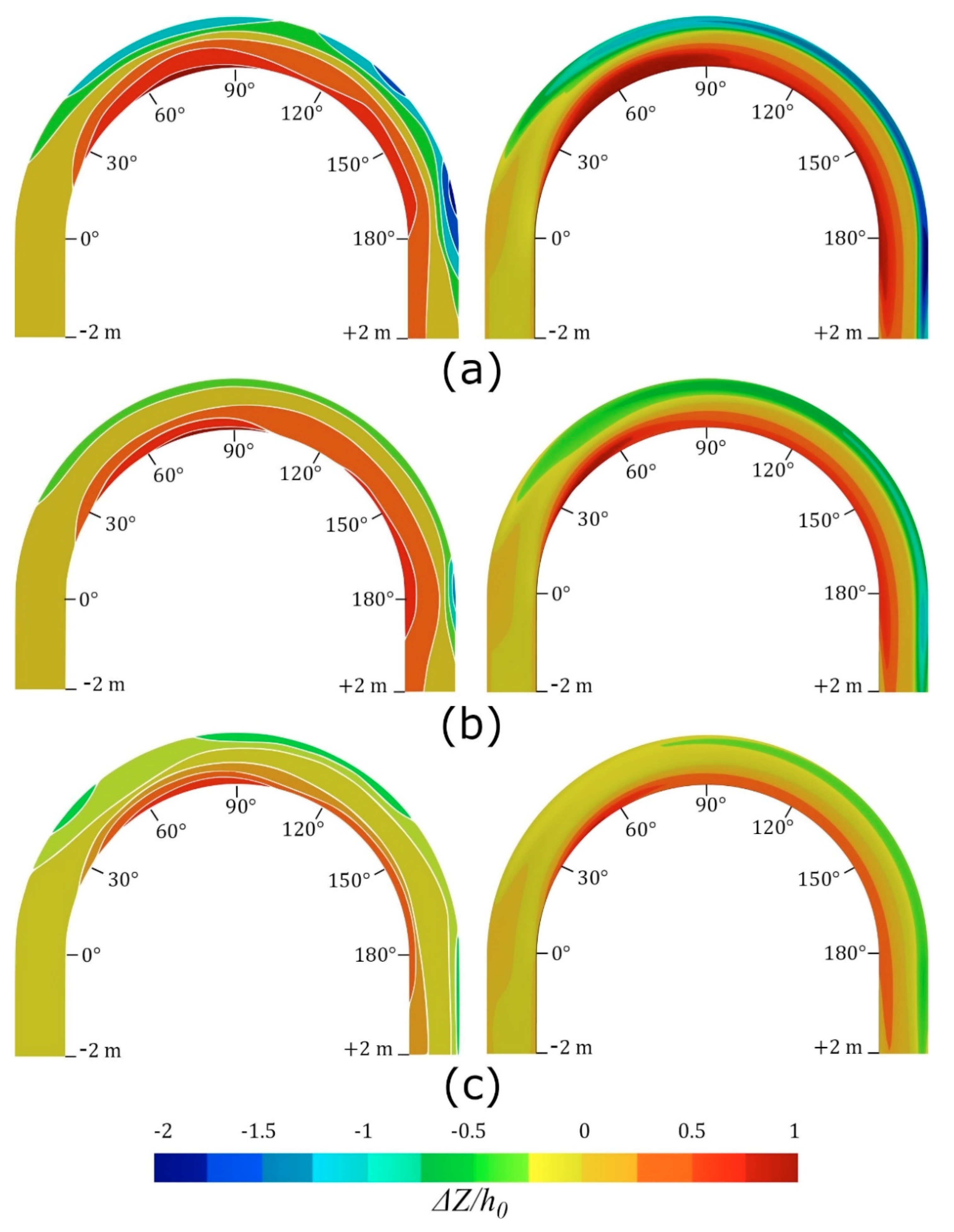
3.1. Testing the Performance of Different Optimization Methods
- PEST#2 (ks = d90, ALT = 2dmax, and VFS = 55%)
- PEST#3 (ks = 2d90, ALT = 4dmax, and VFS = 45%)
- PEST#4 (ks = 5d90, ALT = 2dmax, and VFS = 50%)
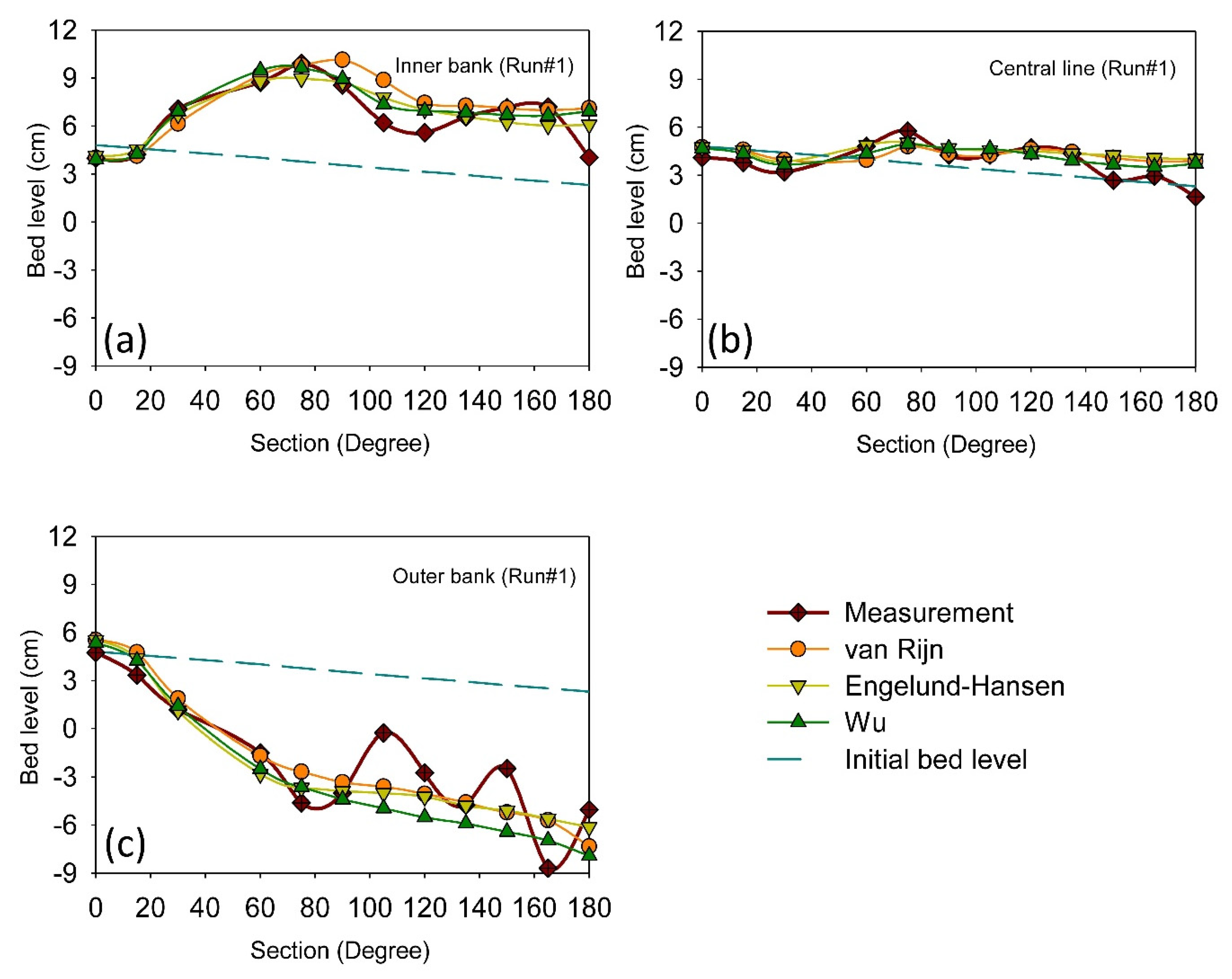
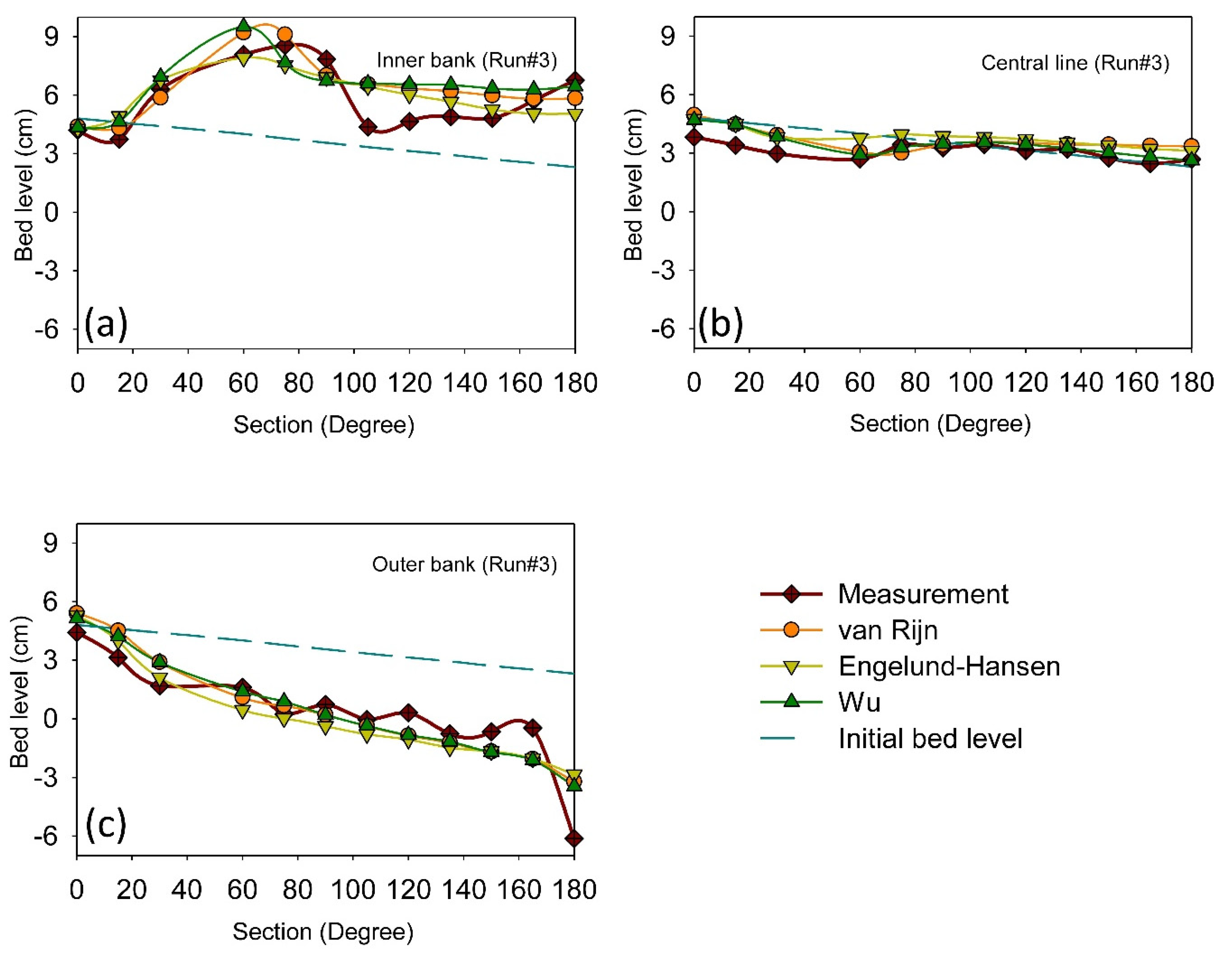
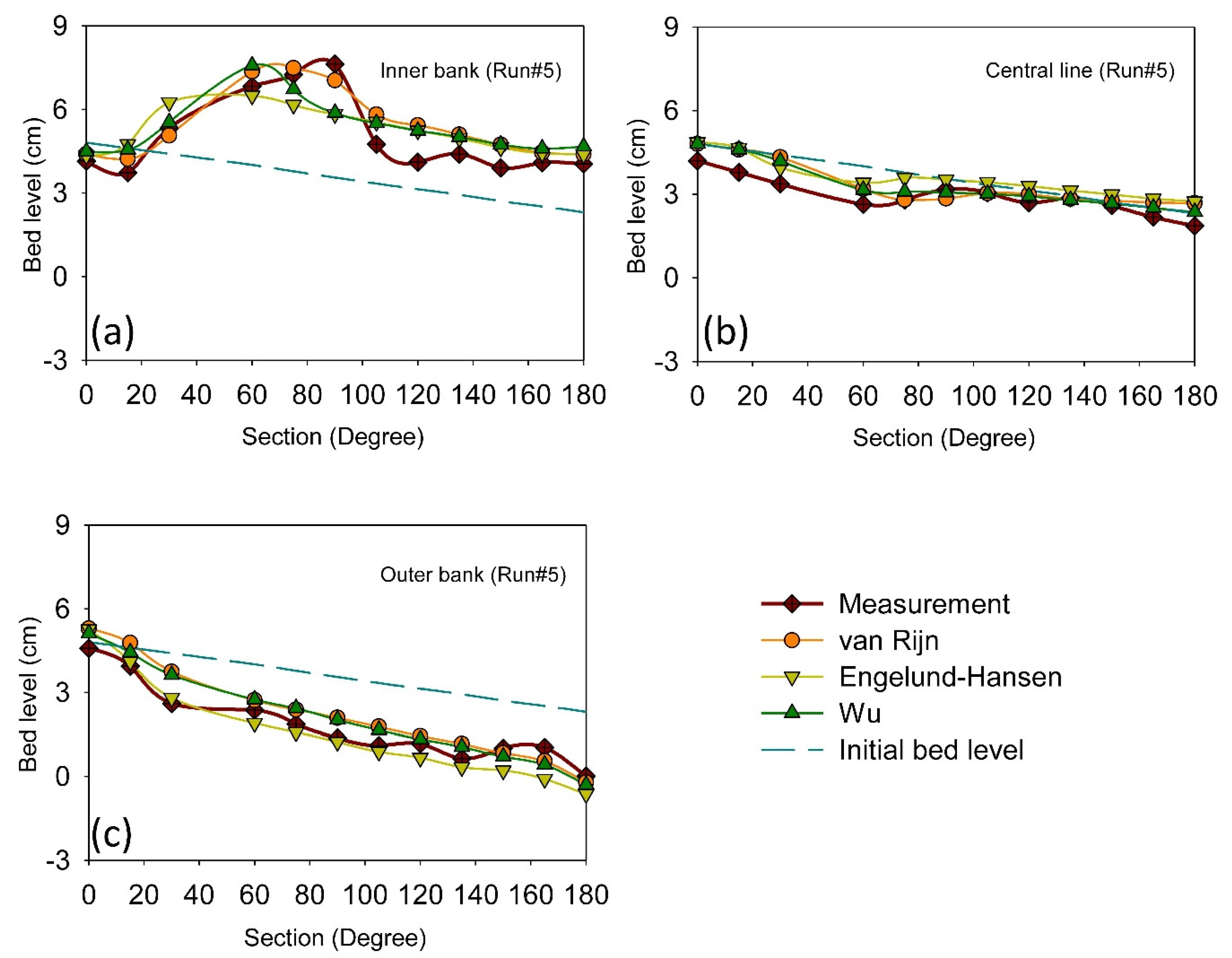
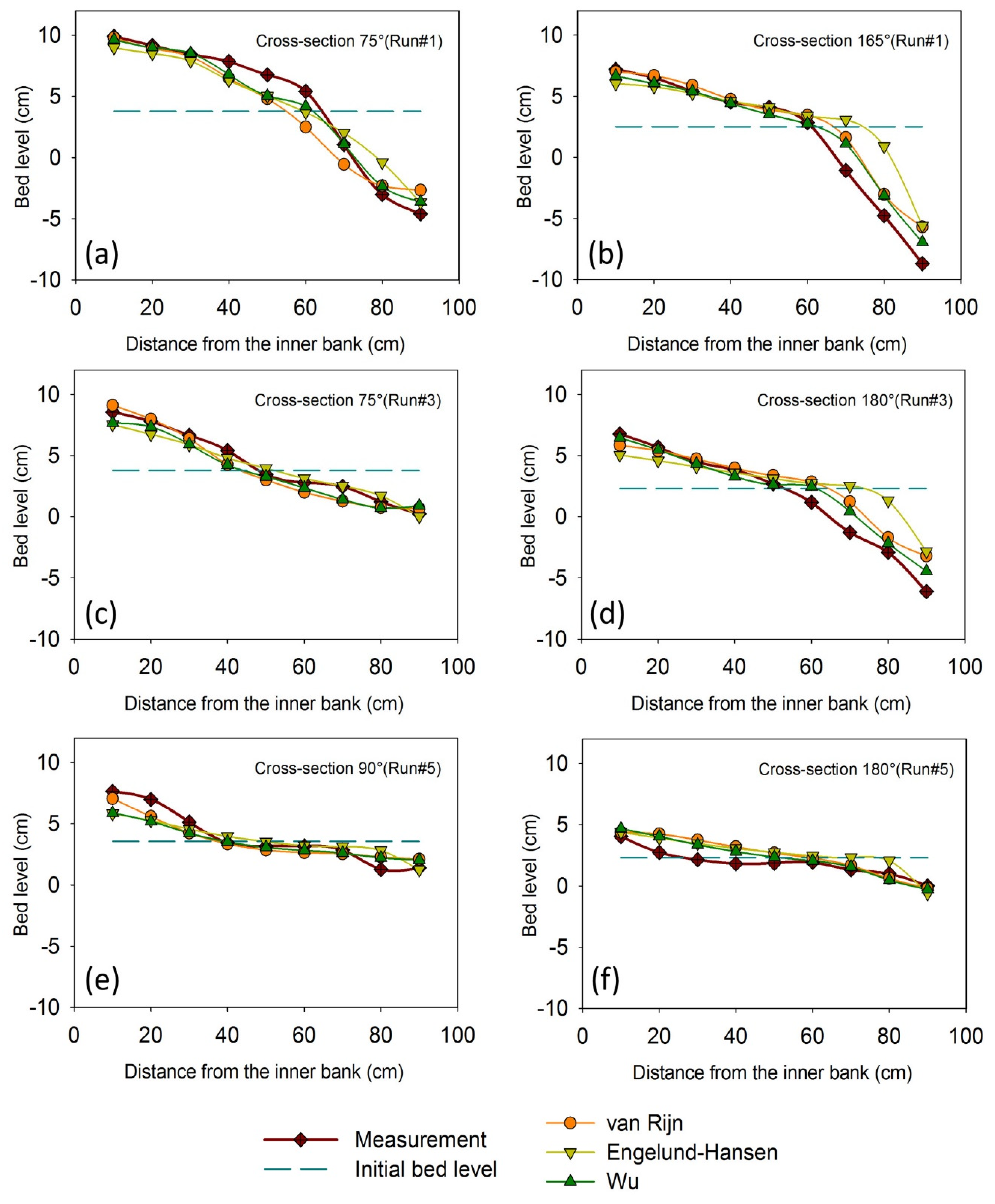
3.2. Application of the Selected Calibration Method for Additional Numerical Setups
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- McIntyre, N.; Wheater, H.; Lees, M. Estimation and propagation of parametric uncertainty in environmental models. J. Hydroinf. 2002, 4, 177–198. [Google Scholar] [CrossRef]
- Thomann, R.V. The future “golden age” of predictive models for surface water quality and ecosystem management. J. Environ. Eng. 1998, 124, 94–103. [Google Scholar] [CrossRef]
- Cunge, J.A. Of data and models. J. Hydroinf. 2003, 5, 75–98. [Google Scholar] [CrossRef]
- Oberkampf, W.L.; Trucano, T.G.; Hirsch, C. Verification, validation, and predictive capability in computational engineering and physics. Appl. Mech. Rev. 2004, 57, 345–384. [Google Scholar] [CrossRef]
- Kleijnen, J.P.C. Verification and validation of simulation models. Eur. J. Oper. Res. 1995, 82, 145–162. [Google Scholar] [CrossRef]
- Oreskes, N.; Shrader-Frechette, K.; Belitz, K. Verification, validation, and confirmation of numerical models in the earth sciences. Science 1994, 263, 641–646. [Google Scholar] [CrossRef]
- Bahremand, A.; De Smedt, F. Distributed hydrological modeling and sensitivity analysis in Torysa Watershed, Slovakia. Water Resour. Manag. 2008, 22, 393–408. [Google Scholar] [CrossRef]
- Muleta, M.K.; Nicklow, J.W. Sensitivity and uncertainty analysis coupled with automatic calibration for a distributed watershed model. J. Hydrol. 2005, 306, 127–145. [Google Scholar] [CrossRef]
- Sargent, R.G. Verification and validation of simulation models. J. Simul. 2013, 7, 12–24. [Google Scholar] [CrossRef]
- Oberkampf, W.L.; Trucano, T.G. Verification and validation benchmarks. Nucl. Eng. Des. 2008, 238, 716–743. [Google Scholar] [CrossRef]
- Rebba, R.; Mahadevan, S.; Huang, S. Validation and error estimation of computational models. Reliab. Eng. Syst. Saf. 2006, 91, 1390–1397. [Google Scholar] [CrossRef]
- Refsgaard, J.C.; Henriksen, H.J. Modelling guidelines—Terminology and guiding principles. Adv. Water Resour. 2004, 27, 71–82. [Google Scholar] [CrossRef]
- Acuña, G.J.; Ávila, H.; Canales, F.A. River model calibration based on design of experiments theory. A case study: Meta River, Colombia. Water 2019, 11, 1382. [Google Scholar]
- Troy, T.J.; Wood, E.F.; Sheffield, J. An efficient calibration method for continental-scale land surface modeling: Efficient calibration for large-scale land surface modeling. Water Resour. Res. 2008. [Google Scholar] [CrossRef]
- Hogue, T.S.; Sorooshian, S.; Gupta, H.; Holz, A.; Braatz, D. A multistep automatic calibration scheme for river forecasting models. J. Hydrometeorol. 2000, 1, 524–542. [Google Scholar] [CrossRef]
- Madsen, H. Automatic calibration of a conceptual rainfall–runoff model using multiple objectives. J. Hydrol. 2000, 235, 276–288. [Google Scholar] [CrossRef]
- Moradkhani, H.; Sorooshian, S. General review of rainfall-runoff modeling: Model calibration, data assimilation, and uncertainty analysis. In Hydrological Modelling and the Water Cycle; Sorooshian, S., Hsu, K.-L., Coppola, E., Tomassetti, B., Verdecchia, M., Visconti, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 63, pp. 1–24. [Google Scholar]
- Madsen, H.; Wilson, G.; Ammentorp, H.C. Comparison of different automated strategies for calibration of rainfall-runoff models. J. Hydrol. 2002, 261, 48–59. [Google Scholar] [CrossRef]
- Boyle, D.P.; Gupta, H.V.; Sorooshian, S. Toward improved calibration of hydrologic models: Combining the strengths of manual and automatic methods. Water Resour. Res. 2000, 36, 3663–3674. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Botterweg, P. The user’s influence on model calibration results: An example of the model SOIL, independently calibrated by two users. Ecol. Model. 1995, 81, 71–81. [Google Scholar] [CrossRef]
- Vidal, J.-P.; Moisan, S.; Faure, J.-B.; Dartus, D. River model calibration, from guidelines to operational support tools. Environ. Model. Softw. 2007, 22, 1628–1640. [Google Scholar] [CrossRef]
- Vidal, J.-P.; Moisan, S.; Faure, J.-B.; Dartus, D. Towards a reasoned 1D river model calibration. J. Hydroinf. 2005, 7, 91–104. [Google Scholar] [CrossRef][Green Version]
- Madsen, H. Parameter estimation in distributed hydrological catchment modelling using automatic calibration with multiple objectives. Adv. Water Resour. 2003, 26, 205–216. [Google Scholar] [CrossRef]
- Mugunthan, P.; Shoemaker, C.A.; Regis, R.G. Comparison of function approximation, heuristic, and derivative-based methods for automatic calibration of computationally expensive groundwater bioremediation models. Water Resour. Res. 2005. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Schulin, R.; van Genuchten, M.T. Estimating unsaturated soil hydraulic parameters using ant colony optimization. Adv. Water Resour. 2001, 24, 827–841. [Google Scholar] [CrossRef]
- Finley, J.R.; Pintér, J.D.; Satish, M.G. Automatic model calibration applying global optimization techniques. Environ. Model. Assess. 1998, 3, 117–126. [Google Scholar] [CrossRef]
- Beven, K. A manifesto for the equifinality thesis. J. Hydrol. 2006, 320, 18–36. [Google Scholar] [CrossRef]
- Beven, K. Prophecy, reality and uncertainty in distributed hydrological modelling. Adv. Water Resour. 1993, 16, 41–51. [Google Scholar] [CrossRef]
- Straten, G.T.V.; Keesman, K.J. Uncertainty propagation and speculation in projective forecasts of environmental change: A lake-eutrophication example. J. Forecast. 1991, 10, 163–190. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. GLUE: 20 years on. Hydrol. Process. 2014, 28, 5897–5918. [Google Scholar] [CrossRef]
- Beven, K.; Freer, J. Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology. J. Hydrol. 2001. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Bates, B.C.; Campbell, E.P. A markov Chain Monte Carlo scheme for parameter estimation and inference in conceptual rainfall-runoff modeling. Water Resour. Res. 2001, 37, 937–947. [Google Scholar] [CrossRef]
- Razavi, S.; Tolson, B.A.; Matott, L.S.; Thomson, N.R.; MacLean, A.; Seglenieks, F.R. Reducing the computational cost of automatic calibration through model preemption: Model preemption approach in automatic calibration. Water Resour. Res. 2010. [Google Scholar] [CrossRef]
- Meert, P.; Pereira, F.; Willems, P. Surrogate modeling-based calibration of hydrodynamic river model parameters. J. Hydro. Environ. Res. 2018, 19, 56–67. [Google Scholar] [CrossRef]
- Deslauriers, S.; Mahdi, T.-F. Flood modelling improvement using automatic calibration of two dimensional river software SRH-2D. Nat. Hazards 2018, 91, 697–715. [Google Scholar] [CrossRef]
- Evangelista, S.; Giovinco, G.; Kocaman, S. A multi-parameter calibration method for the numerical simulation of morphodynamic problems. J. Hydrol. Hydromech. 2017, 65, 175–182. [Google Scholar] [CrossRef]
- Lavoie, B.; Mahdi, T.-F. Comparison of two-dimensional flood propagation models: SRH-2D and Hydro_AS-2D. Nat. Hazards 2017, 86, 1207–1222. [Google Scholar] [CrossRef]
- McKibbon, J.; Mahdi, T.-F. Automatic calibration tool for river models based on the MHYSER software. Nat. Hazards 2010, 54, 879–899. [Google Scholar] [CrossRef]
- Fabio, P.; Aronica, G.T.; Apel, H. Towards automatic calibration of 2-D flood propagation models. Hydrol. Earth Syst. Sci. 2010, 14, 911–924. [Google Scholar] [CrossRef]
- Wasantha Lal, A.M. Calibration of riverbed roughness. J. Hydraul. Eng. 1995, 121, 664–671. [Google Scholar] [CrossRef]
- Doherty, J. PEST Model-Independent Parameter Estimation User Manual Part I, 6th ed.; Watermark Numerical Computing: Brisbane, Australia, 2016. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Hansen, N.; Ostermeier, A. Adapting arbitrary normal mutation distributions in evolution strategies: The covariance matrix adaptation. In Proceedings of the IEEE International Conference on Evolutionary Computation, Nagoya, Japan, 20–22 May 1996. [Google Scholar]
- Yen, C.; Lee, K.T. Bed topography and sediment sorting in channel bend with unsteady flow. J. Hydraul. Eng. 1995, 121, 591–599. [Google Scholar] [CrossRef]
- Ferguson, R.I.; Church, M. A Simple universal equation for grain settling velocity. J. Sediment. Res. 2004, 74, 933–937. [Google Scholar] [CrossRef]
- Olsen, N.R.B. A Three Dimensional Numerical Model for Simulation of Sediment Movement in Water Intakes with Multiblock Option; Department of Hydraulic and Environmental Engineering, The Norwegian University of Science and Technology: Trondheim, Norway, 2014. [Google Scholar]
- Saam, L.; Mouris, K.; Wieprecht, S.; Haun, S. Three-dimensional numerical modelling of reservoir flushing to obtain long-term sediment equilibrium. In Proceedings of the 38th IAHR World Congress, Panama City, Panama, 1–6 September 2019. [Google Scholar]
- Mouris, K.; Beckers, F.; Haun, S. Three-dimensional numerical modeling of hydraulics and morphodynamics of the Schwarzenbach reservoir. E3s Web Conf. 2018, 40, 03005. [Google Scholar] [CrossRef]
- Esmaeili, T.; Sumi, T.; Kantoush, S.; Kubota, Y.; Haun, S.; Rüther, N. Three-dimensional numerical study of free-flow sediment flushing to increase the flushing efficiency: A case-study reservoir in Japan. Water 2017, 9, 900. [Google Scholar] [CrossRef]
- Harb, G.; Haun, S.; Schneider, J.; Olsen, N.R.B. Numerical analysis of synthetic granulate deposition in a physical model study. Int. J. Sediment Res. 2014, 29, 110–117. [Google Scholar] [CrossRef]
- Haun, S.; Kjærås, H.; Løvfall, S.; Olsen, N.R.B. Three-dimensional measurements and numerical modelling of suspended sediments in a hydropower reservoir. J. Hydrol. 2013, 479, 180–188. [Google Scholar] [CrossRef]
- Haun, S.; Olsen, N.R.B. Three-dimensional numerical modelling of the flushing process of the Kali Gandaki hydropower reservoir. Lakes Reserv. Sci. Policy Manag. Sustain. Use 2012, 17, 25–33. [Google Scholar] [CrossRef]
- Haun, S.; Olsen, N.R.B.; Feurich, R. Numerical modeling of flow over trapezoidal broad-crested weir. Eng. Appl. Comput. Fluid Mech. 2011, 5, 397–405. [Google Scholar] [CrossRef]
- Wilson, C.A.M.E.; Yagci, O.; Rauch, H.-P.; Olsen, N.R.B. 3D numerical modelling of a willow vegetated river/floodplain system. J. Hydrol. 2006, 327, 13–21. [Google Scholar] [CrossRef]
- Rüther, N.; Olsen, N.R. Three-dimensional modeling of sediment transport in a narrow 90° channel bend. J. Hydraul. Eng. 2005, 131, 917–920. [Google Scholar] [CrossRef]
- Olsen, N.R.B. Three-dimensional CFD modeling of self-forming meandering channel. J. Hydraul. Eng. 2003, 129, 366–372. [Google Scholar] [CrossRef]
- Booker, D.J. Hydraulic modelling of fish habitat in urban rivers during high flows. Hydrol. Process. 2003, 17, 577–599. [Google Scholar] [CrossRef]
- Wilson, C.A.M.E.; Boxall, J.B.; Guymer, I.; Olsen, N.R.B. Validation of a three-dimensional numerical code in the simulation of pseudo-natural meandering flows. J. Hydraul. Eng. 2003, 129, 758–768. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Pearson Education Ltd.: Harlow, UK, 2007. [Google Scholar]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Rodi, W. Turbulence Models and Their Application in Hydraulics, 1st ed.; Routledge: Rotterdam, The Netherlands, 1993. [Google Scholar]
- Olsen, N.R.B.; Haun, S. Free surface algorithms for 3D numerical modelling of reservoir flushing. In Proceedings of the River flow 2010, Federal Waterways Engineering and Research Institute (BAW), Braunschweig, Germany, 8–10 September 2010; Volume 2010, pp. 1105–1110. [Google Scholar]
- Schlichting, H. Boundary Layer Theory; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Fischer-Antze, T.; Rüther, N.; Olsen, N.R.B.; Gutknecht, D. Three-dimensional (3D) modeling of non-uniform sediment transport in a channel bend with unsteady flow. J. Hydraul. Res. 2009, 47, 670–675. [Google Scholar] [CrossRef]
- Haun, S.; Olsen, N.R.B. Three-dimensional numerical modelling of reservoir flushing in a prototype scale. Int. J. River Basin Manag. 2012, 10, 341–349. [Google Scholar] [CrossRef]
- Engelund, F.; Hansen, E. A Monograph on Sediment Transport in Alluvial Streams; Teknisk Vorlag: Copenhagen, Denmark, 1967. [Google Scholar]
- Van Rijn, L.C. Sediment transport, part I: Bed load transport. J. Hydraul. Eng. 1984, 110, 1431–1456. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S.S.Y.; Jia, Y. Nonuniform sediment transport in alluvial rivers. J. Hydraul. Res. 2000, 38, 427–434. [Google Scholar] [CrossRef]
- Soltani, M.; Laux, P.; Mauder, M.; Kunstmann, H. Inverse distributed modelling of streamflow and turbulent fluxes: A sensitivity and uncertainty analysis coupled with automatic optimization. J. Hydrol. 2019, 571, 856–872. [Google Scholar] [CrossRef]
- Usman, M.; Reimann, T.; Liedl, R.; Abbas, A.; Conrad, C.; Saleem, S. Inverse parametrization of a regional groundwater flow model with the aid of modelling and GIS: Test and application of different approaches. ISPRS Int. J. Geo. Inf. 2018, 7, 22. [Google Scholar] [CrossRef]
- Necpálová, M.; Anex, R.P.; Fienen, M.N.; Del Grosso, S.J.; Castellano, M.J.; Sawyer, J.E.; Iqbal, J.; Pantoja, J.L.; Barker, D.W. Understanding the DayCent model: Calibration, sensitivity, and identifiability through inverse modeling. Environ. Model. Softw. 2015, 66, 110–130. [Google Scholar] [CrossRef]
- Rode, M.; Suhr, U.; Wriedt, G. Multi-objective calibration of a river water quality model—Information content of calibration data. Ecol. Model. 2007, 204, 129–142. [Google Scholar] [CrossRef]
- Baginska, B.; Milne-Home, W.; Cornish, P.S. Modelling nutrient transport in Currency Creek, NSW with AnnAGNPS and PEST. Environ. Model. Softw. 2003, 18, 801–808. [Google Scholar] [CrossRef]
- Liu, C.; Batelaan, O.; Smedt, F.D.; Poórová, J.; Velcická, L. Automated calibration applied to a GIS-based flood simulation model using PEST. In Floods, from Defence to Management; van Alphen, J., van Beek, E., Taal, M., Eds.; Taylor-Francis Group: London, UK, 2005; pp. 317–326. [Google Scholar]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Levenberg, K. A method for the solution of certain nonlinear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Price, W.L. Global optimization algorithms for a CAD workstation. J. Optim. Theory Appl. 1987, 55, 133–146. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V.K. Optimal use of the SCE-UA global optimization method for calibrating watershed models. J. Hydrol. 1994, 158, 265–284. [Google Scholar] [CrossRef]
- Duan, Q.Y.; Gupta, V.K.; Sorooshian, S. Shuffled complex evolution approach for effective and efficient global minimization. J. Optim. Theory Appl. 1993, 76, 501–521. [Google Scholar] [CrossRef]
- Hansen, N. The CMA evolution strategy: A tutorial. arXiv 2016, arXiv:1604.00772. [Google Scholar]
- Shi, Y.; Eberhart, R.C. Parameter selection in particle swarm optimization. In Evolutionary Programming VII; Porto, V.W., Saravanan, N., Waagen, D., Eiben, A.E., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; pp. 591–600. [Google Scholar]
- García, M.H. Sedimentation Engineering: Processes, Measurements, Modeling, and Practice; Environmental and Water Resources Institute (EWRI), ASCE Manuals and Reports on Engineering Practice, American Society of Civil Engineers: Reston, VA, USA, 2008. [Google Scholar]
- Hunziker, R.P. Fraktionsweiser Geschiebetransport. Ph.D. Thesis, ETH, Zurich, Switzerland, 1995. [Google Scholar]
- Malcherek, A. Sedimenttransport und Morphodynamik; Scriptum Institut für Wasserwesen, Bundeswehr University Munich: Munich, Germany, 2007. [Google Scholar]
| Sediment Size Classes | ||||||||
|---|---|---|---|---|---|---|---|---|
| Size (mm) | 0.25 | 0.42 | 0.84 | 1.19 | 2.00 | 3.36 | 4.76 | 8.52 |
| Proportion (%) | 6.55 | 10.56 | 25.36 | 15.06 | 20.11 | 13.02 | 4.88 | 4.46 |
| Cumulative proportion (%) | 6.55 | 17.11 | 42.47 | 57.53 | 77.64 | 90.66 | 95.54 | 100 |
| Fall velocity (m/s) | 0.03 | 0.06 | 0.11 | 0.14 | 0.20 | 0.26 | 0.32 | 0.43 |
| Run# | Peak Flow Discharge (m3/s) | Peak Flow Depth (cm) | Duration (min) |
|---|---|---|---|
| 1 | 0.0750 | 12.9 | 180 |
| 3 | 0.0613 | 11.3 | 240 |
| 5 | 0.0436 | 9.10 | 420 |
| Calibration Results | Calibration Method | ||||||
|---|---|---|---|---|---|---|---|
| PEST#1 | PEST#2 | PEST#3 | PEST#4 | SCE-UA | CMA-ES | PSO | |
| ks (cm) | 0.904 | 0.894 | 0.899 | 0.903 | 0.898 | 0.892 | 0.904 |
| ALT (cm) | 1.639 | 1.644 | 1.629 | 1.638 | 1.635 | 1.631 | 1.647 |
| VFS (%) | 48.1 | 47.9 | 48.4 | 48 | 48.1 | 48.1 | 47.9 |
| Minimum of SSR (cm) | 0.28249 | 0.28251 | 0.28240 | 0.28249 | 0.28247 | 0.28247 | 0.28241 |
| Number of model runs | 26 | 30 | 28 | 27 | 176 | 440 | 448 |
| Calibration Parameters | Sediment Transport Formula | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Wu | Van Rijn | Engelund-Hansen | |||||||
| Run#1 | Run#3 | Run#5 | Run#1 | Run#3 | Run#5 | Run#1 | Run#3 | Run#5 | |
| ks (cm) | 1.52 | 1.34 | 0.90 | 0.63 | 0.61 | 0.37 | 0.48 | 0.31 | 0.25 |
| ALT (cm) | 2.04 | 1.85 | 1.64 | 2.20 | 1.94 | 1.24 | 1.31 | 1.12 | 0.74 |
| VFS (%) | 49 | 51 | 48 | 60 | 60 | 60 | 52 | 51 | 53 |
| Goodness of Fit | Sediment Transport Formula | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Wu | Van Rijn | Engelund-Hansen | |||||||
| Run#1 | Run#3 | Run#5 | Run#1 | Run#3 | Run#5 | Run#1 | Run#3 | Run#5 | |
| R2 (-) | 0.90 | 0.89 | 0.95 | 0.90 | 0.89 | 0.94 | 0.88 | 0.83 | 0.90 |
| RMSE (cm) | 1.49 | 1.04 | 0.67 | 1.57 | 1.08 | 0.69 | 1.63 | 1.33 | 0.81 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shoarinezhad, V.; Wieprecht, S.; Haun, S. Comparison of Local and Global Optimization Methods for Calibration of a 3D Morphodynamic Model of a Curved Channel. Water 2020, 12, 1333. https://doi.org/10.3390/w12051333
Shoarinezhad V, Wieprecht S, Haun S. Comparison of Local and Global Optimization Methods for Calibration of a 3D Morphodynamic Model of a Curved Channel. Water. 2020; 12(5):1333. https://doi.org/10.3390/w12051333
Chicago/Turabian StyleShoarinezhad, Vahid, Silke Wieprecht, and Stefan Haun. 2020. "Comparison of Local and Global Optimization Methods for Calibration of a 3D Morphodynamic Model of a Curved Channel" Water 12, no. 5: 1333. https://doi.org/10.3390/w12051333
APA StyleShoarinezhad, V., Wieprecht, S., & Haun, S. (2020). Comparison of Local and Global Optimization Methods for Calibration of a 3D Morphodynamic Model of a Curved Channel. Water, 12(5), 1333. https://doi.org/10.3390/w12051333





