Wave Glider Observations of Surface Waves During Three Tropical Cyclones in the South China Sea
Abstract
:1. Introduction
2. Data and Method
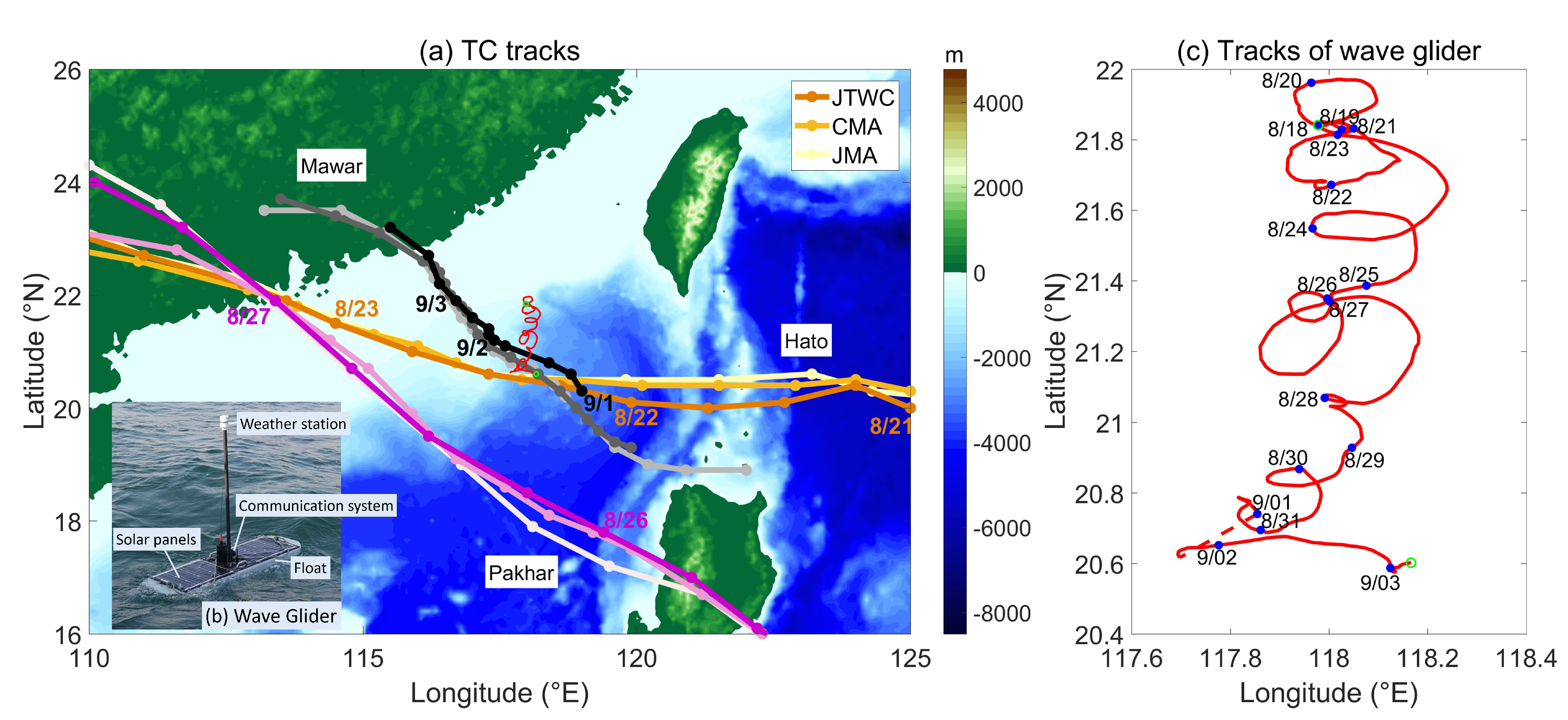
2.1. Wave Glider
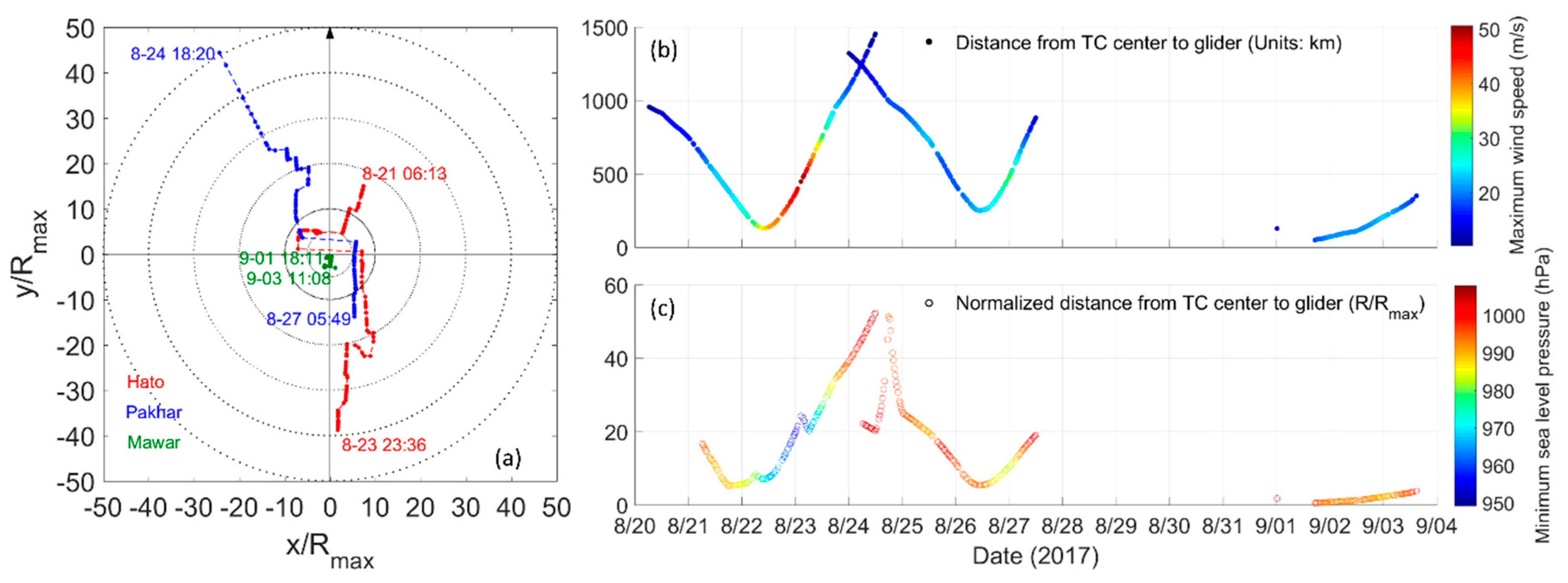
2.2. Tropical Cyclones
2.3. Ocean Surface Roughness
2.4. Ideal Wind Model
3. Results
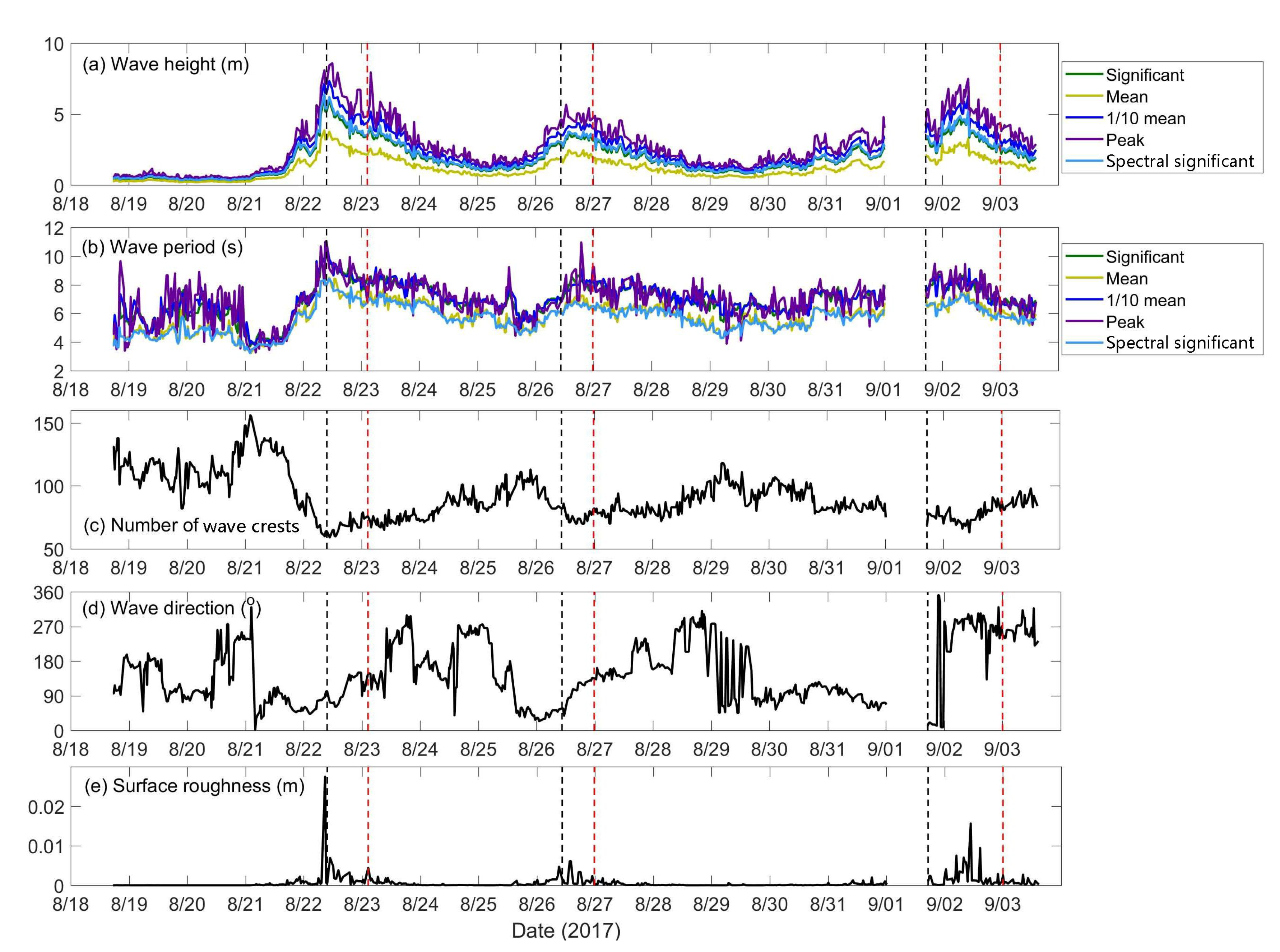
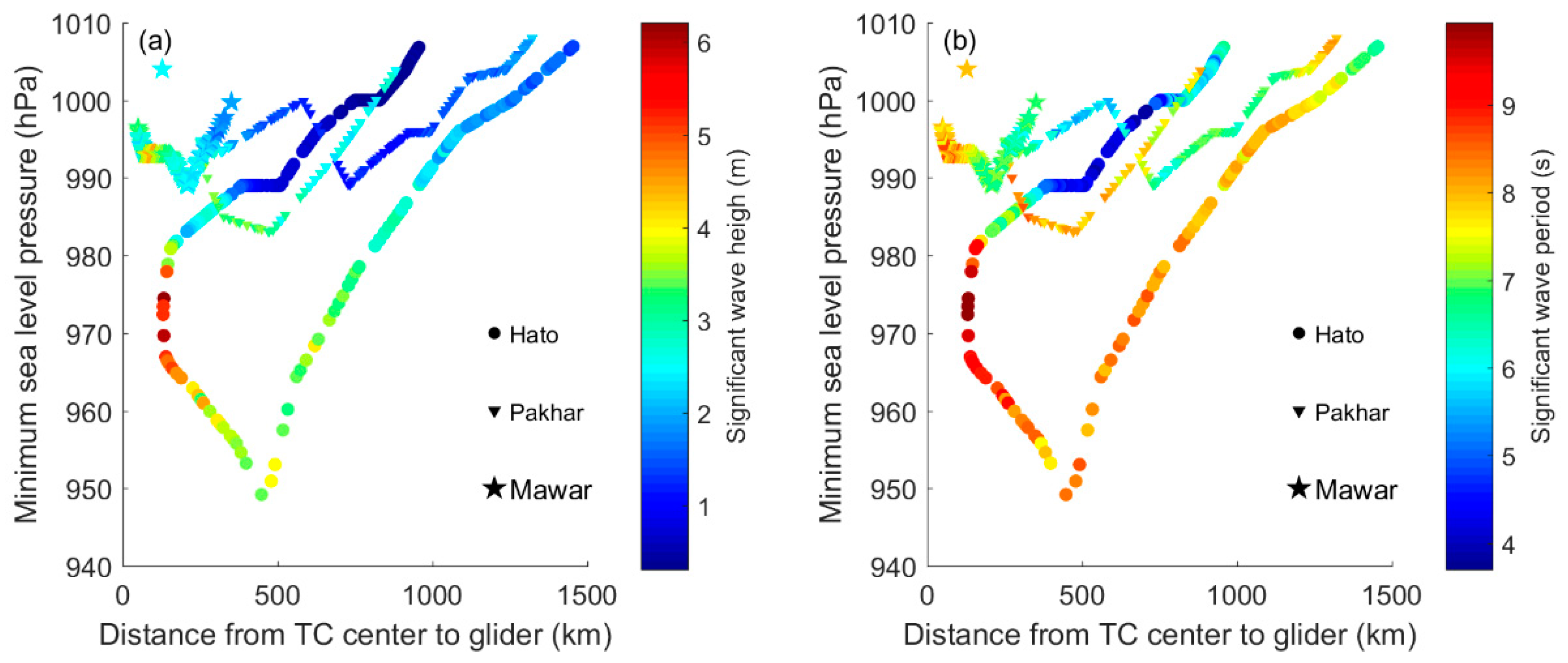
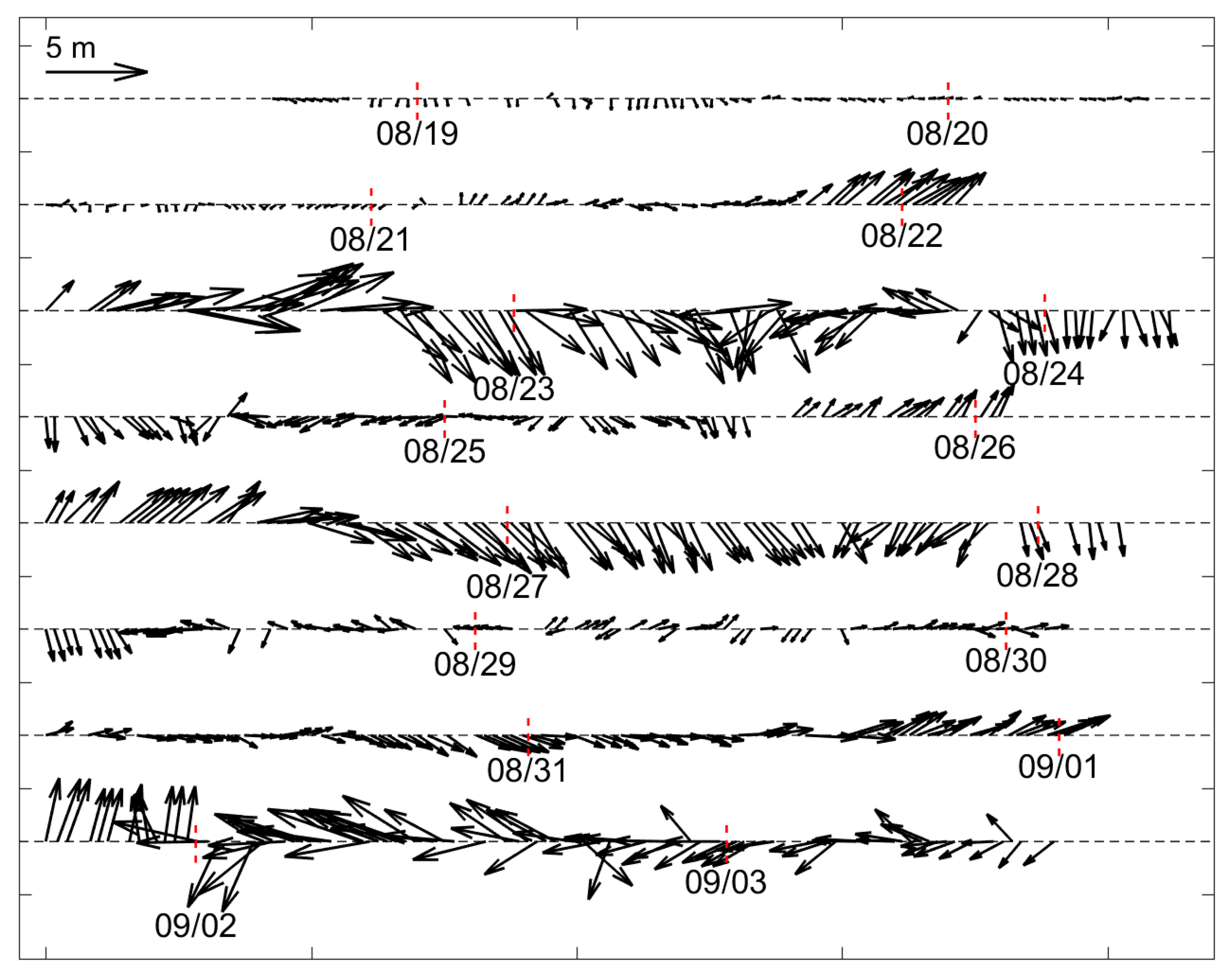
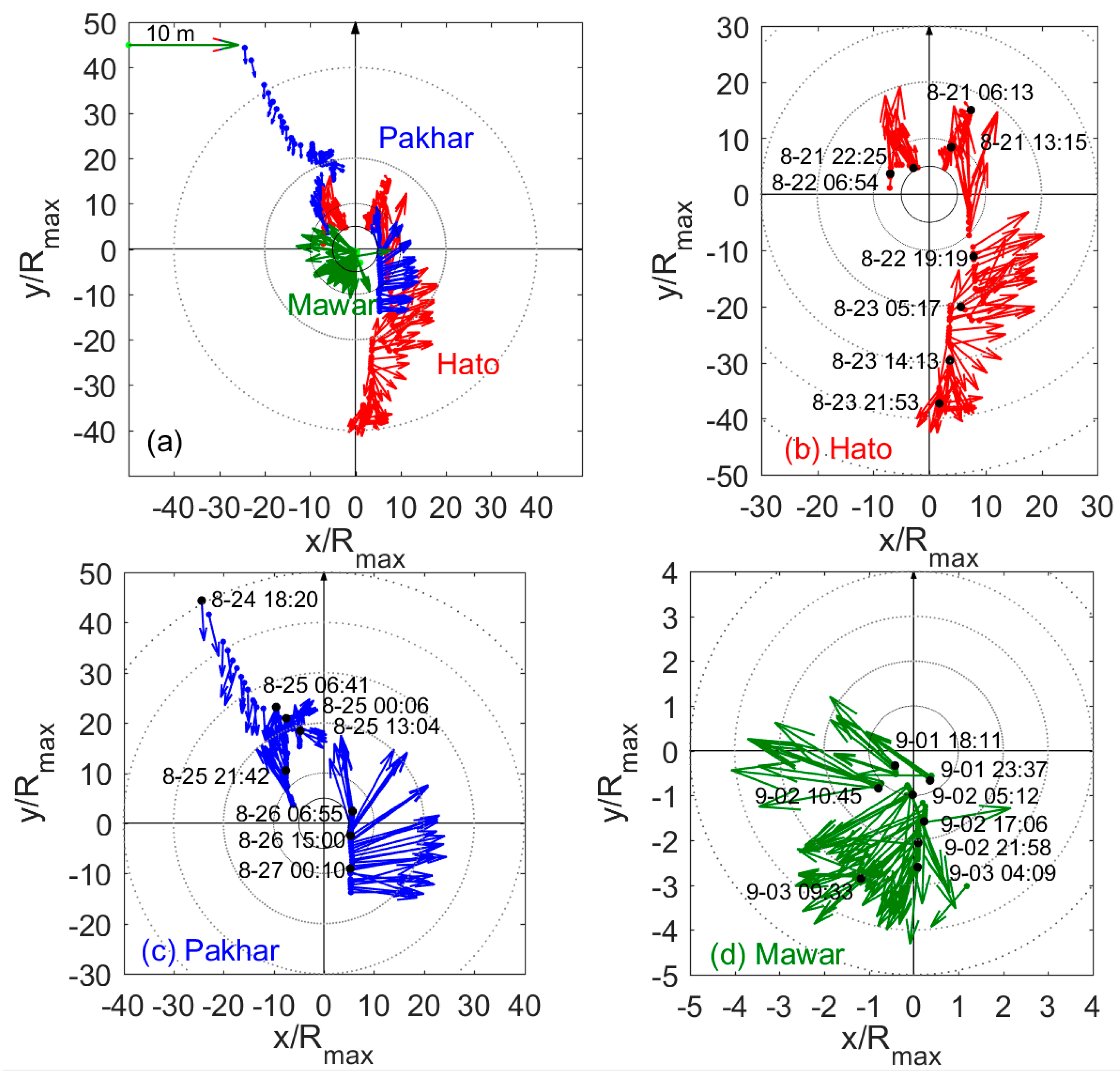
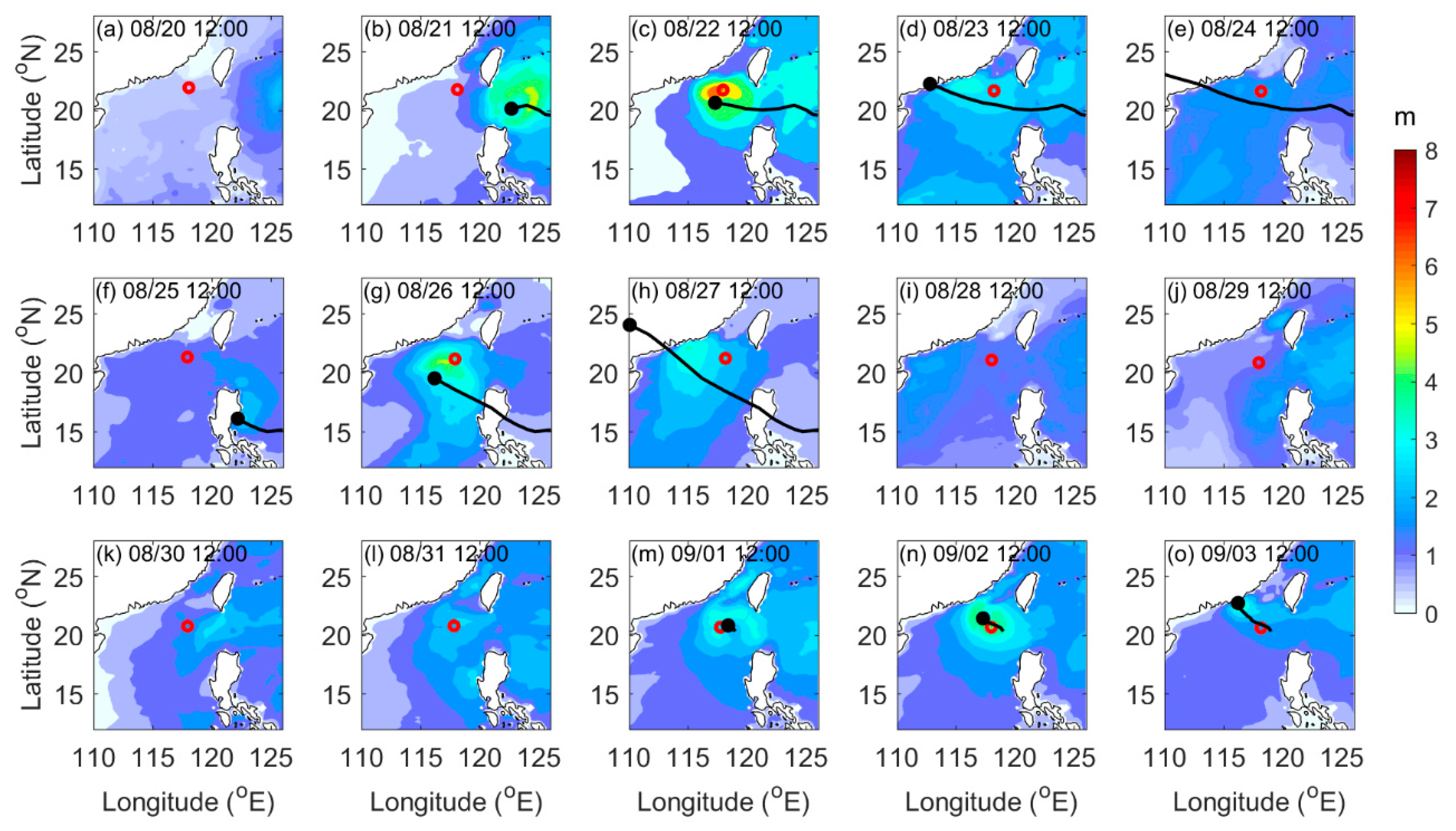
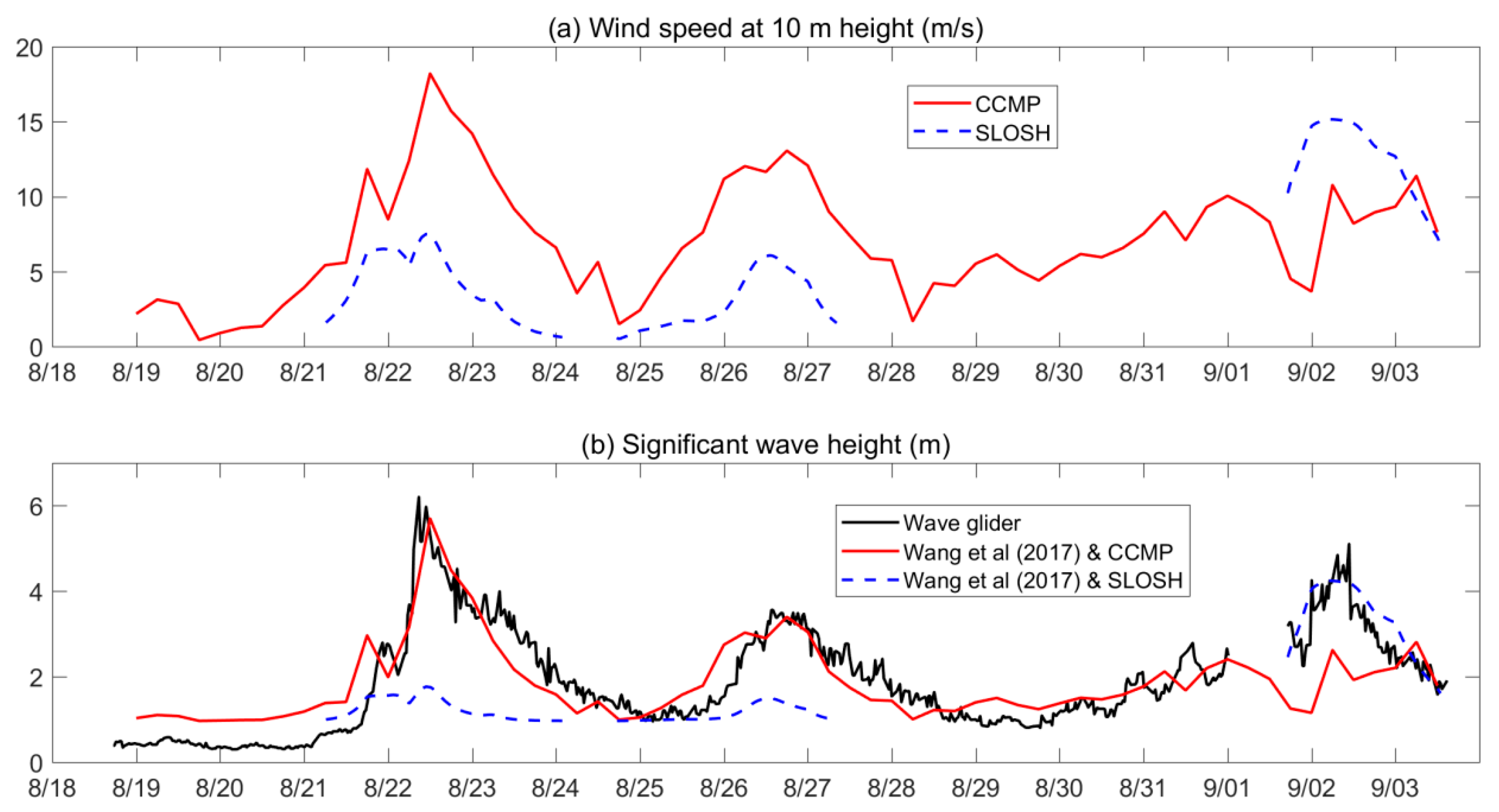
3.1. Surface Waves During Hato, Pakhar, and Mawar
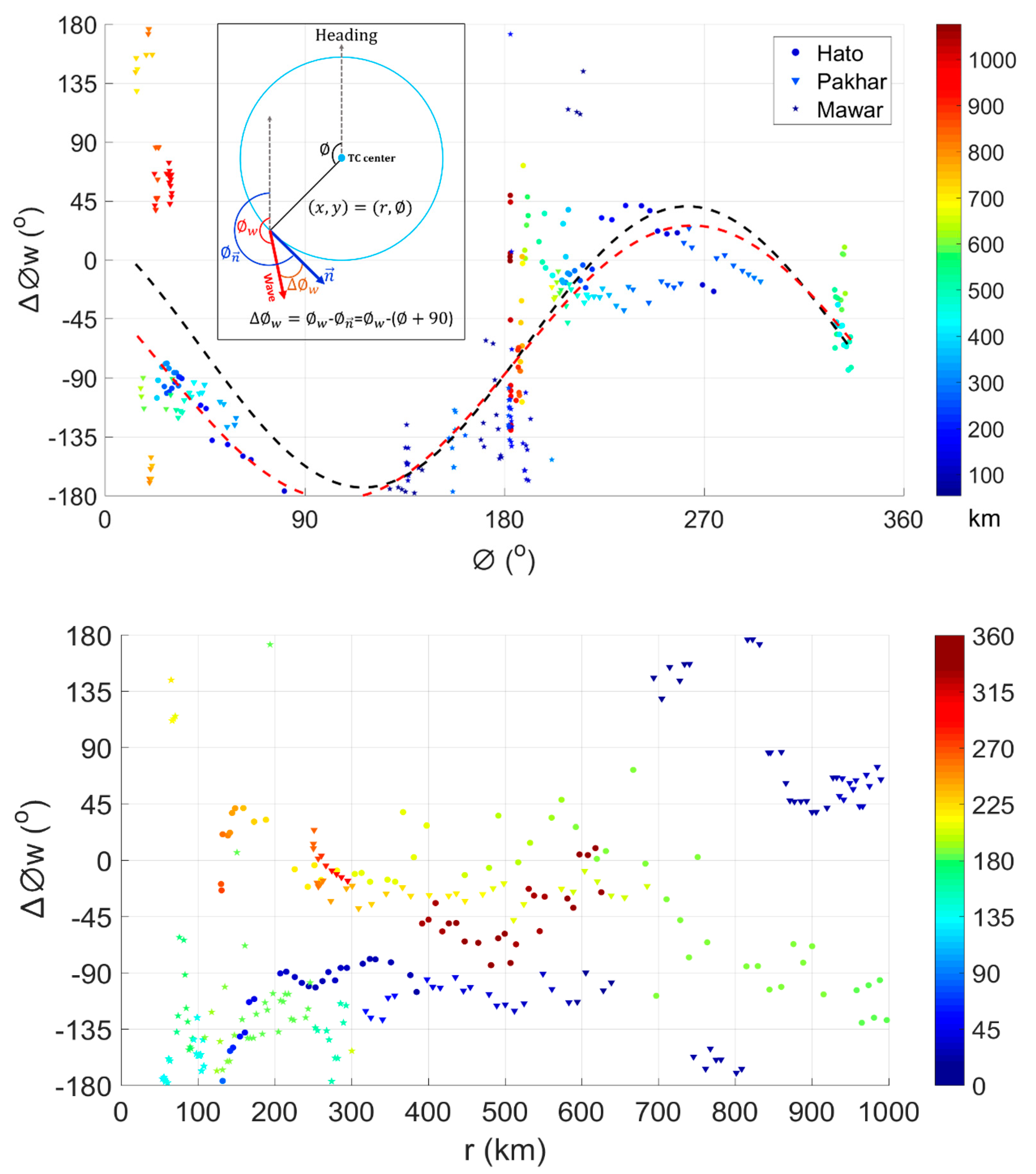
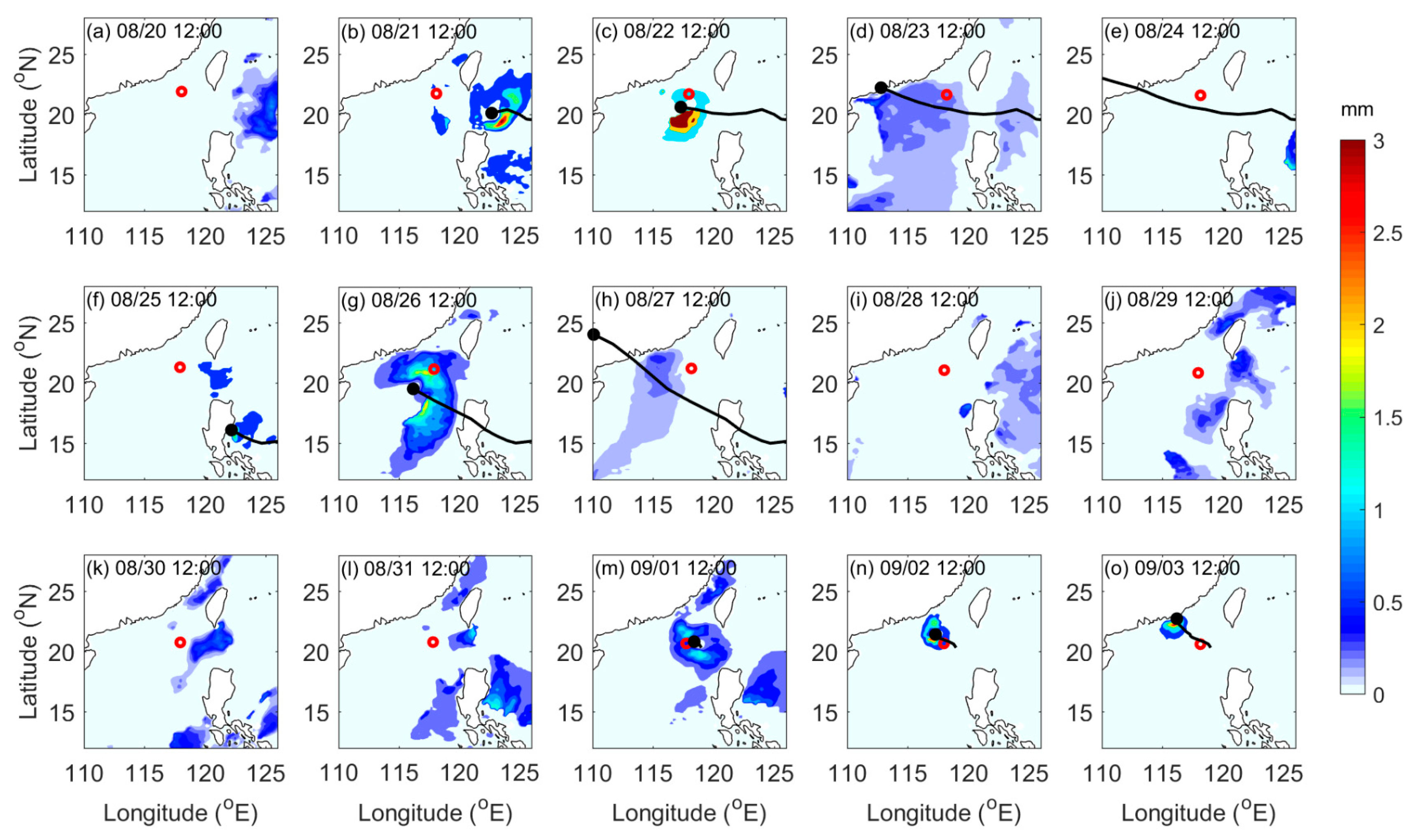
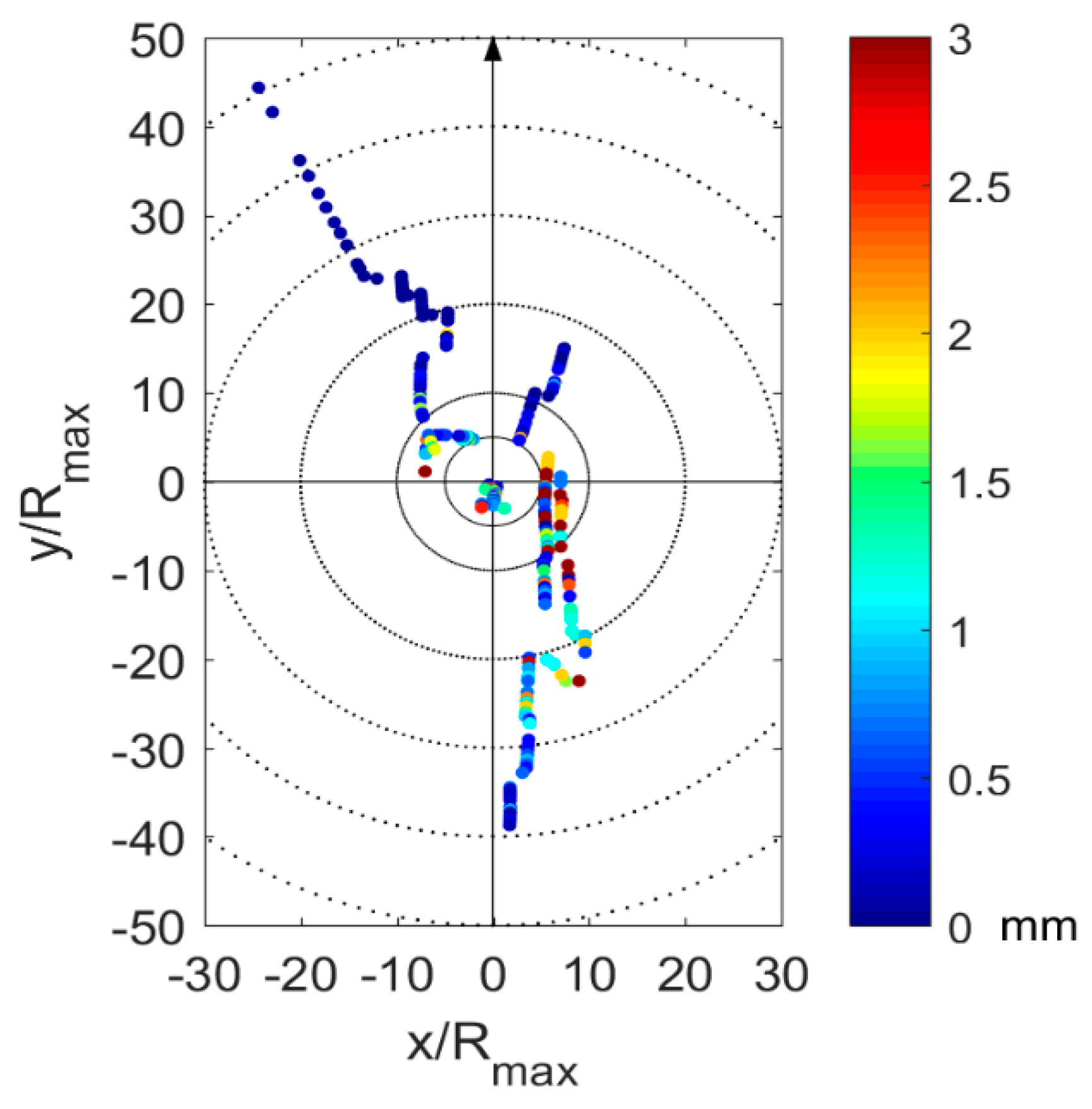
3.2. Ocean Surface Roughness
4. Discussion
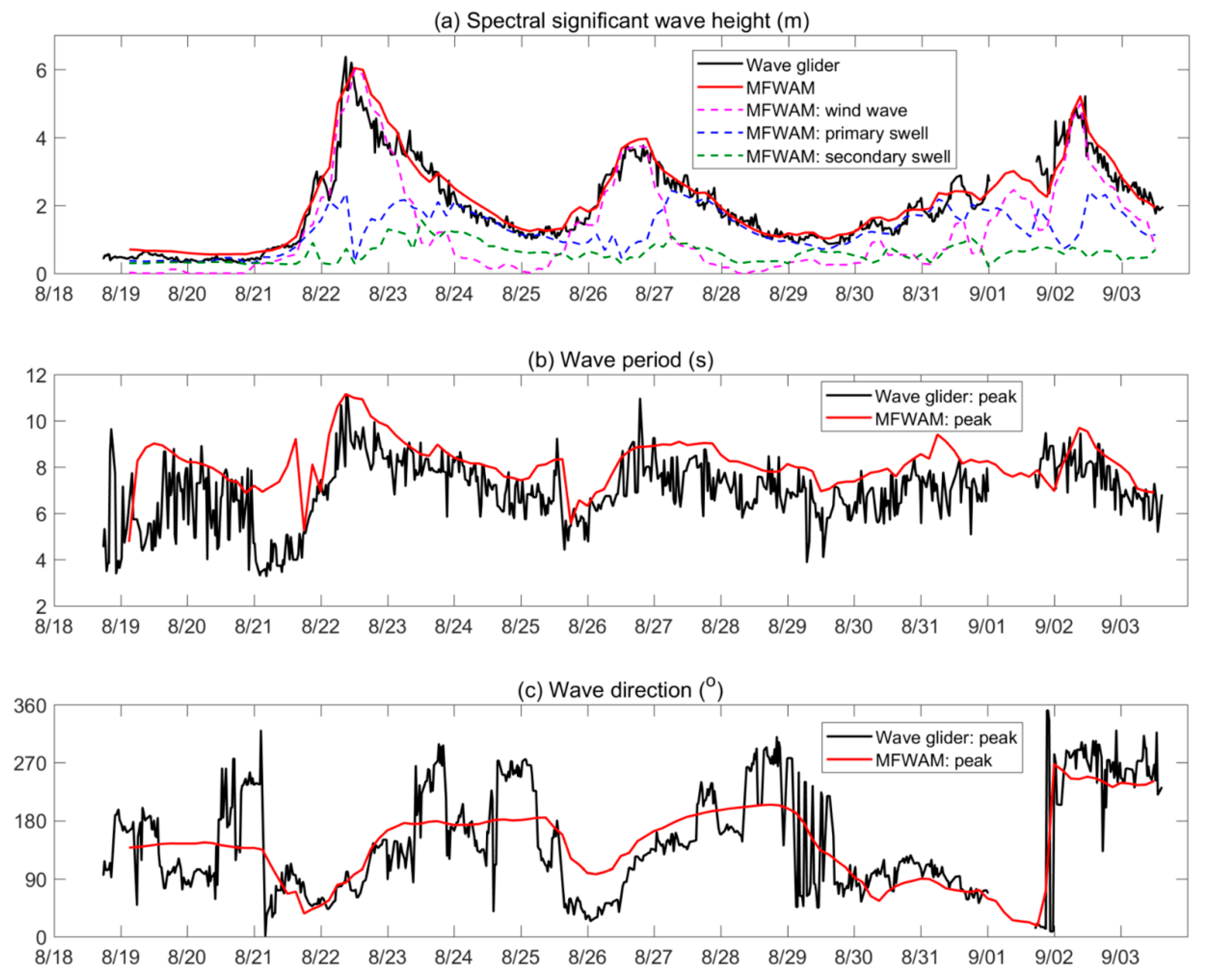
4.1. Assessment for Wave Modelling
4.2. Ocean Surface Roughness
4.3. Future Needs
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, H.; Wu, R.; Chen, D.; Liu, X.; He, H.; Tang, Y.; Ke, D.; Shen, Z.; Li, J.; Xie, J.; et al. Net modulation of upper ocean thermal structure by Typhoon Kalmaegi (2014). J. Geophys. Res. Oceans 2018, 123, 7154–7171. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, D.; Zhou, L.; Liu, X.; Ding, T.; Zhou, B. Upper ocean response to Typhoon Kalmaegi (2014). J. Geophys. Res. Oceans 2016, 121, 6520–6535. [Google Scholar] [CrossRef]
- Collins III, C.O.; Potter, H.; Lund, B.; Tamura, H.; Graber, H.C. Directional wave spectra observed during intense tropical cyclones. J. Geophys. Res. Oceans 2018, 123, 773–793. [Google Scholar] [CrossRef]
- Drost, E.J.F.; Lowe, R.J.; Ivey, G.N.; Jones, N.L.; Péquignet, C.A. The effects of tropical cyclone characteristics on the surface wave fields in Australia’s North West region. Cont. Shelf Res. 2017, 139, 35–53. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.-P.; Oey, L.-Y. Hindcast of waves and currents in Hurricane Katrina. Bull. Amer. Meteor. Soc. 2008, 89, 487–496. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Han, G.; Yang, J.; Chen, D.; Zheng, G.; Chen, N. Using satellite altimetry to calibrate the simulation of typhoon Seth storm surge off Southeast China. Remote Sens. 2018, 10, 657. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Chen, C.; Beardsley, R.C.; Xu, Q.; Qi, J.; Lin, H. Impact of current-wave interaction on storm surge simulation: A case study for Hurricane Bob. J. Geophys. Res. Oceans 2013, 118, 2685–2701. [Google Scholar] [CrossRef] [Green Version]
- Donelan, M.A.; Haus, B.K.; Reul, N.; Plant, W.J.; Stiassnie, M.; Graber, H.C.; Brown, O.B.; Saltzman, E.S. On the limiting aerodynamic roughness of the ocean in very strong winds. Geophys. Res. Lett. 2004, 31, L18306. [Google Scholar] [CrossRef] [Green Version]
- Soloviev, A.V.; Lukas, R.; Donelan, M.A.; Haus, B.K.; Ginis, I. The air-sea interface and surface stress under tropical cyclones. Sci. Rep. 2014, 4, 5306. [Google Scholar] [CrossRef]
- Olabarrieta, M.; Warner, J.C.; Armstrong, B.; Zambon, J.B.; He, R. Ocean–atmosphere dynamics during Hurricane Ida and Nor’Ida: An application of the coupled ocean–atmosphere–wave–sediment transport (COAWST) modeling system. Ocean Model. 2012, 43, 112–137. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.F.; Han, G.J.; Wang, D.X.; Wei, L.; He, Z.J. Effect of surface wave breaking on the surface boundary layer of temperature in the Yellow Sea in summer. Ocean Model. 2011, 38, 267–279. [Google Scholar]
- Zhang, X.; Han, G.; Wang, D.; Deng, Z.; Li, W. Summer surface layer thermal response to surface gravity waves in the Yellow Sea. Ocean Dyn. 2012, 62, 983–1000. [Google Scholar] [CrossRef]
- He, H.; Wu, Q.; Chen, D.; Sun, J.; Liang, C.; Jin, W.; Xu, Y. Effects of surface waves and sea spray on air–sea fluxes during the passage of Typhoon Hagupit. Acta Ocean. Sin. 2018, 37, 1–7. [Google Scholar] [CrossRef]
- Powell, M.D.; Vickery, P.J.; Reinhold, T.A. Reduced drag coefficient for high wind speeds in tropical cyclones. Nature 2003, 422, 279–283. [Google Scholar] [CrossRef]
- Makin, V.K. A Note on the drag of the sea surface at hurricane winds. Boundary Layer Meteorol. 2005, 115, 169–176. [Google Scholar] [CrossRef]
- Holthuijsen, L.H.; Powell, M.D.; Pietrzak, J.D. Wind and waves in extreme hurricanes. J. Geophys. Res. Oceans 2012, 117, C09003. [Google Scholar] [CrossRef] [Green Version]
- Stoney, L.; Walsh, K.; Babanin, A.V.; Ghantous, M.; Govekar, P.; Young, I. Simulated ocean response to tropical cyclones: The effect of a novel parameterization of mixing from unbroken surface waves. J. Adv. Modell. Earth Syst. 2017, 9, 759–780. [Google Scholar] [CrossRef]
- Toffoli, A.; McConochie, J.; Ghantous, M.; Loffredo, L.; Babanin, A.V. The effect of wave-induced turbulence on the ocean mixed layer during tropical cyclones: Field observations on the Australian North-West Shelf. J. Geophys. Res. Oceans 2012, 117, C00J24. [Google Scholar] [CrossRef] [Green Version]
- Aijaz, S.; Ghantous, M.; Babanin, A.V.; Ginis, I.; Thomas, B.; Wake, G. Nonbreaking wave-induced mixing in upper ocean during tropical cyclones using coupled hurricane-ocean-wave modeling. J. Geophys. Res. Oceans 2017, 122, 3939–3963. [Google Scholar] [CrossRef] [Green Version]
- Wright, L.D.; Friedrichs, C.T. Gravity-driven sediment transport on continental shelves: A status report. Cont. Shelf Res. 2006, 26, 2092–2107. [Google Scholar] [CrossRef]
- Walsh, J.P.; Nittrouer, C.A. Understanding fine-grained river-sediment dispersal on continental margins. Mar. Geol. 2009, 263, 34–45. [Google Scholar] [CrossRef]
- Zhang, W.; Cui, Y.; Santos, A.; Hanebuth, T.J.J. Storm-driven bottom sediment transport on a high-energy narrow shelf (NW Iberia) and development of mud depocenters. J. Geophys. Res. Oceans 2016, 121, 5751–5772. [Google Scholar] [CrossRef]
- Zhang, W.; Harff, J.; Schneider, R.; Meyer, M.; Zorita, E.; Hünicke, B. Holocene morphogenesis at the southern Baltic Sea: Simulation of multi-scale processes and their interactions for the Darss–Zingst peninsula. J. Mar. Syst. 2014, 129, 4–18. [Google Scholar] [CrossRef]
- Young, I.R. Observations of the spectra of hurricane generated waves. Ocean Eng. 1998, 25, 261–276. [Google Scholar] [CrossRef]
- Young, I.R. A review of the sea state generated by hurricanes. Mar. Struct. 2003, 16, 201–218. [Google Scholar] [CrossRef]
- Young, I.R. Directional spectra of hurricane wind waves. J. Geophys. Res. 2006, 111, C08020. [Google Scholar] [CrossRef]
- Hwang, P.A. Fetch- and duration-limited nature of surface wave growth inside tropical cyclones: With applications to air–sea exchange and remote sensing. J. Phys. Oceanogr. 2016, 46, 41–56. [Google Scholar] [CrossRef]
- Hwang, P.A.; Fan, Y.; Ocampo-Torres, F.J.; García-Nava, H. Ocean surface wave spectra inside tropical cyclones. J. Phys. Oceanogr. 2017, 47, 2393–2417. [Google Scholar] [CrossRef]
- Hwang, P.A.; Fan, Y. Effective fetch and duration of tropical cyclone wind fields estimated from simultaneous wind and wave measurements: Surface wave and_air–sea exchange computation. J. Phys. Oceanogr. 2017, 47, 447. [Google Scholar] [CrossRef]
- Beeden, R.; Maynard, J.; Puotinen, M.; Marshall, P.; Dryden, J.; Goldberg, J.; Williams, G. Impacts and recovery from severe tropical cyclone Yasi on the Great Barrier Reef. PLoS ONE 2015, 10, e0121272. [Google Scholar] [CrossRef]
- Esquivel-Trava, B.; Ocampo-Torres, F.J.; Osuna, P. Spatial structure of directional wave spectra in hurricanes. Ocean Dyn. 2015, 65, 65–76. [Google Scholar] [CrossRef]
- Young, I.R. Parameteric hurricane wave prediction model. J. Waterw. Port Coast. Ocean Eng. 1988, 114, 637–652. [Google Scholar] [CrossRef]
- Young, I.R.; Vinoth, J. An “extended fetch” model for the spatial distribution of tropical cyclone wind–waves as observed by altimeter. Ocean Eng. 2013, 70, 14–24. [Google Scholar] [CrossRef]
- Wang, D.W.; Mitchell, D.A.; Teague, W.J.; Jarosz, E.; Hulbert, M.S. Extreme waves under Hurricane Ivan. Science 2005, 309, 896. [Google Scholar] [CrossRef] [Green Version]
- Moon, I.-J.; Ginis, I.; Hara, T.; Tolman, H.L.; Wright, C.W.; Walsh, E.J. Numerical simulation of sea surface directional wave spectra under hurricane wind forcing. J. Phys. Oceanogr. 2003, 33, 1680–1706. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.; Ginis, I.; Hara, T.; Wright, C.W.; Walsh, E.J. Numerical simulations and observations of surface wave fields under an extreme tropical cyclone. J. Phys. Oceanogr. 2009, 39, 2097–2116. [Google Scholar] [CrossRef]
- Hu, K.; Chen, Q. Directional spectra of hurricane-generated waves in the Gulf of Mexico. Geophy. Res. Lett. 2011, 38, L19608. [Google Scholar] [CrossRef]
- Wright, C.W.; Walsh, E.J.; Vandemark, D.; Krabill, W.B.; Garcia, A.W.; Houston, S.H.; Powell, M.D.; Black, P.G.; Marks, F.D. Hurricane directional wave spectrum spatial variation in the open ocean. J. Phys. Oceanogr. 2001, 31, 2472–2488. [Google Scholar] [CrossRef]
- Xu, Y.; He, H.; Song, J.; Hou, Y.; Li, F. Observations and modeling of typhoon waves in the South China Sea. J. Phys. Oceanogr. 2017, 47, 1307–1324. [Google Scholar] [CrossRef]
- Hwang, P.A.; Walsh, E.J. Propagation directions of ocean surface waves inside tropical cyclones. J. Phys. Oceanogr. 2018, 48, 1495–1511. [Google Scholar] [CrossRef]
- Beal, R.C.; Gerling, T.W.; Irvine, D.E.; Monaldo, F.M.; Tilley, D.G. Spatial variations of ocean wave directional spectra from the Seasat synthetic aperture radar. J. Geophys. Res. 1986, 91, 2433–2449. [Google Scholar] [CrossRef]
- Holt, B.; Gonzalez, F.I. SIR-B observations of dominant ocean waves near Hurricane Josephine. J. Geophys. Res. 1986, 91, 8595–8598. [Google Scholar] [CrossRef]
- Walsh, E.J.; Wright, C.W.; Vandemark, D.; Krabill, W.B.; Garcia, A.W.; Houston, S.H.; Murillo, S.T.; Powell, M.D.; Black, P.G.; Marks, F.D., Jr. Hurricane directional wave spectrum spatial variation at landfall. J. Phys. Oceanogr. 2002, 32, 1667–1684. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Li, X.; Perrie, W.; Hwang, P.A.; Zhang, B.; Yang, X. A hurricane wind speed retrieval model for C-band RADARSAT-2 Cross-Polarization ScanSAR Images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4766–4774. [Google Scholar] [CrossRef]
- Schmidt, K.M.; Swart, S.; Reason, C.; Nicholson, S.-A. Evaluation of satellite and reanalysis wind products with in situ Wave Glider wind observations in the Southern Ocean. J. Atmos. Ocean. Technol. 2017, 34, 2551–2568. [Google Scholar] [CrossRef]
- Mitarai, S.; McWilliams, J.C. Wave glider observations of surface winds and currents in the core of Typhoon Danas. Geophy. Res. Lett. 2016, 43, 11–312. [Google Scholar] [CrossRef]
- Li, C.; Sang, H.; Sun, X.; Qi, Z. Hydrographic and meteorological observation demonstration with wave glider “black pearl”. In Intelligent Robotics and Applications. Lecture Notes in Computer Science; ICIRA 2017; Huang, Y., Wu, H., Liu, H., Yin, Z., Eds.; Springer: Cham, Switzerland, 2017; Volume 10462, pp. 790–800. [Google Scholar]
- Chu, J.-H.; Sampson, C.R.; Levine, A.S.; Fukada, E. The Joint Typhoonwarning Center Tropical Cyclone Best-Tracks, 1945–2000; Naval Research Laboratory: Washington, DC, USA, 2002. [Google Scholar]
- Ying, M.; Zhang, W.; Yu, H.; Lu, X.; Feng, J.; Fan, Y.; Zhu, Y.; Chen, D. An overview of the China meteorological administration tropical cyclone database. J. Atmos. Ocean. Technol. 2014, 31, 287–301. [Google Scholar] [CrossRef] [Green Version]
- Koide, N.; Nishimura, S. Comparative study of dvorak analysis in the western north pacific. Technical Review No. 19 (March 2017) RSMC Tokyo-Typhoon Center 2017. Available online: http://www.jma.go.jp/jma/jma-eng/jma-center/rsmc-hp-pub-eg/techrev/text19-1.pdf (accessed on 1 May 2020).
- Taylor, P.K.; Yelland, M.J. The dependence of sea surface roughness on the height and steepness of the waves. J. Phys. Oceanogr. 2001, 31, 572–590. [Google Scholar] [CrossRef] [Green Version]
- Fairall, C.W.; Bradley, E.F.; Hare, J.E.; Grachev, A.A.; Edson, J.B. Bulk parameterization of air-sea fluxes: Updates and verification for the COARE algorithm. J. Clim. 2003, 16, 571–591. [Google Scholar] [CrossRef]
- Jelesnianski, C.P. Numerical computation of storm surges without bottom stress. Mon. Weather Rev. 1966, 94, 374–379. [Google Scholar] [CrossRef]
- Hwang, P.A.; Burrage, D.M.; Wang, D.W.; Wesson, J.C. Ocean surface roughness spectrum in high wind condition for microwave backscatter and emission computations. J. Atmos. Ocean. Technol. 2013, 30, 2168–2188. [Google Scholar] [CrossRef]
- Hwang, P.A.; Wang, D.W.; Teague, W.J.; Jacobs, G.A.; Wesson, J.; Burrage, D.; Miller, J. Anatomy of the Ocean Surface Roughness; NRL/FR/7330-02-10036; Naval Research Laboratory, Stennis Space Center: Mississippi, MS, USA, 2002; p. 45. [Google Scholar]
- Fernandez, E.; Aouf, L. Product User Manual for Global Ocean Waves Analysis and Forecasting Product Global_Analysis_Forecast_Wav_001_027, Copernicus Marine Environment Monitoring Service. 2018. Available online: https://resources.marine.copernicus.eu/documents/PUM/CMEMS-GLO-PUM-001-027.pdf (accessed on 1 May 2020).
- Wang, C.; Fei, J.; Ding, J.; Hu, R.; Huang, X.; Cheng, X. Development of a new significant wave height and dominant wave period parameterization scheme. Ocean Eng. 2017, 135, 170–182. [Google Scholar] [CrossRef] [Green Version]
| Hato | Pakhar | Mawar | |
|---|---|---|---|
| Distance to tropical cyclone track (, km) | 130.347 (447.815) | 250.633 (471.136) | −49.441 (207.916) |
| Longitude (°E) | 117.802 (113.735) | 116.655 (113.446) | 117.704 (116.698) |
| Latitude (°N) | 20.523 (21.84) | 19.247 (21.843) | 21.061 (21.903) |
| Time | 8/22 09:41 (8/23 02:33) | 8/26 10:29 (8/26 23:43) | 9/1 17:13 (9/3 00:03) |
| Maximum wind speed (, m/s) | 35.6 (50.7) | 22.5 (30.6) | 17.67 (23.1) |
| Minimum Air pressure (, hPa) | 972 (949) | 994 (983) | 996 (989) |
| Translation speed (, m/s) | 6.65 (8.80) | 10.14 (10.07) | 3.49 (2.11) |
| Radius of maximum wind (, km) | 18.52 (18.52) | 46.3 (46.3) | 101.86 (92.6) |
| Non-dimensional TC translation speed, ()* | 7.02 (8.76) | 4.68 (4.12) | 0.71 (0.47) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, D.; Zhang, H.; Zhang, W.; Zhou, F.; Sun, X.; Zhou, Y.; Ke, D. Wave Glider Observations of Surface Waves During Three Tropical Cyclones in the South China Sea. Water 2020, 12, 1331. https://doi.org/10.3390/w12051331
Tian D, Zhang H, Zhang W, Zhou F, Sun X, Zhou Y, Ke D. Wave Glider Observations of Surface Waves During Three Tropical Cyclones in the South China Sea. Water. 2020; 12(5):1331. https://doi.org/10.3390/w12051331
Chicago/Turabian StyleTian, Di, Han Zhang, Wenyan Zhang, Feng Zhou, Xiujun Sun, Ying Zhou, and Daoxun Ke. 2020. "Wave Glider Observations of Surface Waves During Three Tropical Cyclones in the South China Sea" Water 12, no. 5: 1331. https://doi.org/10.3390/w12051331
APA StyleTian, D., Zhang, H., Zhang, W., Zhou, F., Sun, X., Zhou, Y., & Ke, D. (2020). Wave Glider Observations of Surface Waves During Three Tropical Cyclones in the South China Sea. Water, 12(5), 1331. https://doi.org/10.3390/w12051331









