Complex Networks Theory for Evaluating Scaling Laws and WDS Vulnerability for Potential Contamination Events
Abstract
1. Introduction
2. Materials and Methods
2.1. Complex Networks
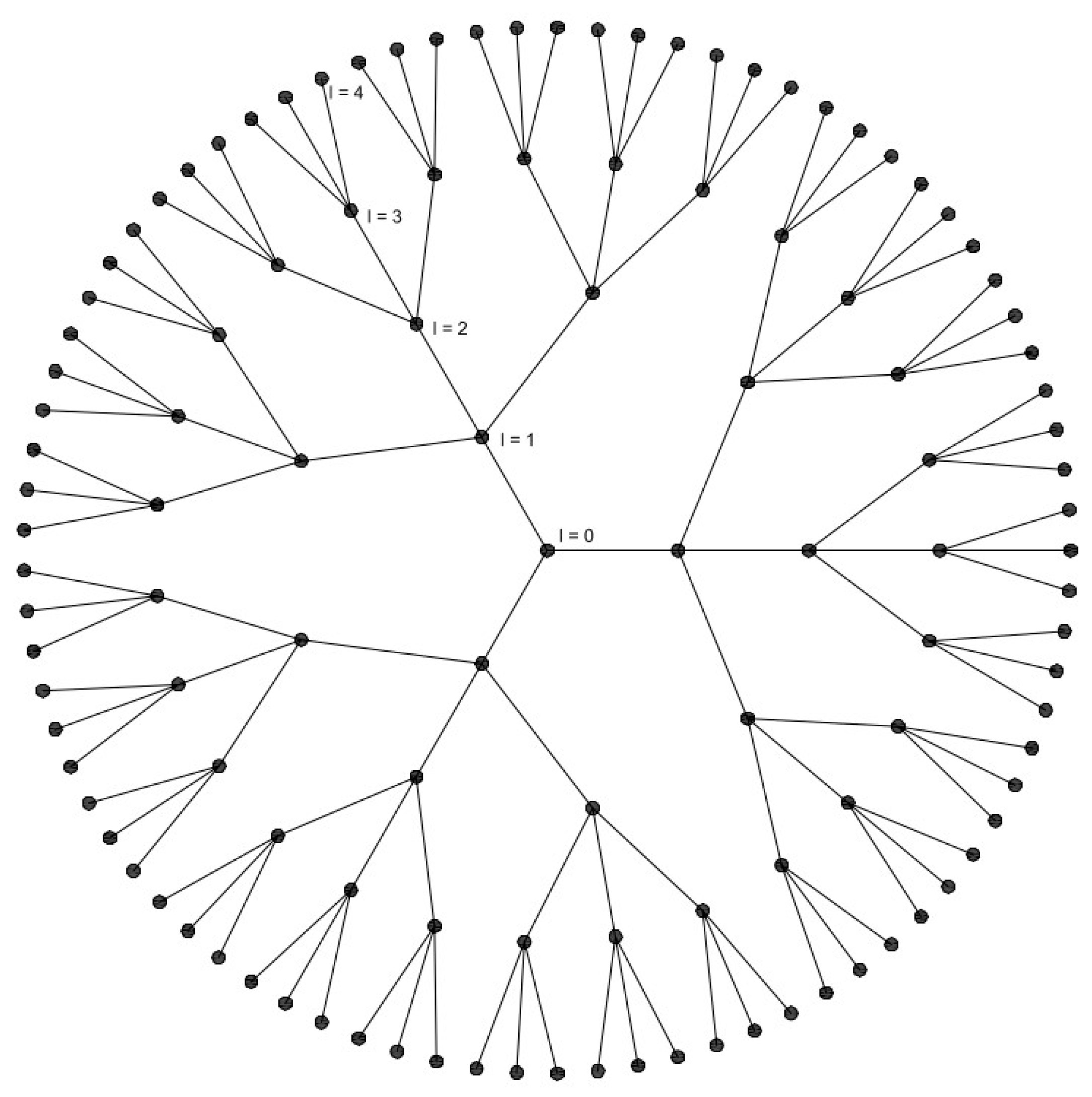
2.2. Cayley Regular Graphs
2.3. Methodology for Determining the Virtual Network and Its Distribution Functions
- Extended period simulations and source tracing analyses are performed with Epanet, one for each junction as a trace node, with sufficient simulation time in order to reach steady-state (or cyclic) conditions.
- A directed functional network is built, where the adjacency matrix is characterized by having 1 at position ij (for i ≠ j) if, and only if, the contaminant injected at the i-th node reaches the j-th node, with a predefined concentration threshold (typically, 0.1%).
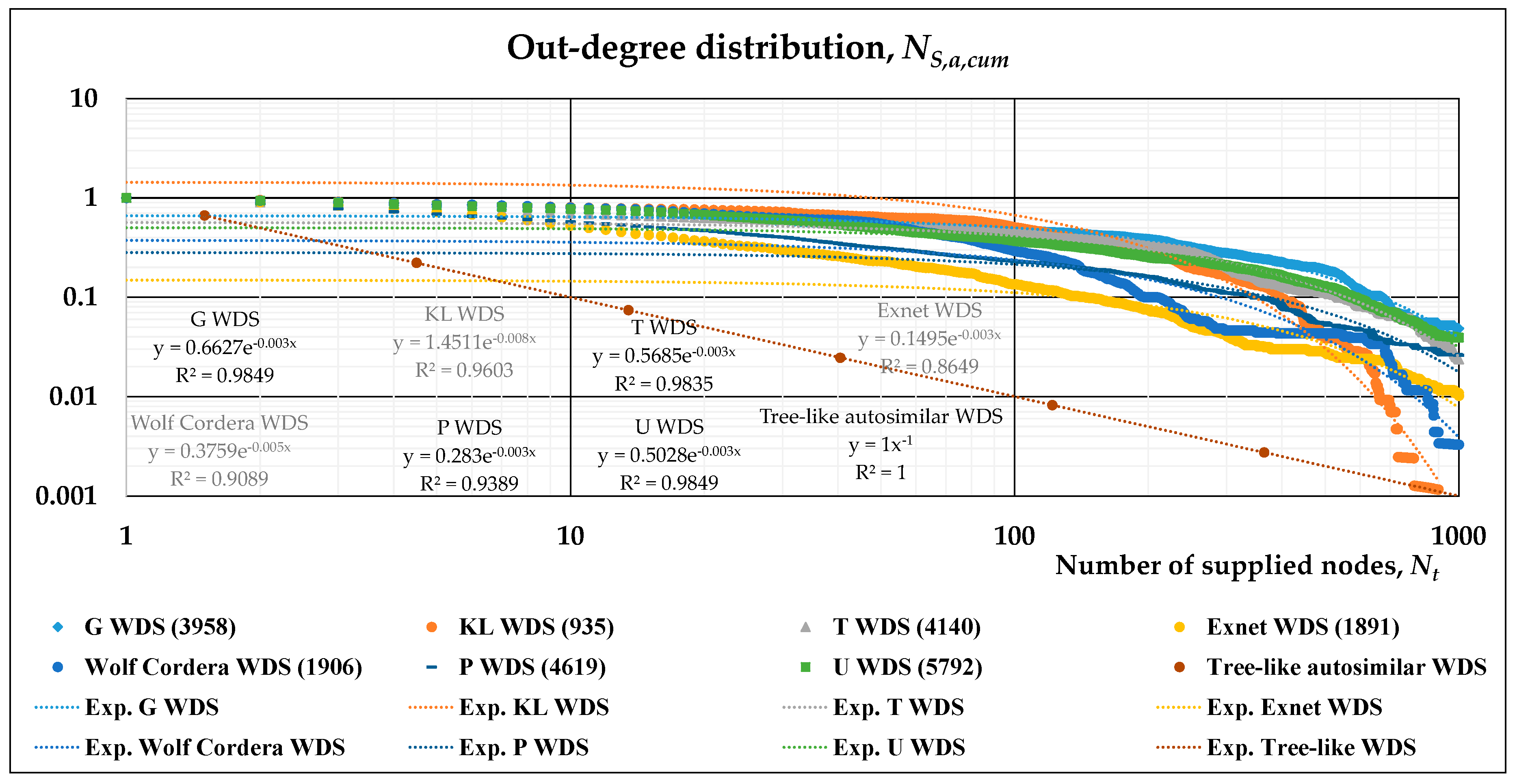
- The out-degree distribution of this directed, complex network is what we have previously called NS,a,cum(l’), and may be plotted on a log-log scale with respect to Nt(l’), the number of nodes supplied.
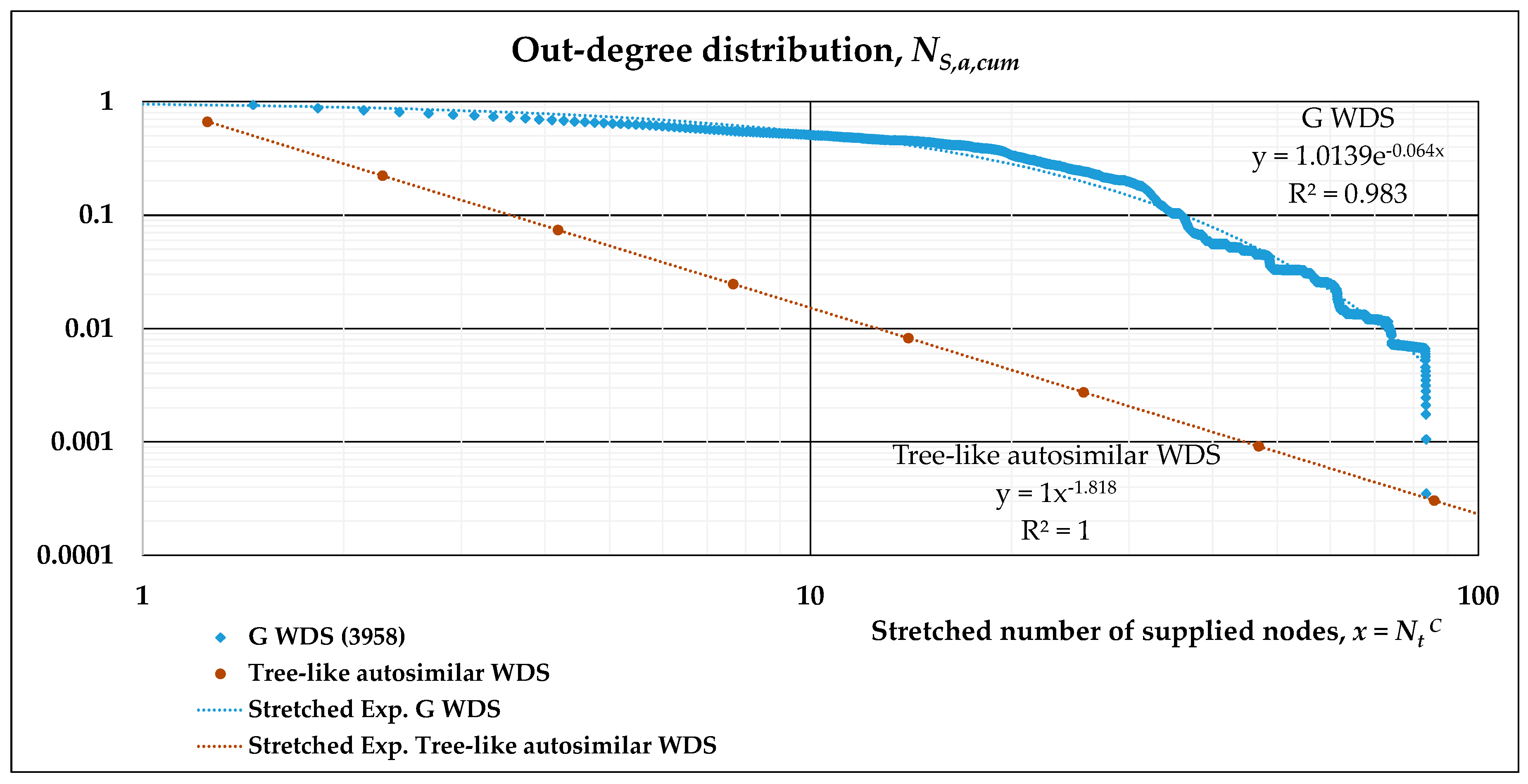
- A stretched exponential function is fitted to the results of numerical simulations in such log-log plots. This allows the evaluation of its scaling behavior and can be compared to the power-law distribution describing the tree-like regular network. Accordingly, two separate fittings may also be obtained, namely, a power-law and an exponential function for subsequent analytical derivation.
- The analytical formula derived in Section 2.4 allows an estimate of the vulnerability of the system. Thus, the more “distant” (in a probabilistic sense) the two distributions are, the more different the behavior of the real WDS is from a purely tree-like and auto-similar network, resulting in higher values of the index.
2.4. Analytical Expression of the Vulnerability Index: A Pragmatic Derivation
3. Results
3.1. Characteristics of the Real WDSs Adopted for the Analyses
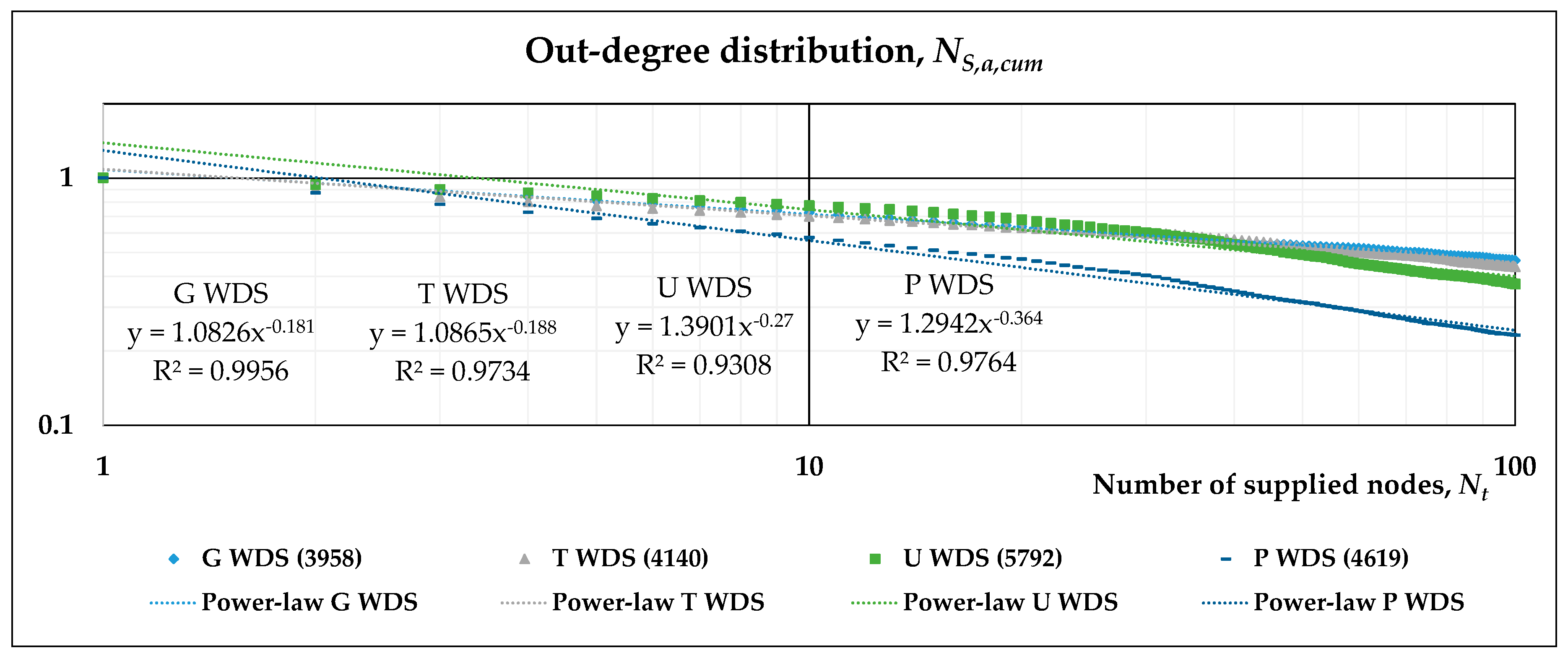
3.2. Scaling Laws of Different WDSs
3.3. Scaling Laws Obtained by Different Fittings
3.4. Determination of the Vulnerability Index for the Real Networks: A Pragmatic Method
4. Discussion and Concluding Remarks
Funding
Conflicts of Interest
References
- Bartram, J.; Corrales, L.; Davison, A.; Deere, D.; Drury, D.; Gordon, B.; Howard, G.; Rinehold, A.; Stevens, M. Water Safety Plan Manual: Step-by-Step Risk Management for Drinking-Water Suppliers; World Health Organization: Geneva, Switzerland, 2009. [Google Scholar]
- Ministry of Health. A Framework on How to Prepare and Develop Water Safety Plans for Drinking-Water Supplies; Ministry of Health: Wellington, New Zealand, 2014.
- Rosén, L.; Lindhe, A.; Hokstad, P.; Sklet, S.; Røstum, J.; Pettersson, T.J.R. Generic Framework for Integrated Risk Management in Water Safety Plans. In Proceedings of the 6th Nordic Drinking Water Conference, Oslo, Norway, 9–11 June 2008; pp. 193–203. [Google Scholar]
- Lockhart, G.; Oswald, W.E.; Hubbard, B.; Medlin, E.; Gelting, R.J. Development of indicators for measuring outcomes of water safety plans. J. Water Sanit. Hyg. Dev. 2014, 4, 171–181. [Google Scholar] [CrossRef] [PubMed]
- Shuang, Q.; Liu, H.J.; Porse, E. Review of the Quantitative Resilience Methods in Water Distribution Networks. Water 2019, 11, 1189. [Google Scholar] [CrossRef]
- Jung, D.; Lee, S.; Kim, J.H. Robustness and Water Distribution Systems: State-of-the-Art Review. Water 2019, 11, 974. [Google Scholar] [CrossRef]
- Huang, J.; McBean, E.A.; James, W. A Review of Reliability Analysis for Water Quality in Water Distribution Systems. J. Water Manag. Modeling 2005, R223, 107–130. [Google Scholar] [CrossRef]
- Rathi, S.; Gupta, R. Sensor Placement Methods for Contamination Detection in Water Distribution Networks: A Review. Procedia Eng. 2014, 89, 181–188. [Google Scholar] [CrossRef]
- Newman, M.E.J. Networks: An Introduction; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Barabási, A.L. The network takeover. Nat. Phys. 2012, 8, 14–16. [Google Scholar] [CrossRef]
- Giustolisi, O.; Simone, A.; Ridolfi, L. Network structure classification and features of water distribution systems. Water Resour. Res. 2017, 53, 3407–3423. [Google Scholar] [CrossRef]
- Yazdani, A.; Jeffrey, P. A complex network approach to robustness and vulnerability of spatially organized water distribution networks. arXiv 2010, arXiv:1008.1770. [Google Scholar]
- Yazdani, A.; Otoo, R.A.; Jeffrey, P. Resilience enhancing expansion strategies for water distribution systems: A network theory approach. Environ. Model. Softw. 2011, 26, 1574–1582. [Google Scholar] [CrossRef]
- Shuang, Q.; Zhang, M.; Yuan, Y. Node vulnerability of water distribution networks under cascading failures. Reliab. Eng. Syst. Saf. 2014, 124, 132–141. [Google Scholar] [CrossRef]
- Berardi, L.; Ugarelli, R.; Rostum, J.; Giustolisi, O. Assessing mechanical vulnerability in water distribution networks under multiple failures. Water Resour. Res. 2014, 50, 2586–2599. [Google Scholar] [CrossRef]
- Fu, C.; Wang, Y.; Wang, X. Research on complex networks’ repairing characteristics due to cascading failure. Phys. A 2017, 482, 317–324. [Google Scholar] [CrossRef]
- Gutiérrez-Pérez, J.A.; Herrera, M.; Pérez-García, R.; Ramos-Martínez, E. Application of graph-spectral methods in the vulnerability assessment of water supply networks. Math. Comput. Model. 2013, 57, 1853–1859. [Google Scholar] [CrossRef]
- Gutiérrez-Pérez, J.A.; Herrera, M.; Izquierdo, J.; Pérez-García, R. An approach based on ranking elements to form supply clusters in Water Supply Networks as a support to vulnerability assessment. In Proceedings of the International Environmental Modelling and Software Society (iEMSs), Leipzig, Germany, 1–5 July 2012; pp. 1544–1551. [Google Scholar]
- Yazdani, A.; Jeffrey, P. A note on measurement of network vulnerability under random and intentional attacks. J. Math. Model. Algorithms 2010, 4, 1–9. [Google Scholar]
- Sheng, N.; Jia, Y.W.; Xu, Z.; Ho, S.L.; Kan, C.W. A complex network based model for detecting isolated communities in water distribution networks. Chaos 2013, 23, 043102. [Google Scholar] [CrossRef] [PubMed]
- Giustolisi, O.; Ridolfi, L. A novel infrastructure modularity index for the segmentation of water distribution networks. Water Resour. Res. 2014, 50, 7648–7661. [Google Scholar] [CrossRef]
- Giustolisi, O.; Ridolfi, L.; Berardi, L. General metrics for segmenting infrastructure networks. J. Hydroinf. 2015, 17, 505–517. [Google Scholar] [CrossRef]
- Simone, A.; Giustolisi, O.; Laucelli, D.B. A proposal of optimal sampling design using a modularity strategy. Water Resour. Res. 2016, 52, 6171–6185. [Google Scholar] [CrossRef]
- Nazempour, R.; Monfared, M.A.S.; Zio, E. A complex network theory approach for optimizing contamination warning sensor location in water distribution networks. arXiv 2016, arXiv:1601.02155. [Google Scholar] [CrossRef]
- Giudicianni, C.; Di Nardo, A.; Di Natale, M.; Greco, R.; Santonastaso, G.F.; Scala, A. Topological Taxonomy of Water Distribution Networks. Water 2018, 10, 444. [Google Scholar] [CrossRef]
- Santonastaso, G.F.; Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Greco, R. Scaling-Laws of Flow Entropy with Topological Metrics of Water Distribution Networks. Entropy 2018, 20, 95. [Google Scholar] [CrossRef]
- Giustolisi, O.; Ridolfi, L.; Simone, A. Embedding the intrinsic relevance of vertices in network analysis: The case of centrality metrics. Sci. Rep. 2020, 10, 1–11. [Google Scholar] [CrossRef]
- Newman, M.E.J. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Estrada, E. The Structure of Complex Networks; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Estrada, E.; Knight, P.A. A First Course in Network Theory; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Erdös, P.; Rényi, A. On random graphs I. Publ. Math. Debr. 1959, 6, 290–297. [Google Scholar]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.-L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Strogatz, S.H. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef]
- Mandelbrot, B. The Fractal Geometry of Nature; W.H. Freeman & Co. Ltd: New York, NY, USA, 1982. [Google Scholar]
- Barthélemy, M. Spatial networks. Phys. Rep. 2001, 499, 1–101. [Google Scholar] [CrossRef]
- Nicolini, M.; Giacomello, C.; Deb, K. Case study: Calibration and optimal leakage management for a real water distribution network. J. Water Resour. Plan. Manag. 2011, 137, 134–142. [Google Scholar] [CrossRef]
- Nicolini, M.; Patriarca, A. Model calibration and system simulation from real-time monitoring of water distribution networks. In Proceedings of the 3rd International Conference on Computer Research and Development, Shangai, China, 11–13 March 2011; pp. 51–55. [Google Scholar]
- Nicolini, M.; Giacomello, C.; Mion, M.; Scarsini, M. Numerical modeling and leakage reduction in the water distribution system of Udine. Procedia Eng. 2014, 70, 1241–1250. [Google Scholar] [CrossRef]
- Bi, W.; Dandy, G.C.; Maier, H.R. Improved genetic algorithm optimization of water distribution system design by incorporating domain knowledge. Environ. Model. Softw. 2015, 69, 370–381. [Google Scholar] [CrossRef]
- Farmani, R.; Savic, D.; Walters, G. EXNET benchmark problem for multi-objective optimization of large water systems. In Modelling and Control for Participatory Planning and Managing Water Systems; International Federation of Automatic Control (IFAC): Venice, Italy, 2004. [Google Scholar]
- Lippai, I. Colorado Springs Utilities Case Study: Water System Calibration/Optimization; ASCE: Reston, VA, USA, 2005. [Google Scholar]
- Simone, A.; Ridolfi, L.; Berardi, L.; Laucelli, D.; Giustolisi, O. Complex Network Theory for Water Distribution Network Analysis. In Proceedings of the 13th Hydroinformatics International Conference, Palermo, Italy, 1–6 July 2018. [Google Scholar]
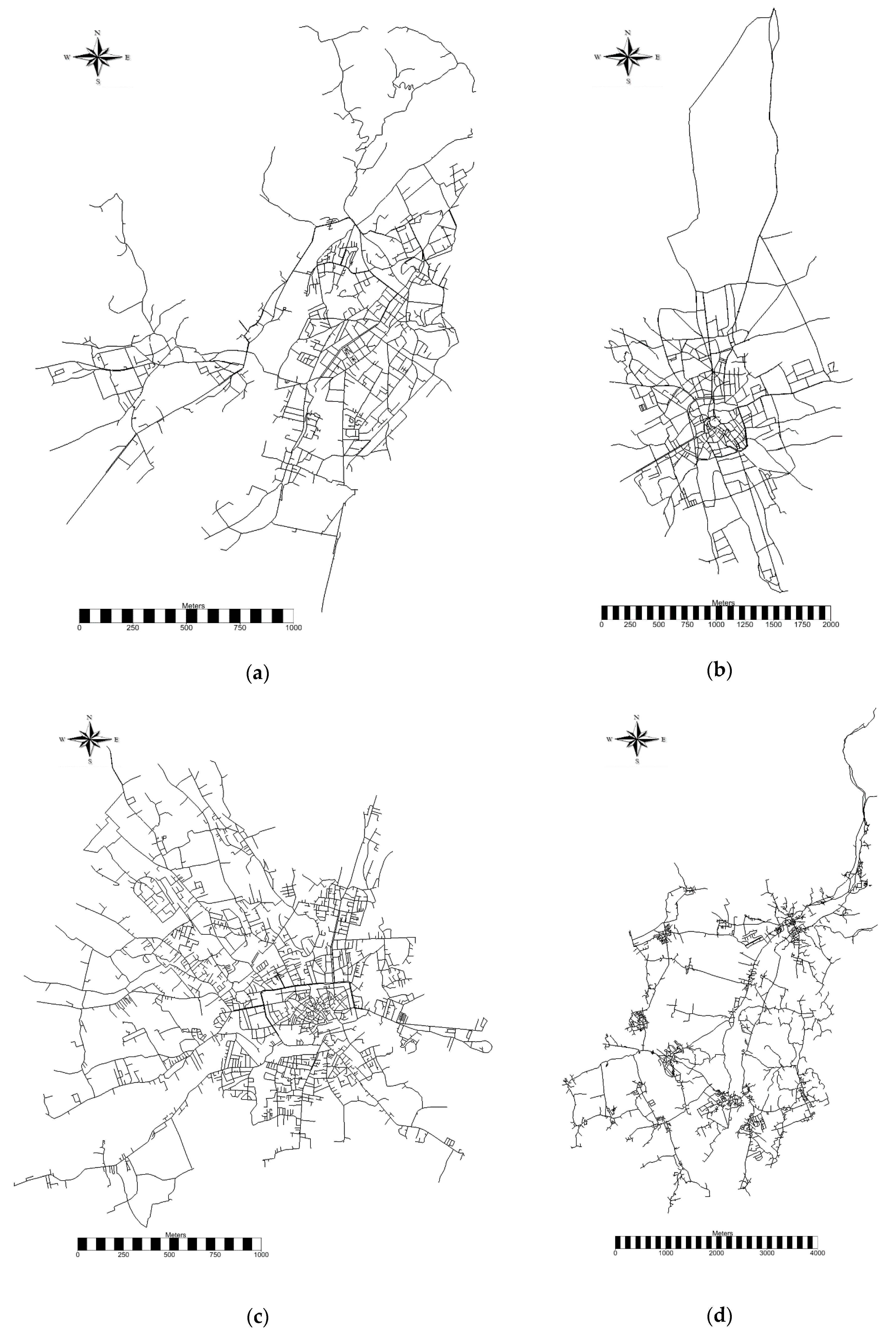
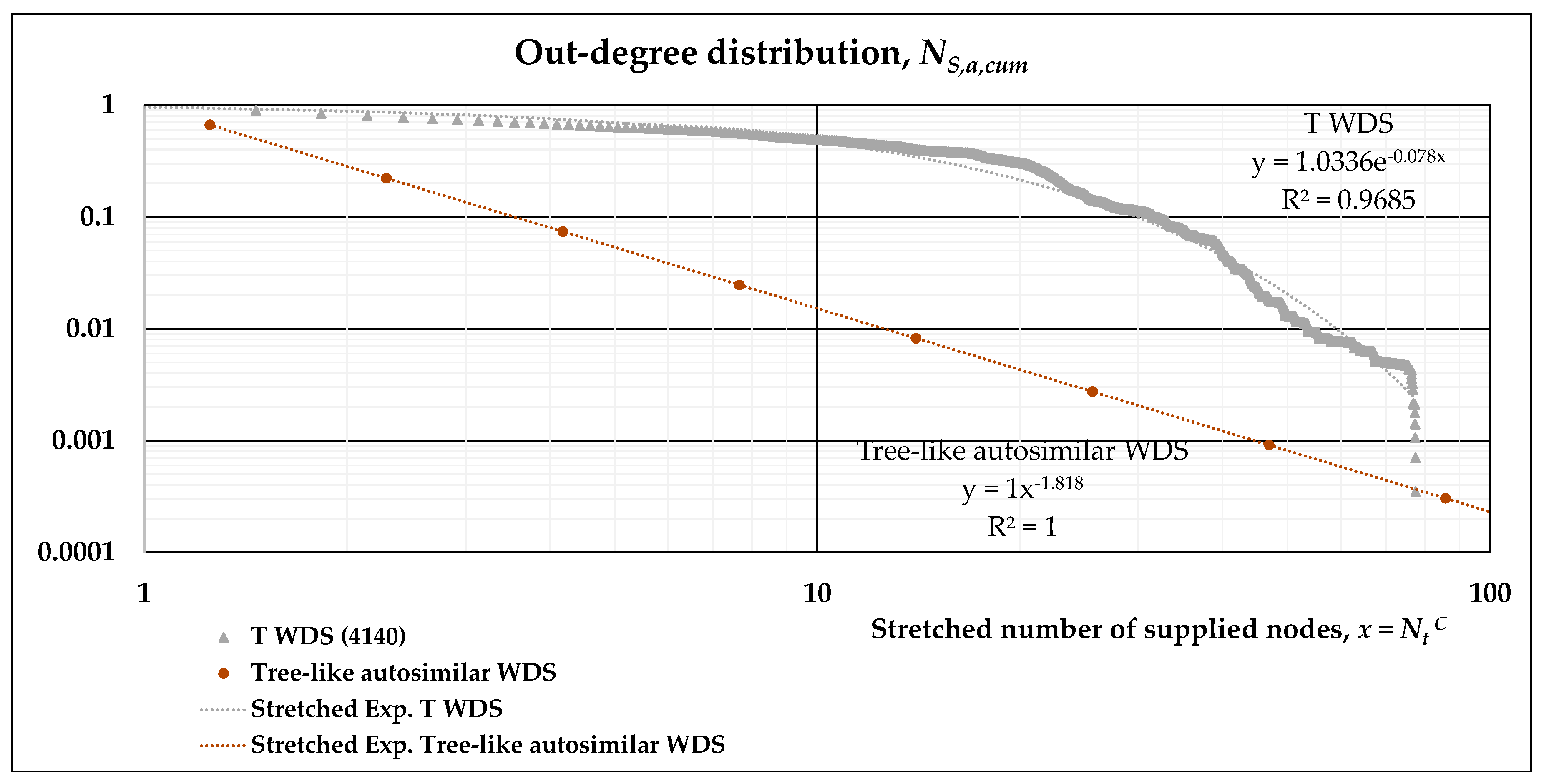
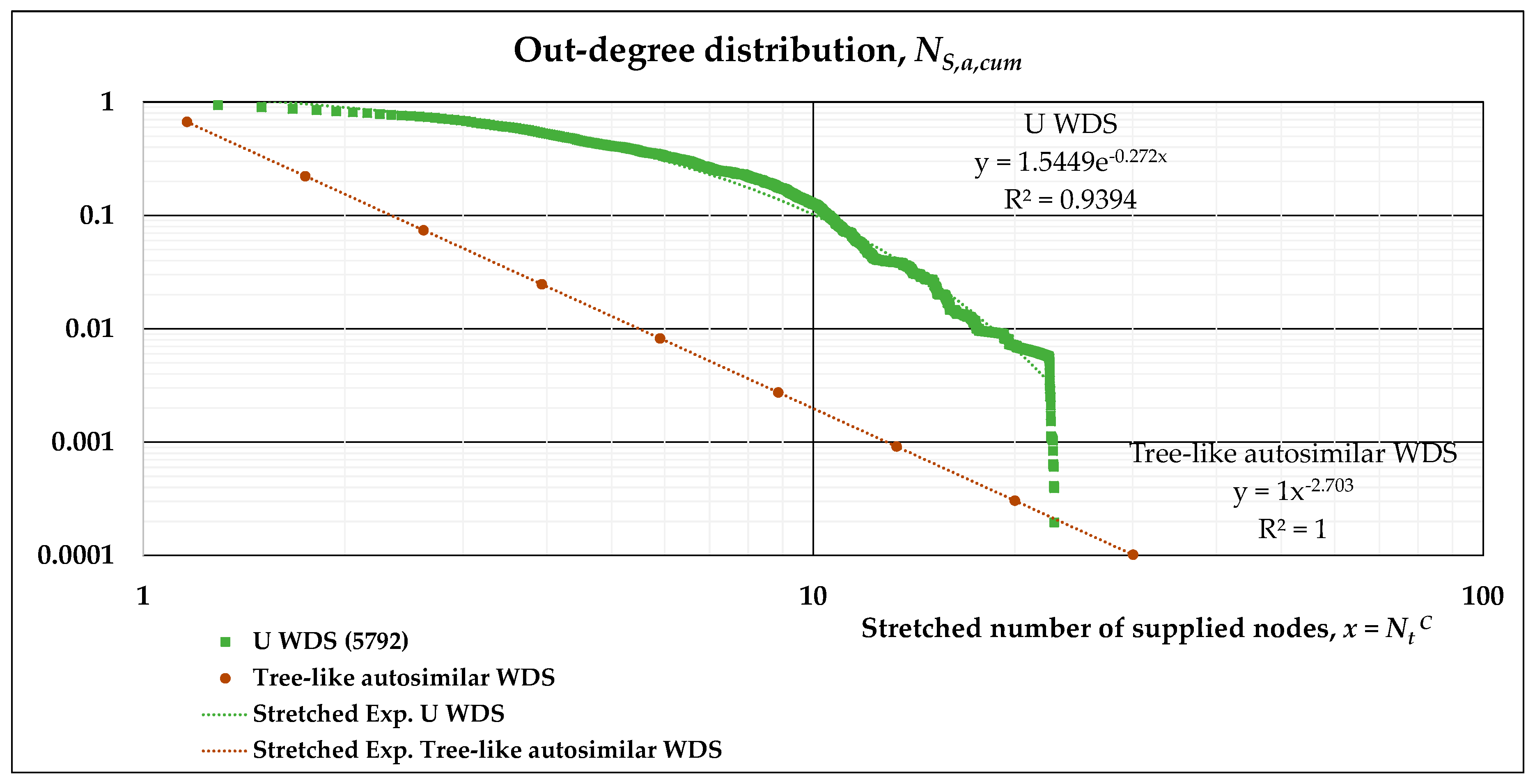
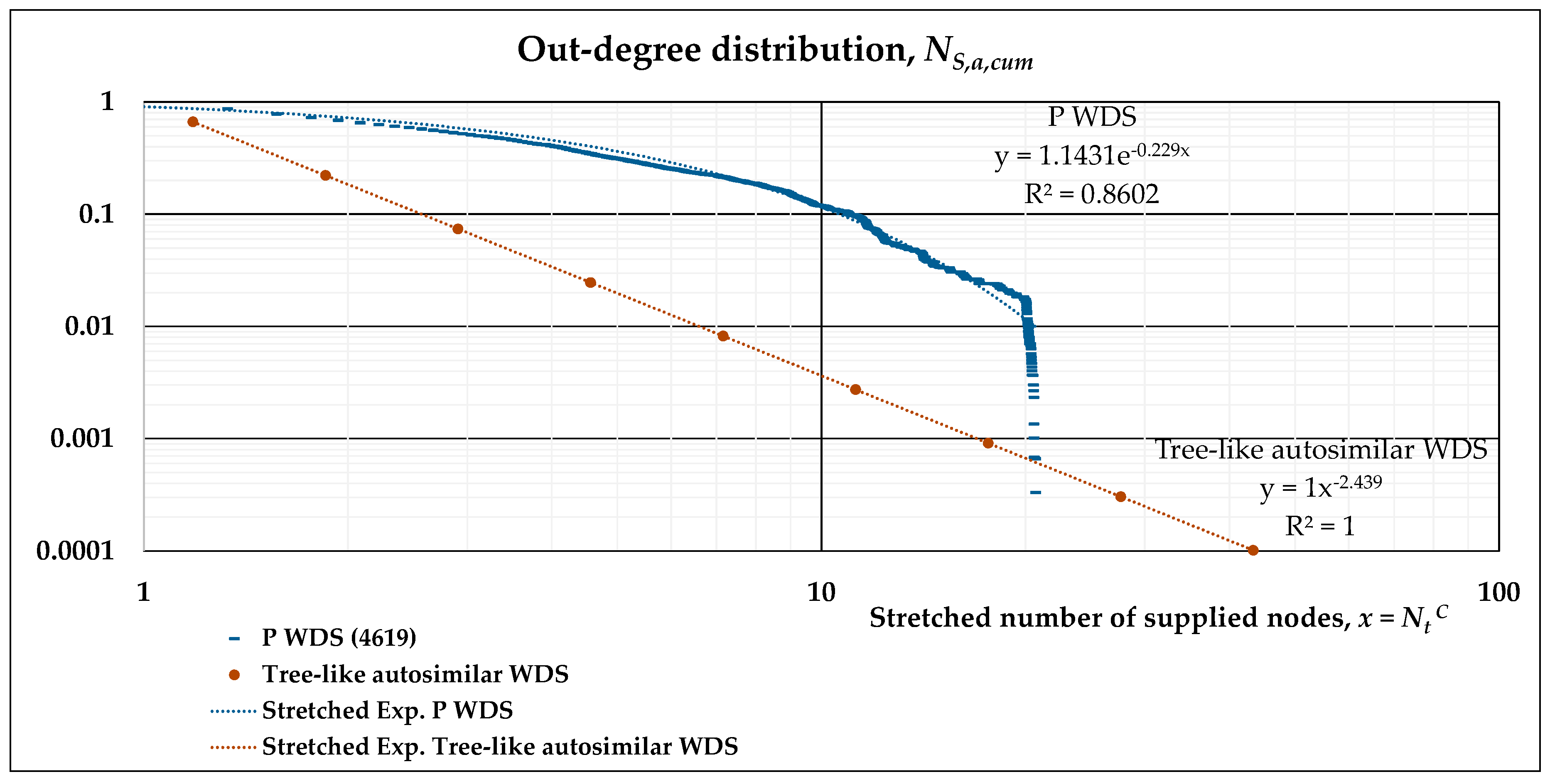
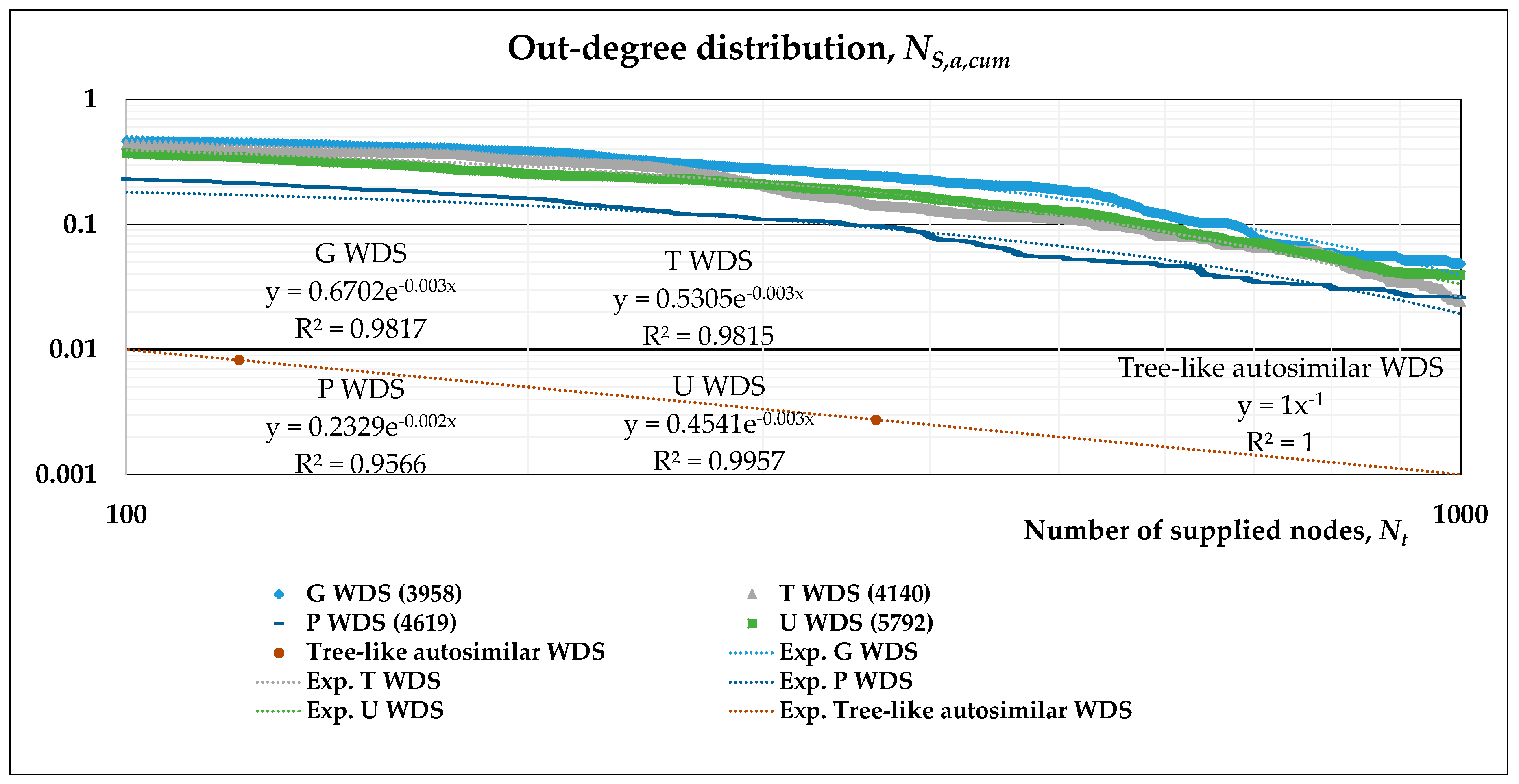
| WDS | n | p | t | L (km) | Pop | ρ | <k> | <ℓ> | D | <Cc> |
|---|---|---|---|---|---|---|---|---|---|---|
| G | 3958 | 4170 | 5 | 201 | 45,000 | 0.001 | 2.11 | 50.04 | 137 | <0.001 |
| T | 4140 | 4601 | 20 | 326 | 85,000 | 0.001 | 2.22 | 46.82 | 130 | 0.009 |
| U | 5772 | 6453 | 19 | 408 | 97,000 | <0.001 | 2.23 | 49.58 | 127 | 0.001 |
| P | 4619 | 5115 | 26 | 756 | 66,000 | <0.001 | 2.21 | 60.93 | 165 | 0.020 |
| WDS | n | m | ρ | ρu | <kout> | <ℓ> | <ℓu> | D | Du | <Cc> | <Cc,u> |
|---|---|---|---|---|---|---|---|---|---|---|---|
| G | 3958 | 281,185 | 0.018 | 0.0359 | 71.042 | 1.1114 | 2.0970 | 5 | 8 | 0.204 | 0.443 |
| T | 4140 | 286,719 | 0.017 | 0.0335 | 69.256 | 1.5126 | 2.3657 | 8 | 13 | 0.184 | 0.433 |
| U | 5772 | 343,422 | 0.010 | 0.0206 | 59.498 | 2.0941 | 3.6016 | 11 | 10 | 0.289 | 0.583 |
| P | 4619 | 219,646 | 0.010 | 0.0206 | 47.553 | 1.6635 | 3.6291 | 5 | 14 | 0.270 | 0.578 |
| WDS | A | B | C |
|---|---|---|---|
| G | 1.0139 | 0.064 | 0.550 |
| T | 1.0336 | 0.078 | 0.551 |
| U | 1.5449 | 0.272 | 0.370 |
| P | 1.1431 | 0.229 | 0.410 |
| WDS | α | β | γ | δ | VI |
|---|---|---|---|---|---|
| G | 1.0826 | 0.181 | 0.6627 | 0.003 | 205.73 |
| T | 1.0865 | 0.188 | 0.5685 | 0.003 | 182.91 |
| U | 1.3901 | 0.270 | 0.5028 | 0.003 | 165.83 |
| P | 1.2942 | 0.364 | 0.2830 | 0.003 | 98.22 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nicolini, M. Complex Networks Theory for Evaluating Scaling Laws and WDS Vulnerability for Potential Contamination Events. Water 2020, 12, 1296. https://doi.org/10.3390/w12051296
Nicolini M. Complex Networks Theory for Evaluating Scaling Laws and WDS Vulnerability for Potential Contamination Events. Water. 2020; 12(5):1296. https://doi.org/10.3390/w12051296
Chicago/Turabian StyleNicolini, Matteo. 2020. "Complex Networks Theory for Evaluating Scaling Laws and WDS Vulnerability for Potential Contamination Events" Water 12, no. 5: 1296. https://doi.org/10.3390/w12051296
APA StyleNicolini, M. (2020). Complex Networks Theory for Evaluating Scaling Laws and WDS Vulnerability for Potential Contamination Events. Water, 12(5), 1296. https://doi.org/10.3390/w12051296




