Abstract
Urban water resources are the basis for the formation and development of cities and the source of urban water supply. However, with the acceleration of urbanization and the explosion of urban populations, the contradiction between water supply and demand in some areas, especially in big cities, has become increasingly prominent. It is simply not sufficient to rely on local conventional water resources to meet urban water demand, and a single source water supply mode has a higher vulnerability, resulting in greater safety risks in urban or regional water supply systems. Therefore, giving full play to the water supply capacity and carrying out multi-source water supplies are necessary and urgent. This paper gives an overview of the optimal allocation of multi-source for urban water supply concerning variation tendency, modeling methods and facing challenges. Based on the variation tendency of water consumption and water supply pattern in China, Tianjin is taken as a typical city for systematically outlining water supply changes and cause analysis. Subsequently, the modeling methods for proposing the optimal allocation scheme are summarized, which are composed of defining the topological relation, constructing the mathematical model and seeking the optimal solution. Ultimately, the current and emerging challenges are discussed including emergency operation of multi-source water supply and joint operation of water quality and quantity. These summaries and prospects provide a valuable reference for giving full play to the multi-source water supply capacity and carrying out relevant research so as to propose the optimal allocation scheme in urban multi-source water supply systems.
1. Introduction
Water is an essential natural resource for the sustainable economic and social development and, more importantly, for the human survival and development [1]. Water shortage has become one of the major problems worldwide, in general, and in China, in particular [2]. With less than 6% of total global water resources but one fifth of the global population, China is facing serious challenges to its water resources management, particularly in rural areas [3]. The sixth census in 2011 showed that China’s average per capita share of water resources (about 2100 m3) is only about 25% of the world average [4]. It was reported that of the 669 cities, 400 suffer from insufficient water supply and 110 suffer from severe water shortage; of the 32 cities with a population at or exceeding 1 million, 30 suffer from chronic water shortage; of the 14 coastal open cities, 9 suffer from acute water shortage [5]. Now, China is one of the 13 most water-stressed countries in the world. Apart from the low per capita availability of water resources, there is a mismatch between the spatial distribution of water resources and geographic regions with high population densities, especially in north China where water resources are particularly scarce [6]. By the end of 2010, the 11 coastal provinces lay alone the 1800 km coastal line, occupying 13.7% of China’s territory with 43.0% of China’s population [7]. The north of the country, similar in land area and population to the south, held only 18% of the total water despite having 65% of the total arable land [8]. In recent decades, accounting for the influence of climate change, land cover change and human activities, drought and water logging disasters, and water ecological security problems have been increasingly prominent; its impact on water availability for humans can jeopardize human life. It is demonstrated that climate change has already aggravated and may further the water challenge in China, worsening the water shortages and intensifying the conflicts among water users [9]. Moreover, in most areas, especially in northwest and north China, water resources utilization has approached or exceeded its threshold [10]. Water resource constraints can slow down the socio-economic growth rate and the speed of urbanization process, destroying the projected targets of eradicating poverty and realizing sustainable development [11].
Urban water resources refer to all kinds of water resources that can be used by cities, with sufficient quantity and quality, consisting of both conventional water resources (e.g., surface water, groundwater, transferring water) and non-conventional water resources (e.g., reclaimed water, desalted water, rain-flood water, et al.) [12]. Not only do urban water resources provide domestic water for urban residents, but they also supply production water for industry, agriculture and ecology. However, due to the expansion of urban scale and the explosion of population, the total urban water consumption has increased year by year. The contradiction between water supply and demand has intensified day by day, and the situation of urban water shortages has become more and more severe. Thus, a large number of reservoirs, groundwater and interbasin water transfer projects are constructed as main measures to alleviate water shortage. Groundwater is an indispensable source of water supply in some inland areas where water shortage is severe, and 35%–50% or so of water supply in north China comes from groundwater [13]. Interbasin water governance is one of the most effective means to solve the shortages of water resources in inland arid and semiarid regions, because interbasin water management has more advantages than basin water management, such as the allocation space for the water resource is greater and there is greater regulation and water storage capacity [14]. Reclaimed water as the second water source can contribute to mitigating water shortages and improving aquatic environment quality [15]. Taking Beijing as an example, its reclaimed water supply increased from 205 million m3 in 2003 to 800 million m3 in 2013, accounting for about 22% of the total annual water supply [16]. Rain-flood water in summer and desalinated water in coastal areas can also be important supplementary water sources for urban use. Total seawater desalination capacity increased from 10,000 m3/d in 2000 to approximately 660,000 m3/d in 2011, and the five provinces including Liaoning, Shandong, Hebei, Tianjin and Zhejiang accounted for 99.5% of the national total capacity [7]. Furthermore, brackish water, mineral water and karstic water in some areas serve as emergency water sources. The Yunnan-Guizhou Plateau is the largest and most diversified karst region in the world. It is estimated that annual average karst water resources available for utilization in Yunnan and Guizhou are 9.95 billion m3 and 8.88 billion m3, respectively [17].
The rational development and utilization of above water resources can provide a variety of water sources on the one hand, and improve the urban water-supply guarantee rate on the other hand. However, water sources may differ considerably in temporal and spatial distribution, water quality, available water supply and water-supply guarantee rate [18]. For example, groundwater as a water source has good quality and high water-supply guarantee rate, but it is difficult to recover once overexploited [19]. Reservoir water as a water source can be renewed and restored every year, but it is susceptible to pollution. Reclaimed water as a water source is less affected by the season and the climate, having the characteristic of excellent quality and stable quantity, but it is mostly used for industrial water and municipal water [16]. Moreover, multi-source competition, substantial uncertainty and special water supply rules are likely to lead to water conflicts in the water distribution process. Thus, it is difficult to cope with the scientific problems existing in urban water supply systems and give full play to the multi-source water supply capacity. As a result, there is an urgent need to consider the optimal allocation of multi-source water supplies. Firstly, this paper introduces Tianjin’s water supply changes and cause analysis based on analyzing water consumption and water supply pattern in China. Then, this paper summarizes the modeling methods for proposing the optimal allocation scheme of a multi-source water supply, from the point of topological relations, modeling constructions and model solutions. Finally, this paper discusses the current challenges of urban multi-source water supply in China.
2. Variation Tendency of Multi-Source Water Supply in China
2.1. Water Consumption and Water Supply Pattern in China
According to Water Resources Bulletin released by the Ministry of Water Resources of China, water uses mainly include industrial water consumption, agricultural water consumption, domestic water consumption and ecological water consumption [20]. The water consumption data in China are shown in Figure 1. The agricultural water consumption accounted for the largest water use from 2005 to 2018; the proportion of water used in agriculture showed a trend of decreasing first before 2010, then rising before 2014, and then falling again. Compared to the agricultural water consumption, other water users in the total water consumption were lower, only accounting for 36.4%–38.7%. During the period of 2005–2014, all the aspects of major cities, including the population growth, the urbanization rate, the economic development and the people’s living standard, maintained an upward trend, which required much more water resources to support them [21]. Furthermore, It was found that population growth was the main cause of increased domestic water consumption in most cities, and the water consumption per capita per day was positively associated with gross domestic product (GDP) per capita, urban area, precipitation, temperature and urban population [22]. Therefore, the domestic water consumption and the ecological water consumption increased significantly since 2005. The proportion of domestic water consumption in the total water consumption increased from 12.0% in 2005 to 14.3% in 2018, and the related figures rose from 67.5 billion m3 to 86 billion m3. The proportion of ecological water consumption in the total water consumption increased from 1.6% in 2005 to 3.3% in 2018, and the number rose from 9.3 billion m3 to 20.1 billion m3. Unlike domestic water and ecological water, the consumption of industrial water fluctuated before 2011 and then descended, due to the improvement of circulating water systems and the reform of industrial water saving technology [23].
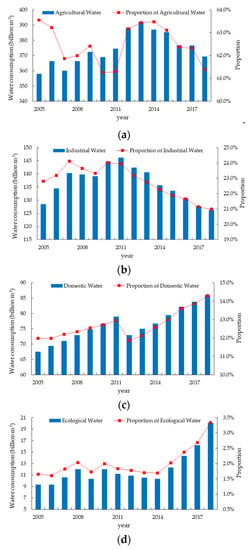
Figure 1.
Annual water consumption by various water users and its share in total water consumption as follows: (a) agricultural water; (b) industrial water; (c) domestic water; (d) ecological water.
In contrast, water sources mainly include surface water, groundwater and other sources. Water supply data in China are shown in Figure 2. Surface water was always the largest water supply source from 2005 to 2018; the proportion of surface water in the total water supply showed a trend of descending first and ascending in succession, varying from 80.7% to 82.3%. The proportion of groundwater in the total water supply was almost constant between 2005 and 2014, and it dropped significantly since 2015. In the last few years, the water supply of groundwater in 2018 was only 86.1% of that in 2012, which was strongly influenced by the promotion and implementation of the most stringent water management system, the reduction of seawater desalination cost, the heightening price levies of the groundwater resources, and the operation of some interbasin water transfer projects [24]. As a result, the water supply of other sources showed an annual increase in the basic trend, but a modest one. The proportion of other sources in the total water supply increased from 0.4% in 2005 to 1.4% in 2018, and the number rose from 2.2 billion m3 to 8.6 billion m3.
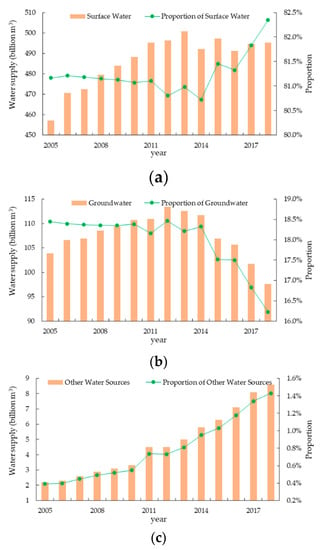
Figure 2.
Annual water supply by various water sources and its share in total water supply as follows: (a) surface water; (b) groundwater; (c) other water sources.
2.2. Water Supply Changes and Cause Analysis in a Typical City
It is well known that the water shortage in northern China is severe and the water shortage in the Haihe River Basin is the most prominent. In order to explore the water supply changes and its cause analysis in Chinese cities, it is essential to select a typical water-scarce city to implement case analysis. As a result, Tianjin is regarded as a typical water-scarce city in northern China, considering that scholars at home and abroad have carried out a lot of research in this city and Tianjin has the lowest per capita water resources in mainland China [25]. Tianjin is situated on the banks of the Haihe River, and it is an important city and main communication center of North China with its comprehensive industrial base and international modernized port. In the late 1970s, water shortage, water pollution and land subsidence caused by over-extraction of groundwater restrained the local economic development and people’s normal life considerably [26]. Subsequently, influenced by overwhelming urbanization, industrialization and economic development, as well as possible shrinkage of water supplies that resulted from extreme weather occurrence, water infrastructure breakdown and water quality deterioration, the contradiction between water supply and water demand was sharpening. At present, Tianjin has the lowest per capita water resources in mainland China, and it is far off the average level of the world. In 2017, per capita water resources in Tianjin was only 83.6 m3, while that in China was 2074.5 m3, and the former is only about 1/25 of the latter. Furthermore, up to 76% of surface water had been utilized in the region at the beginning of the 21st century, which was significantly greater than the 40% global threshold [27].
Interbasin water transfers incorporated with optimal allocation models had become crucial measures to address urban water shortage problems [28]. With the implementation of three major water transfer projects (i.e., the Luan River-to-Tianjin Water Diversion Project, the Yellow River-to-Tianjin Emergency Water Diversion Project, the South-to-North Water Transfer Project), the bottleneck that water resources had been was eased effectively [29,30]. In 2015, the transferring water from the Luan River and the Yangtze River totaled 0.66 and 0.38 billion m3, respectively, accounting for 39% of the total water supply [31]. Moreover, comprehensively utilizing and reasonably allocating conventional water resources (i.e., surface water, transit water, and groundwater) and nonconventional water resources (i.e., desalted water, and reclaimed water) were equally important for Tianjin’s urban water supply [18]. According to Water Resources Bulletin released by the Tianjin Municipal Water Conservancy Bureau, the water supply of other water sources was 0.455 billion m³in 2018, accounting for 16.0% of the total water supply, while the other water sources were only 0.002 billion m³in 2003, less than 0.1% of the total water supply [32].
Due to the improvement of industrial water efficiency, the high-technology, low-energy and low-emission emerging industries gradually replaced the high-water-consumption, high-pollution and low-efficiency traditional industries. The total industrial output value of Tianjin rose from 266.3 billion yuan in 1998 to 1007.5 billion yuan in 2007, with an increase of 278.4%, while the total production water supply of Tianjin declined from 346 million m³ to 336 million m³, with a decrease of 3%. Another research showed that industrial expansion was responsible for an increase in annual water use of 78 million m³, while technical advances and water efficiency measures contributed annual water savings of about 76 million m³ [33]. In addition, in order to ease the increasingly prominent water crisis, Tianjin put the most stringent water management system into practice, which has achieved remarkable results by setting out water use efficiency targets. In 2013, water use per unit of GDP was reduced to 17.52 m3, less than one-sixth of the national average, and water use per unit of industrial added value was reduced to 8.3 m3, representing the highest industrial water efficiency in China [34].
It was worth mentioning that the reform of water price mechanism made a big difference to total urban water consumption [35]. In response to the phenomenon that waste of urban domestic water was serious, Tianjin raised the residential water prices twelve times between 1996 and 2012, increasing the water price from 0.65 yuan/m3 in 1997 to 4.9 yuan/m3 in 2012. The direct action of water price reform was to give full play to water saving and enhance people’s water-saving consciousness. More importantly, it was an effective way to adjust the distribution of water resources to promote the conservation of water resources and propel urban sustainable development. Furthermore, the adjustment of water consumption structure in the central city, especially the development of the third industry and modern service industry, also played an important role in alleviating the contradiction between supply and demand in Tianjin. From 2004 to 2010, the water utilization structure of Tianjin tended to be disordered and balanced, which meant that the dominance of a single water consumption type decreased and the equilibrium degree increased generally [36].
Based on the above influencing factors, the construction of a more complex urban water supply model appears inevitable, that involves multi-objectives, multi-variables and multi-constraints; some special water supply rules are also taken into account. In 2015, Tianjin’s water users were mainly oriented to domestic water, production water and ecological water, while water sources supplied to Tianjin including surface water, groundwater, reclaimed water, desalinated seawater and transferring water. Eleven water resource divisions and 19 water plants were also considered within the scope of urban water supply in Tianjin [37].
3. Modeling Methods for Optimal Allocation of Multiple Water Sources
Multi-source optimal allocation is a significant means to handle contradiction between water supply and demand in water shortage cities. Its core ideas can be interpreted as follows: the premise of ensuring the safety of the urban water supply, considering the uncertainty of multi-source with the help of advanced decision theory and computer technology, intervening in spatial and temporal distribution of water resources, and allocating multi-source uniformly [38]. Meanwhile, meeting requirements of different water users in terms of water quality and water quantity, reducing water supply costs and giving full play to engineering benefits, realizing the optimal allocation of multi-source. According to the selected research area, the modeling methods for proposing the optimal allocation scheme are mainly composed of three parts, namely defining the topological relation, constructing the mathematical model and seeking the optimal solution. A common flow chart of the research on multi-source water supply is shown in Figure 3.
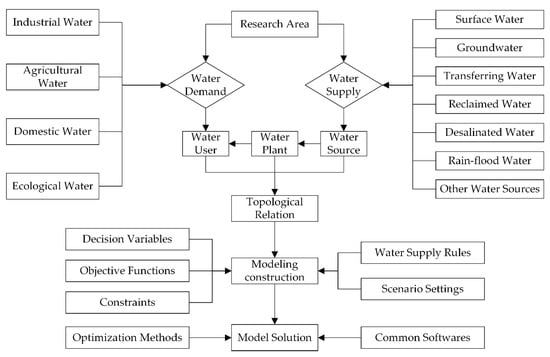
Figure 3.
The flow chart of research on multi-source water supply.
3.1. Topological Relation
Urban multi-source water supply is based on combining multiple water sources, multiple water plants, multiple water users, and other auxiliary elements (e.g., pipelines, sluice gates, pump stations, water intake, and water outlet) together. Simplifying urban water supply networks and generalizing the topological relation between water sources, water plants, and water users, are the foundations for establishing a multi-source optimal allocation model. System generalization is a physical process that generalizes different system entities with common properties into conceptual elements expressed in various parameters [39]. Considering the complexities of the water supply system, the graph theory based on point, line and surface elements is adopted, the topological structure involving multiple water sources, water plants and water users is referenced, and then the actual multi-source water supply system can be abstracted to a generalized water supply network. In the graph theory, point elements indicate entities in the water supply network, while line elements indicate the relation between associated entities and surface elements indicate that where entities are belong to [40]. In the topological structure, only the relation among the position of elements is considered, while the shape and size of the elements are not considered. Furthermore, aiming at giving a general view of the supply and demand relation, as well as making different sub-study areas partitioned and visualized, district metering areas (DMAs), defined as achieving the portioning of a water distribution network, can be applied for large-scale multi-source water supply networks [41].
In the topological relations of multi-source water supply, the water plant is regarded as the intermediate node between the water source and the water user all the times, because it can play an important role in delivering water, storing water and regulating water in the water supply system. Along with the increase in the water sources and the water users, the past one-to-one relation between water sources, water plants and water users is unable to meet requirements of urban water supply [18]. Instead, the one-to-many relation, the many-to-one relation or the many-to-many relation between water sources, water plants and water users are gradually emerging (Figure 4). When it comes to the transfer water, it can deliver water to the water user directly without passing through the water installation, and it can deliver water to the water user passing through the water plant. What needs illustration is that the transferring water can even deliver water to the diversion outlet by means of main line projects, followed by branch line projects delivering water to the water plant. Therefore, for a specified water source delivering water to a specified water user, not just one water supply route, several water supply routes are possible in the water supply system in practice [37]. Consequently, the many-to-many relation between water sources, water plants and water users in the actual water supply network is much more complex than that in Figure 4d.
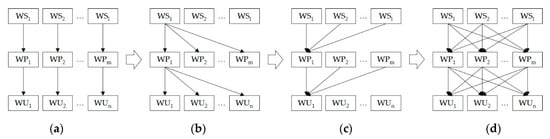
Figure 4.
Four urban multi-source water supply modes are as follows: (a) one to one; (b) one to many; (c) many to one; (d) many to many (Note: WU, WP WU mean water source, water plant, water user, respectively. l, m, n mean numbers of water source, water plant, water user, respectively).
Considering the complexity in the topological relations of multi-source water supply, it is necessary to conduct a more efficient water supply system. Centralized systems, decentralized systems and hybrid systems are widely applied in the water supply network. Centralized water supply systems have ensured adequate water supply, sanitation and drainage services to its inhabitants in cities, but these water infrastructures are considered to be unsuitable to address future challenges in some circumstances [42]. Contrary to the centralized water supply system, a decentralized water supply system can reduce reliance on traditional water sources and provide long-term ecological sustainability. However, there are numerous unknowns and uncertainties that need to be handled, such as long term reliability, operation and maintenance costs [43]. Hybrid water supply systems, defined as the combination of decentralized water supply options with a centralized system, has replaced the centralized system and the decentralized system, for its innovative approaches to respond to water scarcity caused by population growth and uncertainties in climate change [44,45]. Overall, hybrid systems can provide a balance involving centralized systems and decentralized systems together, and it is acknowledged to be pivotal towards achieving a more sustainable urban water system [42].
3.2. Modeling Construction
Decision variables, objective functions and constraints are essential elements for establishing a mathematical programming model, particularly in the multi-source optimal allocation model. The methodology of determining the optimal water supply scheme is to minimize or maximize the objective functions by seeking the optimal solution of decision variables subject to constraints [12]. Thus, proposing reasonable objective functions is the key to establishing an optimal water supply scheme. In most circumstances, the maximum water-supply guarantee rate and the minimum surplus water are assumed to be the fundamental objectives. In addition, objective functions are closely connected with regional economic development, water resources management policies and requirements of decision makers. For cities suffering from seawater invasion or over-exploitation of groundwater, the objective functions may be the minimum groundwater exploitation or the maximum groundwater recharge. Considering the groundwater recharge is a supplement for groundwater resources, Huang et al. recommended the lower or upper limit of groundwater recharge under larger water demand pressure to ensure groundwater exploration without overdraw [46]. For cities placing more emphasis on economic cost, the objective functions may be the minimum annual water supply cost or the maximum net benefit. Wang et al. proposed that the maximum GDP of the whole river basin, the minimum water deficit and the minimum ecological water deficit represent economic benefits, social benefits, and ecological benefits in the Heihe River Basin, respectively [47]. For cities paying more attention to available water supply, the objectives functions may be the maximum water supply or the minimum water shortage. In order to optimize the structure of the water supply system and promote reasonable development of the limited water resources in arid river basin, Li et al. considered the minimum rate of relative water scarcity would be an appropriate tool to relieve the issues of water resource shortages [48].
Water resources allocation rules are composed of water supply rules and water rules. Taking the water supply rules as an example, water supply rules are applied into achieving transmission between water sources and water users through regulating the effects of various projects [39]. On one hand, there is a matter of priorities in water supply sources. Characteristics of water sources, such as availability, cost and reliability, are main factors affecting the priority of urban multi-source water supply. Generally speaking, the priority of multiple water sources is in a sequence of recycled water, surface water, and groundwater. Local conventional water resources are used to be a supplement when the transferring water is not sufficient to satisfy urban water demands. On the other hand, there are corresponding water supply relations between water sources and water users. As far as the conventional water resources are concerned, a great deal of groundwater extraction for use in industrial production, agricultural irrigation and people’s lives are main factors leading to the large amount of groundwater consumption [13]. Surface water has a wide field of application, such as in everyday life, industry, agriculture and ecology, while the transferring water is mainly used in life, agriculture and industry [12]. When it comes to the unconventional water resources, reclaimed water can be utilized in landscape irrigation, the replenishment of environmental water, and industrial uses in many different ways such as cooling-water, processing, and boiler feed water [15]. Moreover, utilizing reclaimed water to recharge underground aquifers has been a new development in China in recent years. Seawater desalination has been primarily used in water treatment, iron and steel manufacturing, petrochemical industry, and environment protections [7]. Rainwater is an important way to improve the urban water environment in the course of urbanization, but it is usually affected by the natural condition, such as climate, distribution of rainfall in different season and rainwater quality.
In order to provide managers with an optimized set of water supply target values, multiple water supply and demand scenarios are established in the context of limited water resource availability, increased water demand brought by socio-economic development and additional uncertainties resulting from climate change in the water supply system. Cheng et al. researched sustainable water resources management strategies integrated with climate change and socio-economic scenarios, and these strategies were suitable for meeting the challenges of water resources shortage and severe conflicts among the users competing for limited water resources [9]. Based on stochastic weather generator (LARS-WG) simulating future change scenarios, Pingale et al. presented different climate change scenarios that were incorporated in non-linear mathematical model of water resources allocation, and calibrated rainfall runoff model (SWMM) and groundwater model (MODFLOW) were used to generate surface water and groundwater, respectively [49]. In order to examine the consequences of various climate change scenarios and adaptive management options on urban water supply, multiple combined measures were developed by Hao et al. to represent possible changes to the water supply-demand relations in Chifeng [50]. Cai et al. established two scenarios in the different planning years to analyze the environmental impacts of water allocation system in Dalian. Scenario 1 represented the baseline of water supply options considering physical restrictions of the existing water supply infrastructure capacities, while scenario 2 considered possible expansions of the existing infrastructures under random water availabilities [51]. Wang et al. took Urumqi as a case study to investigate the risk of water supply and demand under multiple demand scenarios, and the generated decision alternatives could help decision makers to identify desired strategies related to water allocation plans [52]. In summary, in order to propose the optimal water allocation scheme by delivering water from multiple sources to satisfy the demands of different users, multiple water supply and demand scenarios have been presented based on considering the variation of available water resources and regional water demand.
3.3. Model Solution
Urban multi-source water supply is a multi-objective stochastic sequential decision-making problem in essence. Optimization models, such as mathematical programming algorithms, heuristic algorithms and hybrid algorithms, are important means for realizing the optimal allocation of multi-source, especially for large-scale urban water supply systems. Some optimizer solvers or advanced modeling systems, designed for linear, nonlinear, and mixed integer optimization problems, are also support tools for solving the formulated multi-source allocation models [18].
3.3.1. Optimization Model
A number of mathematical programming algorithms have been proposed for optimal allocation of multiple water sources. Simplex method is commonly used to solve linear programming (LP) problems. Rather than enumerating all feasible solutions and choosing the best one, simplex method begins at an arbitrary corner of the basic solution set and then moves to an adjacent corner point [53]. LP can guarantee the optimal solution on the premise that all equations must be linear. Thus, the use of LP may be problematic for the complex multi-source water supply problems, where there are multiple objectives or even contradictions between different objectives [54]. The step method (STEM) proposed by Benayoun could be used for solving multi-objective optimization problem through an interactive procedure between the decision maker and a model [55]. Han et al. established an urban multi-source, multi-user and multi-objective optimization model concerning the maximal benefit of economy, society and environment, and STEM was adopted to solve this multi-objective model [12]. Binary linear programming, integer linear programming and mixed integer linear programming have been put forward to address the nonlinearity and non-convexity of the objective functions and constraints, while sequential quadratic programming could be used to solve constrained nonlinear optimization problems [56]. Dynamic programming (DP) is applicable for optimizing decision making processes, the core idea of which is to decompose a complex problem into multi-stage decision making processes. Considering the curse of dimensionality of DP, many improved algorithms, such as discrete differential dynamic programming (DDDP) and progressive optimality algorithm (POA), have been proposed. Nevertheless, it is important to note that DDDP cannot guarantee the global optimal solution and may converge to the local optimal solution, while POA can only guarantee the local optimal solution, and the global optimal solution can be obtained only for convex problems [53].
Complexities and uncertainties, such as water inflow levels, water demand consumption and the related benefits and costs, are often derived from climate change and human activities, which potentially result in a variable and complex state of urban multi-source water supply [57]. In these cases, the traditional deterministic optimization algorithms are no longer applicable. Therefore, many inexact mathematical programming algorithms are put forward to describe and handle uncertain elements presented in a multi-source water supply system. The majority of these methods focused on three common expressions of uncertainty, including the probability distribution, the interval parameter, and the fuzzy number set, as well as their combinations [58]. Due to the latter could not adequately reflect the dynamic variations of system conditions, especially for sequential structure of large-scale problems, a number of multi-stage programming methods are developed as extensions of two-stage programming methods [59]. On the basis of the multi-stage programming (MP) framework, some potential approaches, such as the interval multi-stage programming (IMP) method involving the interval parameter, the multi-stage stochastic programming (MSP) method involving the probability distribution, and the multi-stage fuzzy programming (MFP) method involving the fuzzy number set, are proposed to handle uncertain elements in the water supply system. Subsequently, a multi-stage stochastic fuzzy programming (MSFP) method and an interval multi-stage stochastic programming (IMSP) method are developed by incorporating MSP with MFP and IMP, respectively. Ultimately, an interval multi-stage stochastic fuzzy programming (IMSFP) method is introduced, which could tackle uncertainties expressed as both interval values and probability distributions, as well as fuzzy sets [60,61]. In addition, some other methods considering various uncertainties and complexities within a general urban water supply management framework are desired. A multi-stage quadratic programming (MQP) method is capable of dealing with nonlinearity in the objective function, as well as obtaining a global optimal solution under a number of system conditions [62]. A multi-stage chance-constraints programming (MCCP) method is developed to address independent random variables in the constraints, while a multi-stage robust programming (MRP) method could effectively capture the expected values of the two planning phases and the deviations of different scenarios [63]. Figure 5 illustrates the general framework of the IMSFP evolving from the MP.
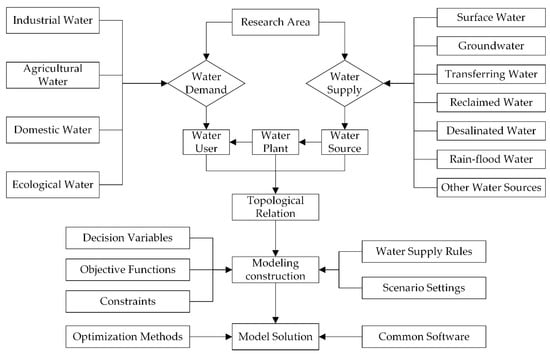
Figure 5.
Schematic of interval multi-stage stochastic fuzzy programming (IMSFP) model.
For optimal allocation models characterized by multi-objective, multi-variable and high-dimensional, some traditional mathematical programming algorithms are not satisfactory in their convergence, calculation efficiency, and parameter sensitivity. The curse of dimensionality in large-scale allocation optimization models often makes solutions become difficult or leads to results that are inconsistent with reality [64]. Inspired by various mechanisms of biological evolution (e.g., reproduction, mutation, crossover, selection), evolutionary algorithms (EAs) are the most well-established class of metaheuristics for solving multi-source water supply problems, due to their ability to find the best solution with an acceptable computational cost, but solutions formed by EAs are not necessarily optimal [65]. Popular modern EAs, including particle swarm optimization (PSO) algorithm, ant colony optimization (ACO) algorithm and genetic algorithm (GA), have become increasingly popular in urban multi-source allocation. PSO is a global optimization algorithm proposed by Eberhart and Kennedy, which is derived by simulating social behavior such as birds flocking to a promising position. PSO has the advantages of high efficiency and simplicity, which make it easy to obtain the optimal solution in complex spaces through the cooperation and competition among individuals. Chen et al. established a multi-objective optimal allocation model to alleviate the conflict over Kunming’s water resources allocation under different circumstances, and PSO was adopted to obtain optimized water resources allocation plans in the year 2020 and 2030 [66]. Modified PSO algorithms, such as multi-objective particle swarm optimization (MOPSO) and particle swarm optimization with mutation similarity (PSOMS), could be used to solve water resources allocation problems. MOPSO is able to store nondominated solutions using an external repository, with a fitness sharing approach promoting diversity and a mutation operator improving global search. PSOMS shows rapid convergence and suitable results compared with the basic PSO and GA; it can also be improved to provide the Pareto frontier that is needed to properly select the optimal solution in uncertain conditions [67]. ACO is inspired by the foraging behaviors of real ant colonies and the positive feedback mechanisms that all ants travel along the optimal pathway. That is to say, ACO works on the same principle as the way ants find the shortest paths between their nest and food sources. Different versions of ACO have proved to be flexible and powerful in solving number of spatially and temporally complex water resources problems in discrete and continuous domains with single or multiple objectives [68]. Based on the ACO, Pareto ant colony algorithm (PACA) is proposed with the aim of limiting local pheromone scope and updating global pheromone levels dynamically. PACA is suitable for optimizing the large-scale allocation of water resources, by means of incorporating intelligent searching, parallel computing, global optimization, robustness, indirect communication and a positive feedback mechanism [69]. Hou et al. adopted an improved PACA to obtain the optimal spatial allocation scheme based on remote sensing and GIS technology, and the improved PACA could reach an effective compromise between global search ability and convergence speed [70]. GA is able to search for many non-inferior solutions in parallel by maintaining a population of solutions, operating simultaneously on the entire population of potential solutions instead of producing successive iterations of a single element. Liu et al. developed an optimization model of water allocation in saltwater intrusion area, and GA was employed to optimize the modules composed of the maximization of economic interest, maximization of social satisfaction and the minimization of the amounts of polluted water [71]. Aiming at addressing computational complexity of non-dominated sorting genetic algorithm (NSGA) and ensuring good convergence, NSGA-II is proposed by Deb et al. for its fast non-dominated sorting procedure, elitist-preserving approach and parameterless niching operator [72]. NSGA-II is applicable for solving the wide range of water management problems such as water allocation and water quality management, because it can obtain Pareto optimal frontier and optimal equilibrium solution [73]. Considering different combination scenarios, Yu et al. investigated the impact of desalinated seawater’s variable costs on a multi-source water supply through a cost-benefit analysis method based on a multi-objective optimization model [74]. Chang et al. implemented intelligent water resources allocation strategies for reservoir operation optimization and water shortage rate estimation, and NSGA-II could suitably search the optimal allocation series and obtain much lower seasonal water shortage [75].
Recently, some hybrid algorithms, namely, synthetically considering separate advantages of different algorithms, have been proposed to improve the effectiveness and efficiency of EAs or multi-objective evolutionary algorithms (MOEAs) by combining different algorithms and strategies into a unified framework [76]. An adjustable PSO-GA hybrid algorithm was developed by Chang et al. to obtain a promising solution with a robust and efficient search, and this algorithm could balance the advantages of PSO and GA concerning natural selection and good knowledge sharing [77]. In order to overcome the dependence of PSO on initial swarm and the deficiency of vulnerability to local optimum, Qu et al. proposed a PSO algorithm based on the immune evolutionary algorithm (IEA) to fully utilize the global search characteristics of IEA and the local search capacity of PSO [78]. Wang et al. proposed an improved multi-objective optimization model that considers eco-environmental water demand for allocating water resources, and a hybrid genetic simulated annealing algorithm (HGSAA) that incorporates the GA and simulated annealing (SA) algorithm was introduced to solve the highly non-linear model and avoid local and pre-mature convergence [79]. Apart from the combinations of different EAs, several multialgorithms, such as a multi-algorithm genetically adaptive for single objective optimization (AMALGAM), Borg multiobjective evolutionary algorithm (Borg MOEA) and genetically adaptive leaping algorithm for approximation and diversity (GALAXY), were raised for population evolution that is always efficient for a diverse set of optimization problems. The Borg MOEA is suitable for combining convergence speed, randomized restarts, and auto-adaptive multioperator recombination into a unified optimization framework [80]. AMALGAM is able to evoke the image of a procedure that merges the strengths of different optimization algorithms [81]. The merit of GALAXY is to alleviate the parameterization issue and the high computational overhead [76]. By these multialgorithms, it is possible to achieve significant improvements in the efficiency of evolutionary search by running multiple optimization algorithms simultaneously, using concepts of global information sharing and genetically adaptive offspring creation. Thus, multialgorithms can provide opportunities for solving previously intractable optimization problems. Nevertheless, these multialgorithms mainly focus on dealing with the discrete, combinatorial and multiobjective design of water distribution systems, while there are few researches on the multi-objective optimal allocation of urban multi-source water supply.
3.3.2. Common Software
Linear interactive and general optimizer (LINGO) is designed by LINDO of the United States, and it is characterized by a built-in modeling language, a dozen internal functions to create the optimized model, multiple interfaces supplied with other data files such as text files, Excel spreadsheet files, and database files. LINGO has four internal solution programs, including a direct solution program, a linear optimization solution program, a nonlinear optimization solution program, and a branch-and-bound management program. LINGO also has global and multi-start solvers, which are capable of achieving global solutions for non-convex and non-linear problems [49]. Thus, LINGO is widely applied into solving multi-source allocation problems for its concise programming language, fast execution and high solution efficiency [47]. In order to provide suggestions and theoretical guidance for regional water distribution implementation in Tianjin, Zhang et al. chose the LINGO to simulate water resource allocation schemes and carry out detailed analyses of the supply and demand of users [18]. Wang et al. established an inexact multi-stage dual-stochastic programming model to manage these uncertainties around the supply and demand in Urumqi, and this optimization programming was calculated and operated with the modeling language running on the LINGO solver [52]. Xu et al. adopted the LINGO to code and tackle the stochastic multi-objective chance-constrained programming model, because LINGO has the advantages of generating a variety of solutions under specific combinations of weighted coefficients and constraints-violation levels [82].
General algebraic modeling system (GAMS) is an advanced computer software developed by the World Bank and GAMS Corporation of the United States in the early 1990s. Compared with other computer languages, GAMS is more oriented to the analysis of synthetic problems, and it is quite an effective tool for large and complex mathematical programming problems, such as linear, nonlinear, mixed integer and other optimization problems. To employ the advantages of both rule-based and optimization-based simulation methods, He et al. proposed the optimal allocation model of water resources where the highly skilled expert experience had been considered as well as the improved optimal water allocation model developed by the GAMS [83]. Zheng et al. proposed a modified rule for seasonal water allocation and introduced a risk analysis model to assess the performance improvement of the proposed rule, and the GAMS was used to compute this multi-objective optimization model [84]. Zarghami et al. researched the demand management and the transfer option in integrated urban water management, and the gradient-based algorithm in the GAMS solver was used to manage a multi-objective optimization model [85]. Modular in core nonlinear optimization system (MINOS) algorithm combing the reduced gradient method with the quasi-Newton method is widely used for large complex linear and nonlinear problems. Vieira et al. used the MINOS algorithm to determine the best operation for large-scale multi-source water supply systems that depend on surface water and groundwater [86]. Zero one optimization method (ZOOM) algorithm jointly developed by Marsten and Singhal has been accepted as the essential method for addressing mixed integer programming problems.
Apart from LINGO and GAMS, other optimization software such as IBM ILOG CPLEX, Gurobi, XPressMP, can also be used to propose the optimal allocation scheme of a multi-source water supply. Likewise, some open source software plays an important and irreplaceable role in solving the problem of multi-source water supply. As an open source software used throughout the world to model water distribution systems, EPANET was developed as a tool for understanding the movement and fate of drinking water constituents within distribution systems, and it can be used for many different types of applications in distribution systems analysis. In addition, some river basin management modeling tools, such as WASP, REALM, MODSIM and RiverWare, can be used to develop specific water resources allocation schemes in the multi-source water supply system. Taking the REALM as an example, REALM is a generalized computer simulation software package that models the harvesting and bulk distribution of water resources within a water supply system, and it is made up of the input processing, the simulation and the output processing [87]. Based on the historic streamflow and climatic data, REALM modelling tool can be successfully employed for a wide range of investigations on water resource planning and management. Moreover, a range of system components and operating rules are taken into account highlighting the flexibility of REALM, especially in using a wide range of data inputs that represent potential hydrological scenarios [88].
4. Future Challenges for Urban Multi-Source Water Supply
With the rapid social and economic development and urbanization, increasing attention has been paid to the water shortage and the deterioration of water quality. Although multi-source water supply could significantly improve the safety of urban water supply, new challenges emerge for the allocation and management of urban water supply. In this section, future challenges for an urban multi-source water supply in China are discussed.
4.1. Emergency Scheduling of Multiple Water Sources
Compared to the water supply system with a single source, a multi-source water supply is able to provide protection against the effects of emergencies (e.g., sudden water pollution, drought and engineering accident) effectively. Moreover, a multi-source water supply can provide a strong guarantee for the sustainable development of the social economy, and reduce the risks and vulnerabilities. However, most cities with a multi-source water supply always respond to emergencies temporarily and passively, especially water pollution incidents. Considering several unforeseeable incidents comprise some emergencies, it is of great importance to implement emergency scheduling of multi-source to improve the reliability and robustness of the urban water supply system.
Emergency scheduling, just as its name implies, can be a series of necessary measures taken by the government and other public institutions to protect the safety of urban water supplies, and the main feature of which is to sacrifice of part of the interests to save the overall situation in exceptional circumstances [89]. Wang et al. designed an emergency scheduling decision support system (DSS) to eliminate the impact of sudden contamination incidents occurring upstream in multi-source water supply systems, and it is demonstrated that this DSS tool is instrumental in emergency scheduling for the water company to quickly and effectively respond to sudden contamination incidents [90]. Xu et al. proposed an integrated bi-level structure and a dynamic strategy for more effective and efficient water transfers and allocations, in which the bi-level structure works to deal with space dimension conflicts in drought emergencies, and the dynamic strategy is used to deal with time dimension conflicts [91]. Gao et al. incorporated emergency management into DSS to provide more effective emergency scheduling plans under extreme conditions, and the regenerated water supply strategy between different reservoirs is capable of reducing the impact of a severe drought year on Dalian [92]. These researches on emergency scheduling mainly focus on: assuming that a sudden accident occurs at a certain location in the urban water supply system, performing optimal allocation analysis under this accident, and providing decision-making guidance for emergency scheduling. Nevertheless, an orderly and complete emergency scheduling procedure is still in necessity in order to guide real-time scheduling of multi-source water supplies under special circumstances. Moreover, methods to minimize accident losses and quickly formulate emergency water supply schemes remain to be determined and suffer from a lack of research. Therefore, it is still a great challenge to accurately simulate and promptly analyze an emergency incident so as to propose the optimal allocation scheme of a multi-source water supply.
4.2. Joint Operation of Water Quality and Quantity
In the urban water supply system, the diversification of water sources is just one part leading to a great difference in the water quality, the other part is that physical or chemical changes may occur in various components of the mixed water. Moreover, water users not only emphasize the available water quantity, but also put forward more demands on the water supply quality. Therefore, the joint operation of water quality and quantity has become the development trend in urban multi-source water supplies.
Considering the unreasonable distribution in the prototype test of the water diversion from Yangtze River to Taihu Lake, Dong et al. established a coupled water quality and quantity model based on numerical simulation. Results showed that distribution of water diversion was more reasonable in space, and the water quality concentration under the optimal operation was significantly reduced compared to that in actual operation [93]. Mahjouri et al. developed two methodologies for a large-scale water allocation problem and it was demonstrated that the water quality in rivers satisfies the standards in both cases [94]. Zhao et al. adopted a decentralized control model in the joint operation of water quality and quantity, and a water quality and quantity feedback mechanism was added in this model in order to give full play of the directive function of water quality simulation results [95]. A high-performance integrated control framework was proposed by Galelli et al. to support the real-time operation of urban water supply storages affected by water quality problems, and Delft3D-FLOW was used to simulate nonsteady flow and transport phenomena in Marina Reservoir [96]. To sum up, researches on the joint operation of water quality and quantity pay more attention to the river basin, while research in the urban water supply systems are still lacking. Moreover, water quality is often taken as a constraint in the multi-source optimal allocation model, or water quantity and quality are simulated separately, in which case the simulation results of water quality are not used to improve the water regulation scheme. Therefore, highlighting the feedback and guidance of water quality calculation to water quantity calculation and realizing the coupling model of water quality and quantity control will be the focus of the next step.
5. Conclusions
Urban water resources are the basis for the formation and development of cities and the source of urban water supply. It is simply not sufficient to rely on a single water resource to meet urban water demand and a multi-source water supply has become significant means to handle contradiction between water supply and demand in water shortage cities. This paper gives an overview of the optimal allocation of multi-source systems for urban water supplies concerning variation tendency, modeling methods and facing challenges. Based on the variation tendency of the water consumption and water supply pattern in China, Tianjin is taken as a typical city to outline water supply change and its cause analysis. Then, pivotal modeling methods that can be used for generating the optimal allocation scheme for an urban water supply are summarized from the view of the topological relations, the modeling constructions and the modelling solutions. Considering an urban multi-source water supply is a multi-objective stochastic sequential decision-making problem in essence, representative optimization models are an important means for realizing the optimal allocation of multi-source, including mathematical programming algorithms, heuristic algorithms and hybrid algorithms. In addition, some common software designed for multiple optimization problems, are also support tools for solving the formulated multi-source allocation models. Finally, current and emerging challenges, such as the emergency operation of multi-source water supplies, and joint operation of water quality and quantity, are also discussed in this paper. These summaries and prospects provide a valuable reference for giving full play to the multi-source water supply capacity and for carrying out relevant researches to propose the optimal allocation scheme in an urban multi-source water supply system.
Author Contributions
P.S., C.W. and W.Z. conducted the research, designed and wrote the paper; W.L., J.S. and X.W. helped to revise the paper; X.L. and H.W. gave the comments. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China (51709275), the Zhejiang Water Conservancy Science and Technology Project (RA1703), the Young Elite Scientists Sponsorship Program by CAST (219QNRC001) and the Fundamental Research Funds of IWHR (WR0145B012020).
Acknowledgments
The anonymous reviewers and the editor are thanked for providing insightful and detailed reviews that greatly improved the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, H.; Jin, G.; Yu, Y. Review of river basin water resource management in China. Water 2018, 10, 425. [Google Scholar] [CrossRef]
- Feng, K.; Hubacek, K.; Pfister, S.; Yu, Y.; Sun, L. Virtual scarce water in China. Environ. Sci. Technol. 2014, 48, 7704–7713. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Geng, Y.; Heck, P.; Xue, B. A review of China’s rural water management. Sustainability 2015, 7, 5773. [Google Scholar] [CrossRef]
- Chang, I.; Wu, J. Review on natural resources utilization in China. Manag. Sci. Eng. 2011, 5, 16–21. [Google Scholar]
- Liu, J.; Raven, P.H. China’s environmental challenges and implications for the world. Crit. Rev. Env. Sci. Tec. 2010, 40, 823–851. [Google Scholar] [CrossRef]
- Lu, Y.; Song, S.; Wang, R.; Liu, Z.; Meng, J.; Sweetman, A.J.; Jenkins, A.; Ferrier, R.C. Impacts of soil and water pollution on food safety and health risks in China. Environ. Int. 2015, 77, 5–15. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Chen, D.; Wang, Q.; Zhang, Z. Seawater desalination in China: Retrospect and prospect. Chem. Eng. J. 2014, 242, 404–413. [Google Scholar] [CrossRef]
- Piao, S.; Ciais, P.; Huang, Y.; Shen, Z.; Peng, S.; Li, J.; Zhou, L.; Liu, H. The impacts of climate change on water resources and agriculture in China. Nature 2010, 467, 43–51. [Google Scholar] [CrossRef] [PubMed]
- Cheng, H.; Hu, Y. Improving China’s water resources management for better adaptation to climate change. Clim. Chang. 2012, 112, 253–282. [Google Scholar] [CrossRef]
- Bao, C.; Fang, C. Water resources constraint force on urbanization in water deficient regions: A case study of the Hexi Corridor, arid area of NW China. Ecol. Econ. 2007, 62, 508–517. [Google Scholar] [CrossRef]
- Bao, C.; Fang, C. Water resources flows related to urbanization in China: Challenges and perspectives for water management and urban development. Water Resour. Manag. 2012, 26, 531–552. [Google Scholar] [CrossRef]
- Han, Y.; Xu, S.; Xu, X. Modeling multisource multiuser water resources allocation. Water Resour. Manag. 2008, 22, 911–923. [Google Scholar] [CrossRef]
- Dou, X. A critical review of groundwater utilization and management in China’s inland water shortage areas. Water Policy 2016, 18, 1367–1383. [Google Scholar] [CrossRef]
- Dou, X. China’s inter-basin water management in the context of regional water shortage. Sustain. Water Resour. Manag. 2018, 4, 519–526. [Google Scholar] [CrossRef]
- Yi, L.; Jiao, W.; Chen, X.; Chen, W. An overview of reclaimed water reuse in China. J. Environ. Sci.-China 2011, 23, 1585–1593. [Google Scholar] [CrossRef]
- Lyu, S.; Chen, W.; Zhang, W.; Fan, Y.; Jiao, W. Wastewater reclamation and reuse in China: Opportunities and challenges. J. Environ. Sci.-China 2016, 39, 86–96. [Google Scholar] [CrossRef]
- Wu, C.; Déry, S.; Wu, W.; Liu, X.; Xiong, J.; Gao, W. A review of water resources utilization and protection in Southwest China. Sci. Cold Arid Reg. 2015, 7, 736–746. [Google Scholar]
- Zhang, S.; Yang, J.; Wan, Z.; Yi, Y. Multi-water source joint scheduling model using a refined water supply network: Case study of Tianjin. Water 2018, 10, 1580. [Google Scholar] [CrossRef]
- Li, P. Groundwater quality in western China: Challenges and paths forward for groundwater quality research in western China. Expos. Health 2016, 8, 305–310. [Google Scholar] [CrossRef]
- Ministry of Water Resources of the People’s Republic of China. China Water Resources Bulletin 2005–2018; China Water & Power Press: Beijing, China, 2018. (In Chinese) [Google Scholar]
- Lu, S.; Gao, X.; Li, W.; Jiang, S.; Huang, L. A study on the spatial and temporal variability of the urban residential water consumption and its influencing factors in the major cities of China. Habitat Int. 2018, 78, 29–40. [Google Scholar] [CrossRef]
- Fan, L.; Gai, L.; Tong, Y.; Li, R. Urban water consumption and its influencing factors in China: Evidence from 286 cities. J. Clean. Prod. 2017, 166, 124–133. [Google Scholar] [CrossRef]
- Gu, A.; Teng, F.; Wang, Y. China energy-water nexus: Assessing the water-saving synergy effects of energy-saving policies during the eleventh Five-year Plan. Energ. Convers. Manag. 2014, 85, 630–637. [Google Scholar] [CrossRef]
- Zuo, Q.; Jin, R.; Ma, J.; Cui, G. China pursues a strict water resources management system. Environ. Earth Sci. 2014, 72, 2219–2222. [Google Scholar] [CrossRef]
- Guo, J.; Ren, G.; Xiong, M.; Huang, H. The spatiotemporal pattern of rainy-season precipitation in the Haihe River Basin, North China. Hydrology 2019, 6, 73–91. [Google Scholar] [CrossRef]
- Bai, X.; Imura, H. Towards sustainable urban water resource management: A case study in Tianjin, China. Sustain. Dev. 2001, 9, 24–35. [Google Scholar] [CrossRef]
- Shang, Y.; Lu, S.; Shang, L.; Li, X.; Shi, H.; Li, W. Decomposition of industrial water use from 2003 to 2012 in Tianjin, China. Technol. Forecast. Soc. 2017, 116, 53–61. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, J.; Xu, Z.; Zhang, C. Effect of frequency of multi-source water supply on regional guarantee rate of water use. Water 2019, 11, 1356. [Google Scholar] [CrossRef]
- Song, X.; Kong, F.; Zhan, C. Assessment of water resources carrying capacity in Tianjin City of China. Water Resour. Manag. 2011, 25, 857–873. [Google Scholar] [CrossRef]
- Men, B.; Wu, Z.; Liu, H.; Li, Y.; Zhao, Y. Research on hedging rules based on water supply priority and benefit loss of water shortage—A case study of Tianjin, China. Water 2019, 11, 778. [Google Scholar] [CrossRef]
- Ji, L.; Sun, P.; Ma, Q.; Jiang, N.; Huang, G.; Xie, Y. Inexact two-stage stochastic programming for water resources allocation under considering demand uncertainties and response—A case study of Tianjin, China. Water 2017, 9, 414. [Google Scholar] [CrossRef]
- Water Bureau of Tianjin. Water Resources Bulletin of Tianjin 2000–2018; Water Bureau of Tianjin: Tianjin, China, 2018. (In Chinese) [Google Scholar]
- Shang, Y.; Wang, J.; Ye, Y.; Lei, X.; Gong, J.; Shi, H. An analysis of the factors that influence industrial water use in Tianjin, China. Int. J. Water Resour. D 2017, 33, 81–92. [Google Scholar] [CrossRef]
- Shang, Y.; Lu, S.; Li, X.; Sun, G.; Shang, L.; Shi, H.; Lei, X.; Ye, Y.; Sang, X.; Wang, H. Drivers of industrial water use during 2003–2012 in Tianjin, China: A structural decomposition analysis. J. Clean. Prod. 2017, 140, 1136–1147. [Google Scholar] [CrossRef]
- Gu, Q.; Chen, Y.; Pody, R.; Cheng, R.; Zheng, X.; Zhang, Z. Public perception and acceptability toward reclaimed water in Tianjin. Resour. Conserv. Recycl. 2015, 104, 291–299. [Google Scholar] [CrossRef]
- Zhang, C.; Dong, L.; Liu, Y.; Qiao, H. Analysis on impact factors of water utilization structure in Tianjin, China. Sustainability 2016, 8, 241. [Google Scholar] [CrossRef]
- Yu, B.; Liang, G.; He, B.; Dong, L.; Zhou, H. Modeling of joint operation for urban water-supply system with multi-water sources and its application. Adv. Water Sci. 2015, 26, 874–884. (In Chinese) [Google Scholar]
- Zhang, Y.; Tian, F.; Hu, H.; Qi, Z. Joint operation model of multiple water sources in Beijing. J. Hydraul. Eng. 2014, 45, 844–849. (In Chinese) [Google Scholar]
- Song, W.; Yuan, Y.; Jiang, Y.; Lei, X.; Shu, D. Rule-based water resource allocation in the Central Guizhou Province, China. Ecol. Eng. 2016, 87, 194–202. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M. A heuristic design support methodology based on graph theory for district metering of water supply networks. Eng. Optimiz. 2011, 43, 193–211. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Santonastaso, G.F.; Tzatchkov, V.G. Water network sectorization based on graph theory and energy performance indices. J. Water Res. Plan. Man. 2014, 140, 620–629. [Google Scholar] [CrossRef]
- Sapkota, M.; Arora, M.; Malano, H.; Moglia, M.; Sharma, A.; George, B.; Pamminger, F. An overview of hybrid water supply systems in the context of urban water management: Challenges and opportunities. Water 2015, 7, 153. [Google Scholar] [CrossRef]
- Moglia, M.; Alexander, K.S.; Sharma, A. Discussion of the enabling environments for decentralised water systems. Water Sci. Technol. 2011, 63, 2331–2339. [Google Scholar] [CrossRef]
- Sapkota, M.; Arora, M.; Malano, H.; Moglia, M.; Sharma, A.; George, B.; Pamminger, F. An integrated framework for assessment of hybrid water supply systems. Water 2016, 8, 4. [Google Scholar] [CrossRef]
- Marlow, D.R.; Moglia, M.; Cook, S.; Beale, D.J. Towards sustainable urban water management: A critical reassessment. Water Res. 2013, 47, 7150–7161. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Chen, J.; Zeng, S.; Sun, F.; Dong, X. A stochastic optimization approach for integrated urban water resource planning. Water Sci. Technol. 2013, 67, 1634–1641. [Google Scholar] [CrossRef][Green Version]
- Wang, Z.; Yang, J.; Deng, X.; Lan, X. Optimal water resources allocation under the constraint of land use in the Heihe River Basin of China. Sustainability 2015, 7, 1558. [Google Scholar] [CrossRef]
- Li, Z.; Quan, J.; Li, X.; Wu, X.; Wu, H.; Li, Y.; Li, G. Establishing a model of conjunctive regulation of surface water and groundwater in the arid regions. Agric. Water Manag. 2016, 174, 30–38. [Google Scholar] [CrossRef]
- Pingale, S.M.; Jat, M.K.; Khare, D. Integrated urban water management modelling under climate change scenarios. Resour. Conserv. Recycl. 2014, 83, 176–189. [Google Scholar] [CrossRef]
- Hao, L.; Sun, G.; Liu, Y.; Qian, H. Integrated modeling of water supply and demand under management options and climate change scenarios in Chifeng City, China. J. Am. Water Resour. As. 2015, 51, 655–671. [Google Scholar] [CrossRef]
- Cai, Y.; Yue, W.; Xu, L.; Yang, Z.; Rong, Q. Sustainable urban water resources management considering life-cycle environmental impacts of water utilization under uncertainty. Resour. Conserv. Recycl. 2016, 108, 21–40. [Google Scholar] [CrossRef]
- Wang, B.; Li, W.; Huang, G.; Liu, L.; Ji, L.; Li, Y. Urban water resources allocation under the uncertainties of water supply and demand: A case study of Urumqi, China. Environ Earth Sci. 2015, 74, 3543–3557. [Google Scholar] [CrossRef]
- Guo, S.; Chen, J.; Liu, P.; Li, Y. State-of-the-art review of joint operation for multi-reservoir systems. Adv. Water Sci. 2010, 21, 496–503. (In Chinese) [Google Scholar]
- Han, Y.; Huang, Y.; Wang, G.; Maqsood, I. A multi-objective linear programming model with interval parameters for water resources allocation in Dalian City. Water Resour. Manag. 2011, 25, 449–463. [Google Scholar] [CrossRef]
- Benayoun, R.; de Montgolfier, J.; Tergny, J.; Laritchev, O. Linear programming with multiple objective functions: Step method (stem). Math. Program. 1971, 1, 366–375. [Google Scholar] [CrossRef]
- Liu, S.; Papageorgiou, L.G.; Gikas, P. Integrated management of non-conventional water resources in anhydrous islands. Water Resour. Manag. 2012, 26, 359–375. [Google Scholar] [CrossRef]
- Fan, Y.; Huang, G.; Huang, K.; Baetz, B.W. Planning water resources allocation under multiple uncertainties through a generalized fuzzy two-stage stochastic programming method. IEEE Trans. Fuzzy Syst. 2015, 23, 1488–1504. [Google Scholar] [CrossRef]
- Qin, X.S.; Xu, Y. Analyzing urban water supply through an acceptability-index-based interval approach. Adv. Water Resour. 2011, 34, 873–886. [Google Scholar] [CrossRef]
- Maqsood, I.; Huang, G.H.; Scott Yeomans, J. An interval-parameter fuzzy two-stage stochastic program for water resources management under uncertainty. Eur. J. Oper. Res. 2005, 167, 208–225. [Google Scholar] [CrossRef]
- Wang, S.; Huang, G. Identifying optimal water resources allocation strategies through an interactive multi-stage stochastic fuzzy programming approach. Water Resour. Manag. 2012, 26, 2015–2038. [Google Scholar] [CrossRef]
- Lu, H.; Huang, G.; He, L. Inexact rough-interval two-stage stochastic programming for conjunctive water allocation problems. J. Environ. Manag. 2009, 91, 261–269. [Google Scholar] [CrossRef]
- Li, Y.P.; Huang, G.H. Inexact multistage stochastic quadratic programming method for planning water resources systems under uncertainty. Environ. Eng. Sci. 2007, 24, 1361–1378. [Google Scholar] [CrossRef]
- Fu, Q.; Li, T.; Cui, S.; Liu, D.; Lu, X. Agricultural multi-water source allocation model based on interval two-stage stochastic robust programming under uncertainty. Water Resour. Manag. 2018, 32, 1261–1274. [Google Scholar] [CrossRef]
- Yan, Z.; Sha, J.; Liu, B.; Tian, W.; Lu, J. An ameliorative whale optimization algorithm for multi-objective optimal allocation of water resources in Handan, China. Water 2018, 10, 87. [Google Scholar] [CrossRef]
- Nicklow, J.; Reed, P.; Savic, D.; Dessalegne, T.; Harrell, L. State of the art for genetic algorithms and beyond in water resources planning and management. J. Water Res. Plan. Man. 2010, 136, 412–432. [Google Scholar] [CrossRef]
- Chen, J.; Yu, C.; Cai, M.; Wang, H.; Zhou, P. Multi-objective optimal allocation of urban water resources while considering conlict resolution based on the PSO algorithm: A case study of Kunming, China. Sustainability 2020, 12, 1337. [Google Scholar] [CrossRef]
- Zarghami, M.; Hajykazemian, H. Urban water resources planning by using a modified particle swarm optimization algorithm. Resour. Conserv. Recycl. 2013, 70, 1–8. [Google Scholar] [CrossRef]
- Afshar, A.; Massoumi, F.; Afshar, A.; Mariño, M.A. State of the art review of ant colony optimization applications in water resource management. Water Resour. Manag. 2015, 29, 3891–3904. [Google Scholar] [CrossRef]
- Liu, X.; Li, X.; Shi, X.; Huang, K.; Liu, Y. A multi-type ant colony optimization (MACO) method for optimal land use allocation in large areas. Int. J. Geogr. Inf. Sci. 2012, 26, 1325–1343. [Google Scholar] [CrossRef]
- Hou, J.; Mi, W.; Sun, J. Optimal spatial allocation of water resources based on Pareto ant colony algorithm. Int. J. Geogr. Inf. Sci. 2014, 28, 213–233. [Google Scholar] [CrossRef]
- Liu, D.; Chen, X.; Lou, Z. A model for the optimal allocation of water resources in a saltwater intrusion area: A case study in Pearl River Delta in China. Water Resour. Manag. 2010, 24, 63–81. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evolut. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Tabari, M.M.R.; Soltani, J. Multi-objective optimal model for conjunctive use management using SGAs and NSGA-II models. Water Resour. Manag. 2013, 27, 37–53. [Google Scholar] [CrossRef]
- Yu, B.; Zhang, C.; Jiang, Y.; Li, Y.; Zhou, H. Conjunctive use of inter-basin transferred and desalinated water in a multi-source water supply system based on cost-benefit analysis. Water Resour. Manag. 2017, 31, 3313–3328. [Google Scholar] [CrossRef]
- Chang, F.; Wang, Y.; Tsai, W. Modelling intelligent water resources allocation for multi-users. Water Resour. Manag. 2016, 30, 1395–1413. [Google Scholar] [CrossRef]
- Wang, Q.; Savić, D.A.; Kapelan, Z. GALAXY: A new hybrid MOEA for the optimal design of water distribution systems. Water Resour. Res. 2017, 53, 1997–2015. [Google Scholar] [CrossRef]
- Chang, J.; Bai, T.; Huang, Q.; Yang, D. Optimization of water resources utilization by PSO-GA. Water Resour. Manag. 2013, 27, 3525–3540. [Google Scholar] [CrossRef]
- Qu, G.; Lou, Z. Application of particle swarm algorithm in the optimal allocation of regional water resources based on immune evolutionary algorithm. J. Shanghai Jiaotong Univ. (Sci.) 2013, 18, 634–640. [Google Scholar] [CrossRef]
- Wang, X.; Sun, Y.; Song, L.; Mei, C. An eco-environmental water demand based model for optimising water resources using hybrid genetic simulated annealing algorithms. Part I. Model development. J. Environ. Manag. 2009, 90, 2628–2635. [Google Scholar] [CrossRef]
- Hadka, D.; Reed, P. Borg: An auto-adaptive many-objective evolutionary computing framework. Evol. Comput. 2013, 21, 231–259. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Robinson, B.A. Improved evolutionary optimization from genetically adaptive multimethod search. Proc. Natl Acad. Sci. USA 2007, 104, 708–711. [Google Scholar] [CrossRef]
- Xu, Y.; Li, W.; Ding, X. A stochastic multi-objective chance-constrained programming model for water supply management in Xiaoqing River Watershed. Water 2017, 9, 378. [Google Scholar] [CrossRef]
- He, H.; Chen, A.; Yin, M.; Ma, Z.; You, J.; Xie, X.; Wang, Z.; An, Q. Optimal allocation model of water resources based on the prospect theory. Water 2019, 11, 1289. [Google Scholar] [CrossRef]
- Zheng, H.; Wang, Z.; Hu, S.; Malano, H. Seasonal water allocation: Dealing with hydrologic variability in the context of a water rights system. J. Water Res. Plan. Man. 2013, 139, 76–85. [Google Scholar] [CrossRef]
- Zarghami, M. Urban water management using fuzzy-probabilistic multi-objective programming with dynamic efficiency. Water Resour. Manag. 2010, 24, 4491–4504. [Google Scholar] [CrossRef]
- Vieira, J.; Cunha, M.C.; Nunes, L.; Monteiro, J.P. Optimization of the operation of large-scale multisource water-supply systems. J. Water Res. Plan. Man. 2011, 137, 150–161. [Google Scholar] [CrossRef]
- George, B.; Malano, H.; Davidson, B.; Hellegers, P.; Bharati, L.; Massuel, S. An integrated hydro-economic modelling framework to evaluate water allocation strategies I: Model development. Agric. Water Manag. 2011, 98, 733–746. [Google Scholar] [CrossRef]
- Perera, B.J.C.; James, B.; Kularathna, M.D.U. Computer software tool REALM for sustainable water allocation and management. J. Environ. Manag. 2005, 77, 291–300. [Google Scholar] [CrossRef]
- Shao, W.; Luo, L.; Wang, J.; Liu, J.; Zhou, J.; Xiang, C.; Wang, H. The coordination of routine and emergency water resources management: Progress in China. Water Int. 2018, 43, 943–962. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, S.; Liu, W.; Kapelan, Z.; Savic, D. Decision support system for emergency scheduling of raw water supply systems with multiple sources. Front. Environ. Sci. Eng. 2013, 7, 777–786. [Google Scholar] [CrossRef]
- Xu, J.; Ma, N.; Lv, C. Dynamic equilibrium strategy for drought emergency temporary water transfer and allocation management. J. Hydrol. 2016, 539, 700–722. [Google Scholar] [CrossRef]
- Gao, Y.; Li, Y.; Song, T.; Wang, C. A decision support system for water supply emergency management with multiple sources. J. Water Supply Res. Technol. Aqua. 2016, 65, 135–144. [Google Scholar] [CrossRef]
- Dong, Z.; Bian, G.; Wang, C.; Li, D. Joint operation of water quantity and quality based on numerical model. Adv. Water Sci. 2009, 20, 184–189. (In Chinese) [Google Scholar]
- Mahjouri, N.; Ardestani, M. Application of cooperative and non-cooperative games in large-scale water quantity and quality management: A case study. Environ. Monit. Assess. 2011, 172, 157–169. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, L.; Zhang, Y.; Liu, F. Study on the coupling model for water quality and quantity control in the urban raw water system. J. Hydraul. Eng. 2012, 43, 1373–1380. (In Chinese) [Google Scholar]
- Galelli, S.; Castelletti, A.; Goedbloed, A. High-performance integrated control of water quality and quantity in urban water reservoirs. Water Resour. Res. 2015, 51, 9053–9072. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).