Comparing Activation Functions in Modeling Shoreline Variation Using Multilayer Perceptron Neural Network
Abstract
:1. Introduction
2. Materials and Methods
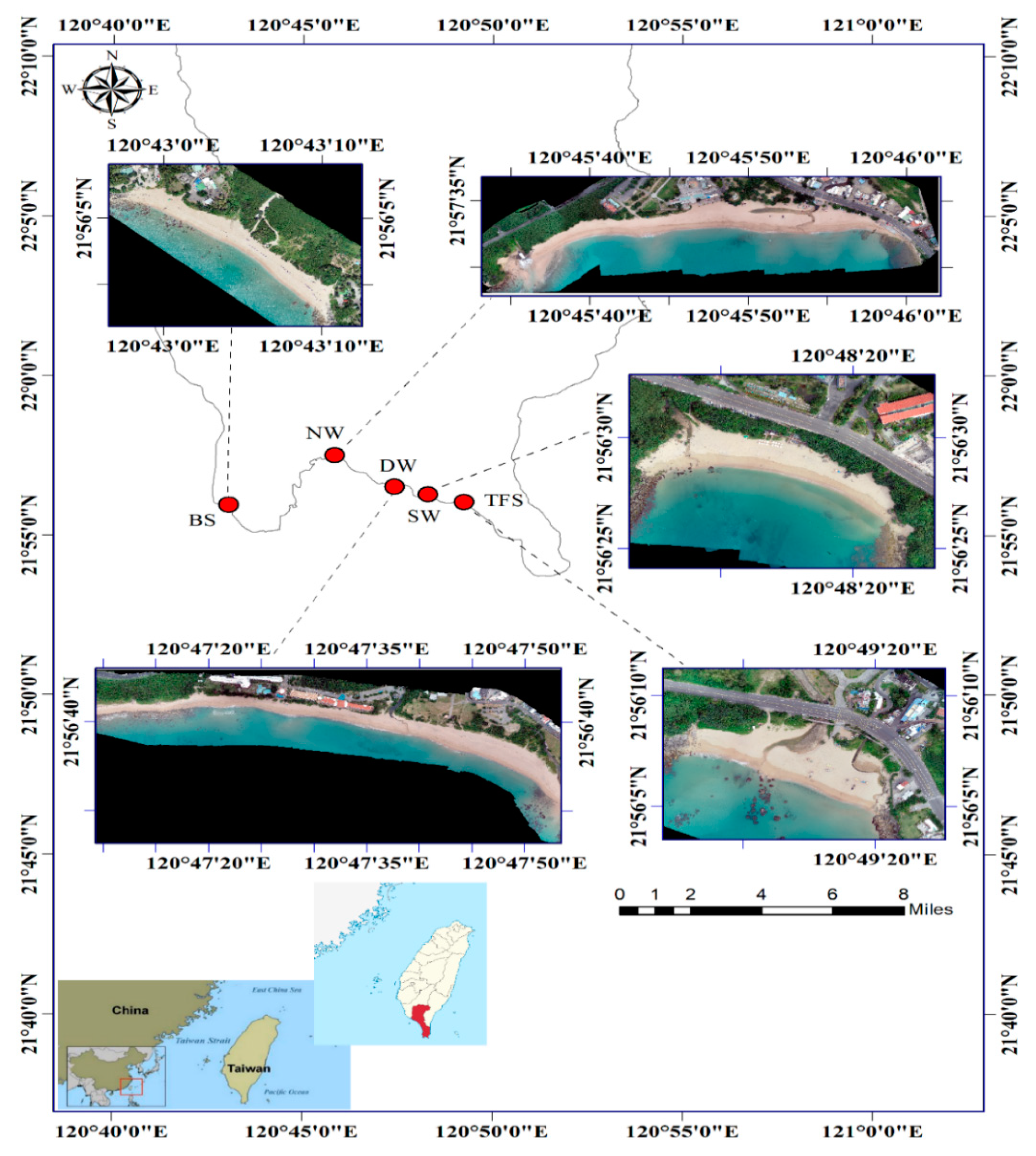
2.1. Study Area and Data Collection
2.2. Artificial Neural Networks (ANNs)
Multilayer Perceptron Neural Network (MLP)
2.3. Activation Functions
2.3.1. Identity Function
2.3.2. Hyperbolic Tan Function (Tanh)
2.3.3. Logistic Function (Logistic)
2.3.4. Exponential Function
2.3.5. Sine function
2.4. Models Evaluation
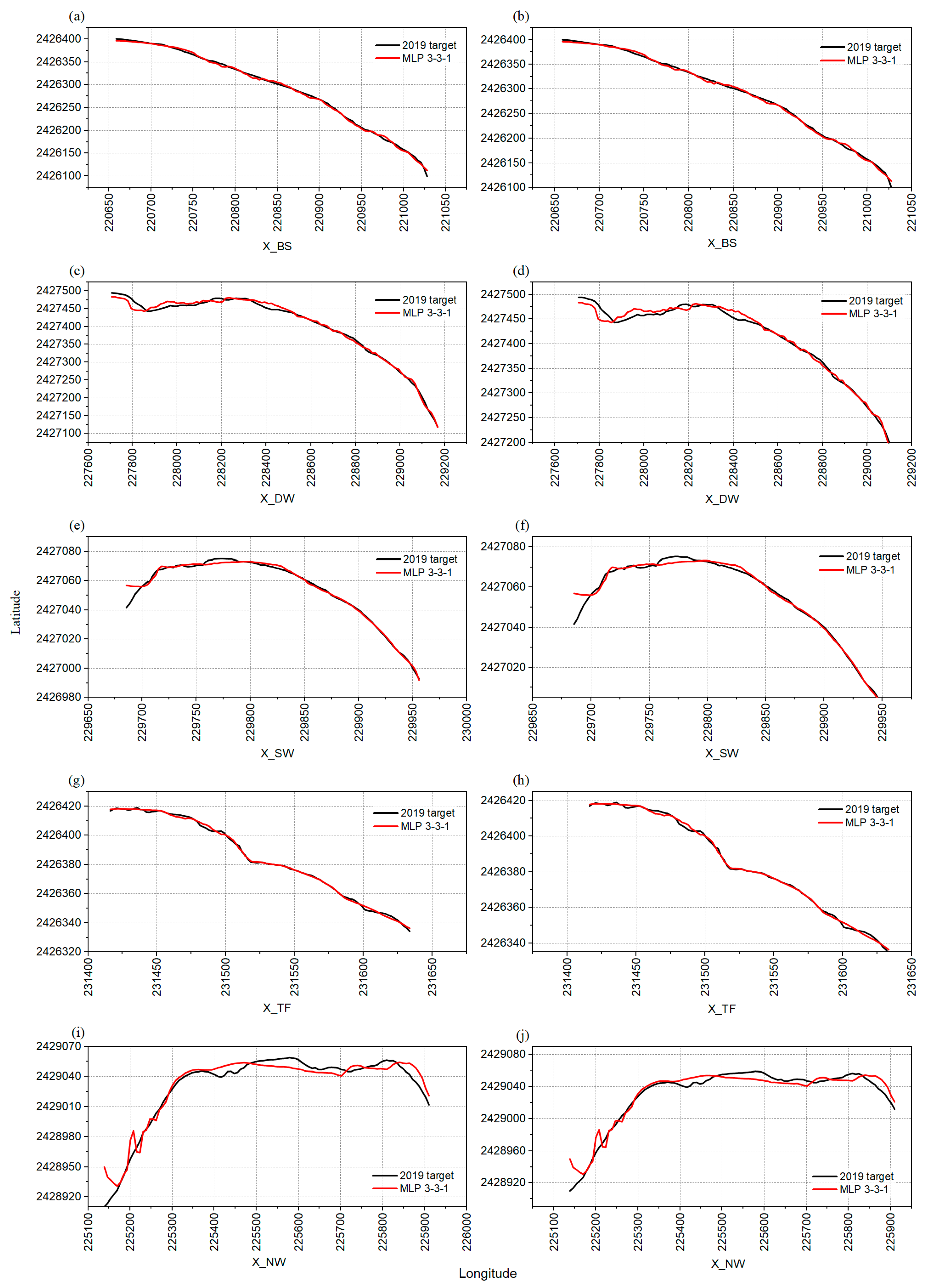
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Papakonstantinou, A.; Topouzelis, K.; Pavlogeorgatos, G. Coastline Zones Identification and 3D Coastal Mapping Using UAV Spatial Data. ISPRS Int. J. Geo-Inf. 2016, 5, 75. [Google Scholar] [CrossRef] [Green Version]
- Neill, S.P.; Elliott, A.J.; Hashemi, M.R. A model of inter-annual variabilityin beach levels. Cont. Shelf Res. 2008, 28, 1769–1781. [Google Scholar] [CrossRef]
- Iglesias, G.; López, I.; Castro, A.; Carballo, R. Neural network modelling of planform geometry of headland-bay beaches. Geomorphology 2009, 103, 577–587. [Google Scholar] [CrossRef]
- Muñoz-Perez, J.J.; Medina, R. Comparison of long-, medium- and short-term variations of beach profiles with and without submerged geological control. Coast. Eng. 2010, 57, 241–251. [Google Scholar]
- López, I.; Aragonés, L.; Villacampa, Y.; Compañ, P. Artificial neural network modeling of cross-shore profile on sand beaches: The coast of the province of Valencia (Spain). Mar. Georesour. Geotechnol. 2017, 36, 698–708. [Google Scholar]
- Rodriguez-Delgado, C.; Bergillos, R.J.; Iglesias, G. An artificial neural network model of coastal erosion mitigation through wave farms. Environ. Model. Softw. 2019, 119, 390–399. [Google Scholar] [CrossRef]
- Liu, L.-W.; Wang, Y.-M. Modelling Reservoir Turbidity Using Landsat 8 Satellite Imagery by Gene Expression Programming. Water 2019, 11, 1479. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.; Wanik, D.W.; Cerrai, D.; Bhuiyan, M.A.E.; Anagnostou, E.N. Quantifying Uncertainty in Machine Learning-Based Power Outage Prediction Model Training: A Tool for Sustainable Storm Restoration. Sustainability 2020, 12, 1525. [Google Scholar] [CrossRef] [Green Version]
- Cerrai, D.; Wanik, D.W.; Bhuiyan, M.A.E.; Zhang, X.; Yang, J.; Frediani, M.E.B.; Anagnostou, E.N. Predicting Storm Outages Through New Representations of Weather and Vegetation. IEEE Access 2019, 7, 29639–29654. [Google Scholar] [CrossRef]
- Bhuiyan, M.A.E.; Begum, F.; Ilham, S.J.; Khan, R.S. Advanced wind speed prediction using convective weather variables through machine learning application. Appl. Comput. Geosci. 2019, 1, 10002. [Google Scholar]
- Kumar, A.; Ramsankaran, R.A.A.J.; Brocca, L.; Munoz-Arriola, F. A Machine Learning Approach for Improving Near-Real-Time Satellite-Based Rainfall Estimates by Integrating Soil Moisture. Remote Sens. 2019, 11, 2221. [Google Scholar] [CrossRef] [Green Version]
- Hazra, A.; Maggioni, V.; Houser, P.; Antil, H.; Noonan, M. A Monte Carlo-based multi-objective optimization approach to merge different precipitation estimates for land surface modeling. J. Hydrol. 2019, 570, 454–462. [Google Scholar] [CrossRef]
- Bhuiyan, M.A.E.; Nikolopoulos, E.I.; Anagnostou, E.N.; Quintana-Seguí, P.; Barella-Ortiz, A. A nonparametric statistical technique for combining global precipitation datasets: Development and hydrological evaluation over the Iberian Peninsula. Hydrol. Earth Syst. Sci. 2018, 22, 1371–1389. [Google Scholar] [CrossRef] [Green Version]
- Zorzetto, E.; Marani, M. Extreme value metastatistical analysis of remotely sensed rainfall in ungauged areas: Spatial downscaling and error modelling. Adv. Water Resour. 2020, 135, 103483. [Google Scholar] [CrossRef]
- Jeatrakul, P.; Wong, K.W. Comparing the performance of different neural networks for binary classification problems. In Proceedings of the 2009 Eighth International Symposium on Natural Language Processing, Bangkok, Thailand, 20–22 October 2009; pp. 111–115. [Google Scholar]
- Tfwala, S.S.; Wang, Y.M. Estimating Sediment Discharge Using Sediment Rating Curves and Artificial Neural Networks in the Shiwen River, Taiwan. Water 2016, 8, 53. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.M.; Wang, Y.M.; Tsou, I. Using artificial neural network approach for modelling rainfall-runoff due to typhoon. J. Earth Syst. Sci. 2013, 122, 399–405. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.M.; Traore, S.; Kerh, T.; Leu, J.M. Modelling Reference Evapotranspiration Using Feed Forward Backpropagation Algorithm in Arid Regions of Africa. Irrig. Drain. 2011, 60, 404–417. [Google Scholar] [CrossRef]
- Awolusi, T.F.; Oke, O.L.; Akinkurolere, O.O.; Sojobi, A.O.; Aluko, O.G. Performance comparison of neural network training algorithms in the modeling properties of steel fiber reinforced concrete. Heliyon 2019, 5, e01115. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.M.; Traore, S. Time-lagged recurrent network for forecasting episodic event suspended sediment load in typhoon prone area. Int. J. Phys. Sci. 2009, 4, 519–528. [Google Scholar]
- Sentas, A.; Psilovikos, A. Comparison of ARIMA and transfer function (TF) models in water temperature simulation in dam-lake Thesaurus, eastern Macedonia, Greece. In Proceedings of the International Symposium: Environmental Hydraulics, Athens, Greece, 23–25 June 2010; pp. 929–934. [Google Scholar]
- Afzaal, H.; Farooque, A.A.; Abbas, F.; Acharya, B.; Esau, T. Groundwater Estimation from Major Physical Hydrology Components Using Artificial Neural Networks and Deep Learning. Water 2019, 12, 5. [Google Scholar] [CrossRef] [Green Version]
- Zubier, K.M.; Eyouni, L.S. Investigating the role of atmospheric variables on sea level variations in the eastern central red sea using an artificial neural network approach. Oceanologia 2020. [Google Scholar] [CrossRef]
- Karamoutsou, L.; Psilovikos, A. The use of artificial neural network in water quality prediction in lake Kastoria, Greece. In Proceedings of the 14th Conference of the Hellenic Hydrotechnical Association (H.H.A.), Volos, Greece, 16–17 May 2019. [Google Scholar]
- Kerh, T.; Hsu, G.S.; Gunaratnam, D. Forecasting of Nonlinera Shoreline Variation Based on Aerial Survey Map by Nueral Network Approach. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 1211–1222. [Google Scholar] [CrossRef]
- Manaf, S.A.; Mustapha, N.; Sulaiman, M.N.; Husin, N.A.; Hamid, M.R.A. Artificial Neural Networks for Satellite Image Classification of Shoreline Extraction for Land and Water Classes of the North West Coast of Peninsular Malaysia. Adv. Sci. Lett. 2018, 24, 1382–1387. [Google Scholar] [CrossRef]
- Kariyama, I.D. Temperature Based Feed Forward Backpropagation Artificial Neural Network for Estimating Reference Crop Evapotranspiration in the Upper West Region. Int. J. Sci. Technol. Res. 2014, 3, 357–364. [Google Scholar]
- Peponi, A.; Morgado, P.; Trindade, J. Combining Artificial Neural Networks and GIS Fundamentals for Coastal Erosion Prediction Modeling. Sustainability 2019, 11, 975. [Google Scholar] [CrossRef] [Green Version]
- Khotanzad, A.; Chung, C. Application of multi-layer perceptron neural networks to vision problems. Neural Comput. Appl. 1998, 7, 249–259. [Google Scholar] [CrossRef]
- Tfwala, S.S.; Wang, Y.-M.; Lin, Y.-C. Prediction of Missing Flow Records Using Multilayer Perceptron and Coactive Neurofuzzy Inference System. Sci. World J. 2013, 2013, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Chi, Y.N.; Chi, J. Saltwater anglers toward marine environmental threats using multilayer perceptron neural network framework. Int. J. Data Sci. Adv. 2020, 2, 6–17. [Google Scholar]
- Cömert, Z.; Kocamaz, A.F. A study of artificial neural network training alorithms classification of cardiotocography signals. Bitlis Eren Univ. J. Sci. Technol. 2017, 7, 93–103. [Google Scholar]
- Kulp, S.A.; Strauss, B.H. Coastaldem: A global coastal digital elevation model improved from SRTM using a neural network. Remote Sens. Environ. 2018, 206, 231–239. [Google Scholar] [CrossRef]
- Fernández, J.R.M.; Vidal, J.d.l.C.B. Fast selection of the sea clutter preferential distribution with neural networks. Eng. Appl. Artif. Intell. 2018, 70, 123–129. [Google Scholar] [CrossRef]
- Saputro, D.R.S.; Widyaningsih, P. Limited memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) method for the parameter estimation on geographically weighted ordinal logistic regression model (GWOLR). AIP Conf. Proc. 2017, 1868, 040009. [Google Scholar]
- Attoh-Okine, N.O. Analysis of learning rate and momentum term in backpropagation neural network algorithm trained to predict pavement performance. Adv. Eng. Softw. 1999, 30, 291–302. [Google Scholar] [CrossRef]
- Arminger, G.; Enache, D. Statistical models and artificial neural networks. In Data Anaysis and Information Systems; Bock, H.-H., Polasek, W., Eds.; Springer: Berlin/Heidelberg, Germany, 1996; pp. 243–260. [Google Scholar]
- Urban, S.; Basalla, M.; van der Smagt, P. Available online: https://arxiv.org/abs/1711.11059.pdf (accessed on 25 March 2020).
- Glorot, X.; Bordes, A.; Bengio, Y. Available online: http://proceedings.mlr.press/v15/glorot11a/glorot11a.pdf (accessed on 25 March 2020).
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Parascandolo, G.; Huttunen, H.; Virtanen, T. Available online: https://openreview.net/forum?id=Sks3zF9eg (accessed on 25 March 2020).



| Location | Function | Training | Validation | Testing | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | KGE | r | RMSE | KGE | r | RMSE | KGE | r | ||||||||
| BS | Exponential | 4.092 | 0.995 | 0.999 | 1.000 | 1.005 | 1.963 | 0.991 | 0.999 | 1.000 | 0.991 | 4.092 | 0.973 | 1.000 | 1.000 | 0.973 |
| Identity | 4.944 | 0.961 | 0.994 | 1.000 | 1.039 | 5.099 | 0.962 | 0.997 | 1.000 | 1.038 | 3.912 | 0.987 | 0.995 | 1.000 | 1.012 | |
| Logistic | 3.195 | 0.995 | 0.999 | 1.000 | 1.005 | 2.856 | 0.993 | 0.999 | 1.000 | 0.993 | 3.153 | 0.988 | 0.999 | 1.000 | 0.988 | |
| Sine | 8.685 | 0.961 | 0.994 | 1.000 | 1.039 | 7.712 | 0.962 | 0.997 | 1.000 | 1.038 | 6.653 | 0.987 | 0.995 | 1.000 | 1.012 | |
| Tahn | 7.003 | 0.977 | 0.996 | 1.000 | 1.023 | 7.411 | 0.996 | 0.997 | 1.000 | 0.997 | 6.587 | 0.995 | 0.996 | 1.000 | 0.998 | |
| DW | Exponential | 11.318 | 0.973 | 0.992 | 1.000 | 1.026 | 5.093 | 0.978 | 0.995 | 1.000 | 1.022 | 9.479 | 0.995 | 0.998 | 1.000 | 0.996 |
| Identity | 13.914 | 0.985 | 0.994 | 1.000 | 1.014 | 5.572 | 0.978 | 0.996 | 1.000 | 1.021 | 12.153 | 0.983 | 0.993 | 1.000 | 1.016 | |
| Logistic | 9.042 | 0.989 | 0.995 | 1.000 | 1.010 | 8.531 | 0.987 | 0.997 | 1.000 | 1.013 | 8.120 | 0.993 | 0.994 | 1.000 | 0.996 | |
| Sine | 9.820 | 0.985 | 0.994 | 1.000 | 1.014 | 8.812 | 0.978 | 0.996 | 1.000 | 1.021 | 8.330 | 0.983 | 0.993 | 1.000 | 1.016 | |
| Tahn | 8.459 | 0.996 | 0.996 | 1.000 | 1.002 | 8.210 | 0.985 | 0.997 | 1.000 | 0.985 | 7.782 | 0.994 | 0.994 | 1.000 | 1.001 | |
| NW | Exponential | 7.504 | 0.951 | 0.975 | 1.000 | 1.042 | 6.303 | 0.763 | 0.981 | 1.000 | 1.237 | 6.647 | 0.794 | 0.988 | 1.000 | 1.205 |
| Identity | 14.263 | 0.932 | 0.969 | 1.000 | 1.061 | 10.096 | 0.798 | 0.972 | 1.000 | 1.200 | 17.322 | 0.702 | 0.985 | 1.000 | 1.298 | |
| Logistic | 6.513 | 0.968 | 0.982 | 1.000 | 1.027 | 6.955 | 0.741 | 0.985 | 1.000 | 1.258 | 5.898 | 0.716 | 0.983 | 1.000 | 1.284 | |
| Sine | 8.100 | 0.932 | 0.969 | 1.000 | 1.061 | 6.400 | 0.798 | 0.972 | 1.000 | 1.200 | 8.295 | 0.702 | 0.985 | 1.000 | 1.298 | |
| Tahn | 7.031 | 0.970 | 0.981 | 1.000 | 1.023 | 7.01913 | 0.854 | 0.969 | 1.000 | 1.143 | 8.179 | 0.870 | 0.983 | 1.000 | 1.129 | |
| SW | Exponential | 1.489 | 0.996 | 0.998 | 1.000 | 1.004 | 5.283 | 0.972 | 0.986 | 1.000 | 1.024 | 3.995 | 0.942 | 0.957 | 1.000 | 1.039 |
| Identity | 1.751 | 0.968 | 0.994 | 1.000 | 1.032 | 5.570 | 0.946 | 0.979 | 1.000 | 1.050 | 4.280 | 0.913 | 0.942 | 1.000 | 1.065 | |
| Logistic | 1.693 | 0.991 | 0.997 | 1.000 | 1.008 | 5.113 | 0.966 | 0.987 | 1.000 | 1.032 | 3.751 | 0.950 | 0.960 | 1.000 | 1.031 | |
| Sine | 2.351 | 0.968 | 0.994 | 1.000 | 1.032 | 5.927 | 0.946 | 0.979 | 1.000 | 1.050 | 4.670 | 0.913 | 0.942 | 1.000 | 1.065 | |
| Tahn | 1.417 | 0.997 | 0.998 | 1.000 | 1.003 | 4.052 | 0.984 | 0.991 | 1.000 | 1.014 | 3.181 | 0.960 | 0.973 | 1.000 | 1.029 | |
| TFS | Exponential | 1.155 | 0.998 | 0.999 | 1.000 | 1.002 | 1.326 | 0.998 | 0.999 | 1.000 | 0.999 | 1.206 | 0.987 | 0.999 | 1.000 | 0.994 |
| Identity | 2.190 | 0.969 | 0.985 | 1.000 | 0.973 | 2.194 | 0.979 | 0.985 | 1.000 | 1.015 | 2.505 | 0.942 | 0.985 | 1.000 | 1.056 | |
| Logistic | 1.051 | 0.999 | 0.999 | 1.000 | 0.999 | 0.982 | 0.999 | 1.000 | 1.000 | 1.001 | 0.916 | 0.994 | 0.999 | 1.000 | 0.987 | |
| Sine | 4.735 | 0.969 | 0.985 | 1.000 | 0.973 | 4.297 | 0.979 | 0.985 | 1.000 | 1.015 | 5.104 | 0.942 | 0.985 | 1.000 | 1.056 | |
| Tahn | 1.550 | 0.998 | 0.998 | 1.000 | 0.998 | 1.599 | 0.986 | 0.999 | 1.000 | 1.014 | 1.537 | 0.983 | 0.998 | 1.000 | 1.017 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.-C.; Wang, Y.-M. Comparing Activation Functions in Modeling Shoreline Variation Using Multilayer Perceptron Neural Network. Water 2020, 12, 1281. https://doi.org/10.3390/w12051281
Chen J-C, Wang Y-M. Comparing Activation Functions in Modeling Shoreline Variation Using Multilayer Perceptron Neural Network. Water. 2020; 12(5):1281. https://doi.org/10.3390/w12051281
Chicago/Turabian StyleChen, Je-Chian, and Yu-Min Wang. 2020. "Comparing Activation Functions in Modeling Shoreline Variation Using Multilayer Perceptron Neural Network" Water 12, no. 5: 1281. https://doi.org/10.3390/w12051281
APA StyleChen, J.-C., & Wang, Y.-M. (2020). Comparing Activation Functions in Modeling Shoreline Variation Using Multilayer Perceptron Neural Network. Water, 12(5), 1281. https://doi.org/10.3390/w12051281






