Improvement of Non-Hydrostatic Hydrodynamic Solution Using a Novel Free-Surface Boundary Condition
Abstract
:1. Introduction
2. Methods
2.1. Governant Equations
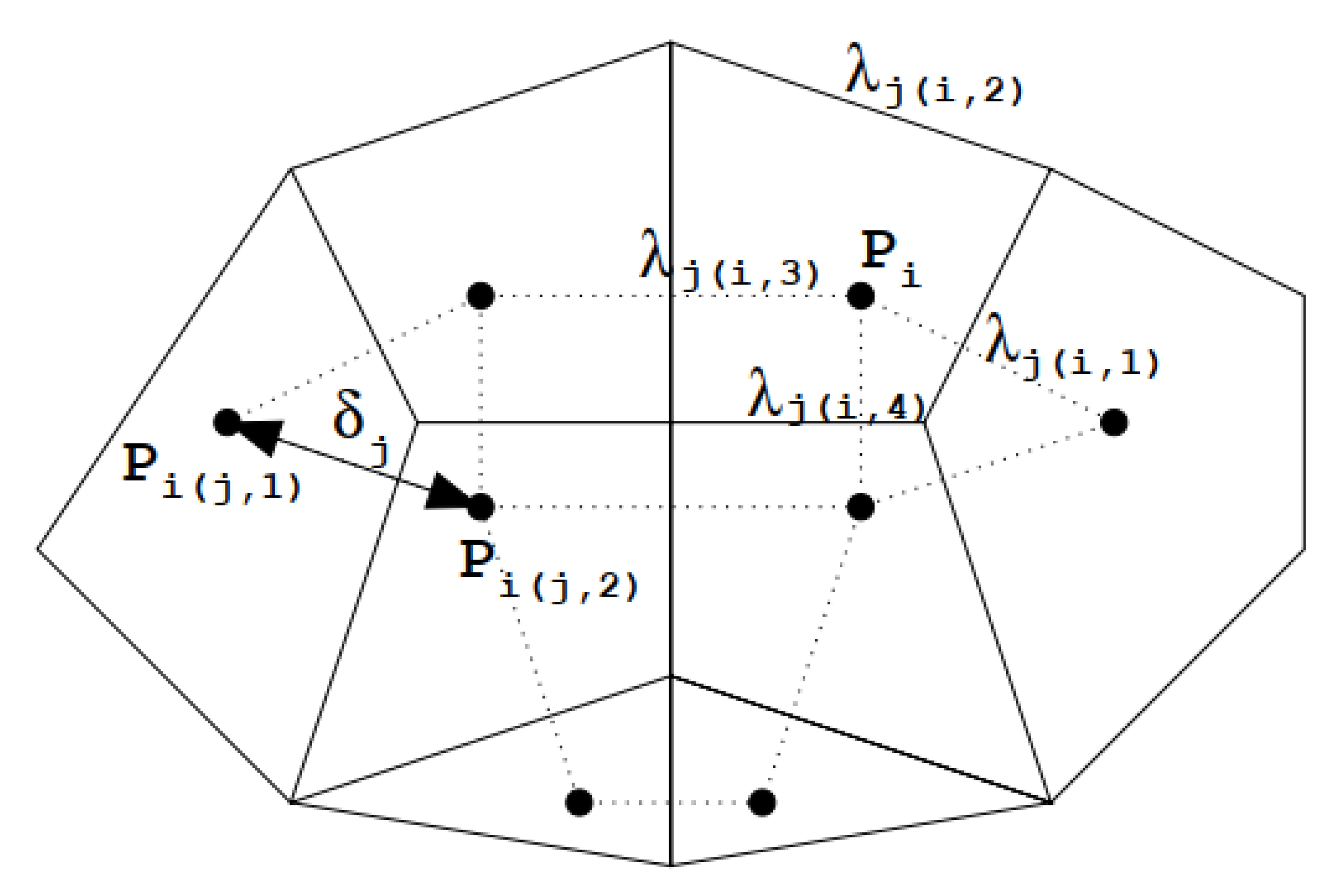
2.2. Grid and Variables Locations
2.3. Numerical Approximation
- Definition of initial parameters, initial conditions, and boundary conditions.
- Solution of convective terms using the Eulerian–Lagrangian Method.
- Determination of the provisional free-surface elevation () through the preconditioned conjugate gradient iterations until the residual norm is smaller than a given tolerance .
- Numeric solution of provisional velocity field ( and ).
- Solution of non-hydrostatic pressure (q) through the preconditioned conjugate gradient iterations until the residual norm is smaller than a given tolerance .
- Numeric correction of velocity field and free surface elevation.
2.3.1. Non-Hydrostatic Pressure Discretization
2.3.2. Free-Surface Boundary Condition Treatment
- (i)
- For bottom and middle layers (i.e., to ), the Equation (17) is applied using its original form;
- (ii)
- For the top layer (), Equation (17) is adapted to take into account the influence of FSFS height () in and :
- (iii)
- For the FSFS layer (), Equation (18) is adapted to take into account the height and the velocity field in the layer M. Preliminary simulations showed that making a stable solution is achieved for any vertical discretization:
2.4. Numerical Experiments
- a
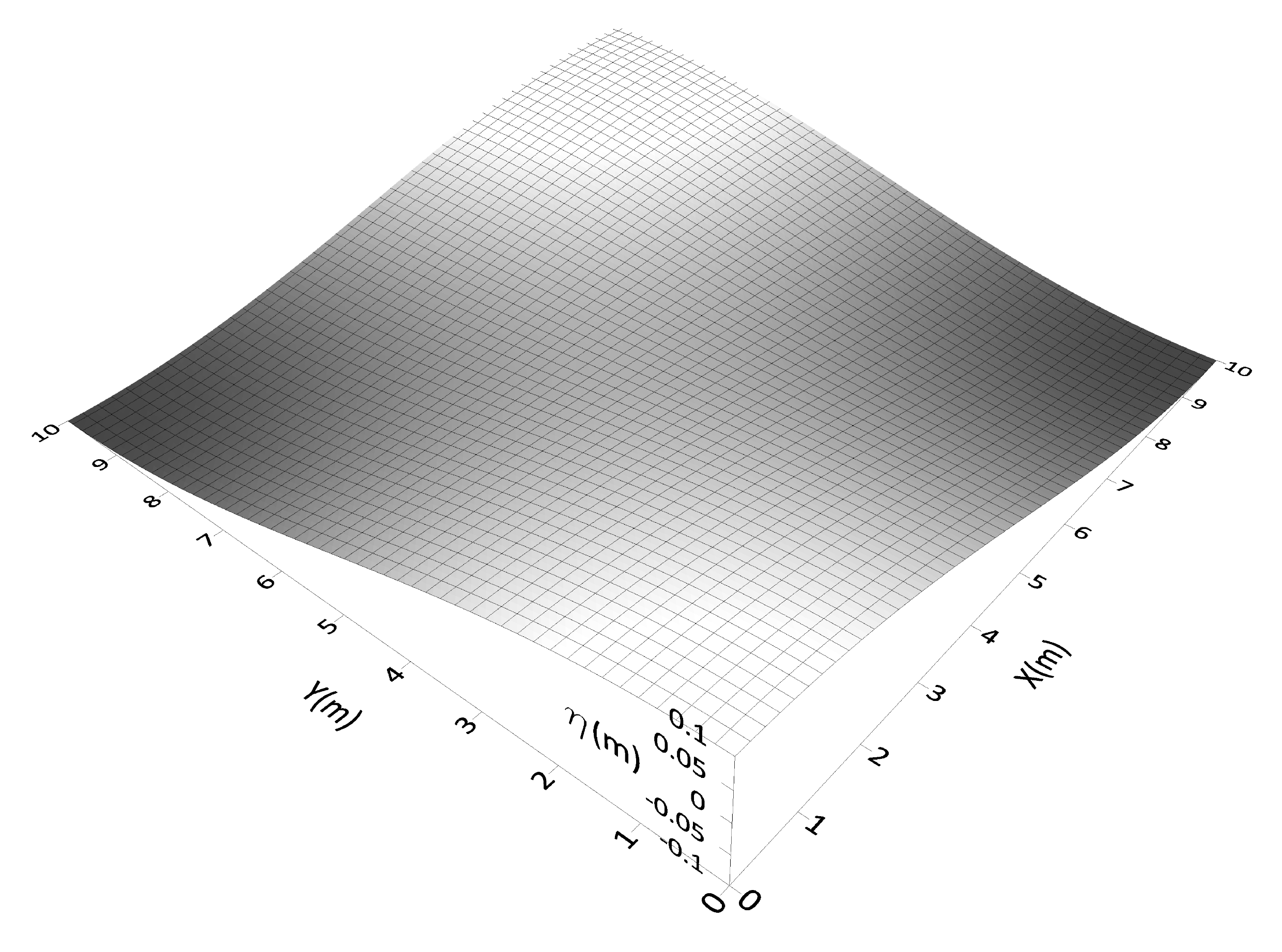
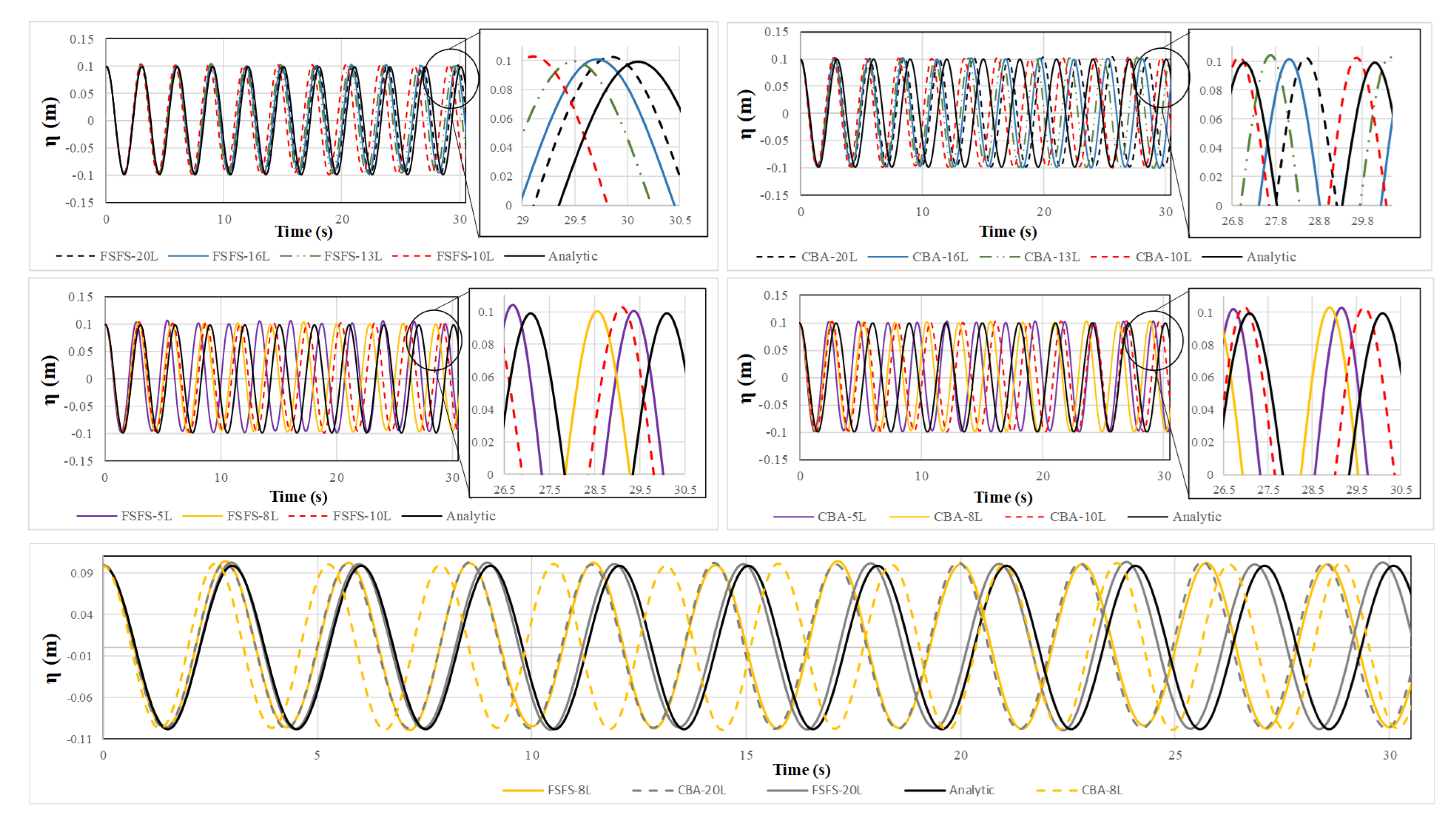
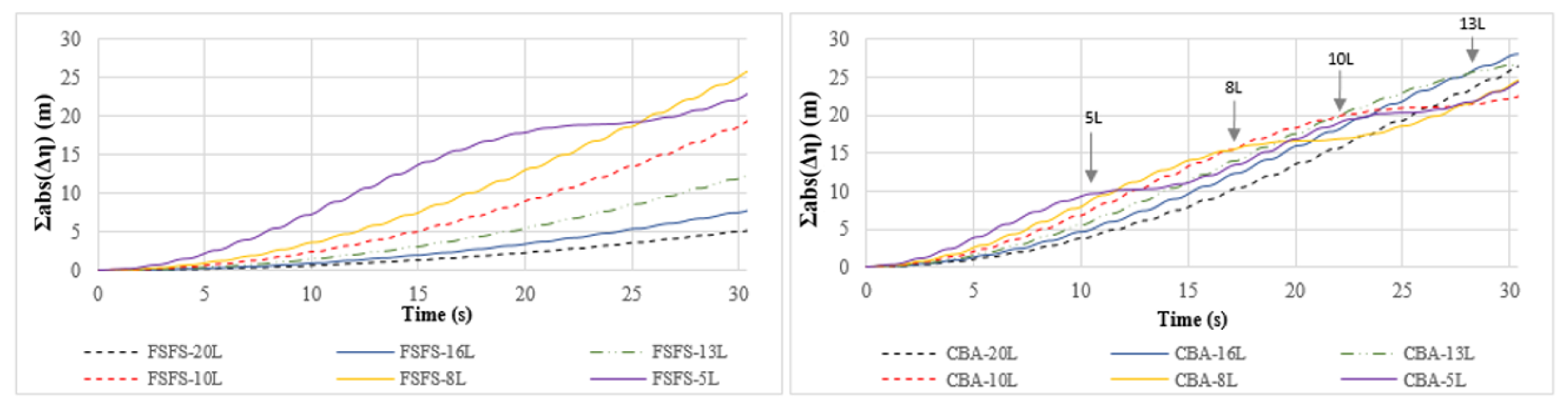
- Standing waves in a three-dimensional closed basin: This test was widely applied in the literature to verify the model’s ability to simulate 3D linear waves comparing the analytic solution with the numerical solution in regard to phase and amplitude representation [8,9,11,20]. We evaluated the model capability in calculating the wave celerity and frequency wave dispersion with the Classic Boundary Approach (hereafter named CBA) and with the proposed FSFS boundary condition. We used six different vertical resolutions (20~5 layers), as most of the previous studies do, and since previous analyses showed that more than 20 layers do not have substantial improvement over 20 layers non-hydrostatic solution. We compare the free surface elevation cumulative phase error, the mean one time-step computational cost, the number of wave periods, and the relation with the free surface vertical velocity after 30 s of simulation in comparison with the analytical solution. We also compared the free surface elevation results with some metrics (RMSE, BIAS, Volume Error, KGE, NSE). At last, we statistically tested the residual series (the difference between analytic and simulated results) with the non-parametric Kruskal–Wallis test followed by a post-hoc Nemenyi to identify significant differences concerning the analytic results. The mean time of one time-step simulation was computed using an Intel® Xenon® CPU-E5-1620 3.7 GHz computer with 32 GB of RAM in a Fortran-based numerical model.
- b
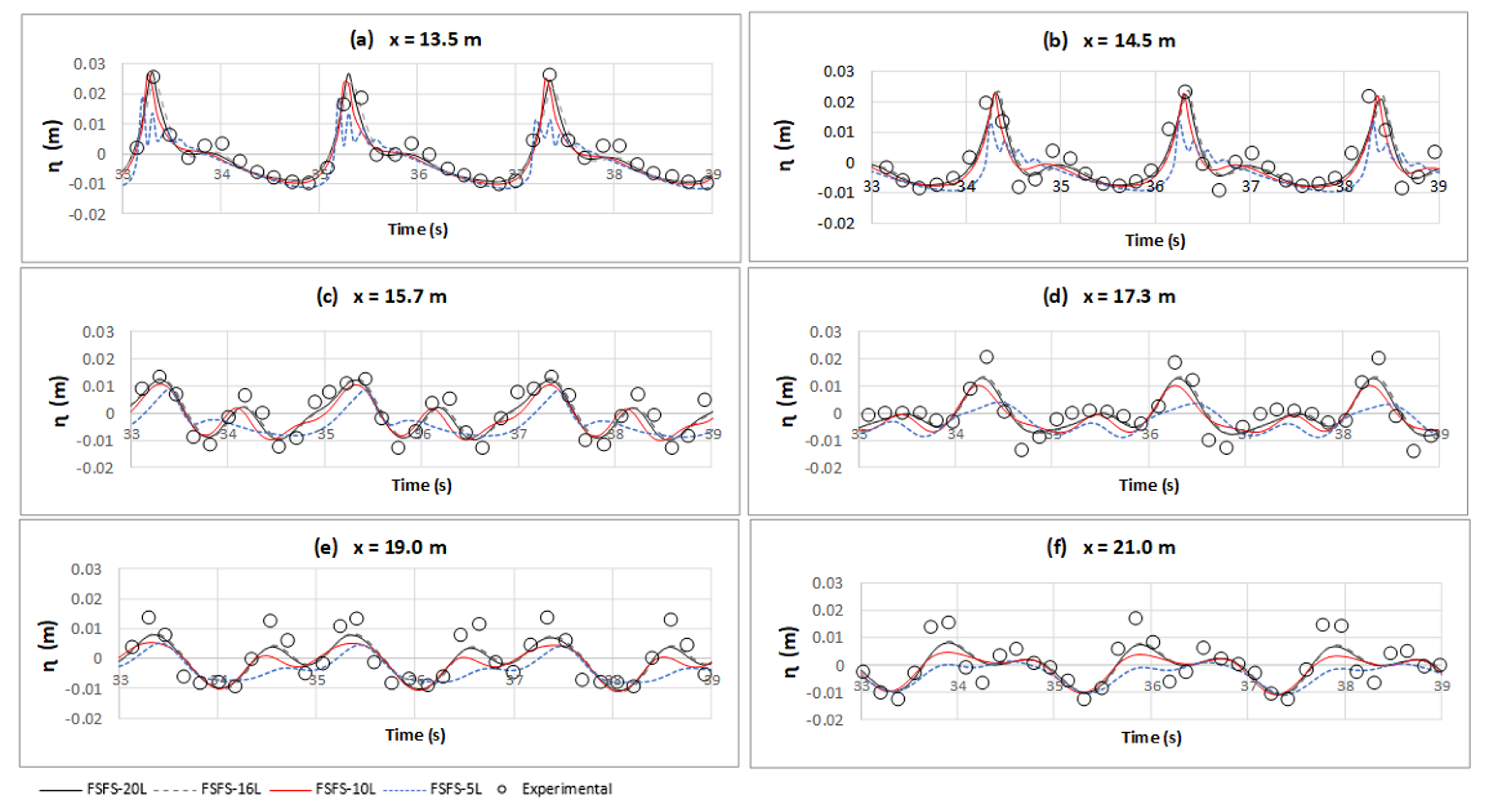
- The wave propagation over a submerged bar: This test case was an experimental model idealized by [32], and was frequently used to validate numerical models (e.g., [7,8,24,26,28,33]). This experiment was used to evaluate accuracy to represent a non-linear wave pattern due to physical changes at the bottom, by comparing free surface elevation between the FSFS approach with a different vertical resolution between simulated and experimental results. To evaluate the model’s performance was used a few metrics (RMSE, BIAS, Volume Error, KGE, NSE) and the statistical test non-parametric Kruskal–Wallis test followed by a post-hoc Nemenyi test applied at residuals series.
3. Results
3.1. 3D Standing Waves in a Closed Basin
3.2. Wave Propagation over a Submerged Bar
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Valipour, R.; Bouffard, D.; Boegman, L.; Rao, Y.R. Near-inertial waves in Lake Erie. Limnol. Oceanogr. 2015, 60, 1522–1535. [Google Scholar] [CrossRef]
- De Brito, A.N., Jr.; Fragoso, C.R., Jr.; Larson, M. Tidal exchange in a choked coastal lagoon: A study of Mundaú Lagoon in northeastern Brazil. Reg. Stud. Mar. Sci. 2018, 17, 133–142. [Google Scholar] [CrossRef]
- Vilas, M.P.; Marti, C.L.; Adams, M.P.; Oldham, C.E.; Hipsey, M.R. Invasive macrophytes control the spatial and temporal patterns of temperature and dissolved oxygen in a shallow lake: A proposed feedback mechanism of macrophyte loss. Front. Plant Sci. 2017, 8, 2097. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soulignac, F.; Vinçon-Leite, B.; Lemaire, B.J.; Martins, J.R.S.; Bonhomme, C.; Dubois, P.; Mezemate, Y.; Tchiguirinskaia, I.; Schertzer, D.; Tassin, B. Performance Assessment of a 3D Hydrodynamic Model Using High Temporal Resolution Measurements in a Shallow Urban Lake. Environ. Model. Assess. 2017, 22, 309–322. [Google Scholar] [CrossRef]
- Munar, A.M.; Cavalcanti, J.R.; Bravo, J.M.; Fan, F.M.; da Motta-Marques, D.; Fragoso, C.R., Jr. Coupling large-scale hydrological and hydrodynamic modeling: Toward a better comprehension of watershed-shallow lake processes. J. Hydrol. 2018, 564, 424–441. [Google Scholar] [CrossRef]
- Zhang, J.; Liang, D.; Liu, H. A hybrid hydrostatic and non-hydrostatic numerical model for shallow flow simulations. Estuar. Coast. Shelf Sci. 2018, 205, 21–29. [Google Scholar] [CrossRef]
- Stelling, G.; Zijlema, M. An accurate and efficient finite-difference algorithm for non-hydrostatic free-surface flow with application to wave propagation. Int. J. Numer. Methods Fluids 2003, 43, 1–23. [Google Scholar] [CrossRef]
- Yuan, H.; Wu, C.H. An implicit three-dimensional fully non-hydrostatic model for free-surface flows. Int. J. Numer. Methods Fluids 2004, 46, 709–733. [Google Scholar] [CrossRef]
- Zijlema, M.; Stelling, G.S. Further experiences with computing non-hydrostatic free-surface flows involving water waves. Int. J. Numer. Methods Fluids 2005, 48, 169–197. [Google Scholar] [CrossRef]
- Lv, B. A higher-efficient three-dimensional numerical model for small amplitude free surface flows. China Ocean Eng. 2014, 28, 617–628. [Google Scholar] [CrossRef]
- Liu, X.; Ma, D.G.; Zhang, Q.H. A higher-efficient non-hydrostatic finite volume model for strong three-dimensional free surface flows and sediment transport. China Ocean Eng. 2017, 31, 736–746. [Google Scholar] [CrossRef]
- Escalante, C.; Fernández-Nieto, E.; de Luna, T.M.; Castro, M. An Efficient Two-Layer Non-hydrostatic Approach for Dispersive Water Waves. J. Sci. Comput. 2019, 79, 273–320. [Google Scholar] [CrossRef]
- Wadzuk, B.M.; Hodges, B.R. Hydrostatic and Non-Hydrostatic Internal Wave Models; Technical report; Center for Research in Water Resources, University of Texas at Austin: Austin, TX, USA, 2004. [Google Scholar]
- Bohacek, J.; Kharicha, A.; Ludwig, A.; Wu, M.; Karimi-Sibaki, E.; Paar, A.; Brandner, M.; Elizondo, L.; Trickl, T. A (non-) hydrostatic free-surface numerical model for two-layer flows. Appl. Math. Comput. 2018, 319, 301–317. [Google Scholar] [CrossRef]
- Escalante, C.; de Luna, T.M.; Castro, M. Non-hydrostatic pressure shallow flows: GPU implementation using finite volume and finite difference scheme. Appl. Math. Comput. 2018, 338, 631–659. [Google Scholar] [CrossRef] [Green Version]
- Kanarska, Y.; Maderich, V. A non-hydrostatic numerical model for calculating free-surface stratified flows. Ocean Dyn. 2003, 53, 176–185. [Google Scholar] [CrossRef]
- Wang, K.; Jin, S.; Liu, G. Numerical modelling of free-surface flows with bottom and surface-layer pressure treatment. J. Hydrodyn. 2009, 21, 352–359. [Google Scholar] [CrossRef]
- Casulli, V. A semi-implicit finite difference method for non-hydrostatic, free-surface flows. Int. J. Numer. Methods Fluids 1999, 30, 425–440. [Google Scholar] [CrossRef]
- Namin, M.; Lin, B.; Falconer, R. An implicit numerical algorithm for solving non-hydrostatic free-surface flow problems. Int. J. Numer. Methods Fluids 2001, 35, 341–356. [Google Scholar] [CrossRef]
- Monteiro, L.R.; Schettini, E.B.C. Comparação entre a aproximação hidrostática e a não-hidrostática na simulação numérica de escoamentos com superfície livre. Rev. Bras. De Recur. Hídricos 2015, 20, 1051–1062. [Google Scholar]
- Bergh, J.; Berntsen, J. The surface boundary condition in nonhydrostatic ocean models. Ocean Dyn. 2010, 60, 301–315. [Google Scholar] [CrossRef]
- Jankowski, J.A. A Non-Hydrostatic Model for Free Surface Flows. Ph.D. Thesis, Inst. für Strömungsmechanik und Elektronisches Rechnen im Bauwesen, University of Hannover, Hannover, Germany, 1999. [Google Scholar]
- Casulli, V.; Lang, G. Mathematical Model UnTRIM, Validation Document 1.0; The Federal Waterways Engineering and Research Institute (BAW): Hamburg, Germany, 2004. [Google Scholar]
- Cui, H.; Pietrzak, J.; Stelling, G. Improved efficiency of a non-hydrostatic, unstructured grid, finite volume model. Ocean Model. 2012, 54, 55–67. [Google Scholar] [CrossRef]
- Lu, X.; Dong, B.; Mao, B.; Zhang, X. A two-dimensional depth-integrated non-hydrostatic numerical model for nearshore wave propagation. Ocean Model. 2015, 96, 187–202. [Google Scholar] [CrossRef]
- Dingemans, M. Comparison of computations with Boussinesq-like models and laboratory measurements. In Memo in Framework of MAST Project (G8-M), Delft Hydraulics Memo H1684. 12; Deltares: Delft, The Netherlands, 1994. [Google Scholar]
- Fringer, O.; Armfield, S.; Street, R. Reducing numerical diffusion in interfacial gravity wave simulations. Int. J. Numer. Methods Fluids 2005, 49, 301–329. [Google Scholar] [CrossRef]
- Yin, J.; Sun, J.W.; Wang, X.G.; Yu, Y.H.; Sun, Z.C. A hybrid finite-volume and finite difference scheme for depth-integrated non-hydrostatic model. China Ocean Eng. 2017, 31, 261–271. [Google Scholar] [CrossRef]
- Casulli, V. Semi-implicit finite difference methods for the two-dimensional shallow water equations. J. Comput. Phys. 1990, 86, 56–74. [Google Scholar] [CrossRef]
- Casulli, V.; Cheng, R.T. Semi-implicit finite difference methods for three-dimensional shallow water flow. Int. J. Numer. Methods Fluids 1992, 15, 629–648. [Google Scholar] [CrossRef]
- Hodges, B.R.; Imberger, J.; Saggio, A.; Winters, K.B. Modeling basin-scale internal waves in a stratified lake. Limnol. Oceanogr. 2000, 45, 1603–1620. [Google Scholar] [CrossRef] [Green Version]
- Beji, S.; Battjes, J. Experimental investigation of wave propagation over a bar. Coast. Eng. 1993, 19, 151–162. [Google Scholar] [CrossRef]
- Beji, S.; Battjes, J. Numerical simulation of nonlinear wave propagation over a bar. Coast. Eng. 1994, 23, 1–16. [Google Scholar] [CrossRef]
- Park, J.C.; Kim, M.H.; Miyata, H. Fully non-linear free-surface simulations by a 3D viscous numerical wave tank. Int. J. Numer. Methods Fluids 1999, 29, 685–703. [Google Scholar] [CrossRef]
- Walters, R.A. A semi-implicit finite element model for non-hydrostatic (dispersive) surface waves. Int. J. Numer. Methods Fluids 2005, 49, 721–737. [Google Scholar] [CrossRef]
- Chen, X. A fully hydrodynamic model for three-dimensional, free-surface flows. Int. J. Numer. Methods Fluids 2003, 42, 929–952. [Google Scholar] [CrossRef]

| N°L | FSFS | CBA | ||||
|---|---|---|---|---|---|---|
| N° T | N° T | |||||
| 20-Layers | 2.8 | 10 | 0.3 | 2.62 | 10 | 1.6 |
| 16-Layers | 2.21 | 10 | 0.4 | 2.14 | 10 | 2 |
| 13-Layers | 1.68 | 10 | 0.6 | 1.67 | 10 | 2.4 |
| 10-Layers | 1.54 | 10 | 1 | 1.45 | 11 | 3.1 |
| 8-Layers | 1.51 | 10 | 1.5 | 1.34 | 11 | 3.8 |
| 5-Layers | 1.22 | 11 | 2.1 | 1.08 | 12 | 4.6 |
| Metrics | FSFS-20L | FSFS-16L | FSFS-13L | FSFS-10L | FSFS-8L | FSFS-5L |
|---|---|---|---|---|---|---|
| RMSE (mm) | 7.40 | 11.52 | 18.29 | 30.53 | 45.30 | 89.20 |
| BIAS (mm) | 0.32 | 0.32 | −0.77 | −2.11 | −3.54 | −7.61 |
| Error (%) | 9.25 | 14.28 | 22.55 | 37.79 | 56.60 | 114.13 |
| KGE | 0.93 | 0.93 | 0.82 | 0.52 | 0.18 | −0.88 |
| NSE | 0.99 | 0.97 | 0.93 | 0.81 | 0.57 | −0.66 |
| Metrics | CBA-20L | CBA-16L | CBA-13L | CBA-10L | CBA-8L | CBA-5L |
|---|---|---|---|---|---|---|
| RMSE (mm) | 47.06 | 57.68 | 68.75 | 83.48 | 95.63 | 107.80 |
| BIAS (mm) | −4.35 | −5.65 | −6.88 | −7.96 | −7.57 | −1.06 |
| Error (%) | 58.94 | 72.70 | 87.10 | 106.42 | 123.39 | 145.02 |
| KGE | 0.004 | −0.30 | −0.61 | −0.91 | −0.93 | −0.20 |
| NSE | 0.54 | 0.31 | 0.017 | −0.45 | −0.90 | −1.42 |
| N°-L | FSFS-20L | FSFS-16L | FSFS-13L | FSFS-10L | FSFS-8L |
|---|---|---|---|---|---|
| FSFS-16L | 0.97833 | - | - | - | - |
| FSFS-13L | 0.24554 | 0.69401 | - | - | - |
| FSFS-10L | <0.05 | <0.05 | 0.05269 | - | - |
| FSFS-8L | <0.05 | <0.05 | <0.05 | <0.05 - | |
| FSFS-5L | <0.05 | <0.05 | <0.05 | 0.70396 | 0.5515 |
| Station a: x = 13.5 m | Station d: x = 17.3 m | |||||||
|---|---|---|---|---|---|---|---|---|
| Metrics | 20L | 16L | 10L | 5L | 20L | 16L | 10L | 5L |
| RMSE (mm) | 2.67 | 2.31 | 3.40 | 5.23 | 4.12 | 4.08 | 5.57 | 8.05 |
| BIAS (mm) | −0.67 | −0.70 | −1.26 | −2.70 | −0.60 | −0.44 | −1.34 | −3.14 |
| Error (%) | 26.47 | 25.37 | 34.07 | 53.94 | 59.29 | 57.97 | 79.03 | 116.84 |
| KGE | −0.95 | −1.06 | −2.69 | −6.92 | −4.57 | −3.06 | −11.30 | −27.85 |
| NSE | 0.92 | 0.94 | 0.87 | 0.69 | 0.76 | 0.76 | 0.56 | 0.08 |
| Station b: x = 14.5 m | Station e: x = 19.0 m | |||||||
| RMSE (mm) | 3.68 | 4.21 | 4.18 | 6.74 | 4.30 | 4.23 | 5.69 | 7.22 |
| BIAS (mm) | −0.80 | −0.73 | −1.23 | −2.58 | −0.65 | −0.50 | −1.39 | −3.28 |
| Error (%) | 37.73 | 43.83 | 44.30 | 76.27 | 48.15 | 47.35 | 62.91 | 75.29 |
| KGE | −0.83 | −0.68 | −1.80 | −4.88 | −54.45 | −41.24 | −117.00 | −277.78 |
| NSE | 0.82 | 0.77 | 0.77 | 0.41 | 0.72 | 0.72 | 0.50 | 0.20 |
| Station c: x = 15.7 m | Station f: x = 21.0 m | |||||||
| RMSE (mm) | 3.91 | 3.64 | 5.45 | 7.64 | 4.57 | 4.59 | 5.61 | 7.09 |
| BIAS (mm) | −0.63 | −0.48 | −1.37 | −3.32 | −0.65 | −0.48 | −1.38 | −3.25 |
| Error (%) | 44.46 | 40.98 | 62.63 | 88.06 | 56.63 | 56.12 | 67.62 | 76.43 |
| KGE | −1.13 | −0.63 | −3.58 | −10.09 | −9.80 | −7.09 | −22.02 | −53.11 |
| NSE | 0.79 | 0.82 | 0.60 | 0.21 | 0.69 | 0.68 | 0.53 | 0.24 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cunha, A.H.F.; Fragoso, C.R., Jr.; Chalegre, C.L.B.; Motta-Marques, D. Improvement of Non-Hydrostatic Hydrodynamic Solution Using a Novel Free-Surface Boundary Condition. Water 2020, 12, 1271. https://doi.org/10.3390/w12051271
Cunha AHF, Fragoso CR Jr., Chalegre CLB, Motta-Marques D. Improvement of Non-Hydrostatic Hydrodynamic Solution Using a Novel Free-Surface Boundary Condition. Water. 2020; 12(5):1271. https://doi.org/10.3390/w12051271
Chicago/Turabian StyleCunha, Augusto Hugo Farias, Carlos Ruberto Fragoso, Jr., Cayo Lopes Bezerra Chalegre, and David Motta-Marques. 2020. "Improvement of Non-Hydrostatic Hydrodynamic Solution Using a Novel Free-Surface Boundary Condition" Water 12, no. 5: 1271. https://doi.org/10.3390/w12051271
APA StyleCunha, A. H. F., Fragoso, C. R., Jr., Chalegre, C. L. B., & Motta-Marques, D. (2020). Improvement of Non-Hydrostatic Hydrodynamic Solution Using a Novel Free-Surface Boundary Condition. Water, 12(5), 1271. https://doi.org/10.3390/w12051271






