Abstract
Demand for reliable estimates of streamflow has increased as society becomes more susceptible to climatic extremes such as droughts and flooding, especially at small scales where local population centers and infrastructure can be affected by rapidly occurring events. In the current study, the Hydrology Laboratory-Research Distributed Hydrologic Model (HL-RDHM) (NOAA/NWS, Silver Spring, MD, USA) was used to explore the accuracy of a distributed hydrologic model to simulate discharge at watershed scales ranging from 20 to 2500 km2. The model was calibrated and validated using observed discharge data at the basin outlets, and discharge at uncalibrated subbasin locations was evaluated. Two precipitation products with nominal spatial resolutions of 12.5 km and 4 km were tested to characterize the role of input resolution on the discharge simulations. In general, model performance decreased as basin size decreased. When sub-basin area was less than 250 km2 or 20–40% of the total watershed area, model performance dropped below the defined acceptable levels. Simulations forced with the lower resolution precipitation product had better model evaluation statistics; for example, the Nash–Sutcliffe efficiency (NSE) scores ranged from 0.50 to 0.67 for the verification period for basin outlets, compared to scores that ranged from 0.33 to 0.52 for the higher spatial resolution forcing.
1. Introduction
Hydrologic models are essential for improving our understanding of the various components of the hydrologic cycle and are valuable tools for water resources modeling, drought and flood forecasting, and climate change impact assessment studies. In recent decades, efforts have been made to advance hydrologic modeling and forecasting through the use of spatially distributed models [1,2,3,4,5,6]. Spatially distributed models are supported by readily available geographic information system (GIS) data and rapidly increasing computing power, and it has been anticipated that spatially distributed models would provide more accurate and timely hydrologic information due to their innate ability to account for basin heterogeneities and spatially distributed inputs [7,8,9,10,11]. Critically, distributed models are able to simulate hydrologic responses at interior locations within the basin drainage network, a benefit not afforded by lumped models.
Quantifying hydrologic variability across a range of scales is a primary focus of the prediction in ungauged basins (PUB) initiative, where ungauged basins are described as “one with inadequate records (in terms of both data quantity and quality) of hydrological observations to enable computation of hydrological variables of interest at the appropriate spatial and temporal scales, and to the accuracy acceptable for practical applications” [12]. Despite decades of research, hydrologic behavior in ungauged basins is still often misunderstood or misrepresented in model applications [13]. This is largely because there is an incomplete process understanding of the multi-scale spatial-temporal heterogeneities across different landscapes and climates [14].
From an operational standpoint, distributed models provide an opportunity to expand the information available in forecasts, including streamflow at interior locations, uncertainty assessment, and soil moisture conditions [10,11,15,16]. Fang et al. [17] showed that the use of appropriately structured flexible, distributed models with a-priori estimation from on-site measurements could produce robust estimations of snowpack, soil moisture, and streamflow at multiple scales. Another study by Reed et al. [18], as part of the first phase of the Distributed Model Inter-Comparison Project (DMIP), reported that when calibrated to the outlet of larger parent basins, distributed models produced reasonable performance at interior locations where no explicit calibration was conducted. However, when these models were calibrated at the outlet of relatively smaller parent basins, a degradation of the performance at interior locations was observed. They argued that the lack of explicit calibration at interior sites does not fully explain poor model performance at these points.
Given the increasing demands for higher resolution information at scales necessary to support water resources relevant forecasts [14], the Office of Hydrologic Development (OHD) developed the Hydrology Laboratory Research Distributed Hydrologic Model (HL-RDHM) [1,2]. The HL-RDHM uses the spatially distributed version of the Sacramento Soil Moisture Accounting model (SAC-SMA) [19] and supports investigations such as forecasting at an increased number of locations (interior points), improving flash flood information, and utilizing a framework to test new spatially distributed products [20]. While distributed models can represent the spatial variability of watershed response in a more realistic manner than the traditional lumped modeling, it is also necessary to properly account for the spatial variability of precipitation to accurately characterize the hydrologic response [21,22]. In this study, we aim (1) to quantify how the accuracy of simulated discharge changes with basin scale for a distributed model calibrated only to the outlet, and (2) to characterize the impact of the spatial resolution of precipitation inputs on the accuracy of simulated streamflow across basin scales. Both these objectives further the understanding of modeling and forecasting for small ungauged basins.
Using the HL-RDHM framework, we tested two precipitation products with varying spatial resolutions, the North American Land Data Assimilation System Phase 2 (NLDAS-2) with a nominal 12.5 km resolution and the Stage IV quantitative precipitation estimate with an approximate 4 km resolution, as hydrologic model input. Discharge simulations were conducted for three watersheds in the North-Central United States for the evaluation period 2003–2016. The model was calibrated with observed discharge from each watershed outlet, defined as the location of a United States Geological Survey (USGS) gage. Interior locations were left uncalibrated and used to evaluate model performance and predictive uncertainty for interior ungauged basins.
2. Materials and Methods
2.1. Hydrologic Model
The HL-RDHM is a spatially distributed hydrologic model that includes a rainfall-runoff model (the Sacramento Soil Moisture Accounting Model; SAC-SMA) (NOAA/NWS, Silver Spring, MD, USA), a snow model (SNOW-17) (NOAA/NWS, Silver Spring, MD, USA), and hillslope watershed and channel routing models to simulate hydrologic processes. We used the modified version of the SAC-SMA, referred to as the SAC-SMA Heat Transfer model (SAC-HT) (NOAA/NWS, Silver Spring, MD, USA), within the HL-RDHM V3.5.1. The SAC-HT incorporates a physically-based frozen ground model [23]. The SAC-HT accounts for storage and flow in the subsurface using a two-layer soil structure. Each zone has free water storages that represent water drained by gravitational forces and tension water storages that represent water removed through evaporation and transpiration. Discharge contributions to the stream occur from both upper and lower zones representing surface runoff, interflow, and baseflow processes. Surface runoff occurs when precipitation exceeds the interflow and percolation capacities and the upper zone tension storage is full [24]. The SNOW-17 is a snow accumulation and ablation model that uses air temperature as an index to determine energy exchange across the snow–air interface [25]. The surface and subsurface flow routing processes are based on hillslope slope, roughness, and drainage density. Water is routed from upstream to downstream cells by using a cell-to-cell connectivity file. The connectivity sequence was developed by the OHD and defined using surface flow directions derived from a digital elevation model (DEM). Inputs to the model are precipitation, temperature, and potential evapotranspiration (PET). PET is commonly input as daily values that are uniformly interpolated into the specified model time step.
The spatial resolution of the HL-RDHM is based on the Next Generation Weather Radar (NEXRAD) Hydrologic Rainfall Analysis Project (HRAP) grid coordinate system [1,8]. The HRAP coordinate system is a polar stereographic projection at a nominal grid spacing of 4 km × 4 km, or 1 HRAP pixel; however true pixel size varies with latitude [26]. Model simulations were run at an hourly time step and at the default 1 HRAP spatial resolution with a yearlong initialization period (2002) to allow model states to equilibrate.
2.2. Study Area
Three basins in the north central United States, one basin in Iowa and two basins in Minnesota (Figure 1), were selected for study based on discharge data availability at and upstream of the basin outlet. All watersheds are within the Upper Mississippi River basin and are forecast points of the National Weather Service (NWS) North Central River Forecast Center (NCRFC) in Chanhassen, MN. The drainage area of the basins range from 542 km2 to 3493 km2 (Table 1, Table 2 and Table 3). Each basin is partitioned into 5–8 subbasins (Figure 1) depending on the location of available upstream data. The subbasins, or interior locations, range in size from 19 km2 to 2429 km2 (Table 1, Table 2 and Table 3).
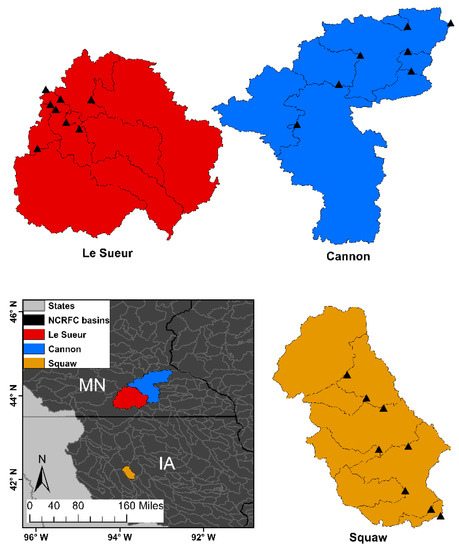
Figure 1.
Study basins with outlets of the main watershed and subbasins denoted by a black triangle. Inset shows the location of the study basins relative to one another.

Table 1.
Squaw Creek basin and subbasins gage sites. The outlet of Squaw Creek watershed, denoted with “*”, has United States Geological Survey station ID 05470500 and US National Weather Service ID AMWI4.

Table 2.
Le Sueur River basin and subbasins gage sites. The outlet of Le Sueur River watershed, denoted with “*”, has United States Geological Survey station ID 05320500 and US National Weather Service ID RPDM5.

Table 3.
Cannon River basin and subbasins gage sites. Outlet of the Cannon River watershed, denoted with “*”, has United States Geological Survey station ID 05355200 and US National Weather Service ID WLCM5.
The study area has topographic relief of less than 200 m of total elevation change [27]. The landscape surrounding the Squaw and Le Sueur basins, located in Iowa and Southern Minnesota, is dominated by agriculture with large areas of row crops such as corn and soybeans. This agricultural land is typically made up of the nutrient-rich Mollisol soil order defined by the United States Department of Agriculture soil taxonomy. Land use in South-Eastern Minnesota, the location of the Cannon River basin, is predominantly agriculture or forestland. Based on the Natural Resources Conservation Service Soil Survey Geographic (SSURGO) database, soils in the Cannon River basin are a combination of both mollisols and alfisols; the alfisols soil group is a clay-enriched subsurface region most commonly found in forested areas. In Iowa and Southern Minnesota, artificial drainage networks are commonly used to drain soils and lower the water table to promote crop growth. Field monitoring studies have suggested that drainage from tiles increases annual baseflow in streams [28,29]. Tile drainage is not explicitly included in the utilized model.
Each study basin experiences similar climatic conditions, and depending on the time of year, is subject to various meteorological extremes. In summer months, convective thunderstorms are common due to moisture transported from the Gulf of Mexico. These convective systems account for most of the annual precipitation for the study area, occurring from early spring into late summer. Annual precipitation amounts averaged over 12 years ranges from 773 mm in southern Minnesota (45° N) to 950 mm in central Iowa (42° N) (Table 4). Conversely, winters are cool and drier with precipitation commonly occurring in the form of snow.

Table 4.
Average annual precipitation totals (mm) for 2002–2013 period from the North Central River Forecast Center (NCRFC) mean areal precipitation (MAP) data, NLDAS-2, and Stage IV; precipitation adjustment factors (Adj Factor) for NLDAS-2 and Stage IV; and average annual precipitation for NLDAS-2 and Stage IV after the adjustment factor was applied.
2.3. Discharge Data
Hourly and daily discharge data for the basin outlets were obtained from the USGS (Table 1, Table 2 and Table 3). Discharge observations at upstream sites within the Minnesota basins were available from the Minnesota Department of Natural Resources (MN DNR) Stream Hydrology Unit [30]. The MN DNR collects and quality controls discharge data following the USGS protocols. Data for upstream sites in the Squaw Creek were collected by the Iowa Flood Center (IFC) [5] using a network of automated stage sensors. These sensors collect and relay stage data to a central database at 15 min intervals. The data are available in near real-time through the Iowa Flood Information System (IFIS) [31]. There were 22 bridge-mounted stage sensors installed in Squaw Creek at the time of this study; a subset of these sites were selected based on data quality and site accessibility.
To convert IFC stage data to discharge, we obtained model-generated rating curves developed by the IFC using site-specific one-dimensional HEC-RAS models built from Iowa statewide LIDAR data, existing cross-sectional survey data, and bridge plans (Ricardo Mantilla, University of Iowa, personal communication, 2 February 2016). Throughout 2015 and 2016, we conducted periodic field measurements to verify and reduce uncertainty in the modeled curves. Between four to eight manual discharge measurements were taken at each upstream location in Squaw Creek. During periods of lower flows, where channel depths were less than 1.5 feet, a wading measurement was conducted using a hand-held FlowTracker, which employs an Acoustic Doppler Velocimeter (ADV). For moderate to high flows, measurements were taken from the bridge using an Acoustic Doppler Current Profiler (ADCP). A measurement transect was completed by navigating the boat in a straight line normal to the direction of flow, while the ADCP collects depth, distance, and velocity data. A minimum of four transects were made to ensure the average difference of the discharge from each transect was less than 6%. Manual discharge measurements were added to modeled rating curves and a polynomial equation was applied to fit a curve through both modeled and measured points along the curve.
2.4. Model Inputs
PET data were obtained from the OHD and consisted of long-term average PET at the HRAP resolution. The PET values represent mid-month values from which daily values are linearly interpolated. PE adjustment factors for each month account for the seasonal variability in vegetation through the course of a year [20].
Hourly air temperature (at 2-m) and precipitation from the NLDAS-2 were used. These data are derived using the National Center for Environmental Protection’s (NCEP) Eta-model-based Data Assimilation System (EDAS) [32]. The NLDAS-2 [33] hourly precipitation product is created by NCEP through merger of satellite, radar, and observation-based data and generated at a 1/8th degree (~12.5 km) spatial resolution [34]. In this study, the geographic coordinates of each 1/8th degree pixel were converted to the HRAP coordinate system and disaggregated into a 4-km resolution for input into the HL-RDHM. NLDAS-2 precipitation grids are available from 1996 to present.
Given the focus on localized, summer rainfall events, we included a second analysis using the NCEP Stage IV product, which has a higher spatial resolution than the NLDAS-2. Stage IV is a mosaic of the multi-sensor hourly/6-hourly Stage III analyses produced by the 12 RFCs in the continental United States (CONUS) via manual quality control performed on the Stage III data. Stage IV has a spatial resolution of 16 km2 and is a combination of ground-based gage observations and radar calculated reflectivity. The hydrological and meteorological communities commonly use this product as a reference for gridded rainfall estimates due to its national coverage and high spatial and temporal resolutions [35,36]. Hourly Stage IV data is available at HRAP resolution from 2002 to present.
Initial model simulations indicated discharge tended to be underestimated with both precipitation inputs. Studies have indicated a low bias in the NLDAS-2 derived precipitation product, depending on the region [33,37]. Similarly, Prat and Nelson [38] determined that Stage IV exhibits a considerable low bias in comparison with surface observations on a seasonal scale, with differences ranging from −18% to −2% for winter and from −28% to 8% for summer. In our analysis, we found that the NLDAS-2 and Stage IV inputs were consistently lower than the mean areal precipitation (MAP) data provided by the NCRFC (our ground-truth) for each study basin. To correct for the low bias, a precipitation adjustment factor was developed by calculating the average difference between the individual precipitation product (NLDAS-2 and Stage IV) and the MAP data from 2002 to 2013 (Table 4) following an approach used in Spies et al. [27]. This precipitation adjustment factor can be defined within HL-RDHM and is applied to each HRAP pixel in the specified basin.
2.5. Model Calibration and Validation
There are 16 parameters in the HL-RDHM used to reflect basin characteristics and parameter values can vary by grid. Default a-priori parameter grids [8] were used as an initial starting point for parameter calibration for each basin. To improve calibration efficiency, basin-scale parameter multipliers, rather than the parameters in each grid, were calibrated and applied to the a-priori parameter grids. This method greatly reduces the number of parameters needed in the calibration process, while maintain the spatial information provided by the a-priori parameters [20]. Prior studies show that this technique is an effective way of improving a-priori model parameter grids [1,27,39].
The parameter multipliers were calibrated using an automated Stepwise Line Search (SLS) procedure [20]. The SLS technique successively steps through each parameter to optimize the multi-scale objective function for each parameter. If values remain static for three consecutive loops, the parameter multiplier is removed from further manipulation. Ten parameters were selected for calibration with multiplier ranges based on previous studies [27,40,41,42,43,44,45]. Identifying the maximum and minimum multipliers for each parameter was done using the following method [27]:
where xmin and xmax represent the minimum and maximum multipliers, pmin and pmax are the minimum and maximum values for the parameter, and α indicating the mean basin a-priori parameter value.
The model was calibrated for each precipitation input (NLDAS-2 and Stage IV) separately and using observed discharge at the outlet as the calibration criteria. To assess the accuracy of the model for simulating discharge at interior points that may be ungauged, no calibration was done using data from interior locations. The data set spans 2002–2016 for which we have a continuous record of input data. The calibration (2003–2009) and validation (2010–2016) period used a one year initialization period (2002) to allow model states to equilibrate. The calibration period contained both very wet and dry periods.
To capture the flashy response times of the small upstream basins, it was necessary to run the HL-RDHM at an hourly time step, requiring the use of hourly discharge aggregated from the instantaneous data. To verify the suitability of the hourly USGS discharge data for this study, we calibrated the HL-RDHM parameters to both hourly (real-time) and daily (quality controlled) observed discharge in two separate trials for each site, using both precipitation inputs. Time periods with missing hourly data (occurring for winter months due to icing), were omitted from the calibration process. Overall, the differences in model evaluation scores (defined in Section 2.6) were minor; calibration to hourly data produced higher NSE scores while the calibration to daily data produced better Pbias scores. Given the minimal differences between using hourly and daily discharge data for calibration, study results will focus on the hourly simulations.
2.6. Evaluation Statistics
Four statistical metrics were used to evaluate simulated discharge: Percent Bias (Pbias), coefficient of determination (R2), Nash–Sutcliffe efficiency (NSE), and mean absolute percent deviation (MAPD) are shown below.
Pbias measures the relative tendency of simulated flows to be larger or smaller than observed counterparts. Positive values indicate overestimation, negative values indicate underestimation, and the optimal value is zero. NSE measures the relative magnitude of the residual variance compared to the measured data variance. Values range from −∞ to 1.0, with 1.0 being the optimal value where model simulation match observed discharge. MAPD is the mean absolute error as a percentage of the deviation from observed.
Model evaluation criteria established by Moriasi et al. [46] define a model simulation as “satisfactory” if NSE > 0.50 and Pbias ±25% for streamflow simulations with a monthly timestep. Given that models exhibit poorer performance when evaluated at shorter time steps [47], we used an NSE > 0.40 threshold to identify a result as acceptable for an individual basin at the hourly timestep. R2, Pbias, and MAPD are percent error metrics and are suitable for comparing across different data sets [48], they are used evaluated how model error changes across basin scales.
3. Results
3.1. Model Performance with NLDAS-2 Precipitation
Model performance measures indicated that the HL-RDHM reproduced the observed hourly flows at each outlet with reasonably low Pbias and good correlation (Table 5). MAPD values for the calibration ranged from 37.6% to 57.2%. Statistics tended to be poorer for the validation periods compared to the calibration period, for example, NSE scores at basin outlets ranged from 0.57 to 0.75 for the calibration period and from 0.50 to 0.67 for the validation period. Pbias was lowest for AMWI4 and WLCM4. Pbias scores indicated that discharge for RPDM5 was overestimated for the calibration period, which could be a result of the overestimated baseflow in the RPDM5 (Figure 2). Several larger events (one in 2010 and a few in 2015) were observed to be underestimated and likely resulted in the switch to a negative Pbias for RPDM5 during the validation period. In general, simulated hydrographs at basin outlets generally matched the observed discharge for low and intermediate flows, while high flows were often underestimated in the both calibration and validation periods (Figure 2). Event timing was simulated relatively accurately although the simulated peak was delayed in a few events.

Table 5.
Percent bias (Pbias), coefficient of determination (R2), Nash-Sutcliffe efficiency (NSE) and mean absolute percent deviation (MAPD) for the calibration (cal) and validation (val) period for model runs using NLDAS-2 forcing. * Denotes basin outlet.
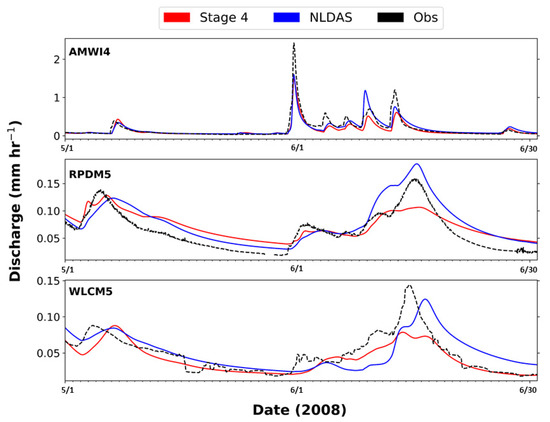
Figure 2.
Simulated vs. observed discharge hydrographs for basin outlets for March–September 2008, which is during the calibration period.
R2 and NSE scores were highest for the basin outlet and generally decreased from downstream to upstream points for AMWI4 and RPDM5 (Table 5). There were four upstream sites with unsatisfactory NSE scores in the calibration period (as defined in Section 2.6): LICOBB, CAMORR, LCANNO, and CASOGN. These sites were among the smallest subbasins, representing less than 17% of the area of the watershed (Table 2; Table 3). PINECR also had an unsatisfactory NSE score, but only had one year of available data for the validation period, making it difficult to formulate conclusions. NSE values were above the acceptable threshold level for most downstream points, with basins sizes of 224 km2 (SQ4), 807 km2 (BIGCOB), and 588 km2 (CAMORR) having NSE above 0.40 in the verification period. MAPD values for these subbasin locations were 27.5% (SQ4), 61.9% (BIGCOB), and 49.3% (CAMORR). These basins represent 40%, 28%, and 17% of the total basin area for the Squaw, LeSueur, and Cannon watersheds, respectively. Results for Pbias were varied, with only AMWI4 showing a consistent trend of increasingly poorer performance from downstream to upstream (Table 5).
There was a general trend of decreasing MAPD with basin area (Figure 3) across all watersheds, and in particular for the LeSueur and Cannon watersheds. The smallest subbasins in each watershed studied had distinctly poorer MAPD than the parent basin; these represent 10%, 7%, and 5% of the total watershed area for the Cannon, LeSueur, and Squaw watersheds, respectively (Figure 3). Two smaller basins within the Squaw Creek watershed (Prairie and Onion) showed relatively small MAPD and were outliers in this general correlation of improved MAPD with larger basin size. However, Prairie and Onion had Pbias values greater than 40%, which was among the worst across all watersheds (Table 5) and above the ±25% acceptable threshold set by Moriasi et al. [46]. The outlet of Squaw (AMWI4) also had a higher MAPD than several of the subbasins; however, this site had the best R2 and low Pbias (Table 5).
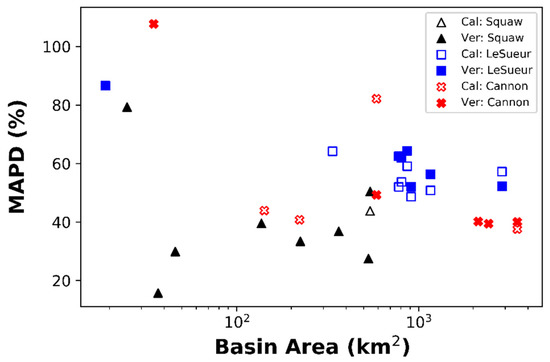
Figure 3.
Mean absolute percent deviation (MAPD) versus basin area (plotted on a log scale) for all watersheds and subwatersheds for the calibration (Cal) and verification (Ver) periods for simulated discharge produced from NLDAS-2 inputs.
3.2. Model Performances with Stage IV Precipitation
Simulations using the higher resolution Stage IV precipitation product showed more variability in statistical results compared to the NLDAS-2 data, with NSE values from the calibration period ranging from −2.8 to 0.77 and from −0.78 to 0.67 for validation (Table 6). NSE scores for basin outlets met the acceptable threshold of 0.4 for the calibration period. For the verification period, only WLCM5 and RPDM5 had NSE values above the 0.40 threshold and only three subbasins passed this threshold (Table 6). Discharge was commonly overestimated during the calibration period and underestimated during the validation period.

Table 6.
Percent bias (Pbias), coefficient of determination (R2), Nash-Sutcliffe efficiency (NSE) and mean absolute percent deviation (MAPD) for the calibration (cal) and validation (val) period for model runs using Stage IV forcing. * Denotes basin outlet.
Similar to the NLDAS-2 driven simulations, statistics generally improved from small to larger basin areas. Although, MAPD from the Stage IV simulations were less correlated to the basin area (Figure 4) compared to NLDAS-2 simulations, for individual watersheds there was a trend towards smaller MAPD with increased basin size (Figure 4, Table 6). The smallest subbasins again performed the worst. Overall, MAPD scores were slightly larger for the Stage IV simulations, particularly for the LeSueur basin.
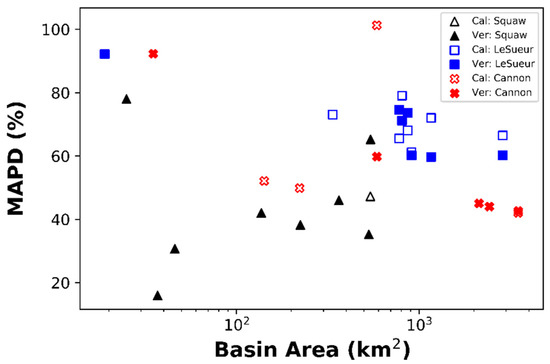
Figure 4.
Mean absolute percent deviation (MAPD) versus basin area (plotted on a log scale) for all watersheds and subwatersheds for the calibration (Cal) and verification (Ver) periods for simulated discharge produced from Stage IV inputs.
3.3. Comparison of NLDAS-2 and Stage IV Simulations
The summary statistics indicated that the HL-RDHM model performance was better for discharge simulations using the NLDAS-2 precipitation product compared to the Stage IV precipitation. MAPD was lower for the NLDAS-2 simulations for both the calibration and verification period for all but two of the smallest subbasins (one in Cannon and one in Squaw) (Table 5; Table 6). Overall, there was no clear pattern with respect to which precipitation data produced the best model performance for various basin scales. However, there was a moderately strong inverse correlation between the average annual precipitation intensity of the Stage IV data and NSE (Figure 5). Although, the HL-RDHM simulations tended to have the lowest NSE scores in years with the highest average intensities for Stage IV input, there is considerable scatter, and therefore uncertainty, in this result. NSE scores are more consistent across precipitation regimes for the NLDAS-2 simulations with no correlation to annual precipitation intensity.
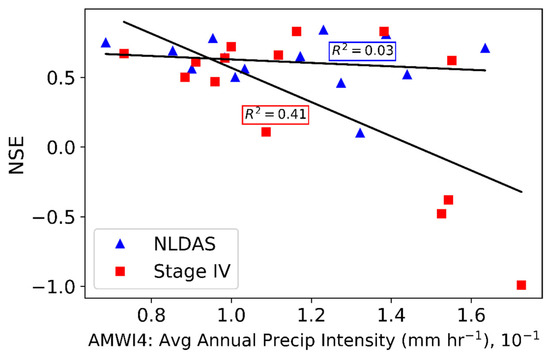
Figure 5.
Average Nash-Sutcliffe efficiency (NSE) values as a function of average precipitation intensity for NLDAS and Stage IV for the period of 2003–2016. NSE; IV; R2.
Analysis of simulated hydrographs revealed that Stage IV simulations tended to produce higher peaks, and often overestimated small events. Hydrographs from Squaw Creek April–July 2014 are given as a typical example (Figure 6). Stage IV data often resulted in over-estimated discharge peaks, with larger errors in the spring months as illustrated by simulations for April (Figure 6). In contrast, NLDAS-2 produced a better match to observations during this April period.
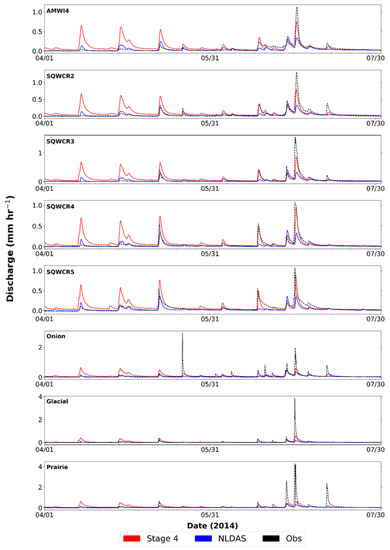
Figure 6.
Simulated and observed discharge for the Squaw Creek watershed for the period of 1 April 2014 to 31 July 2014. SQWCR.
During the wet warm season of May and June, model results alternated between periods of good and poor agreement between the two data sets. Commonly, we observed that the higher intensities of the Stage IV data led to larger peak discharges in late spring and often better simulated peaks when compared to NLDAS-2. In the example shown in Figure 5, the Stage IV produced much higher and more accurate peaks, than NLDAS-2 during June.
The larger, flashy events in the smaller watersheds tended to be underestimated in simulations from both data sets (e.g., Figure 6 Onion, Glacial, and Prairie). This under-simulation explains the negative Pbias scores and low NSE scores reported for the smallest watersheds (Table 5; Table 6). Simulated hydrographs for the smallest subwatersheds commonly showed little event response as seen for Glacial and Prairie subwatersheds (Figure 6); this was also observed in LBEAUF in the LeSueur River basin.
4. Discussion
The simulation results for each basin outlet and corresponding upstream location indicated that model efficiencies increase with increasing basin size. Based on our findings, we infer that the HL-RDHM model can produce satisfactory streamflow estimates for basins down to ~250 km2. Below this threshold, model skill became less consistent and more variable, especially for basins less than 50 km2. We found NSE values to be below the acceptable threshold for subbasins that represented less than 20–40% of the total watershed area. The NSE <0.40 threshold generally corresponded to Pbias value >±30%, R2 value <0.30, and MAPD values >30%.
The scale effect can be explained by a simpler rainfall–runoff relationship in larger basins as these larger systems integrate many of the complexities seen at small scales, thus creating better modeling conditions for larger basins [49]. At the smallest scales studied, both model calibration and the resolution of the input data can become problematic [50]. We calibrated only using information at the basin outlet and the decreased model skill with upstream sites may be associated with the calibration results being unable to reflect the various physical and hydrologic characteristics of subbasins, especially when estimating high flows in smaller subbasins [51].
Spies et al. [27] suggested that the HL-RDHM (specifically the SAC-HT) may not be able to capture the full range of hydrologic conditions experienced by watersheds in this region. For this same study area, they found that model performance was better during the wetter months of spring when watershed response was faster, whereas performance was poorer in the drier late summer when watershed response was damped due to lower soil moisture and higher surface roughness from extensive row crop vegetation cover. Spies et al. [27] noted that the model was limited in its ability to represent the watershed consistently well across all time periods; in this study we find the model is also unable to represent watersheds consistently well at all spatial scales tested. In both studies, a single set of parameters was identified for each watershed. Parameters that are varied in time and space may improve model performance in this region.
The use of the 4 km resolution of the HRAP cell network may be another source of model error. It is plausible that the watershed area specified in the connectivity file (used for routing) could be significantly different from the USGS estimate, 10% or more in some cases [52]. This issue is more common in basins less than 1000 km2 because basin boundaries cannot be precisely captured by the coarse resolution grid [20]. This is a significant challenge for small basins where the confluence of multiple streams could be occurring within a single cell.
Basin characteristics, such as basin slope, may also play a role in the accuracy of the simulations. Spies et al. [27] found that the HL-RDHM performed the worst in basins characterized by relatively flat topography (<1.0% average slope) for this same general study area. However, differences in the average slopes for the basins studied here vary less than 1–2%. In basins with low slopes and poorly drained soils, agricultural tiles the presence of subsurface tile drainage adds to the uncertainty of simulations because they were not explicitly represented in the model.
Overall, model statistics were better when using the NLDAS-2 product rather than Stage IV. Our conclusions surrounding these two precipitation products are similar to Wu et al. [53], who determined that out of nine Quantitative Precipitation Estimate (QPE) products, including Stage IV, model skill was highest for simulations forced with NLDAS-2 precipitation. Wu et al. [53], who also studied basins in Eastern Iowa but with a much larger drainage area (ranging from 2816 km2 to 32,381 km2), determined that when using NLDAS-2 precipitation to force model simulations, model performance tends to increase for downstream basins.
The importance of the spatial representation of precipitation likely increases with decreasing basin size, particularly when simulating discharge at the smallest scales. Smaller basins have less capacity to dampen out inputs and corresponding input errors, therefore, small-scale variability and bias in precipitation inputs has the potential to cause greater errors in simulated streamflow for small basins [18,54]. Faurès et al. [55] demonstrated that even for very small basins less than 1 km2 subject to convective events, precipitation variability must be considered. However, Brath et al. [56] investigated a basin in north central Italy with a drainage area 1050 km2, which is considered “mid-sized” relative to watersheds used in our study, and suggested that the spatial representation of rainfall was not important to the streamflow response at the outlet.
Stage IV is often regarded as the reference or ground-truth in Quantitative Precipitation Estimate (QPE) [57]. However, Chen et al. [57] concluded that Stage IV hourly data underestimated roughly 10% of precipitation volume in the NCRFC region. A primary reason for this is the limited sensitivity of the radar to frozen precipitation, resulting in underrepresented precipitation across the United States. As temperatures fall below freezing or a temperature inversion occurs, the effective range of the WSR-88D radar used to generate Stage IV data decreases, decreasing the likelihood of accurately retrieving frozen precipitation. In Iowa, many of these events may be viewed as insignificant because light or frozen precipitation do not generally result in flooding events. However, these precipitation types can be frequent enough to influence local water budgets and affect soil moisture [57], which in turn influence the accuracy of simulated low flow discharges and initial soil moisture conditions leading into larger events in the spring and summer. Precipitation either missed or underrepresented during the winter months may have affected the calculated precipitation adjustment factor, which is used to improve the water budget of the model. The adjustment factor was created using analysis of precipitation throughout the year. If the accuracy of the precipitation data varied by season, for example underrepresented winter precipitation but accurate summer precipitation, the adjustment factor may have been larger than necessary to account for the erroneously low precipitation in the cold months. This could negatively affect discharge simulations by increasing the intensity of summer events and lead to overestimation of high flows. We could have further manipulated the adjustment factor to improve results for Stage IV simulations, but to remain consistent in our approach we chose to adjust the Stage IV input the same way as the NLDAS-2.
The accuracy of the discharge data at non-USGS sites may also be influencing results, and for the Squaw Creek basin in particular. Mantilla and Krajewski [58] state that the accuracy of the LiDAR derived cross-section used to create the modeled rating curves is not optimal, a primary reason for not including them in routine forecasts. We had few manual measurements with which to validate the rating curve for larger flows in the Squaw Creek. Due to the time period during which measurements were taken and the short time to peak in the small basins (<6 h), observations are limited to flows in the intermediate range for larger subbasins and sub-intermediate flows for small basins. Thus, discharge estimates for high stage observations likely are the most uncertain.
5. Conclusions
While distributed models are capable of producing simulations at interior points, data limitations make understanding how well the model perform at a range of spatial scales challenging. The objective of the current study was to investigate how the accuracy of a spatially distributed model, when calibrated only to the basin outlet, changes with respect to basin size to gain insight into forecasting in small, likely ungauged, basins. The ability of the HL-RDHM to produce NSE values above 0.4 for several upstream locations indicates the potential for using this distributed model to simulate discharge at interior basins, when only calibrating the model to the basin outlet. However, for the NLDAS-2 precipitation product, the skill of the model decreased for subbasins less than 250 km2, this represents 20–40% of the total basin area depending on the watershed. For basins smaller than 250 km2, the relationship of model skill to basin area becomes less predictable. These basin size thresholds were larger when using the Stage IV, and average model performance was poorer when using Stage IV precipitation.
In the cases shown, the coarser resolution NLDAS-2 product performed better overall, although for some mid-summer events the finer resolution Stage IV produced more accurate hydrographs. This study corroborates others illustrating that inputs with higher spatial and/or temporal resolution may not necessarily result in more accurate simulations of hydrologic variables [39,54,59,60], including subbasin streamflow. The continued improvement of spatially distributed inputs, calibration approaches, and model structures will increase the potential for using a spatially distributed model to advance current emergency management and decision-support services. Application of distributed models at finer watershed scales should be a continued focus of model development research.
Author Contributions
Conceptualization, T.M. and K.F.; methodology, T.M., K.F. and T.H.; software, T.M.; formal analysis, T.M.; investigation, T.M. and K.F.; data curation, T.M.; writing—original draft preparation, T.M.; writing—review and editing, T.M., K.F., T.H.; visualization, T.M. and K.F.; supervision, K.F.; project administration, K.F. and T.H.; resources, K.F.; funding acquisition, K.F. and T.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by NASA ROSES Grant (NNX15AB28G). Partial support was also provided by NOAA CSTAR Award (NA17NWS4680005).
Acknowledgments
Special thanks to Mike DeWeese and staff at the US National Weather Service North Central River Forecast Center with model assistance and data acquisition. Also thanks to Ricardo Mantilla of the Iowa Flood Center and University of Iowa for providing rating curves for stream gages in the Squaw Creek and Skunk River in Iowa.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Koren, V.; Reed, S.; Smith, M.; Zhang, Z.; Seo, D.-J. Hydrology laboratory research modeling system (HL-RMS) of the US national weather service. J. Hydrol. 2004, 291, 297–318. [Google Scholar]
- Koren, V.; Smith, M.; Cui, Z.; Cosgrove, B.; Werner, K.; Zamora, R. Modification of Sacramento Soil Moisture Accounting Heat Transfer Component (SAC-HT) for Enhanced Evapotranspiration. NOAA Tech. Rep. NWS 53; U.S. Dep. Commer. NOAA/NWS: Silver Spring, MD, USA, 2010; 72p.
- Alfieri, L.; Burek, P.; Dutra, E.; Krzeminski, B.; Muraro, D.; Thielen, J.; Pappenberger, F. GloFAS–Global Ensemble Streamflow Forecasting and Flood Early Warning GloFAS–global ensemble streamflow forecasting and flood early warning. Hydrol. Earth Syst. Sci. 2013, 17, 1161–1175. [Google Scholar] [CrossRef]
- Yucel, I.; Onen, A.; Yilmaz, K.K.; Gochis, D.J. Calibration and evaluation of a flood forecasting system: Utility of numerical weather prediction model, data assimilation and satellite-based rainfall. J. Hydrol. 2015, 523, 49–66. [Google Scholar]
- Krajewski, W.F.; Ceynar, D.; Demir, I.; GosKa, R.; Kruger, A.; Langel, C.; Mantilla, R.; Niemeier, J.; Quintero, F.; Seo, B.-C.; et al. Real-time flood forecasting and information system for the state of Iowa. Bull. Am. Meteorol. Soc. 2017, 98, 539–554. [Google Scholar] [CrossRef]
- Salas, F.R.; Somos-valenzuela, M.A.; Dugger, A.; Maidment, D.R.; Gochis, D.J.; David, H.; Yu, W.; Ding, D.; Clark, E.P.; Noman, N. Towards real-time continental scale streamflow simulation in continuous and discrete space. JAWRA J. Am. Water Resour. Assoc. 2018, 54, 7–27. [Google Scholar]
- Beven, K. How far can we go in distributed hydrological modelling? Hydrol. Earth Syst. Sci. 2001, 5, 1–12. [Google Scholar] [CrossRef]
- Koren, V.; Smith, M.; Duan, Q. Use of a Priori parameter estimates in the derivation of spatially consistent parameter sets of rainfall-runoff models. In Calibration of Watershed Models; Duan, Q., Gupta, H.V., Sorooshian, S., Rousseau, A.N., Turcotte, R., Eds.; American Geophysical Union: Washington, DC, USA, 2003; pp. 239–254. [Google Scholar]
- Blöschl, G.; Reszler, C.; Komma, J. A spatially distributed flash flood forecasting model. Environ. Model. Softw. 2008, 23, 464–478. [Google Scholar] [CrossRef]
- Hapuarachchi, H.A.P.; Wang, Q.J.; Pagano, T.C. A review of advances in flash flood forecasting. Hydrol. Process. 2011, 25, 2771–2784. [Google Scholar]
- Fatichi, S.; Vivoni, E.R.; Ogden, F.L.; Ivanov, V.Y.; Mirus, B.; Gochis, D.; Downer, C.W.; Camporese, M.; Davison, J.H.; Ebel, B.; et al. An overview of current applications, challenges, and future trends in distributed process-based models in hydrology. J. Hydrol. 2016, 537, 45–60. [Google Scholar]
- Sivapalan, M. Prediction in ungauged basins: A grand challenge for theoretical hydrology. Hydrol. Process. 2003, 17, 3163–3170. [Google Scholar]
- Hrachowitz, M.; Savenije, H.H.G.; Blöschl, G.; McDonnell, J.J.; Sivapalan, M.; Pomeroy, J.W.; Arheimer, B.; Blume, T.; Clark, M.P.; Ehret, U.; et al. A decade of Predictions in Ungauged Basins (PUB)–A review. Hydrol. Sci. J. 2013, 58, 1198–1255. [Google Scholar]
- National Research Council. Challenges and Opportunities in the Hydrologic Sciences; The National Academies Press: Washington, DC, USA, 2012; 200p. [Google Scholar]
- Khakbaz, B.; Imam, B.; Sorooshian, S.; Koren, V.I.; Cui, Z.; Smith, M.B.; Restrepo, P. Modification of the National Weather Service Distributed Hydrologic Model for subsurface water exchanges between grids. Water Resour. Res. 2011, 47, 1–17. [Google Scholar]
- Kauffeldt, A.; Wetterhall, F.; Pappenberger, F.; Salamon, P.; Thielen, J. Technical review of large-scale hydrological models for implementation in operational flood forecasting schemes on continental level. Environ. Model. Softw. 2016, 75, 68–76. [Google Scholar] [CrossRef]
- Fang, X.; Pomeroy, J.W.; Ellis, C.R.; Macdonald, M.K.; Debeer, C.M.; Brown, T. Multi-variable evaluation of hydrological model predictions for a headwater basin in the Canadian Rocky Mountains. Hydrol. Earth Syst. Sci. 2013, 17, 1635–1659. [Google Scholar]
- Reed, S.; Koren, V.; Smith, M.; Zhang, Z.; Moreda, F.; Seo, D.-J.; DMIP Participants. Overall distributed model intercomparison project results. J. Hydrol. 2004, 298, 27–60. [Google Scholar] [CrossRef]
- Burnash, R.J.C.; Ferral, L.; McGuire, R.A. A Generalized Streamflow Simulation System: Conceptual Models for Digital Computers, Technical Report; Joint Federal and State River Forecast Center: Sacramento, CA, USA, 1973; 204p.
- NWS. Hydrology Laboratory-Research Distributed Hydrologic Model (HL-RDHM) User Manual V.3.5.0; U.S. Dep. Commer. NOAA/NWS: Silver Spring, MD, USA, 2016; 147p.
- Smith, M.B.; Koren, V.I.; Zhang, Z.; Reed, S.M.; Pan, J.-J.; Moreda, F. Runoff response to spatial variability in precipitation: An analysis of observed data. J. Hydrol. 2004, 298, 267–286. [Google Scholar]
- Kavetski, D.; Kuczera, G.; Franks, S.W. Bayesian analysis of input uncertainty in hydrological modeling: 1. Theory. Water Resour. Res. 2006, 42, W03407. [Google Scholar] [CrossRef]
- Koren, V.; Smith, M.; Cui, Z. Physically-based modifications to the Sacramento Soil Moisture Accounting model. Part A: Modeling the effects of frozen ground on the runoff generation process. J. Hydrol. 2014, 519, 3475–3491. [Google Scholar]
- Burnash, R.J.C. The NWS River Forecast System-Catchment Modeling. In Computer Models of Watershed Hydrology; Singh, V., Ed.; Water Resources Publication: Colorado, CO, USA, 1995; pp. 311–366. [Google Scholar]
- Anderson, E. Snow Accumulation and Ablation Model–SNOW-17. In NWSRFS User Documentation; Office of Hydrology, NOAA/NWS: Silver Spring, MD, USA, 2006; p. 44. [Google Scholar]
- Reed, S.M.; Maidment, D.R. Coordinate Transformations for using NEXRAD data in GIS-based hydrologic modeling. J. Hydrol. Eng. 1999, 4, 174–182. [Google Scholar] [CrossRef]
- Spies, R.R.; Franz, K.J.; Hogue, T.S.; Bowman, A.L. Distributed Hydrologic Modeling Using Satellite-Derived Potential Evapotranspiration. J. Hydrometeorol. 2015, 16, 129–146. [Google Scholar] [CrossRef]
- Schilling, K.E.; Libra, R.D. Increased baseflow in Iowa over the second half of the 20th century. J. Am. Water Resour. Assoc. 2003, 39, 851–860. [Google Scholar]
- Schilling, K.E.; Helmers, M. Effects of subsurface drainage tiles on streamflow in Iowa agricultural watersheds: Exploratory hydrograph analysis. Hydrol. Process. 2008, 4506, 4497–4506. [Google Scholar]
- Minnesota Department of Natural Resources (MDNR). Cooperative Stream Gaging (CSG). Available online: www.dnr.state.mn.us/waters/csg (accessed on 16 June 2016).
- Demir, I.; Krajewski, W.F. Towards an integrated Flood Information System: Centralized data access, analysis, and visualization. Environ. Model. Softw. 2013, 50, 77–84. [Google Scholar]
- Rogers, E.; Deaven, D.G.; DiMego, G.J. The Regional analysis system for the operational “Early” Eta model: Original 80-km configuration and recent changes. Weather Forecast. 1995, 10, 810–825. [Google Scholar]
- Xia, Y.; Mitchell, K.; Ek, M.; Cosgrove, B.; Sheffield, J.; Luo, L.; Alonge, C.; Wei, H.; Meng, J.; Livneh, B.; et al. Continental-scale water and energy flux analysis and validation for North American Land Data Assimilation System project phase 2 (NLDAS-2): 2. Validation of model-simulated streamflow. J. Geophys. Res. Atmos. 2012, 117, D03110. [Google Scholar]
- Mitchell, K.E. The multi-institution North American Land Data Assimilation System (NLDAS): Utilizing multiple GCIP products and partners in a continental distributed hydrological modeling system. J. Geophys. Res. 2004, 109, 1–32. [Google Scholar]
- Wu, H.; Adler, R.F.; Hong, Y.; Tian, Y.; Policelli, F. Evaluation of Global Flood Detection Using Satellite-Based Rainfall and a Hydrologic Model. J. Hydrometeorol. 2012, 13, 1268–1284. [Google Scholar] [CrossRef]
- Seo, D.; Lakhankar, T.; Mejia, J.; Cosgrove, B.; Khanbilvardi, R. Evaluation of operational national weather service gridded flash flood guidance over the Arkansas Red River basin. J. Am. Water Resour. Assoc. 2013, 49, 1296–1307. [Google Scholar]
- Nan, Z.; Wang, S.; Liang, X.; Adams, T.E.; Teng, W.; Liang, Y. Analysis of Spatial Similarities Between NEXRAD and NLDAS Precipitation Data Products. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 371–385. [Google Scholar]
- Prat, O.P.; Nelson, B.R. Evaluation of precipitation estimates over CONUS derived from satellite, radar, and rain gauge data sets at daily to annual scales (2002–2012). Hydrol. Earth Syst. Sci. 2015, 19, 2037–2056. [Google Scholar] [CrossRef]
- Bowman, A.L.; Franz, K.J.; Hogue, T.S. Case studies of a MODIS-based potential evapotranspiration input to the Sacramento Soil Moisture Accounting Model. J. Hydrometeorol. 2016, 18, 151–158. [Google Scholar] [CrossRef]
- Hogue, T.S.; Sorooshian, S.; Gupta, H.; Holz, A.; Braatz, D. A Multistep Automatic Calibration Scheme for River Forecasting Models. J. Hydrometeorol. 2000, 1, 524–542. [Google Scholar]
- Anderson, E. Calibration of Conceptual Hydrologic Models for Use in River Forecasting; U.S. Dep. Commer. NOAA/NWS: Silver Spring, MD, USA, 2002; 300p.
- Ajami, N.K.; Gupta, H.; Wagener, T.; Sorooshian, S. Calibration of a semi-distributed hydrologic model for streamflow estimation along a river system. J. Hydrol. 2004, 298, 112–135. [Google Scholar]
- Tang, Y.; Reed, P.; van Werkhoven, K.; Wagener, T. Advancing the identification and evaluation of distributed rainfall-runoff models using global sensitivity analysis. Water Resour. Res. 2007, 43, 1–14. [Google Scholar] [CrossRef]
- Franz, K.J.; Butcher, P.; Ajami, N.K. Addressing snow model uncertainty for hydrologic prediction. Adv. Water Resour. 2010, 33, 820–832. [Google Scholar] [CrossRef]
- Steffens, K.J.; Franz, K.J. Late 20th-century trends in Iowa watersheds: An investigation of observed and modelled hydrologic storages and fluxes in heavily managed landscapes. Int. J. Climatol. 2012, 32, 1373–1391. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Engel, B.; Storm, D.; White, M.; Arnold, J.; Arabi, M. A hydrologic/water quality model application protocol. J. Am. Water Resour. Assoc. 2007, 43, 1223–1226. [Google Scholar]
- Jackson, E.K.; Roberts, W.; Nelsen, B.; Williams, G.P.; Nelson, E.J.; Ames, D.P. Introductory overview: Error metrics for hydrologic modelling–A review of common practices and an open source library to facilitate use and adoption. Environ. Model. Softw. 2019, 119, 32–48. [Google Scholar] [CrossRef]
- Merz, R.; Parajka, J.; Blöschl, G. Scale effects in conceptual hydrological modeling. Water Resour. Res. 2009, 45, 1–15. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M. Scale issues in hydrological modelling: A review. Hydrol. Process. 1995, 9, 251–290. [Google Scholar] [CrossRef]
- Ricard, S.; Bourdillon, R.; Roussel, D.; Turcotte, R. Global Calibration of Distributed Hydrological Models for Large-Scale Applications. J. Hydrol. Eng. 2013, 18, 719–721. [Google Scholar] [CrossRef]
- Reed, S.M. Deriving flow directions for coarse-resolution (1–4 km) gridded hydrologic modeling. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Wu, H.; Adler, R.F.; Tian, Y.; Gu, G.; Huffman, G.J. Evaluation of Quantitative Precipitation Estimations through Hydrological Modeling in IFloodS River Basins. J. Hydrometeorol. 2017, 18, 529–553. [Google Scholar] [CrossRef]
- Yilmaz, K.K.; Hogue, T.S.; Hsu, K.-L.; Sorooshian, S.; Gupta, H.V.; Wagener, T. Intercomparison of Rain Gauge, Radar, and Satellite-Based Precipitation Estimates with Emphasis on Hydrologic Forecasting. J. Hydrometeorol. 2005, 6, 497–517. [Google Scholar] [CrossRef]
- Faurès, J.M.; Goodrich, D.C.; Woolhiser, D.A.; Sorooshian, S. Impact of small-scale spatial rainfall variability on runoff modeling. J. Hydrol. 1995, 173, 309–326. [Google Scholar] [CrossRef]
- Brath, A.; Montanari, A.; Toth, E. Analysis of the effects of different scenarios of historical data availability on the calibration of a spatially-distributed hydrological model. J. Hydrol. 2004, 291, 232–253. [Google Scholar] [CrossRef]
- Chen, S.; Hong, Y.; Gourley, J.J.; Huffman, G.J.; Tian, Y.; Cao, Q.; Yong, B.; Kirstetter, P.E.; Hu, J.; Hardy, J.; et al. Evaluation of the successive V6 and V7 TRMM multisatellite precipitation analysis over the Continental United States. Water Resour. Res. 2013, 49, 8174–8186. [Google Scholar] [CrossRef]
- Mantilla, R.; Krajewski, W.F. Pilot Project for a Hybrid Road-Flooding Forecasting System on Squaw Creek, Final Report, IHRB Project TR-642; Iowa Flood Center, University of Iowa: Iowa City, IA, USA, 2014; 42p. [Google Scholar]
- Franz, K.J.; Karsten, L.R. Calibration of a distributed snow model using MODIS snow covered area data. J. Hydrol. 2013, 494, 160–175. [Google Scholar] [CrossRef]
- Rajib, M.A.; Merwade, V.; Yu, Z. Multi-objective calibration of a hydrologic model using spatially distributed remotely sensed/in-situ soil moisture. J. Hydrol. 2016, 536, 192–207. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).