Development of Decay in Biofilms under Starvation Conditions—Rethinking of the Biomass Model
Abstract
:1. Introduction
- The quantification of cell-decay rate under starvation conditions;
- To identify and quantify degradation of a “new” COD fraction, made accessible under those conditions;
- To quantify the recovery of the biofilm after starvation.
2. Material and Methods
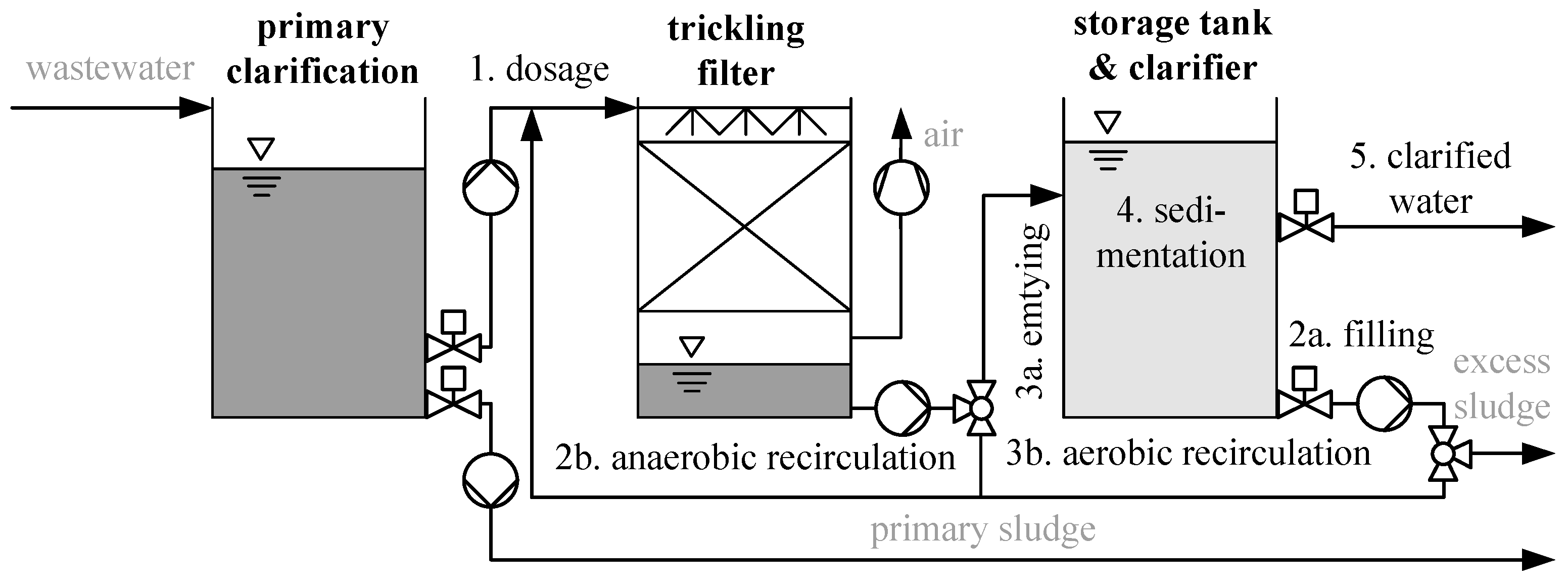
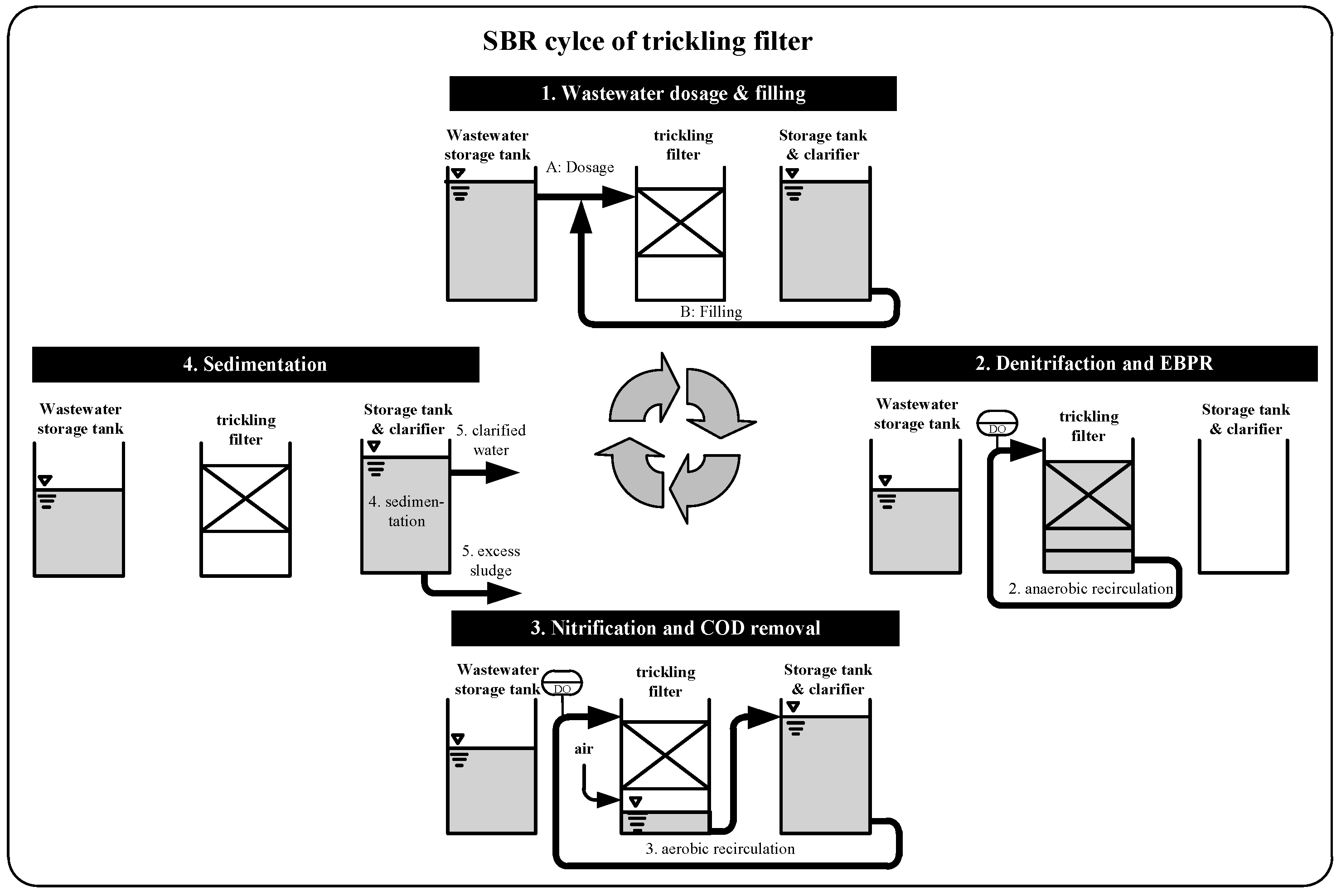
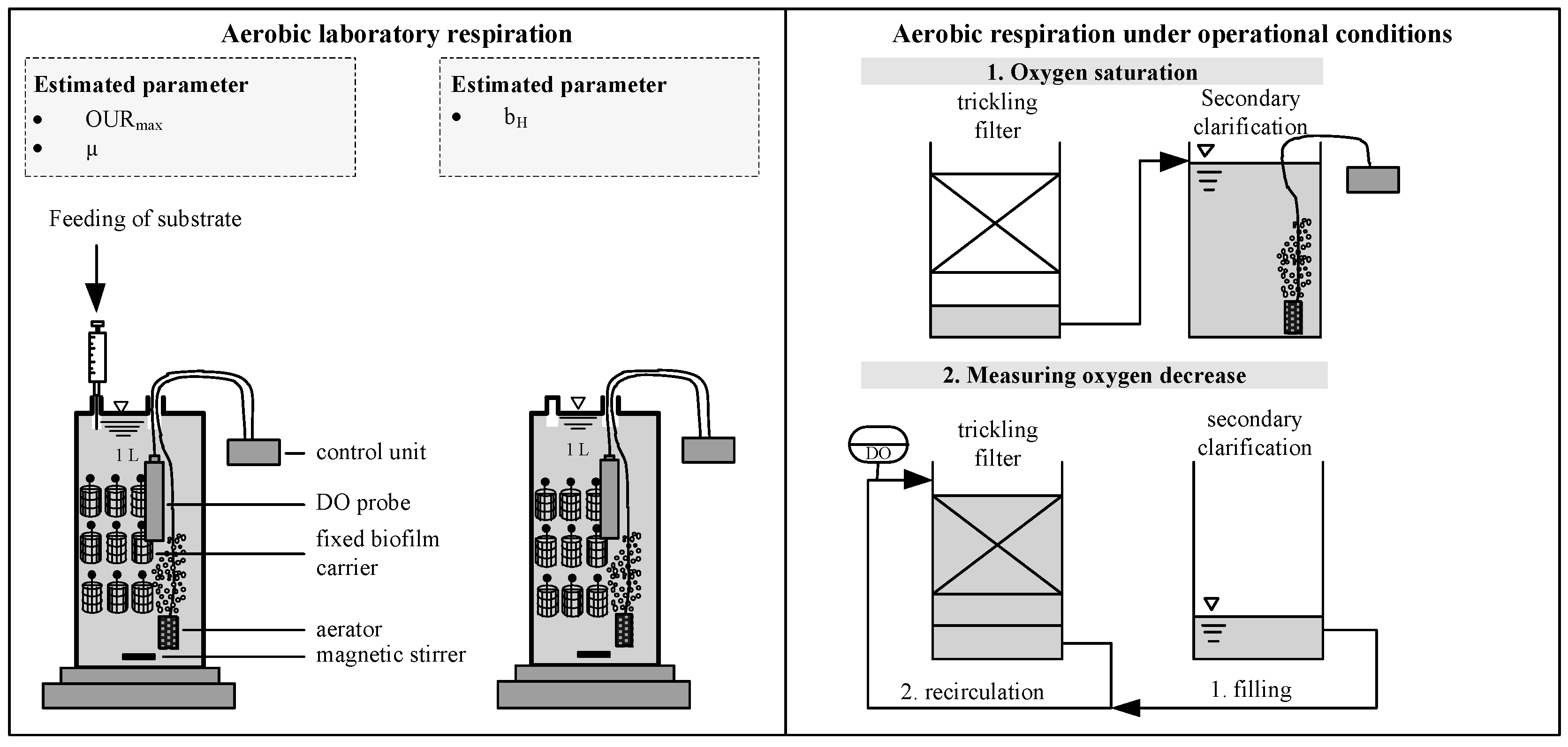
2.1. Design of Wastewater Treatment Plant
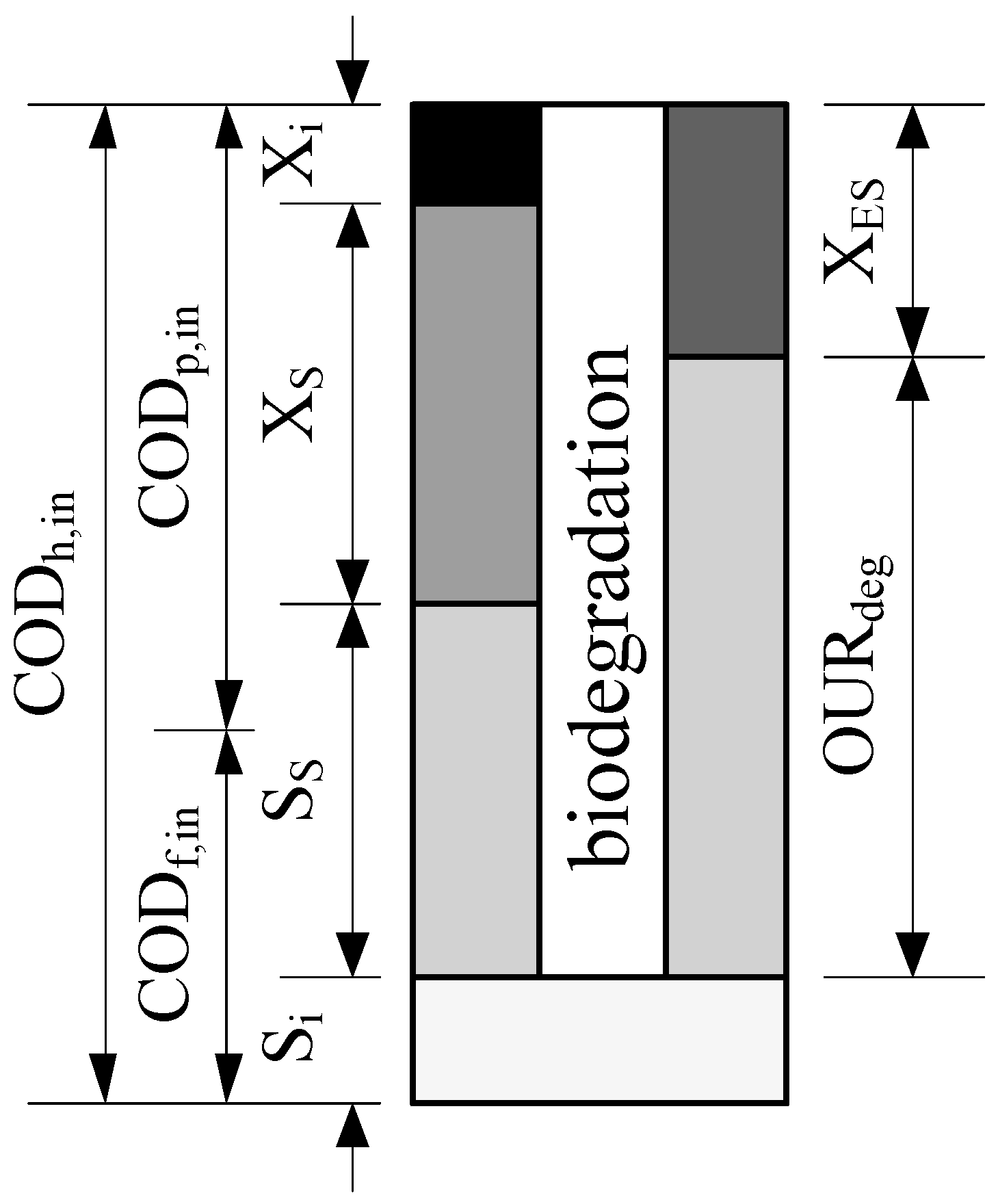
2.2. Analytical Procedure
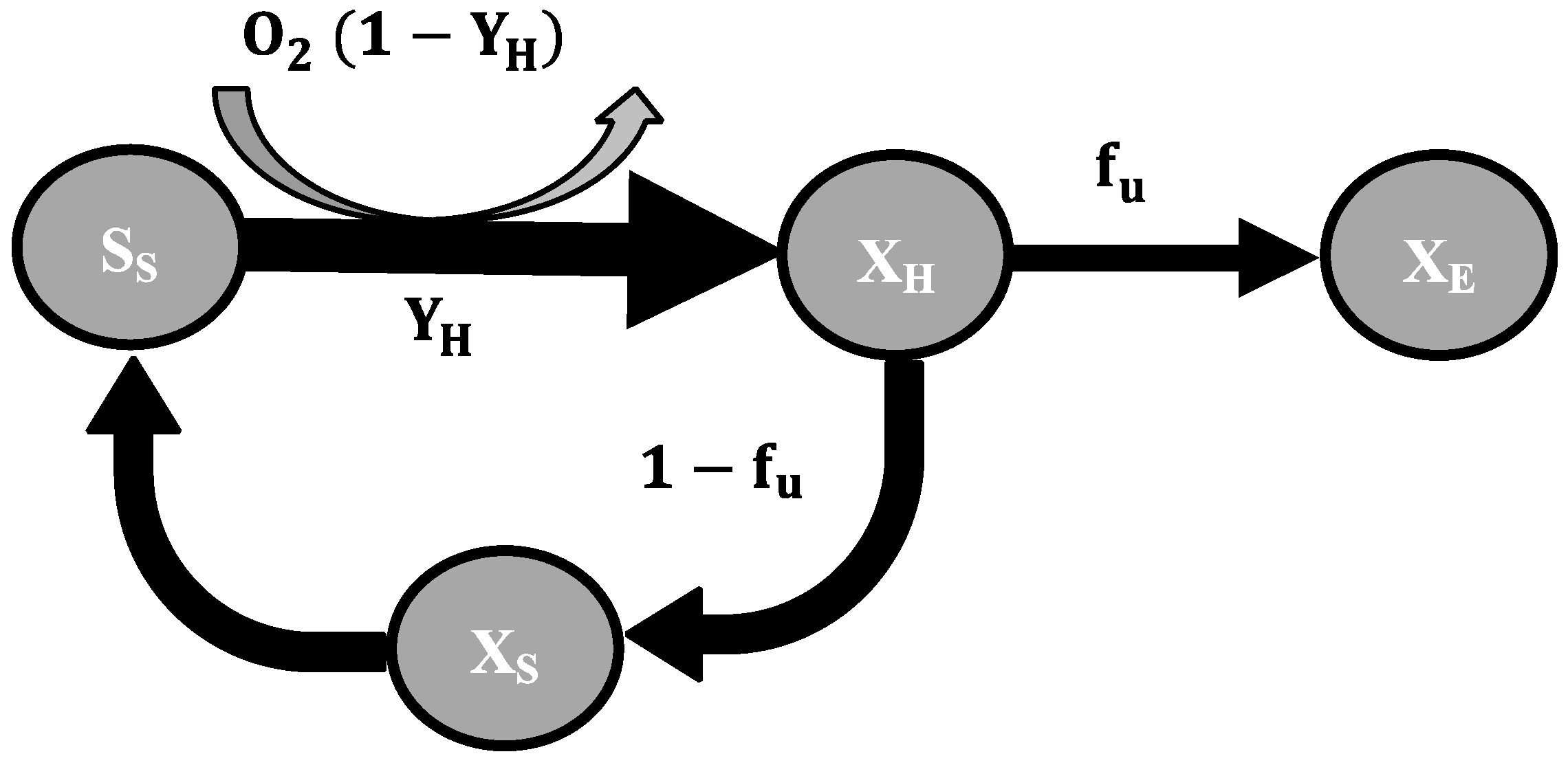
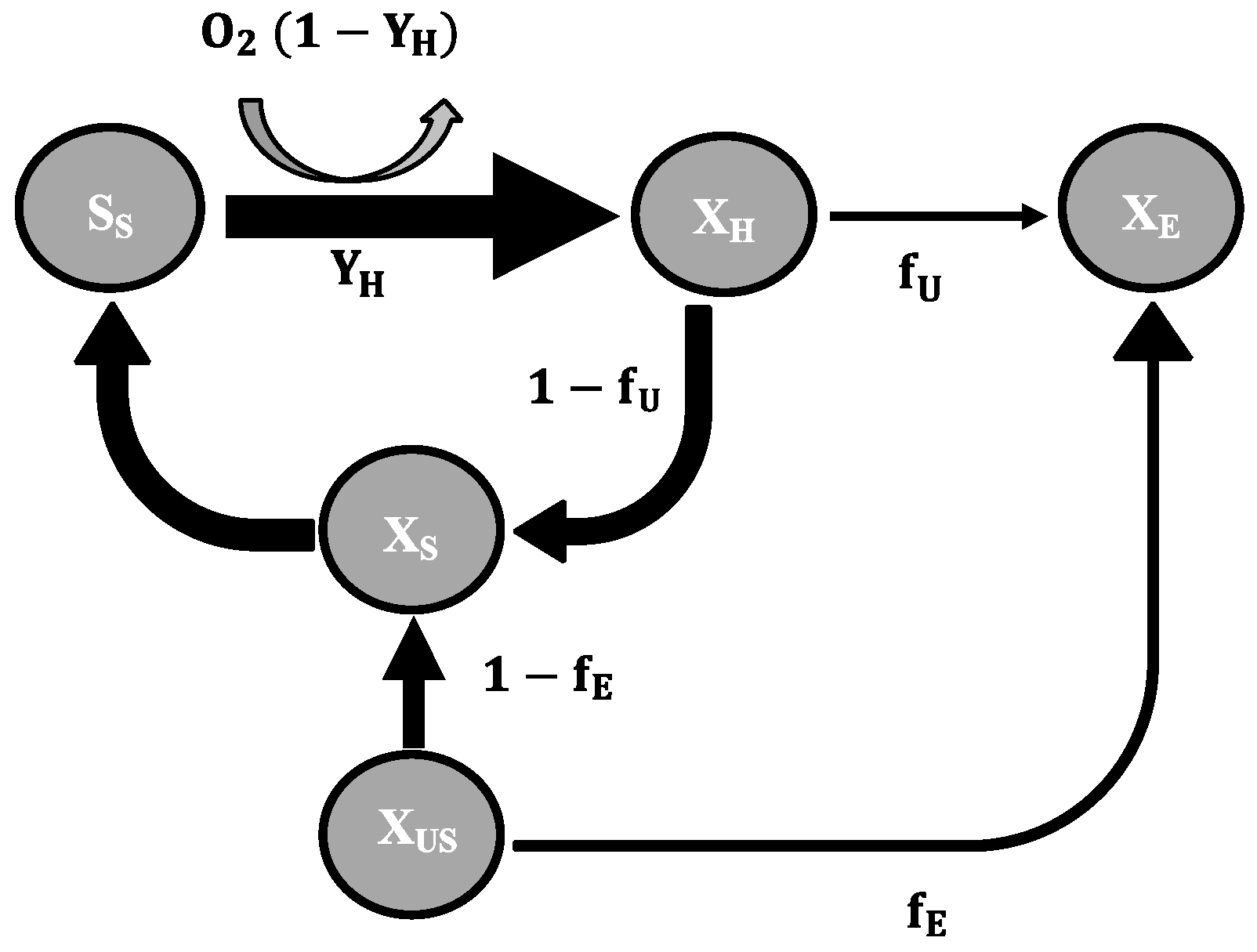
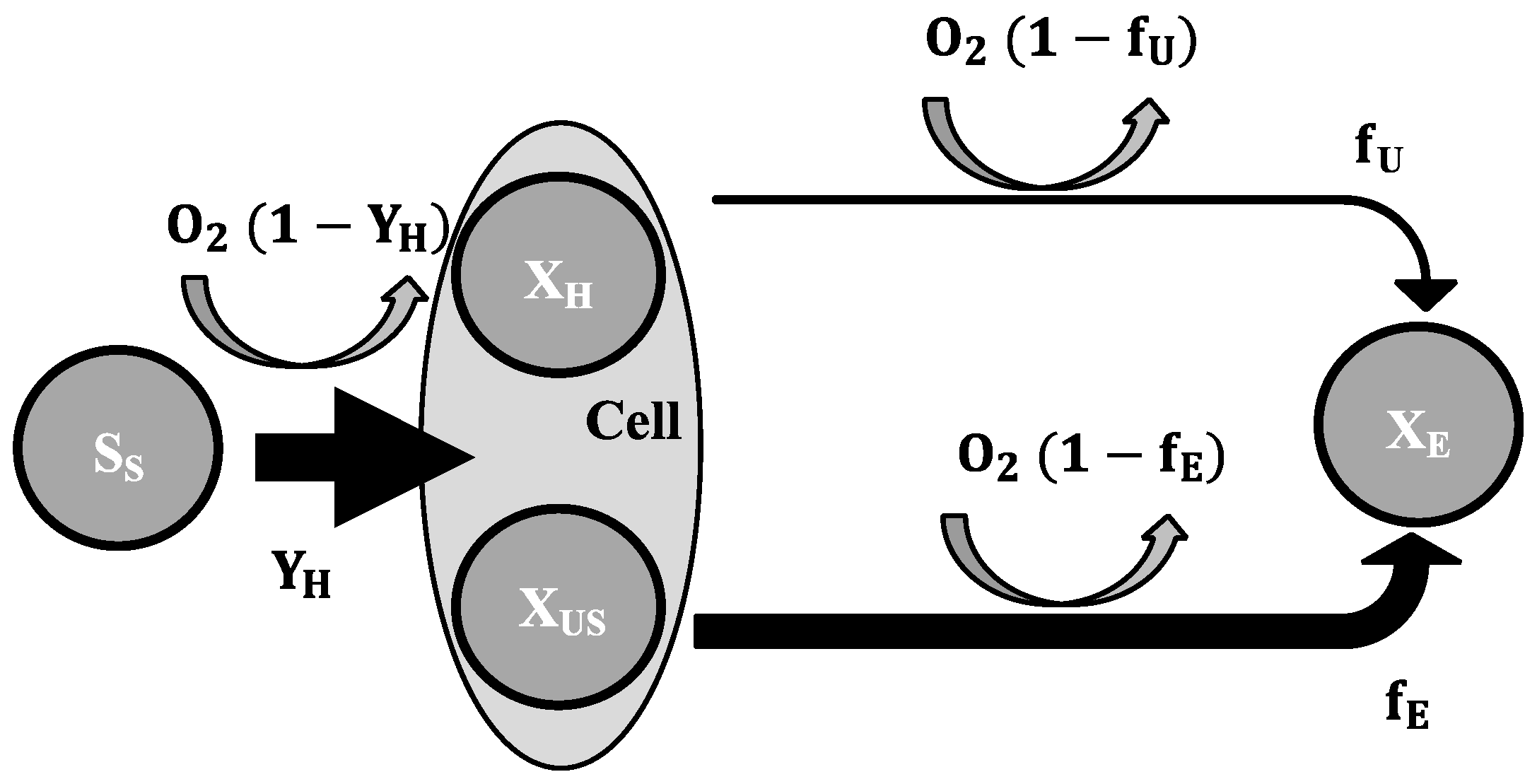
2.3. Mathematical Model
3. Results
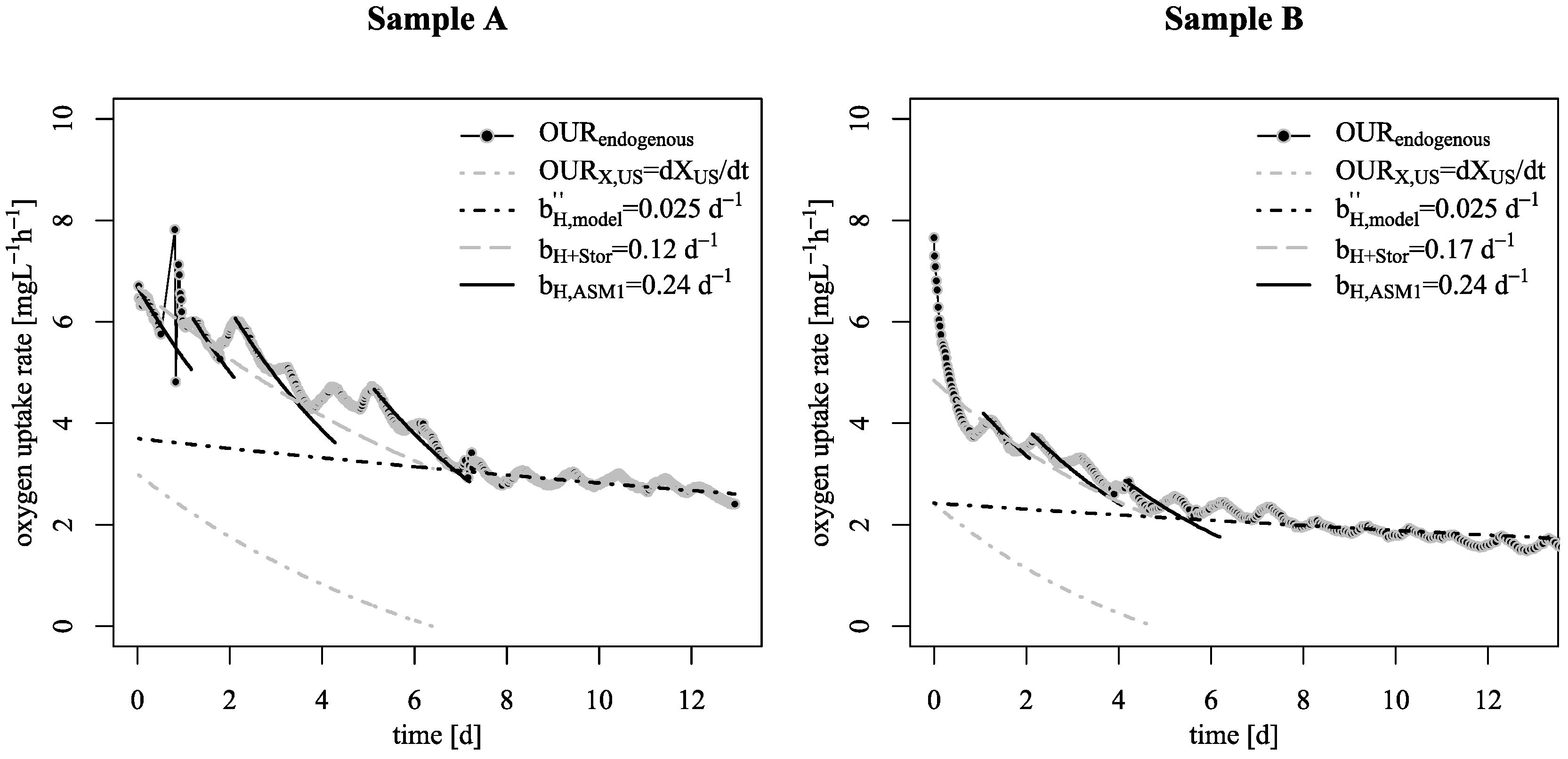
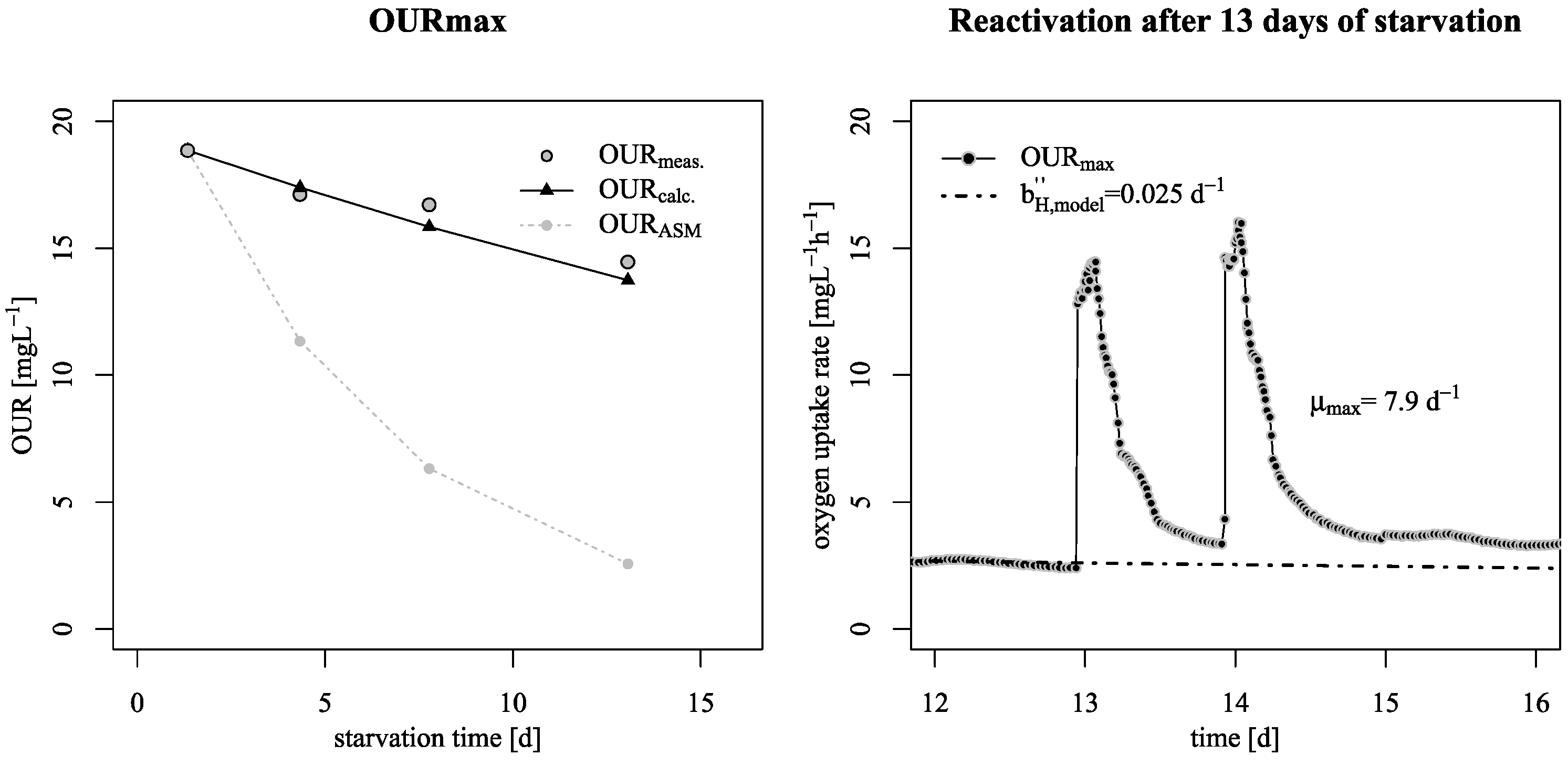
3.1. Decay Rate During Starvation
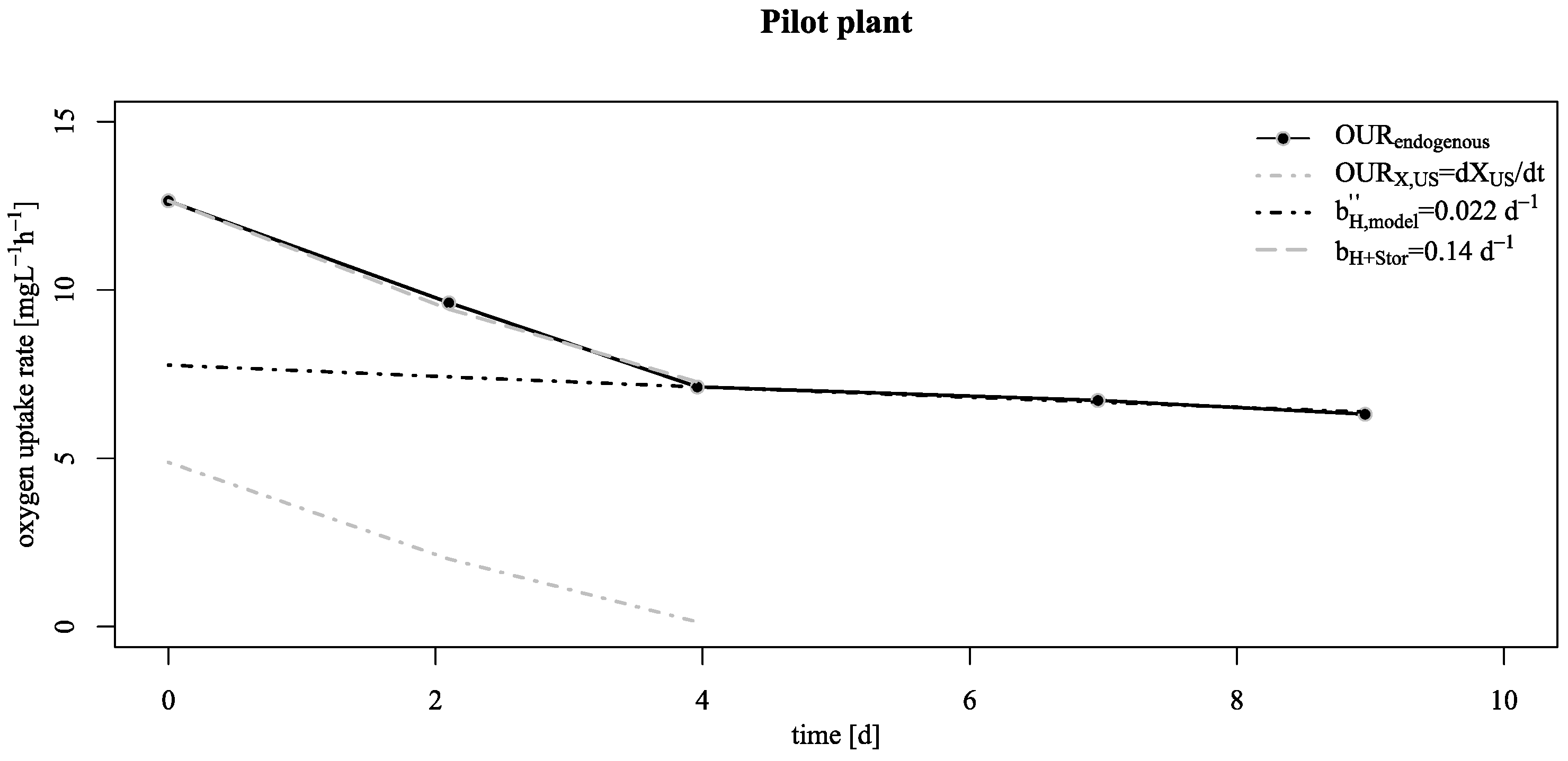
3.2. Verification of the Low Decay Rate in Pilot Scale
4. Discussion
5. Conclusions
- Starvation of biofilm carrier was characterized by wavy increase and decrease of endogenous respiration, ending at a surprisingly low base decay rate. Justifying this effect with either the existing death-regeneration model or the endogenous respiratory model is not a straightforward task;
- A possible explanation approach is the layering and the associated oxygen diffusion limitations, which preserves the lower layers from real degradation of COD but not from decay;
- However, even taking these biofilm specific conditions apart: the base decay rate is considerably lower than the recommended value in existing ASM;
- This lower decay rates allow a conservation of biological activity over long starvation periods as shown by reactivation experiments at the pilot SBR trickling filter;
- To explain these findings, the common one step decay model needs be divided into at least two processes: (i) a fast degradation of cell internal reserves and/or hardly degradable external COD, named here as “ultra-slow” degradable COD XUS and (ii) the net decay of active biomass;
- Based on recent publications, it can be assumed that these findings are transferrable to activated sludge systems;
- The findings have practical consequences for aerobic biologic reactors suffering from long starvation conditions: (i) they should survive those conditions better than commonly presumed, (ii) biomass production is larger and aeration demand is lower than commonly presumed.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Nomenclature | |
| A | surface area |
| ASM | activated sludge model |
| ASS | activated sludge system |
| b | decay rate |
| BF | biofilm |
| COD | chemical oxygen demand |
| D | diffusion coefficient |
| DO | dissolved oxygen |
| EBPR | enhanced biological phosphorus removal |
| f | residue factor |
| k | rate constant |
| L | characteristic length |
| n | number of |
| N | oxygen demand for nitrification |
| OUR | oxygen uptake rate |
| r | rate expression |
| S | dissolved fraction |
| SBR | sequence batch reactor |
| SBR-TFS | SBR-trickling filter system |
| SRT | sludge retention time |
| ß | oxygen penetration factor |
| t | time |
| X | particulate fraction |
| Y | yield coefficient |
| Indices | |
| 0 | initial |
| deg | degraded |
| E | endogenous residue |
| e | endogenous |
| eff | effluent |
| eli | elimination |
| ES | excess sludge |
| f | filtrated |
| F | fluid |
| H | heterotrophic organism |
| H+stor | degradation of heterotrophic organism and storage fraction |
| h | homogeneous |
| i | inert |
| i,BM | inert biomass residue |
| in | influent |
| N | nitrification |
| S | substrate |
| sp | specific |
| tot | total |
| U | unbiodegradable |
| US | ultra slow |
References
- Daigger, G.T.; Grady, C.P.L. An assessment of the role of physiological adaptation in the transient response of bacterial cultures. Biotechnol. Bioeng. 1982, 24, 1427–1444. [Google Scholar] [CrossRef] [PubMed]
- Hood, M.A.; Guckert, J.B.; White, D.C.; Deck, F. Effect of nutrient deprivation on lipid, carbohydrate, DNA, RNA, and protein levels in Vibrio cholerae. Appl. Environ. Microbiol. 1986, 52, 788–793. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- White, D. Physiology and biochemistry of prokaryotes; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Morita, R.Y. Bioavailability of Energy and the Starvation State; Springer: Boston, MA, USA, 1993; pp. 1–23. [Google Scholar]
- Cebollero, E.; Reggiori, F.; Kraft, C. Reticulophagy and ribophagy: Regulated degradation of protein production factories. Int. J. Cell Biol. 2012, 2012, 1–9. [Google Scholar] [CrossRef] [PubMed]
- MacIntosh, G.C.; Bassham, D.C. The connection between ribophagy, autophagy and ribosomal RNA decay. Autophagy 2011, 7, 662–663. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kurland, G.C.; Mikkola, R. The Impact of Nutritional State on the Microevolution of Ribosomes, Starvation in Bacteria; Kjelleberg, S., Ed.; Plenum Press: New York, NY, USA, 1993; pp. 225–237. [Google Scholar]
- Henze, M.; Gujer, W.; Van Loosdrecht, M.C.M.; Mino, T. Activated sludge models ASM1, ASM2, ASM2d and ASM3; IWA Publishing: London, UK, 2000. [Google Scholar]
- Wanner, O.; Gujer, W. A Multispecies Biofilrn Model. Biotechnol. Bioeng. 1986, 28, 314–328. [Google Scholar] [CrossRef]
- Gikas, P.; Livingston, A.G. Specific ATP and specific oxygen uptake rate in immobilized cell aggregates: Experimental results and theoretical analysis using a structured model of immobilized cell growth. Biotechnol. Bioeng. 1997, 55, 660–673. [Google Scholar] [CrossRef]
- McKinney, R.E. Complete mixing activated sludge. Water Sew. Work. 1960, 107, 69. [Google Scholar]
- Gujer, W.; Henze, M.; Mino, T.; Loosdrecht, M.C.M. Van Activated sludge model No. 3. Water Sci. Technol. 1999, 39, 183–193. [Google Scholar] [CrossRef]
- Dold, P.L.; Ekama, G.; Marais, G.v.R. A General Model for the Activated Sludge Process. Water Res. Public Heal. Eng. 1980, 12, 47–77. [Google Scholar]
- Wanner, J.; Kucman, K.; Grau, P. Activated sludge process combined with biofilm cultivation. Water Res. 1988, 22, 207–215. [Google Scholar] [CrossRef]
- Wanner, O.; Morgenroth, E. Biofilm modeling with AQUASIM. Water Sci. Technol. 2004, 49, 137–144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Spanjers, H.; Vanrolleghem, P. Respirometry as a tool for rapid characterization of wastewater and activated sludge. Water Sci. Technol. 1995, 31, 105–114. [Google Scholar] [CrossRef]
- Di Trapani, D.; Capodici, M.; Cosenza, A.; Di Bella, G.; Mannina, G.; Torregrossa, M.; Viviani, G. Evaluation of biomass activity and wastewater characterization in a UCT-MBR pilot plant by means of respirometric techniques. Desalination 2011, 269, 190–197. [Google Scholar] [CrossRef]
- Ramdani, A.; Dold, P.L.; Déléris, S.; Lamarre, D.; Gadbois, A.; Comeau, Y. Biodegradation of the endogenous residue of activated sludge. Water Res. 2010, 44, 2179–2188. [Google Scholar] [CrossRef] [PubMed]
- Tränckner, J.; Wricke, B.; Krebs, P. Estimating nitrifying biomass in drinking water filters for surface water treatment. Water Res. 2008, 42, 2574–2584. [Google Scholar] [CrossRef] [PubMed]
- Cramer, M.; Tränckner, J.; Schelhorn, P.; Kotzbauer, U. Degradation kinetics and COD fractioning of agricultural wastewaters from biogas plants applying biofilm respirometry. Environ. Technol. 2019, 17, 1–11. [Google Scholar] [CrossRef]
- Marais, G.v.R.; Ekama, G.A. The activated sludge process Part 1—Steady state behaviour. Water S.A. 1976, 2, 163–200. [Google Scholar]
- Friedrich, M.; Takács, I.; Tränckner, J. Experimental Assessment of the Degradation of “Unbiodegradable” Organic Solids in Activated Sludge. Water Environ. Res. 2016, 88, 272–279. [Google Scholar] [CrossRef]
- Friedrich, M.; Takács, I.; Tränckner, J. Physiological adaptation of growth kinetics in activated sludge. Water Res. 2015, 85, 22–30. [Google Scholar] [CrossRef]
- Cramer, M.; Rinas, M.; Kotzbauer, U.; Tränckner, J. Surface contamination of impervious areas on biogas plants and conclusions for an improved stormwater management. J. Clean. Prod. 2019, 217, 1–11. [Google Scholar] [CrossRef]
- Ye, L.; Hu, S.; Poussade, Y.; Keller, J.; Yuan, Z. Evaluating a strategy for maintaining nitrifier activity during long-term starvation in a moving bed biofilm reactor (MBBR) treating reverse osmosis concentrate. Water Sci. Technol. 2012, 66, 837–842. [Google Scholar] [CrossRef] [PubMed]
- Buitrón, G.; Moreno-Andrade, I. Biodegradation kinetics of a mixture of phenols in a sequencing batch moving bed biofilm reactor under starvation and shock loads. J. Chem. Technol. Biotechnol. 2011, 86, 669–674. [Google Scholar] [CrossRef]
- Cramer, M.; Tränckner, J.; Kotzbauer, U. Kinetic of denitrification and enhanced biological phosphorous removal (EBPR) of a trickling filter operated in a sequence-batch-reactor-mode (SBR-TF). Environ. Technol. 2019, 1–10. [Google Scholar] [CrossRef]
- Metcalf, E.; Eddy, M. Wastewater Engineering: Treatment and Resource Recovery; McGraw-Hill: New York, NY, USA, 2014. [Google Scholar]
- Friedrich, M.; Takacs, I. A new interpretation of endogenous respiration profiles for the evaluation of the endogenous decay rate of heterotrophic biomass in activated sludge. Water Res. 2013, 47, 5639–5646. [Google Scholar] [CrossRef]
- Dircks, K.; Pind, P.F.; Mosbæk, H.; Henze, M. Yield determination by respirometry—The possible influence of storage under aerobic conditions in activated sludge. Water S.A. 1999, 25, 69–74. [Google Scholar]
- Kwok, W.K.; Picioreanu, C.; Ong, S.L.; Van Loosdrecht, M.C.M.; Ng, W.J.; Heijnen, J.J. Influence of biomass production and detachment forces on biofilm structures in a biofilm airlift suspension reactor. Biotechnol. Bioeng. 1998, 58, 400–407. [Google Scholar] [CrossRef]
- Kuenen, J.G.; Jorgensen, B.B.; Revsbech, N.P. Oxygen Microprofiles of Trickling Filter Biofilms. Water Res. 1986, 20, 1589–1598. [Google Scholar] [CrossRef] [Green Version]
- Virdis, B.; Read, S.T.; Rabaey, K.; Rozendal, R.A.; Yuan, Z.; Keller, J. Biofilm stratification during simultaneous nitrification and denitrification (SND) at a biocathode. Bioresour. Technol. 2011, 102, 334–341. [Google Scholar] [CrossRef]
- Hauduc, H.; Rieger, L.; Oehmen, A.; van Loosdrecht, M.C.M.; Comeau, Y.; Héduit, A.; Vanrolleghem, P.A.; Gillot, S. Critical review of activated sludge modeling: State of process knowledge, modeling concepts, and limitations. Biotechnol. Bioeng. 2013, 110, 24–46. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cramer, M.; Tränckner, J. Development of Decay in Biofilms under Starvation Conditions—Rethinking of the Biomass Model. Water 2020, 12, 1249. https://doi.org/10.3390/w12051249
Cramer M, Tränckner J. Development of Decay in Biofilms under Starvation Conditions—Rethinking of the Biomass Model. Water. 2020; 12(5):1249. https://doi.org/10.3390/w12051249
Chicago/Turabian StyleCramer, Michael, and Jens Tränckner. 2020. "Development of Decay in Biofilms under Starvation Conditions—Rethinking of the Biomass Model" Water 12, no. 5: 1249. https://doi.org/10.3390/w12051249
APA StyleCramer, M., & Tränckner, J. (2020). Development of Decay in Biofilms under Starvation Conditions—Rethinking of the Biomass Model. Water, 12(5), 1249. https://doi.org/10.3390/w12051249





