Using GRanD Database and Surface Water Data to Constrain Area–Storage Curve of Reservoirs
Abstract
1. Introduction
2. Materials and Methods
2.1. Input Datasets
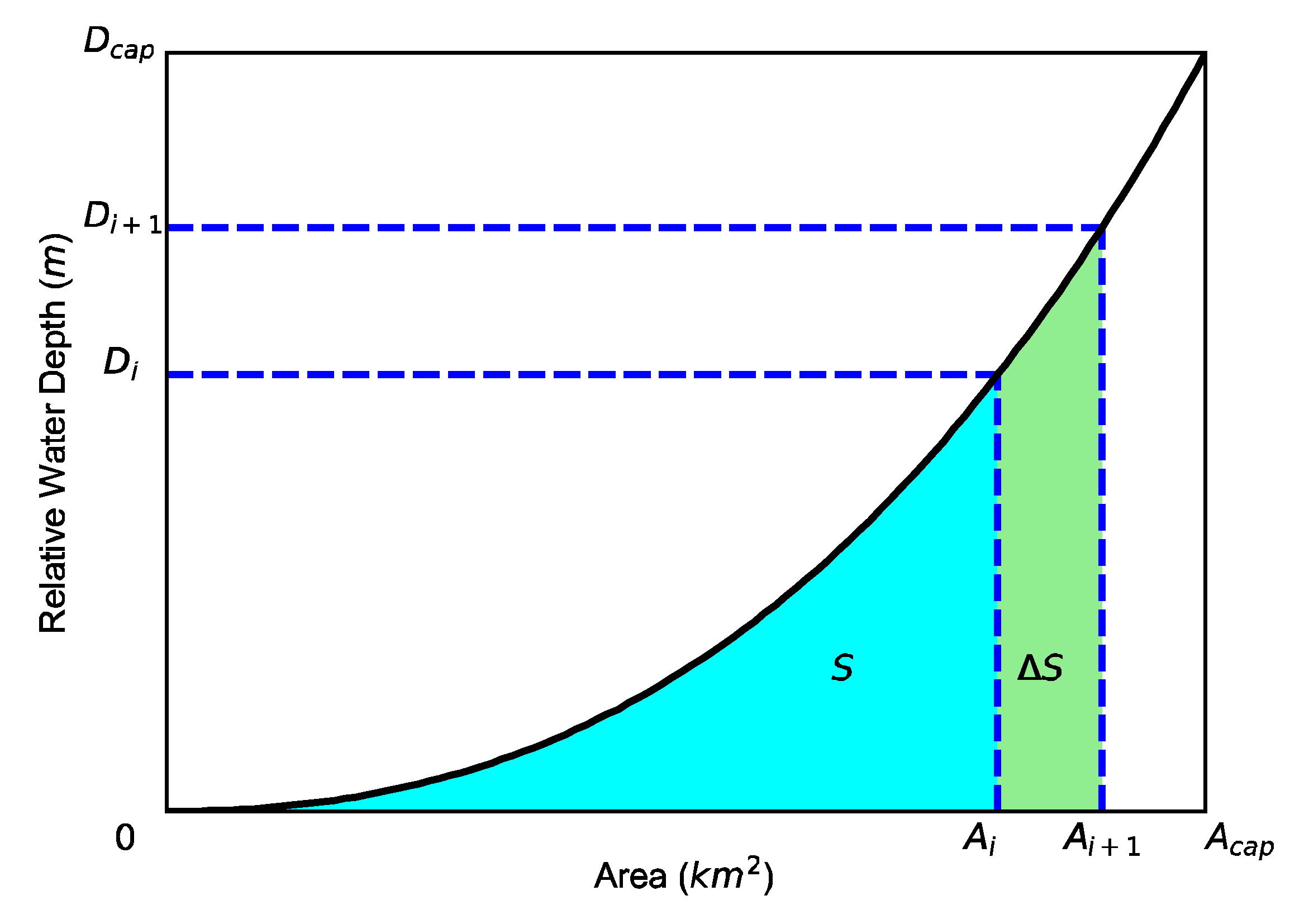
2.2. Methods to Derive Area–Storage Curves
3. Results
4. Conclusions and Discussion
- The coverage polygon of each reservoir. The polygon is based on the original GRanD polygon and expanded by the GSW dataset. The uncertainties in both datasets would propagate to affect the real coverage of the reservoir and in result, affect the area at capacity and the topography delineation from ETOPO1.
- The coarse resolution and vertical accuracy of elevation data. The coarse resolution and limited vertical accuracy of the ETOPO1 could cause great uncertainties even errors and restrict its applicability. A finer-resolution (10–60 m) and higher-accuracy (10–25 cm) DEM with water depth information may be derived after SWOT (Surface Water and Ocean Topography mission) [33] to be launched in the year 2021. SWOT would be able to observe lakes with repeated high-resolution elevation measurements, and when combined with high-resolution surface water data, would enable area–storage curves of global lake/reservoirs with better accuracy in the future. For now, however, the proposed approach in this study, which utilizes the readily available ETOPO1, can serve as an alternative approach with satisfied accuracy to provide area–storage curves for the hydrology community. Furthermore, the disadvantages of ETOPO1 are largely compensated in the calibration process by the GRanD and GSW dataset. Although other high-resolution DEMs may have the potential to derive the area–storage curves with some new modified approaches, it is beyond the scope of this study and may be considered and examined in the future.
- The reported capacity in the GRanD database and the sedimentation effect. The calibration in this study heavily depends on , which is collected from multiple unguaranteed sources with various qualities. Moreover, in this study (as well as in previously mentioned studies), the storage capacity of the reservoir is assumed not to change through time and thus, a stationary capacity is adopted, which means the sedimentation effect [34] is not considered and may introduce bias in reservoirs with severe sediment deposition. Basson (2009) [35] reported that the annual reservoir sedimentation rate is about 0.5%–1% of global reservoir storage volume. It means the adding loss of storage is approximately 50 km3 per year worldwide [36]. The highest average reservoir sedimentation rate occurs in arid regions such as the Middle East, Australia, Africa, and western United States [37,38]. Wang and Hu (2009) [39] reported that sedimentation had reduced the reservoir capacity in China by 66%. The previous study also showed that 80% of the useful storage capacity for hydropower production will be lost by 2035, and whereas 70% of the storage volumes used for irrigation will be lost due to sedimentation by 2025 in Asia [40]. As the sediment filling effect is increasingly widespread, many measures have been carried out to preserve reservoir capacity [41,42]. The variation of reservoir storage capacity is difficult to monitor and predict. Wisser et al. (2013) [43] estimated the loss in storage capacity for global large reservoirs from 1901 to 2010, and found that the net reservoir capacity is declining as a result of sedimentation (∼5% compared to the installed capacity). It should be noted that using the fixed reservoir storage capacity in the GRanD database would introduce uncertainty to the area–storage curve estimates. There is an urgent need to update the storage capacity in the database. We also note that the annual change of reservoir capacity is usually small compared to the install capacity. If the storage capacity had been recently updated, the fixed storage capacity may be used to derive the area–storage curve for reservoir water storage monitoring. Local information, e.g., more accurate dynamic capacity of reservoirs, could be used to calibrate the A-S curves on a local scale if higher accuracy is desired. However, for global-scale studies, the proposed approach should work well with acceptable bias.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chao, B.F.; Wu, Y.H.; Li, Y.S. Impact of Artificial Reservoir Water Impoundment on Global Sea Level. Science 2008, 320, 212–214. [Google Scholar] [CrossRef]
- Döll, P.; Fiedler, K.; Zhang, J. Global-scale analysis of river flow alterations due to water withdrawals and reservoirs. Hydrol. Earth Syst. Sci. 2009, 13, 2413–2432. [Google Scholar] [CrossRef]
- Zhou, T.; Nijssen, B.; Gao, H.; Lettenmaier, D.P. The Contribution of Reservoirs to Global Land Surface Water Storage Variations. J. Hydrometeorol. 2016, 17, 309–325. [Google Scholar] [CrossRef]
- Hanasaki, N.; Kanae, S.; Oki, T. A reservoir operation scheme for global river routing models. J. Hydrol. 2006, 327, 22–41. [Google Scholar] [CrossRef]
- Hanasaki, N.; Kanae, S.; Oki, T.; Masuda, K.; Motoya, K.; Shirakawa, N.; Shen, Y.; Tanaka, K. An integrated model for the assessment of global water resources—Part 1: Model description and input meteorological forcing. Hydrol. Earth Syst. Sci. 2008, 12, 1007–1025. [Google Scholar] [CrossRef]
- Wisser, D.; Fekete, B.M.; Vörösmarty, C.J.; Schumann, A.H. Reconstructing 20th century global hydrography: A contribution to the Global Terrestrial Network-Hydrology (GTN-H). Hydrol. Earth Syst. Sci. 2010, 14, 1–24. [Google Scholar] [CrossRef]
- Pokhrel, Y.; Hanasaki, N.; Koirala, S.; Cho, J.; Yeh, P.J.-F.; Kim, H.; Kanae, S.; Oki, T. Incorporating Anthropogenic Water Regulation Modules into a Land Surface Model. J. Hydrometeorol. 2012, 13, 255–269. [Google Scholar] [CrossRef]
- Voisin, N.; Liu, L.; Hejazi, M.; Tesfa, T.; Li, H.; Huang, M.; Liu, Y.; Leung, L.R. One-Way coupling of an integrated assessment model and a water resources model: Evaluation and implications of future changes over the US Midwest. Hydrol. Earth Syst. Sci. 2013, 17, 4555–4575. [Google Scholar] [CrossRef]
- Biemans, H.; Haddeland, I.; Kabat, P.; Ludwig, F.; Hutjes, R.W.A.; Heinke, J.; Von Bloh, W.; Gerten, D. Impact of reservoirs on river discharge and irrigation water supply during the 20th century. Water Resour. Res. 2011, 47, 1–15. [Google Scholar] [CrossRef]
- Liu, X.; Tang, Q.; Voisin, N.; Cui, H. Projected impacts of climate change on hydropower potential in China. Hydrol. Earth Syst. Sci. 2016, 20, 3343–3359. [Google Scholar] [CrossRef]
- Nazemi, A.; Wheater, H.S. On inclusion of water resource management in Earth system models—Part 2: Representation of water supply and allocation and opportunities for improved modeling. Hydrol. Earth Syst. Sci. 2015, 19, 63–90. [Google Scholar] [CrossRef]
- Gao, H.; Birkett, C.; Lettenmaier, D.P. Global monitoring of large reservoir storage from satellite remote sensing. Water Resour. Res. 2012, 48, 1–12. [Google Scholar] [CrossRef]
- Zhang, S.; Gao, H.; Naz, B.S. Monitoring reservoir storage in South Asia frommultisatellite remote sensing. Water Resour. Res. 2014, 50, 8927–8943. [Google Scholar] [CrossRef]
- Gao, H. Satellite remote sensing of large lakes and reservoirs: From elevation and area to storage. Wiley Interdiscip. Rev. Water 2015, 2, 147–157. [Google Scholar] [CrossRef]
- Crétaux, J.F.; Biancamaria, S.; Arsen, A.; Bergé-Nguyen, M.; Becker, M. Global surveys of reservoirs and lakes from satellites and regional application to the Syrdarya river basin. Environ. Res. Lett. 2015, 10, 015002. [Google Scholar] [CrossRef]
- Zhang, S.; Gao, H. A novel algorithm for monitoring reservoirs under all-weather conditions at a high temporal resolution through passive microwave remote sensing. Geophys. Res. Lett. 2016, 43, 8052–8059. [Google Scholar] [CrossRef]
- Lehner, B.; Liermann, C.R.; Revenga, C.; Vörömsmarty, C.; Fekete, B.; Crouzet, P.; Döll, P.; Endejan, M.; Frenken, K.; Magome, J.; et al. High-resolution mapping of the world’s reservoirs and dams for sustainable river-flow management. Front. Ecol. Environ. 2011, 9, 494–502. [Google Scholar] [CrossRef]
- G-REALM: A Lake/Reservoir Monitoring Tool for Water Resources and Regional Security Assessment. Available online: https://www.pecad.fas.usda.gov/cropexplorer/global_reservoir (accessed on 1 July 2017).
- Crétaux, J.F.; Jelinski, W.; Calmant, S.; Kouraev, A.; Vuglinski, V.; Bergé-Nguyen, M.; Gennero, M.C.; Nino, F.; Abarca Del Rio, R.; Cazenave, A.; et al. SOLS: A lake database to monitor in the Near Real Time water level and storage variations from remote sensing data. Adv. Space Res. 2011, 47, 1497–1507. [Google Scholar] [CrossRef]
- Liebe, J.; van de Giesen, N.; Andreini, M. Estimation of small reservoir storage capacities in a semi-arid environment. Phys. Chem. Earth 2005, 30, 448–454. [Google Scholar] [CrossRef]
- Sawunyama, T.; Senzanje, A.; Mhizha, A. Estimation of small reservoir storage capacities in Limpopo River Basin using geographical information systems (GIS) and remotely sensed surface areas: Case of Mzingwane catchment. Phys. Chem. Earth 2006, 31, 935–943. [Google Scholar] [CrossRef]
- Klein, I.; Gessner, U.; Dietz, A.J.; Kuenzer, C. Global WaterPack—A 250 m resolution dataset revealing the daily dynamics of global inland water bodies. Remote Sens. Environ. 2017, 198, 345–362. [Google Scholar] [CrossRef]
- Pekel, J.-F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef] [PubMed]
- Van Bemmelen, C.W.T.; Mann, M.; de Ridder, M.P.; Rutten, M.M.; van de Giesen, N.C. Determining water reservoir characteristics with global elevation data. Geophys. Res. Lett. 2016, 43, 11278–11286. [Google Scholar] [CrossRef]
- Amante, C.; Eakins, B.W. ETOPO1 1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis; NOAA Technical Memorandum NESDIS NGDC-24; National Geophysical Data Center, NOAA, 2009; p. 19. Available online: http://www.ngdc.noaa.gov/mgg/global/global.html (accessed on 1 June 2017).
- Yamazaki, D.; Ikeshima, D.; Tawatari, R.; Yamaguchi, T.; O’Loughlin, F.; Neal, J.C.; Sampson, C.C.; Kanae, S.; Bates, P.D. A high accuracy map of global terrain elevations. Geophys. Res. Lett. 2017, 44, 5844–5853. [Google Scholar] [CrossRef]
- USBR US Bureau of Reclamation. Available online: https://www.usbr.gov/ (accessed on 1 June 2017).
- Li, Y.; Zhang, C.; Chu, J.; Cai, X.; Zhou, H. Reservoir Operation with Combined Natural Inflow and Controlled Inflow through Interbasin Transfer: Biliu Reservoir in Northeastern China. J. Water Resour. Plan. Manag. 2015, 142, 05015009. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Y.; Chu, J.; Fu, G.; Tang, R.; Qi, W. Use of Many-Objective Visual Analytics to Analyze Water Supply Objective Trade-Offs with Water Transfer. J. Water Resour. Plan. Manag. 2017, 143, 05017006. [Google Scholar] [CrossRef]
- NASA/NGA SRTM Water Body Data Product Specific Guidance, Version 2.0. Available online: http://dds.cr.usgs.gov/srtm/version2_1/SWBD/SWBD_Documentation/ (accessed on 1 June 2017).
- Zhao, G.; Gao, H. Towards Global Hydrological Drought Monitoring Using Remotely Sensed Reservoir Surface Area. Geophys. Res. Lett. 2019, 46, 13027–13035. [Google Scholar] [CrossRef]
- Zhang, C.; Ding, W.; Li, Y.; Tang, Y.; Wang, D. Catchments’ hedging strategy on evapotranspiration for climatic variability. Water Resour. Res. 2016, 52, 9036–9045. [Google Scholar] [CrossRef]
- Biancamaria, S.; Lettenmaier, D.P.; Pavelsky, T.M. The SWOT Mission and Its Capabilities for Land Hydrology. Surv. Geophys. 2016, 37, 307–337. [Google Scholar] [CrossRef]
- Dargahi, B. Reservoir Sedimentation. In Encyclopedia of Lakes and Reservoirs; Bengtsson, L., Herschy, R.W., Fairbridge, R.W., Eds.; Springer: Dordrecht, The Netherlands, 2012; pp. 628–649. [Google Scholar]
- Basson, G. Management of siltation in existing and new reservoirs. In Proceedings of the 23rd Congress of the International Commission on Large Dams ICOLD CIGB, Basilia, Brazil, 25–29 May 2009. [Google Scholar]
- Palmieri, A.; Shah, F.; Annandale, G.; Dinar, A. Reservoir Conservation Volume I: The RESCON Approach; World Bank: Washington, DC, USA, 2003; Available online: http://documents.worldbank.org/curated/en/819541468138875126/RESCON-approach (accessed on 20 February 2020).
- Graf, W.L.; Wohl, E.; Sinha, T.; Sabo, J.L. Sedimentation and sustainability of western American reservoirs. Water Resour. Res. 2010, 46, 1–34. [Google Scholar] [CrossRef]
- George, M.W.; Hotchkiss, R.H.; Huffaker, R. Reservoir sustainability and sediment management. J. Water Resour. Plan. Manag. 2017, 143, 04016077. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, C. Strategies for managing reservoir sedimentation. Int. J. Sediment Res. 2009, 24, 369–384. [Google Scholar] [CrossRef]
- Schleiss, A.J.; Franca, M.J.; Juez, C.; De Cesare, G. Reservoir sedimentation. J. Hydraul. Res. 2016, 54, 595–614. [Google Scholar] [CrossRef]
- Kondolf, G.M.; Gao, Y.; Annandale, G.W.; Morris, G.L.; Jiang, E.; Zhang, J.; Cao, Y.; Carling, P.; Fu, K.; Guo, Q.; et al. Sustainable sediment management in reservoirs and regulated rivers: Experiences from five continents. Earth’s Future 2014, 2, 256–280. [Google Scholar] [CrossRef]
- Espa, P.; Batalla, R.J.; Brignoli, M.L.; Crosa, G.; Gentili, G.; Quadroni, S. Tackling reservoir siltation by controlled sediment flushing: Impact on downstream fauna and related management issues. PLoS ONE 2019, 14, e0218822. [Google Scholar] [CrossRef]
- Wisser, D.; Frolking, S.; Hagen, S.; Bierkens, M.F.P. Beyond peak reservoir storage? A global estimate of declining water storage capacity in large reservoirs. Water Resour. Res. 2013, 49, 5732–5739. [Google Scholar] [CrossRef]
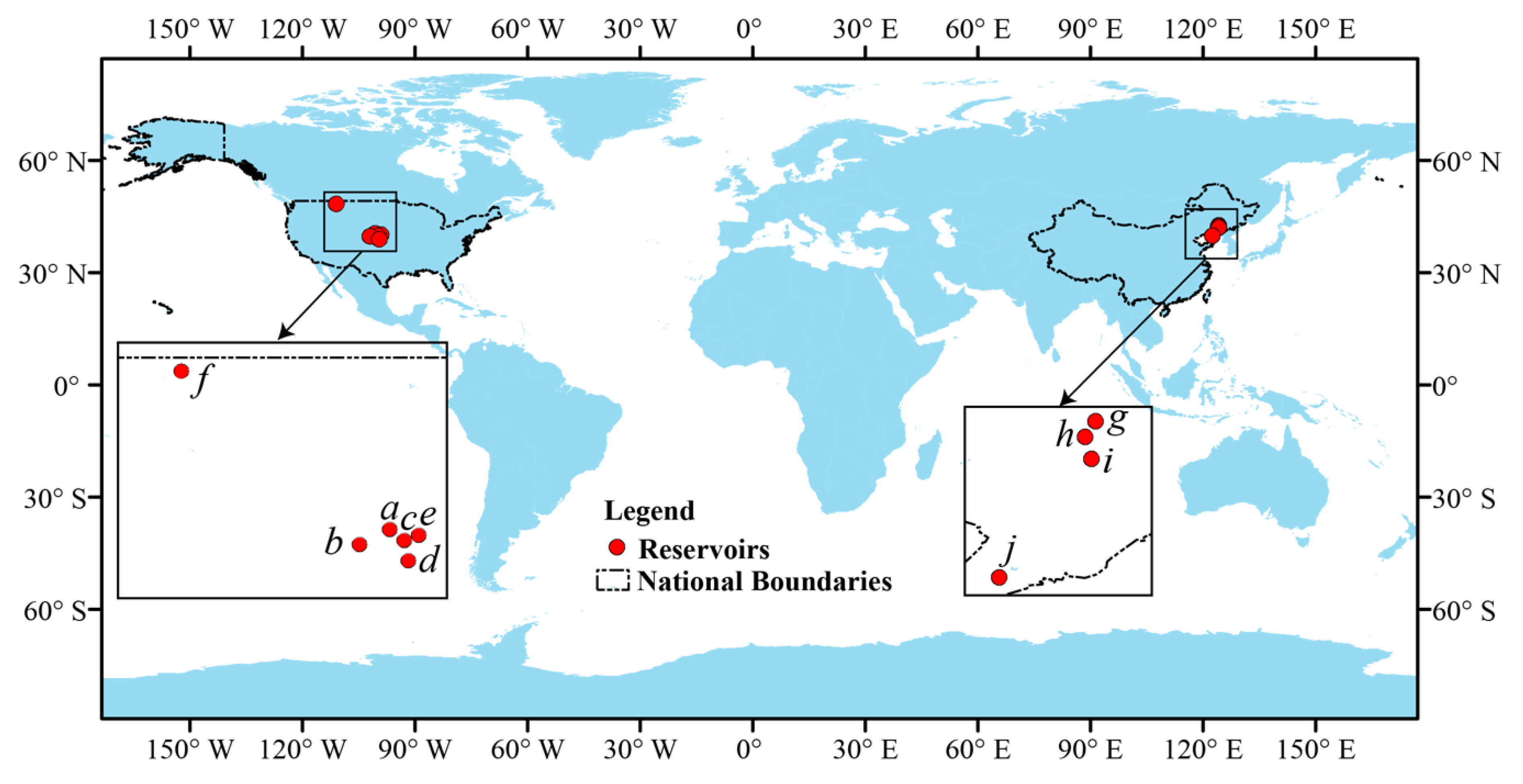
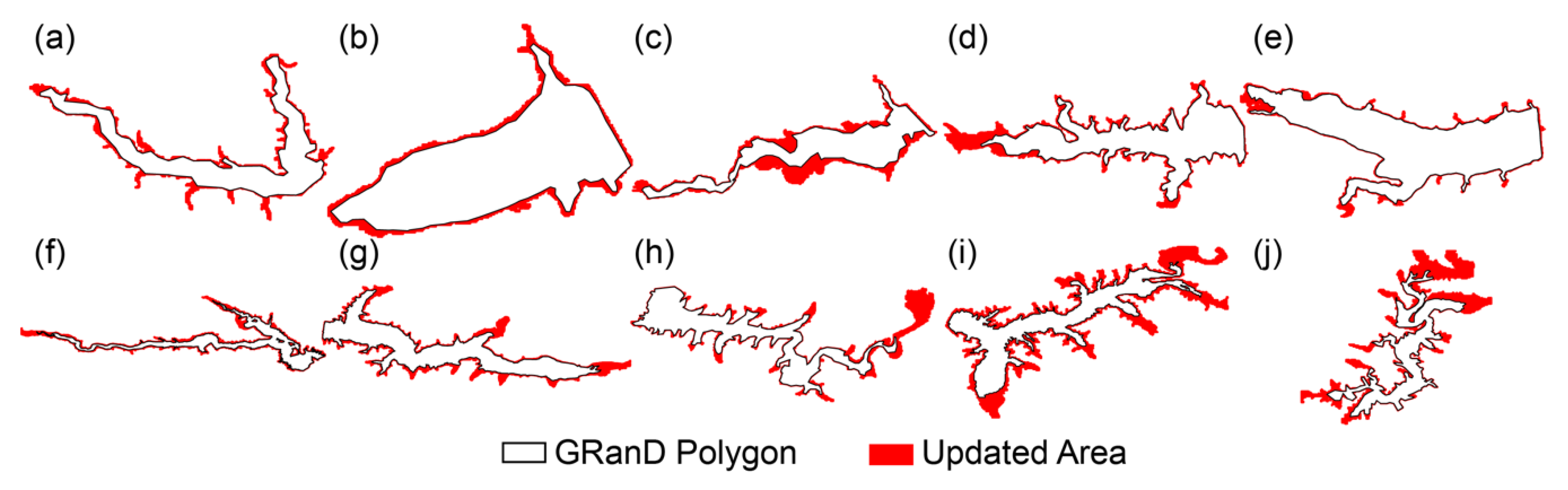
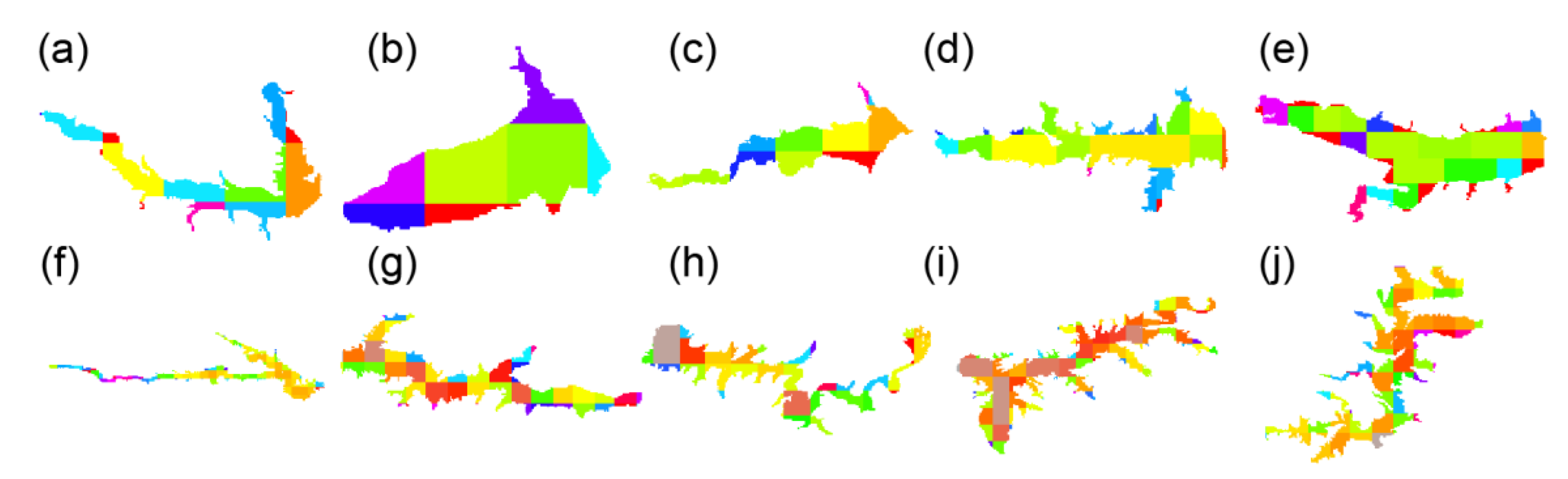
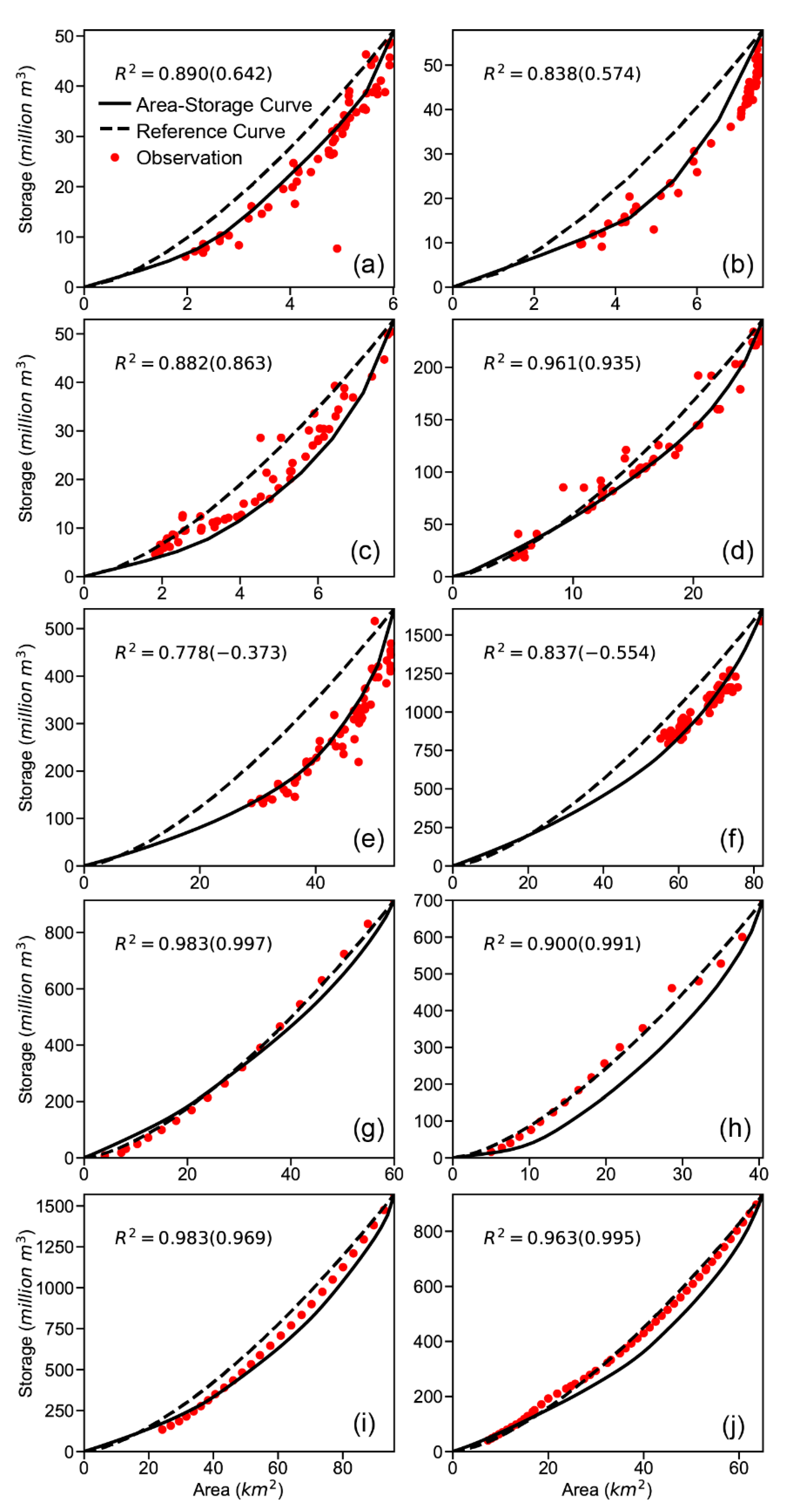
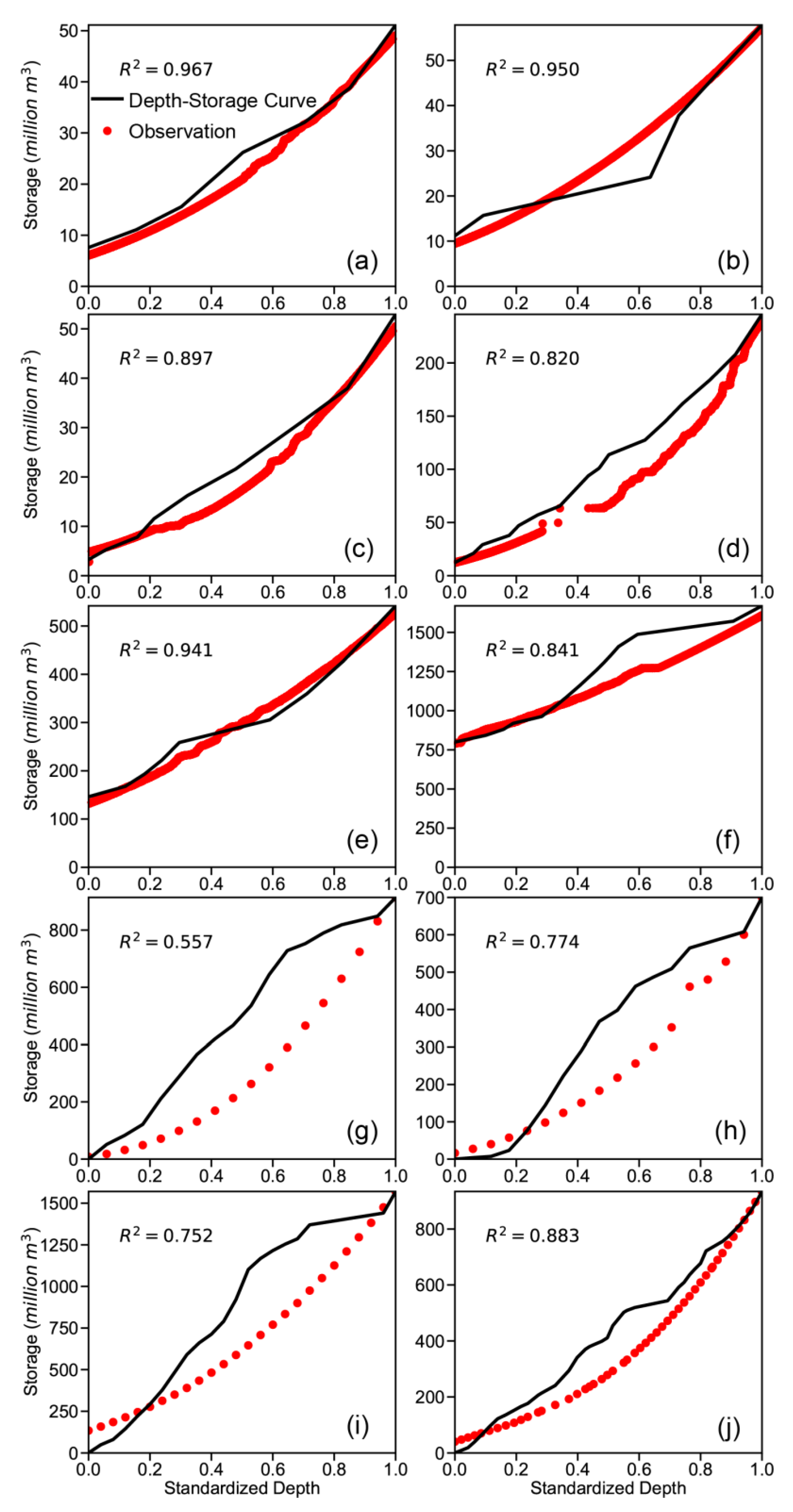
| ID in Figures | GRanD ID | Reservoir Name | Capacity (million m3) | Area at Capacity (km2) | GRanD Area (km2) | Updated Area Ratio (%) |
|---|---|---|---|---|---|---|
| a | 939 | Hugh Butler Lake | 51.1 | 6.0 | 5.0 | 20% |
| b | 958 | Bonny Reservoir | 57.9 | 7.6 | 6.8 | 12% |
| c | 953 | Keith Sebelius Lake | 52.9 | 8.0 | 5.7 | 39% |
| d | 976 | Cedar Bluff Reservoir | 245.7 | 25.8 | 21.2 | 22% |
| e | 948 | Harlan County Lake | 541.8 | 53.6 | 50.0 | 7% |
| f | 300 | Lake Elwell | 1669.5 | 82.4 | 65.2 | 26% |
| g | 5855 | Qinghe Reservoir | 971.0 | 46.1 | 37.1 | 24% |
| h | 5864 | Chaihe Reservoir | 650.0 | 26.2 | 20.8 | 26% |
| i | 5873 | Dahuofang Reservoir | 2187.0 | 79.8 | 51.1 | 56% |
| j | 5913 | Biliuhe Reservoir | 930.0 | 53.2 | 32.2 | 65% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, M.; Tang, Q.; Han, S.; Liu, X.; Cui, H. Using GRanD Database and Surface Water Data to Constrain Area–Storage Curve of Reservoirs. Water 2020, 12, 1242. https://doi.org/10.3390/w12051242
Mu M, Tang Q, Han S, Liu X, Cui H. Using GRanD Database and Surface Water Data to Constrain Area–Storage Curve of Reservoirs. Water. 2020; 12(5):1242. https://doi.org/10.3390/w12051242
Chicago/Turabian StyleMu, Mengfei, Qiuhong Tang, Songjun Han, Xiaomang Liu, and Huijuan Cui. 2020. "Using GRanD Database and Surface Water Data to Constrain Area–Storage Curve of Reservoirs" Water 12, no. 5: 1242. https://doi.org/10.3390/w12051242
APA StyleMu, M., Tang, Q., Han, S., Liu, X., & Cui, H. (2020). Using GRanD Database and Surface Water Data to Constrain Area–Storage Curve of Reservoirs. Water, 12(5), 1242. https://doi.org/10.3390/w12051242







