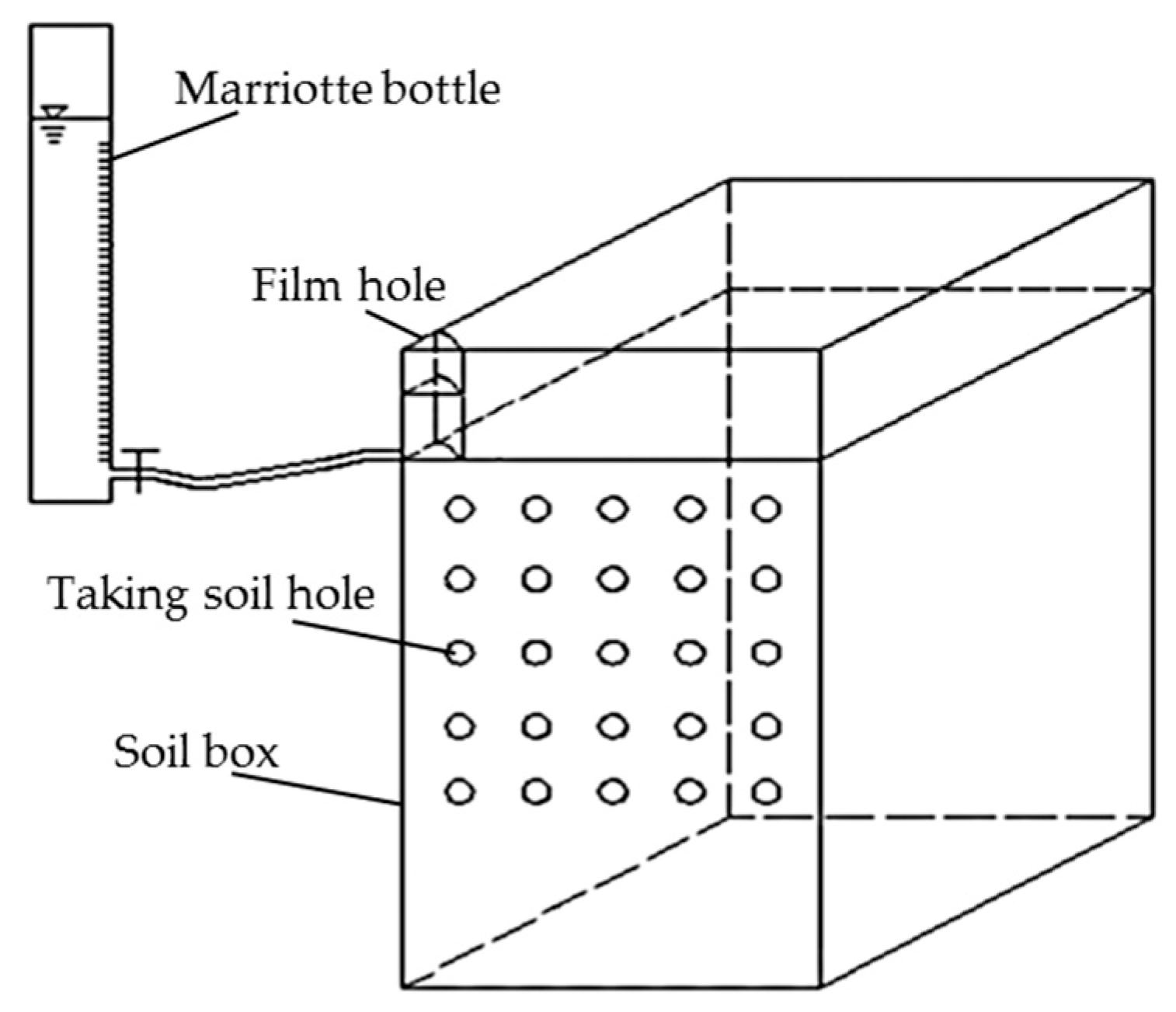
1. Introduction
Water resources are crucial for the production and preservation of human beings, and the shortage of water resources throughout the world is becoming increasingly severe [
1,
2]. The arid and semi-arid region in Northwest China has low rainfall and large evaporation capacity, so water resources, particularly agricultural water, are scarce in this region [
3,
4]. To solve the problem of water shortage in this area, water-saving irrigation technologies, such as sprinkler irrigation and drip irrigation, are widely used. However, for farmers in poor areas, the cost of advanced irrigation systems is relatively high, which is not conducive to their promotion and application. Therefore, a relatively cheap and efficient irrigation technology is urgently required in poorer areas [
5].
In recent years, mulch irrigation has become a high-yielding and efficient agricultural practice, with global applications which can reduce water evaporation, maintain soil temperature and humidity, prevent weed growth, and reduce the use of chemical fertilizers [
6,
7,
8,
9,
10,
11]. Due to the advantages of plastic film mulch, plastic film currently accounts for the largest proportion of agricultural surface mulch [
12,
13]. Currently, China is the world’s largest consumer of plastic mulch, and has the world’s largest mulch area [
14]. With the development of mulching technology, film hole irrigation, a relatively new irrigation method, emerged as the times required [
15]. Film hole irrigation is similar to point source irrigation. Using this method, plastic film is laid flat in a field, and water is transported by plastic film and irrigated through crop holes and special irrigation holes [
16]. Compared to traditional surface irrigation methods, film hole irrigation significantly improves the efficiency of water use [
5,
15,
16,
17,
18]. Therefore, an in-depth study of film hole irrigation will have positive significance for water-saving irrigation.
With the rapid development of computer technology, HYDRUS and other software types have been widely used in the study of unsaturated flow in soil. Because the basic theory of film hole irrigation is not mature, most of the research is still in the stage of laboratory and simulation experiments. Although the laboratory and simulation experiments cannot fully reflect the real situation of the field, they can help us to understand the infiltration process of film hole irrigation more intuitively due to the limitations of many conditions in field experiments. For example, it is impossible to directly observe the shape of wetting body in field experiments, and it is very difficult to determine the distribution of soil water content of the wetting body. Therefore, it is necessary to carry out the laboratory and simulation experiments before the field experiments, in order to study the infiltration mechanism of film hole irrigation. Compared to laboratory experiments, the numerical simulation of film hole irrigation using HYDRUS software can intuitively understand the infiltration process, such as the shape of the wetting front, the distribution of water content in the wetting body, the change law of infiltration rate and the cumulative infiltration with infiltration time. In the past two decades, China has conducted a large number of laboratory and simulation experiments on film hole infiltration, mostly focusing on the infiltration characteristics of single point source and multiple point source of film hole irrigation, and established some empirical models [
15,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27]. Some scholars have discovered that the relationship between cumulative infiltration amount and infiltration time was consistent with the Kostiacov model under the condition of experiment [
25]. However, an empirical model is mainly based on soil infiltration experiment data, and different soil types often correspond to different fitting parameters. Before using an empirical model, a large amount of real experiment data is required in order to determine empirical parameters, which makes it difficult to popularize and apply an empirical model. However, physical models can effectively solve this problem. Fei et al. [
28] established a 3D infiltration model of film hole irrigation based on the Green-Ampt model, which has certain applicability. However, there is no corresponding analytic equation for this model, and calculation software is required to assist in calculating the cumulative infiltration, which, to a certain extent, limits the use of this model.
In fact, the water content distribution characteristics of the wetting body under film hole can more intuitively reflect the infiltration process of film hole irrigation. However, in recent years, most studies on the water content distribution characteristics of the wetting body of film hole irrigation have been qualitative studies, and some empirical models have been established [
29,
30]. However, quantitative models between the cumulative infiltration and the wetting body are still lacking, but different crops have different root distributions and different water requirements. In order to ensure the reasonable application of irrigation water and ensure the accurate supply of limited irrigation water to crop roots, it is necessary to understand the relationship between irrigation volume and water content distribution of the wetting body, which will provide the irrigation basis for water-saving irrigation. Based on this, in this paper, the distribution characteristics of the water content of wetting body were analyzed in laboratory experiments and HYDRUS numerical simulation experiments, and the quantitative relationship between irrigation volume and wetting body was established under the condition of experiments in order to provide some useful insights for accurate irrigation using film hole irrigation. It is expected that this study, under the condition of experiments, can provide some theoretical basis and references for the field experiment and application for film hole irrigation in future.
3. Results and Discussion
3.1. Verification for Numerical Simulation Experiment
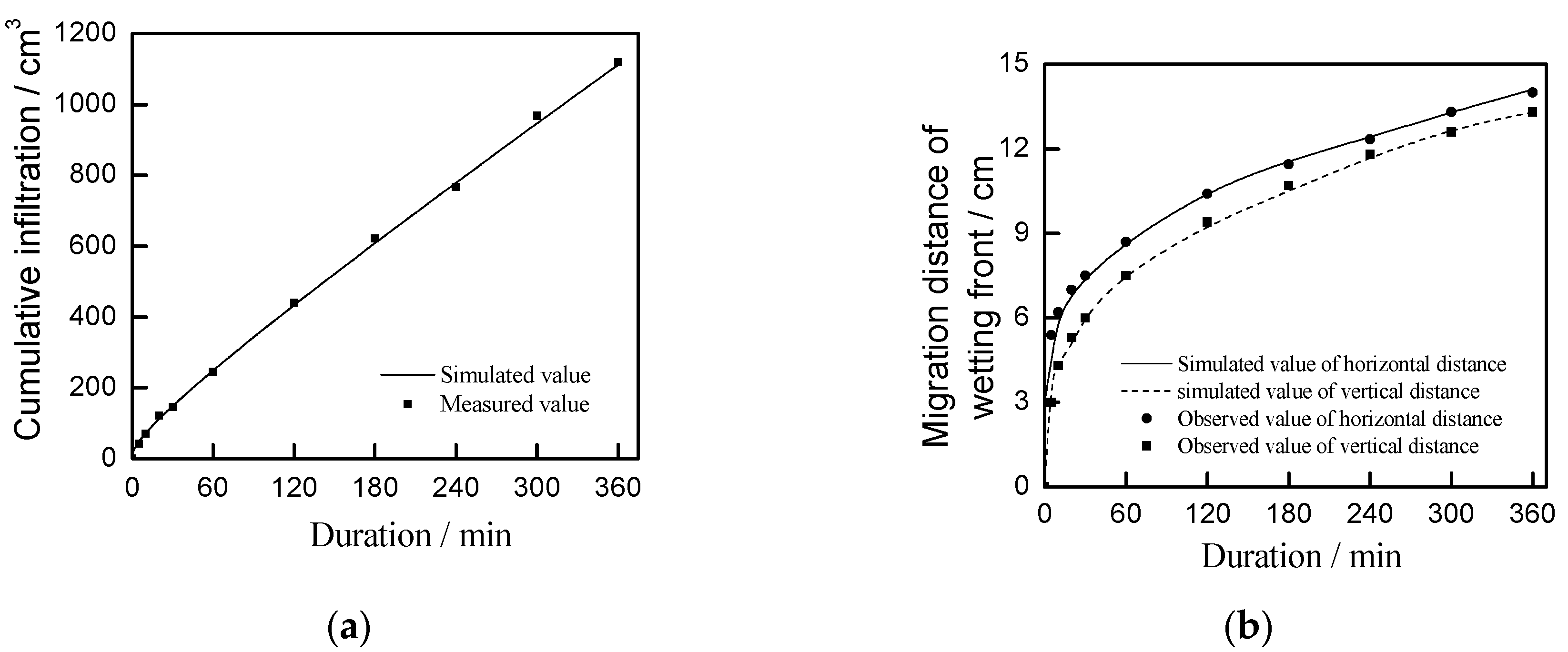
Figure 3a shows the comparison between the simulated and the measured values of cumulative infiltration for Xi’an silt loam, and its determination coefficient R
2 > 0.99.
Figure 3b shows the comparison between simulated and measured values of the migration distance of the wetting front, and its determination coefficients of horizontal and vertical directions are greater than 0.99. The coefficients are all close to 1, which proved that it was accurate to simulate the infiltration process of film hole irrigation using HYDRUS. Therefore, HYDRUS could be used in order to simulate the infiltration process of film hole irrigation in different soils.
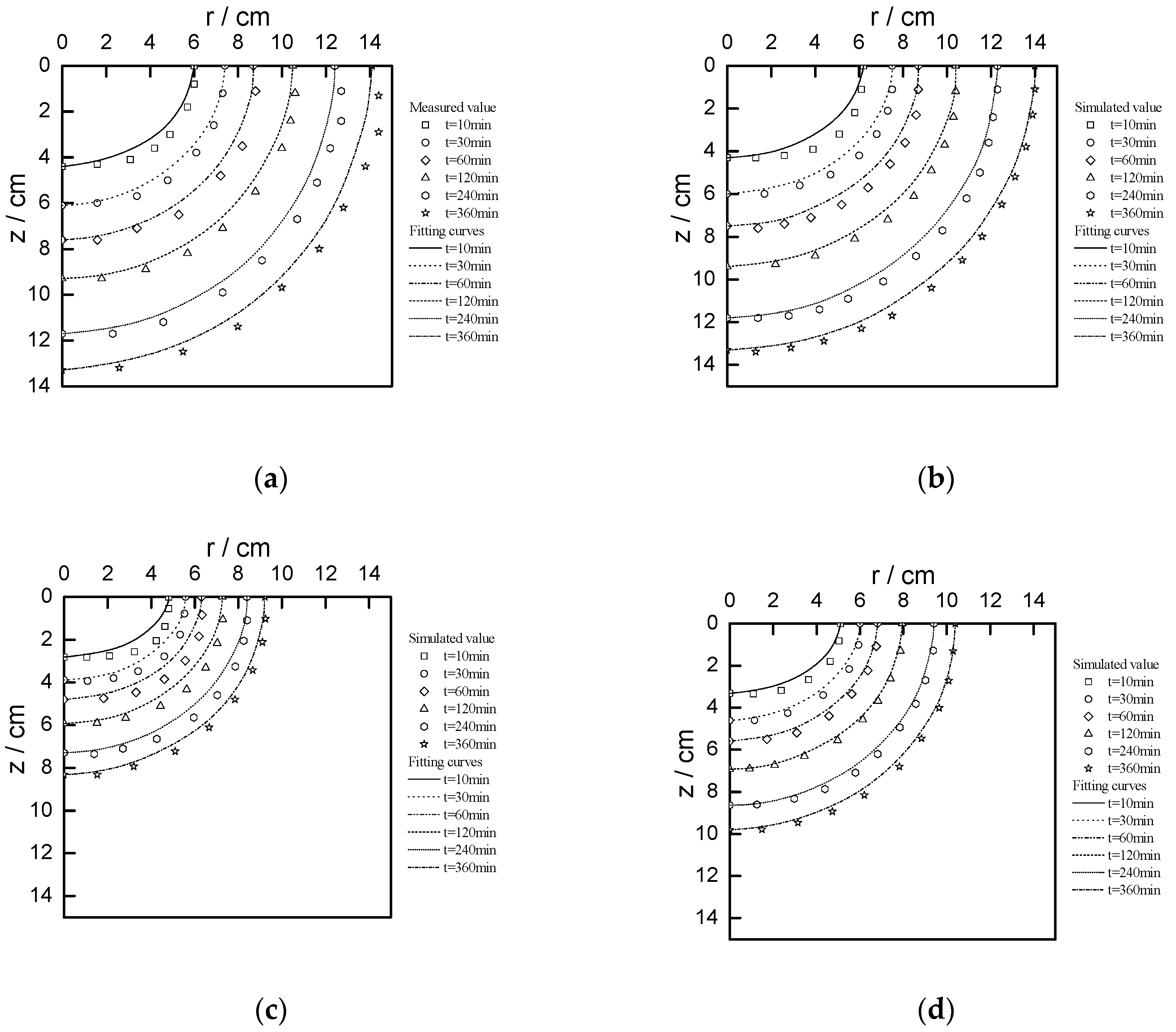
3.2. Wetting Front Shape
Figure 4 shows the variation process of the wetting front with time in five tests (one laboratory test, four numerical simulation tests). It can be observed from this figure that the wetting front continues to advance as the length of time increases, and the curve shape of the wetting front remains close to the elliptic curve at different times. Assuming that the migration distances of the wetting front in horizontal and vertical directions are respectively the semi-major semi-minor axis of the ellipse, the equation of the elliptic curve can then be expressed as:
where
and
are respectively the horizontal and vertical migration distances of the wetting front.
In order to further determine the fitting degree of the wetting front and the elliptic curve, a correlation analysis was conducted on the test results of five groups, as shown in
Table 2. The determination coefficient R
2 of five tests at different times ranges from 0.94 to 1.00, which is close to 1, indicating that it fitted well, so the shape of the wetting front could be expressed using the elliptic equation.
3.3. Distribution Characteristics of Water Content in the Wetting Body
In order to calculate the cumulative infiltration of the wetting body, both the shape of the wetting body and the distribution of the water content in wetting body should be known. In order to study the distribution characteristics of water content in the wetting body of film hole irrigation, a contour map of soil water content in Xi’an silt loam test was drawn (
Figure 5). It can be seen that the soil water content gradually decreases from the center of film hole to the surface of the wetting front, and the rate of change of water content increases gradually, which is consistent with the results of Fei et al. [
28] and Fan et al. [
29].
The water content contour map cannot be used to directly represent the distribution of water content through mathematical functions, but the distribution function of moisture content in the wetting body can be obtained by studying the distribution law of moisture content in the wetting body radius.
Suppose in
Figure 2 that “OF” is the wetting body radius,
β is the angle between the wetting body radius and horizontal direction. The water content distribution of the wetting body radius may be affected by
β, irrigation duration and soil type. Therefore, the control variable method was used to study the influence of various factors on water content distribution. As shown in
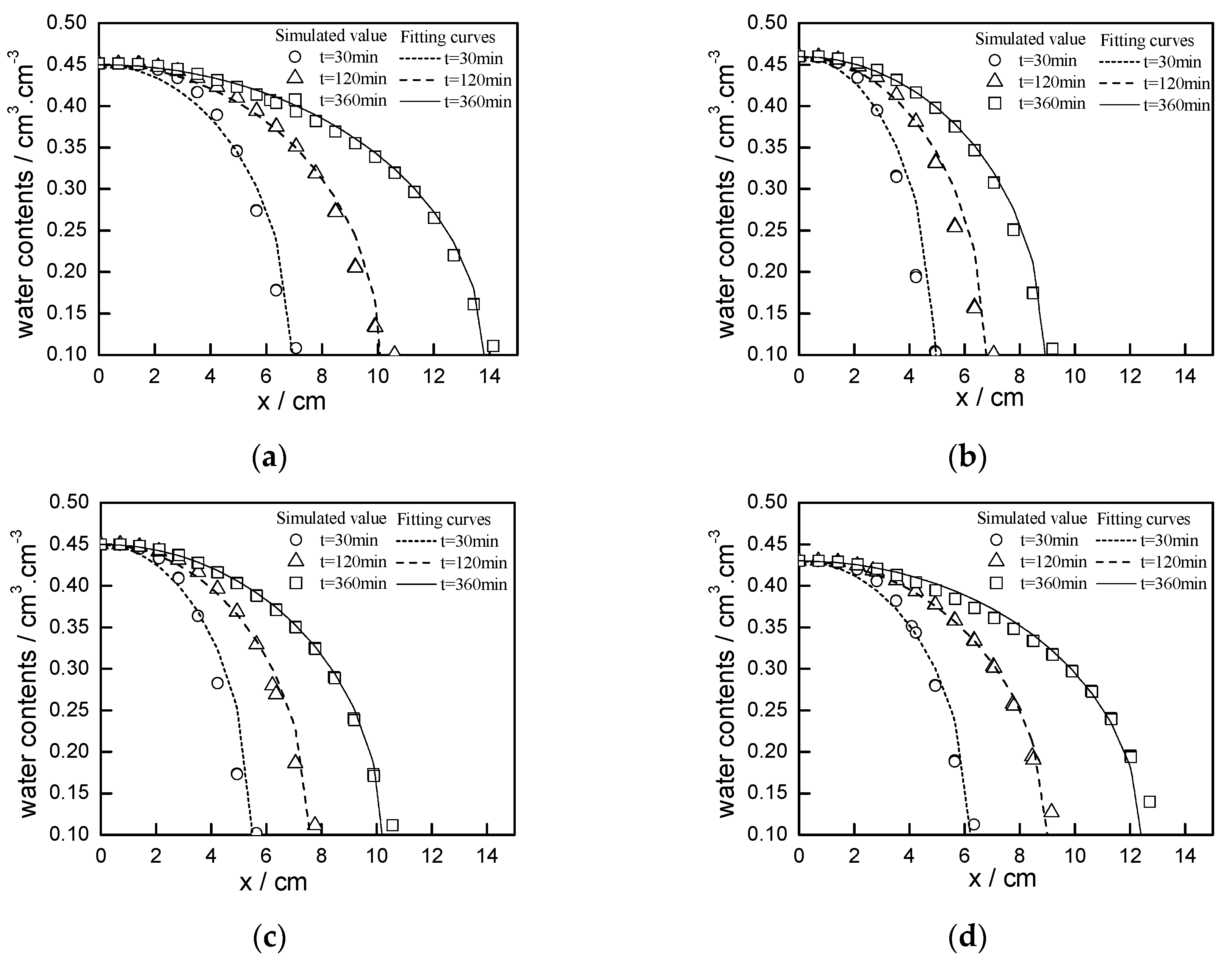
Figure 6, when
β takes different values, R
2 ranges from 0.99 to 1.00, all of which are close to 1, indicating that the water content distribution is well fitted to the elliptic curve. As shown in
Figure 7 and
Table 3, with different soil types and irrigation durations, the water content distribution of the wetting body radius is well fitted to the elliptic curve. Wang et al. [
31] showed that the distribution of soil water content under one-dimensional vertical infiltration can be represented by elliptic curve, and we discovered that the water content distribution of film hole irrigation has similar properties.
In summary, the water content distribution of wetting body radius can be expressed using an ellipse equation. Therefore, according to the characteristics of the ellipse, the water content at any point in the wetting body can be expressed as:
where
is the water content at any point in the wetting body (cm
3/cm
−3);
is the distance between this point and the center of the film hole (cm);
is the radius of the wetting body (cm); and function image of Equation (4) is shown in
Figure 8b. If the
and
of the wetting front are known, the equivalent radius can be expressed as the geometric mean value:
3.4. The Relationship between Cumulative Infiltration and Migration Distance of the Wetting Front
The shape of the wetting body can be expressed using Equation (3), and the water content distribution of the wetting body can be expressed using Equation (4). Therefore, the cumulative infiltration of the wetting body can be calculated by integrating and establishing the coordinate system as shown in
Figure 8a. An element with a volume of
in the wetting body can be chosen, and then the water content change in the element can be expressed as:
where
is element volume (cm
3);
is the water content change in the element (cm
3). The cumulative infiltration can be obtained by integrating Equation (6):
where Ω represents the integral range, i.e., the range of wetting body, Substitute Equation (4) into Equation (7) and calculate the integral result to obtain:
Equation (8) represents the relationship between the cumulative infiltration of film hole irrigation and the equivalent radius of the wetting body. Substitute Equation (5) into Equation (8) to obtain:
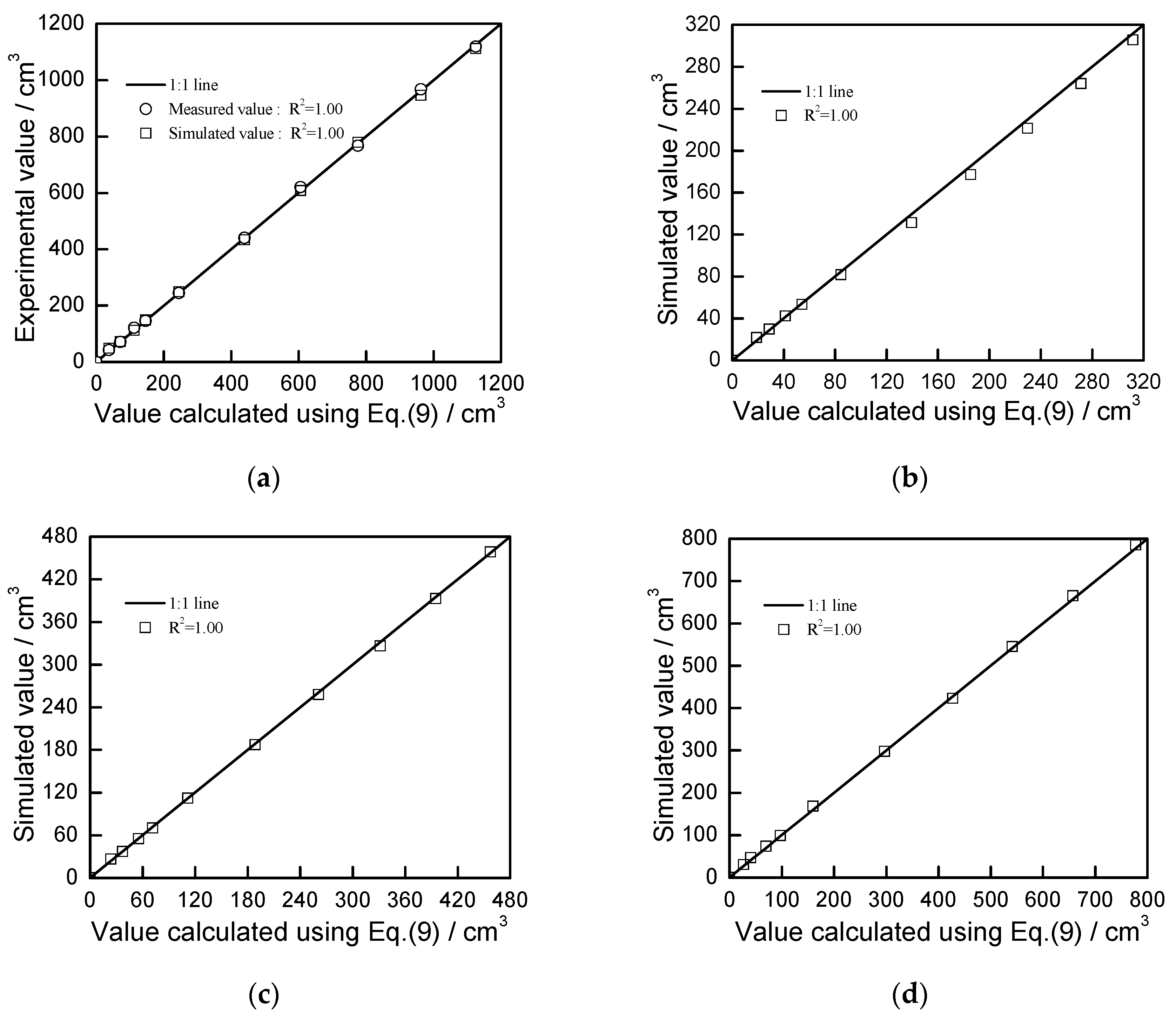
Equation (9) is the relationship between the cumulative infiltration of film hole irrigation and the migration distance of the wetting front. When the horizontal and vertical migration distances of the wetting front are known, cumulative infiltration can be calculated using Equation (9). In order to verify the accuracy of Equation (9), five test results were calculated, as shown in
Figure 9. It can be seen in
Figure 9 that the cumulative infiltration calculated by Equation (9) fits well with the experimental results, and the R
2 are all close to 1, which indicates that the cumulative infiltration of film hole irrigation can be accurately calculated using Equation (9) under the condition of experiment.
At present, the Kostiacov model is most widely used in film hole irrigation [
24,
26,
27], but the Kostiacov model was used to calculate the cumulative infiltration changing with time, while Equation (9) indicates the relationship between the cumulative infiltration and the size or shape of the wetting body. In addition, the Kostiacov model is chiefly based on soil infiltration experiment data, and different soil types often correspond to different fitting parameters. Before using the Kostiacov model, a large amount of real experiment data is required in order to determine model parameters. However, Equation (9) is a physical model for calculating cumulative infiltration, and for different soils, Equation (9) can be used directly without fitting parameters. Although this study is currently in the stage of laboratory and simulation experiment, the conclusion has obvious advantages over the traditional empirical model.
In addition, due to the differences of the different crops in different growth periods, the water distribution characteristic of the wetting body has played a critical role in the growth of crops, and its effect is far greater than the effect of irrigation time. Therefore, under the condition of experiment, Equation (9) is superior to traditional empirical models such as Kostiacov model, to some extent, in calculating the irrigation requirement of crops.
3.5. Irrigation Requirement for Crops
The distribution law of the water content of the wetting body and the calculation formula of cumulative infiltration has been obtained, but the root distribution range of different crops is different, and the required water content of different crops is also different. If the crop roots are distributed within a radius of
(
Figure 8c.), and the water content required by the root of the crop is greater than
, then the equivalent radius of the wetting body should be greater than the radius of the crop root distribution. Therefore, according to Equation (4), when
and
, the equivalent radius
can be calculated as follows:
when
, substitute Equation (10) into Equation (8), in order to obtain the irrigation requirement for crops under the film hole irrigation:
where
represents the irrigation requirement when the root radius of the crop is
and the required water content of the crop roots is
. Equation (11) is applicable for calculating the irrigation volume of the film hole irrigation under the condition that the basic characteristics of crops are known. As the current film hole irrigation is mostly experimental research under bare land conditions, Equation (11) has certain guiding significance for the promotion of the application of film hole irrigation in different crops, which can be popularized and applied to research into different crop conditions in the future.
So far, there exist few quantitative studies on the wetting body characteristics, and there are no reports on the application of film hole irrigation in different crops. Under conditions of the experiment, an ideal model was proposed in this paper, which can calculate the water requirements of different crops in different growth periods. Although Equation (11) is presented under the ideal condition of experiment, it will provide some useful insights for accurate irrigation using film hole irrigation. It is hoped that this study under the condition of experiments can provide some useful theoretical basis and reference for field experiment and application for film hole irrigation in the future.
4. Conclusions
Film hole irrigation is an efficient and water-saving irrigation method which has a wide application prospect in agricultural production. In this paper, using laboratory experiments and HYDRUS numerical simulation experiments, the water infiltration characteristics of film hole irrigation in four different soil types were studied, and the following conclusions were obtained:
(1) HYDRUS software can be used for simulating the process of film hole infiltration under the condition of the laboratory experiment. The simulated values of the cumulative infiltration amount and the migration distance of the wetting front fit well with the measured values, and the coefficient of determination between the simulated values and measured values is close to 1.
(2) For the four different soil types (Xi’an silt loam, silt, silt loam, loam) and different irrigation durations, the shape of the wetting body formed by film hole irrigation is similar to the ellipsoid of rotation, and therefore the curve of the wetting front can be expressed using the elliptic curve equation.
(3) For the four different soil types and the different irrigation durations, the water content distribution of the wetting body radius is approximately the elliptic curve. The cumulative infiltration model was established using the integral method under the condition of experiment. The model provides a theoretical basis for determining the irrigation volume of film hole irrigation and is superior to traditional empirical models such as the Kostiacov model, to some extent, in calculating the irrigation requirement of crops.
(4) Considering the different distribution ranges and the different water content requirements of crop roots, a calculation model of irrigation requirement under the condition of experiment was established, which could be used to calculate crop irrigation volumes based on the radius and required water content for crop roots. This conclusion has some useful implications for promoting the application of film hole irrigation in different crops.
(5) These conclusions are drawn based on the condition of the laboratory and simulation experiment, and the field experiment and application of film hole irrigation needs further in-depth study in future.