Studying the Wake of an Island in a Macro-Tidal Estuary
Abstract
:1. Introduction
2. Materials and Methods
2.1. In Situ Data Collection
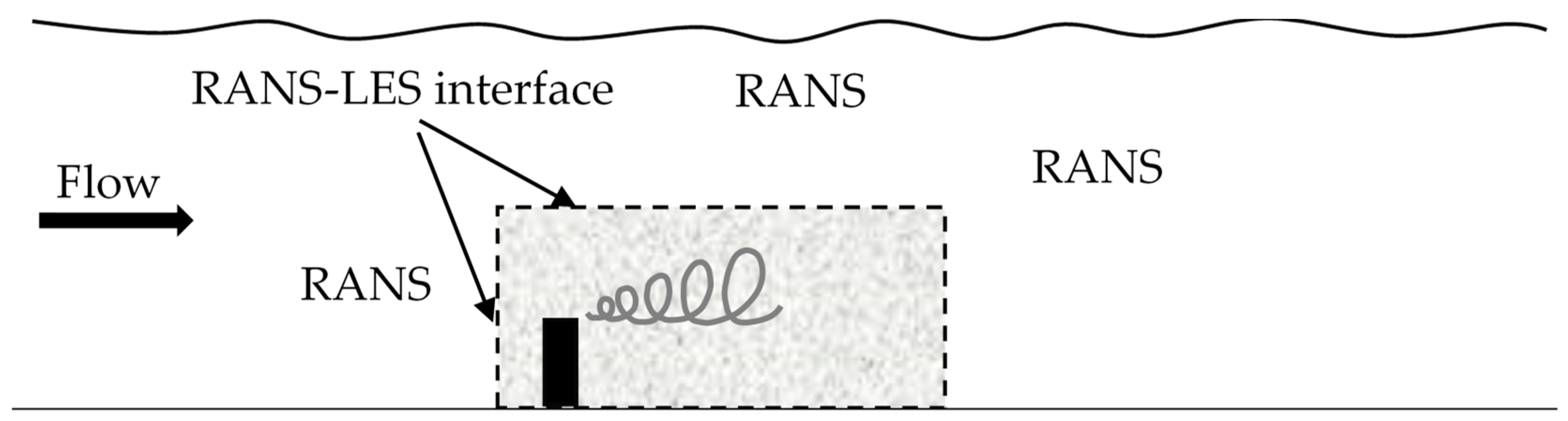
2.2. Modelling System and the Turbulence Models
2.3. Model Setup
2.4. Analysis Tools
3. Results and Discussion
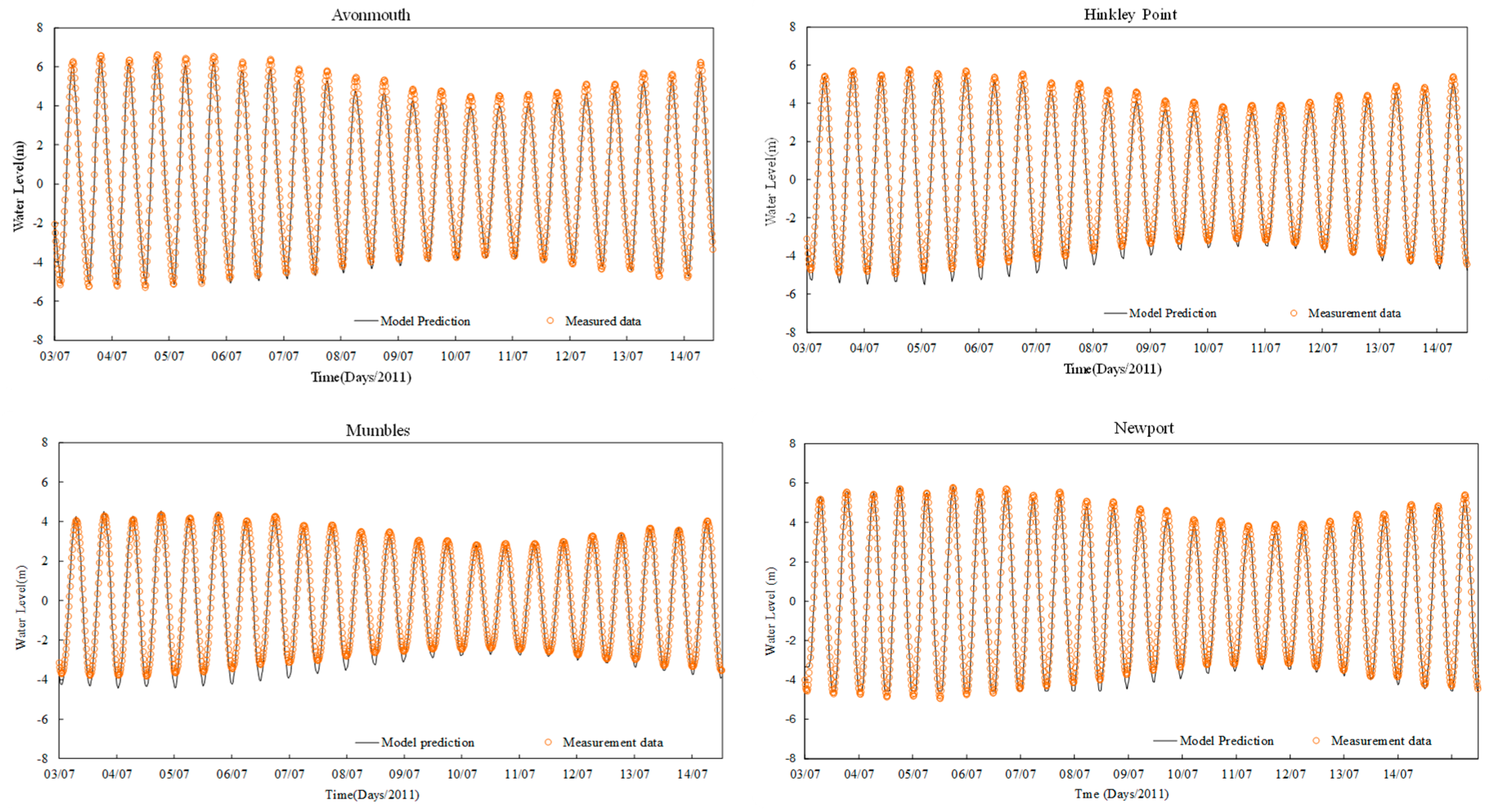
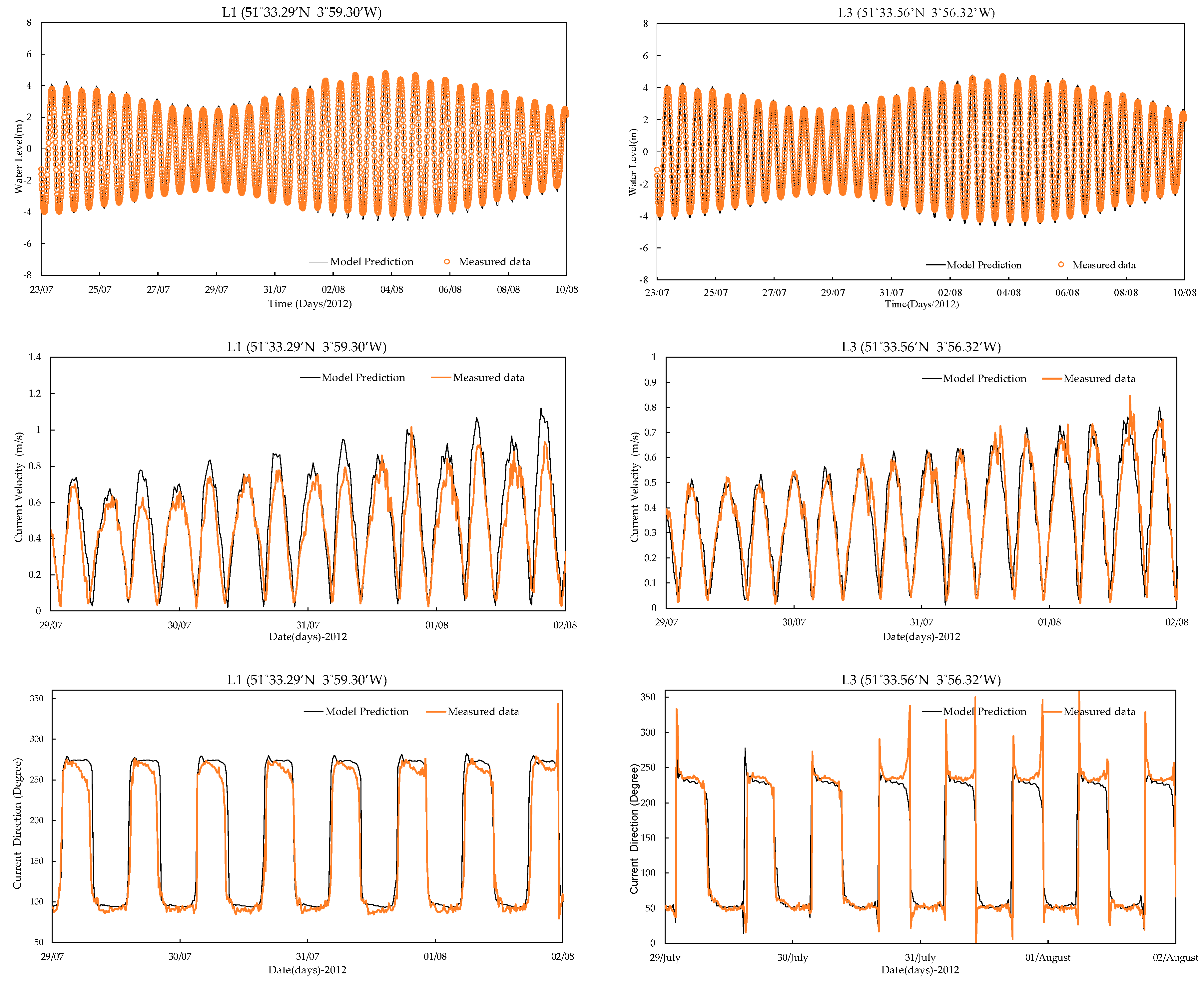
3.1. Model Calibration and Validation
3.2. Comparison of Turbulence Schemes
3.3. Comparison of Different k-ε Solvers
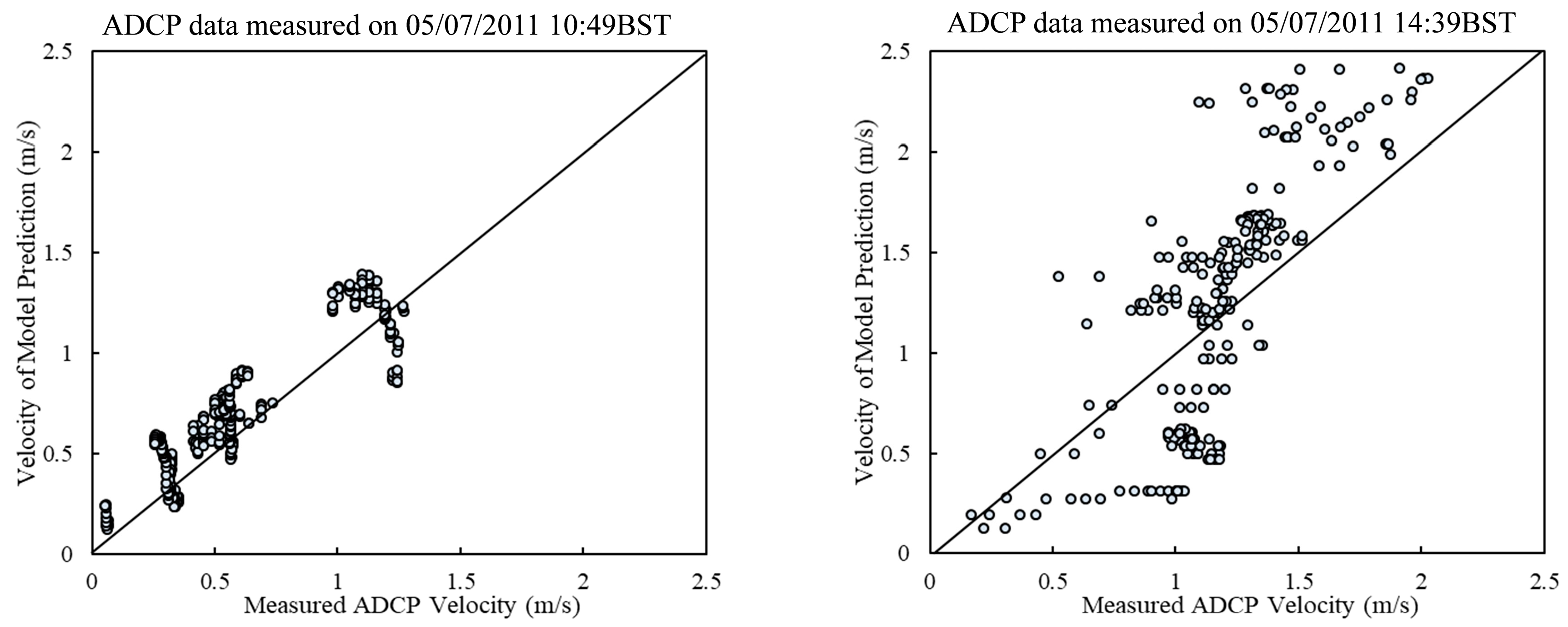
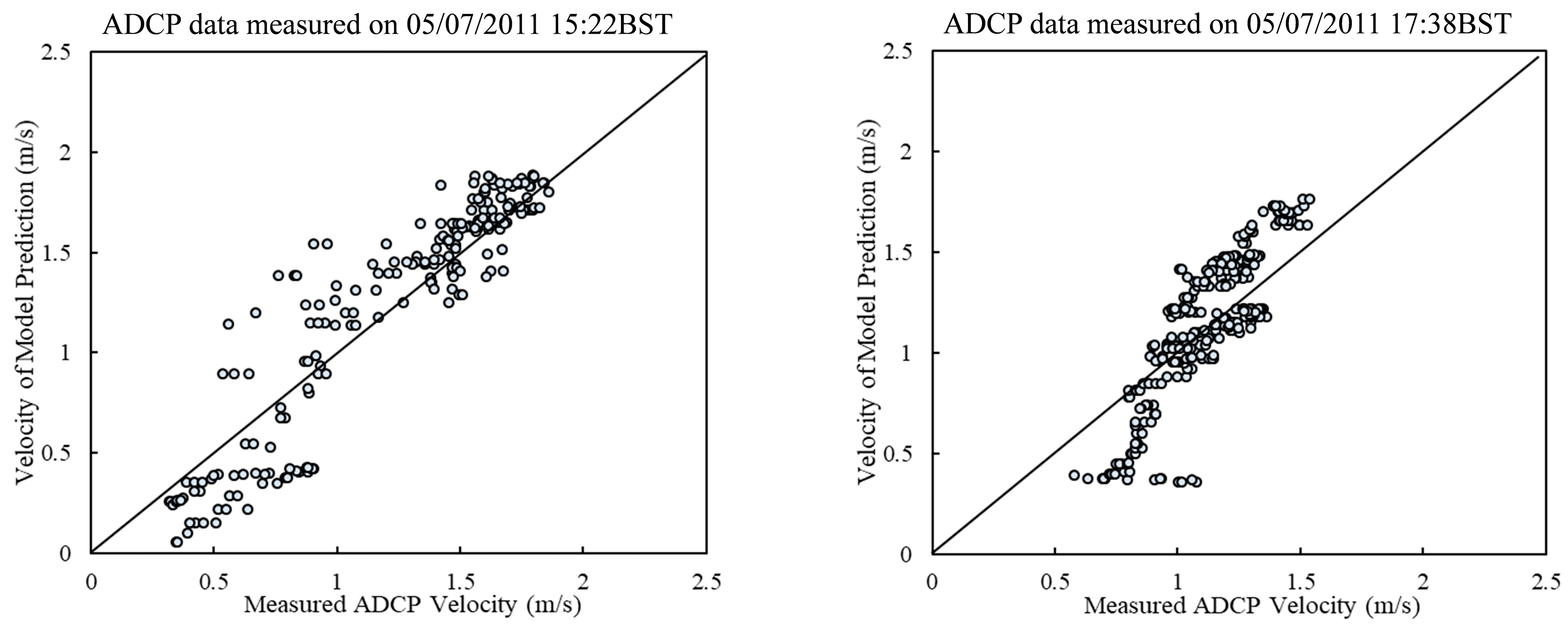
3.4. Model Comparison with ADCP Data
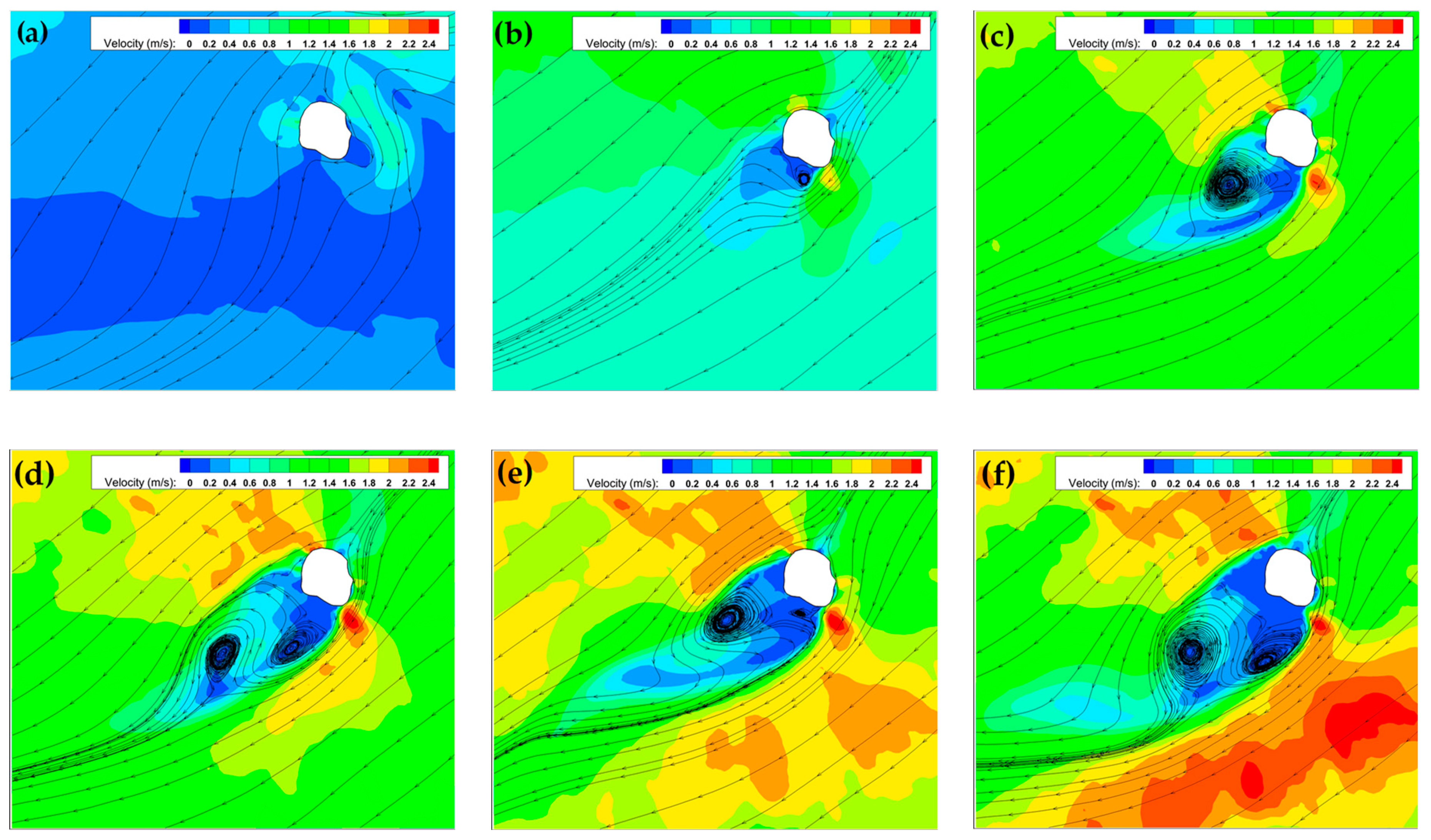
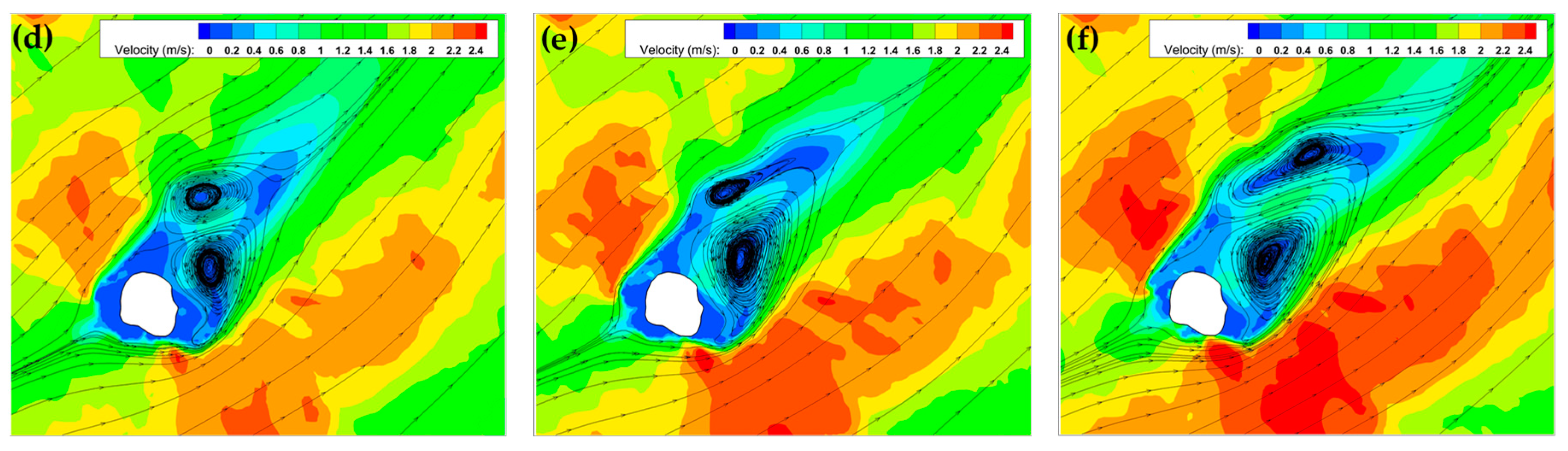
3.5. The Evolution of Wake in the Lee of Island
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Evans, P.; Lazarus, E.D.; Mason-Jones, A.; O’Doherty, D.M.; O’Doherty, T. Wake characteristics of a natural submerged pinnacle and implications for tidal stream turbine installations. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015. [Google Scholar]
- Estrade, P.; Middleton, J.H. A numerical study of island wake generated by an elliptical tidal flow. Cont. Shelf Res. 2010, 30, 1120–1135. [Google Scholar] [CrossRef]
- Hamner, W.M.; Hauri, I.R. Effects of island mass: Water flow and plankton pattern around a reef in the great barrier reef lagoon, Australia. Limnol. Oceanogr. 1981, 26, 1084–1102. [Google Scholar] [CrossRef]
- Pingree, R. The formation of the shambles and other banks by tidal stirring of the seas. J. Mar. Biol. Assoc. UK 1978, 58, 211–226. [Google Scholar] [CrossRef] [Green Version]
- Dyer, K.R.; Huntley, D.A. The origin, classification and modelling of sand banks and ridges. Cont. Shelf Res. 1999, 19, 1285–1330. [Google Scholar] [CrossRef]
- Neill, S.P.; Scourse, J.D. The formation of headland/island sandbanks. Cont. Shelf Res. 2009, 29, 2167–2177. [Google Scholar] [CrossRef]
- Li, Y.; Song, Z.; Peng, G.; Fang, X.; Li, R.; Chen, P.; Hong, H. Modeling Hydrodynamics in a harbor area in the Daishan Island, china. Water 2019, 11, 192. [Google Scholar] [CrossRef] [Green Version]
- Gou, H.; Luo, F.; Li, R.; Dong, X.; Zhang, Y. Modeling study on the hydrodynamic environmental impact caused by the sea for regional construction near the Yanwo Island in Zhoushan, China. Water 2019, 11, 1674. [Google Scholar] [CrossRef] [Green Version]
- Neill, S.P.; Jordan, J.R.; Couch, S.J. Impact of tidal energy converter (TEC) arrays on the dynamics of headland sand banks. Renew. Energy 2012, 37, 387–397. [Google Scholar] [CrossRef]
- Finkl, C.W.; Charlier, R. Electrical power generation from ocean currents in the straits of Florida: Some environmental considerations. Renew. Sustain. Energy Rev. 2009, 13, 2597–2604. [Google Scholar] [CrossRef]
- Stansby, P.; Chini, N.; Lloyd, P. Oscillatory flows around a headland by 3d modelling with hydrostatic pressure and implicit bed shear stress comparing with experiment and depth-averaged modelling. Coast Eng. 2016, 116, 1–14. [Google Scholar] [CrossRef]
- Dewey, R.; Richmond, D.; Garrett, C. Stratified tidal flow over a bump. J. Phys. Oceanogr. 2005, 35, 1911–1927. [Google Scholar] [CrossRef]
- Wolanski, E.; Imberger, J.; Heron, M.L. Island wakes in shallow coastal waters. J. Geophys. Res. 1984, 89, 10553–10569. [Google Scholar] [CrossRef]
- Lacey, R.J.; Rennie, C.D. Laboratory investigation of turbulent flow structure around a bed-mounted cube at multiple flow stages. J. Hydraul. Eng. 2011, 138, 71–84. [Google Scholar] [CrossRef]
- Arbic, B.K.; Richman, J.G.; Shriver, J.F.; Timko, P.G.; Metzger, E.J.; Wallcraft, A.J. Global modeling of internal tides: Within an eddying ocean general circulation model. Oceanography 2012, 25, 20–29. [Google Scholar] [CrossRef] [Green Version]
- Blaise, S.; Deleersnijder, E.; White, L.; Remacle, J.-F. Influence of the turbulence closure scheme on the finite-element simulation of the upwelling in the wake of a shallow-water island. Cont. Shelf Res. 2007, 27, 2329–2345. [Google Scholar] [CrossRef]
- Pattiaratchi, C.; James, A.; Collins, M. Island wakes and headland eddies: A comparison between remotely sensed data and laboratory experiments. J. Geophys. Res. 1987, 92, 783–794. [Google Scholar] [CrossRef]
- Coutisa, P.F.; Middleton, J.H. The physical and biological impact of a small island wake in the deep ocean. Deep Sea Res. Part I 2002, 49, 1341–1361. [Google Scholar] [CrossRef]
- Neill, S.P.; Elliott, A.J. In situ measurements of spring–neap variations to unsteady island wake development in the firth of forth, Scotland. Estuar. Coast. Shelf Sci. 2004, 60, 229–239. [Google Scholar] [CrossRef]
- Williams, R.D.; Brasington, J.; Hicks, M.; Measures, R.; Rennie, C.D.; Vericat, D. Hydraulic validation of two-dimensional simulations of braided river flow with spatially continuous aDcp data. Water Resour. Res. 2013, 49, 5183–5205. [Google Scholar] [CrossRef] [Green Version]
- Ahmadian, R.; Olbert, A.I.; Hartnett, M.; Falconer, R.A. Sea level rise in the severn estuary and bristol channel and impacts of a severn barrage. Comput. Geosci. 2014, 66, 94–105. [Google Scholar] [CrossRef]
- Dastgheib, A.; Roelvink, J.; Wang, Z. Long-term process-based morphological modeling of the Marsdiep tidal basin. Mar. Geol. 2008, 256, 90–100. [Google Scholar] [CrossRef]
- Jones, J.E.; Davies, A.M. Storm surge computations for the west coast of britain using a finite element model (TELEMAC). Ocean Dyn. 2008, 58, 337–363. [Google Scholar] [CrossRef] [Green Version]
- Falconer, R.A.; Wolanski, E.; Mardapitta-Hadjipandeli, L. Modeling tidal circulation in an island’s wake. J. Waterw. Port Coast. Ocean Eng. 1986, 112, 234–254. [Google Scholar] [CrossRef]
- Draper, S.; Borthwick, A.G.; Houlsby, G.T. Energy potential of a tidal fence deployed near a coastal headland. Philos. Trans. A Math. Phys. Eng. Sci. 2013, 371, 20120176. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Falconer, R.A.; Xia, J.; Lin, B.; Ahmadian, R. The Severn Barrage and other tidal energy options: Hydrodynamic and power output modeling. Sci. China Ser. E 2009, 52, 3413–3424. [Google Scholar] [CrossRef]
- Neill, S.P.; Angeloudis, A.; Robins, P.E.; Walkington, I.; Ward, S.L.; Masters, I.; Lewis, M.J.; Piano, M.; Avdis, A.; Piggott, M.D.; et al. Tidal range energy resource and optimization—Past perspectives and future challenges. Renew. Energy 2018, 127, 763–778. [Google Scholar] [CrossRef]
- Angeloudis, A.; Falconer, R.A.; Bray, S.; Ahmadian, R. Representation and operation of tidal energy impoundments in a coastal hydrodynamic model. Renew. Energy 2016, 99, 1103–1115. [Google Scholar] [CrossRef] [Green Version]
- Čož, N.; Ahmadian, R.; Falconer, R.A. Implementation of a full momentum conservative approach in modelling flow through tidal structures. Water 2019, 11, 1917. [Google Scholar] [CrossRef] [Green Version]
- Ahmadian, R.; Falconer, R.A.; Bockelmann-Evans, B. Comparison of hydro-environmental impacts for ebb-only and two-way generation for a severn barrage. Comput. Geosci. 2014, 71, 11–19. [Google Scholar] [CrossRef]
- Galland, J.C.; Goutal, N.; Hervouet, J.M. Telemac: A new numerical model for solving shallow water equations. Adv. Water Resour. 1991, 14, 138–148. [Google Scholar] [CrossRef]
- Hervouet, J.M. Hydrodynamics of Free Surface Flows: Modelling with the Finite Element Method, 1st ed.; John Wiley and Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Matta, E. Multi-dimensional Flow and Transport Modeling of a Surface Water Body in a Semi-Arid Area. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 2018. [Google Scholar]
- Jourieh, A. Multi-dimensional Numerical Simulation of Hydrodynamics and Transport Processes in Surface Water Systems in Berlin. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 2013. [Google Scholar]
- Elder, J. The dispersion of marked fluid in turbulent shear flow. J. Fluid Mech. 1959, 5, 544–560. [Google Scholar] [CrossRef]
- Fischer, H.B.; List, J.E.; Koh, R.C.Y.; Imberger, J.; Brooks, N.H. Mixing in Inland and Coastal Waters, 1st ed.; Academic Press: San Diego, CA, USA, 1979. [Google Scholar]
- Wu, W.; Wang, P.; Chiba, N. Comparison of five depth-averaged 2D turbulence models for river flows. Arch. Hydro-Eng. Environ. Mech. 2004, 51, 183–200. [Google Scholar]
- Steffler, P.; Blackburn, J. Two-dimensional depth averaged model of river hydrodynamics and fish habitat. In River2D User’s Manual; University of Alberta: Edmonton, AB, Canada, 2002; Available online: http://www.river2d.ualberta.ca/Downloads/documentation/River2D.pdf (accessed on 5 January 2020).
- Rastogi, A.K.; Rodi, W. Predictions of heat and mass transfer in open channels. J. Hydraul. Div. 1978, 104, 397–420. [Google Scholar]
- Rodi, W.; Constantinescu, G.; Stoesser, T. Large-eddy Simulation in Hydraulics; CRC Press: London, UK, 2013. [Google Scholar]
- Martins, F.A.B.D.C.; Fernandes, E.H. Hydrodynamic model intercomparison for the Patos Lagoon (Brazil). In Proceedings of EMS 2004 IASTED Org; Ubertini, L., Ed.; ACTA Press: Calgary, AB, Canada, 2008; pp. 123–126. [Google Scholar]
- Abu-Bakar, A.; Ahmadian, R.; Falconer, R.A. Modelling the transport and decay processes of microbial tracers in a macro-tidal estuary. Water Res. 2017, 123, 802–824. [Google Scholar] [CrossRef]
- Ji, Z.-G. Hydrodynamics and Water Quality: Modeling Rivers, Lakes, and Estuaries, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2017; p. 574. [Google Scholar]
- POL. Continental Shelf Model: Fine Grid(CS3 and CS3-3D). 2011. Available online: https://noc-innovations.co.uk/ocean-innovations/sites/ocean-innovations/files/documents/model-info-CS3.pdf (accessed on 5 January 2020).
- Maréchal, D. A Soil-Based Approach to Rainfall-Runoff Modelling in Ungauged Catchments for England and Wales. Ph.D. Thesis, Cranfield University, Silsoe, UK, 2004. Available online: https://dspace.lib.cranfield.ac.uk/handle/1826/915 (accessed on 2 January 2020).
- Walstra, D.; Van Rijn, L.; Blogg, H.; Van Ormondt, M. Evaluation of a hydrodynamic area model based on the COAST3D data at Teignmouth 1999. In Proceedings of the Coastal Dynamics 2001 Conference, Lund, Sweden, 11–15 June 2001. [Google Scholar]
- Pawlowicz, R.; Beardsley, B.; Lentz, S. Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE. Comput. Geosci. UK 2002, 28, 929–937. [Google Scholar] [CrossRef]
- Shewchuk, J.R. An Introduction to the Conjugate Gradient Method without the Agonizing Pain; Techical Report; School of Computer Science, Carnegie Mellon University: Pittsburgh, PA, USA, 1994. [Google Scholar]
- Tomczak, M. Island wakes in deep and shallow water. J. Geophys. Res. Oceans 1988, 93, 5153–5154. [Google Scholar] [CrossRef]
- Neill, S.P.; Elliott, A.J. Observations and simulations of an unsteady island wake in the Firth of Forth, Scotland. Ocean Dyn. 2004, 54, 324–332. [Google Scholar] [CrossRef]
- Cramp, A.; Coulson, M.; James, A.; Berry, J. A note on the observed and predicted flow patterns around islands—Flat Holm, the Bristol Channel. Int. J. Remote Sens. 1991, 12, 1111–1118. [Google Scholar] [CrossRef]
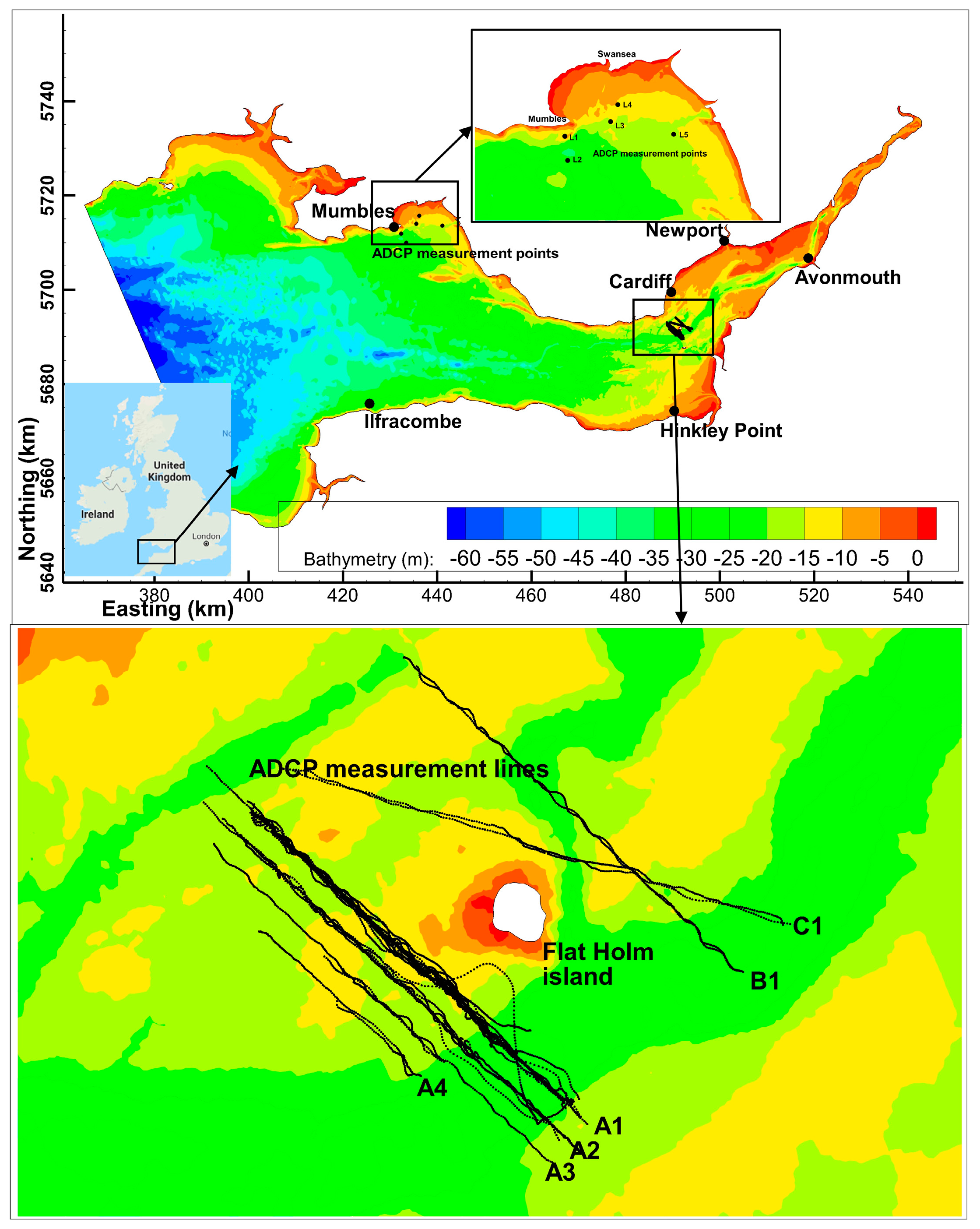




| Date | Time (GMT) | Measure Route | Date | Time (GMT) | Measure Route |
|---|---|---|---|---|---|
| 5 July 2011 | 09:05 | A1 | 1 August 2011 | 09:27 | A4 |
| 09:49 | A1 | 09:55 | A3 | ||
| 11:00 | A1 | 10:08 | A2 | ||
| 11:34 | A1 | 10:40 | A1 | ||
| 12:29 | A1 | 11:04 | A4 | ||
| 13:00 | A1 | 11:20 | A3 | ||
| 13:39 | A1 | 11:40 | A2 | ||
| 14:22 | A1 | 12:02 | A1 | ||
| 15:00 | A1 | 30 September 2011 | 09:37 | A2 | |
| 16:38 | A1 | 10:56 | A1 | ||
| 7 July 2011 | 15:10 | A2 | 11:49 | A2 | |
| 15:47 | A2 | 12:33 | A1 | ||
| 16:55 | B1 | ||||
| 15:37 | B1 | ||||
| 18:50 | D1 | ||||
| 19:31 | D1 |
| Water Level Statistical Analysis | ||
| Site | Coefficient of Determination (R2) | Root Mean Squared Error RMSE (m) |
| Avonmouth | 0.992 | 0.359 |
| Hinkley | 0.988 | 0.351 |
| Mumbles | 0.964 | 0.420 |
| Newport | 0.932 | 0.767 |
| ADCP L1 | 0.99 | 0.260 |
| ADCP L2 | 0.993 | 0.213 |
| ADCP L3 | 0.992 | 0.232 |
| ADCP L4 | 0.992 | 0.231 |
| ADCP L5 | 0.993 | 0.214 |
| Swansea Bay ADCPs Measured Velocity Magnitude | ||
| Site | Mean Absolute Error (MAE(m/s)) | Relative Mean Absolute Error (RMAE) |
| ADCP L1 | 0.122 | 0.222 |
| ADCP L2 | 0.083 | 0.145 |
| ADCP L3 | 0.057 | 0.142 |
| ADCP L4 | 0.045 | 0.191 |
| ADCP L5 | 0.076 | 0.230 |
| Tidal Gauges | Data Classification | M2 Amplitude (m) | M2 Phase (deg) | S2 Amplitude (m) | S2 Phase (deg) | N2 Amplitude (m) | N2 Phase (deg) |
|---|---|---|---|---|---|---|---|
| Mumbles | Observation | 3.16 | 59.98 | 1.25 | 227.95 | 0.37 | 282.18 |
| Prediction | 3.17 | 57.49 | 1.22 | 225.58 | 0.49 | 271.09 | |
| Difference | 0.56% | −4.15% | −2.82% | −1.04% | 33.26% | −3.93% | |
| Hinkley | Observation | 3.97 | 66.84 | 1.58 | 243.97 | 0.63 | 285.55 |
| Prediction | 4.03 | 65.56 | 1.55 | 238.59 | 0.61 | 283.40 | |
| Difference | 1.49% | −1.94% | −2.15% | −2.26% | −2.18% | −0.76% | |
| Newport | Observation | 4.18 | 86.51 | 1.65 | 267.42 | 0.63 | 307.12 |
| Prediction | 4.26 | 78.43 | 1.62 | 254.62 | 0.64 | 298.68 | |
| Difference | 1.96% | −9.35% | −1.63% | −4.79% | 1.57% | −2.75% | |
| Avonmouth | Observation | 4.30 | 91.48 | 1.69 | 274.06 | 0.67 | 313.47 |
| Prediction | 4.29 | 86.04 | 1.60 | 264.46 | 0.64 | 308.15 | |
| Difference | −0.38% | −5.96% | −5.45% | −3.50% | −4.83% | −1.70% |
| Scenario | Turbulence Model | MAE (m/s) | RMAE |
|---|---|---|---|
| 1 | Constant viscosity model | 0.3744 | 0.3672 |
| 2 | Elder model | 0.3950 | 0.3705 |
| 3 | k-ε model | 0.3597 | 0.3266 |
| 4 | Smagorinski model | 0.3735 | 0.3708 |
| Scenario | Solver in Telemac-2D Model with k-ε Turbulence Model | MAE | RMAE |
|---|---|---|---|
| 1 | Conjugate Gradient | 0.3597 | 0.3266 |
| 2 | Conjugate Residual | 0.3420 | 0.3129 |
| 3 | Conjugate Gradient on Normal Equation | 0.3556 | 0.3254 |
| 4 | Minimum Error | 0.3625 | 0.3298 |
| 5 | Squared Conjugate Gradient | 0.3607 | 0.3274 |
| 6 | BICGSTAB (Biconjugate Stabilized Gradient) | 0.3535 | 0.3231 |
| 7 | GMRES (Generalised Minimum Residual) | 0.3544 | 0.3251 |
| Figure | Moment | U0 (m/s) | D (m) | Kz (m2 s−1) | L (m) | P |
|---|---|---|---|---|---|---|
| Figure 9a | HW | 0.42 | 16.2 | 0.2 | 700 | 0.79 |
| Figure 9b | HW + 0.5 h | 0.51 | 15.4 | 0.2 | 700 | 0.86 |
| Figure 9c | HW + 1.0 h | 0.67 | 14.6 | 0.2 | 700 | 1.02 |
| Figure 9d | HW + 1.5 h | 0.82 | 14.1 | 0.2 | 700 | 1.16 |
| Figure 9e | HW + 2.0 h | 1.05 | 13.5 | 0.2 | 700 | 1.37 |
| Figure 9f | HW + 3.0 h | 1.09 | 13.1 | 0.2 | 700 | 1.34 |
| Figure 10a | LW | 0.62 | 8.5 | 0.2 | 700 | 0.32 |
| Figure 10b | LW + 0.5 h | 0.68 | 9.3 | 0.2 | 700 | 0.42 |
| Figure 10c | LW + 1.0 h | 0.79 | 9.9 | 0.2 | 700 | 0.55 |
| Figure 10d | LW + 1.5 h | 0.95 | 10.6 | 0.2 | 700 | 0.76 |
| Figure 10e | LW + 2.0 h | 0.89 | 11.9 | 0.2 | 700 | 0.90 |
| Figure 10f | LW + 3.0 h | 1.1 | 12.4 | 0.2 | 700 | 1.21 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, B.; Ahmadian, R.; Evans, P.; Falconer, R.A. Studying the Wake of an Island in a Macro-Tidal Estuary. Water 2020, 12, 1225. https://doi.org/10.3390/w12051225
Guo B, Ahmadian R, Evans P, Falconer RA. Studying the Wake of an Island in a Macro-Tidal Estuary. Water. 2020; 12(5):1225. https://doi.org/10.3390/w12051225
Chicago/Turabian StyleGuo, Bin, Reza Ahmadian, Paul Evans, and Roger A. Falconer. 2020. "Studying the Wake of an Island in a Macro-Tidal Estuary" Water 12, no. 5: 1225. https://doi.org/10.3390/w12051225
APA StyleGuo, B., Ahmadian, R., Evans, P., & Falconer, R. A. (2020). Studying the Wake of an Island in a Macro-Tidal Estuary. Water, 12(5), 1225. https://doi.org/10.3390/w12051225







