The Dynamic Yield Response Factor of Alfalfa Improves the Accuracy of Dual Crop Coefficient Approach under Water and Salt Stress
Abstract
:1. Introduction
2. Materials and Methods
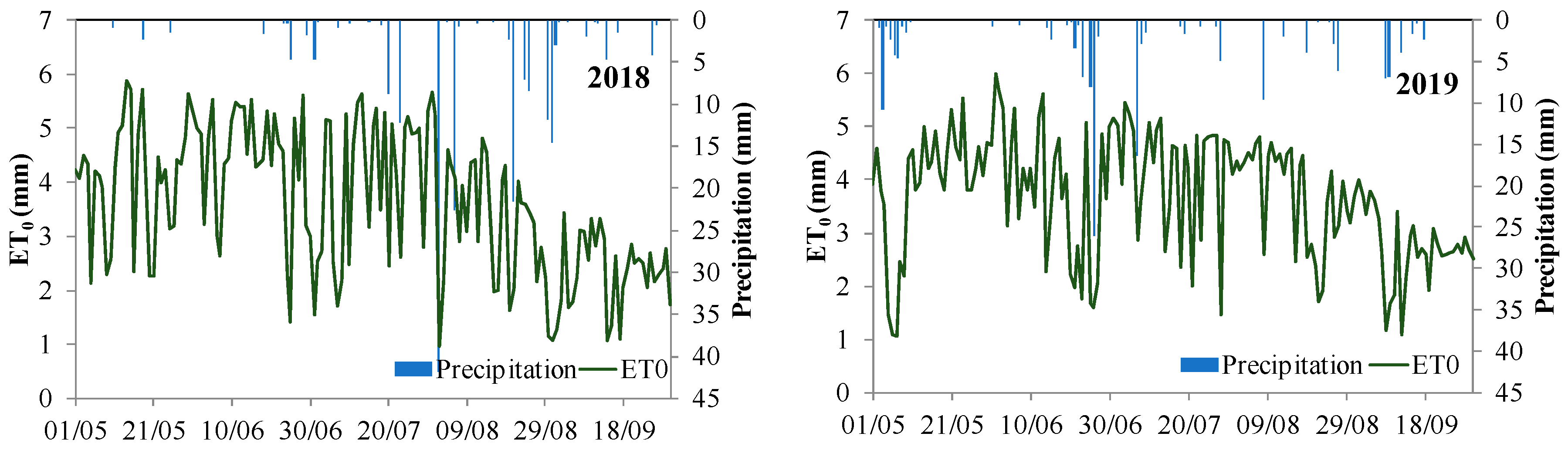
2.1. Experimental Site and Design
2.2. Field Measurements
2.3. The Dual Kc Approach
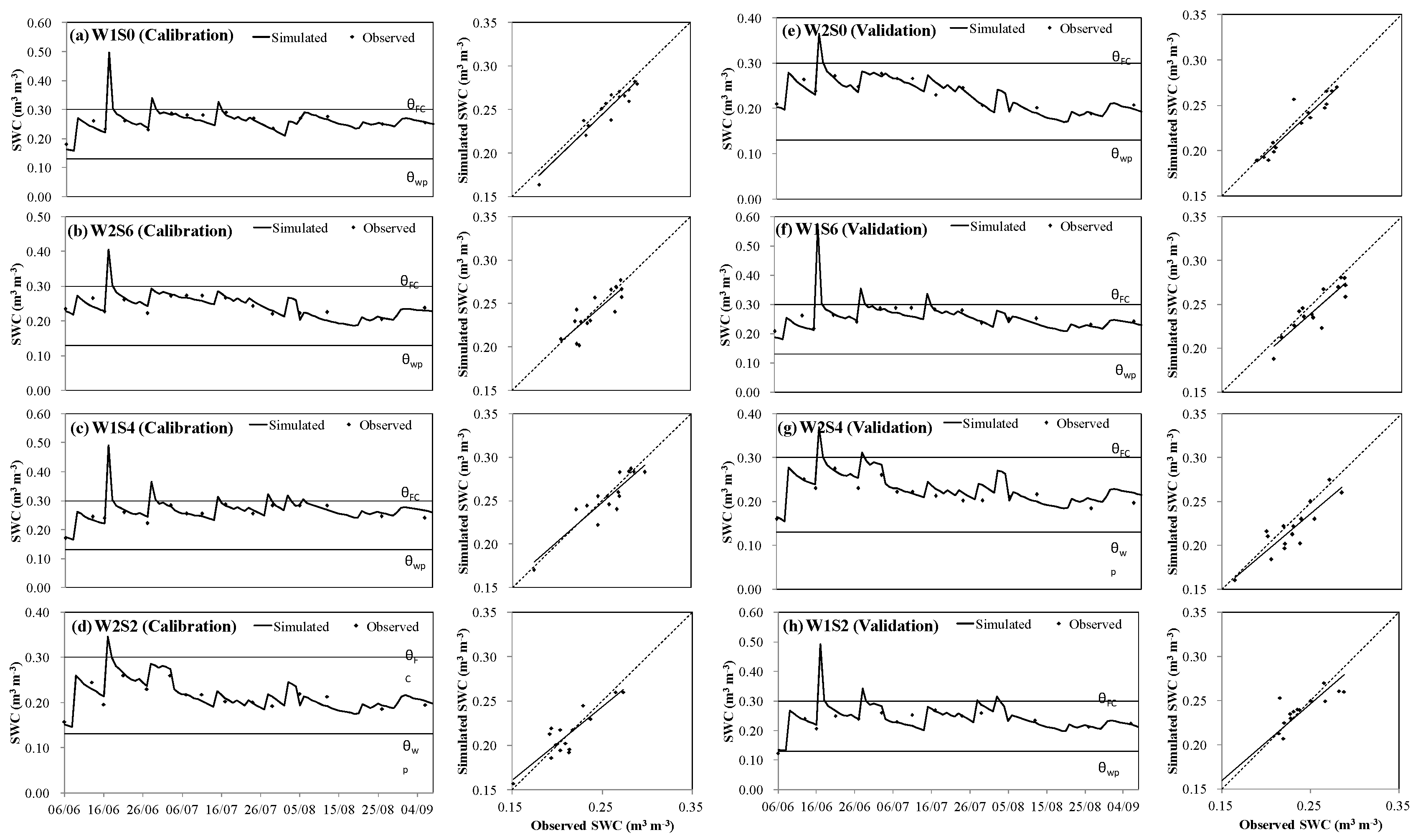
2.4. Model Calibration and Validation
3. Results and Discussion
3.1. Daily Crop Coefficients and ET Components
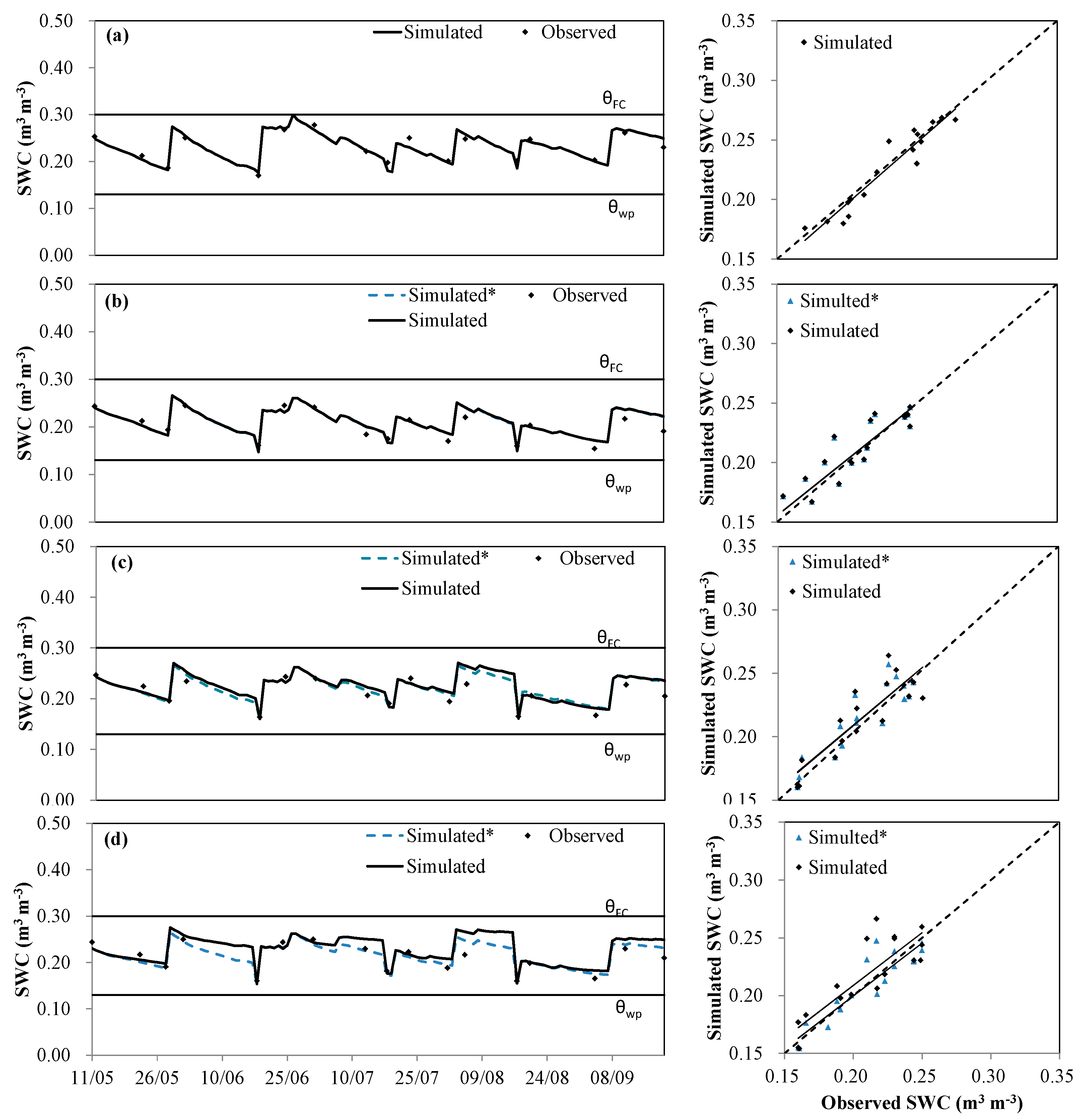
3.2. Evaluation of the Effect of Dynamic Ky on ET
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rengasamy, P. World salinization with emphasis on Australia. J. Exp. Bot. 2006, 57, 1017–1023. [Google Scholar] [CrossRef] [Green Version]
- Singh, A. Poor-drainage-induced salinization of agricultural lands: Management through structural measures. Land Use Policy 2019, 82, 457–463. [Google Scholar] [CrossRef]
- Lindenmayer, R.B.; Hansen, N.C.; Brummer, J.; Pritchett, J.G. Deficit irrigation of alfalfa for water-savings in the Great Plains and Intermountain West: A review and analysis of the literature. Agron. J. 2011, 103, 45–50. [Google Scholar] [CrossRef]
- Schneekloth, J.; Andale, A. Seasonal Water Needs and Opportunities for Limited Irrigation for Colorado Crops. Colorado State University Extension, 2009. Available online: https://extension.colostate.edu (accessed on 24 April 2020).
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper No.56; FAO-Food and Agriculture Organization of the United Nations: Rome, Italy, 1998; p. 300. [Google Scholar]
- Cavero, J.; Faci, J.M.; Medina, E.T.; Martínez-Cob, A. Alfalfa forage production under solid-set sprinkler irrigation in a semiarid climate. Agric. Water Manag. 2017, 191, 184–192. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Su, D. Alfalfa water use and yield under different sprinkler irrigation regimes in north arid regions of China. Sustainability 2017, 9, 1–15. [Google Scholar]
- Skaggs, T.H.; Poss, J.A.; Shouse, P.J.; Grieve, C.M. Irrigating forage crops with saline waters: 1. Volumetric lysimeter studies. Vadose Zone J. 2006, 5, 815–823. [Google Scholar] [CrossRef]
- Cao, X.; Li, H.; Zheng, H.; Wang, J.; Feng, Y. Water consumption characteristic and water requirement calculation of alfalfa under different drip irrigation treatments. Water Sav. Irrig. 2016, 12, 15–19, (In Chinese with English abstract). [Google Scholar]
- Greenwood, K.L.; Lawson, A.R.; Kelly, K.B. The water balance of irrigated forages in northern Victoria, Australia. Agric. Water Manag. 2009, 96, 847–858. [Google Scholar] [CrossRef]
- Hunsaker, D.J.; Pinter, P.J., Jr.; Cai, H. Alfalfa basal crop coefficients for FAO-56 procedures in the desert regions of the southwestern US. Trans. ASAE 2002, 45, 1799–1815. [Google Scholar] [CrossRef]
- Jensen, M.E.; Allen, R.G. Evolution of practical ET estimating methods. In Proceedings of the National Irrigation Symposium Decennial Symposium, Phoenix, AZ, USA, 14–16 November 2000. [Google Scholar]
- Anapalli, S.S.; Ahuja, L.R.; Gowda, P.H.; Ma, L.; Marek, G.; Evett, S.R.; Howell, T.A. Simulation of crop evapotranspiration and crop coefficients with data in weighing lysimeters. Agric. Water Manag. 2016, 177, 274–283. [Google Scholar] [CrossRef] [Green Version]
- Agam, N.; Evett, S.R.; Tolk, J.A.; Kustas, W.P.; Colaizzi, P.D.; Alfieri, J.G.; McKee, L.G.; Copeland, K.S.; Howell, T.A.; Chávez, J.L. Evaporative loss from irrigated interrows in a highly advective semi-arid agricultural area. Adv. Water Resour. 2012, 50, 20–30. [Google Scholar] [CrossRef] [Green Version]
- Pereira, L.S.; Paredes, P.; Rodrigues, G.C.; Neves, M. Modeling malt barley water use and evapotranspiration partitioning in two contrasting rainfall years. Assessing AquaCrop and SIMDualKc models. Agric. Water Manag. 2015, 159, 239–254. [Google Scholar] [CrossRef]
- Wei, Z.; Paredes, P.; Liu, Y.; Chi, W.W.; Pereira, L.S. Modelling transpiration, soil evaporation and yield prediction of soybean in North China Plain. Agric. Water Manag. 2015, 147, 43–53. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, Y.; Xu, D.; Zhao, N.; Lei, B.; Rosa, R.D.; Paredes, P.; Paço, T.A.; Pereira, L.S. The dual crop coefficient approach to estimate and partitioning evapotranspiration of the winter wheat–summer maize crop sequence in North China Plain. Irrig. Sci. 2013, 31, 1303–1316. [Google Scholar] [CrossRef]
- Zhao, N.; Liu, Y.; Cai, J.; Paredes, P.; Rosa, R.D.; Pereira, L.S. Dual crop coefficient modelling applied to the winter wheat–summer maize crop sequence in North China Plain: Basal crop coefficients and soil evaporation component. Agric. Water Manag. 2013, 117, 93–105. [Google Scholar] [CrossRef]
- Zhao, P.; Li, S.; Li, F.; Du, T.; Tong, L.; Kang, S. Comparison of dual crop coefficient method and Shuttleworth–Wallace model in evapotranspiration partitioning in a vineyard of northwest China. Agric. Water Manag. 2015, 160, 41–56. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S. Estimating crop coefficients from fraction of groundcover and height. Irrig. Sci. 2009, 28, 17–34. [Google Scholar] [CrossRef] [Green Version]
- Howell, T.A.; Evett, S.R.; Tolk, J.A.; Schneider, A.D. Evapotranspiration of full-, deficit-irrigated, and dryland cotton on the northern Texas high plains. J. Irrig. Drain. Eng. 2004, 130, 277–285. [Google Scholar] [CrossRef]
- Paco, T.A.; Ferreira, M.I.; Rosa, R.D.; Paredes, P.; Rodrigues, G.C.; Conceicao, N.; Pacheco, C.A.; Pereira, L.S. The dual crop coefficient approach using a density factor to simulate the evapotranspiration of a peach orchard: SIMDualKc model versus eddy covariance measurements. Irrig. Sci. 2012, 30, 115–126. [Google Scholar] [CrossRef]
- Salarian, M.; Alizadeh, A.; Davary, K.; Ansari, H. The impact of water stress and salinity on water requirement and crop coefficient of greenhouse bell pepper. Adv. Environ. Biol. 2014, 8, 88–99. [Google Scholar]
- Pereira, L.S. Water, agriculture and food: Challenges and issues. Water Resour. Manag. 2017, 31, 2985–2999. [Google Scholar] [CrossRef]
- Rosa, R.D.; Ramos, T.B.; Pereira, L.S. The dual Kc approach to assess maize and sweet sorghum transpiration and soil evaporation under saline conditions: Application of the SIMDualKc model. Agric. Water Manag. 2016, 177, 77–94. [Google Scholar] [CrossRef]
- Ran, H.; Kang, S.; Li, F.; Tong, L.; Ding, R.; Du, T.; Li, S.; Zhang, X. Performance of AquaCrop and SIMDualKc models in evapotranspiration partitioning on full and deficit irrigated maize for seed production under plastic film-mulch in an arid region of China. Agric. Syst. 2017, 151, 20–32. [Google Scholar] [CrossRef]
- Abdelraheem, A.; Esmaeili, N.; O’Connell, M.; Zhang, J. Progress and perspective on drought and salt stress tolerance in cotton. Ind. Crop. Prod. 2019, 130, 118–129. [Google Scholar] [CrossRef]
- Farooq, M.; Hussain, M.; Wakeel, A.; Siddique, K.H.M. Salt stress in maize: Effects, resistance mechanisms, and management. A review. Agron. Sustain. Dev. 2015, 35, 461–481. [Google Scholar] [CrossRef] [Green Version]
- Munns, R.; Tester, M. Mechanisms of salinity tolerance. Annu. Rev. Plant Biol. 2008, 59, 651–681. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, I.M.; Dai, H.; Zheng, W.; Cao, F.; Zhang, G.; Sun, D.; Wu, F. Genotypic differences in physiological characteristics in the tolerance to drought and salinity combined stress between Tibetan wild and cultivated barley. Plant Physiol. Biochem. 2013, 63, 49–60. [Google Scholar] [CrossRef]
- Wang, Q.M.; Huo, Z.L.; Zhang, L.D.; Wang, J.H.; Zhao, Y. Impact of saline water irrigation on water use efficiency and soil salt accumulation for spring maize in arid regions of China. Agric. Water Manag. 2016, 163, 125–138. [Google Scholar] [CrossRef]
- Yang, H.; Du, T.; Mao, X.; Ding, R.; Shukla, M.K. A comprehensive method of evaluating the impact of drought and salt stress on tomato growth and fruit quality based on EPIC growth model. Agric. Water Manag. 2019, 213, 116–127. [Google Scholar] [CrossRef]
- Zhang, H.; Li, D.; Zhou, Z.; Zahoor, R.; Chen, B.; Meng, Y. Soil water and salt affect cotton (Gossypium hirsutum L.) photosynthesis, yield and fiber quality in coastal saline soil. Agric. Water Manag. 2017, 187, 112–121. [Google Scholar] [CrossRef]
- Minhas, P.S.; Ramos, T.B.; Ben-Gal, A.; Pereira, L.S. Coping with salinity in irrigated agriculture: Crop evapotranspiration and water management issues. Agric. Water Manag. 2020, 227, 105832. [Google Scholar] [CrossRef]
- Paredes, P.; Wei, Z.; Liu, Y.; Xu, D.; Xin, Y.; Zhang, B.; Pereira, L.S. Performance assessment of the FAO AquaCrop model for soil water, soil evaporation, biomass and yield of soybeans in North China Plain. Agric. Water Manag. 2015, 152, 57–71. [Google Scholar] [CrossRef] [Green Version]
- Paredes, P.; D’Agostino, D.; Assif, M.; Todorovic, M.; Pereira, L.S. Assessing potato transpiration, yield and water productivity under various water regimes and planting dates using the FAO dual Kc approach. Agric. Water Manag. 2018, 195, 11–24. [Google Scholar] [CrossRef]
- Yuan, C.; Feng, S.; Huo, Z.; Ji, Q. Effects of deficit irrigation with saline water on soil water-salt distribution and water use efficiency of maize for seed production in arid Northwest China. Agric. Water Manag. 2019, 212, 424–432. [Google Scholar] [CrossRef]
- Hu, M.; Kang, S.; Zhang, J.; Li, F.; Du, T.; Tong, L. Potential use of saline water for irrigating shelterbelt plants in the arid region. Irrig. Drain. 2012, 61, 107–115. [Google Scholar] [CrossRef]
- Jiang, J.; Huo, Z.; Feng, S.; Zhang, C. Effect of irrigation amount and water salinity on water consumption and water productivity of spring wheat in Northwest China. Field Crop. Res. 2012, 137, 78–88. [Google Scholar] [CrossRef]
- Rosa, R.D.; Paredes, P.; Rodrigues, G.C.; Fernando, R.M.; Alves, I.; Pereira, L.S.; Allen, R.G. Implementing the dual crop coefficient approach in interactive software: 2. Model testing. Agric. Water Manag. 2012, 103, 62–77. [Google Scholar] [CrossRef]
- Ding, R.; Kang, S.; Zhang, Y.; Hao, X.; Tong, L.; Du, T. Partitioning evapotranspiration into soil evaporation and transpiration using a modified dual crop coefficient model in irrigated maize field with ground-mulching. Agric. Water Manag. 2013, 127, 85–96. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Smith, M.; Raes, D.; Wright, J.L. FAO-56 dual crop coefficient method for estimating evaporation from soil and application extensions. J. Irrig. Drain. Eng. 2005, 131, 2–13. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Pereira, L.S.; Fernando, R.M. Fluxes through the bottom boundary of the root zone in silty soils: Parametric approaches to estimate groundwater contribution and percolation. Agric. Water Manag. 2006, 84, 27–40. [Google Scholar] [CrossRef]
- Paredes, P.; Pereira, L.S.; Rodrigues, G.C.; Botelho, N.; Torres, M.O. Using the FAO dual crop coefficient approach to model water use and productivity of processing pea (Pisum sativum L.) as influenced by irrigation strategies. Agric. Water Manag. 2017, 189, 5–18. [Google Scholar] [CrossRef]
- Xu, C.; Liu, H.; Zhao, L. Calculating alfalfa irrigation quota by FAO Penman-Monteith equation. Trans. CSAE 2005, 21, 30–34, (In Chinese with English abstract). [Google Scholar]
- Tao, X.; Su, D.; Kou, D.; Qiao, Y. Effects of irrigation methods on growth and water use efficiency of alfalfa in arid northwest China. Acta Agrestia Sinica 2016, 24, 114–120, (In Chinese with English abstract). [Google Scholar]
- Qassim, A.; Dunin, F.; Bethune, M. Water balance of centre pivot irrigated pasture in northern Victoria, Australia. Agric. Water Manag. 2008, 95, 566–574. [Google Scholar] [CrossRef]
- Jiang, X.; Kang, S.; Tong, L.; Li, F.; Li, D.; Ding, R.; Qiu, R. Crop coefficient and evapotranspiration of grain maize modified by planting density in an arid region of northwest China. Agric. Water Manag. 2014, 142, 135–143. [Google Scholar] [CrossRef]
- Lovelli, S.; Perniola, M.; Ferrara, A.; Di Tommaso, T. Yield response factor to water (Ky) and water use efficiency of Carthamus tinctorius L. and Solanum melongena L. Agric. Water Manag. 2007, 92, 73–80. [Google Scholar] [CrossRef]
- Saeidi, R.; Sotoodehnia, A.; Etedali, H.R.; Nazari, B.; Kaviani, A. Effect of water salinity and soil nitrogen deficiency on Ks-coefficient and readily available water of maize. J. Water Soil 2018, 32, 865–878. [Google Scholar]



| Parameters. | Initial Values | Calibrated |
|---|---|---|
| Crop coefficients | ||
| Kcb ini | 0.3 | 0.3 |
| Kcb mid | 1.15 | 1.15 |
| Kcb end | 1.1 | 1.1 |
| Ky | 1.1 | 1.2 |
| p | 0.55 | 0.50 |
| Soil evaporation | ||
| REW (mm) | 6–10 | 10 |
| TEW (mm) | 15–30 | 30 |
| Ze (m) | 0.1–0.15 | 0.12 |
| Deep percolation | ||
| ap (mm) | 360 | 310 |
| bp | –0.0173 | –0.065 |
| Salinity | ||
| b (%/(dS m−1)) | 7.3 | 6.0 |
| ECe threshold (dS m−1) | 2.0 | 2.0 |
| Year | Treatments | b | R2 | RMSE (m3 m−3) | AAE (m3 m−3) | EF | dIA |
|---|---|---|---|---|---|---|---|
| 2018 | W1S0 | 1.00 | 0.91 | 0.011 | 0.009 | 0.84 | 0.96 |
| W2S0 | 0.92 | 0.89 | 0.011 | 0.009 | 0.86 | 0.96 | |
| W1S2 | 0.94 | 0.82 | 0.015 | 0.115 | 0.80 | 0.95 | |
| W2S2 | 0.94 | 0.78 | 0.014 | 0.012 | 0.74 | 0.94 | |
| W1S4 | 0.91 | 0.82 | 0.013 | 0.011 | 0.80 | 0.95 | |
| W2S4 | 0.89 | 0.77 | 0.017 | 0.014 | 0.63 | 0.91 | |
| W1S6 | 0.90 | 0.79 | 0.016 | 0.012 | 0.62 | 0.91 | |
| W2S6 | 0.89 | 0.70 | 0.013 | 0.011 | 0.64 | 0.91 | |
| 2019 | W1S0 | 1.02 | 0.91 | 0.010 | 0.008 | 0.89 | 0.97 |
| W2S2 | 0.94 | 0.81 | 0.014 | 0.012 | 0.78 | 0.95 | |
| W2S4 | 0.93 | 0.76 | 0.016 | 0.012 | 0.69 | 0.92 | |
| W2S6 | 0.91 | 0.72 | 0.020 | 0.016 | 0.61 | 0.90 | |
| 2019 * | W2S2 | 0.94 | 0.82 | 0.014 | 0.012 | 0.79 | 0.95 |
| W2S4 | 0.94 | 0.82 | 0.013 | 0.011 | 0.77 | 0.94 | |
| W2S6 | 0.92 | 0.83 | 0.013 | 0.010 | 0.82 | 0.95 |
| Year | Treatments | b | R2 | RMSE (mm−1) | AAE (mm d−1) | EF | dIA |
|---|---|---|---|---|---|---|---|
| 2018 | W1S0 | 0.97 | 0.90 | 0.744 | 0.629 | 0.64 | 0.92 |
| W2S0 | 0.97 | 0.87 | 0.716 | 0.598 | 0.63 | 0.91 | |
| W1S2 | 0.97 | 0.90 | 0.795 | 0.716 | 0.54 | 0.89 | |
| W2S2 | 0.92 | 0.87 | 0.795 | 0.688 | 0.59 | 0.90 | |
| W1S4 | 0.94 | 0.88 | 0.756 | 0.654 | 0.59 | 0.90 | |
| W2S4 | 0.90 | 0.87 | 0.793 | 0.643 | 0.67 | 0.92 | |
| W1S6 | 0.91 | 0.83 | 0.778 | 0.625 | 0.65 | 0.91 | |
| W2S6 | 0.90 | 0.76 | 0.773 | 0.636 | 0.53 | 0.89 | |
| 2019 | W1S0 | 0.99 | 0.90 | 0.651 | 0.583 | 0.53 | 0.90 |
| W2S2 | 1.00 | 0.89 | 0.748 | 0.669 | 0.40 | 0.87 | |
| W2S4 | 1.07 | 0.87 | 0.769 | 0.664 | 0.39 | 0.88 | |
| W2S6 | 1.09 | 0.82 | 0.777 | 0.641 | 0.39 | 0.88 | |
| 2019 * | W2S2 | 1.00 | 0.89 | 0.749 | 0.670 | 0.40 | 0.87 |
| W2S4 | 1.02 | 0.89 | 0.764 | 0.674 | 0.40 | 0.87 | |
| W2S6 | 1.01 | 0.84 | 0.764 | 0.638 | 0.41 | 0.88 |
| Treatments | ET (mm) | Ya (kg ha−1) | Ky |
|---|---|---|---|
| W1S0 | 383 | 19979 | 1.20 |
| W2S0 | 361 | 18579 | 1.23 |
| W1S2 | 376 | 19530 | 1.23 |
| W2S2 | 344 | 17219 | 1.37 |
| W1S4 | 354 | 17881 | 1.42 |
| W2S4 | 304 | 13463 | 1.60 |
| W1S6 | 332 | 15810 | 1.60 |
| W2S6 | 301 | 12009 | 1.87 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Kang, S.; Ding, R.; Du, T.; Tong, L.; Li, S. The Dynamic Yield Response Factor of Alfalfa Improves the Accuracy of Dual Crop Coefficient Approach under Water and Salt Stress. Water 2020, 12, 1224. https://doi.org/10.3390/w12051224
Hu Y, Kang S, Ding R, Du T, Tong L, Li S. The Dynamic Yield Response Factor of Alfalfa Improves the Accuracy of Dual Crop Coefficient Approach under Water and Salt Stress. Water. 2020; 12(5):1224. https://doi.org/10.3390/w12051224
Chicago/Turabian StyleHu, Yanzhe, Shaozhong Kang, Risheng Ding, Taisheng Du, Ling Tong, and Sien Li. 2020. "The Dynamic Yield Response Factor of Alfalfa Improves the Accuracy of Dual Crop Coefficient Approach under Water and Salt Stress" Water 12, no. 5: 1224. https://doi.org/10.3390/w12051224





