Comparative Hydrodynamic Analysis by Using Two−Dimensional Models and Application to a New Bridge
Abstract
:1. Introduction
2. Materials and Methods
2.1. Hydrodinamic Model
2.2. Comparative Analysis
2.3. Description of the SHEE Software
3. Study Case for a New Bridge
4. Results and Discussion
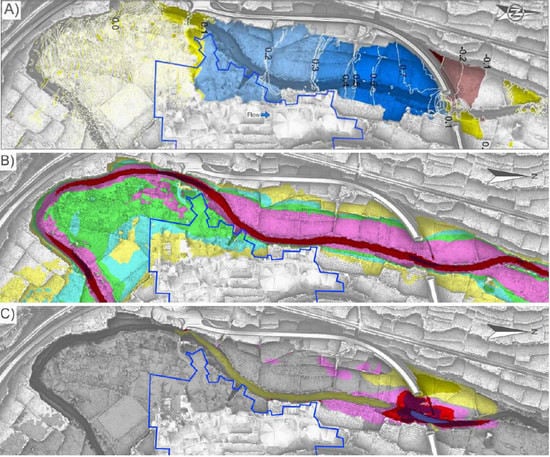
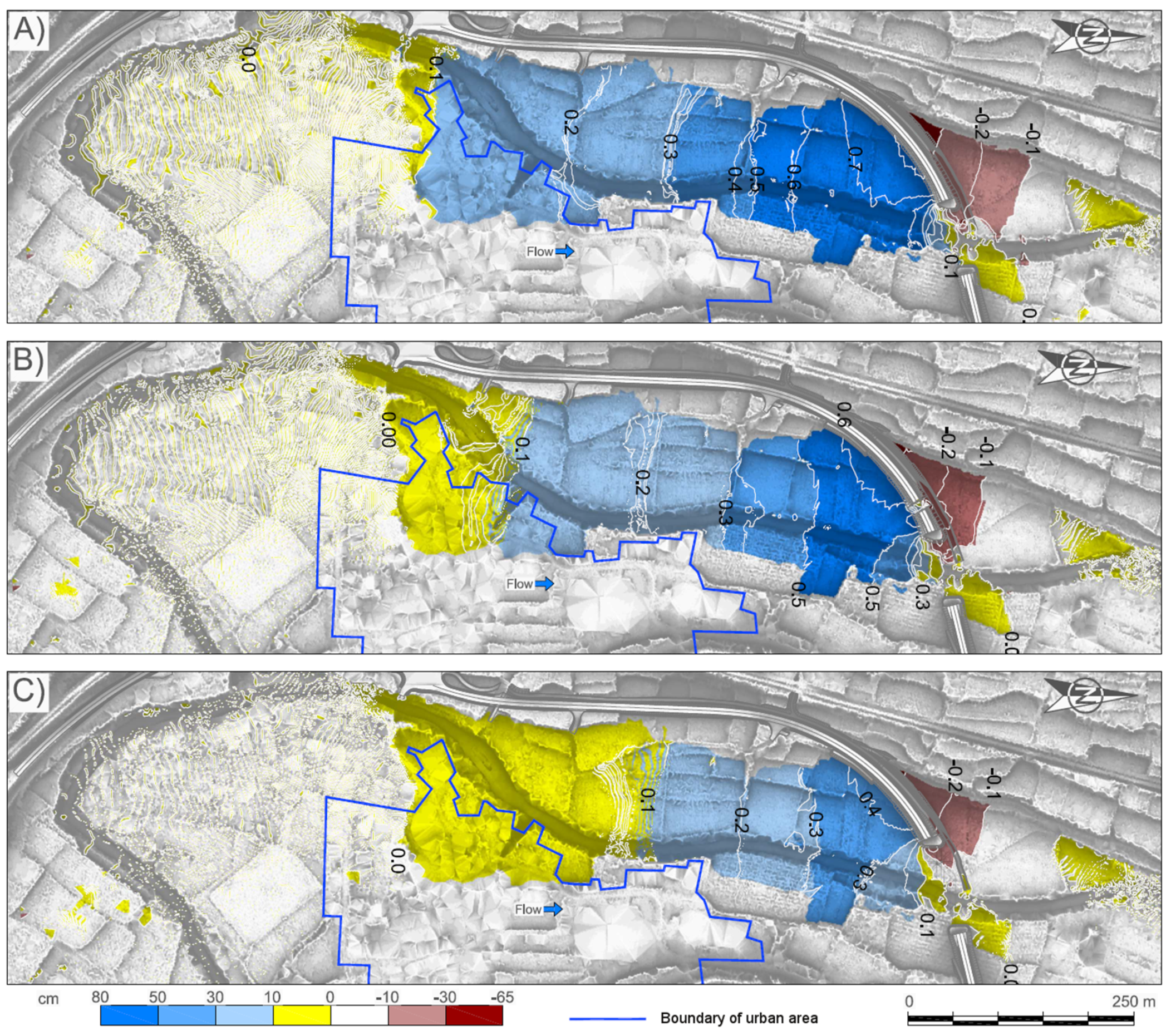
4.1. Study of Bridge Alternatives and Selection of the Most Suitable One
4.2. Hydraulic Detail Study of the Suitable Alternative (Option 3)
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tayefi, V.; Lane, S.N.; Hardy, R.J.; Yu, D. A comparison of one- and two-dimensional approaches to modelling flood inundation over complex upland floodplains. Hydrol. Process. 2007, 21, 3190–3202. [Google Scholar] [CrossRef]
- Cook, A.; Merwade, V. Effect of topographic data, geometric configuration and modeling approach on flood inundation mapping. J. Hydrol. 2009, 377, 131–142. [Google Scholar] [CrossRef]
- Costabile, P.; Macchione, F. Analysis of one-dimensional modelling for flood routing in compound channels. Water Resour. Manag. 2012, 26, 1065–1087. [Google Scholar] [CrossRef]
- Costabile, P.; Macchione, F. Enhancing river model set-up for 2-D dynamic flood modelling. Environ. Model. Softw. 2015, 67, 89–107. [Google Scholar] [CrossRef]
- Papaioannou, G.; Loukas, A.; Vasiliades, L.; Aronica, G.T. Flood inundation mapping sensitivity to riverine spatial resolution and modelling approach. Nat. Hazards 2016, 83, 117–132. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Tegos, A.; Oikonomou, A.; Pagana, V.; Koukouvinos, A.; Mamassis, N.; Koutsoyiannis, D.; Efstratiadis, A. Comparative evaluation of 1D and quasi-2D hydraulic models based on benchmark and real-world applications for uncertainty assessment in flood mapping. J. Hydrol. 2016, 534, 478–492. [Google Scholar] [CrossRef]
- Liu, Z.; Merwade, V.; Jafarzadegan, K. Investigating the role of model structure and surface roughness in generating flood inundation extents using one- and two-dimensional hydraulic models. J. Flood Risk Manag. 2019, 12, e12347. [Google Scholar] [CrossRef] [Green Version]
- Fleischmann, A.; Paiva, R.; Collischonn, W. Can regional to continental river hydrodynamic models be locally relevant? A cross-scale comparison. J. Hydrol. 2019, 3, 100027. [Google Scholar] [CrossRef]
- Mignot, E.; Paquier, A.; Haider, S. Modeling floods in a dense urban area using 2D shallow water equations. J. Hydrol. 2006, 327, 186–199. [Google Scholar] [CrossRef] [Green Version]
- Apel, H.; Aronica, G.T.; Kreibich, Z.A.; Thieken, H. Flood risk analyses—How detailed do we need to be? Nat. Hazards 2009, 49, 79–98. [Google Scholar] [CrossRef]
- Yu, D.; Lane, S.N. Interactions between subgrid-scale resolution, feature representation and grid-scale resolution in flood inundation modelling. Hydrol. Process. 2011, 25, 36–53. [Google Scholar] [CrossRef] [Green Version]
- Pina, R.D.; Ochoa-Rodriguez, S.; Simões, N.E.; Mijic, A.; Marques, A.S.; Maksimović, C. Semi- vs. Fully-distributed urban stormwater models: Model set up and comparison with two real case studies. Water 2016, 8, 58. [Google Scholar] [CrossRef] [Green Version]
- Ashraf, U.A.; Flint, M.M. Analysis of peak flow distribution for bridge collapse sites. Water 2020, 12, 52. [Google Scholar] [CrossRef] [Green Version]
- Rehan, B.M. Accounting public and individual flood protection measures in damage assessment: A novel approach for quantitative assessment of vulnerability and flood risk associated with local engineering adaptation options. J. Hydrol. 2018, 563, 863–873. [Google Scholar] [CrossRef]
- Ward, P.J.; Jongman, B.; Aerts, J.C.J.H.; Bates, P.D.; Botzen, W.J.W.; Diaz Loaiza, A.; Hallegatte, S.; Kind, J.M.; Kwadijk, J.; Scussolini, P.; et al. A global framework for future costs and benefits of river-flood protection in urban areas. Nat. Clim. Chang. 2017, 7, 642–646. [Google Scholar] [CrossRef]
- Aerts, J.C.J.H.; Botzen, W.J.W.; Emanuel, K.; Lin, N.; De Moel, H.; Michel-Kerjan, E.O. Climate adaptation: Evaluating flood resilience strategies for coastal megacities. Science 2014, 344, 473–475. [Google Scholar] [CrossRef]
- Bladé, E.; Cea, L.; Corestein, G.; Escolano, E.; Puertas, J.; Vázquez-Cendón, E.; Dolz, J.; Coll, A. Iber: Herramienta de simulación numérica del flujo en ríos. In Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería; Elsevier: Amsterdam, The Netherlands, 2014; Volume 30, pp. 1–10. ISSN 0213-1315. [Google Scholar] [CrossRef] [Green Version]
- Cea, L.; Bladé, E. A simple and efficient unstructured finite volume scheme for solving the shallow water equations in overland flow applications. Water Resour. Res. 2015, 51, 5464–5486. [Google Scholar] [CrossRef] [Green Version]
- Cea, L.; Bermudez, M.; Puertas, J.; Blade, E.; Corestein, G.; Escolano, E.; Conde, A.; Bockelmann-Evans, B.; Ahmadian, R. IberWQ: New simulation tool for 2D water quality modelling in rivers and shallow estuaries. J. Hydroinformatics 2016, 18, 816–830. [Google Scholar] [CrossRef] [Green Version]
- García-Feal, O.; González-Cao, J.; Gómez-Gesteira, M.; Cea, L.; Domínguez, J.M.; Fornella, A. An accelerated tool for flood modelling based on Iber. Water 2018, 10, 1459. [Google Scholar] [CrossRef] [Green Version]
- García-Feal, O.; Gonzalez-Cao, J.; Cea, L.; Formella, A.; Domínguez, J.M. Iber as a tool to analyse flooding scenarios. Proceedings of First International Electronic Conference on the Hydrological Cycle; MDPI: Basel, Switzerland, 2017. [Google Scholar] [CrossRef]
- Sanz-Ramos, M.; Amengual, A.; Bladé, E.; Romero, R.; Roux, H. Flood forecasting using a coupled Hydrological and Hydraulic Model (based on FVM) and high resolution Meteorological Model. In Proceedings of the River Flow 2018—Ninth International Conference on Fluvial Hydraulics, Lyon-Villeurbanne, France, 5–8 September 2018; Paquier, A., Rivière, N., Eds.; E3S Web of Conferences 40 (September): Lyon-Villeurbanne, France, 2018; p. 06028. [Google Scholar] [CrossRef]
- Sopelana, J.; Cea, L.; Ruano, S. A continuous simulation approach for the estimation of extreme flood inundation in coastal river reaches affected by meso and macrotides. Nat. Hazards 2018, 93, 1337–1358. [Google Scholar] [CrossRef]
- Bermúdez, M.; Zischg, A.P. Sensitivity of flood loss estimates to building representation and flow depth attribution methods in micro-scale flood modelling. Nat. Hazards 2018, 92, 1633–1648. [Google Scholar] [CrossRef] [Green Version]
- Bermúdez, M.; Cea, L.; Puertas, J.; Sopelana, J.; Ruano, S. Application of least squares support vector machine regression for historical reconstruction and real-time prediction of flood inundation. In Proceedings of the 5th IAHR Europe Congress, Trento, Italy, 12−14 June 2018. [Google Scholar]
- Uber, M.; Nord, G.; Legout, C.; Cea, L. A combination of high resolution hydro-sedimentary data and distributed numerical modelling to understand internal catchment erosion processes. In Proceedings of the XXII Computational Methods in Water Resources, Saint−Malo, France, 3−7 June 2018. [Google Scholar]
- Cea, L.; Legout, C.; Grangeon, T.; Nord, G. Impact of model simplifications on soil erosion predictions: Application of the GLUE methodology to a distributed event-based model at the hillslope scale. Hydrol. Process. 2016, 30, 1096–1113. [Google Scholar] [CrossRef]
- Corestein, G.; Bladé, E.; Niñerola, D. Modelling bedload transport for mixed flows in presence of a non−erodible bed layer. In River Flow 2014; CRC Press: Boca Raton, FL, USA, 2014; pp. 1611–1618. [Google Scholar] [CrossRef]
- Cea, L.; Bladé, E.; Corestein, G.; Fraga, I.; Espinal, M.; Puertas, J. Comparative analysis of several sediment transport formulations applied to dam−break flows over erodible beds. In EGU General Assembly Abstracts; EGU General Assembly: Vienna, Austria, 2014. [Google Scholar]
- Caro, C.A.; Lesmes, C.; Bladé, E. Drying and transport processes in distributed hydrological modelling based on finite volume schemes (IBER model). In Proceedings of the 9th Annual International Symposium on Agricultural Research, Athens, Greece, 11−14 July 2016; p. 33. [Google Scholar]
- Ruiz Villanueva, V.; BladéCastellet, E.; Díez-Herrero, A.; Bodoque, J.M.; Sánchez-Juny, M. Two-dimensional modelling of large wood transport during flash floods. Earth Surf. Process. Landf. 2013, 39, 438–449. [Google Scholar] [CrossRef]
- Ruiz-Villanueva, V.; Bladé, E.; Sánchez-Juny, M.; Marti-Cardona, B.; Díez-Herrero, A.; Bodoque, J.M. Two-dimensional numerical modeling of wood transport. J. Hydroinformatics 2014, 16, 1077–1096. [Google Scholar] [CrossRef]
- Ruiz-Villanueva, V.; Bodoque, J.M.; Díez-Herrero, A.; Bladé, E. Large wood transport as significant influence on flood risk in a mountain village. Nat. Hazards 2014, 74, 967–987. [Google Scholar] [CrossRef] [Green Version]
- Ruiz Villanueva, V.; Diez Herrero, A.; Bodoque del Pozo, J.M.; Blade Castellet, E.; Sanchez Juny, M. Large wood transport influence on flash flood risk in a mountain village in central Spain. In Engineering Geology for Society and Territory—Volume 3; Springer International Publishing: Cham, Switzerland, 2015; pp. 123–126. [Google Scholar] [CrossRef]
- Ruiz-Villanueva, V.; Mazzorana, B.; Bladé, E.; Bürkli, L.; Iribarren-Anacona, P.; Mao, L.; Nakamura, F.; Ravazzolo, D.; Rickenmann, D.; Sanz-Ramos, M.; et al. Characterization of wood-laden flows in rivers. Earth Surf. Process. Landf. 2019, 44, 1694–1709. [Google Scholar] [CrossRef]
- Bladé, E.; Ruiz Villanueva, V.; Sánchez-Juny, M. Strategies in the 2D numerical modelling of wood transport in rivers. In River Flow; Garcia & Hanes, Taylor & Francis Group, Eds.; Proceeding of the Eight International Conference on Fluvial Hydraulics: St.Louis, MO, USA, 2016; pp. 2333–2340. ISBN 978-1-138-02913-2. [Google Scholar] [CrossRef]
- Ramos-Fuertes, A.; Marti-Cardona, B.; Bladé, E.; Dolz, J. Envisat/ASAR images for the calibration of wind drag action in the doñana wetlands 2D hydrodynamic model. Remote Sens. 2013, 6, 379–406. [Google Scholar] [CrossRef] [Green Version]
- Areu-Rangel, O.; Cea, L.; Bonasio, R.; Espinosa-Echevarria, V.J. Impact of Uuban growth and changes in land use on river flood hazard in Villahermosa, Tabasco (Mexico). Water 2019, 11, 304. [Google Scholar] [CrossRef] [Green Version]
- Bermúdez, M.; Neal, J.C.; Bates, P.D.; Coxon, G.; Freer, J.E.; Cea, L.; Puertas, J. Quantifying local rainfall dynamics and uncertain boundary conditions into a nested regional-local flood modeling system. Water Resour. Res. 2017, 53, 2770–2785. [Google Scholar] [CrossRef] [Green Version]
- Fraga, I.; Cea, L.; Puertas, J. Effect of rainfall uncertainty on the performance of physically-based rainfall-runoff models. Hydrol. Process. 2018. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez-Cao, J.; García-Feal, O.; Cea, L.; Gómez-Gesteira, M. Preservation of the cultural heritage from floods using the numerical code Iber. In Proceedings of the 1st International Electronic Conference on Hydrological Cycle, Ourense, Spain, 12–16 November 2017; Volume 1. [Google Scholar] [CrossRef] [Green Version]
- Bermúdez, M.; Cea, L.; Puertas, J. A rapid flood inundation model for hazard mapping based on least squares support vector machine regression. J. Flood Risk Manag. 2018. [Google Scholar] [CrossRef] [Green Version]
- Castelltort, F.X.; Ribé, M.; Balasch, J.C.; Bladé, E. 2D numerical flow modelling of a river confluence in order to know the geomorphic consequences of the backwater effect. In EGU General Assembly, Held 223–28; EGU General Assembly: Vienna, Austria, 2017. [Google Scholar]
- Sanz-Ramos, M.; Bladé, E.; Alcázar, J.; Palau, A. Application of Iber hydraulic simulation model for assessing physical habitat suitability (WUA) for fish. In Proceedings of the 12th ISE2018 | International Symposium on Ecohydraulics, Tokyo, Japan, 19–24 August 2018. [Google Scholar]
- Surendran, S.; Gibbs, G.; Wade, S.; Udale-Clarke, H. Supplementary Note on Flood Hazard Ratings and Thresholds for Development Planning and Control Purpose—Clarification of the Table 13.1 of FD2320/TR2 and Figure 3.2 of FD2321/TR1; Environment Agency: Bristol, UK, 2008. [Google Scholar]
- Defra and Agency. Framework and Guidance for Assessing and Managing Flood Risk for New Development; FD2320 Technical Report 2; Flood Risk Assessment Guidance for New Development; did the report for Defra/EA Flood and Coastal Defence R&D Programme; HR Wallingford: Wallingford, UK, October 2005.
- Defra and Agency. The Flood Risks to People Methodology; Flood Risks to People Phase 2; FD2321 Technical Report 1; did the report for Defra/EA Flood and Coastal Defence R&D Programme; HR Wallingford: Wallingford, UK, March 2006.
- Mateo-Lázaro, J.; Sánchez-Navarro, J.A.; García-Gil, A.; Edo-Romero, V. Frequency analysis and classification of real hydrometeorological episodes in three basins of NE Spain. Geogaceta 2013, 53, 117–120. [Google Scholar]
- Mateo-Lázaro, J.; Sánchez-Navarro, J.A.; García-Gil, A.; Edo-Romero, V. Developing and programming a watershed traversal algorithm (WTA) in GRID−DEM and adapting it to hydrological processes. Comput. Geosci. 2013, 51, 418–429. [Google Scholar]
- Mateo-Lázaro, J.; Sánchez-Navarro, J.A.; García-Gil, A.; Edo-Romero, V. Sensitivity analysis of main variables present on flash flood processes. Application in two Spanish catchments: Arás and Aguilón. Environ. Earth Sci. 2014, 71, 2925–2939. [Google Scholar]
- Mateo-Lázaro, J.; Sánchez-Navarro, J.A.; García-Gil, A.; Edo-Romero, V. 3D-geological structures with digital elevation models using GPU programming. Comput. Geosci. 2014, 70, 147–153. [Google Scholar]
- Mateo-Lázaro, J.; Sánchez-Navarro, J.A.; García-Gil, A.; Edo-Romero, V. A new adaptation of linear reservoir models in parallel sets to assess actual hydrological events. J. Hydrol. 2015, 524, 507–521. [Google Scholar] [CrossRef]
- Mateo-Lázaro, J.; Sánchez-Navarro, J.A.; García-Gil, A.; Edo-Romero, V. Flood Frequency Analysis (FFA) in Spanish catchments. J. Hydrol. 2016, 538, 598–608. [Google Scholar] [CrossRef]
- Mateo-Lázaro, J.; Sánchez-Navarro, J.A.; García-Gil, A.; Edo-Romero, V.; Castillo-Mateo, J. Modelling and layout of drainage−levee devices in river sections. Eng. Geol. 2016, 214, 11–19. [Google Scholar] [CrossRef]
- Mateo-Lázaro, J.; Sánchez-Navarro, J.A.; Edo-Romero, V.; Castillo-Mateo, J. Application of the Spanish criteria for the water management policy in the creation of new infrastructure. Geogaceta 2017, 61, 51–54. [Google Scholar]
- Mateo-Lázaro, J.; Castillo-Mateo, J.; Sánchez-Navarro, J.A.; Fuertes-Rodriguez, V.; García-Gil, A.; Edo-Romero, V. New analysis method for continuous base-flow and availability of water resources based on parallel linear reservoir models. Water Sect. Water Resour. Manag. Gov. 2018, 10, 465. [Google Scholar] [CrossRef] [Green Version]
- Mateo-Lázaro, J.; Castillo-Mateo, J.; Sánchez-Navarro, J.A.; Fuertes-Rodriguez, V.; García-Gil, A.; Edo-Romero, V. Assessment of the role of snowmelt in a flood event in a gauged catchment. Water Hydrol. Sect. 2019, 11, 506. [Google Scholar] [CrossRef] [Green Version]
- García-Gil, A.; Vázquez-Suñé, E.; Sánchez-Navarro, J.A.; Mateo-Lázaro, J. Recovery of energetically overexploited urban aquifers using surface water. J. Hydrol. 2015, 531, 602–611. [Google Scholar] [CrossRef]
- García-Gil, A.; Vázquez-Suñé, E.; Sánchez-Navarro, J.A.; Mateo-Lázaro, J.; Alcaraz, M. The propagation of complex flood−induced head wavefronts through a heterogeneous alluvial aquifer and its applicability in groundwater flood risk management. J. Hydrol. 2015, 527, 402–419. [Google Scholar] [CrossRef]
- Chapman, L.; Thornes, J.E. Real-time sky-view factor calculation and approximation. J. Atmos. Ocean. Technol. 2004, 21, 730–741. [Google Scholar] [CrossRef]
- Zaksek, K.; Ostir, K.; Kokalj, Z. Sky-view factor as a relief visualization technique. Remote Sens. 2011, 3, 398–415. [Google Scholar] [CrossRef] [Green Version]
- Kastendeuch, P.P. Amethod to estimate skyview factors from digital elevation models. Int. J. Climatol. 2013, 33, 1574–1578. [Google Scholar] [CrossRef]
- SNCZI. Available online: https://sig.mapama.gob.es/snczi/visor.html?herramienta=DPHZI (accessed on 1 April 2020).

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mateo-Lázaro, J.; Castillo-Mateo, J.; García-Gil, A.; Sánchez-Navarro, J.Á.; Fuertes-Rodríguez, V.; Edo-Romero, V. Comparative Hydrodynamic Analysis by Using Two−Dimensional Models and Application to a New Bridge. Water 2020, 12, 997. https://doi.org/10.3390/w12040997
Mateo-Lázaro J, Castillo-Mateo J, García-Gil A, Sánchez-Navarro JÁ, Fuertes-Rodríguez V, Edo-Romero V. Comparative Hydrodynamic Analysis by Using Two−Dimensional Models and Application to a New Bridge. Water. 2020; 12(4):997. https://doi.org/10.3390/w12040997
Chicago/Turabian StyleMateo-Lázaro, Jesús, Jorge Castillo-Mateo, Alejandro García-Gil, José Ángel Sánchez-Navarro, Víctor Fuertes-Rodríguez, and Vanesa Edo-Romero. 2020. "Comparative Hydrodynamic Analysis by Using Two−Dimensional Models and Application to a New Bridge" Water 12, no. 4: 997. https://doi.org/10.3390/w12040997