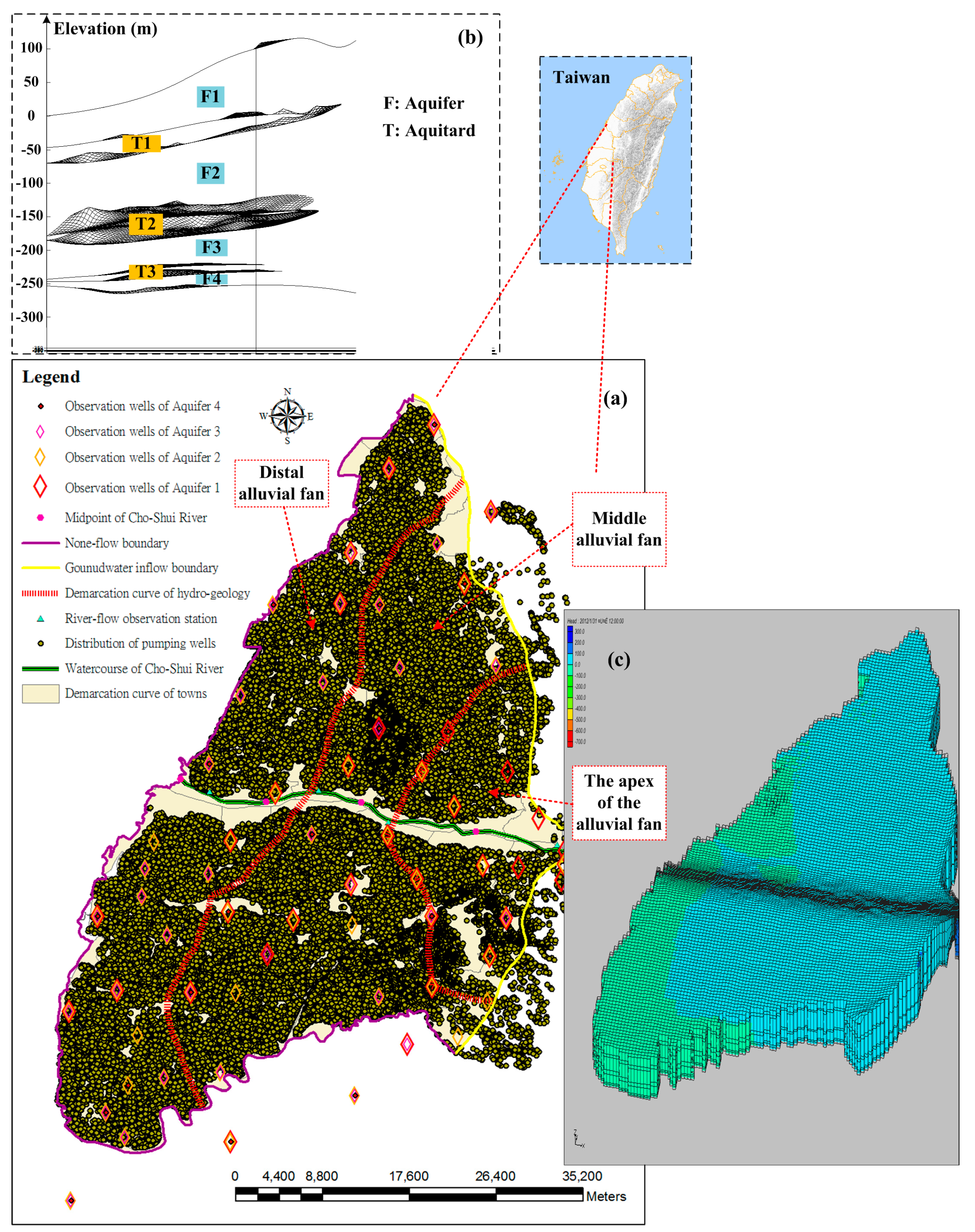
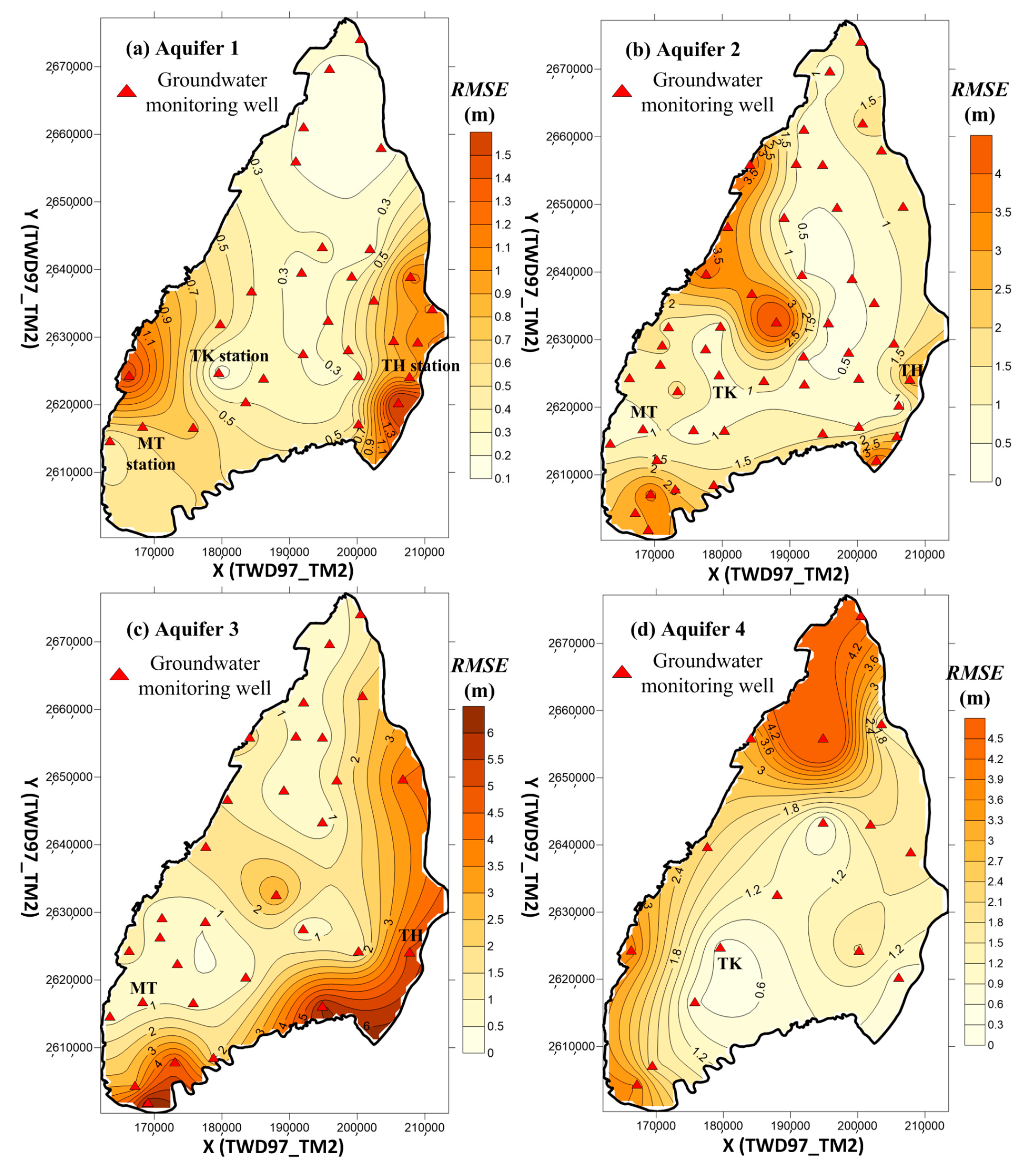
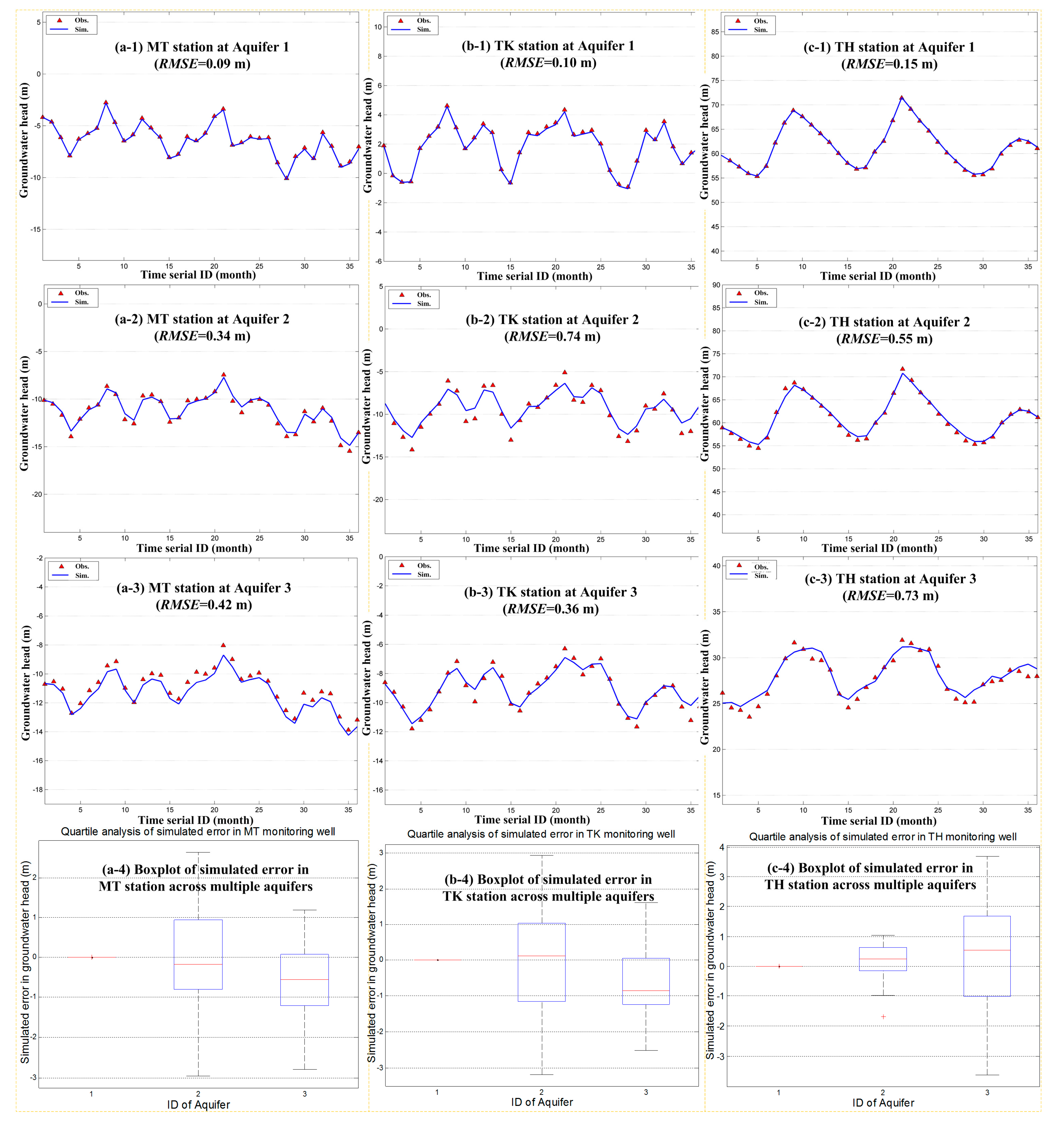
2.1. Proposing Optimization Model for Model Calibration in a Multi-Layer Groundwater System
Traditionally, for model calibration purposes, a set of the hydrogeological parameters or source/sink patterns (
) are optimized from a limited number of observations (
). If the classical least-squares error (LSE) is used to represent the output simulated groundwater head error, the objective function can be expressed as the minimization problem in Equation (2a) [
37]. In this study, the order differs substantially between the storage coefficient in confined aquifers and the specific yield in unconfined aquifers, which are the dominant independent groundwater head fluctuation variables, thus, this study devises the LSE of the simulated and observed storage hydrograph (
and
) as the objective function to optimize the parameter vector
. The proposing minimized objective function is expressed in Equation (2b):
where
is the simulated groundwater head at an observation well based on an estimated value of
;
and
are the observed storage and the simulated storage, corresponding to the observed and simulated groundwater head of aquifer
f in region
for time step
calculated according to Hsu et al. [
16], respectively; and
F is the total number of aquifers. Equation (2b) assumes that a groundwater system has
observation wells in aquifer
f with several time steps
, and uses
to represent subscript symbols
and
by single subscript symbols
and
. To formulate the optimization model, the zonation approach [
38,
39] is used to partition the parameter space according to the observation well location.
Assume that the spatiotemporal pumpage pattern can be estimated beforehand, and the storage coefficients and specific yield values can be obtained from pumping tests. Then, the parameter vector estimated in the optimization model includes aquifer hydraulic conductivity , riverbed leakage conductivity , aquitard leakance conductivity , and the source patterns of surface recharge and boundary recharge . The parameter vector has L entries and in which is the hydraulic conductivity of aquifer f in region []; is the riverbed hydraulic conductivity of river in region []; is the vertical hydraulic conductivity of aquitard f in region []; is the surface recharge of region for time step ; is the boundary recharge of aquifer f and arc for time step []; and , , , and are the total time step number, total number of rivers, total sectional number of river , and total boundary arcs of aquifer f, respectively.
The optimization model contains four constraints: (1) the spatiotemporal pattern of multiple recharges should subject to mass balance, (2) the simulation of groundwater head should obey governing Equation (1), (3) the upper and lower bounds of in situ hydrogeological parameters, and (4) the allocated upper and lower bounds of surface recharge. In a real case, the identification of hydrogeological parameters and recharges often form a large-scale highly nonlinear problem.
2.2. Modification of Traditional Algorithms in Nonlinear Programming for Proposing SR3 VLS Quasi-Newton Algorithm to Solve Hydrogeological Parameters
In nonlinear programming, Newton’s method attempts to find the roots of
by constructing a sequence
from the initial guess
that converges towards some value
satisfying
. This
is a stationary point of
where the second-order Taylor expansion
of an objective function
around
is:
Ideally, we want to pick
such that
is a stationary point of
. Using this Taylor expansion as an approximation, we can at least solve for the
corresponding to the root of the expansion’s derivative:
The above-mentioned iterative scheme can be generalized to several dimensions by replacing the derivative with the gradient,
and the reciprocal of the second derivative with the inverse of the Hessian matrix,
. The iterative scheme obtained on doing so is as follows:
If all second-order partial derivatives of
exist and are continuous over the function domain, then the Hessian matrix
of
is usually defined as follows:
At a local minimum, the Hessian is positive semi-definite. The geometric interpretation of the Gauss–Newton method is that at each iteration,
is approximated by a quadratic function around
, and a small scalar step size
was taken to the minimum (or maximum) of that function, as expressed in Equation (8a). The Jacobian quasi-Newton method uses the Jacobian matrix
to approximate the Hessian matrix
iteratively, as expressed in Equation (8b). The Levenberg–Marquardt algorithm adds an identity matrix
to the Hessian
, with the scale adjusted iteratively as needed, in which the increment vector is rotated towards the direction of steepest descent, as expressed in Equation (8c). Considering a disadvantage arises for large damping factor values
, Fletcher (1971) proposed each gradient component can be scaled by curvature, so that there is larger movement along directions where the gradient is smaller [
17], which avoids slow convergence in the direction of a small gradient. Therefore, the identity matrix was replaced with the diagonal matrix comprising diagonal elements of
, which is used to solve linear ill-posed problems, as expressed in Equation (8d). The BFGS quasi-Newton algorithm is used for solving unconstrained nonlinear optimization problems by setting the search direction
for the analog solution of the Newton equation, where
approximates the Hessian matrix, as expressed in Equation (8e).
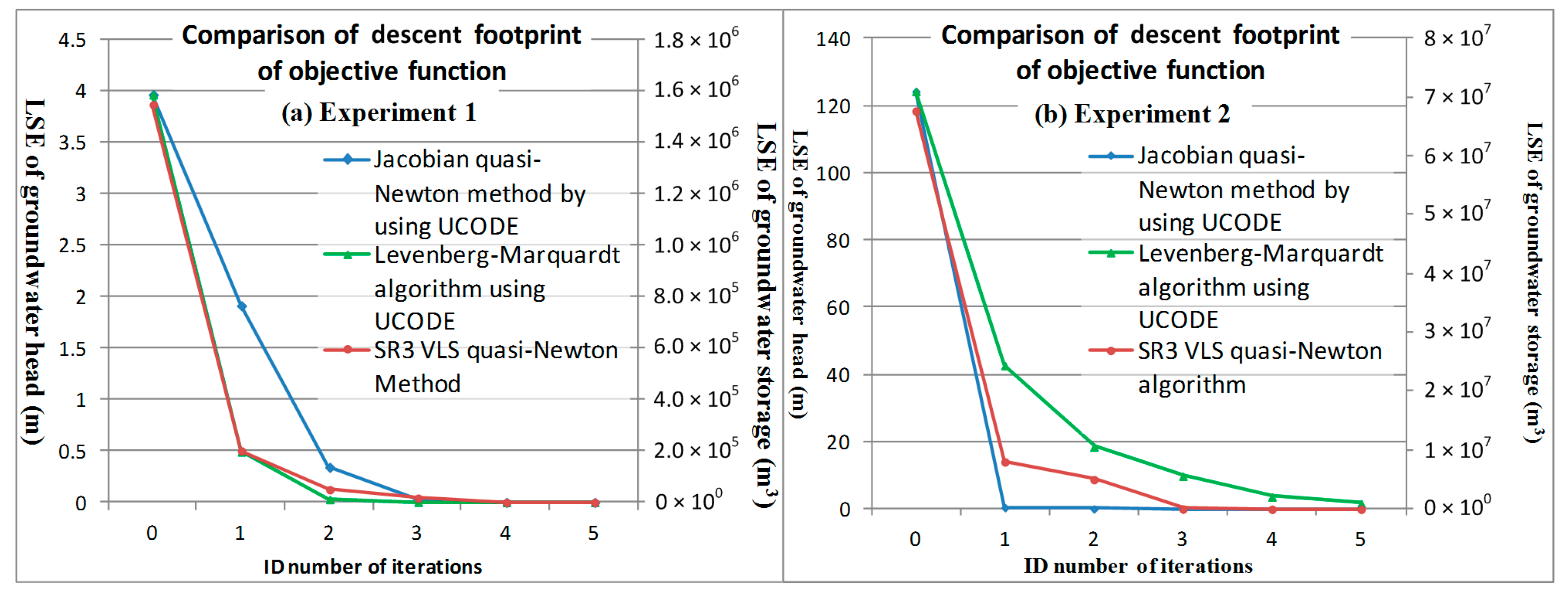
To accelerate convergence, jump over local minima, and achieve a well-posed problem, this study uses a vectorized limited switchable step size in the inverse problem of transmissive groundwater whose parameters include both hydrogeology and source simultaneously. Therefore, we achieve , detect the minima area, approach global optimum, and solve nonlinear ill-posed problems, this study modifies LMA and imports a third rank structure from BFGS for solving constrained nonlinear parameter identification problems, which uses a low-rank factor loading score and a high-rank loading score analyzed from the simulated storage difference to approximate the Hessian and calculate the correction matrix, as expressed in Equation (8f).
In Equation (8b–d),
is the Jacobian matrix of
defined in Equation (9a). In Equation (8e), set
and
, the approximate Hessian matrix
in the BFGS algorithm is updated by the addition of two matrices as expressed in Equation (9b), subjected to symmetry and positive definiteness of
. Both
and
are symmetric rank-one matrices, and their sum is a rank two updated matrix. Imposing the secant condition [
40]
and choosing
and
, the secant BFGS scale factors
and
are expressed in Equation (9c).
In the proposing SR3 VLS quasi-Newton algorithm in Equation (8f),
,
and
are symmetric rank-one matrices; however, their sum is a rank three matrix. The row vectors of the low-rank and high-rank loading score matrix, namely
and
, are permutated from
and
, as expressed in Equation (10a–c) and in Equation (10d–f), respectively, in which the low-rank component
j is 1, and the high-rank component
j is from 2 to
Sf. This study uses the factor score
and the factor loading
calculated from the simulated storage difference
through SVD between iteration
k and
k − 1 to compute the elements of
and
, as expressed in Equations (13)–(16), thereby eliminating the need for additional model runs to approximate the Hessian.
is the diagonalized standard deviation matrix of
, where
, and
. Before SVD, the simulated storage difference
will first be normalized by the average
and standard deviation
for each zonal
and each aquifer
f across multiple simulated time steps
, such that the average of the simulated storage difference of each zone equals to 0 and the variance equals to 1. Hence, the vectorized step size
is a switchable and limited set between
and
, namely
.
According to this design, this study uses the orthogonal component of loading scores
and
to correct the direction to better approximate the Hessian. That is, the modified algorithm uses the vector-expanded matrix
and
to scale each high-rank component of the loading scores according to the orthogonal properties eigenvalue
to approximate the Hessian and explore different local minima positions, so there is larger movement along the directions for each parameter where the gradient is smaller. Accordingly, this study designs the symmetry rank three loading scores
,
, and
to solve nonlinear ill-posed problems, thus, properly handling the approximated Hessian elements by scale and correction at all iterations. The calculation of the scale matrix
and
are formulated as follows:
In large-scale groundwater modeling with a large number of parameters and numerical grids, the transient simulation time increases substantially [
41]. To imitate the real complex alluvial groundwater hydrogeology in practice, meticulously detailed parameterization of aquifer’s/aquitard’s shape is unavoidable. Hence, computing and storing the full Hessian matrix directly may be infeasible, unavailable, and too expensive to compute at all iterations in hydrogeological parameter identification. Furthermore, the convergence of the Jacobian quasi-Newton is not guaranteed. The approximation
required to ignore the second-order derivative terms may be valid in two conditions [
17], for which convergence is to be expected: the function values
are small in magnitude, at least around the minimum; and the functions are only slightly nonlinear, so that
is relatively small in magnitude. Moreover, when the (non-negative) Marquardt damping factor
(scalar) optimized by a line search changes, the shift vector must be recalculated. Furthermore, in cases with multiple minima, the algorithm converges to the global minimum only if the initial guess is close to the final solution [
20]. However, for well-behaved functions and reasonable starting parameters, the LMA tends to be slightly slower than the Jacobian quasi-Newton. Besides, letting
be positive definite in the BFGS updates should satisfy the curvature condition
and
be positive definite. A key reason leading to the above challenges is the scalar nature of the step size
in the Jacobian quasi-Newton, the Marquardt damping factor
in LMA, and the secant scale factors
and
in BFGS. Hence, this study uses the designed preserved approximate Hessians with positive definite and numerically stable selections from the various combinations of low–high rank loading scores along with the vectorized limited switchable step sizes to detect the area of the global minimum and approach the global optimum in a multi-minima problem.
2.3. Modification from Traditional Scalar Line Search to Vectorized Multi-Order Derivative Exact Double False Position Bracketing Using SVD-Related Rank and Depth
The traditional double false position provides the exact solution for a root-finding problem, which determines a scalar
such that
, while a nonlinear objective function
can be successively improved by iteration
. If
is a continuous function and there exist two points
and
such that
and
are of opposite signs, then, by the intermediate value theorem, the function
has a root
in the interval
. The simplest two-point bracketing is the bisection method, which estimates the solution as the bracketing interval midpoint as expressed in Equation (12a). If the functional value of the new calculated estimate
has the same sign as
, the new bracketing interval becomes
. The fact that false position method always converges, and has advantages that minimize slowdowns, recommends it when speed is needed [
22], in which the solved
is expressed in Equation (12b). The Illinois algorithm dampens one of the endpoint values by a factor of 1/2 to force the next
to occur on that side of
guaranteeing superlinear convergence, as shown in Equation (12c). The Anderson−Bjork algorithm multiplies
by
m in Equation (12c), as expressed in Equation (12d).
For the vectorized step size root finding problem, which is more difficult and complicated, the double false position can be used and written algebraically in the form: determine
such that
, if the known conditions are
at the
-th iteration in the exact optimization procedure of the vectorized step size. If
is a nonlinear continuous function and there exist two vectors
and
such that each corresponding element of vectors
and
are of opposite signs, then by the intermediate value theorem, the function
has a root
in the interval
. In a conventional iterative nonlinear programming for parameter identification, the information
in Equation (6) is not used for exact approximation. Hence, this study modifies the double false position method for estimating new parameter vector guesses
through a series of non-derivative, first-order derivative, and SVD depth component-based halving vectors of the objective function simultaneously in vector form, as shown in Equation (12e).
where
is the
lth unit vector;
is the halving vector of the proposing 0 order derivative’s double false position method;
,
, and
are the halving vectors of the vectorized Anderson−Björk algorithm, vectorized Illinois algorithm, and vectorized conventional false position method, respectively [
22]; and
is the halving vector of the proposing SVD depth rank component-based double false position method, which uses the
jth component in
dth depth as the high-rank loading score
for the Hessian correction.
This study uses symmetry rank three loading score quasi-Newton associated with vectorized step size for solving massive parameters in transmissive groundwater. This study specializes the step size for each parameter with a switchable limited scheme; thus, this approach helps reduce the difference between different kinds of parameters (transmissivity and source/sink) and improves the convergence rate and searching direction by modifying the parameter step size. To achieve small error in the large parameters
and the desired rapid convergence in the objective function
, an exact line search approach, which computes the vectorized limited switchable step size that optimizes how far vector of parameters
should move along the calculated direction, is proposing. This study proposes a systematic strengthening approach of vectorized multi-order derivative exact double false position bracketing using SVD-related rank and depth, which guarantee convergence for solving the vectorized step size corresponding to different kinds of hydrogeological parameters and recharges. The detailed procedure is listed in Step 4 of
Section 2.4.
2.4. Procedures of the Methodology
Step 1: Set the iteration counter of identified parameters , and make an initial guess for the minimum.
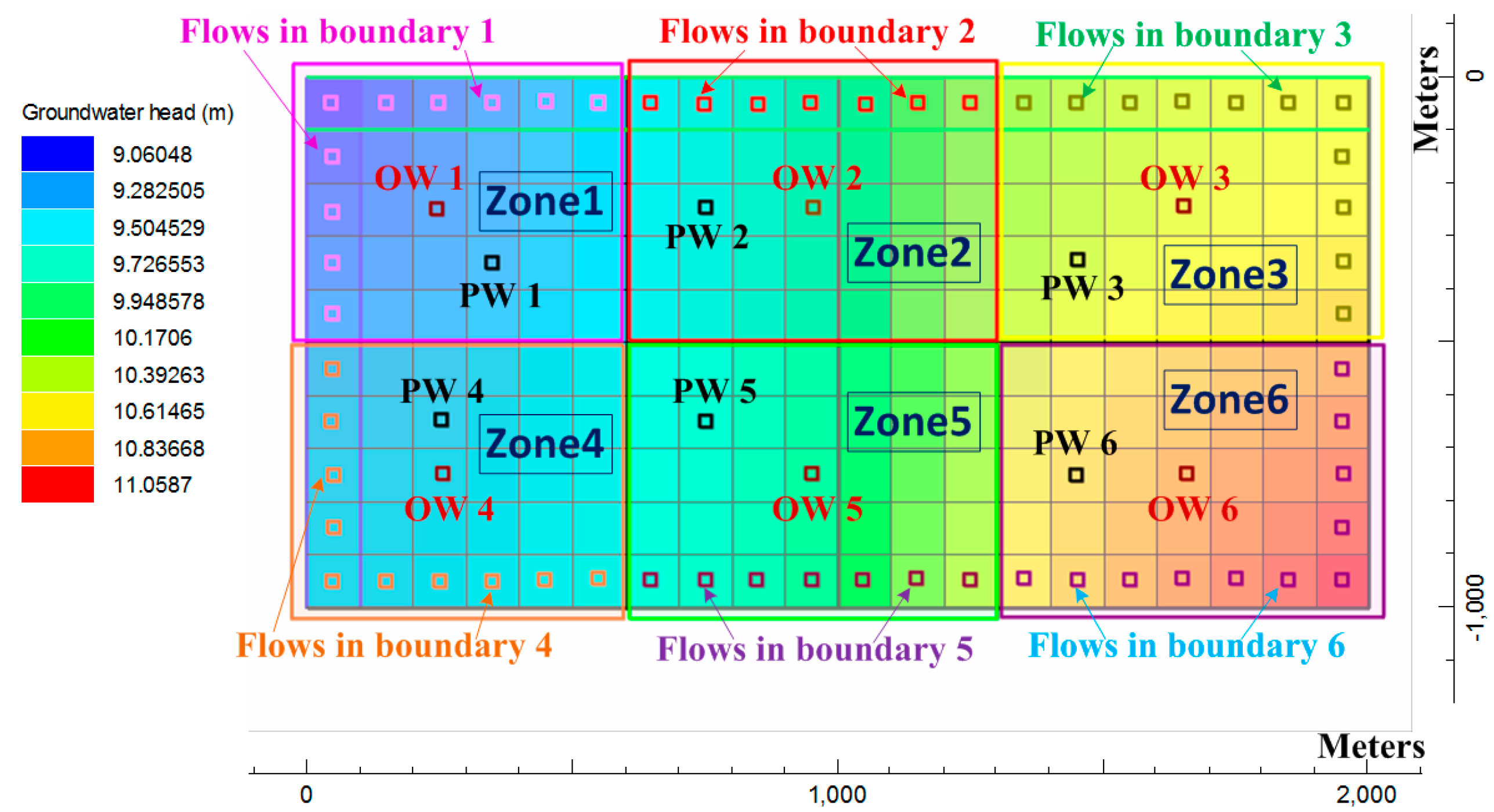
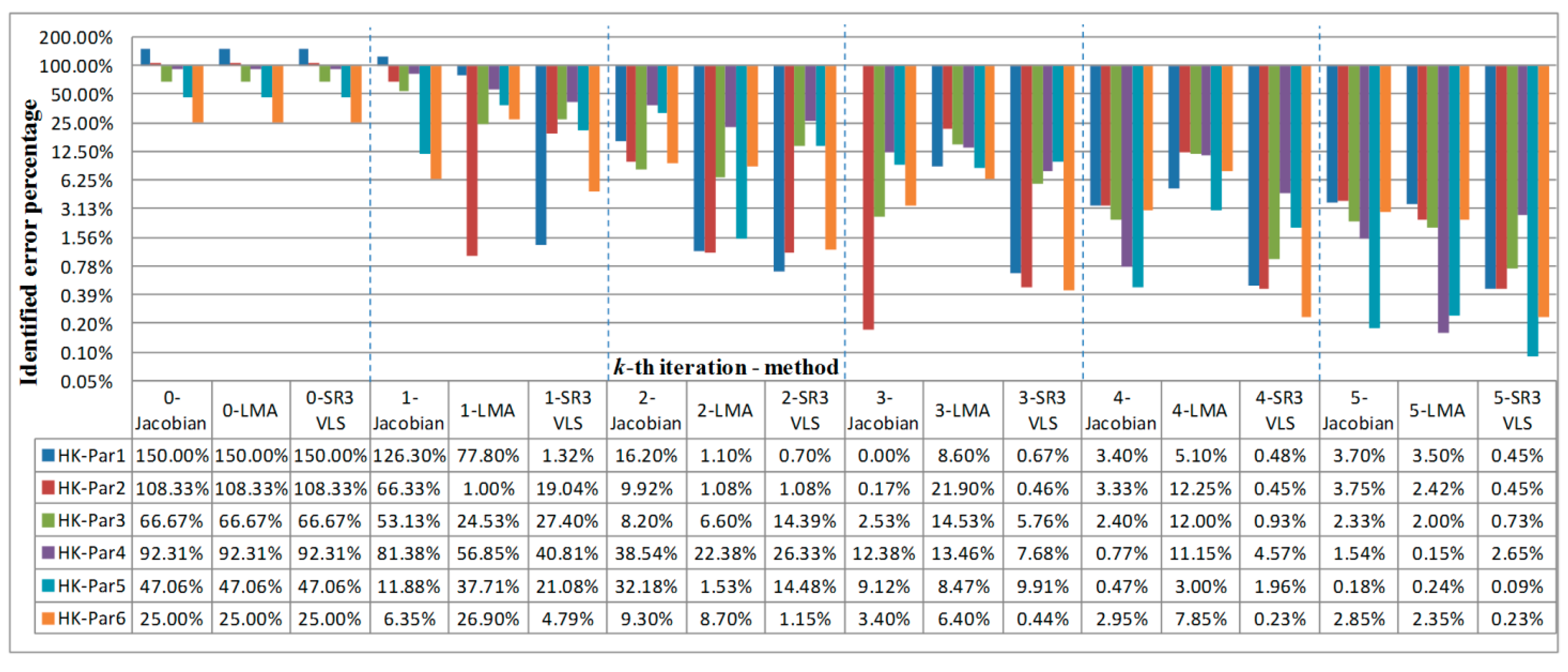
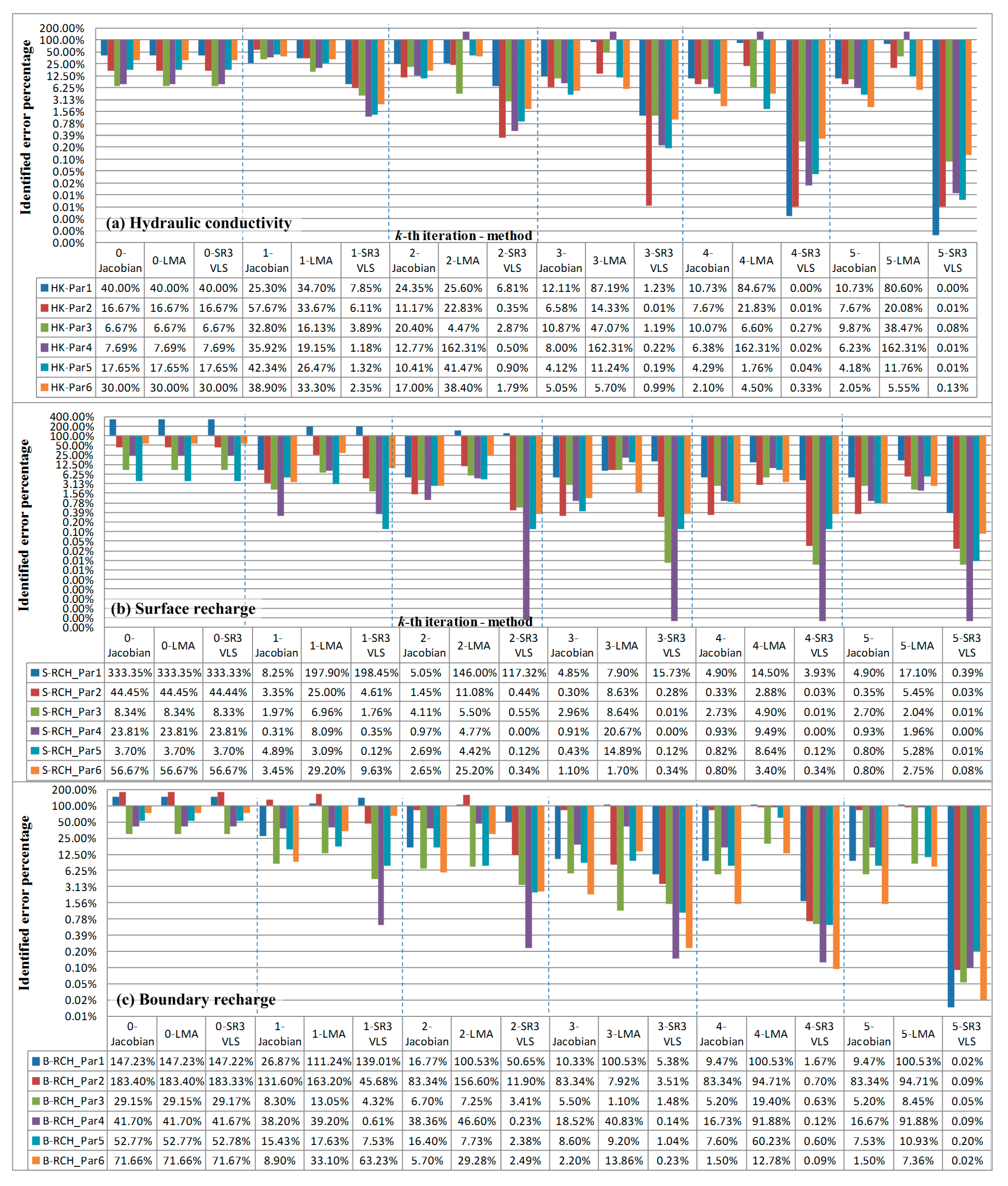
Step 1-1: In hypothetical experiment 1, the initial guess of is set as a relatively large value.
Step 1-2: In hypothetical experiment 2, the initial guesses of and are set as mean values of the calculated lumped recharge, and those of , and are set as medium guess values.
Step 1-3: In practical application, the spatiotemporal recharge pattern is estimated by multiplying the temporal pattern calculated by using the lumped storage hydrograph fluctuation and the previously estimated pumpage according to Hsu et al. [
16], with the initial guess of the spatial pattern estimated according to the factor loadings calculated from the computed distributed inflow hydrographs (
storage + pumpage). The initial estimate of the hydrogeological parameters is assigned according to the in situ pumping tests.
Step 2: Compute the second-order derivative descent direction through the symmetry rank three storage-based loading scores.
Step 2-1: Simulate the spatiotemporal groundwater head pattern by using the MODFLOW from pumpage, recharge and parameters, boundary conditions, and initial conditions. The modular MODFLOW-2005, which is a computer code that solves the groundwater flow equation, was used to simulate the finite-difference flow through aquifers [
42].
Step 2-2: Compute lumped and distributed groundwater storage hydrographs, based on the in situ storage coefficient and specific yield (Sy) estimated from pumping tests, drilled hydrogeological structure, and observed/simulated groundwater head hydrographs.
Step 2-3: Use various multi-rank loading score combinations calculated from the simulated storage difference using SVD between iteration k and k − 1 to approximate Hessians, and then use selected positive definite and numerically stable approximations with calculated to search for the global minimum.
Step 3: Choose to minimize over .
Step 3-1: Set the root-finding iteration counter and make an initial interval for the minimum.
Step 3-2: Use a series of potentially faster double false position methods including the proposing vectorized multi-order derivative exact double false position bracketing using SVD-related rank and depth, vectorized Anderson−Björk algorithm, vectorized Illinois algorithm, and vectorized conventional false position method to calculate as shown in Equation (12e), in which they are always converging and avoid slowdowns.
Step 3-3: Select the calculated with the largest shrinking rate and the same sign as .
Step 3-4: If the shrinking rate drops below 0.5, the bisection is used to calculate .
Step 3-5: The new bracketing interval becomes . Let and return to Step 3-2.
Step 3-6: Until the bracketing interval of step sizes < tolerance.
Step 4: Update . Set and return to Step 2-1.
Step 5: Until the descent gradient of objective function < tolerance.
2.5. SVD of the Change in Storage between kth and (k − 1)th Iteration for Hessian Approximation
First, we normalize the data (the average of each storage fluctuation variable equals to 0, and the variance equals to 1) and divide all elements of each row of
X by the sample standard deviation of the variable
for an aquifer
f, that is,
where
and
are the sample’s variance and the average of the change in storage between
kth and (
k − 1)
th iteration at the
sf-th observation well in aquifer
f, respectively. Set
.
SVD can produce a series of datasets consisting of non-correlated new variables (partial simulated storage difference by a parameter factor) for the original analyzed spatiotemporal variables (simulated change in storage between
kth and (
k − 1)
th iteration). Considering the SVD of the deviation matrix
X:
where the row vector of the
order matrix
is an orthonormal left singular vector
,
;
,
is a singular value. The row vector of the
order matrix
is an orthonormal right singular vector
,
. The singular value
determines the eigenvalue
. Next, let
be the correlation coefficient between the
observation well’s change in storage and the
jth principal component coefficient, called factor loading, and let
be the
order factor loading matrix. Because
and
contain the standardized data, substituting
, we can derive:
The principal component analysis provides a description model for the simulated spatiotemporal change in storage between the
kth and (
k − 1)
th iterations by using SVD. The deviation matrix
X can be expressed by the factor score
and the factor loading
F as follows:
According to the mathematical meaning, the above formula can be interpreted as: there are
L independent parameters caused the change in storage following perturbation by
. The factor score (transpose) matrix
stores
observations for
L factors in aquifer
f, where vector
records the
observation of the
Sf factors, as shown in
Figure 1.
The signal (temporal step size) first passes through a mixing process which called the factor loading F (customized spatial direction), where determines the loading weight (namely, the correlation coefficient) from the lth parameter’s factor perturbed between the kth and (k − 1)th iterations to the change in storage at observation well . Then, L variables pass through the stretching process D (standard deviation) to enlarge or reduce the range of correction values. Finally, shift a again to generate the component of the change in storage between the kth and (k − 1)th iterations .