A Design for Vortex Suppression Downstream of a Submerged Gate
Abstract
1. Introduction
2. Flume Experiments
3. Computational Model
3.1. Numerical Framework
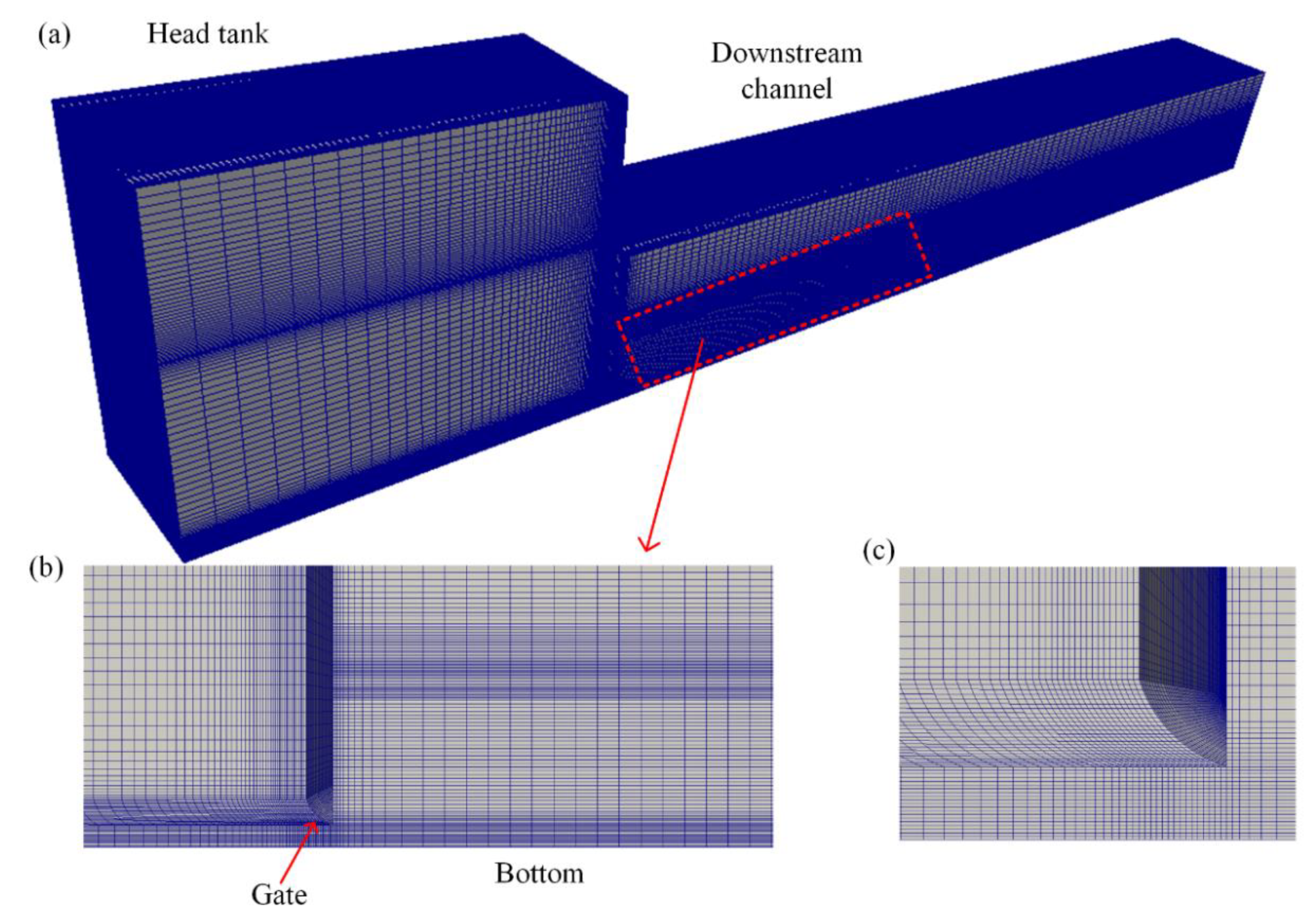
3.2. Mesh and Boundary Conditions
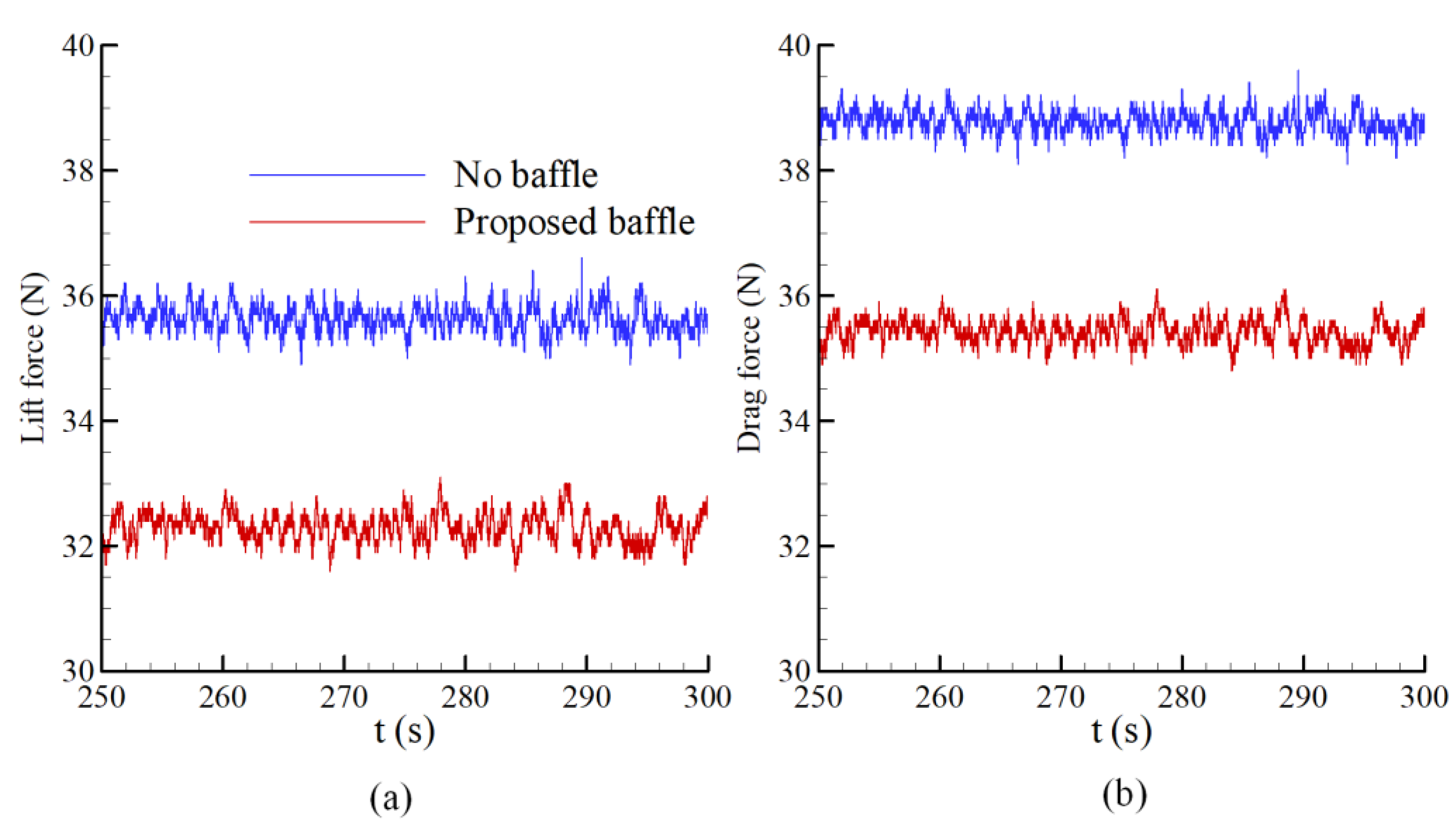
4. Results and Discussion
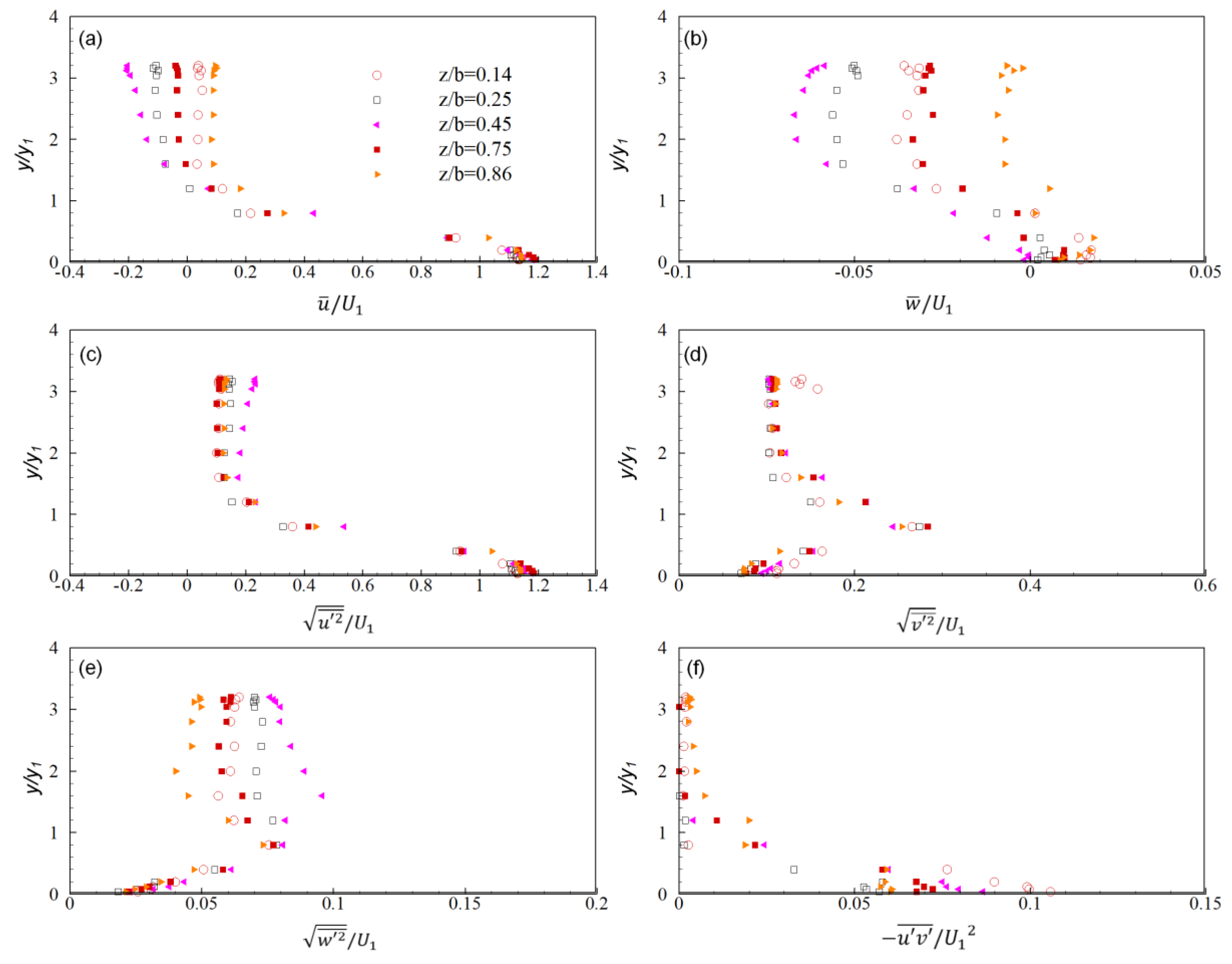
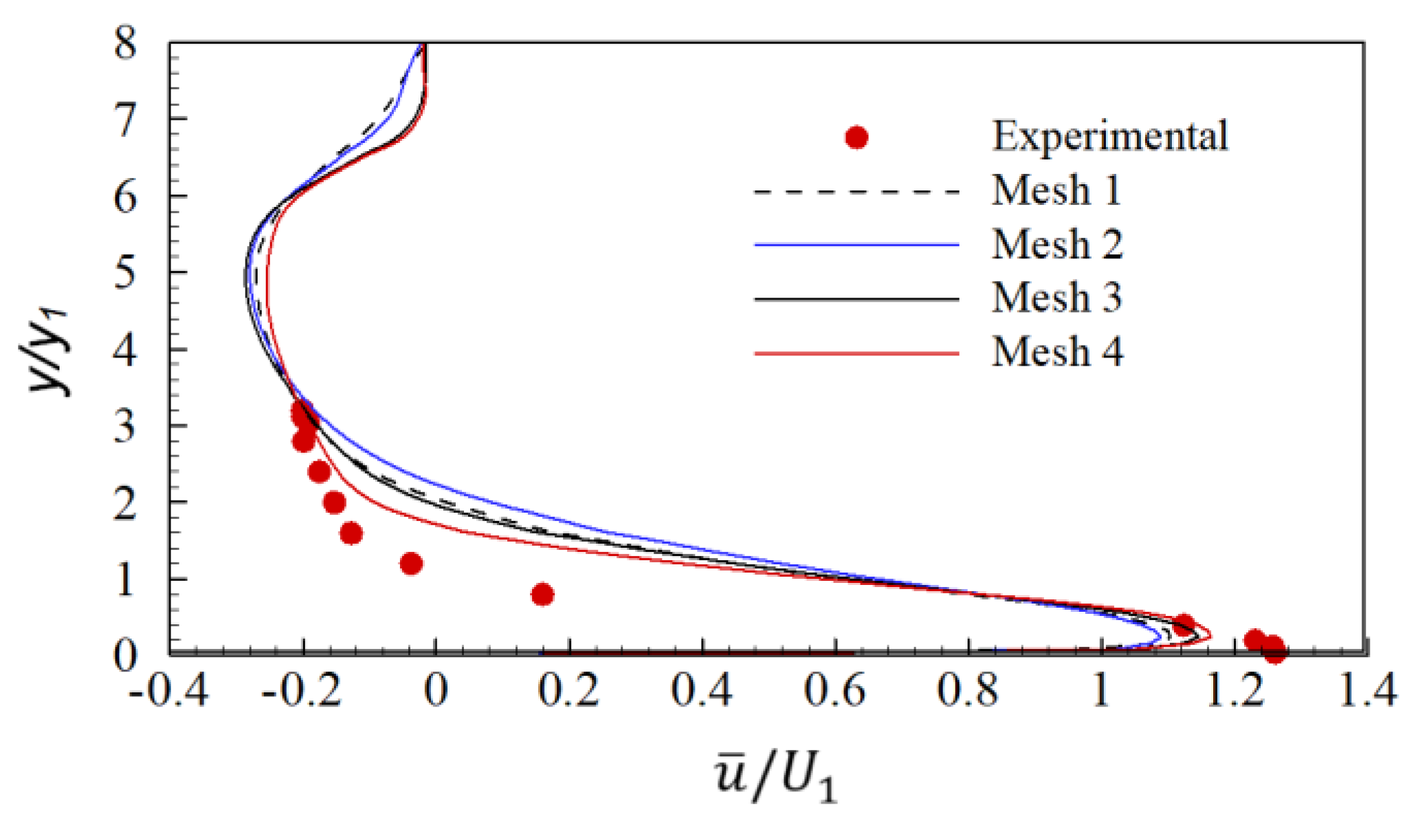
4.1. Mesh Independent Study and Validation
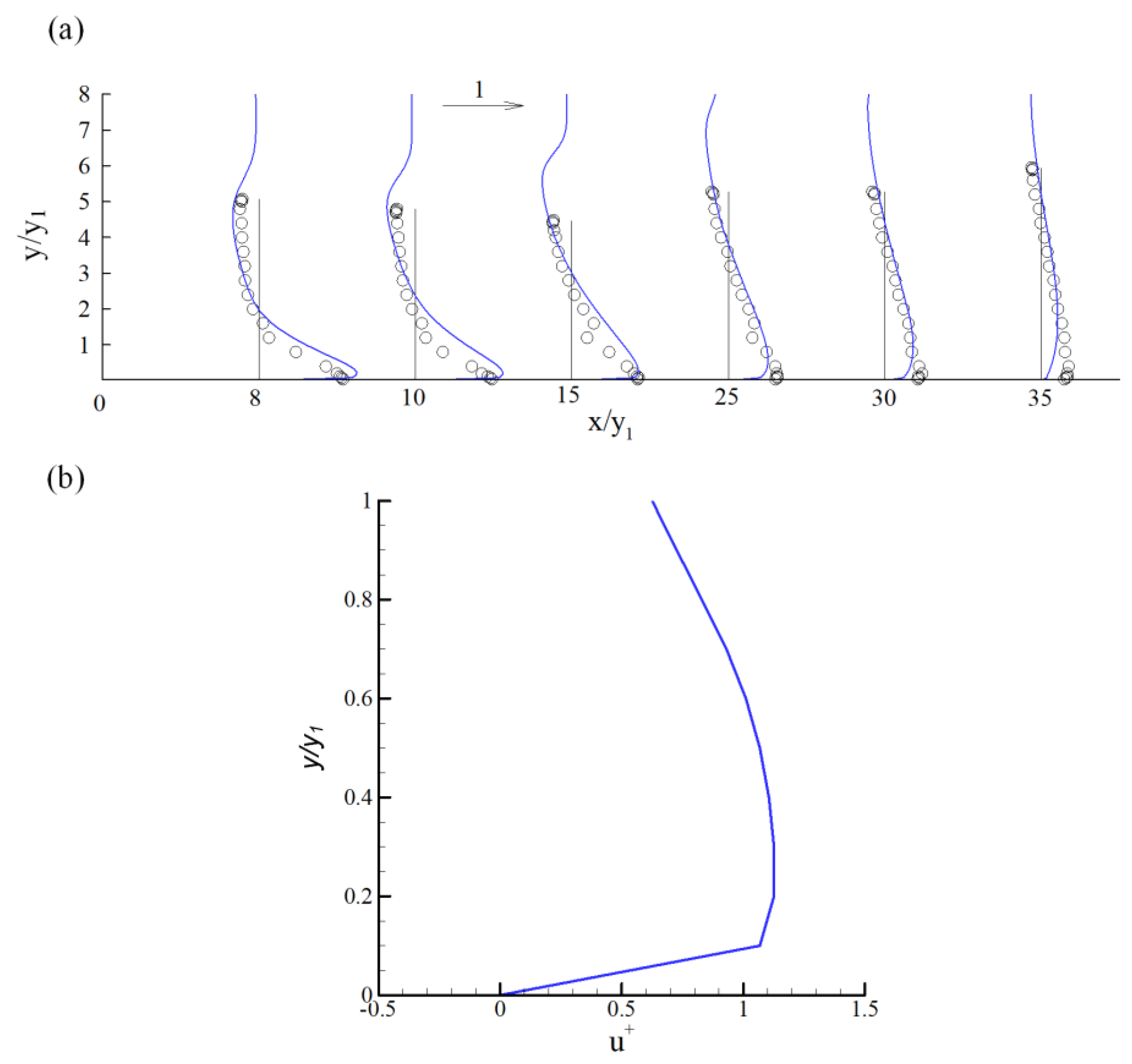
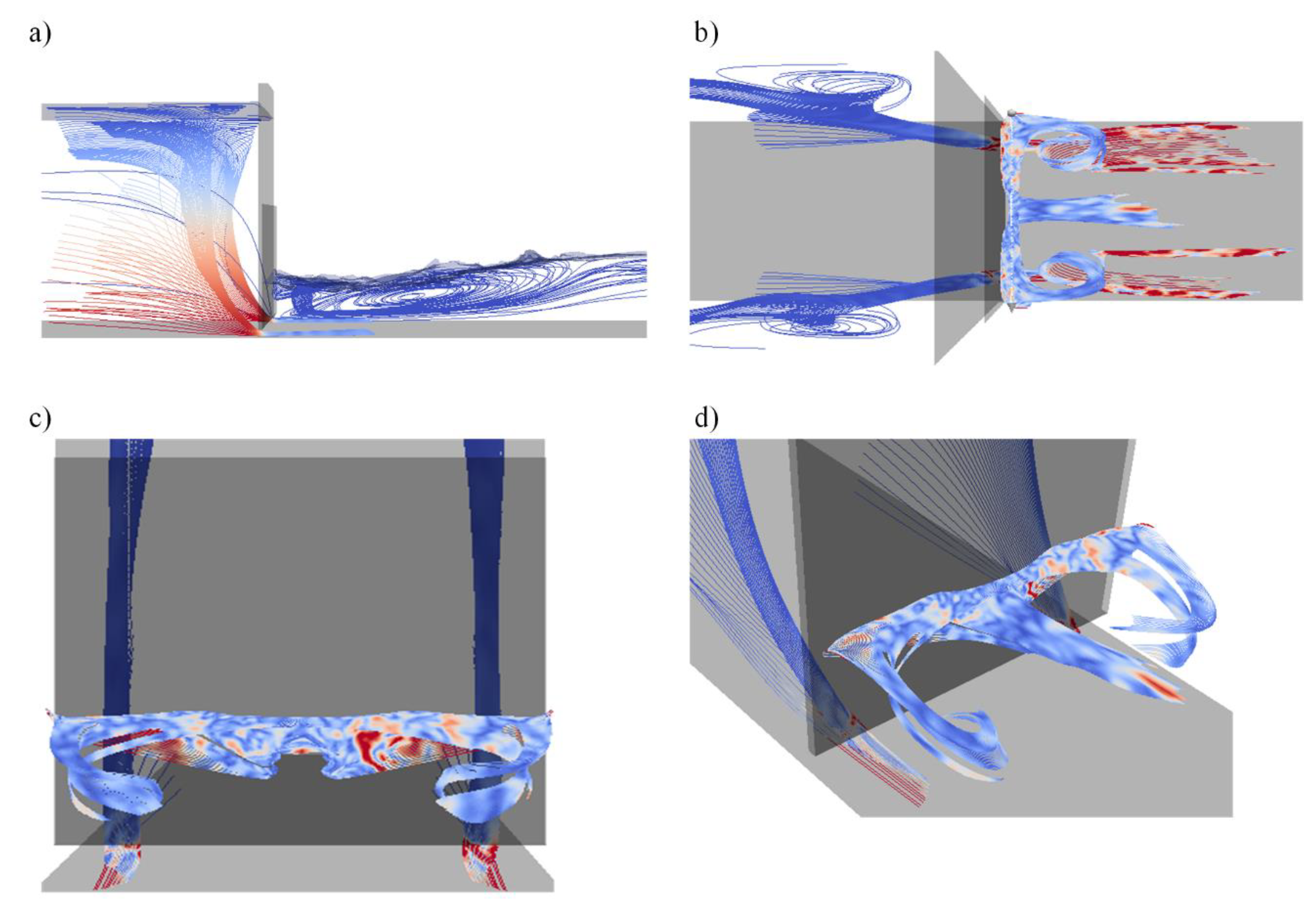
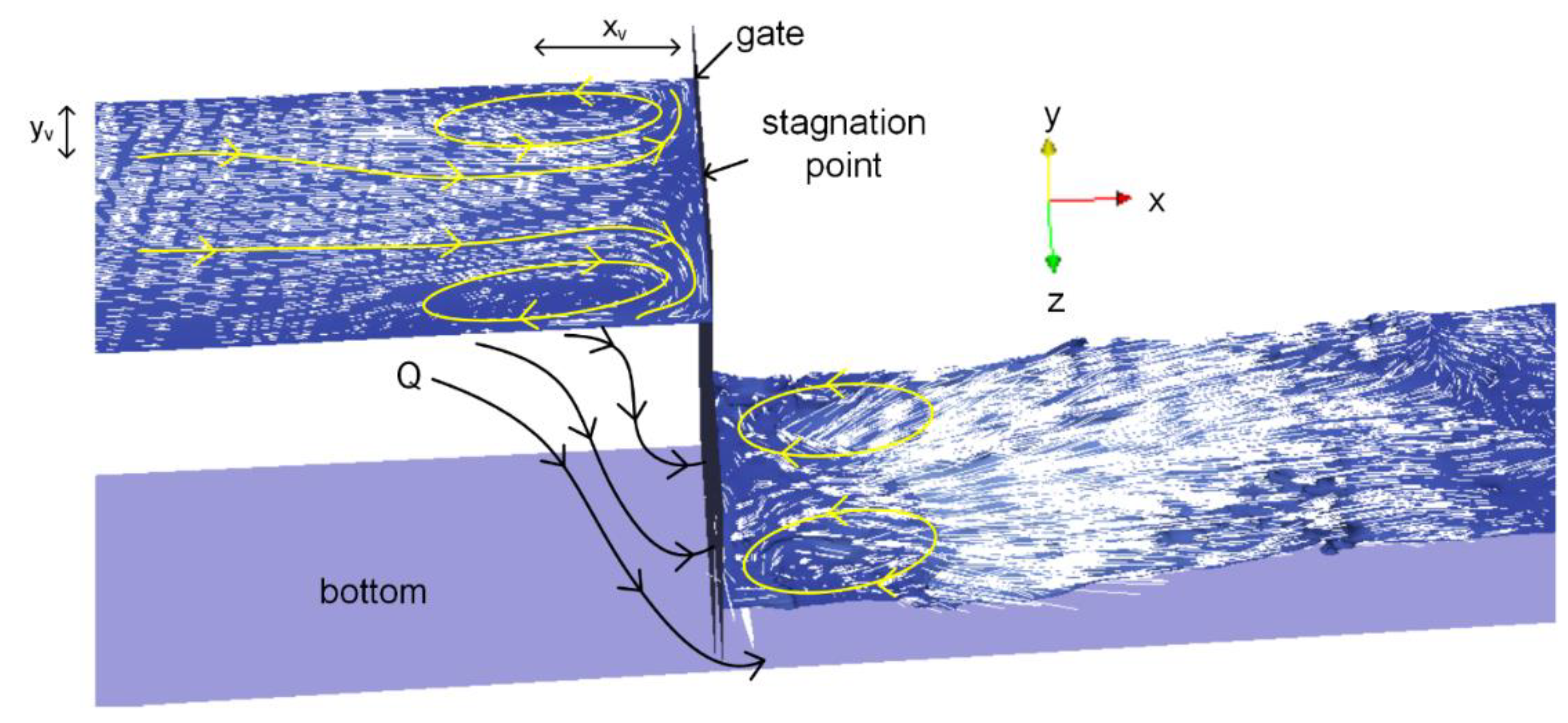
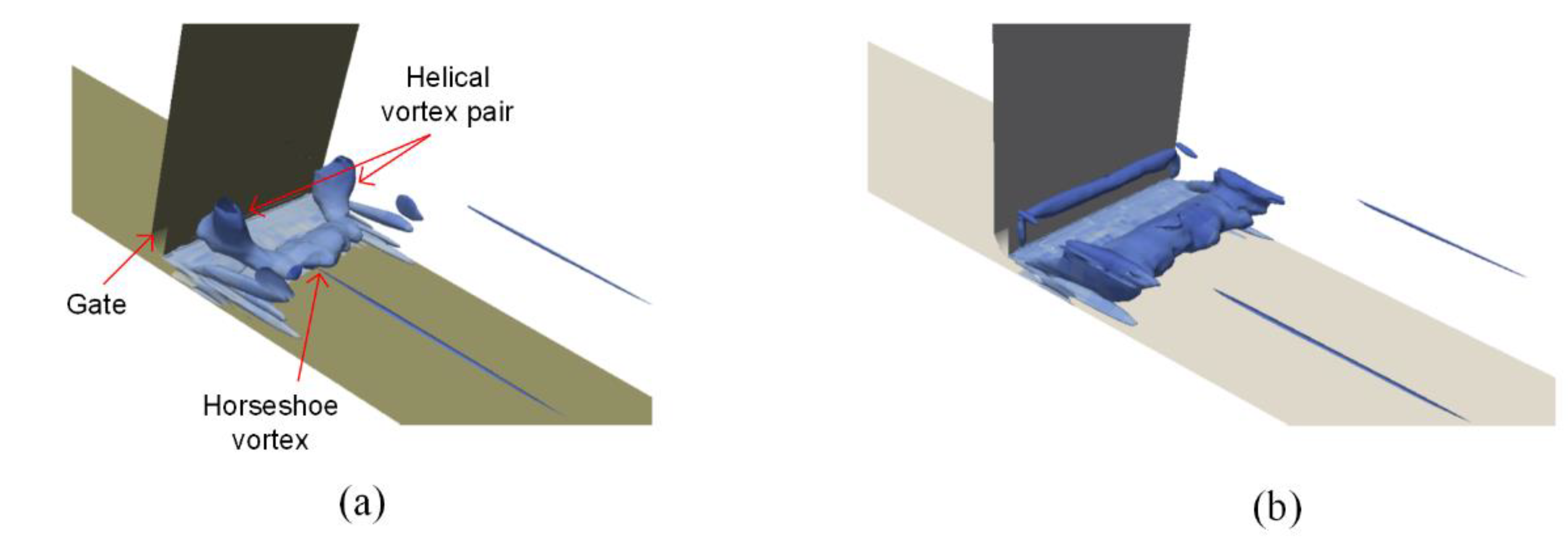
4.2. Mean Flow Structure around the Gate
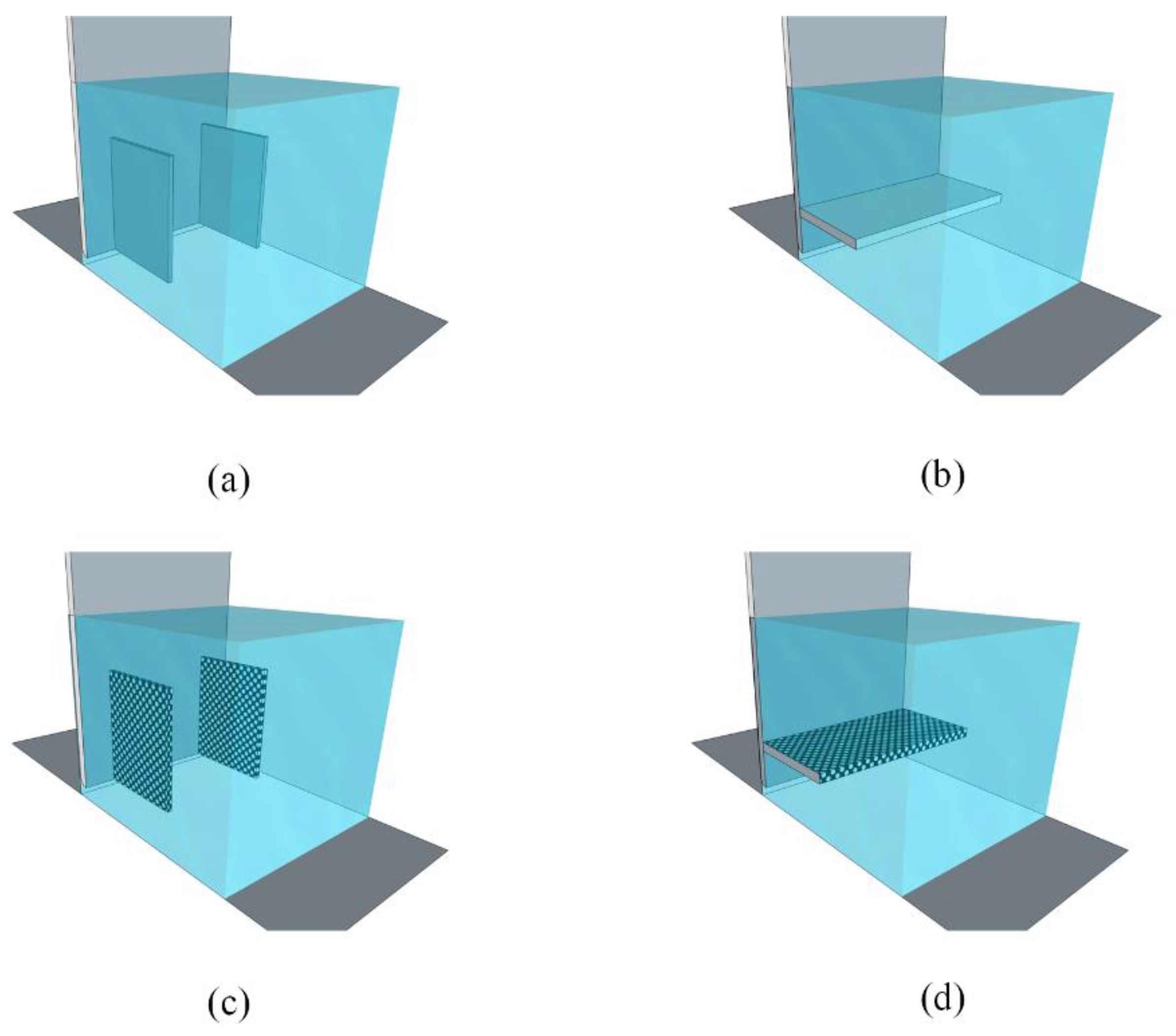
4.3. Development of anti-Vortex Elements
4.4. Performance of the Vortex Breaker for Different Flow Conditions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Long, D.; Steffler, P.M.; Rajaratnam, N. LDA study of flow structure in submerged hydraulic jump. J. Hydraul. Res. 1990, 28, 437–460. [Google Scholar] [CrossRef]
- Demirel, E. Measured and simulated flow downstream of the submerged sluice gate. Water Environ. J. 2015, 29, 446–455. [Google Scholar] [CrossRef]
- Liu, M.; Rajaratnam, N.; Zhu, D.Z. Turbulence Structure of Hydraulic Jumps of Low Froude Numbers. J. Hydraul. Eng. 2004, 130, 511–520. [Google Scholar] [CrossRef]
- De Dios, M.; Bombardelli, F.A.; García, C.M.; Liscia, S.O.; Lopardo, R.A.; Parravicini, J.A. Experimental characterization of three-dimensional flow vortical structures in submerged hydraulic jumps. HydroResearch 2017, 15, 1–12. [Google Scholar] [CrossRef]
- Dey, S.; Sarkar, A. Response of velocity and turbulence in submerged wall jets to abrupt changes from smooth to rough beds and its application to scour downstream of an apron. J. Fluid Mech. 2006, 556, 387. [Google Scholar] [CrossRef]
- Dey, S.; Sarkar, A. Characteristics of Turbulent Flow in Submerged Jumps on Rough Beds. J. Eng. Mech. 2008, 134, 49–59. [Google Scholar] [CrossRef]
- Bhargava, V.P.; Narasimhan, S. Pressure fluctuations on gates. J. Hydraul. Res. 1989, 27, 215–231. [Google Scholar] [CrossRef]
- Thang, N.D.; Naudascher, E. Vortex-excited vibrations of underflow gates. J. Hydraul. Res. 1986, 24, 133–151. [Google Scholar] [CrossRef]
- Billeter, P.; Staubli, T. Flow-induced multıple-mode vıbratıons of gates wıth submerged dıscharge. J. Fluids Struct. 2000, 14, 323–338. [Google Scholar] [CrossRef]
- Erdbrink, C.; Krzhizhanovskaya, V.V.; Sloot, P. Reducing cross-flow vibrations of underflow gates: Experiments and numerical studies. J. Fluids Struct. 2014, 50, 25–48. [Google Scholar] [CrossRef]
- Long, D.; Steffler, P.M.; Rajaratnam, N. A numerical study of submerged hydraulic jumps. J. Hydraul. Res. 1991, 29, 293–308. [Google Scholar] [CrossRef]
- Ma, F.; Hou, Y.; Prinos, P. Numerical calculation of submerged hydraulic jumps Calcul numérique des sauts hydrauliques submergés. J. Hydraul. Res. 2001, 39, 493–503. [Google Scholar] [CrossRef]
- Javan, M.; Eghbalzadeh, A. 2D numerical simulation of submerged hydraulic jumps. Appl. Math. Model. 2013, 37, 6661–6669. [Google Scholar] [CrossRef]
- Cassan, L.; Belaud, G. Experimental and Numerical Investigation of Flow under Sluice Gates. J. Hydraul. Eng. 2012, 138, 367–373. [Google Scholar] [CrossRef]
- Jesudhas, V.; Roussinova, V.; Balachandar, R.; Barron, R. Submerged Hydraulic Jump Study Using DES. J. Hydraul. Eng. 2017, 143, 04016091. [Google Scholar] [CrossRef]
- Nortek, A. Vectrino Velocimeter User Guide; Tech. Rep.; Nortek AS: Vangkroken, Norway, 2019. [Google Scholar]
- Wahl, T.L. Analyzing ADV data using WinADV. In Proceedings of the Joint Conference on Water Resources Engineering and Water Resources Planning & Management, ASCE, Reston, VA, USA, 31 July–2 August 2000; pp. 1–10. [Google Scholar]
- Yeh, H.H. Vorticity-generation mechanisms in bores. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1991, 432, 215–231. [Google Scholar]
- OpenFOAM. The OpenFOAM Foundation; OpenCFD Ltd. Bracknell: London, UK, 2015. [Google Scholar]
- Hirt, C.; Nichols, B. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Wu, S.; Rajaratnam, N. Free jumps, submerged jumps and wall jets. J. Hydraul. Res. 1995, 33, 197–212. [Google Scholar] [CrossRef]
- Kizilaslan, M.A.; Demirel, E.; Aral, M.M. Efficiency Enhancement of Chlorine Contact Tanks in Water Treatment Plants: A Full-Scale Application. Processes 2019, 7, 551. [Google Scholar] [CrossRef]
- Roth, A.; Hager, W.H. Underflow of standard sluice gate. Exp. Fluids 1999, 27, 339–350. [Google Scholar] [CrossRef]
- Sperry, J.M.; Peirce, J.J. A Model for Estimating the Hydraulic Conductivity of Granular Material Based on Grain Shape, Grain Size, and Porosity. Ground Water 1995, 33, 892–898. [Google Scholar] [CrossRef]
- Morgan, N.A. PHYSICAL PROPERTIES OF MARINE SEDIMENTS AS RELATED TO SEISMIC VELOCITIES. Geophysics 1969, 34, 529–545. [Google Scholar] [CrossRef]
- Kizilaslan, M.A.; Demirel, E.; Aral, M.M. Effect of Porous Baffles on the Energy Performance of Contact Tanks in Water Treatment. Water 2018, 10, 1084. [Google Scholar] [CrossRef]


| Q (L/s) | y1 (mm) | U1 (m/s) | F1 | R | y2 (mm) | yt (mm) | S |
|---|---|---|---|---|---|---|---|
| 21 | 25 | 2.1 | 4.24 | 98,824 | 137.93 | 230 | 0.67 |
| Grid | Number of cells (× 106) | ||||||
|---|---|---|---|---|---|---|---|
| Mesh 1 | 0.7 | 2.20 | 53.05 | 176.09 | 0.25 | 23.10 | 83.36 |
| Mesh 2 | 1.85 | 0.84 | 26.95 | 91.86 | 0.22 | 13.42 | 45.65 |
| Mesh 3 | 2.60 | 0.93 | 27.38 | 90.09 | 0.14 | 12.82 | 41.50 |
| Mesh 4 | 4.10 | 1.15 | 28.16 | 94.74 | 0.04 | 9.86 | 35.42 |
| 0.31 | 2.76 × 109 | 5.24 × 104 |
| 0.504 | 7.1 × 107 | 4.78 × 103 |
| 0.802 | 6.26 × 105 | 3.54 × 102 |
| Design | Dissipation Ratio | ||
|---|---|---|---|
| No baffle | N/A | 39.066 | - |
| Vertical solid | N/A | 34.417 | 11.90% |
| Horizontal solid | N/A | 36.898 | 13.25% |
| Vertical porous | 0.3 | 36.898 | 5.55% |
| Vertical porous | 0.5 | 36.905 | 5.53% |
| Vertical porous | 0.8 | 34.816 | 10.88% |
| Horizontal porous | 0.3 | 32.504 | 16.80% |
| Horizontal porous | 0.5 | 34.417 | 11.90 |
| Horizontal porous | 0.8 | 36.210 | 7.31 |
| Dissipation Ratio | ||
|---|---|---|
| 0.10 | 34.423 | 16.80% |
| 0.15 | 32.504 | 11.89% |
| 0.31 | 28.594 | 26.80% |
| Case | Q (lt/s) | y1 (mm) | U1 (m/s) | F1 | Re | S | Vortex Dissipation Ratio (%) | ||
|---|---|---|---|---|---|---|---|---|---|
| No Baffle | Breaker | ||||||||
| Case 1 | 21 | 25 | 2.1 | 4.24 | 9.9 × 104 | 0.67 | 39.066 | 28.594 | 26.81 |
| Case 2 | 15 | 25 | 1.5 | 3.03 | 7.1 × 104 | 0.67 | 34.838 | 25.880 | 25.71 |
| Case 3 | 25 | 25 | 2.5 | 5.05 | 1.2 × 105 | 0.67 | 37.764 | 27.947 | 26.00 |
| Case 4 | 21 | 25 | 2.1 | 4.24 | 9.9 × 104 | 0.96 | 30.402 | 23.782 | 21.78 |
| Case 5 | 21 | 25 | 2.1 | 4.24 | 9.9 × 104 | 0.50 | 42.627 | 29.787 | 30.12 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demirel, E.; Aral, M.M. A Design for Vortex Suppression Downstream of a Submerged Gate. Water 2020, 12, 750. https://doi.org/10.3390/w12030750
Demirel E, Aral MM. A Design for Vortex Suppression Downstream of a Submerged Gate. Water. 2020; 12(3):750. https://doi.org/10.3390/w12030750
Chicago/Turabian StyleDemirel, Ender, and Mustafa M. Aral. 2020. "A Design for Vortex Suppression Downstream of a Submerged Gate" Water 12, no. 3: 750. https://doi.org/10.3390/w12030750
APA StyleDemirel, E., & Aral, M. M. (2020). A Design for Vortex Suppression Downstream of a Submerged Gate. Water, 12(3), 750. https://doi.org/10.3390/w12030750






