Hydropower Generation Through Pump as Turbine: Experimental Study and Potential Application to Small-Scale WDN
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Tests
- Test Series 1: Both rotational PAT speed N and inverter frequency were kept constant during each test, the former imposed at the test bench, the latter at the feed pump. From test to test, the speed varied in the range N = 650–2350 rpm, while the frequency ranging 35–50 Hz, with step of 5 Hz.
- Test Series 2: N, inverter frequency, and discharge Q were kept constant during each test. Such test series was conducted (i) imposing the rotational speed at the test bench; (ii) fixing the feed-pump frequency; and (iii) regulating the valves. This enabled us to have the same flow-rate values, ranging within Q = 5–9 L/s, for each tested speed, this ranging N = 650–1250 rpm.
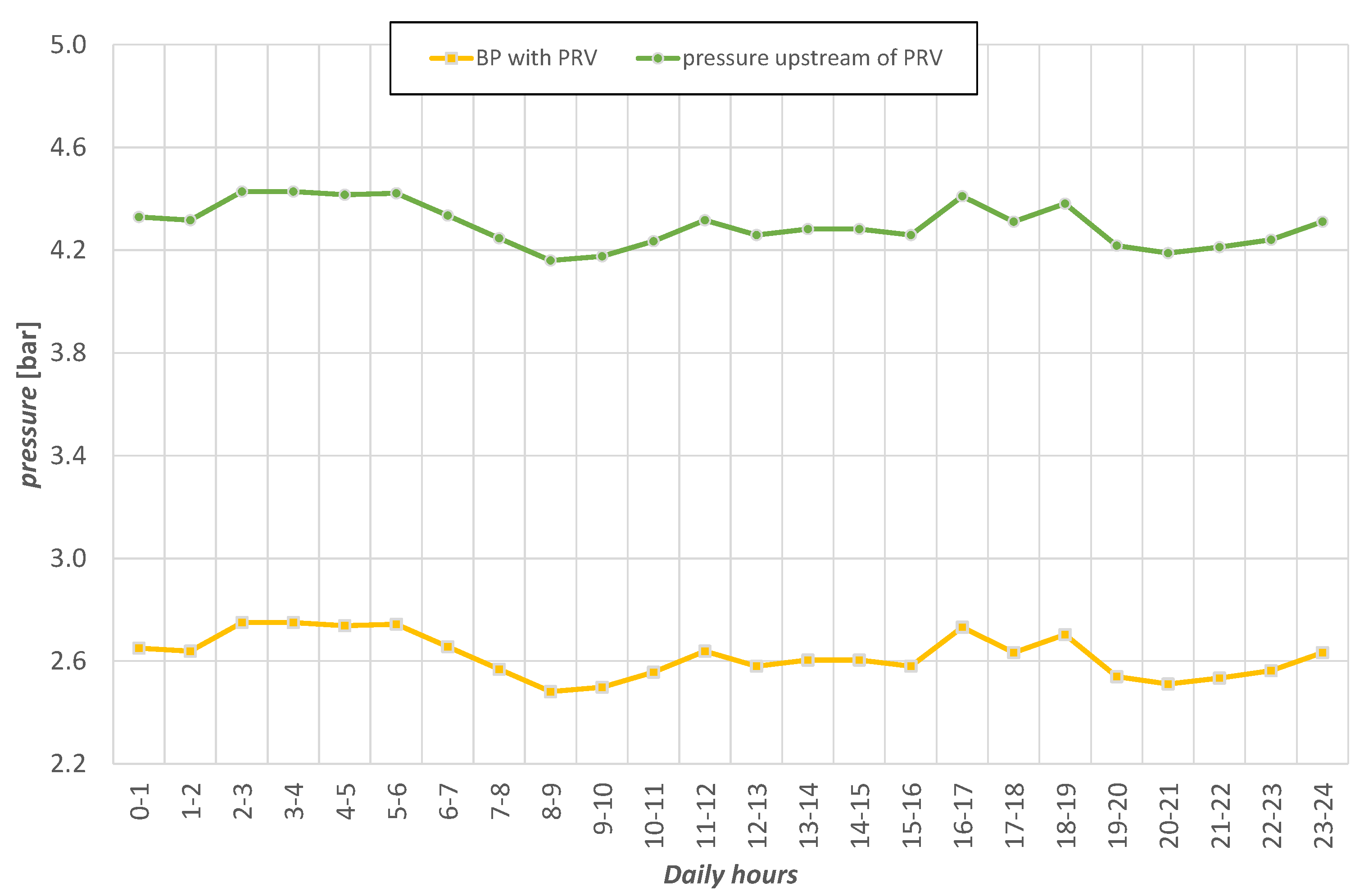
2.2. Application
3. Results
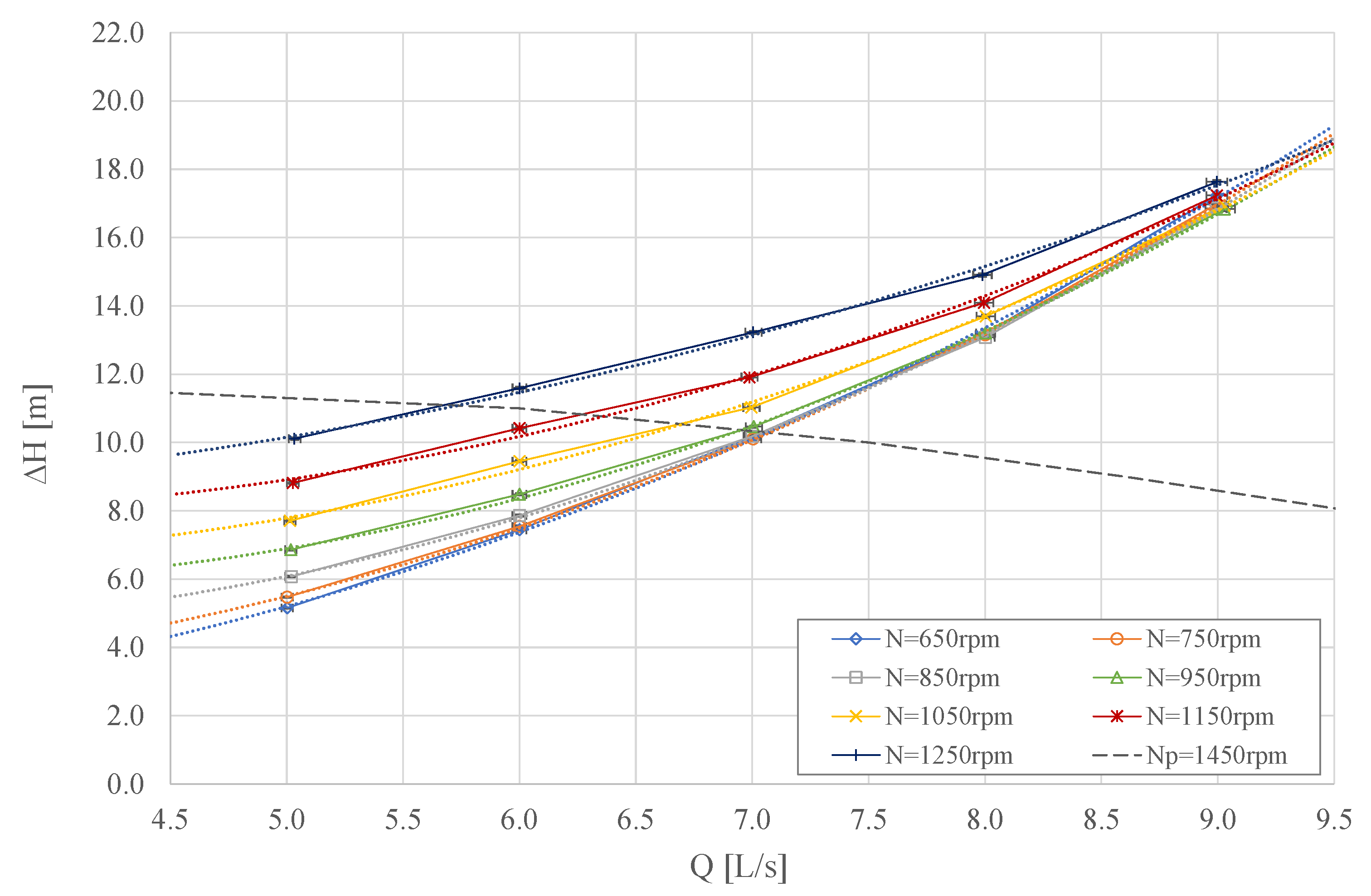
3.1. Hydraulic Properties
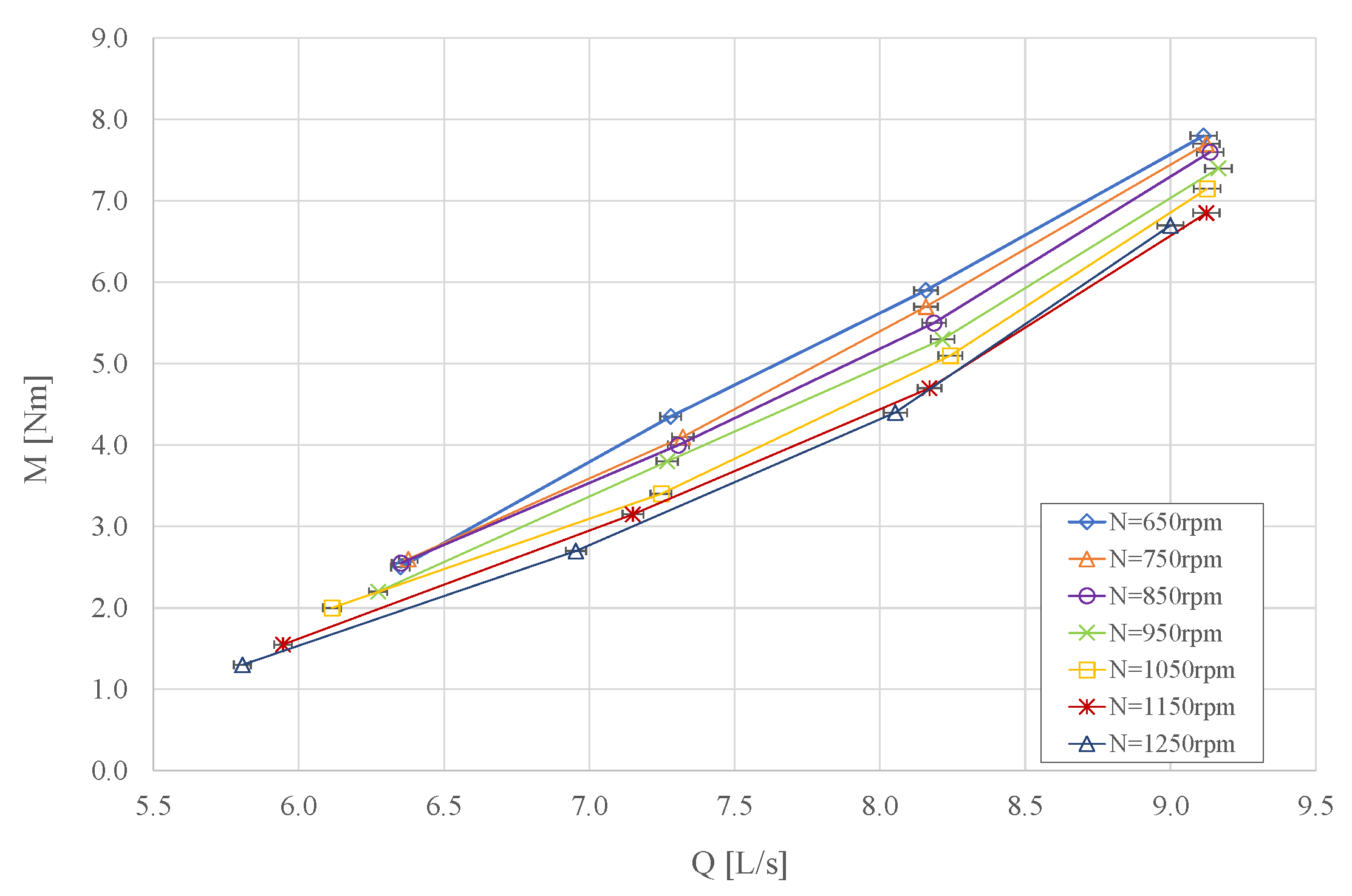
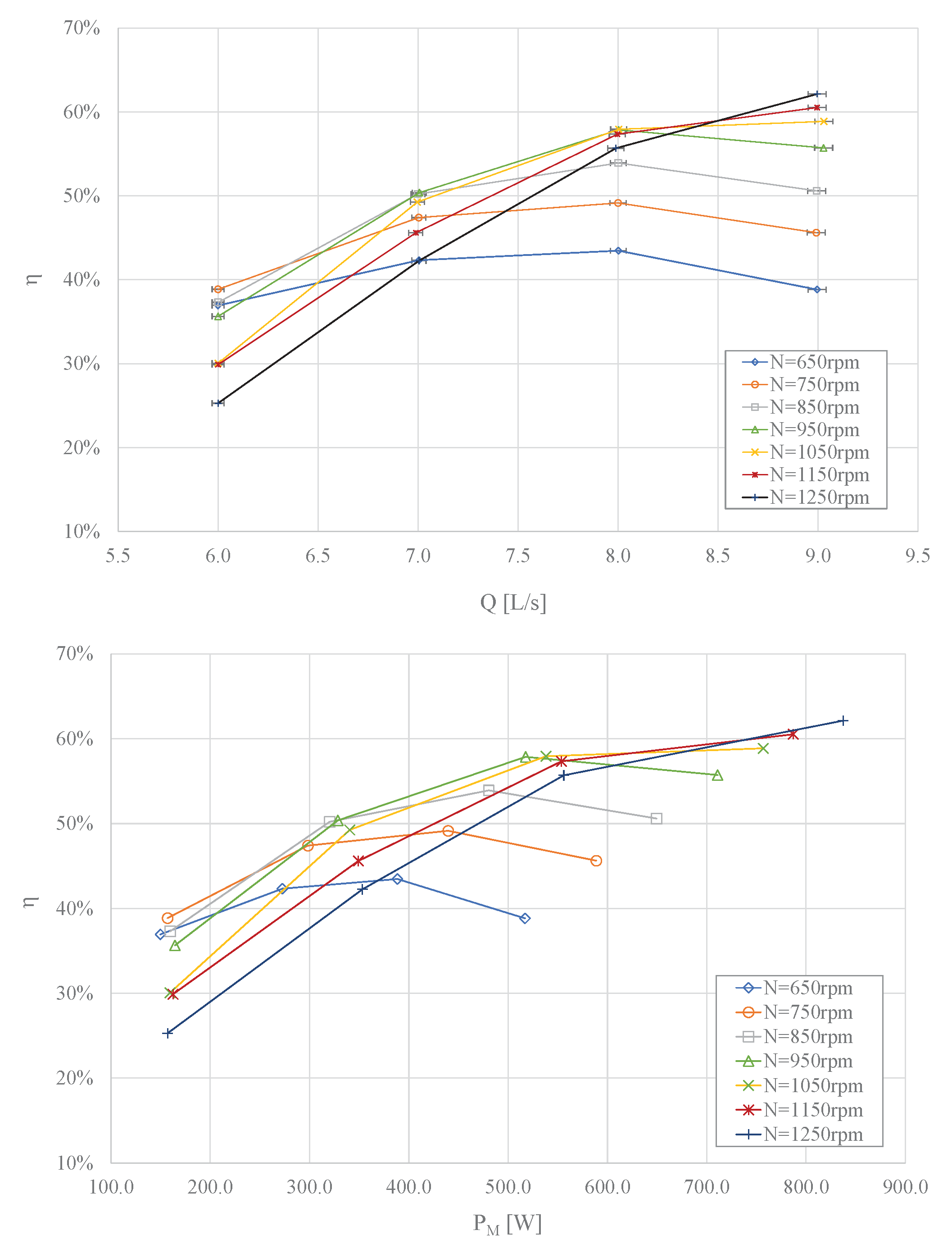
3.2. Mechanical Properties
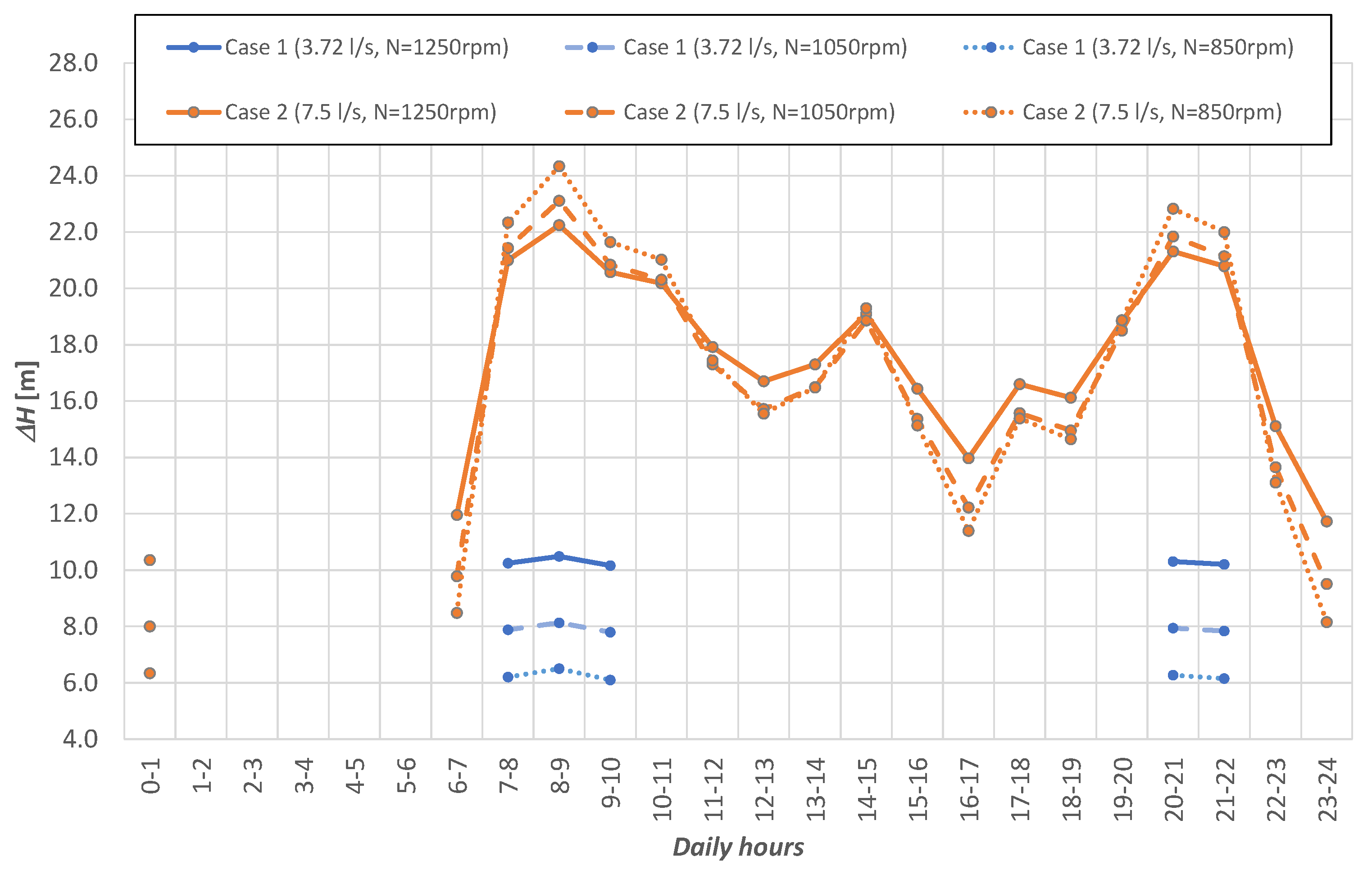
3.3. Application
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Derakhshan, S.; Nourbakhsh, A. Experimental study of characteristic curves of centrifugal pumps working as turbines in different specific speeds. Exp. Therm. Fluid Sci. 2008, 32, 800–807. [Google Scholar] [CrossRef]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H.M. Energy production in water distribution networks: A PAT design strategy. Water Resour. Manag. 2012, 26, 3947–3959. [Google Scholar] [CrossRef]
- Fontana, N.; Giugni, M.; Portolano, D. Losses reduction and energy production in water-distribution networks. J. Water Resour. Plan. Manag. 2012, 138, 237–244. [Google Scholar] [CrossRef]
- Sammartano, V.; Aricò, C.; Carravetta, A.; Fecarotta, O.; Tucciarelli, T. Banki-Michell optimal design by computational fluid dynamics testing and hydrodynamic analysis. Energies 2013, 6, 2362–2385. [Google Scholar] [CrossRef]
- Stefanizzi, M.; Torresi, M.; Fortunato, B.; Camporeale, S. Experimental investigation and performance prediction modeling of a single stage centrifugal pump operating as turbine. Energy Procedia 2017, 126, 589–596. [Google Scholar] [CrossRef]
- Delgado, J.; Ferreira, J.; Covas, D.; Avellan, F. Variable speed operation of centrifugal pumps running as turbines. Experimental investigation. Renew. Energy 2019, 142, 437–450. [Google Scholar] [CrossRef]
- Morani, M.C.; Carravetta, A.; Fecarotta, O.; McNabola, A. Energy Transfer from the Freshwater to the Wastewater Network Using a PAT-Equipped Turbopump. Water 2020, 12, 38. [Google Scholar] [CrossRef] [Green Version]
- Darvini, G.; Soldini, L. Pressure control for WDS management. A case study. Procedia Eng. 2015, 119, 984–993. [Google Scholar] [CrossRef] [Green Version]
- Pugliese, F.; De Paola, F.; Fontana, N.; Giugni, M.; Marini, G. Experimental characterization of two pumps as turbines for hydropower generation. Renew. Energy 2016, 99, 180–187. [Google Scholar] [CrossRef]
- Jain, S.V.; Patel, R.N. Investigations on pump running in turbine mode: A review of the state-of-the-art. Renew. Sustain. Energy Rev. 2014, 30, 841–868. [Google Scholar] [CrossRef]
- Novara, D.; Carravetta, A.; McNabola, A.; Ramos, H. Cost model for pumps as turbines in run-of-river and in-pipe microhydropower applications. J. Water Resour. Plan. Manag. 2019, 145, 04019012. [Google Scholar] [CrossRef]
- Barbarelli, S.; Amelio, M.; Florio, G. Experimental activity at test rig validating correlations to select pumps running as turbines in microhydro plants. Energy Convers. Manag. 2017, 149, 781–797. [Google Scholar] [CrossRef]
- Venturini, M.; Alvisi, S.; Simani, S.; Manservigi, L. Comparison of Different Approaches to Predict the Performance of Pumps as Turbines (PATs). Energies 2018, 11, 1016. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.S.; Derakhshan, S.; Kong, F.Y. Theoretical, numerical and experimental prediction of pump as turbine performance. Renew. Energy 2012, 48, 507–513. [Google Scholar] [CrossRef]
- Rossi, M.; Righetti, M.; Renzi, M. Pump-as-Turbine for energy recovery applications: The case study of an aqueduct. Energy Procedia 2016, 101, 1207–1214. [Google Scholar] [CrossRef]
- De Marchis, M.; Milici, B.; Volpe, R.; Messineo, A. Energy saving in water distribution network through pump as turbine generators: Economic and environmental analysis. Energies 2016, 9, 877. [Google Scholar] [CrossRef] [Green Version]
- Renzi, M.; Rudolf, P.; Štefan, D.; Nigro, A.; Rossi, M. Installation of an axial Pump-as-Turbine (PaT) in a wastewater sewer of an oil refinery: A case study. Appl. Energy 2019, 250, 665–676. [Google Scholar] [CrossRef]
- Morabito, A.; Hendrick, P. Pump as turbine applied to micro energy storage and smart water grids: A case study. Appl. Energy 2019, 241, 567–579. [Google Scholar] [CrossRef]
- Kramer, M.; Terheiden, K.; Wieprecht, S. Pumps as turbines for efficient energy recovery in water supply networks. Renew. Energy 2018, 122, 17–25. [Google Scholar] [CrossRef] [Green Version]
- Sammartano, V.; Sinagra, M.; Filianoti, P.; Tucciarelli, T. A Banki–Michell turbine for in-line water supply systems. J. Hydraul. Res. 2017, 55, 686–694. [Google Scholar] [CrossRef]
- Sammartano, V.; Filianoti, P.; Sinagra, M.; Tucciarelli, T.; Scelba, G.; Morreale, G. Coupled hydraulic and electronic regulation of cross-flow turbines in hydraulic plants. J. Hydraul. Eng. 2017, 143, 04016071. [Google Scholar] [CrossRef]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H.M. PAT design strategy for energy recovery in water distribution networks by electrical regulation. Energies 2013, 6, 411–424. [Google Scholar] [CrossRef] [Green Version]
- Carravetta, A.; Derakhshan Houreh, S.; Ramos, H.M. Pumps as turbines. In Springer Tracts in Mechanical Engineering; Springer: Cham, Switzerland, 2018; p. 236. [Google Scholar]
- Tricarico, C.; Morley, M.S.; Gargano, R.; Kapelan, Z.; De Marinis, G.; Savic, D.; Granata, F. Integrated optimal cost and pressure management for water distribution systems. Procedia Eng. 2014, 70, 1659–1668. [Google Scholar] [CrossRef] [Green Version]
- Carravetta, A.; Fecarotta, O.; Ramos, H. A new low-cost installation scheme of PATs for pico-hydropower to recover energy in residential areas. Renew. Energy 2018, 125, 1003–1014. [Google Scholar] [CrossRef]
- Lydon, T.; Coughlan, P.; McNabola, A. Pressure management and energy recovery in water distribution networks: Development of design and selection methodologies using three pump-as-turbine case studies. Renew. Energy 2017, 114, 1038–1050. [Google Scholar] [CrossRef]
- Muhammetoğlu, A.; Muhammetoğlu, H. Excess Pressure in Municipal Water Supply Systems as a Renewable Energy Source: Antalya Case Study. In Recycling and Reuse Approaches for Better Sustainability; Springer: Berlin, Germany, 2019; pp. 113–126. [Google Scholar]
- Alberizzi, J.C.; Renzi, M.; Nigro, A.; Rossi, M. Study of a Pump-as-Turbine (PaT) speed control for a Water Distribution Network (WDN) in South-Tyrol subjected to high variable water flow rates. Energy Procedia 2018, 148, 226–233. [Google Scholar] [CrossRef]
- Du, J.; Yang, H.; Shen, Z.; Chen, J. Micro hydro power generation from water supply system in high rise buildings using pump as turbines. Energy 2017, 137, 431–440. [Google Scholar] [CrossRef]
- Milano, V. ACQUEDOTTI; Hoepli: Milan, Italy, 2012. (In Italian) [Google Scholar]
- Creaco, E.; Franchini, M.; Todini, E. Generalized resilience and failure indices for use with pressure-driven modeling and leakage. J. Water Resour. Plan. Manag. 2016, 142, 04016019. [Google Scholar] [CrossRef]
- Darvini, G.; Ruzza, V.; Salandin, P. Performance Assessment of Water Distribution Systems Subject to Leakage and Temporal Variability of Water Demand. J. Water Resour. Plan. Manag. 2020, 146, 04019069. [Google Scholar] [CrossRef]
- Tricarico, C.; De Marinis, G.; Gargano, R.; Leopardi, A. Peak residential water demand. In Proceedings of the Institution of Civil Engineers-Water Management; Thomas Telford Ltd.: London, UK, 2007; Volume 160, pp. 115–121. [Google Scholar]
- IEC. Hydraulic Turbines, Storage Pumps and Pump-Turbines—Model Acceptance Tests; International Electrotechnical Commission: Geneva, Switzerland, 1999; European Standard EN 60193:1999. [Google Scholar]
- Balacco, G.; Carbonara, A.; Gioia, A.; Iacobellis, V.; Piccinni, A. Evaluation of peak water demand factors in Puglia (Southern Italy). Water 2017, 9, 96. [Google Scholar] [CrossRef] [Green Version]
- Favi, C.; Di Giuseppe, E.; D’Orazio, M.; Rossi, M.; Germani, M. Building retrofit measures and design: A probabilistic approach for LCA. Sustainability 2018, 10, 3655. [Google Scholar] [CrossRef] [Green Version]
- Baldoni, E.; Coderoni, S.; D’Orazio, M.; Di Giuseppe, E.; Esposti, R. The role of economic and policy variables in energy-efficient retrofitting assessment. A stochastic Life Cycle Costing methodology. Energy Policy 2019, 129, 1207–1219. [Google Scholar] [CrossRef]








| Flow rate value at BEP | 7 L/s |
|---|---|
| Head at BEP | 10 m |
| Best efficiency value | 0.75 |
| Fixed rotating speed N | 1450 rpm |
| Specific speed | 12.63 |
| Impeller diameter | 65 mm |
| Liquid processed | H2O ( = 1000 kg/m3) |
| # | Component | Specifications |
|---|---|---|
| 1 | Open tank | 2.0 m × 1.0 m × 2.5 m |
| 1 | Feed pump | Caprari multistage vertical electric pump |
| ( kW, m, L/s) | ||
| 2 | Flowmeters | 1 instant-measuring (Riels) |
| 1 electromagnetic Endress+Hauser [acc.: ±0.5%] | ||
| 4 | Flow-regulation valves | 2 butterfly valves (V1, V3) |
| 1 diaphragm valve (V2) | ||
| 1 globe valve (Vu) | ||
| 3 | Pressure meters | 1 barometer |
| 2 electronic Endress+Hauser [acc.: ±0.3%] | ||
| 1 | PAT | Rotos axial pump |
| (1.23 kW, max head 12 m, max flow 11.2 L/s) | ||
| 1 | Test bench | Borghi&Saveri |
| Case | Description | n | d [lpd] | α | [L/s] |
|---|---|---|---|---|---|
| 1 | Servigliano | 2377 | 130 | 1.04 | 3.72 |
| 2 | PAT optimized | 4792 | 130 | 1.04 | 7.50 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Postacchini, M.; Darvini, G.; Finizio, F.; Pelagalli, L.; Soldini, L.; Di Giuseppe, E. Hydropower Generation Through Pump as Turbine: Experimental Study and Potential Application to Small-Scale WDN. Water 2020, 12, 958. https://doi.org/10.3390/w12040958
Postacchini M, Darvini G, Finizio F, Pelagalli L, Soldini L, Di Giuseppe E. Hydropower Generation Through Pump as Turbine: Experimental Study and Potential Application to Small-Scale WDN. Water. 2020; 12(4):958. https://doi.org/10.3390/w12040958
Chicago/Turabian StylePostacchini, Matteo, Giovanna Darvini, Fiorenza Finizio, Leonardo Pelagalli, Luciano Soldini, and Elisa Di Giuseppe. 2020. "Hydropower Generation Through Pump as Turbine: Experimental Study and Potential Application to Small-Scale WDN" Water 12, no. 4: 958. https://doi.org/10.3390/w12040958
APA StylePostacchini, M., Darvini, G., Finizio, F., Pelagalli, L., Soldini, L., & Di Giuseppe, E. (2020). Hydropower Generation Through Pump as Turbine: Experimental Study and Potential Application to Small-Scale WDN. Water, 12(4), 958. https://doi.org/10.3390/w12040958







