Abstract
This paper presents a comparison between two procedures for the generation of water demand time series at both single user and nodal scales, a top-down and a bottom-up procedure respectively. Both procedures are made up of two phases. The top-down procedure adopted includes a non-parametric disaggregation based on the K-nearest neighbours approach. Therefore, once the temporal aggregated water demand patterns have been defined (first phase), the disaggregation is used to generate water demand time series at lower levels of spatial aggregation (second phase). In the bottom-up procedure adopted, demand time series for each user and for each time step are generated applying a beta probability distribution with tunable bounds or a gamma distribution with shift parameter (first phase). Then, a Copula based re-sort is applied to the demand time series generated to impose existing rank cross-correlations between users and at all temporal lags (second phase). For the sake of comparison, two case studies were considered, both of which are related to a smart water network in Naples (Italy). The results obtained show that the bottom-up procedure performs significantly better than the top-down procedure in terms of rank-cross correlations at fine scale. However, the top-down procedure showed a better performance in terms of skewness and rank cross-correlation when the aggregated demands were considered. Finally, the level of aggregation in nodes was found to affect the performance of both the procedures considered.
1. Introduction
Accurate estimates of nodal demands are of fundamental importance for numerical simulation of water distribution networks (WDNs) behavior. Accurate estimates lead to consistent results in terms of nodal outflows and pressure-heads [1]. The assessment of nodal demands is usually carried out through two different approaches [2], the top-down and the bottom-up approach respectively.
According to the first approach, firstly the total water demand pattern of the whole WDN considered is defined and then the total demand is disaggregated into the individual nodes of the model. In its most common deterministic application, once the water demand pattern has been defined at high levels of spatial aggregation, the nodal water demand patterns are usually obtained by disaggregating the total amount of water supplied in proportion to the average demand at each node. Therefore, this approach does not consider both the random character of water demands and their variability. Indeed, it is assumed that all nodes are characterized by an identical demand pattern implying a maximum correlation in space between the temporal patterns. However, the importance of taking into account the variability of water demands was highlighted by several studies [3,4,5,6]. Therefore, with the aim of taking into account the random nature of the water demand, stochastic procedures for the disaggregation of time series were adopted. Among them, several procedures belonging to the hydrological field allow preservation of the main statistics (such as mean, variance and skewness) of the disaggregated series [7,8,9,10]. The disaggregation procedures present in the literature can essentially rely on two different approaches, the parametric approach [11,12,13] and the non-parametric approach [14,15,16]. Essentially, the parametric approach requires a priori assumptions about the probability distributions of the demands, while the nonparametric procedures need observed nodal demands for their application.
The second demand reconstruction approach provides the bottom-up reconstruction starting from the single nodes. The nodal demands are then represented as stochastic variables. However, the stochastic nodal demands can be obtained by temporal aggregating the results of pulse generation models [17]. Among them, certain models reproduce arrival time, intensity and duration of all pulses coming from individual appliances and fixtures (such as dishwashers, washing machines, shower, etc.) in the generic household allocated to the WDN node operating at very small time steps, i.e., of the order of seconds [18,19]. Due to the large computational burden of these procedures different approaches are used when synthetical nodal demands at larger time step (i.e., of the order of minutes or hours) are needed. In this event, as an example, the overall pulse model proposed by Gargano et al. [20] or the random multinomial processes developed by Alvisi et al. [21] can be used.
Though various applications of top-down and bottom-up approaches exist in the scientific literature, as reported above, few comparative works have been presented so far [22], aimed at assessing the effectiveness of such approaches in both water resources planning [23] and in identifying main energy inefficiencies in water systems [24]. However, the present paper was aimed at presenting this comparison in a real case study, made up of a smart water network in Naples (Italy), highlighting the differences in synthetic time series generation in terms of statistics, such as media, standard deviation, skewness and correlations.
In the following sections, the demand reconstruction procedures are first briefly explained. Then, the results of their applications to two case studies, both consisting of hourly consumption data, are reported. Finally, the obtained results are discussed in order to carry out a comparison between the two procedures.
2. Materials and Methods
In the following sections two procedures for generating synthetic time series are presented. The first procedure presented is based on the top-down non-parametric disaggregation developed by Nowak et al. [16]. Once the temporal water demand pattern at a high level of spatial aggregation has been defined, the disaggregation procedure allows generation of water demand time series at lower levels of spatial aggregation.
The second procedure is the bottom-up procedure developed by Creaco et al. [25] for the reconstruction of consistent demand time series at WDN users starting from the measured demand time series from a smart meter district.
2.1. Top-Down Procedure
Let us assume a district with N nodes (or users). After subdividing the generic day into time steps , the first procedure proposed in this paper allows generation of the water demand time series of the generic j-th node (or user) in the generic i-th , starting from the total amount of water Qi supplied at the i-th time step. The procedure is made up of two phases [26]. The first phase consists of using a stochastic [27] or non-parametric algorithm [28] to generate the total water demand time series of the area (i.e., one demand time series for each of the day). In the present work, the total demand at the generic time step of the day is sampled from a beta probability distribution with tunable bounds, which enables preserving mean, variance and skewness of the total demand time series [25]. A copula resorting is applied on the generated time series to preserve temporal correlations on the total demand at all temporal lags. These latter are derived from the measured time series through the Spearman index [29]. Specifically, a multivariate normal probability distribution, with means and standard deviations equal to 0 and 1 respectively, is used as copula [30]. The multivariate normal distribution is then used to generate time series expressing the rank cross correlations to be imposed on demand time series between users at all temporal lags.
Therefore, for the parametrization of the procedure mean , standard deviation and skewness for each total demand time series must be assessed ( parameters). Furthermore, the minimum value of the total demand time series is needed ( parameters) in order to implement the beta probability distribution (make reference to Creaco et al. 2020 [25] for further explanations). Finally, temporal cross-correlations between total demand time series must be evaluated. In this respect, two aspects should be considered: firstly, each time series is fully correlated with itself, secondly the correlation between two time series is symmetrical ( parameters). Concluding, the number of parameters to be assessed adds up to .
In the second phase, a spatial disaggregation is applied to generate the water demand time series of each node. In the present work the non-parametric disaggregation proposed by Nowak et al. [16] is used. Assuming an hourly time-step, according to the non-parametric disaggregation the generation of the nodal demand is obtained by the random resampling from the conditional probability density function f (qh|Qh), where Qh and qh are the random variables representing the aggregate demand in the h-th hour and the disaggregated demand in the h-th hour respectively. In the model presented in Nowak et al. [16], the conditional density function is carried out using a K-nearest neighbours (K-NN) approach applied on the basis of the observed aggregate series. Specifically, let us assume the length of the generated and measured aggregated time series respectively equal to and , where and are the numbers of days of generated and measured time series respectively. K-nearest neighbours to each generated value of the aggregated series (, with ) are identified from the measured aggregate demands related to the same hour h (, with ). According to a heuristic approach, the optimal number K is equal to [28]. However, the neighbours are computed based on the absolute value of the difference between the observed and generated aggregate values (). Therefore, the K values with the smallest are selected. Then, after being reordered from the nearest to the farthest, the K-nearest neighbours are assigned a weight according to their position j in the reordered vector [28]:
One of the K-nearest neighbours is selected based on a weighted resampling and the corresponding proportions for each of the N nodes for the h-th hour of the d-th day are calculated on the basis of measured demands:
where is the generic disaggregated measured value of the j-th node for the h-th hour of the d-th day and is the associated aggregated value.
Finally, the obtained proportions are multiplied by the generated aggregated value to provide the generated disaggregated values :
2.2. Bottom-Up Procedure
In this work the procedure developed by Creaco et al. [25] was applied as bottom-up procedure, enabling the generation of demand time series for each of the N nodes (or users) considered for any time step .
Then, the procedure is made up of two phases. In the first phase it is assumed that the daily demand of the generic j-th user in the i-th follows the beta probability distribution with tunable bounds.
The generated demand time series respect the basic statistics (mean, variance, and skewness). However, they fail to preserve the existing rank cross correlations between users and at various temporal lags. Therefore, in the second phase, the generated demand time series are re-sorted through a copula to impose existing rank cross-correlations. These latter are derived from the measured time series through the Spearman index [29]. Specifically, a multivariate normal probability distribution, with means and standard deviations equal to 0 and 1 respectively, is used as copula [30]. The multivariate normal distribution is then used to generate time series expressing the rank cross correlations to be imposed on demand time series between users at various lags.
At the generic i-th of the time steps, the total demand Qi is finally obtained as the sum of the N values obtained after the copula based re-sorting.
As regards the parameterization of the procedure, the assessment of mean , standard deviation , skewness and the minimum value of each demand time series is required ( parameters). Moreover, cross-correlations between demand time series must be evaluated, assuming the same as in the previous procedure ( parameters). Finally, the number of parameters to be assessed is equal to .
2.3. Case Studies
Two case studies were analysed in this work.
For both case studies the hourly consumption data from a smart water network located in a suburban area of Naples (Italy) were considered. In this area, called Soccavo, the municipal water company “Acqua Bene Comune Napoli” (ABC) implemented a smart WDN replacing almost 5000 traditional water meters with smart meters, aiming to reconstruct the total district consumption. For the sake of comparison with the results obtained in the previous work carried out by Creaco et al. [25], in the first case study (Case study 1) the data of 100 users for 31 days, from 1 January 2018 to 31 January 2018, were considered.
The second case study (Case study 2) is made up of 1000 users from the same smart water district, monitored from 1 October 2017 to 31 October 2017. Therefore, the case studies essentially differ because of the number of users. It must be noted that in both case studies only one month was considered since the parameters of the procedures presented are characterized by monthly variations.
The daily patterns of aggregated measured hourly demand in the 31 days considered in both case studies are shown in Figure 1, highlighting similar characteristics of water consumption in the network.
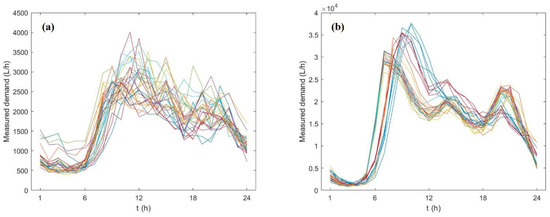
Figure 1.
Patterns of aggregated measured hourly demand for 31 days for both Case study 1 (a) and Case study 2 (b).
In both case studies, the generated demand time series were obtained by assuming the typical day of generation to be subdivided into = 24 time steps with = 1 hr.
Furthermore, the generation of demand time series was performed for a number of days and was reiterated for 500 times for both procedures.
3. Results
In the following sections the results obtained applying both the top-down and bottom-up procedures to both case studies are reported. In the comparison between basic statistics of measured and generated demand time series the average values over the 500 iterations were considered for the latter series.
3.1. Results—Case Study 1
For the sake of comparison with the results obtained by Creaco et al. [25], the top-down procedure was applied to the Case study 1 performing two applications: in the first application (Application 1) the top-down procedure was applied in order to generate single user and aggregated water demand time series. In the second application (Application 2), nodal demands were considered grouping the users in 20 nodes. In Application 2, the measured demand time series of the generic node were estimated as the sum of the demand time series of the related users. Therefore, the procedure was parameterized based on the measured single user and nodal demand time series, respectively in Application 1 and in Application 2.
As regards the single user demands of Application 1, Figure 2a shows the comparison between measured and generated hourly demands in terms of mean values, highlighting a perfect fit (). Almost the same result () was obtained for the standard deviation values, as shown in Figure 2b. The fit in terms of skewness values (Figure 2c) is almost perfect () as well. As regards the cross-correlations, in Figure 2d the dots representing the rank cross correlations at lag 0, i.e., the spatial correlations between the N user demands in the same hour, are differentiated from the others. Indeed, the values of the rank cross-correlations at lag 0 show a good fit (). However, the top-down procedure failed to preserve the rank cross correlations between users and at various temporal lags (). As already shown by Alvisi et al. [26], the non-parametric approach is unable to preserve the correlations between the demands associated with one hour and those of the previous hour, since for each hour the data are disaggregated independently of those related to other hours.
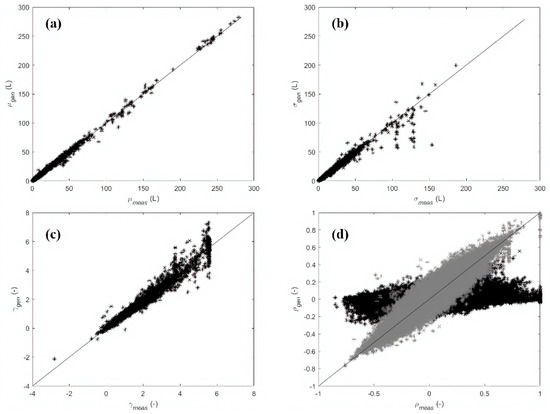
Figure 2.
Case study 1 (Application 1)—Comparison between measured and generated hourly demands at single user level: (a) mean values , (b) standard deviation values , (c) skewness , (d) rank cross-correlations (black) and (gray).
Figure 3 shows the results at the level of the aggregated demand time series. As shown in Figure 3a,b,d, the comparison between measured and generated aggregated hourly demands in terms of mean, standard deviation and rank cross-correlations values highlights a perfect agreement (). As regards the skewness values (Figure 3c), the fit is again almost perfect ().
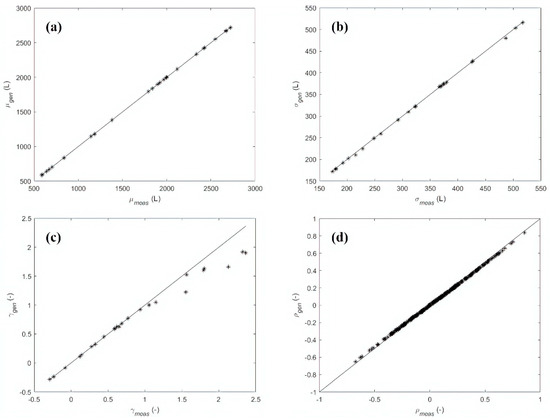
Figure 3.
Case study 1 (Application 1)—Comparison between measured and generated aggregated hourly demands: (a) mean values , (b) standard deviation values , (c) skewness , (d) rank cross-correlations .
The graphs in Figure 4 show the results obtained in Application 2 for generated hourly demands at single node level, leading to similar considerations to Application 1. Indeed, though respecting the basic statistics in terms of mean, variance and skewness the top-down procedure was unable to reproduce the existing rank cross-correlations between nodes at various temporal lags.
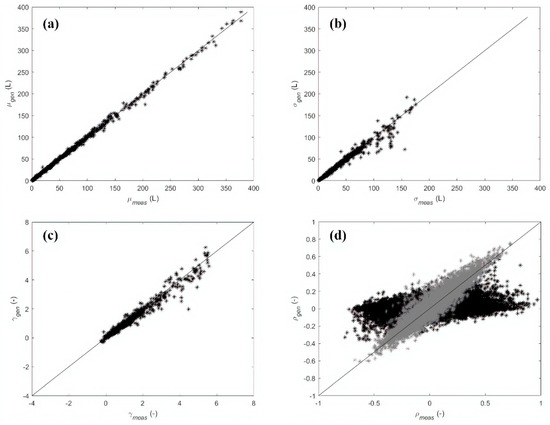
Figure 4.
Case study 1 (Application 2)—Comparison between measured and generated hourly demands at single node level: (a) mean values , (b) standard deviation values , (c) skewness , (d) rank cross-correlations (black) and (gray).
Finally, the comparison of measured and generated aggregated hourly demands is reported in Figure 5. The performance on the aggregated scale is excellent as in the Application 1, demonstrating the effectiveness of the procedure in total district consumption reconstruction.
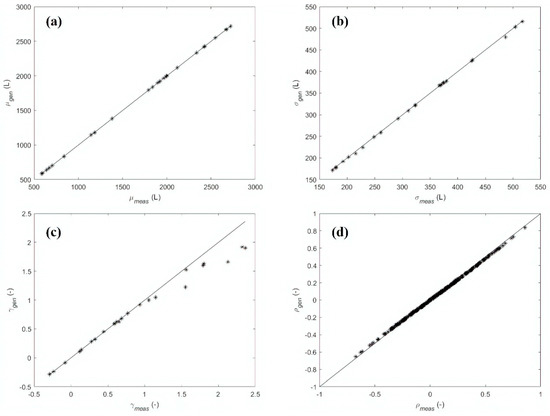
Figure 5.
Case study 1 (Application 2)—Comparison between measured and generated aggregated hourly demands: (a) mean values , (b) standard deviation values , (c) skewness , (d) rank cross-correlations .
The Table 1 summarizes the results discussed above along with the results obtained by Creaco et al. [22].

Table 1.
Comparison of mean values , standard deviation values , skewness , rank cross-correlations and of measured and generated hourly demands, evaluating the fit in terms of R2 at both single and aggregated scales, for both applications to the first case study and for both the top-down and the bottom-up procedures.
3.2. Results—Case Study 2
Both procedures were applied to the Case study 2 performing three applications: the users were grouped in 10 (Application 1), 50 (Application 2), and 100 (Application 3) nodes, allocating in each node 100, 20, and 10 users respectively.
The results in terms of of the fit obtained by the application of the top-down procedure are shown in Table 2.

Table 2.
Comparison of mean values , standard deviation values , skewness , rank cross-correlations and of measured and generated hourly demands, evaluating the fit in terms of R2 at both single and aggregated scales, for each application of top-down procedure to Case study 2.
For all the three applications, the performance on mean, standard deviation, skewness and cross-correlations at lag 0 at single node level is excellent. However, the fit of rank cross-correlations at lag 0 seems to slightly improve with the increasing level of aggregation in nodes, i.e., with the increasing number of users allocated in each node. In this respect, even though Application 2 and Application 3 confirm the inability of the top-down procedure to reproduce the cross-correlations at various temporal lags, better results are obtained in case of 10 nodes. Indeed, for Application 1, the reaches a value of 0.54. It can be stated then that a high level of aggregation in nodes can improve the performance in terms of cross-correlations for the top-down procedure.
As regards the aggregated demands, the fit is always perfect for all three applications, confirming the effectiveness of the procedure in total district consumption reconstruction.
Table 3 shows the results obtained applying the bottom-up procedure.

Table 3.
Comparison of mean values , standard deviation values , skewness , rank cross-correlations and of measured and generated hourly demands, evaluating the fit in terms of R2 at both single and aggregated scales, for each application of bottom-up procedure to Case study 2.
For all three applications, the bottom-up procedure performs better than the top-down procedure in terms of rank-cross correlations at single node level. Indeed, the fit is always perfect (), attesting to the effectiveness of the copula-based re-sort during the second phase of the procedure. However, on the aggregated scale the performance in terms of skewness is better in case of application of the top-down procedure. As already stated by Creaco et al. [25], the deterioration of the fit in terms of skewness when aggregated demand is considered is due to both the parameterization, which was performed on the single user scale, and the approximations inherent in the modelling. However, the fit of the skewness values seems to improve with the increasing level of aggregation in nodes. Indeed, the maximum value of is reached in case of 10 nodes ().
For explicatory purposes, the graphs in Figure 6 report, for measured and generated aggregated demand time series, the daily temporal patterns of mean μ and their intervals ± 0.5 for both the procedures in Application 2. The means for the measured demand time series were obtained starting from the aggregated measured demands, while those for the generated demand time series are the average values over 500 generations. However, these graphs constitute further evidence of the goodness of the fit at aggregated scale for both procedures.
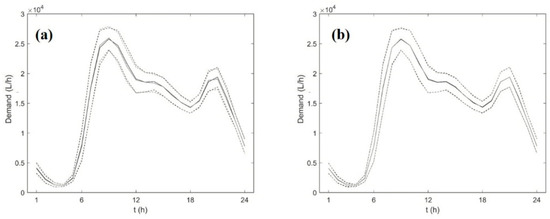
Figure 6.
Case study 2 (Application 2) - Daily temporal patterns of both mean (continuous lines) and intervals ± 0.5 (dotted lines) for measured (black lines) and generated (grey lines) aggregated demands: the generated demands were obtained applying the top-down approach (a) and the bottom-up approach (b) respectively.
4. Discussion
In this section some considerations about the results reported above are made.
Case study 1 was previously used by Creaco et al. [25] for the application of the bottom-up procedure. Therefore, a comparison between the top-down and the bottom-up procedures can be carried out. The results reported in Table 1 show the inability of the top-down procedure to reproduce the cross-correlations at various temporal lags at both single user and nodal scales. However, according to the work of Creaco et al. [25], in both cases (single users and single nodes), the performance in terms of rank cross-correlation of the bottom-up procedure is excellent. Indeed, the of the fit between measured and generated values is equal to 1 at both single user and nodal scales.
However, as regards the aggregated demands better results were obtained by applying the top-down procedure. As mentioned above, for the bottom-up procedure the parameterization performed on the single user scale leads to the deterioration of the fit in terms of skewness and rank cross-correlation when the aggregated demands are considered. Furthermore, better results were obtained applying the bottom-up procedure starting from the nodes of the WDN, rather than from single users.
In this respect, the results obtained in Case study 2 give further evidence of the effectiveness of the bottom-up procedure in generating consistent synthetical patterns of nodal demands.
Account must be taken of the higher burden of parameterization of the bottom-up procedure. Indeed, the top-down procedure requires definition of a lower number of parameters. However, the parameters required by the bottom-up procedure can be easily estimated when smart meter readings are widely available over the WDN. Also, the computational burden is lower for the top-down procedure.
As regards the choice of in the present work, for both procedures, an hourly time step was considered. However, the procedures are expected to be effective also for different values of . Anyway, the bottom-up procedure is mainly based on the application of rank cross-correlations to demand time series. Therefore, its use is more suitable in the case of values in which these correlations are significant, i.e., starting from hourly time step [31]. Furthermore, the bottom-up procedure neglects the pulsed nature of demand, that becomes predominant when is small, i.e., of the order of minutes or seconds.
5. Conclusions
In the present paper, two procedures for the generation of demand time series at both single user and nodal scale were presented. The first procedure consists of a top-down approach based on the disaggregation developed by Nowak et al. [16]. According to this procedure, once the temporally aggregated water demand patterns have been defined, the disaggregation is applied to generate water demand time series at lower levels of spatial aggregation.
The second procedure proposed is made up of a bottom-up procedure. Under this procedure, a copula based re-sort is applied to demand time series of the first attempt generated through a beta or gamma probability distribution to impose existing rank cross-correlations.
Two case studies with different numbers of users were then considered performing various application types.
While the reproduction of mean and standard deviation of demand time series at single users (nodes) and for the total demand is satisfactory for both procedures, differences arise as for demand cross-correlations and skewness.
As expected, the top-down procedure is better at reproducing the total demand, especially in terms of skewness and temporal correlations. The bottom-up procedure prevails, instead, as for cross-correlations between single users (nodes).
Indeed, the top-down procedure proved poorly capable of reproducing the cross-correlations at various temporal lags though results slightly improve in the case of high levels of aggregation in nodes.
As regards the aggregated demands, the top-down procedure showed a better performance in terms of skewness and rank cross-correlation. However, it was found that the application of the bottom-up procedure for the generation of nodal demands, rather than single users’ demands, has positive impacts in respecting rank cross-correlations in the aggregated consumption. Therefore, it can be successfully applied to the generation of nodal demands in a WDN.
Author Contributions
Conceptualization and methodology D.F. and E.C.; software E.C.; validation and resources F.D.P and M.G.; writing—original draft preparation, D.F.; writing—review and editing, D.F. and E.C.; supervision, E.C., F.D.P., M.G. All authors have read and agree to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank Acqua Bene Comune for the consumption data supplied.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Creaco, E.; Pezzinga, G.; Savic, D. On the choice of the demand and hydraulic modeling approach to WDN real-time simulation. Water Resour. Res. 2017, 53, 6159–6177. [Google Scholar] [CrossRef]
- Walski, T.M.; Chase, D.V.; Savic, D.A.; Grayman, W.; Beckwith, S.; Koelle, E. Advanced Water Distribution Modeling and Management; Haestad Press: Waterbury, CT, USA, 2003. [Google Scholar]
- Filion, Y.R.; Karney, B.W.; Adams, B.J. Stochasticity of demand and probabilistic performance of water networks. In World Water Congress 2005: Impacts of Global Climate Change, Proceedings of the 2005 World Water and Environmental Resources Congress, Anchorage, AK, USA, 15–19 May 2005; American Society of Civil Engineers: Reston, VA, USA, 2005. [Google Scholar]
- Filion, Y.; Adams, B.; Karney, B. Cross correlation of demands in water distribution network design. J. Water Resour. Plan. Manag. 2007, 133, 137–144. [Google Scholar] [CrossRef]
- Blokker, E.J.M.; Vreeburg, J.H.G.; Buchberger, S.G.; Van Dijk, J.C. Importance of demand modelling in network water quality models: A review. Drink. Water Eng. Sci. 2008, 1, 27–38. [Google Scholar] [CrossRef]
- Blokker, E.J.M.; Beverloo, H.; Vogelaar, A.J.; Vreeburg, J.H.G.; Van Dijk, J.C. A bottom-up approach of stochastic demand allocation in a hydraulic network model: A sensitivity study of model parameters. J. Hydroinformatics 2011, 13, 714–728. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Manetas, A. Simple disaggregation by accurate adjusting procedures. Water Resour. Res. 1996, 32, 2105–2117. [Google Scholar] [CrossRef]
- Kumar, D.N.; Lall, U.; Petersen, M.R. Multisite disaggregation of monthly to daily streamflow. Water Resour. Res. 2000, 36, 1823–1833. [Google Scholar] [CrossRef]
- Deidda, R.; Badas, M.G.; Piga, E. Space-time scaling in high-intensity Tropical Ocean Global Atmosphere Coupled Ocean-Atmosphere Response Experiment (TOGA-COARE) storms. Water Resour. Res. 2004, 40, W02506. [Google Scholar] [CrossRef]
- Onibon, H.; Lebel, T.; Afouda, A.; Guillot, G. Gibbs sampling for conditional spatial disaggregation of rain fields. Water Resour. Res. 2004, 40, W08401. [Google Scholar] [CrossRef]
- Mejia, J.M.; Rousselle, J. Disaggregation models in hydrology revisited. Water Resour. Res. 1976, 12, 185–186. [Google Scholar] [CrossRef]
- Todini, E. The preservation of skewness in linear disaggregation schemes. J. Hydrol. 1980, 47, 199–214. [Google Scholar] [CrossRef]
- Santos, E.G.; Salas, J.D. Stepwise disaggregation scheme for synthetic hydrology. J. Hydraul. Eng. 1992, 118, 765–784. [Google Scholar] [CrossRef]
- Tarboton, D.G.; Sharma, A.; Lall, U. Disaggregation procedures for stochastic hydrology based on nonparametric density estimation. Water Resour. Res. 1998, 34, 107–119. [Google Scholar] [CrossRef]
- Lee, T.; Salas, J.D.; Prairie, J. An enhanced nonparametric streamflow disaggregation model with genetic algorithm. Water Resour. Res. 2010, 46, W08529. [Google Scholar] [CrossRef]
- Nowak, K.; Prairie, J.; Rajagopalan, B.; Lall, U. A nonparametric stochastic approach for multisite disaggregation of annual to daily streamflow. Water Resour. Res. 2010, 46, W08529. [Google Scholar] [CrossRef]
- Creaco, E.; Blokker, M.; Buchberger, S. Models for generating household water demand pulses: Literature review and comparison. J. Water Resour. Plan. Manag. 2017, 143, 1–11. [Google Scholar] [CrossRef]
- Buchberger, S.G.; Carter, J.T.; Lee, Y.; Schade, T.G. Random Demands, Travel Times and Water Quality in Deadends; AWWA Research Foundation: Denver, CO, USA, 2003. [Google Scholar]
- Blokker, M.; Agudelo-Vera, C.; Moerman, A.; Van Thienen, P.; Pieterse-Quirijns, I. Review of applications for SIMDEUM, a stochastic drinking water demand model with a small temporal and spatial scale. Drink. Water Eng. Sci. 2017, 10, 1–12. [Google Scholar] [CrossRef]
- Gargano, R.; Di Palma, F.; de Marinis, G.; Granata, F.; Greco, R. A stochastic approach for the water demand of residential end users. Urban Water J. 2016, 13, 569–582. [Google Scholar] [CrossRef]
- Alvisi, S.; Ansaloni, N.; Franchini, M. Generation of synthetic water demand time series at different temporal and spatial aggregation levels. Urban Water J. 2014, 11, 297–310. [Google Scholar] [CrossRef]
- Blokker, E.J.M. Stochastic Water Demand Modelling for a Better Understanding of Hydraulics in Water Distribution Networks; Water Management Academic Press: Delft, The Netherlands, 2010; ISBN 9789089570154. [Google Scholar]
- Sheng, Z.; Jia, S.; Michelsen, A.; Abudu, S. Lessons learned from long term water resources plans: Top town vs. bottom up. In International Water Resources Association (IWRA), Proceedings of the XVIth World Water Congress “Bridging Science and Policy”, Cancun, Mexico, 29 May–2 June 2017; International Water Resources Association: Paris, France, 2017; pp. 1–8. [Google Scholar]
- Mamade, A.; Loureiro, D.; Alegre, H.; Covas, D. Top-down and bottom-up approaches for water-energy balance in Portuguese supply systems. Water 2018, 10, 577. [Google Scholar] [CrossRef]
- Creaco, E.; De Paola, F.; Fiorillo, D.; Giugni, M. Bottom-Up Generation of Water Demands to Preserve Basic Statistics and Rank Cross-Correlations of Measured Time Series. J. Water Resour. Plan. Manag. 2020, 146, 1–9. [Google Scholar] [CrossRef]
- Alvisi, S.; Ansaloni, N.; Franchini, M. Comparison of parametric and nonparametric disaggregation models for the top-down generation of water demand time series. Civ. Eng. Environ. Syst. 2016, 33, 3–21. [Google Scholar] [CrossRef]
- Bras, R.L.; Rodriguez-Iturbe, I. Random Functions and Hydrology; Addison-Wesley: Boston, MA, USA, 1984. [Google Scholar]
- Lall, U.; Sharma, A. A nearest neighbor bootstrap for resampling hydrologic time series. Water Resour. Res. 1996, 32, 679–693. [Google Scholar] [CrossRef]
- Spearman, C. The Proof and Measurement of Association between Two Things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar] [CrossRef]
- Nelsen, R.B. An introduction to Copulas (Springer Series in Statistics); Springer: New York, NY, USA, 2006; ISBN 9780387286594. [Google Scholar]
- Moughton, L.J.; Buchberger, S.G.; Boccelli, D.L.; Filion, Y.R.; Karney, B.W. Effect of time step and data aggregation on cross correlation of residential demands. In Proceedings of the 8th Annual Water Distribution Systems Analysis Symposium 2006, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).