Overview of the Chemical and Isotopic Investigations of the Mareza Springs and the Zeta River in Montenegro
Abstract
1. Introduction
2. Materials and Methods
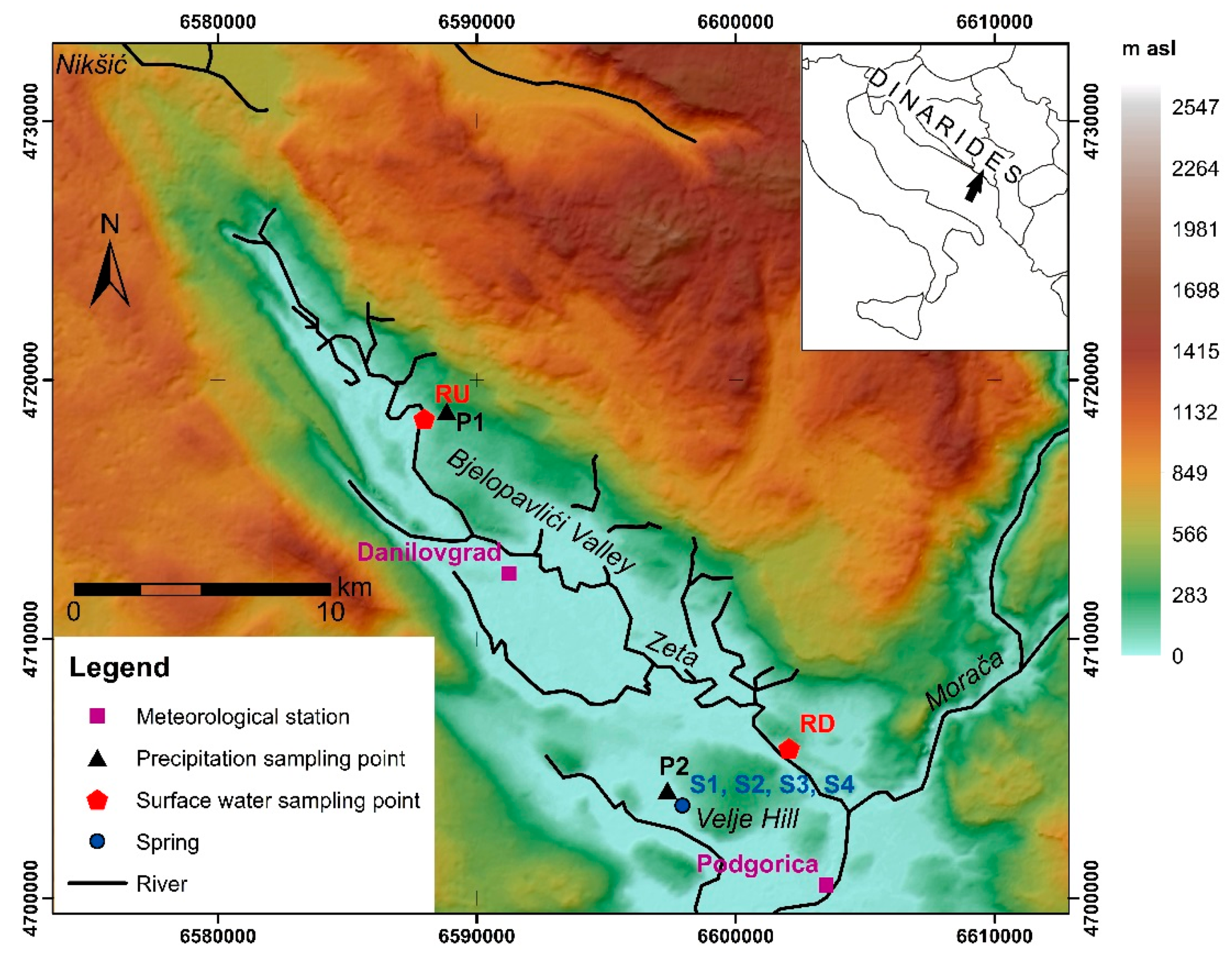
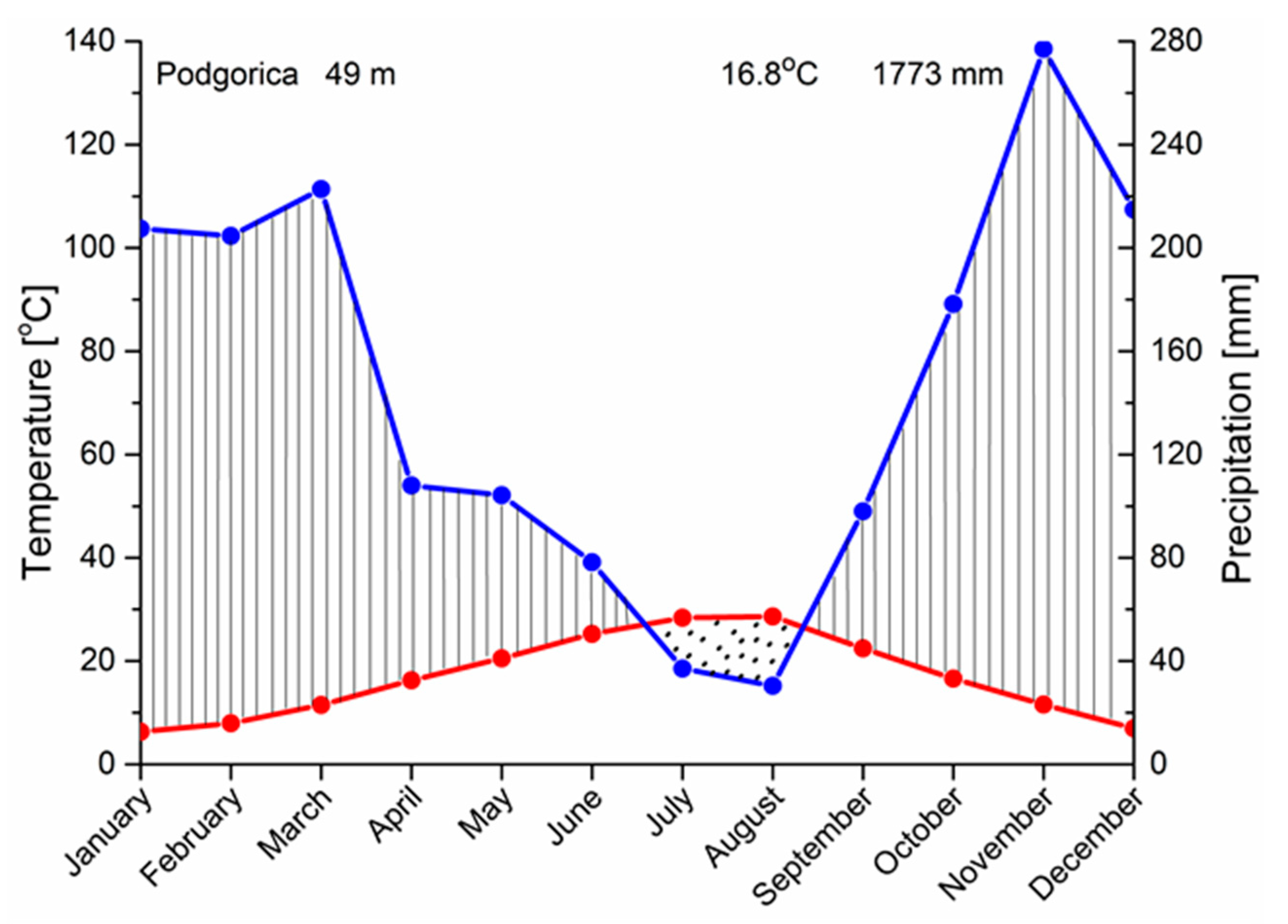
2.1. Study Area
2.2. Sampling Locations
2.3. Sampling
2.4. Methods
2.4.1. Analyses
2.4.2. Calculation of Mean Transit Time (MTT) and Young Water Fraction (Fyw)
3. Results and Discussion
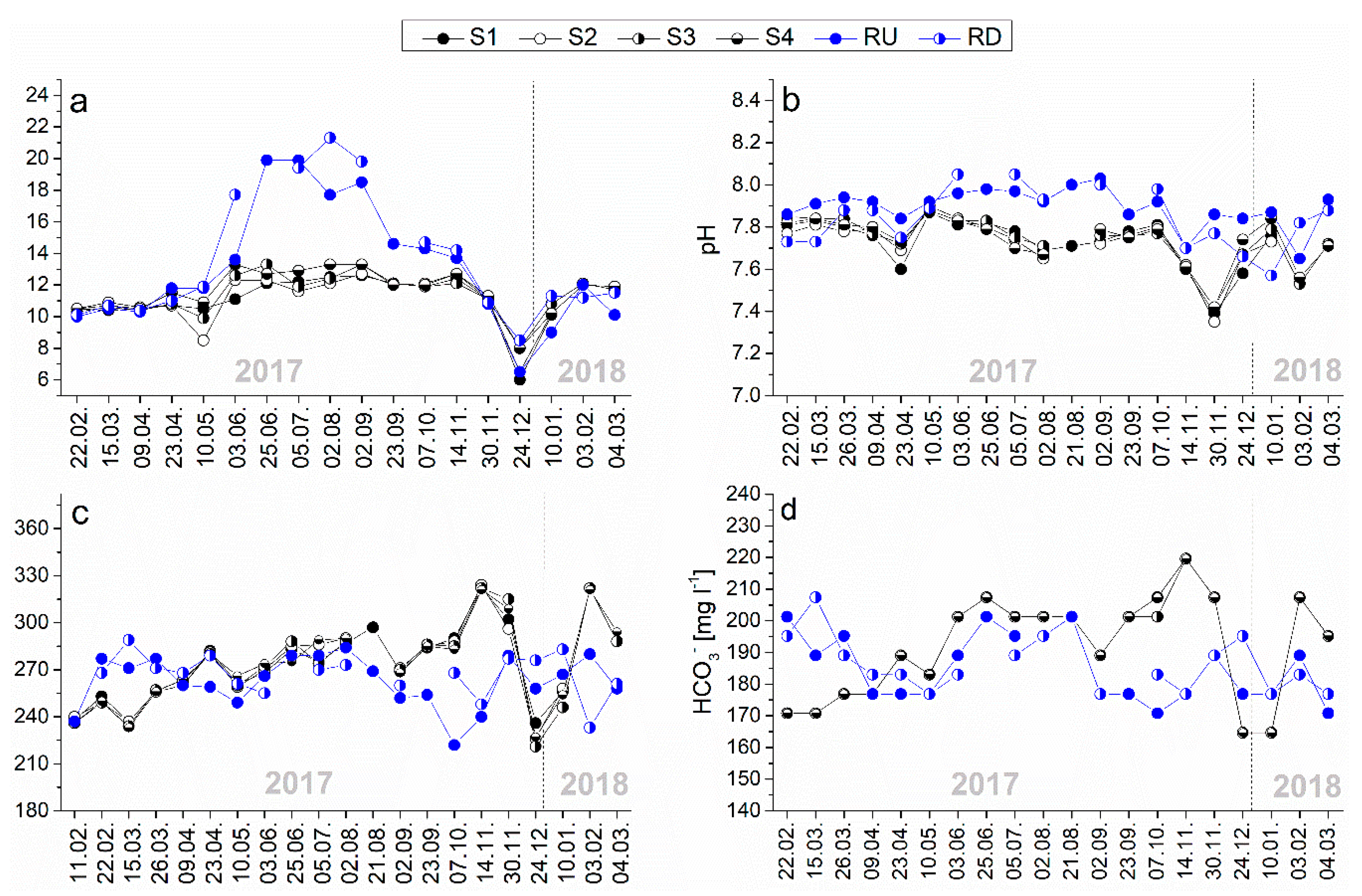
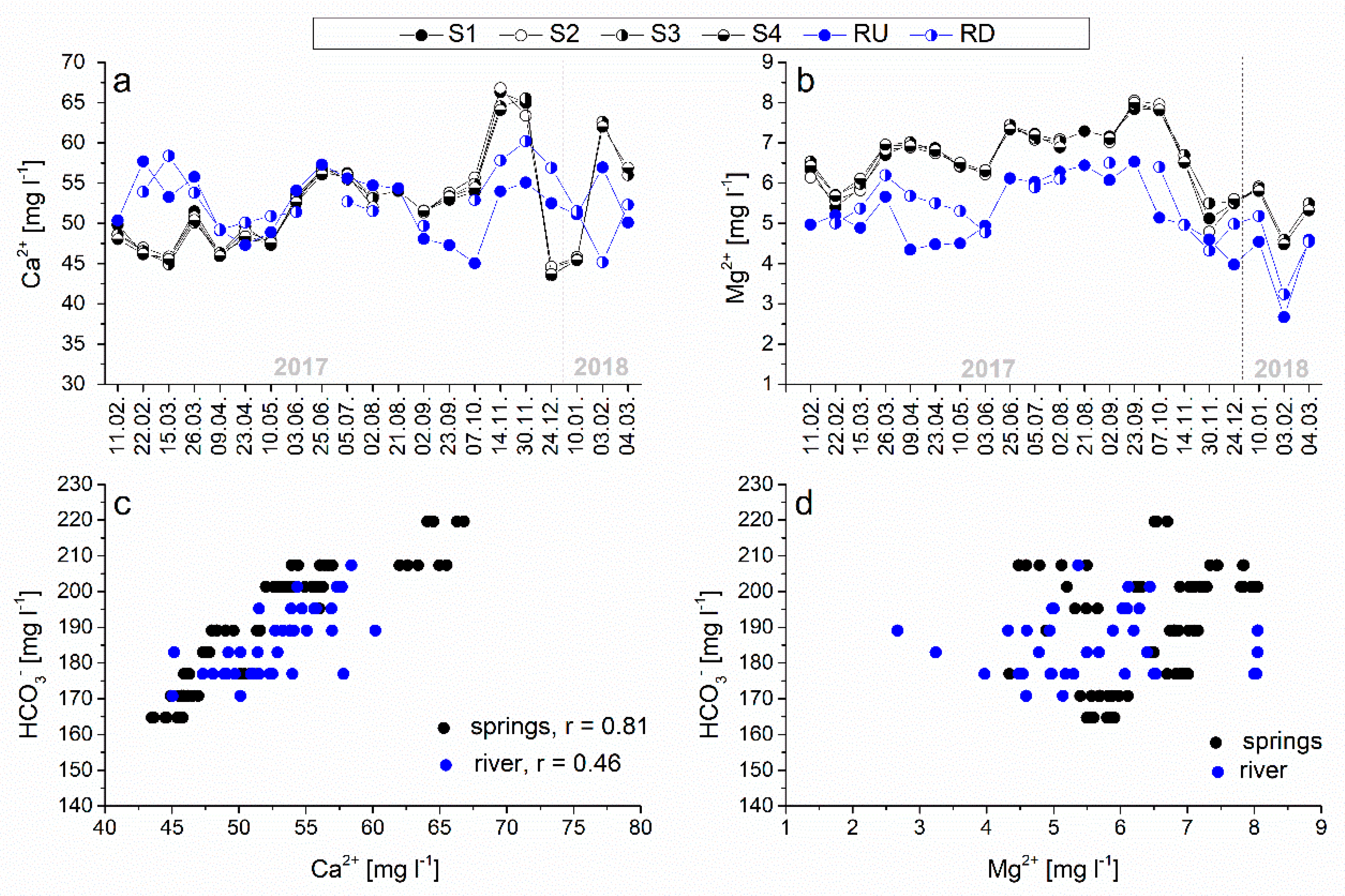
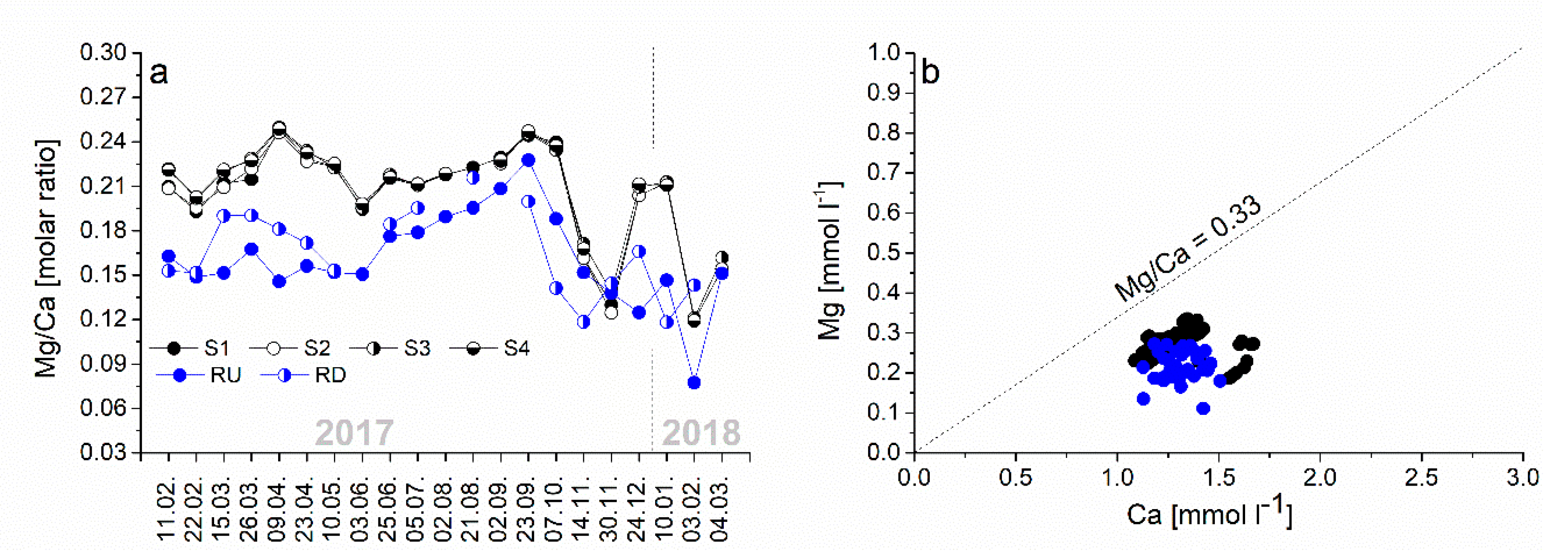
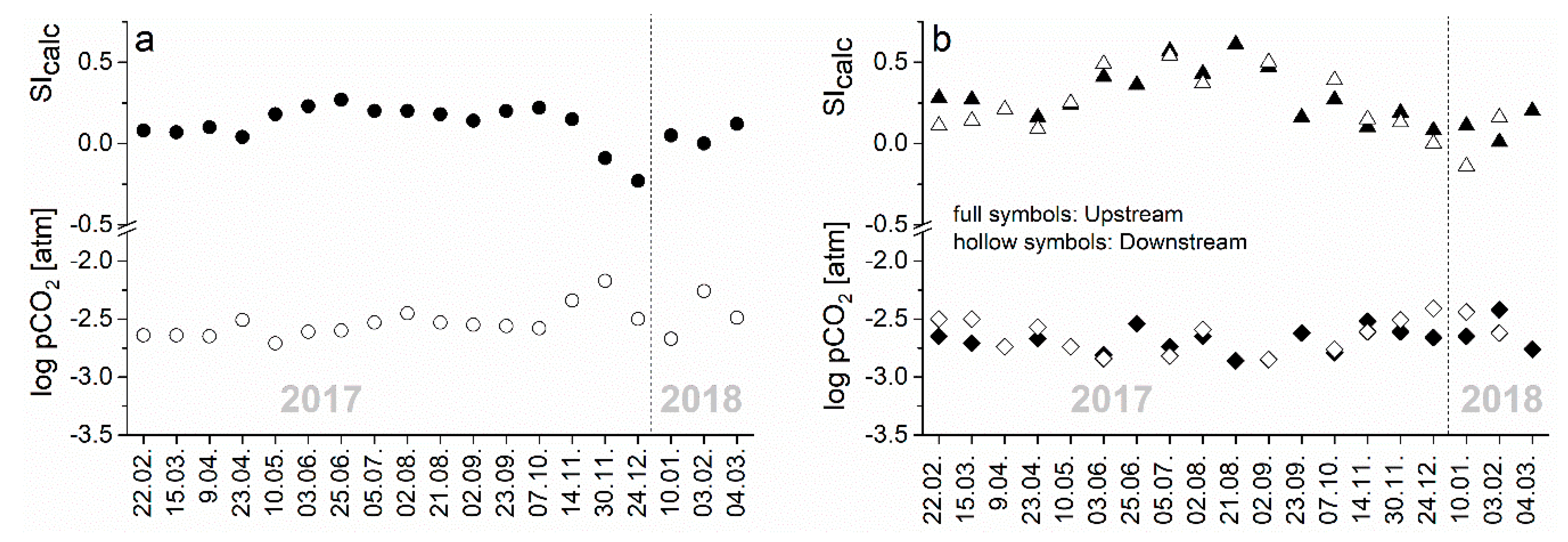
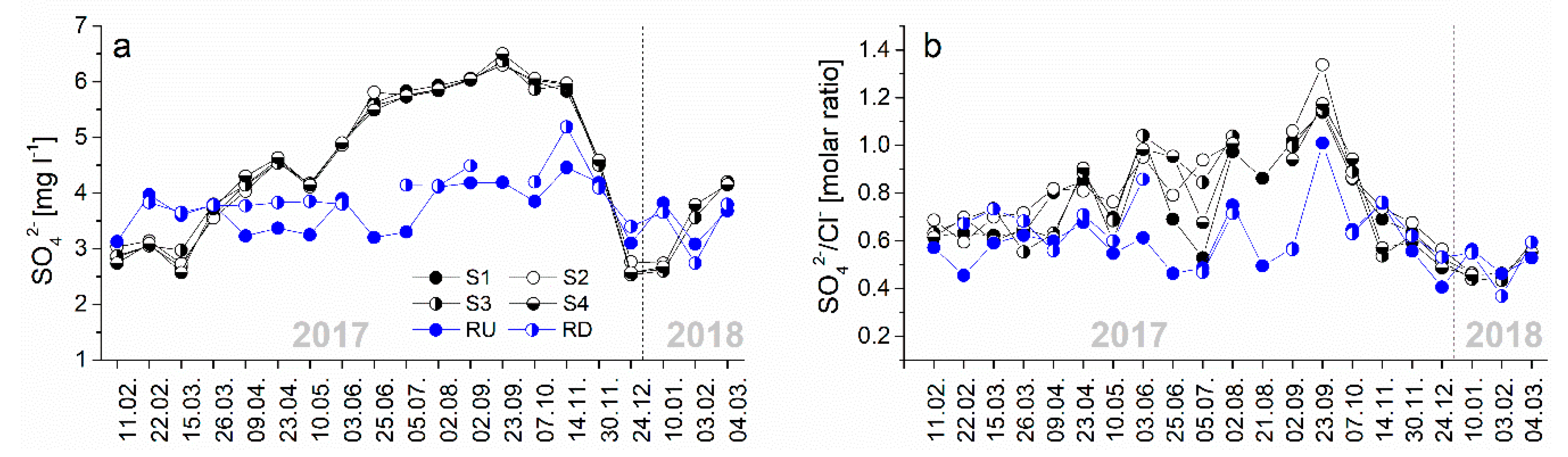
3.1. Physicochemical Parameters
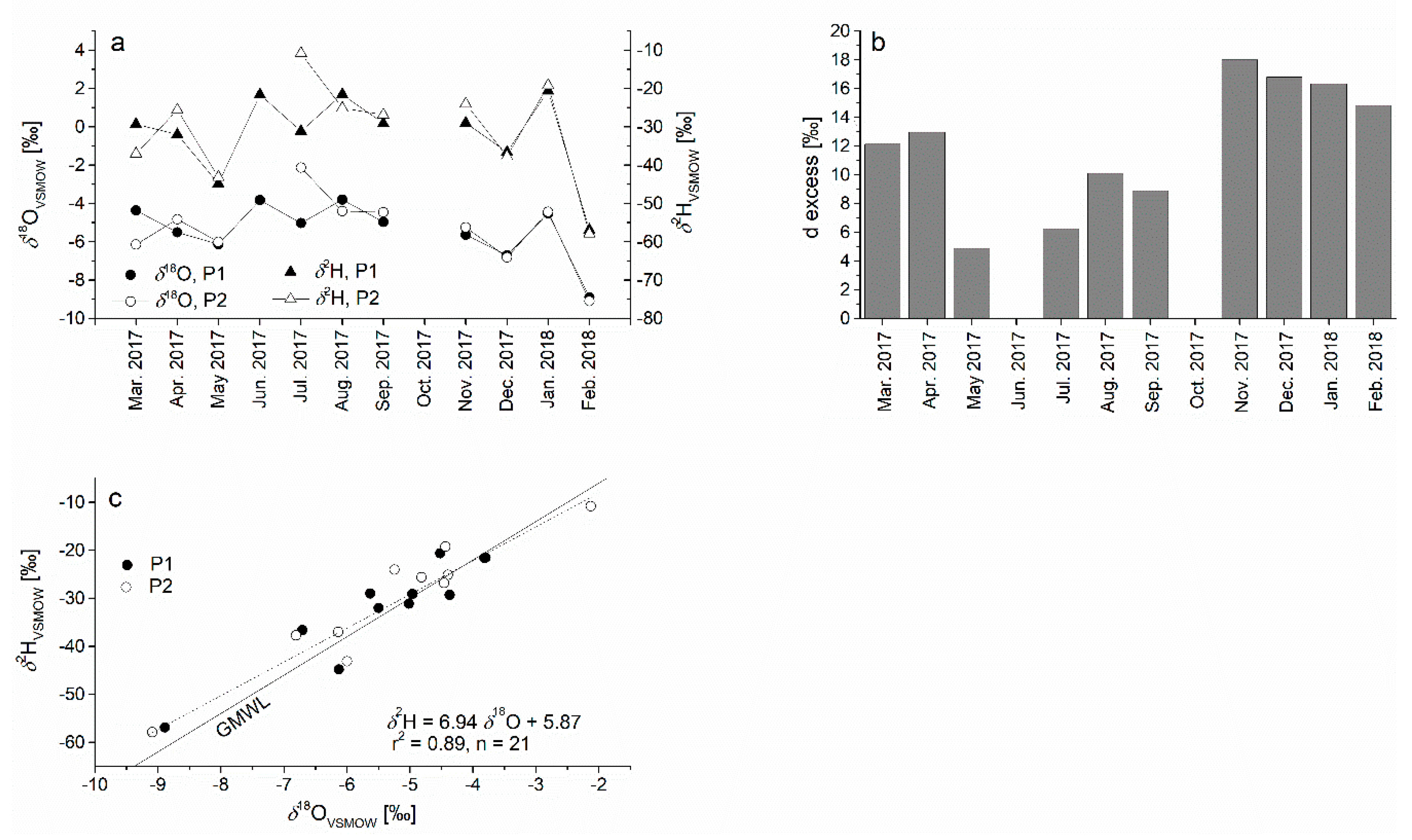
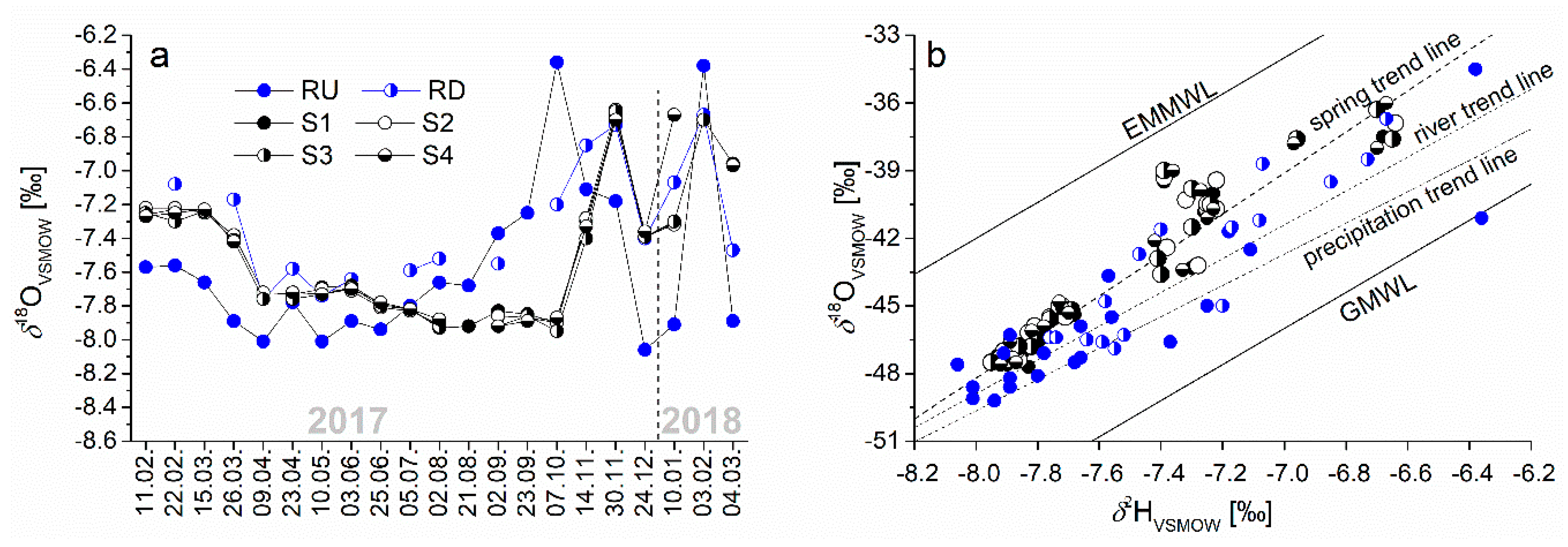
3.2. Isotope Composition of Oxygen and Hydrogen
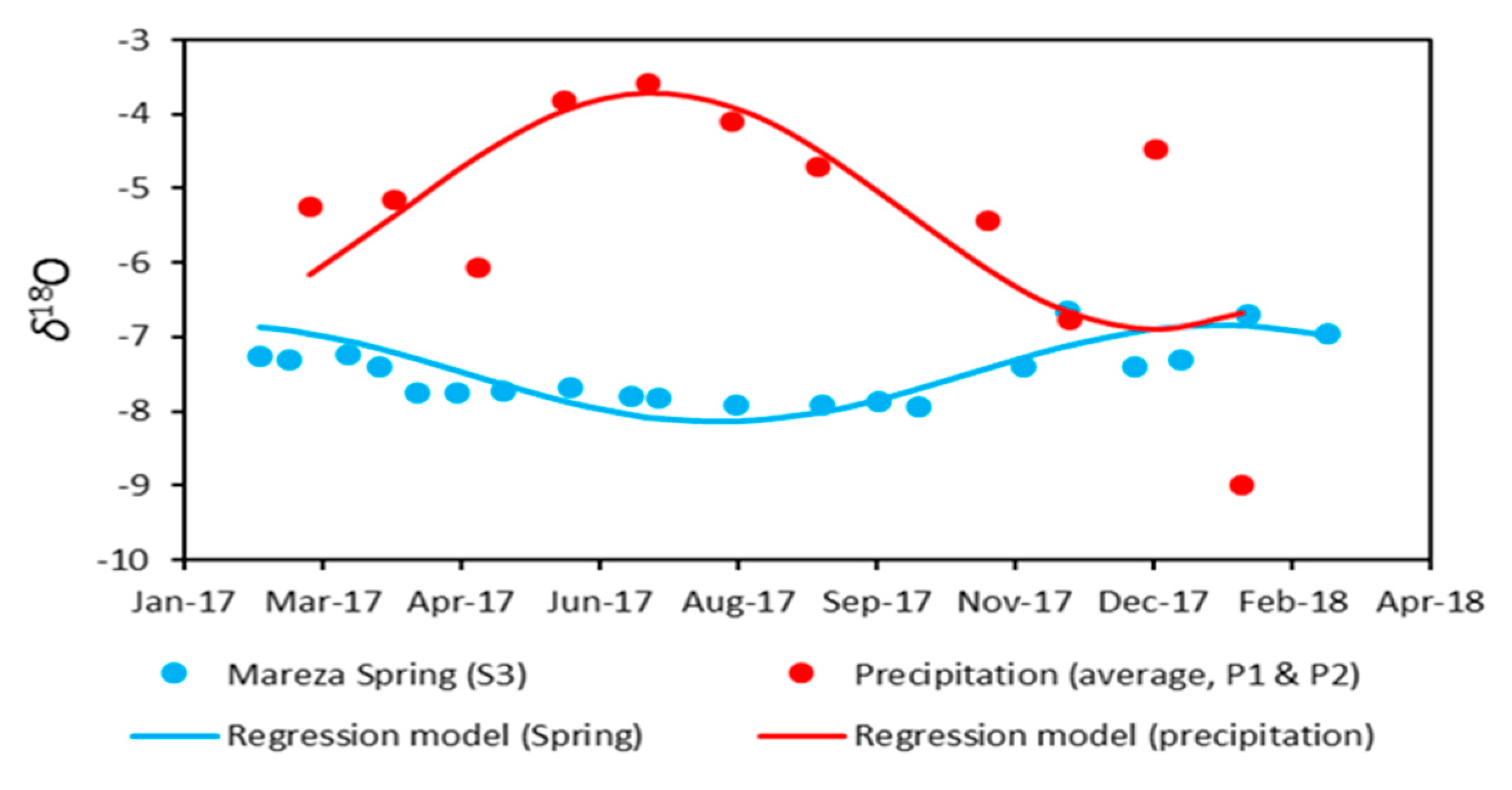
3.2.1. Isotopic Composition of Precipitation
3.2.2. Isotope Composition of the Spring and River Water
3.2.3. Estimated Mean Transit Time (MTT) and Young Water Fraction (Fyw)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- ten Brink, P.; Avramovski, L.; Vermoote, S.; Bassi, S.; Callebaut, K.; Lust, A.; Hunt, A. Benefits for fYRoM and Other Countries of SEE of Compliance with the Environmental Acquis (Task 2); Final Report—Part II: Country Specific Report Montenegro; Report prepared for the European Commission—DG Environment, Arcadis ECOLAS N.V.; Berchem and Institute of European Environmental Policy: Brussels, Belgium, 2007. [Google Scholar]
- Bakalowicz, M. Karst groundwater: A challenge for new resources. Hydrogeol. J. 2005, 13, 148–160. [Google Scholar] [CrossRef]
- Ford, D.; Williams, P. Karst Geomorphology and Hydrology; Unwin Hyman: London, UK, 2007; p. 601. [Google Scholar]
- Chen, X.; Zhang, Z.; Soulsby, C.; Cheng, Q.; Binley, A.; Jiang, R.; Tao, M. Characterizing the heterogeneity of karst critical zone and its hydrological function: An integrated approach. Hydrol. Process. 2018, 32, 1–15. [Google Scholar] [CrossRef]
- White, W.B. Karst hydrology: Recent developments and open questions. Eng. Geol. 2002, 65, 85–105. [Google Scholar] [CrossRef]
- Zhao, M.; Hu, Y.; Zeng, C.; Liu, Z.; Yang, R.; Chen, B. Effects of land cover on variations in stable hydrogen and oxygen isotopes in karst groundwater: A comparative study of three karst catchments in Guizou Province, Southwest China. J. Hydrol. 2018, 565, 374–385. [Google Scholar] [CrossRef]
- Coplen, T.B.; Herczeg, A.L.; Barnes, C. Isotope engineering—Using stable isotopes of the water molecule to solve practical problems. In Environmental Tracers in Subsurface Hydrology; Cook, P., Herczeg, A.L., Eds.; Kluwer Academic Publishers: South Holland, The Nerthelands, 2000; pp. 79–110. [Google Scholar]
- Leibundgut, C.; Maloszewski, P.; Kulls, C. Tracer in Hydrology, 1st ed.; Wiley-Blackwell: Chichester, UK, 2009; p. 432. [Google Scholar]
- Moeck, C.; Radny, D.; Popp, A.; Brennwald, M.; Stoll, S.; Auckenthaler, A.; Berg, M.; Schirmer, M. Characterization of a managed aquifer recharge system using multiple tracers. Sci. Total Environ. 2017, 609, 701–714. [Google Scholar] [CrossRef]
- Dević, N.; Filipović, S. Repercussion of the pressure from the surface area to the geochemical properties of water of karst spring. In Proceedings of the Book of Apstracts 6th Symposium Chemistry and Environmental Protection EnviroChem, Vršac, Serbia, 21–24 May 2013; pp. 220–222. [Google Scholar]
- Krivokapić, S.; Dević, N.; Filipović, S. Research on the natural features of karst water, on the example of some water inatkes. Abstr. Appl. Stud. Agribus. Commer. 2013. [Google Scholar] [CrossRef]
- Dević, N.; Radojević, D.; Filipović, S.; Blečić, V. Prilog poznavanju veze između voda sliva gornje Morače i vodozahvata Mareza. In Proceedings of the XIV Srpski Simpozijum o Hidrogeologiji sa Međunarodnim Učešćem, RGF, Zlatibor, Serbia, 17–20 May 2012; pp. 70–74. [Google Scholar]
- Vujošević, M. Izrada Monitoringa Vode za Piće, na Primjeru Kaptiranih Izvora ”Mareza”. Master’s Thesis, University of Montenegro—Faculty of Natural Sciences and Mathematics, Podgorica, Montenegro, 2013. [Google Scholar]
- Živkovic, K. Istraživanje Kvaliteta Vode Izvorišta “Ljeskovac”—Podgorica za Proizvodnju Flaširane vode za Piće. Master’s Thesis, University of Montenegro—Faculty of Metallurgy and Technology, Podgorica, Montenegro, 2007. [Google Scholar]
- Živković, K.; Zejnilović, R.M.; Jaćimović, Ž.K. Investigation of water and sediments in water from well “Ljeskovac”–Podgorica and possibility of its use in production of bottled water. In Proceedings of the 5th International Conference of the Chemical Societies of the South-Eastern European Countries, Ohrid, FYR Macedonia, 10 September 2006. [Google Scholar]
- McGuire, K.; McDonnell, J.J. Stable isotope tracers in watershed hydrology. In Stable Isotopes in Ecology and Environmental Science, 2nd ed.; Michener, R., Lajtha, K., Eds.; Wiley/Blackwell: Malden, MA, USA, 2007; pp. 334–540. [Google Scholar]
- Gat, J.R.; Gonfiantini, R. Stable Isotope Hydrology: Deuterium and Oxygen-18 in the Water Cycle; IAEA Technical Reports Series; International Atomic Energy Agency: Vienna, Austria, 1981; Volume 63, pp. 861–862. [Google Scholar]
- Gat, J.R. Oxygen and hydrogen isotopes in the hydrologic cycle. Annu. Rev. Earth Planet. Sci. 1996, 24, 225–262. [Google Scholar] [CrossRef]
- Greene, E.A. Tracing recharge from sinking streams over spatial dimensions of kilometers in a karst aquifer. Ground Water 1997, 35, 898–904. [Google Scholar] [CrossRef]
- Kohfahl, C.; Sprenger, C.; Benavente Herrera, J.; Meyer, H.; Fernandez Chacon, P.; Pekdeger, A. Recharge sources and hydrogeochemical evolution of groundwater in semiarid and karstic environments. A field study in the Granada Basin (Southern Spain). Appl. Geochem. 2008, 23, 846–862. [Google Scholar] [CrossRef][Green Version]
- Vandenschrick, G.; van Wesemael, B.; Frot, E.; Pulido-Bosch, A.; Molina, L.; Stiévenard, M.; Souchez, R. Using Stable Isotope Analysis (δD and δ18O) to Characterize the Regional Hydrology of the Sierra de Gador, South East Spain. J. Hydrol. 2002, 265, 43–55. [Google Scholar] [CrossRef]
- Long, A.J.; Putnam, L.D. Linear model describing three components of flow in karst aquifers using 18O data. J. Hydrol. 2004, 296, 254–270. [Google Scholar] [CrossRef]
- Maloszewski, P.; Stichler, W.; Zuber, A.; Rank, D. Identifying the flow systems in a karstic-fissured-porous aquifer, the Schneealpe, Austria, by modelling of environmental 18O and 3H isotopes. J. Hydrol. 2002, 256, 48–59. [Google Scholar] [CrossRef]
- Perrin, J.; Jeannin, P.Y.; Zwahlen, F. Epikarst storage in a karst aquifer: A conceptual model based on isotopic data, Milandre test site, Switzerland. J. Hydrol. 2003, 279, 106–124. [Google Scholar] [CrossRef]
- Schwarz, K.; Barth, J.A.C.; Postigo-Rebollo, C.; Grathwohl, P. Mixing and transport of water in a karst catchment: A case study from precipitation via seepage to the spring. Hydrol. Earth Syst. Sci. 2009, 13, 285–292. [Google Scholar] [CrossRef]
- Katz, B.G.; Coplen, T.B.; Bullen, T.D.; Davis, J.H. Use of chemical and isotopic tracers to characterize the interactions between ground water and surface water in mantled karst. Ground Water 1997, 35, 1014–1028. [Google Scholar] [CrossRef]
- Barbieri, M.; Boschetti, T.; Petitta, M.; Tallini, M. Stable isotope (H-2, O-18 and Sr-87/Sr-86) and hydrochemistry monitoring for groundwater hydrodynamics analysis in a karst aquifer (Gran Sasso, Central Italy). Appl. Geochem. 2005, 20, 2063–2081. [Google Scholar]
- Andreo, B.; Liñán, C.; Carrasco, F.; Jimenez de Cisneros, C.; Caballero, E.; Mudry, J. Influence of rainfall quantity on the isotopic composition (18O and 2H) of water in mountainous areas. Application for groundwater research in the Yunquera-Nieves karst aquifers (S Spain). Appl. Geochem. 2004, 19, 561–574. [Google Scholar] [CrossRef]
- Einsiedl, F.; Maloszewski, P.; Stichler, W. Multiple isotope approach to the determination of the natural attenuation potential of a high-alpine karst system. J. Hydrol. 2009, 365, 113–121. [Google Scholar] [CrossRef]
- Hem, J.D. Study and Interpretation of the Chemical Characteristics of Natural Water, 2nd ed.; US Government Printing Office: Washington, DC, USA, 1975.
- Gibbs, R.J. Mechanism controlling world water chemistry. Science 1970, 17, 1088–1090. [Google Scholar] [CrossRef]
- Kendall, C.; Doctor, D.H. Stable Isotope Applications in Hydrologic Studies. In Treatise on Geochemistry, 1st ed.; Drever, J.I., Ed.; Elsevier: Amsterdam, The Netherlands, 2003; Volume 5, pp. 319–364. [Google Scholar]
- Clark, I.D.; Fritz, P. Environmental Isotopes in Hydrogeology; CRC Press/Lewis Publishers: Palm Beach County, FL, USA, 1997; p. 342. [Google Scholar]
- Glynn, P.D.; Plummer, L.N. Geochemistry and the understanding of ground-water systems. Hydrogeol. J. 2005, 13, 263–287. [Google Scholar] [CrossRef]
- Radulović, V.; Perović, V. Concession Study for Use a Part of Waters for Bottling of Aquifer Mareza PE; Water Supply and Sewage: Podgorica, Montenegro, 2003. [Google Scholar]
- Radulovic, M.; Radulovic, M.; Stevanovic, Z.; Sekulic, G.; Radulovic, V.; Buric, M.; Radojevic, D. Hydrogeology of the Skadar Lake basin (Southeast Dinarides) with an assessment of considerable subterranean inflow. Environ. Earth Sci. 2015, 74, 71–82. [Google Scholar] [CrossRef]
- IAEA/GNIP. Available online: http://www.naweb.iaea.org/napc/ih/documents/other/gnip_manual_v2.02_en_hq.pdf (accessed on 9 June 2017).
- Ternan, J.L. Comments on the use of calcium hardness variability index in the study of carbonate aquifers; with reference to the Central Pennines, England. J. Hydrol. 1972, 16, 317–321. [Google Scholar] [CrossRef]
- White, W.B. Geomorphology and Hydrology of Karst Terrain; Oxford University Press: New York, NY, USA, 1988; p. 480. [Google Scholar]
- Toran, G.L.; Roman, E. CO2 outgassing in a combined fracture and conduit karst aquifer near Lititz Spring, Pennsylvania. Spec. Pap. Geol. Soc. Am. 2006, 404, 275–282. [Google Scholar]
- Drever, J.I. The Geochemistry of Natural Waters-Surface and Groundwater Environments, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1997; p. 436. [Google Scholar]
- Rodgers, P.; Soulsby, C.; Waldon, S.; Tetzlaff, D. Using stable isotope tracers to identify hydrological flow paths, residence times and landscape controls in a mesoscale catchment. Hydrol. Earth Syst. Sci. 2005, 9, 139–155. [Google Scholar] [CrossRef]
- Rusjan, S.; Sapač, K.; Petrič, M.; Lojenc, S.; Bezaka, N. Identifying the hydrological behavior of a complex karst system using stable isotopes. J. Hydrol. 2019, 577. [Google Scholar] [CrossRef]
- Kirchner, J.W. Aggregation in environmental systems—Part 1: Seasonal tracer cycles quantify young water fractions, but not mean transit times in spatially heterogeneous catchments. Hydrol. Earth Syst. Sci. 2016, 20, 279–297. [Google Scholar] [CrossRef]
- Manning, A.H.; Solomon, D.K. Using noble gases to investigate mountain-front recharge. J. Hydrol. 2003, 275, 194–207. [Google Scholar] [CrossRef]
- Barešić, J. Application of Isotopic and Geochemical Methods in Monitoring of Global and Local Changes in Ecological System of Plitvice Lakes. Ph.D. Thesis, University of Zagreb, Zagreb, Croatia, 2009. [Google Scholar]
- Jacobson, R.L.; Langmuir, D. The chemical history of some spring waters in carbonate rocks. Groundwater 1970, 8, 5–9. [Google Scholar] [CrossRef]
- Hess, J.W.; White, W.B. Storm response of the karstic carbonate aquifer of south-central Kentucky. J. Hydrol. 1988, 99, 235–252. [Google Scholar] [CrossRef]
- Edmunds, W.M.; Cook, J.M.; Darling, W.G.; Kinniburgh, D.G.; Miles, D.L.; Bath, A.H.; Morgan-Jones, M.; Andrews, J.N. Baseline geochemical conditions in the Chalk aquifer, Berkshire, UK: A basis for groundwater quality management. Appl. Geochem. 1987, 2, 251–274. [Google Scholar] [CrossRef]
- Cardenal, J.; Benavente, J.; Cruzsanjulian, J.J. Chemical Evolution of Groundwater in Triassic Gypsum-Bearing Carbonate Aquifers (Las-Alpujarras, Southern Spain). J. Hydrol. 1994, 161, 3–30. [Google Scholar] [CrossRef]
- Musgrove, M.; Banner, J.L. Controls on the spatial and temporal variability of vadose dripwater geochemistry: Edwards Aquifer, central Texas. Geochim. Cosmochim. Acta 2004, 68, 1007–1020. [Google Scholar] [CrossRef]
- McMahon, P.B.; Böhlke, J.K.; Christenson, S.C. Geochemistry, radiocarbon ages, and paleorecharge conditions along a transect in the central High Plains aquifer, southwestern Kansas, USA. Appl. Geochem. 2004, 19, 1655–1686. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Appelo, C.A.J. Description of Input and Examples for PHREEQC Version 3—A Computer Program for Speciation, Batch Reaction, One Dimensional Transport and Inverse Geochemical Calculations; U.S. Geological Survey Techniques and Methods: Reston, VA, USA, 2013; Volume 43.
- Appello, C.A.J.; Postma, D. Geochemistry, Groundwater and Pollution, 2nd ed.; A.A. Balkema Publishers: Leiden, The Netherlands, 2005; p. 649. [Google Scholar]
- Langelier, W.F. The analytical control of anti-corrosion water treatment. J. Am. Waterworks Assoc. 1936, 28, 1500–1521. [Google Scholar] [CrossRef]
- Langmuir, D. The geochemistry of some carbonate ground waters in central Pennsylvania. Geochim. Cosmochim. Acta 1971, 35, 1023–1045. [Google Scholar] [CrossRef]
- Langmuir, D. Aqueous Environmental Chemistry; Prentice Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Vitvar, T.; Balderer, W. Estimation of mean water residence times and runoff generation by 180 measurements in a Pre-Alpine catchment (Rietholzbach, Eastern Switzerland). Appl. Geochem. 1997, 12, 787–796. [Google Scholar] [CrossRef]
- Craig, H. Isotopic Variations in Meteoric Waters. Science 1961, 133, 1702–1703. [Google Scholar] [CrossRef]
- Bowen, R. Groundwater, 2nd ed.; Elsevier Applied Science Publishers: London, UK, 1986. [Google Scholar]
- Aggarwal, P.K.; Gat, J.R.; Froehlich, K.F.O. Isotopes in the Water Cycle: Past, Present and Future of a Developing Science; Springer: Berlin, Germany, 2005. [Google Scholar]
- Dansgaard, W. Stable isotopes in precipitation. Tellus 1964, 16, 436–468. [Google Scholar] [CrossRef]
- Kendall, C.; McDonnell, J.J. Isotope Tracers in Catchment Hydrology; Elsevier: Amsterdam, The Netherlands, 1998; p. 840. [Google Scholar]
- Araguás-Araguás, L.; Froehlich, K.; Rozanski, K. Deuterium and oxygen-18 isotope composition of precipitation and atmospheric moisture. Hydrol. Process. 2000, 14, 1341–1355. [Google Scholar] [CrossRef]
- Mook, W.G.; De Vries, J.J. Environmental Isotopes in the Hydrological Cycle. In Principles and Applications; IHP–V, UNESCO, No. 39; IAEA Publish: Vienna, Austria, 2000. [Google Scholar]
- Masson-Delmotte, V.; Jouzel, J.; Landais, A.; Stievenard, M.; Johnsen, S.J.; White, J.W.C.; Werner, M.; Sveinbjornsdottir, A.; Fuhrer, K. GRIP Deuterium excess reveals rapid and orbital-scale changes in Greenland moisture origin. Science 2005, 309, 118–121. [Google Scholar] [CrossRef]
- Aemisegger, F.; Pfahl, S.; Sodemann, H.; Lehner, I.; Seneviratne, S.I.; Wernli, H. Deuterium excess as a proxy for continental moisture recycling and plant transpiration. Atmos. Chem. Phys. 2014, 14, 29721–29784. [Google Scholar] [CrossRef]
- Lewis, S.C.; LeGrande, A.N.; Kelley, M.; Schmidt, G.A. Modeling insights into deuterium excess as an indicator of water vapor source conditions. J. Geophys. Res. Atmos. 2013, 118, 243–262. [Google Scholar] [CrossRef]
- Benetti, M.; Reverdin, G.; Pierre, C.; Merlivat, L.; Risi, C.; SteenLarsen, H.C.; Vimeux, F. Deuterium excess in marine water vapor: Dependency on relative humidity and surface wind speed during evaporation. J. Geophys. Res.-Atmos. 2014, 119, 584–593. [Google Scholar] [CrossRef]
- Pfahl, S.; Sodemann, H. What controls deuterium excess in global precipitation? Clim. Past 2014, 10, 771–781. [Google Scholar] [CrossRef]
- Steen-Larsen, H.C.; Sveinbjornsdottir, A.E.; Peters, A.J.; Masson-Delmotte, V.; Guishard, M.P.; Hsiao, G.; Jouzel, J.; Noone, D.; Warren, J.K.; White, J.W.C. Climatic controls on water vapor deuterium excess in the marine boundary layer of the North Atlantic based on 500 days of in situ, continuous measurements. Atmos. Chem. Phys. 2014, 14, 7741–7756. [Google Scholar] [CrossRef]
- IAEA. Isotopic Composition of Precipitation in the Mediterranean Basin in Relation to Air Circulation Patterns and Climate; IAEA-TECDOC-1453; IAEA: Vienna, Austria, 2005; p. 223. [Google Scholar]
- Froehlich, K.; Gibson, J.J.; Aggarwal, P.K. Deuterium Excess in Precipitation and Its Climatological Significance; IAEA-CSP--13/P; International Atomic Energy Agency (IAEA): Vienna, Austria, 2002. [Google Scholar]
- Cruz-san, J.; Araguas, L.; Rozanski, K.; Benavente, J.; Cardenal, J.; Hidalgo, M.C.; Garcia-Lopez, S.; Martinez-Garrido, J.C.; Moral, F.; Olias, M. Sources of precipitation over South-Eastern Spain and groundwater recharge. An isotopic study. Tellus B 1992, 44, 226–236. [Google Scholar] [CrossRef]
- Đorđević, D.S.; Tošić, I.; Unkašević, M.; Đurašković, P. Water-soluble mainions in precipitation over the southeastern Adriatic region: Chemical composition and long-rang transport. Environ. Sci. Pollut. Res. 2010, 17, 1591–1598. [Google Scholar] [CrossRef]
- Schicker, I.; Radanovics, S.; Seibert, P. Origin and transport of Mediterranean moisture and air. Atmos. Chem. Phys. 2010, 10, 5089–5105. [Google Scholar] [CrossRef]
- Vreča, P.; Krajcar Bronić, I.; Horvatinčić, N.; Barešić, J. Isotopic characteristics of precipitation in Slovenia and Croatia: Comparisom of continental and maritime stations. J. Hydrol. 2006, 330, 457–469. [Google Scholar] [CrossRef]
- IAEA/GNIP. Available online: https://nucleus.iaea.org/wiser/index.aspx (accessed on 8 February 2019).
- Gat, J.R.; Carmi, H. Evolution of the isotopic composition of atmospheric waters in the Mediterranean Sea area. J. Geophys. Res. 1970, 75, 3039–3040. [Google Scholar] [CrossRef]
- Horvatinčić, N.; Krajcar Bronić, I.; Barešić, J.; Obelić, B.; Vidić, S. Tritium and stable isotope distribution in the atmosphere eat the coastal region of Croatia. In Isotopic Composition of Precipitation in the Mediterranean Basin in Relation to Air Circulation Patterns and Climate; TECDOC Series No. 1453; IAEA: Vienna, Austria, 2005; pp. 37–50. [Google Scholar]


| Location | Latitude (°) | Longitude (°) | Altitude (m asl) |
|---|---|---|---|
| P1 | 42.36 | 19.04 | 38 |
| P2 | 42.45 | 19.20 | 32 |
| Danilovgrad meteorological station | 42.55 | 19.1 | 53 |
| Podgorica meteorological station | 42.43 | 19.28 | 49 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Živković, K.; Radulović, M.; Lojen, S.; Pucarević, M. Overview of the Chemical and Isotopic Investigations of the Mareza Springs and the Zeta River in Montenegro. Water 2020, 12, 957. https://doi.org/10.3390/w12040957
Živković K, Radulović M, Lojen S, Pucarević M. Overview of the Chemical and Isotopic Investigations of the Mareza Springs and the Zeta River in Montenegro. Water. 2020; 12(4):957. https://doi.org/10.3390/w12040957
Chicago/Turabian StyleŽivković, Katarina, Milan Radulović, Sonja Lojen, and Mira Pucarević. 2020. "Overview of the Chemical and Isotopic Investigations of the Mareza Springs and the Zeta River in Montenegro" Water 12, no. 4: 957. https://doi.org/10.3390/w12040957
APA StyleŽivković, K., Radulović, M., Lojen, S., & Pucarević, M. (2020). Overview of the Chemical and Isotopic Investigations of the Mareza Springs and the Zeta River in Montenegro. Water, 12(4), 957. https://doi.org/10.3390/w12040957






