High-Resolution Mapping of Japanese Microplastic and Macroplastic Emissions from the Land into the Sea
Abstract
1. Introduction
2. Materials and Methods
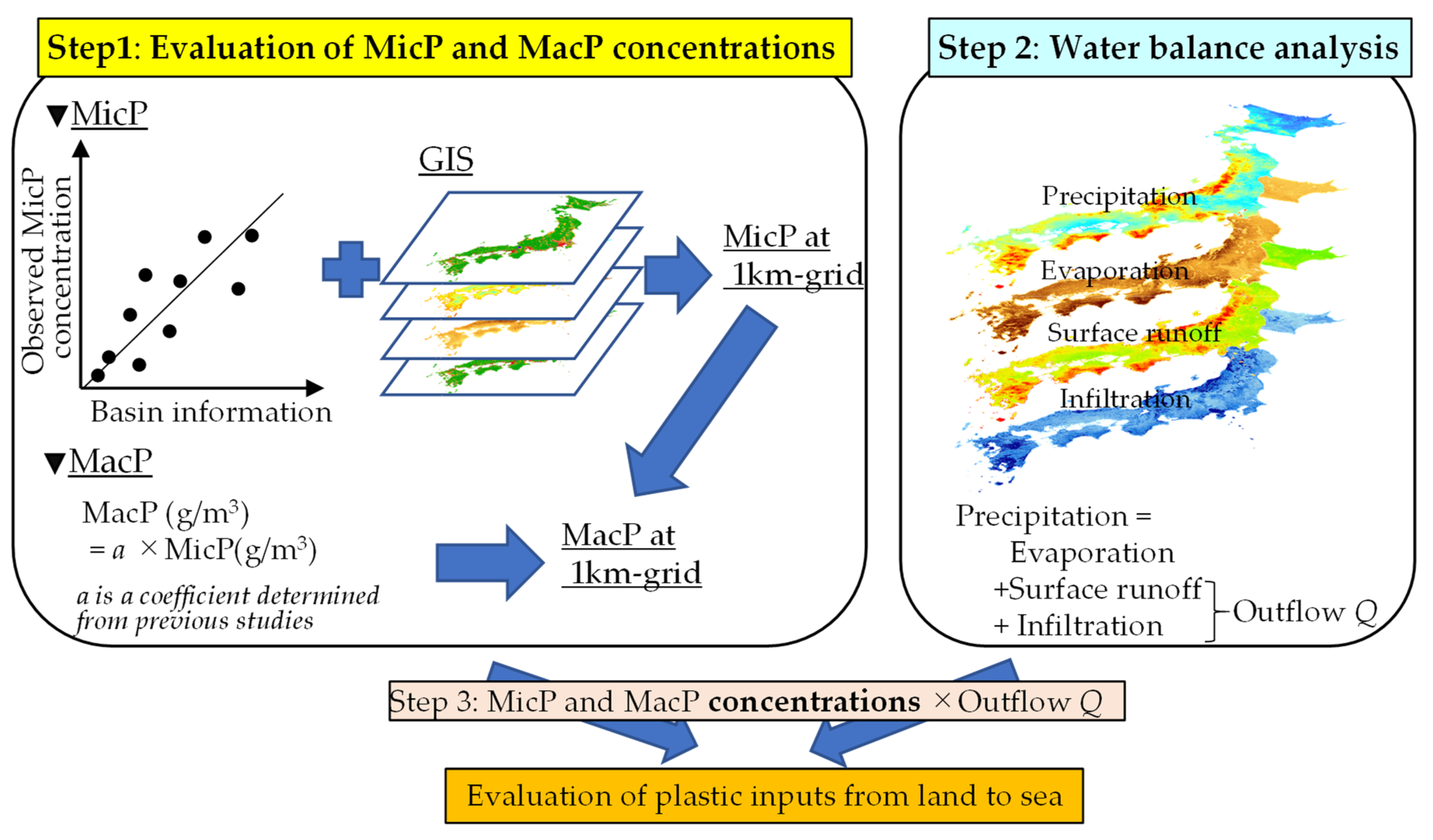
2.1. Conceptual Foundation for Evaluating Plastic input
2.2. Evaluating Riverine MicP and MacP Concentrations
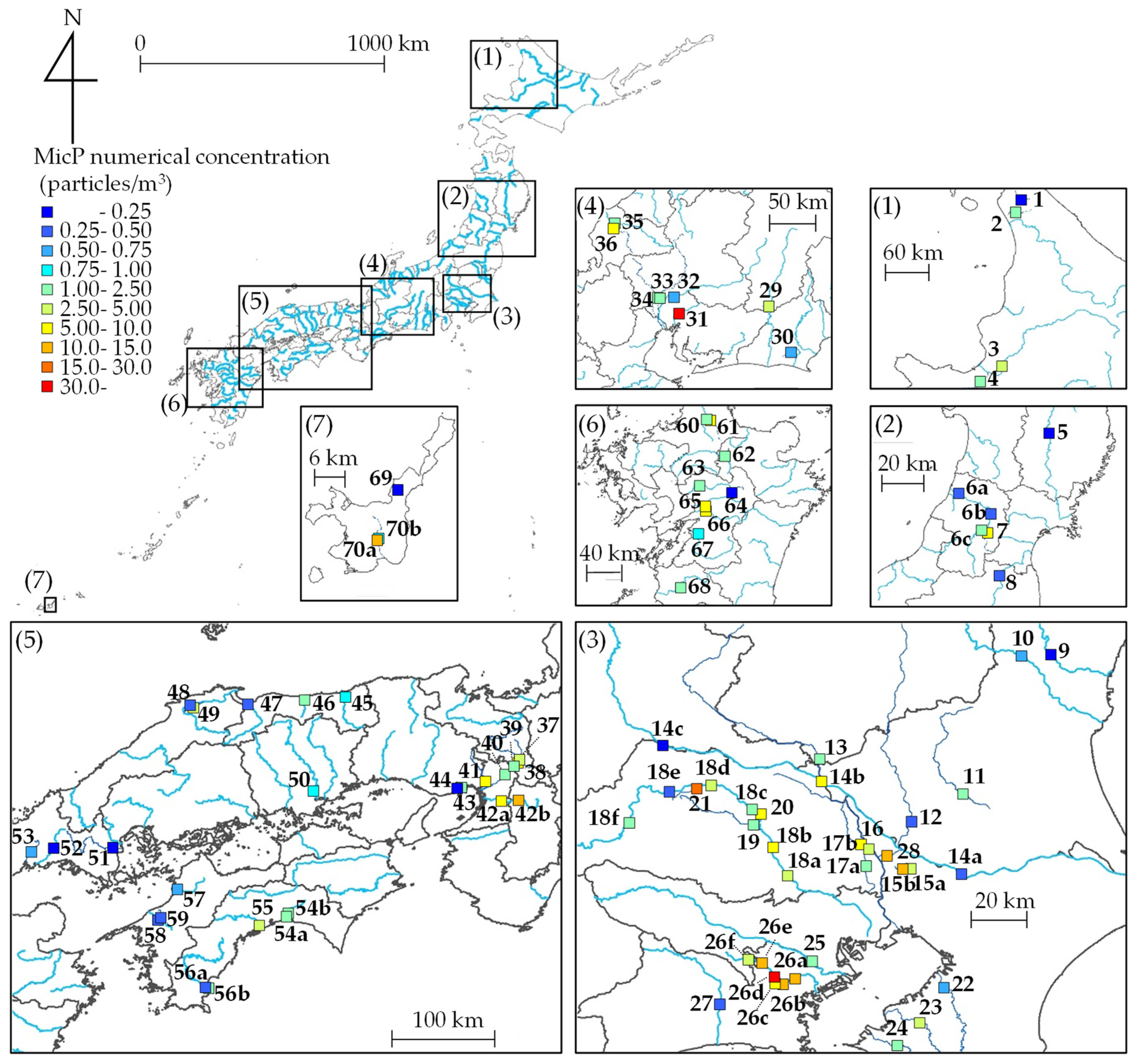
2.2.1. Field Sites
2.2.2. Measuring MicP in Rivers
- From the top of a bridge, the plankton net was deployed onto the surface of the river using a rope. The net position was located at the center of each stream in cross-section;
- The length of the rope was adjusted so that the net was generally fixed near the water surface and set for 5–10 min;
- After a predetermined installation time, the plankton net was raised to the bridge.
2.2.3. Laboratory Analyses of MicP Concentrations
- The sample was filtered using a 0.1 mm net and the sample remaining on the filter was dried;
- The dried sample was immersed in a 30% hydrogen peroxide solution for approximately one week to decompose any organic matter, such as plant debris;
- The sample was filtered again through a 0.1 mm net and the residue was dried for 24 h in a 60 °C incubator;
- The dried sample was spread in a petri dish containing the tap water, and MicP candidate particles were extracted manually one-by-one;
- The masses of the MicP candidate particles were measured using an ultra-micro balance (XPR2UV, Mettler Toledo, Columbus, OH, USA);
- The sizes of the candidate particles > ~0.1 mm were measured. Here, MicP was photographed using an electron microscope (SZX7, Olympus Corp., Tokyo, Japan) with a charge-coupled device (CCD) camera (HDCE-20C, AS ONE Corp., Osaka, Japan). The ImageJ v.1.52t software package (https://imagej.nih.gov/ij/notes.html) was then used to calculate the MicP sizes (maximum length, etc.) from the captured images;
- A Fourier transform infrared spectrophotometer (FTIR, IRAffinity-1S, Shimadzu Corp., Kyoto, Japan) was used to identify the material compositions of the MicP candidate particles to determine whether or not they were indeed plastic.
2.2.4. Evaluating Basin Characteristics
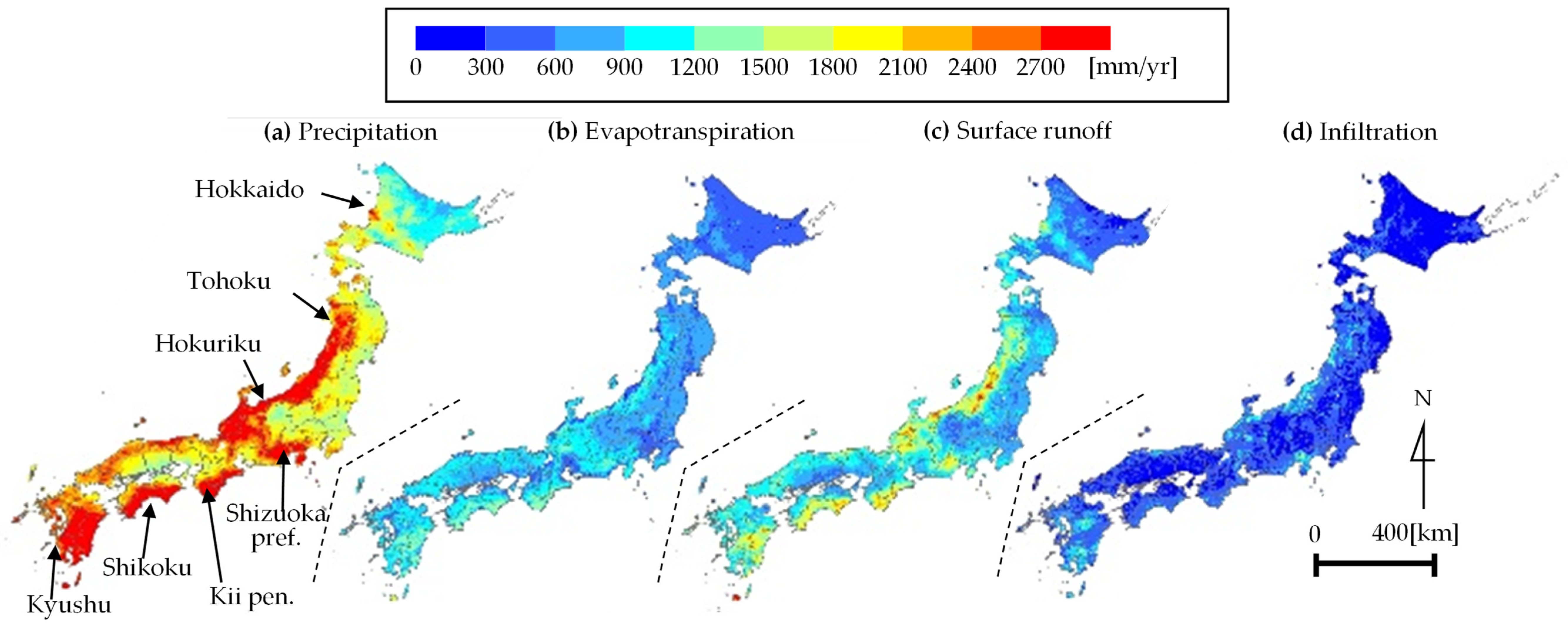
2.3. Water Balance Analysis at a 1 km Mesh Resolution
2.3.1. Outline of Water Balance Analysis
2.3.2. Precipitation
2.3.3. Evapotranspiration
2.3.4. Surface Runoff and Underground Infiltration
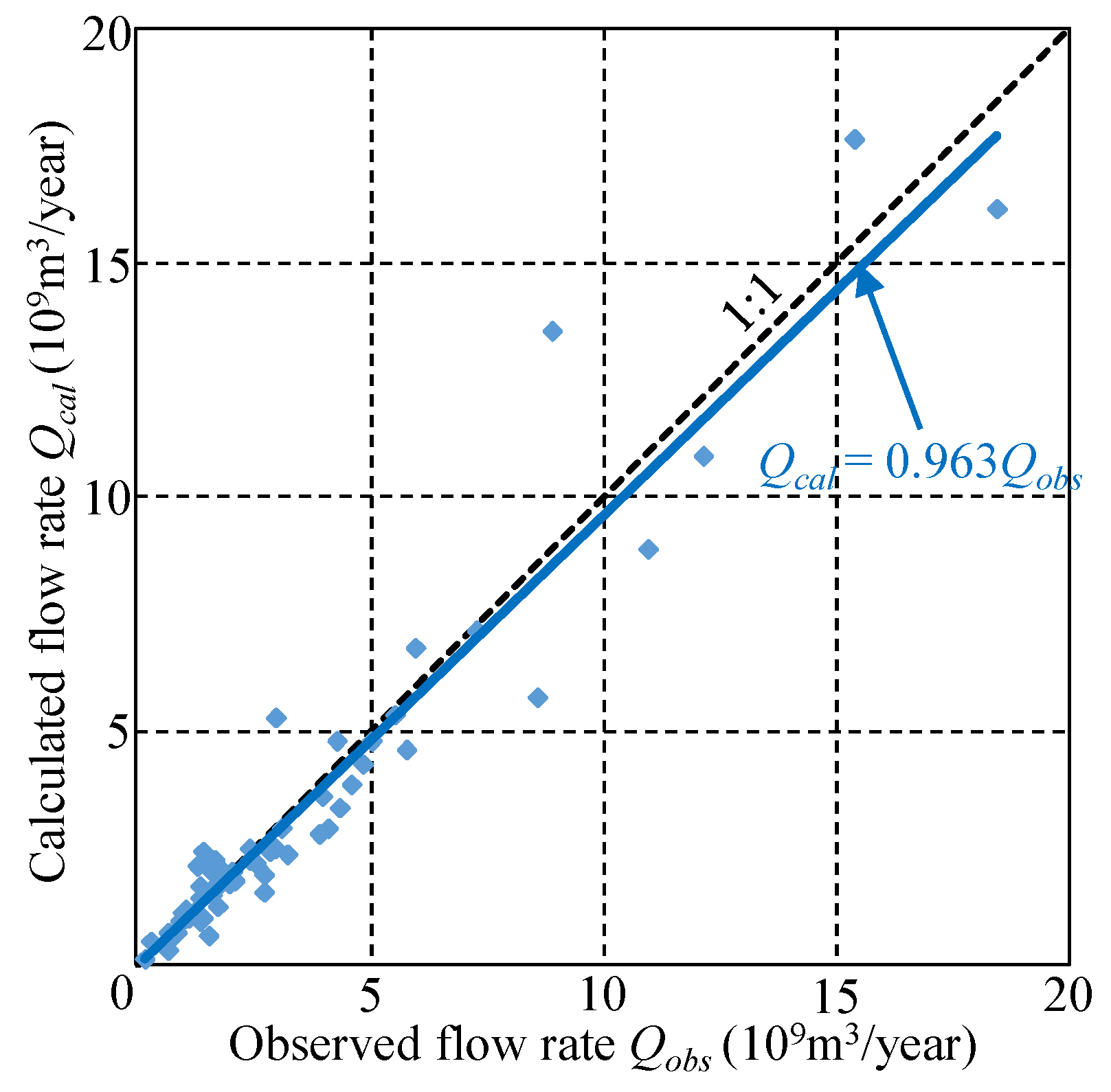
2.3.5. Validating the Water Balance Model
3. Results
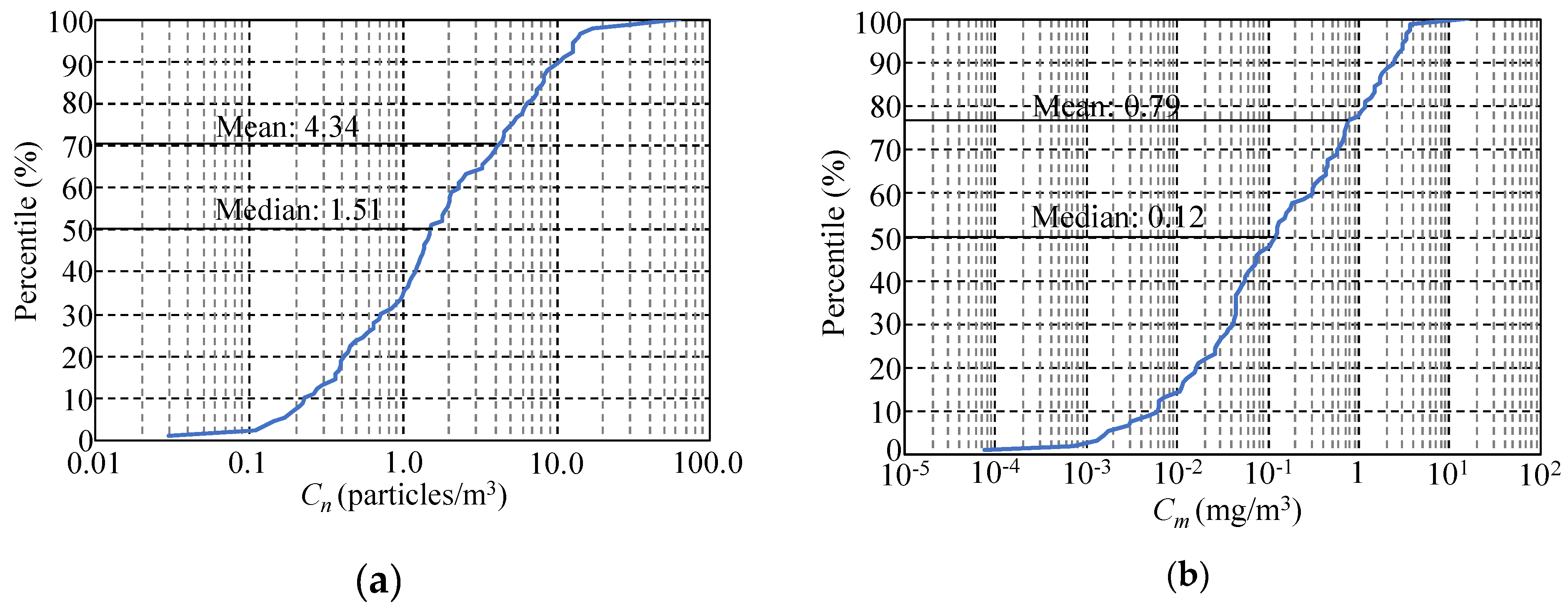
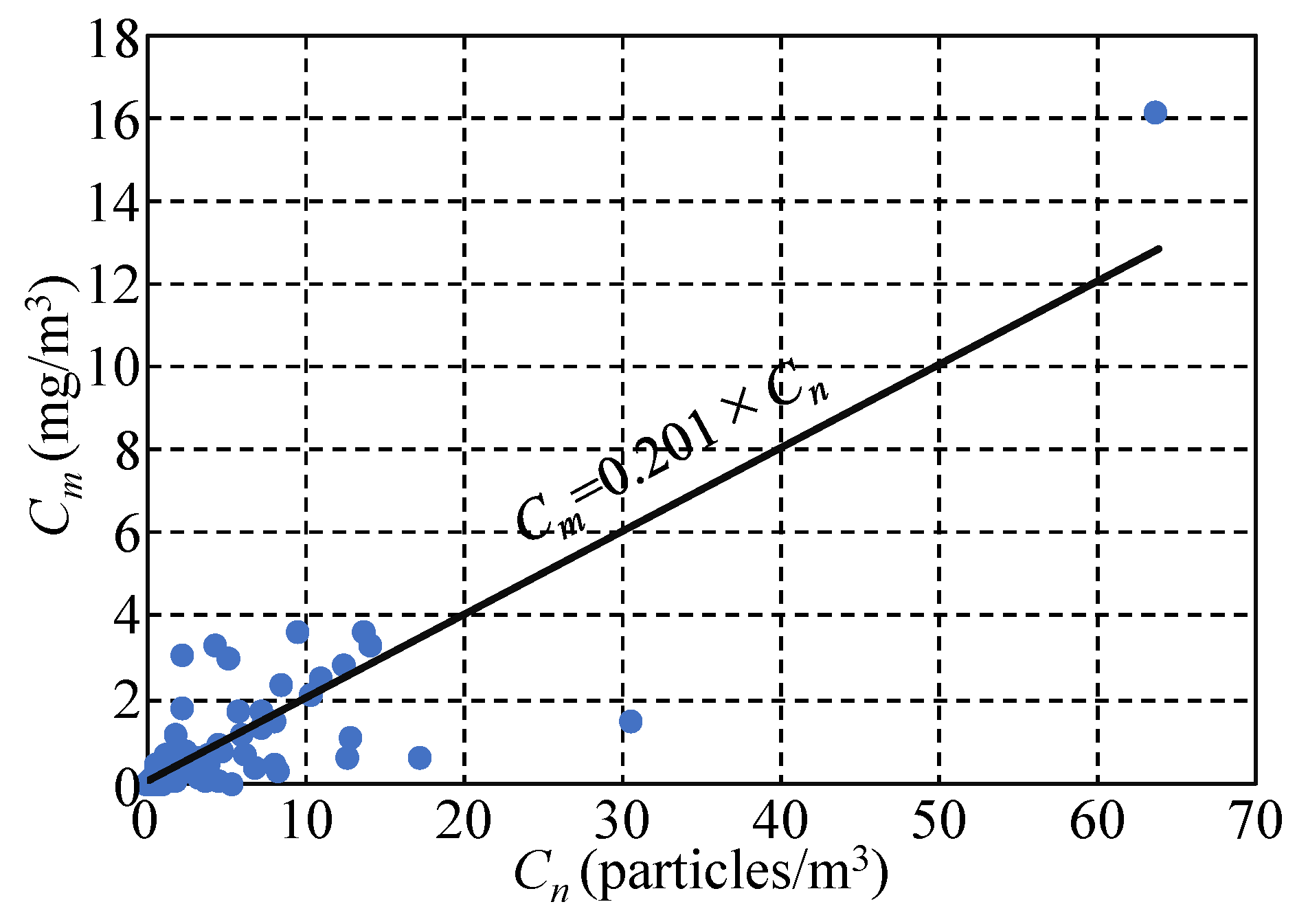
3.1. Characteristics of MicP Concentrations in Japanese Rivers
3.2. Relationship between MicP Concentrations and Basin Characteristics
3.3. Calculated Results for Water Balance Analysis
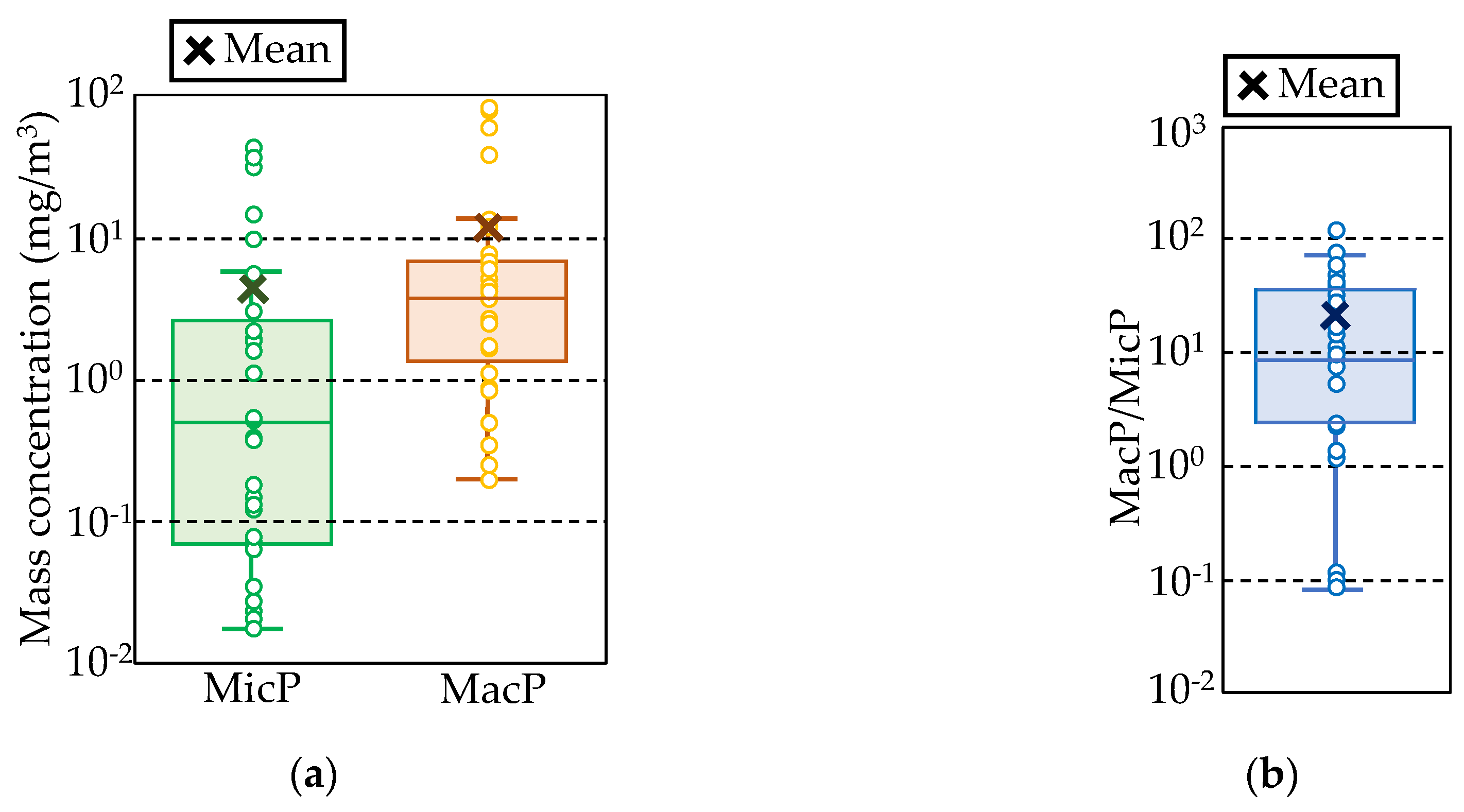
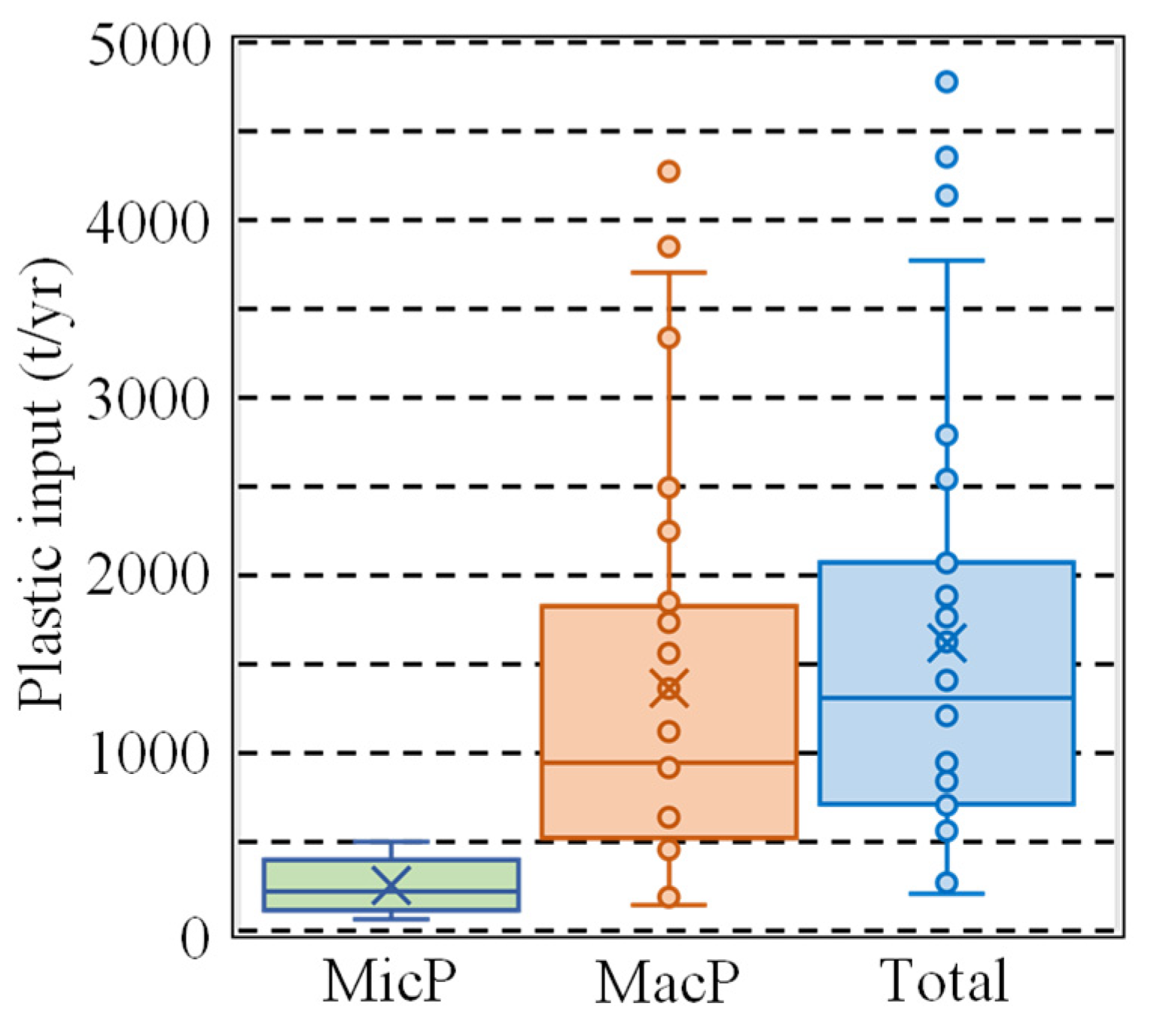
3.4. Calculating Japanese Plastic Emissions from Land to the Sea
4. Discussion
4.1. Total Plastic Input from the Land to the Sea
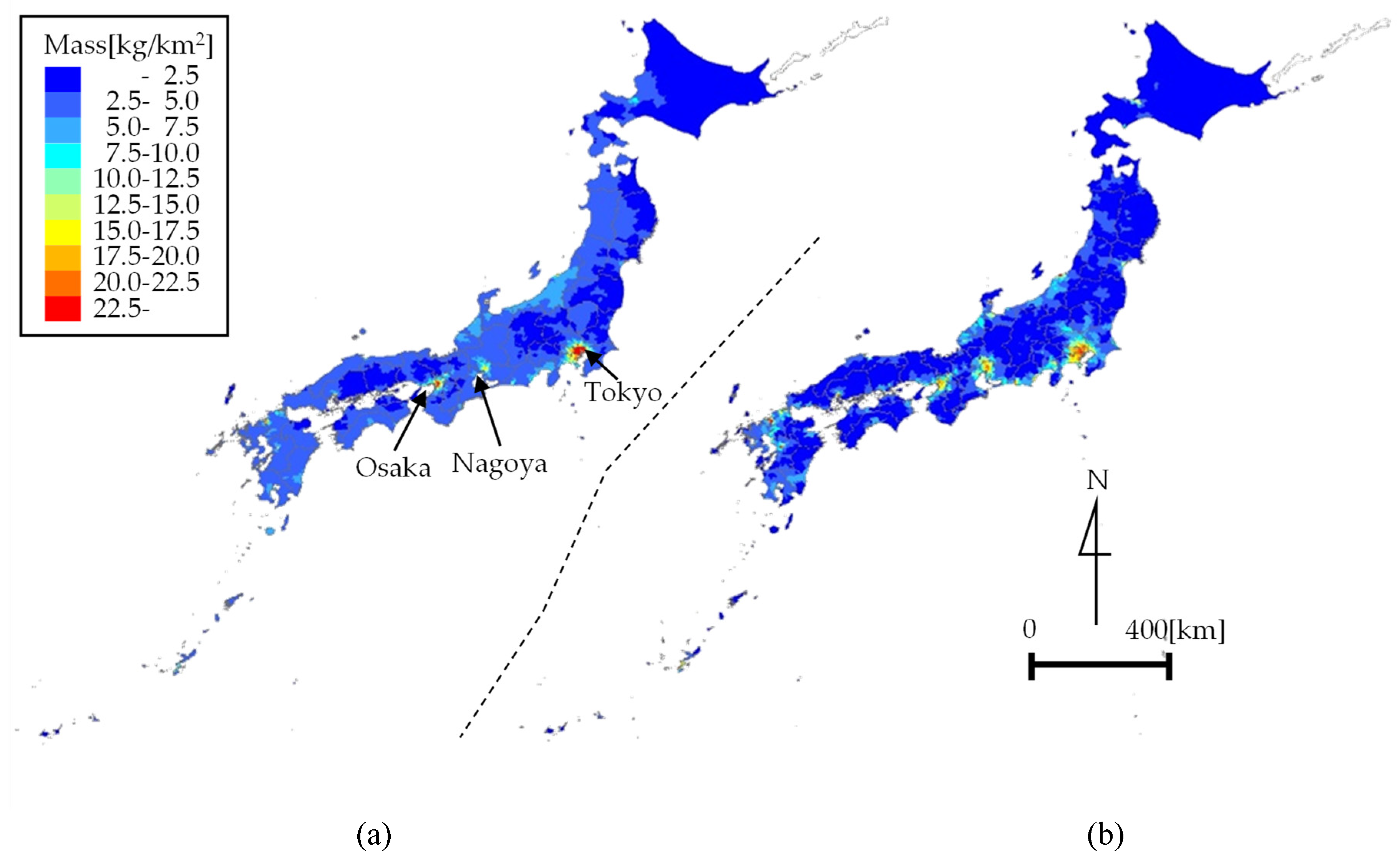
4.2. Map of Plastic Emissions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| No. | River | Survey Site | Cn | Cm | Wp | Wu |
|---|---|---|---|---|---|---|
| 1 | Koetoi R. | Komatsu | 0.19 | 0.00 | 4 | 1 |
| 2 | Shimoebekorobetsu R. | Toyotomi | 1.81 | 0.19 | 6 | 1 |
| 3 | Ishikari R. | Tachihu-oohashi | 4.11 | 0.69 | 38 | 2 |
| 4 | Toyohira R. | Nijunijo-oohashi | 1.24 | 0.06 | 126 | 3 |
| 5 | Kitakami R. | Meiji | 0.14 | 0.00 | 141 | 5 |
| 6a | Mogami R. | Shonai-oohashi | 0.36 | 0.08 | 130 | 6 |
| 6b | Mogami R. | Kurotaki | 0.49 | 0.12 | 182 | 8 |
| 6d | Mogami R. | Konoki | 1.48 | 0.02 | 94 | 6 |
| 7 | Su R. | Ochiai | 8.12 | 1.52 | 362 | 15 |
| 8 | Abukuma R. | Tenjin | 0.39 | 0.01 | 216 | 10 |
| 9 | Kuji R. | Tomioka | 0.03 | 0.00 | 59 | 3 |
| 10 | Naka R. | Nakagawa | 0.70 | 0.03 | 145 | 8 |
| 11 | Sakura R. | Sakaeri | 2.46 | 0.74 | 265 | 17 |
| 12 | Kinu R. | Toyomizu | 0.40 | 0.01 | 54 | 11 |
| 13 | Watarase R. | Nowatari | 1.53 | 0.07 | 429 | 15 |
| 14a | Tone R. | Sakae | 0.37 | 0.07 | 475 | 17 |
| 14b | Tone R. | Tonegawa | 8.68 | 2.36 | 329 | 14 |
| 14c | Tone R. | Bando | 0.17 | 0.03 | 414 | 14 |
| 15a | Ohori R. | Kisaki | 4.40 | 3.31 | 7161 | 85 |
| 15b | Ohori R. | Kachi | 12.88 | 1.08 | 6066 | 82 |
| 16 | Edo R. | Noda | 3.32 | 0.58 | 2366 | 57 |
| 17a | Naka R. | Yoshikoshi | 2.31 | 1.78 | 1784 | 45 |
| 17b | Naka R. | Shinkai | 5.98 | 1.74 | 1000 | 37 |
| 18a | Ara R. | Hanekura | 4.57 | 0.97 | 636 | 17 |
| 18b | Ara R. | Kaihei | 7.40 | 1.37 | 403 | 12 |
| 18c | Ara R. | Onari | 8.35 | 0.32 | 219 | 8 |
| 18d | Ara R. | Kumagaya | 4.59 | 0.05 | 157 | 7 |
| 18e | Ara R. | Tamayodo | 0.44 | 0.02 | 128 | 5 |
| 18f | Ara R. | Kyu-titibu | 1.15 | 0.16 | 78 | 3 |
| 19 | Ichino R. | Matsunaga | 2.09 | 0.43 | 1002 | 42 |
| 20 | Musashi Channel | Gese | 1.31 | 0.04 | 330 | 12 |
| 21 | Yoshino R. | Mannen | 17.27 | 0.59 | 445 | 26 |
| 22 | Yoro R. | Kasumi | 0.71 | 0.00 | 208 | 10 |
| 23 | Obitsu R. | Nakagawa | 3.29 | 0.15 | 110 | 6 |
| 24 | Koito R. | Rokusan | 1.43 | 0.12 | 116 | 5 |
| 25 | Tama R. | Maruko | 1.11 | 0.24 | 2931 | 31 |
| 26a | Tsurumi R. | Shinyokohama | 14.24 | 3.33 | 6619 | 72 |
| 26b | Tsurumi R. | Kamoike | 13.81 | 3.62 | 6877 | 73 |
| 26c | Tsurumi R. | Kawawakitahassaku | 30.67 | 1.52 | 5759 | 67 |
| 26d | Tsurumi R. | Ochiai | 6.15 | 1.16 | 6752 | 72 |
| 26e | Tsurumi R. | Onmawari | 10.52 | 2.11 | 5230 | 66 |
| 26f | Tsurumi R. | Sumiyoshi | 2.59 | 0.32 | 5768 | 23 |
| 27 | Sagami R. | Sagami-oohashi | 0.30 | 0.04 | 446 | 12 |
| 28 | Toneunga R. | Fureai | 12.66 | 2.81 | 1333 | 50 |
| 29 | Hayakido R. | Shibasawa | 3.51 | 0.13 | 35 | 2 |
| 30 | Saka R. | Midori | 0.60 | 0.46 | 600 | 26 |
| 31 | Shonai R. | Shin-meisei | 63.89 | 16.15 | 2045 | 44 |
| 32 | Kiso R. | Kawashima-oohashi | 0.55 | 0.04 | 79 | 2 |
| 33 | Nagara R. | Nagara-oohashi | 1.79 | 0.04 | 110 | 6 |
| 34 | Ibi R. | Ibi-oohashi | 1.01 | 0.01 | 72 | 3 |
| 35 | Kuzuryu R. | Nakakado | 2.01 | 0.06 | 72 | 4 |
| 36 | Asuwa R. | Kujuku | 7.35 | 1.70 | 144 | 5 |
| 37 | Kamo R. | Kyoukawa | 4.93 | 0.77 | 2378 | 30 |
| 38 | Katsura R. | Miyamae | 9.57 | 3.61 | 924 | 14 |
| 39 | Uji R. | Gokou | 1.83 | 1.20 | 333 | 11 |
| 40 | Yodo R. | Hijikata | 2.01 | 0.11 | 491 | 12 |
| 41 | Ina R. | Minamizono | 6.39 | 0.68 | 1261 | 22 |
| 42a | Yamato R. | Taisho | 6.94 | 0.37 | 1266 | 30 |
| 42b | Yamato R. | Gokou-oohashi | 11.09 | 2.52 | 1192 | 31 |
| 43 | Toga R. | Shimokawara | 1.38 | 0.03 | 4276 | 28 |
| 44 | Ikuta R. | Nunohiki | 0.22 | 0.01 | 303 | 3 |
| 45 | Sendai R. | Sendai-oohashi | 0.99 | 0.01 | 83 | 4 |
| 46 | Tenjin R. | Tenjin | 1.95 | 0.04 | 86 | 4 |
| 47 | Hino R. | Shin-hino | 0.45 | 0.04 | 25 | 2 |
| 48 | Hii R. | Mizuho-oohashi | 0.28 | 0.01 | 53 | 4 |
| 49 | Goemon R. | Hinode | 3.98 | 0.45 | 643 | 29 |
| 50 | Asahi R. | Okakita-oohashi | 0.90 | 0.04 | 70 | 4 |
| 51 | Nishiki R. | Gosho-oohashi | 0.11 | 0.00 | 21 | 2 |
| 52 | Saba R. | Okinohara | 0.12 | 0.00 | 19 | 1 |
| 53 | Fushino R. | Takada | 0.65 | 0.02 | 339 | 13 |
| 54a | Mononobe R. | Mononobe | 1.07 | 0.12 | 26 | 1 |
| 54b | Mononobe R. | Matchida | 1.48 | 0.18 | 21 | 1 |
| 55 | Niyodo R. | Niyodo-oohashi | 3.76 | 0.03 | 43 | 2 |
| 56a | Shimanto R. | Rivermouth | 1.35 | 0.04 | 37 | 2 |
| 56b | Shimanto R. | Downstream | 0.39 | 0.00 | 37 | 2 |
| 57 | Shigenobu R. | Deai | 0.64 | 0.06 | 658 | 12 |
| 58 | Yaoshi.R | Seisei | 0.26 | 0.00 | 218 | 8 |
| 59 | Hiji R. | Hatanomae | 0.42 | 0.03 | 93 | 8 |
| 60 | Onga R. | Kanroku | 1.27 | 0.07 | 508 | 19 |
| 61 | Hikosan R. | Okamori | 5.24 | 3.04 | 406 | 17 |
| 62 | Kagetsu R. | Kagetsugawa | 1.37 | 0.05 | 100 | 4 |
| 63 | Kikuchi R. | Yamagaseibu-oohashi | 2.28 | 3.11 | 181 | 11 |
| 64 | Kuro R. | Kurumagaeri | 0.21 | 0.01 | 125 | 9 |
| 65 | Shira R. | Yotsugi | 5.51 | 0.01 | 334 | 12 |
| 66 | Midori R. | Medomachi | 8.25 | 0.43 | 67 | 5 |
| 67 | Kuma R. | Seibu-oohashi | 0.84 | 0.11 | 50 | 3 |
| 68 | Sendai R. | Miyanojo | 1.21 | 0.68 | 68 | 6 |
| 69 | Fukido R. | South side | 0.23 | 0.02 | 0 | 0 |
| 70a | Miyara R. | Kainan | 12.77 | 0.62 | 12 | 2 |
| 70b | Miyara R. | Kawara | 0.97 | 0.31 | 11 | 2 |
| Prefecture | Low | Middle | High | Prefecture | Low | Middle | High |
|---|---|---|---|---|---|---|---|
| Hokkaido | 5.2 | 91.6 | 594.1 | Shiga | 2.1 | 14.1 | 47.2 |
| Aomori | 1.5 | 26.3 | 101.5 | Kyoto | 2.6 | 16.3 | 59.3 |
| Iwate | 0.5 | 33.6 | 158.1 | Osaka | 7.8 | 24.0 | 60.5 |
| Miyagi | 3.8 | 21.8 | 74.0 | Hyogo | 6.3 | 28.8 | 100.7 |
| Akita | 0.8 | 38.1 | 175.3 | Nara | 2.2 | 12.8 | 49.2 |
| Yamagata | 1.2 | 32.7 | 137.9 | Wakayama | 1.4 | 18.7 | 73.9 |
| Fukushima | 2.2 | 35.3 | 136.4 | Tottori | 1.1 | 13.3 | 49.7 |
| Ibaraki | 3.7 | 23.5 | 76.9 | Shimane | 0.6 | 18.9 | 80.2 |
| Tochigi | 3.9 | 21.6 | 73.2 | Okayama | 2.7 | 17.2 | 61.3 |
| Gunma | 3.5 | 18.4 | 62.7 | Hiroshima | 3.2 | 24.0 | 87.9 |
| Saitama | 7.0 | 28.5 | 81.9 | Yamaguchi | 2.0 | 20.8 | 74.6 |
| Chiba | 6.7 | 31.2 | 94.9 | Tokushima | 1.3 | 14.0 | 56.6 |
| Tokyo | 12.7 | 36.0 | 103.4 | Kagawa | 1.1 | 5.9 | 20.0 |
| Kanagawa | 10.0 | 31.6 | 83.0 | Ehime | 1.6 | 18.0 | 67.5 |
| Yamanashi | 1.5 | 12.9 | 47.6 | Kochi | 1.2 | 23.1 | 121.6 |
| Nagano | 2.0 | 36.2 | 138.7 | Fukuoka | 7.6 | 35.1 | 107.2 |
| Niigata | 7.2 | 70.6 | 257.8 | Saga | 2.1 | 12.1 | 38.5 |
| Toyama | 3.9 | 24.1 | 82.7 | Nagasaki | 2.2 | 16.0 | 55.3 |
| Ishikawa | 3.3 | 22.2 | 77.5 | Kumamoto | 4.0 | 33.9 | 122.8 |
| Fukui | 2.4 | 19.8 | 72.0 | Oita | 1.7 | 21.2 | 78.9 |
| Gifu | 5.5 | 43.2 | 162.9 | Miyazaki | 2.5 | 35.5 | 136.0 |
| Shizuoka | 9.0 | 45.0 | 146.1 | Kagoshima | 3.2 | 40.4 | 149.3 |
| Aichi | 8.7 | 40.4 | 117.3 | Okinawa | 2.6 | 11.2 | 36.7 |
| Mie | 5.0 | 26.5 | 91.2 |
References
- Plastics Europe. Association of Plastic Manufacturers; Plastics Europe: Brussles, Belgium, 2016. [Google Scholar]
- Laist, D.W. Overview of the biological effects of lost and discarded plastic debris in the marine environment. Mar. Pollut. Bull. 1987, 18, 319–326. [Google Scholar] [CrossRef]
- Hansen, J. Draft position statement on plastic debris in marine environments. Fisheries 1990, 15, 16–17. [Google Scholar]
- Pruter, A.T. Sources, quantities and distribution of persistent plastics in the marine environment. Mar. Pollut. Bull. 1987, 18, 305–310. [Google Scholar] [CrossRef]
- Gregory, M.R. The hazards of persistent marine pollution: Drift plastics and conservation islands. J. R. Soc. N. Z. 1991, 21, 83–100. [Google Scholar] [CrossRef]
- Gregory, M.R.; Ryan, P.G. Pelagic plastics and other seaborne persistent synthetic debris: A review of Southern Hemisphere perspectives. In Marine Debris—Sources, Impacts and Solutions; Coe, J.M., Rogers, D.B., Eds.; Springer: New York, NY, USA, 1997; pp. 49–66. [Google Scholar]
- Derraik, J.G. The pollution of the marine environment by plastic debris: A review. Mar. Pollut. Bull. 2002, 44, 842–852. [Google Scholar] [CrossRef]
- Law, K.L.; Thompson, R.C. Microplastics in the seas. Science 2014, 345, 144–145. [Google Scholar] [CrossRef]
- Cózar, A.; Echevarría, F.; González-Gordillo, J.I.; Irigoien, X.; Úbeda, B.; Hernández-León, S.; Palma, A.T.; Navarro, S.; García-de-Lomas, J.; Ruiz, A.; et al. Plastic debris in the open ocean. Proc. Natl. Acad. Sci. USA 2014, 111, 10239–10244. [Google Scholar] [CrossRef] [PubMed]
- Shaw, D.G. Pelagic tar and plastic in the Gulf of Alaska and BeringSea: 1975. Sci. Total Environ. 1977, 8, 13–20. [Google Scholar] [CrossRef]
- Williams, A.T.; Simmons, S.L. Estuarine litter at the river/beach interface in the Bristol Channel, United Kingdom. J. Coast. Res. 1997, 13, 1159–1165. [Google Scholar]
- Jambeck, J.R.; Geyer, R.; Wilcox, C.; Siegler, T.R.; Perryman, M.; Andrady, A.; Narayan, R.; Law, K.L. Plastic waste inputs from land into the ocean. Science 2015, 347, 768–771. [Google Scholar] [CrossRef]
- Thompson, R.C.; Olsen, Y.; Mitchell, R.P.; Davis, A.; Rowland, S.J.; John, A.W.G.; McGonigle, D.; Russell, A.E. Lost at sea: Where is all the plastic? Science 2004, 34, 838. [Google Scholar] [CrossRef] [PubMed]
- Carpenter, E.J.; Smith, K.L. Plastics on the Sargasso Sea surface. Science 1972, 175, 1240–1241. [Google Scholar] [CrossRef] [PubMed]
- Rothstein, S.I. Plastic particle pollution of the surface of the Atlantic Ocean: Evidence from a seabird. Condor 1973, 75, 344–345. [Google Scholar] [CrossRef]
- Eriksen, M.; Lebreton, L.C.M.; Carson, H.S.; Thiel, M.; Moore, C.J.; Borerro, J.C.; Galgani, F.; Ryan, P.G.; Reisser, J. Plastic pollution in the world’s oceans: More than 5 trillion plastic pieces weighing over 250,000 tons afloat at sea. PLoS ONE 2014, 9, e111913. [Google Scholar] [CrossRef]
- Mato, Y.; Isobe, T.; Takada, H.; Kanehiro, H.; Ohtake, C.; Kaminuma, T. Plastic resin pellets as a transport medium for toxic chemicals in the marine environment. Environ. Sci. Technol. 2001, 35, 318–324. [Google Scholar] [CrossRef]
- Tanaka, K.; Takada, H.; Yamashita, R.; Mizukawa, K.; Fukuwaka, M.A.; Watanuki, Y. Accumulation of plastic-derived chemicals in tissues of seabirds ingesting marine plastics. Mar. Pollut. Bull. 2013, 69, 219–222. [Google Scholar] [CrossRef]
- Koelmans, A.A.; Besseling, E.; Wegner, A.; Foekema, E.M. Plastic as a carrier of POPs to aquatic organisms: A model analysis. Environ. Sci. Technol. 2013, 47, 7812–7820. [Google Scholar] [CrossRef]
- Browne, M.A.; Dissanayake, A.; Galloway, T.S.; Lowe, D.M.; Thompson, R.C. Ingested microscopic plastic translocates to the circulatory system of the mussel, Mytilus edulis (L). Environ. Sci. Technol. 2008, 42, 5026–5031. [Google Scholar] [CrossRef]
- Boerger, C.M.; Lattin, G.L.; Moore, S.L.; Moore, C.J. Plastic ingestion by planktivorous fishes in the North Pacific Central Gyre. Mar. Pollut. Bull. 2010, 60, 2275–2278. [Google Scholar] [CrossRef]
- Cole, M.; Lindeque, P.; Halsband, C.; Galloway, T.S. Microplastics as contaminants in the marine environment: A review. Mar. Pollut. Bull. 2011, 62, 2588–2597. [Google Scholar] [CrossRef]
- Tanaka, K.; Takada, H. Microplastic fragments and microbeads in digestive tracts of planktivorous fish from urban coastal waters. Sci. Rep. 2016, 6, 34351. [Google Scholar] [CrossRef] [PubMed]
- Andrady, A.L. Microplastics in the marine environment. Mar. Pollut. Bull. 2011, 62, 1596–1605. [Google Scholar] [CrossRef]
- Hidalgo-Ruz, V.; Gutow, L.; Thompson, R.C.; Thiel, M. Microplastics in the marine environment: A review of the methods used for identification and quantification. Environ. Sci. Technol. 2012, 46, 3060–3075. [Google Scholar] [CrossRef]
- Law, K.L.; Moret-Ferguson, S.; Goodwin, D.S.; Zettler, E.R.; DeForce, E.; Kukulka, T.; Proskurowski, G. Distribution of surface plastic debris in the eastern Pacific Ocean from an 11-year. Environ. Sci. Technol. 2014, 48, 4732–4738. [Google Scholar] [CrossRef] [PubMed]
- Law, K.L.; Moret-Ferguson, S.; Maximenko, N.A.; Proskurowski, G.; Peacock, E.E.; Hafner, J.; Reddy, C.M. Plastic accumulation in the North Atlantic subtropical gyre. Science 2015, 329, 1185–1188. [Google Scholar] [CrossRef] [PubMed]
- Isobe, A.; Uchida, K.; Tokai, T.; Iwasaki, S. East Asian seas: A hot spot of pelagic microplastics. Mar. Pollut. Bull. 2015, 101, 618–623. [Google Scholar] [CrossRef]
- Kershaw, P.J.; Rochman, C.M. Sources, fate and effects of microplastics in the marine environment: Part 2 of a global assessment. Rep. Stud. 2016, 93, 216. [Google Scholar]
- Wagner, M.; Scherer, C.; Alvarez-Muñoz, D.; Brennholt, N.; Bourrain, X.; Buchinger, S.; Fries, E.; Grosbois, C.; Klasmeier, J.; Marti, T.; et al. Microplastics in freshwater ecosystems: What we know and what we need to know. Environ. Sci. Eur. 2014, 26, 12. [Google Scholar] [CrossRef]
- Moore, C.J.; Lattin, G.L.; Zellers, A.F. Quantity and type of plastic debris flowing from two urban rivers to coastal waters and beaches of Southern California. Rev. Gest. Costeira Integr. J. Integr. Coast. Zone Manag. 2011, 11, 65–73. [Google Scholar] [CrossRef]
- Eriksen, M.; Mason, S.; Wilson, S.; Box, C.; Zellers, A.; Edwards, W.; Farley, H.; Amato, S. Microplastic pollution in the surface waters of the Laurentian Great Lakes. Mar. Pollut. Bull. 2013, 77, 177–182. [Google Scholar] [CrossRef]
- Mani, T.; Hauk, A.; Walter, U.; Burkhardt-Holm, P. Microplastics profile along the Rhine river. Sci. Rep. 2014, 5, 17988. [Google Scholar] [CrossRef] [PubMed]
- Yonkos, L.T.; Friedel, E.A.; Perez-Reyes, A.C.; Ghosal, S.; Arthur, C.D. Microplastics in four estuarine rivers in the Chesapeake Bay, U.S.A. Environ. Sci. Technol. 2014, 48, 14195–14202. [Google Scholar] [CrossRef] [PubMed]
- Eerkes-Medrano, D.; Thompson, R.C.; Aldridge, D.C. Microplastics in freshwater systems: A review of the emerging threats, identification of knowledge gaps and prioritisation of research needs. Water Res. 2015, 75, 63–82. [Google Scholar] [CrossRef] [PubMed]
- Dris, R.; Gasperi, J.; Rocher, V.; Saad, M.; Renault, N.; Tassin, B. Microplastic contamination in an urban area: A case study in Greater Paris. Environ. Chem. 2015, 12, 592–599. [Google Scholar] [CrossRef]
- McCormick, A.R.; Hoellein, T.J.; London, M.G.; Hittie, J.; Scott, J.W.; Kelly, J.J. Microplastic in surface waters of urban rivers: Concentration, sources, and associated bacterial assemblages. Ecosphere 2016, 7, e01556. [Google Scholar] [CrossRef]
- Murphy, F.; Ewins, C.; Carbonnier, F.; Quinn, B. Wastewater treatment works (WwTW) as a Source of microplastics in the aquatic environment. Environ. Sci. Technol. 2016, 50, 5800–5808. [Google Scholar] [CrossRef]
- Verster, C.; Minnaar, K.; Bouwman, H. Marine and freshwater microplastic research in South Africa. Integr. Environ. Assess. Manag. 2017, 13, 533–535. [Google Scholar] [CrossRef]
- Kataoka, T.; Nihei, Y.; Kudou, K.; Hinata, H. Assessment of the sources and inflow processes of microplastics in the river environments of Japan. Environ. Pollut. 2019, 244, 958–965. [Google Scholar] [CrossRef]
- Lebreton, L.C.M.; van der Zwet, J.; Damsteeg, J.-W.; Slat, B.; Andrady, A.; Reisser, J. River plastic emissions to the world’s oceans. Nat. Commun. 2017, 8, 15611. [Google Scholar] [CrossRef]
- Schmidt, C.; Krauth, T.; Wagner, S. Export of plastic debris by rivers into the sea. Environ. Sci. Technol. 2017, 51, 12246–12253. [Google Scholar] [CrossRef]
- Siegfred, M.; Koelmans, A.A.; Besseling, E.; Kroeze, C. Export of microplastics from land to sea. A modelling approach. Water Res. 2017, 127, 249–257. [Google Scholar] [CrossRef] [PubMed]
- Kudo, K.; Kataoka, T.; Nihei, Y.; Kitaura, F. Estimation of temporal variations and annual flux of microplastics in rivers under low- and high-flow conditions. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2018, 74, 529–534. (In Japanese) [Google Scholar] [CrossRef]
- Kataoka, T.; Hinata, H.; Nihei, Y. Numerical estimation of inflow flux of floating natural macro-debris into Tokyo Bay. Estuar. Coast. Shelf Sci. 2013, 134, 69–79. [Google Scholar] [CrossRef]
- Motovilov, Y.G.; Gottschalk, L.; Engeland, K.; Rodhe, A. Validation of a distributed hydrological model against spatial observations. Agric. For. Meteorol. 1999, 98, 257–277. [Google Scholar] [CrossRef]
- Sayama, T.; Ozawa, G.; Kawakami, T.; Nabesaka, S.; Fukami, K. Rainfall–runoff–inundation analysis of the 2010 Pakistan flood in the Kabul River basin. Hydrol. Sci. J. 2012, 57, 298–312. [Google Scholar] [CrossRef]
- Sawano, S.; Hotta, N.; Tanaka, N.; Suboyama, Y.; Suzuki, M. Development of a simple forest evapotranspiration model using a process-oriented model as a reference to parameterize data from a wide range of environmental conditions. Ecol. Model. 2015, 309–310, 93–109. [Google Scholar] [CrossRef]
- Motoyama, H. Simulation of seasonal snowcover based on air temperature and precipitation. J. Appl. Meteorol. 1990, 29, 1104–1110. [Google Scholar] [CrossRef]
- Suzuki, M.; Fukusima, Y. Estimates of evapotranspiration from land surface in Shiga Prefecture using digitalized square-grid map database. Lake Biwa Study Monogr. 1995, 2, 1–55. [Google Scholar]
- Research Group of Evapotranspiration. Evapotranspiration from paddy field. J. Agric. Meteorol. 1967, 22, 13–21. (In Japanese) [Google Scholar]
- Kondo, J Evaporation from lake or sea surface. Weather 2012, 59, 75–78. (In Japanese)
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw Hill: New York, NY, USA, 1988. [Google Scholar]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2012; p. 821. [Google Scholar]
- Kataoka, T.; Nihei, Y. Quantification of floating riverine macro-debris transport using an image processing approach. Sci. Rep. 2020, 10, 1–11. [Google Scholar] [CrossRef] [PubMed]

| Land Use | E | Qs | Qi | ||
|---|---|---|---|---|---|
| Major | Details | Coefficient f | |||
| Forest | Forests | Equation (1) | 0.5 (Quaternary volcanic rock) 0.8(Other) | Equation (6) | |
| Bushes | Equation (2) | 0.3 | Equation (6) | ||
| Mountainous bushes | P − Qs | 0.95 | 0 | ||
| Agriculture area | Paddy fields | Irrigation | Equation (3) | 0.8 | Equation (6) |
| No irrigation | Equation (2) | 0.3 | Equation (6) | ||
| Other | Equation (2) | 0.3 | Equation (6) | ||
| Urban area | Building sites | Infiltration area | Equation (2) | 0.3 | Equation (6) |
| No-infiltration area | P − Qs | 0.95 | 0 | ||
| Road, railways, and others | P − Qs | 0.95 | 0 | ||
| Other | Golf courses | Equation (2) | 0.3 | Equation (6) | |
| Rivers and lakes | Equation (4) | P − E | 0 | ||
| Variables | Approximation | Number | Mass | ||
|---|---|---|---|---|---|
| Equation | 1012 Particles | Equation | Tons | ||
| Population density, Wp | Linear y | 9 | 1.67 | 10 | 293.6 |
| Linear y + Δy/2 | 7,8,9 | 2.54 | 7,8,10 | 502.8 | |
| Linear y − Δy/2 | 7,8,9 | 0.81 | 7,8,10 | 84.5 | |
| Curve | 13 | 1.39 | 14 | 204.1 | |
| Urban ratio, Wu | Linear y | 11 | 1.41 | 12 | 228.1 |
| Linear y + Δy/2 | 7,8,11 | 2.26 | 7,8,12 | 435.7 | |
| Linear y − Δy/2 | 7,8,11 | 0.55 | 7,8,12 | 65.1 | |
| Curve | 15 | 1.27 | 16 | 217.9 | |
| Low | 0.55 | 65.1 | |||
| Middle | 1.40 | 223.0 | |||
| High | 2.54 | 502.8 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nihei, Y.; Yoshida, T.; Kataoka, T.; Ogata, R. High-Resolution Mapping of Japanese Microplastic and Macroplastic Emissions from the Land into the Sea. Water 2020, 12, 951. https://doi.org/10.3390/w12040951
Nihei Y, Yoshida T, Kataoka T, Ogata R. High-Resolution Mapping of Japanese Microplastic and Macroplastic Emissions from the Land into the Sea. Water. 2020; 12(4):951. https://doi.org/10.3390/w12040951
Chicago/Turabian StyleNihei, Yasuo, Takushi Yoshida, Tomoya Kataoka, and Riku Ogata. 2020. "High-Resolution Mapping of Japanese Microplastic and Macroplastic Emissions from the Land into the Sea" Water 12, no. 4: 951. https://doi.org/10.3390/w12040951
APA StyleNihei, Y., Yoshida, T., Kataoka, T., & Ogata, R. (2020). High-Resolution Mapping of Japanese Microplastic and Macroplastic Emissions from the Land into the Sea. Water, 12(4), 951. https://doi.org/10.3390/w12040951





