Levee Breaching: A New Extension to the LISFLOOD-FP Model
Abstract
:1. Introduction
2. Methods
2.1. Levee Breach Module
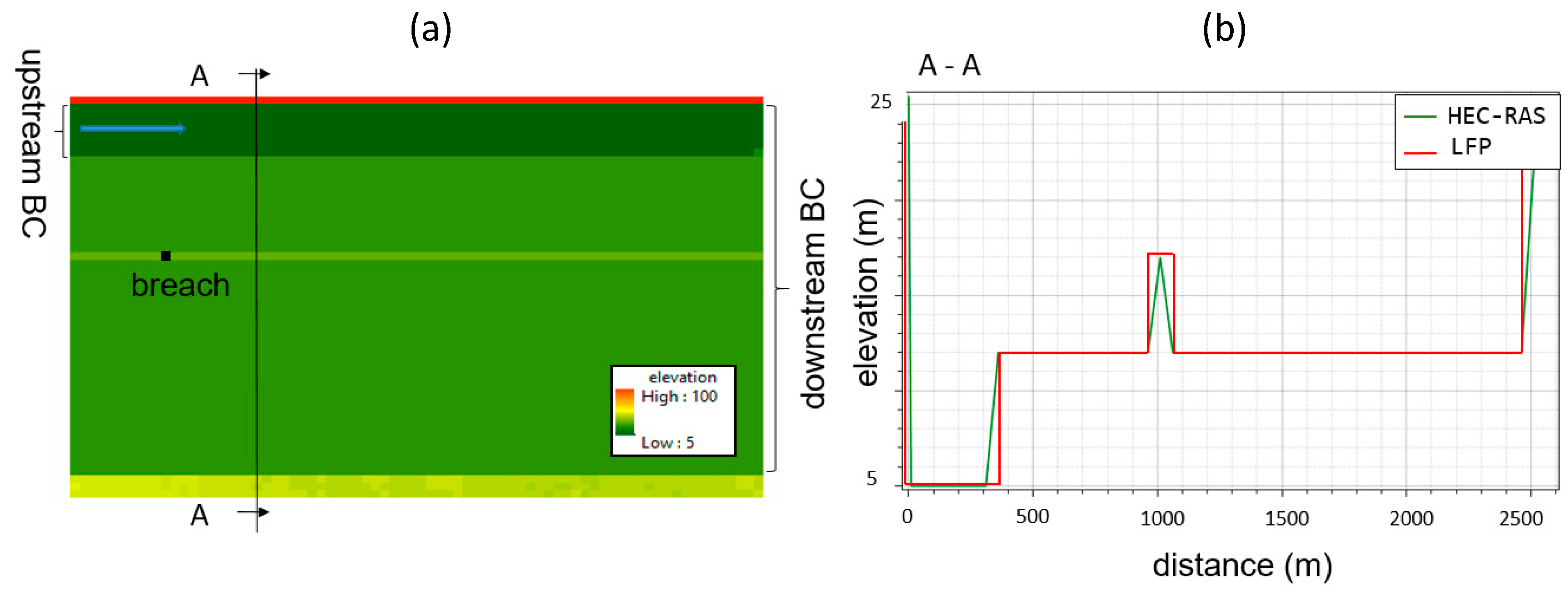
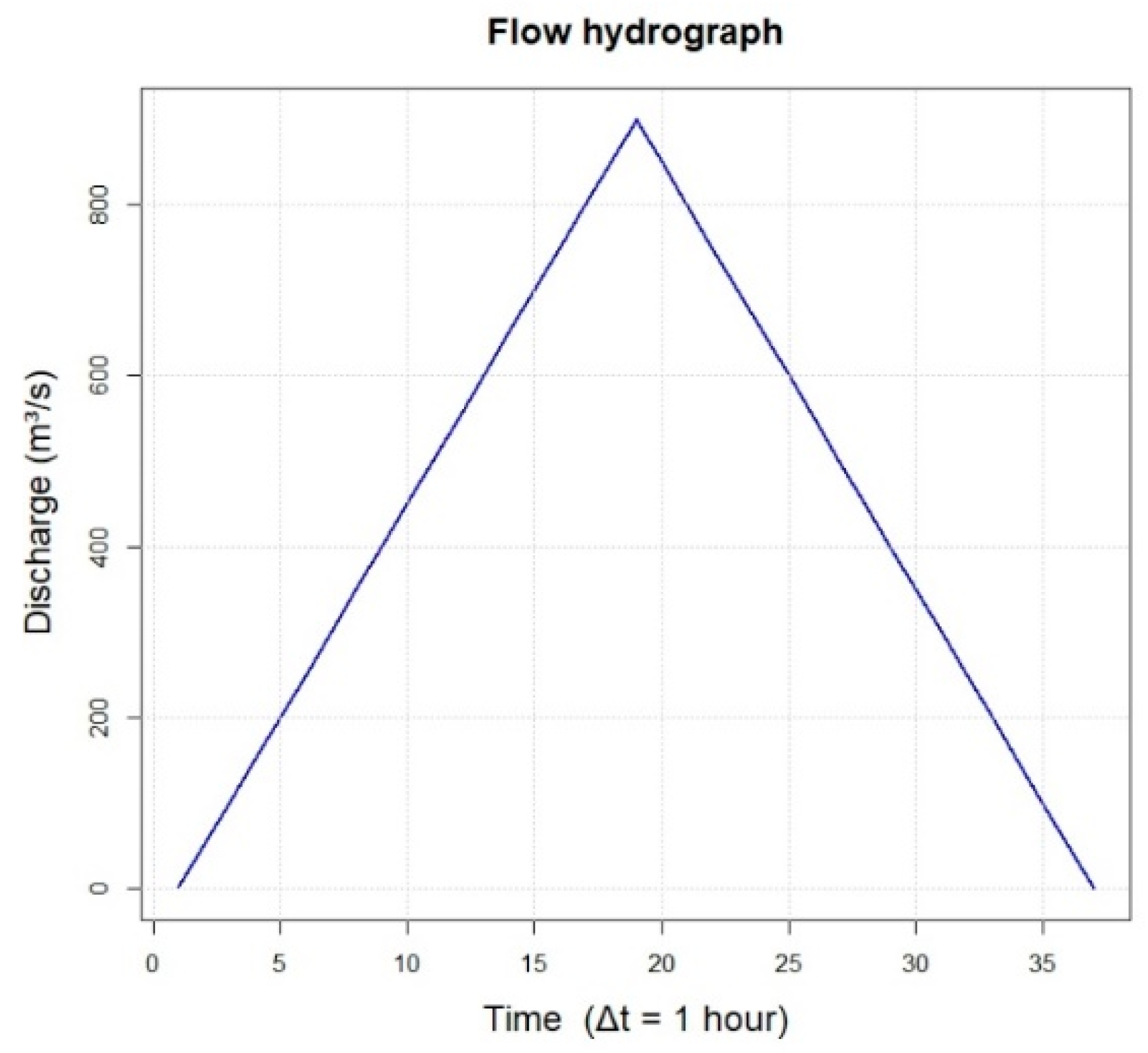
2.2. Synthetic Test Description
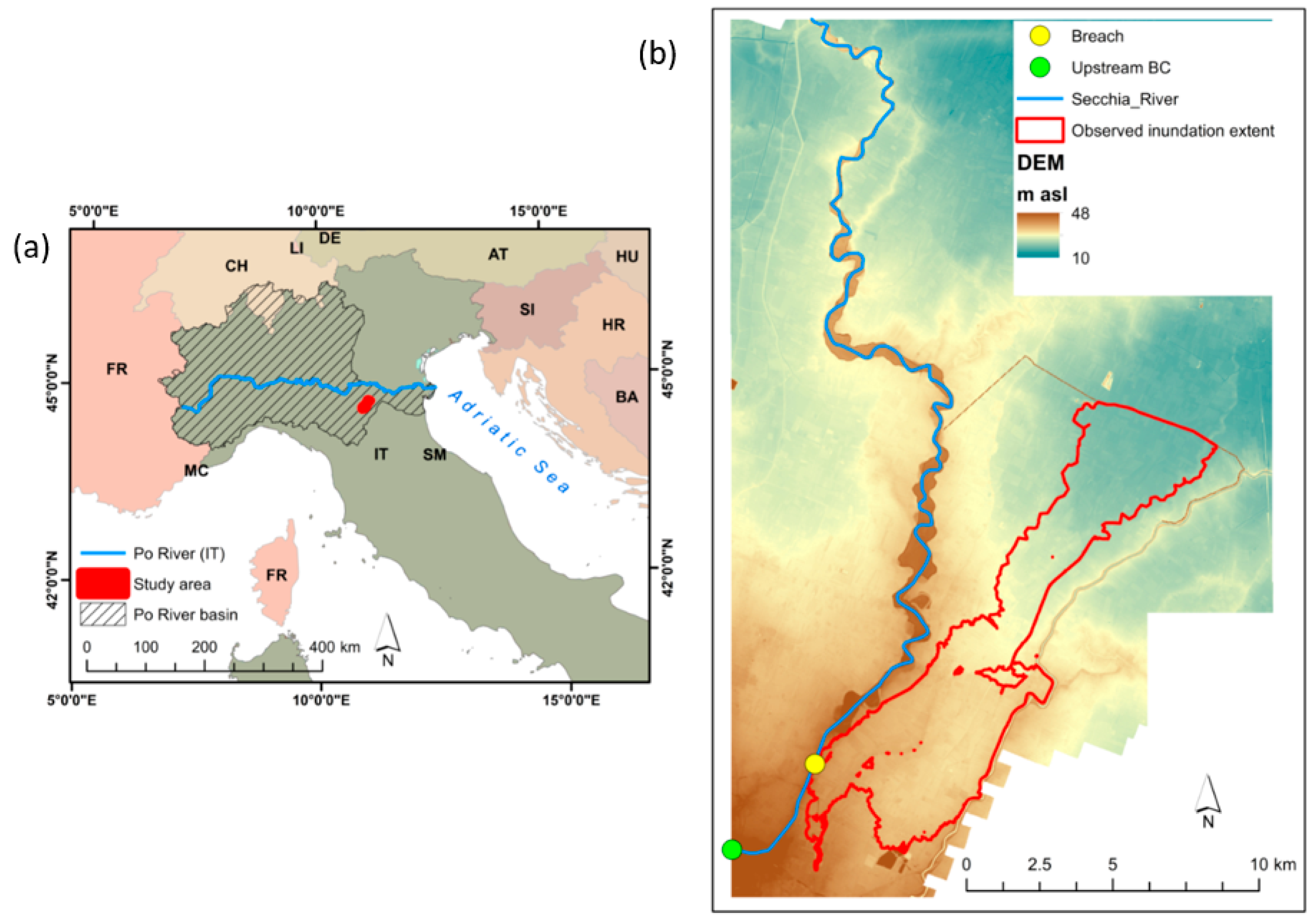
2.3. Secchia Inundation
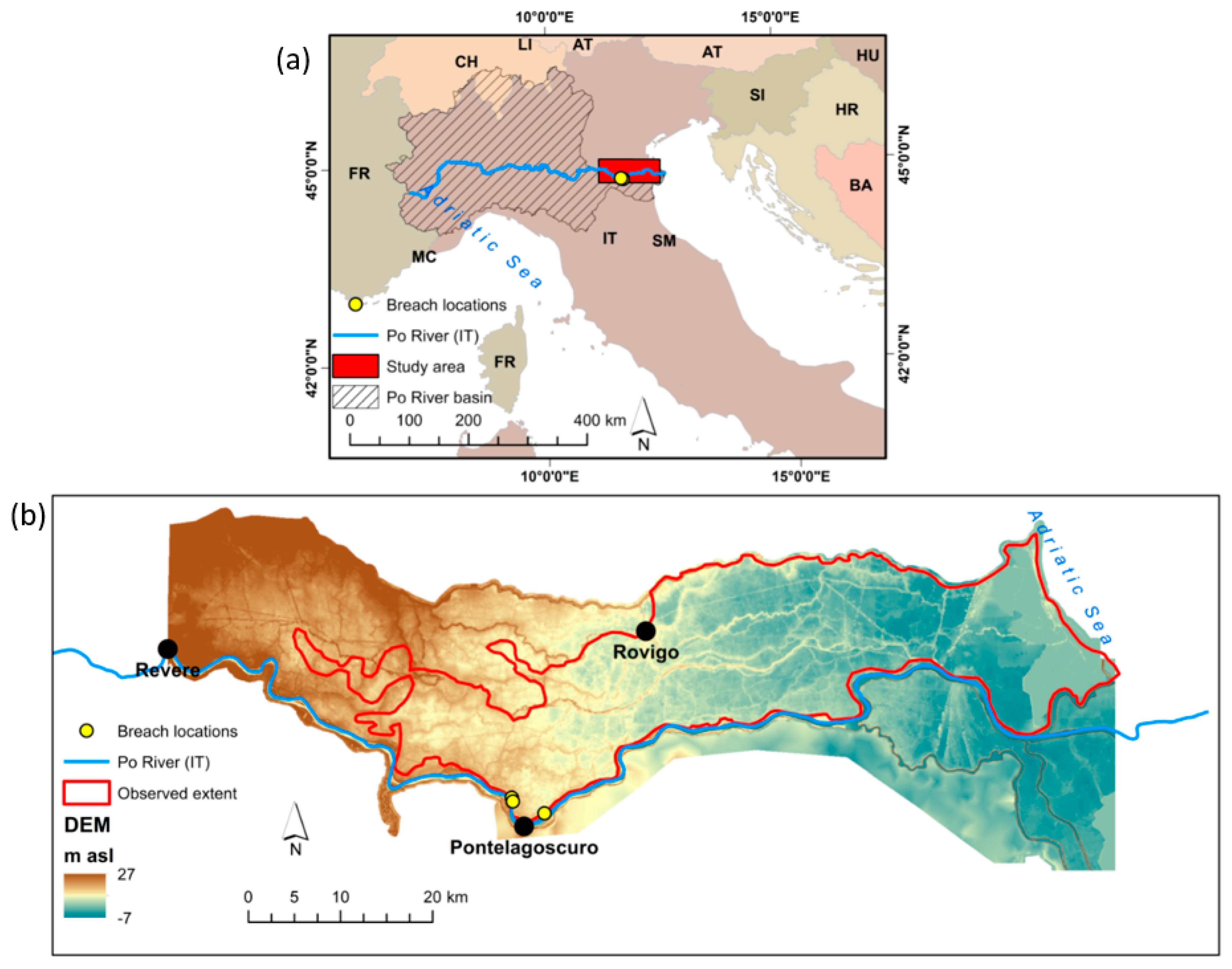
2.4. November 1951 Polesine Catastrophic Flood of the Po River
3. Results
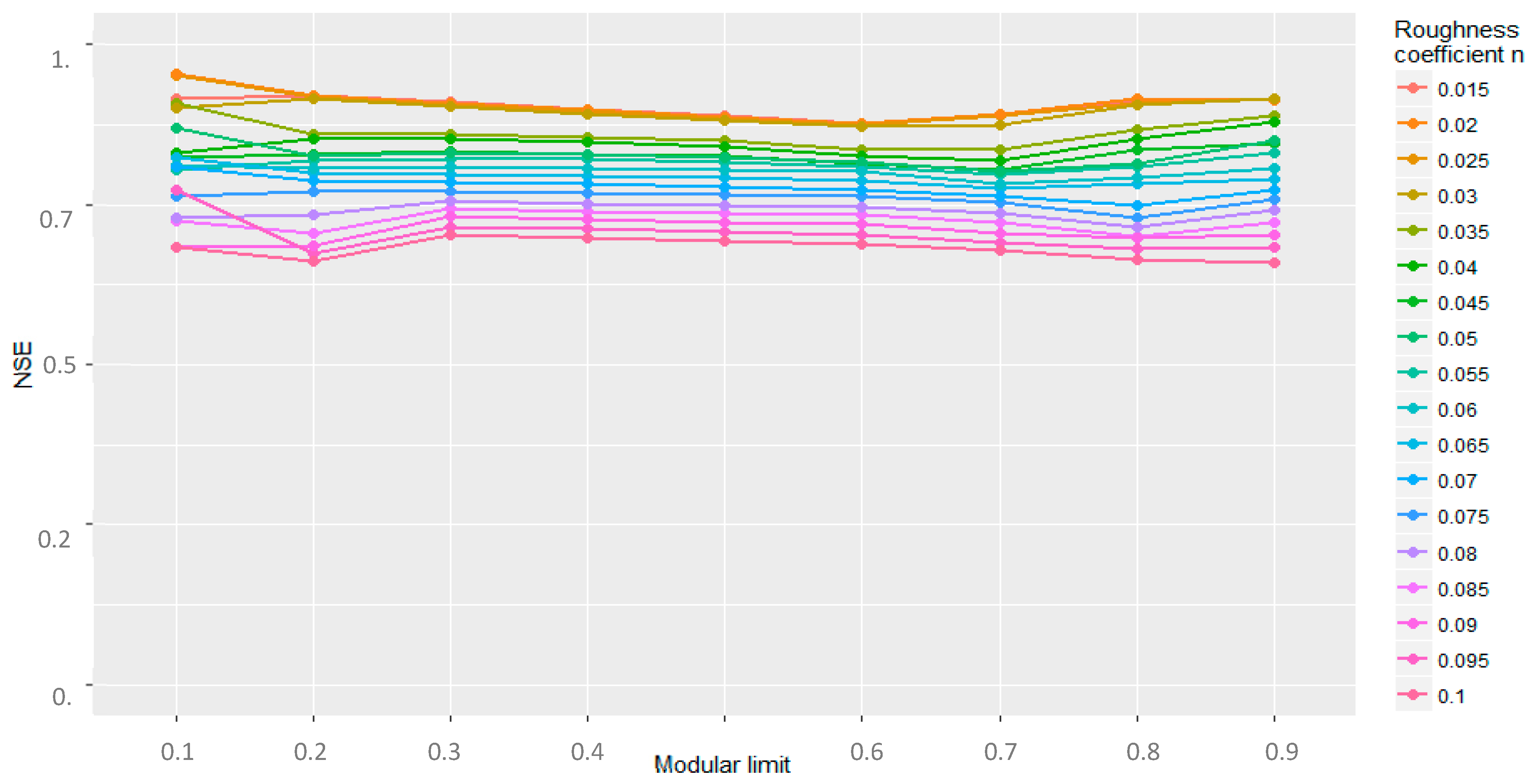
3.1. Synthetic Tests
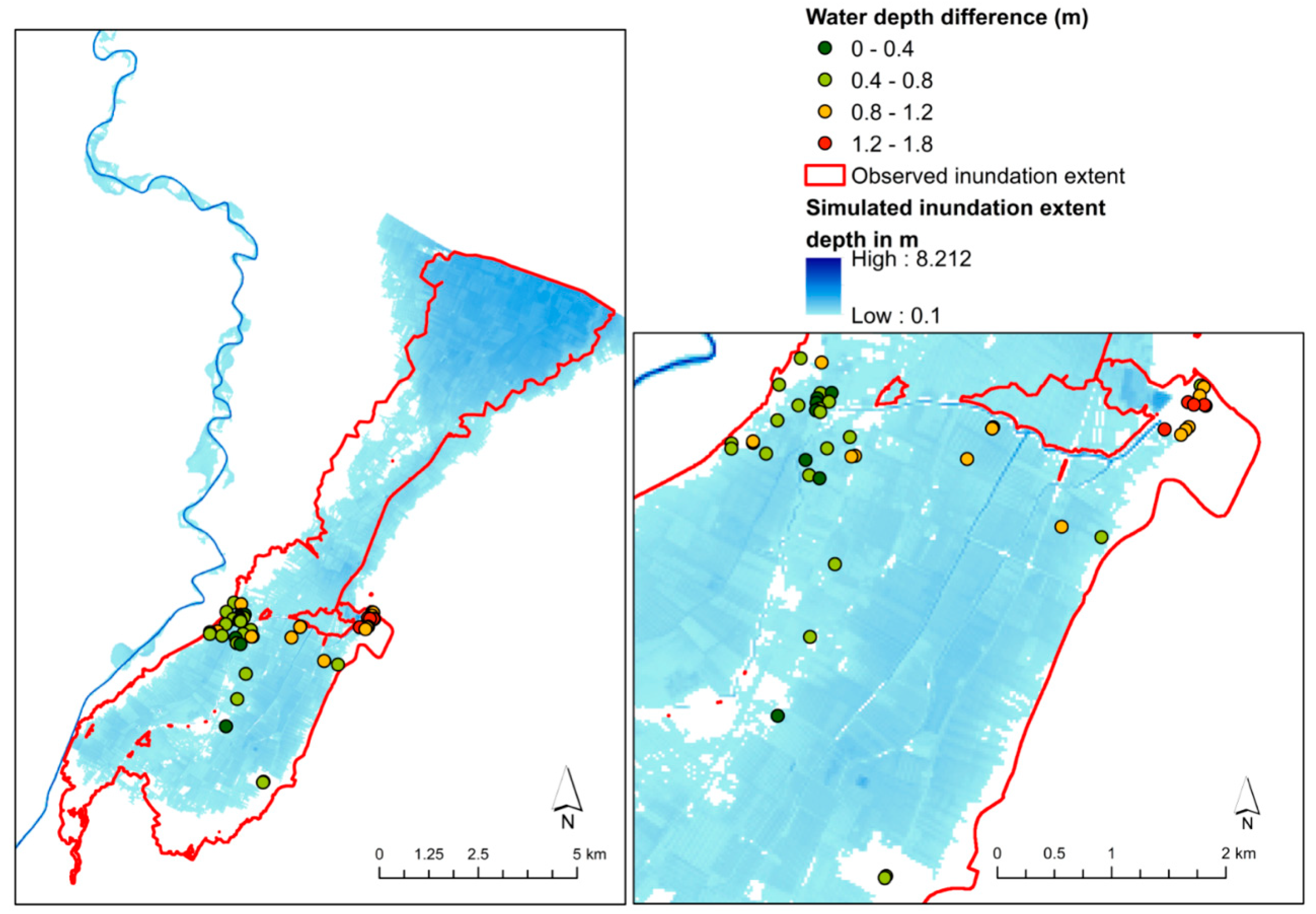
3.2. Secchia Inundation
3.3. November 1951 Polesine Catastrophic Flood, Po River
4. Discussion
4.1. Synthetic Cases
4.2. Historic Events Simulations
4.3. Assumption and Limitation of the Levee Failure Extension
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Centre for Research on the Epidemiology of Disasters. 2018 Review of Disaster Events 2019. Available online: http://www.cred.be/publications (accessed on 22 January 2020).
- Alfieri, L.; Bisselink, B.; Dottori, F.; Naumann, G.; de Roo, A.; Salamon, P.; Wyser, K.; Feyen, L. Global projections of river flood risk in a warmer world. Earth’s Future 2017, 5, 171–182. [Google Scholar] [CrossRef]
- Vorogushyn, S.; Merz, B.; Apel, H. Development of dike fragility curves for piping and micro-instability breach mechanisms. Nat. Hazards Earth Syst. Sci. 2009, 9, 1383–1401. [Google Scholar] [CrossRef]
- Marijnissen, R.; Kok, M.; Kroeze, C.; van Loon-Steensma, J. Re-evaluating safety risks of multifunctional dikes with a probabilistic risk framework. Nat. Hazards Earth Syst. Sci. 2019, 19, 737–756. [Google Scholar] [CrossRef] [Green Version]
- van Mierlo, M.; Vrouwenvelder, A.; Calle, E.; Vrijling, J.; Jonkman, S.N.; de Bruijn, K.; Weerts, A.H. Assessment of flood risk accounting for river system behaviour. International. Int. J. River Basin Manag. 2007, 5, 93–104. [Google Scholar] [CrossRef]
- De Bruijn, K.M.; Diermanse, F.L.; Van Der Doef, M.; Klijn, F. Hydrodynamic System Behaviour: Its Analysis and Implications for Flood Risk Management; EDP Sciences: Les Ulis, France, 2016. [Google Scholar]
- Ludy, J.; Kondolf, G.M. Flood risk perception in lands “protected” by 100-year levees. Nat. Hazards 2012, 61, 829–842. [Google Scholar] [CrossRef]
- Domeneghetti, A.; Carisi, F.; Castellarin, A.; Brath, A. Evolution of flood risk over large areas: Quantitative assessment for the Po river. J. Hydrol. 2015, 527, 809–823. [Google Scholar] [CrossRef]
- Andersen, C.F. The New Orleans Hurricane Protection System: What Went Wrong and Why; A report; ASCE: Reston, VA, USA, 2007. [Google Scholar]
- Larson, L.W. The Great USA Flood of 1993. 1996. Available online: https://www.nwrfc.noaa.gov/floods/papers/oh_2/great.htm (accessed on 17 February 2020).
- Carisi, F.; Schröter, K.; Domeneghetti, A.; Kreibich, H.; Castellarin, A. Development and assessment of uni- and multivariable flood loss models for Emilia-Romagna (Italy). Nat. Hazards Earth Syst. Sci. 2018, 18, 2057–2079. [Google Scholar] [CrossRef] [Green Version]
- Vorogushyn, S.; Bates, P.D.; de Bruijn, K.; Castellarin, A.; Kreibich, H.; Priest, S.; Schröter, K.; Bagli, S.; Blöschl, G.; Domeneghetti, A. Evolutionary leap in large-scale flood risk assessment needed. Wiley Interdiscip. Rev. Water 2018, 5, e1266. [Google Scholar] [CrossRef] [Green Version]
- Sanders, B.F.; Pau, J.C.; Jaffe, D.A. Passive and active control of diversions to an off-line reservoir for flood stage reduction. Adv. Water Resour. 2006, 29, 861–871. [Google Scholar] [CrossRef]
- Vorogushyn, S.; Lindenschmidt, K.-E.; Kreibich, H.; Apel, H.; Merz, B. Analysis of a detention basin impact on dike failure probabilities and flood risk for a channel-dike-floodplain system along the river Elbe, Germany. J. Hydrol. 2012, 436, 120–131. [Google Scholar] [CrossRef] [Green Version]
- Castellarin, A.; Domeneghetti, A.; Brath, A. Identifying robust large-scale flood risk mitigation strategies: A quasi-2D hydraulic model as a tool for the Po river. Phys. Chem. Earth Parts A/B/C 2011, 36, 299–308. [Google Scholar] [CrossRef]
- Viero, D.P.; D’Alpaos, A.; Carniello, L.; Defina, A. Mathematical modeling of flooding due to river bank failure. Adv. Water Resour. 2013, 59, 82–94. [Google Scholar] [CrossRef]
- Wu, W. Earthen Embankment Breaching. J. Hydraul. Eng. 2011, 137, 1549–1564. [Google Scholar] [CrossRef]
- Dazzi, S.; Vacondio, R.; Mignosa, P. Integration of a Levee Breach Erosion Model in a GPU-Accelerated 2D Shallow Water Equations Code. Water Resour. Res. 2019, 137, 1549. [Google Scholar] [CrossRef]
- Morris, M.W.; Kortenhaus, A.; Visser, P.J.; Hassan, M. Breaching Processes. 2009. Available online: http://www.floodsite.net/html/publications2.asp?by=documentDeliverables&byway=desc&documentType=1 (accessed on 19 March 2020).
- Zhong, Q.; Wu, W.; Chen, S.; Wang, M. Comparison of simplified physically based dam breach models. Nat. Hazards 2016, 84, 1385–1418. [Google Scholar] [CrossRef]
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Hunter, N.M.; Bates, P.D.; Horritt, M.S.; Wilson, M.D. Simple spatially-distributed models for predicting flood inundation: A review. Geomorphology 2007, 90, 208–225. [Google Scholar] [CrossRef]
- Chatterjee, C.; Förster, S.; Bronstert, A. Comparison of hydrodynamic models of different complexities to model floods with emergency storage areas. Hydrol. Process. 2008, 22, 4695–4709. [Google Scholar] [CrossRef]
- Kamrath, P.; Disse, M.; Hammer, M.; Köngeter, J. Assessment of Discharge through a Dike Breach and Simulation of Flood Wave Propagation. Nat. Hazards 2006, 38, 63–78. [Google Scholar] [CrossRef]
- Vorogushyn, S.; Merz, B.; Lindenschmidt, K.-E.; Apel, H. A new methodology for flood hazard assessment considering dike breaches. Water Resour. Res. 2010, 46, 125. [Google Scholar] [CrossRef] [Green Version]
- Rodríguez-Blanco, M.L.; Taboada-Castro, M.M.; Taboada-Castro, M.T. Factors controlling hydro-sedimentary response during runoff events in a rural catchment in the humid Spanish zone. Catena 2010, 82, 206–217. [Google Scholar] [CrossRef]
- Luke, A.; Kaplan, B.; Neal, J.; Lant, J.; Sanders, B.; Bates, P.; Alsdorf, D. Hydraulic modeling of the 2011 New Madrid Floodway activation: A case study on floodway activation controls. Nat. Hazards 2015, 77, 1863–1887. [Google Scholar] [CrossRef]
- Mazzoleni, M.; Bacchi, B.; Barontini, S.; Di Baldassarre, G.; Pilotti, M.; Ranzi, R. Flooding Hazard Mapping in Floodplain Areas Affected by Piping Breaches in the Po River, Italy. J. Hydrol. Eng. 2014, 19, 717–731. [Google Scholar] [CrossRef]
- Bates, P.; Horritt, M.S.; Fewtrell, T.J. A simple inertial formulation of the shallow water equations for efficient two-dimensional flood inundation modelling. J. Hydrol. 2010, 387, 33–45. [Google Scholar] [CrossRef]
- Neal, J.; Villanueva, I.; Wright, N.; Willis, T.; Fewtrell, T.; Bates, P. How much physical complexity is needed to model flood inundation? Hydrol. Process. 2012, 26, 2264–2282. [Google Scholar] [CrossRef] [Green Version]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- White, W.R.; Whitehead, E.; Forty, E.J. Extending the Scope of Standard Specifications for Open Channel Flow Gauging Structures. 2000. Available online: http://eprints.hrwallingford.co.uk/891/ (accessed on 13 December 2019).
- Wu, W.; Li, H. A simplified physically-based model for coastal dike and barrier breaching by overtopping flow and waves. Coast. Eng. 2017, 130, 1–13. [Google Scholar] [CrossRef]
- Brunner, G.W. HEC-RAS River Analysis System. Hydraulic Reference Manual. Version 5.0 2016. Available online: https://www.hec.usace.army.mil/software/hec-ras/documentation.aspx (accessed on 11 January 2019).
- Shustikova, I.; Domeneghetti, A.; Neal, J.; Bates, P.; Castellarin, A. Comparing 2D capabilities of HEC-RAS and LISFLOOD-FP on complex topography. Hydrol. Sci. J. 2019, 1–14. [Google Scholar] [CrossRef]
- D’Oria, M.; Mignosa, P.; Tanda, M.G. An inverse method to estimate the flow through a levee breach. Adv. Water Resour. 2015, 82, 166–175. [Google Scholar] [CrossRef]
- Orlandini, S.; Moretti, G.; Albertson, J.D. Evidence of an emerging levee failure mechanism causing disastrous floods in Italy. Water Resour. Res. 2015, 51, 7995–8011. [Google Scholar] [CrossRef] [Green Version]
- Vacondio, R.; Aureli, F.; Ferrari, A.; Mignosa, P.; Palù, A.D. Simulation of the January 2014 flood on the Secchia River using a fast and high-resolution 2D parallel shallow-water numerical scheme. Nat. Hazards 2016, 80, 103–125. [Google Scholar] [CrossRef]
- D’Alpaos, L.; Brath, A.; Fioravante, V.; Gottardi, G.; Mignosa, P.; Orlandini, S. Relazione Tecnico-Scientifica Sulle Cause del Collasso Dell’argine del Fiume Secchia Avvenuto il Giorno 19 Gennaio 2014 Presso la Frazione San Matteo 2014. Available online: http://ambiente.regione.emilia-romagna.it/geologia/notizie/notizie-2014/fiume-secchia (accessed on 18 January 2020).
- Horritt, M.S.; Bates, P.D.; Fewtrell, T.J.; Mason, D.C.; Wilson, M.D. Modelling the hydraulics of the Carlisle 2005 flood event. Proc. Inst. Civ. Eng. -Water Manag. 2010, 163, 273–281. [Google Scholar] [CrossRef]
- Viero, D.P.; Roder, G.; Matticchio, B.; Defina, A.; Tarolli, P. Floods, landscape modifications and population dynamics in anthropogenic coastal lowlands: The Polesine (northern Italy) case study. Sci. Total Environ. 2019, 651, 1435–1450. [Google Scholar] [CrossRef] [PubMed]
- Masoero, A.; Claps, P.; Asselman, N.E.M.; Mosselman, E.; Di Baldassarre, G. Reconstruction and analysis of the Po River inundation of 1951. Hydrol. Process. 2013, 27, 1341–1348. [Google Scholar] [CrossRef] [Green Version]
- SIMPO. Studio E Progettazione Di Massima Delle Sistemazioni Idrauliche Dell’asta Principale Del Po, Dalle Sorgenti Alla Foce, Finalizzata Alla Difesa Ed Alla Conservazione Del Suolo E Nella Utilizzazione Delle Risorse Idriche; Magistrato del Po: Parma, Italy, 1982. [Google Scholar]
- Contributors OSM. OpenStreetMap; Packt Publishing Ltd.: Birmingham, UK, 2012. [Google Scholar]
- Sofia, G.; Fontana, G.D.; Tarolli, P. High-resolution topography and anthropogenic feature extraction: Testing geomorphometric parameters in floodplains. Hydrol. Process. 2014, 28, 2046–2061. [Google Scholar] [CrossRef]
- Krüger, T. Algorithms for Detecting and Extracting Dikes from Digital Terrain Models, 10th ed.; Car, A., Griesebner, G., Strobl, J., Eds.; Wichmann: Berlin, Germany, 2010. [Google Scholar]
- Wing, O.E.; Bates, P.D.; Neal, J.C.; Sampson, C.C.; Smith, A.M.; Quinn, N.; Shustikova, I.; Domeneghetti, A.; Gilles, D.W.; Goska, R.; et al. A new automated method for improved flood defense representation in large-scale hydraulic models. Water Resour. Res. 2019. [Google Scholar] [CrossRef] [Green Version]
- Di Baldassare, G.; Castellarin, A.; Molnar, P.; Brath, A. Probability-weighted hazard maps for comparing different flood risk management strategies: A case study. Nat. Hazards 2009, 50, 479–496. [Google Scholar] [CrossRef]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shustikova, I.; Neal, J.C.; Domeneghetti, A.; Bates, P.D.; Vorogushyn, S.; Castellarin, A. Levee Breaching: A New Extension to the LISFLOOD-FP Model. Water 2020, 12, 942. https://doi.org/10.3390/w12040942
Shustikova I, Neal JC, Domeneghetti A, Bates PD, Vorogushyn S, Castellarin A. Levee Breaching: A New Extension to the LISFLOOD-FP Model. Water. 2020; 12(4):942. https://doi.org/10.3390/w12040942
Chicago/Turabian StyleShustikova, Iuliia, Jeffrey C. Neal, Alessio Domeneghetti, Paul D. Bates, Sergiy Vorogushyn, and Attilio Castellarin. 2020. "Levee Breaching: A New Extension to the LISFLOOD-FP Model" Water 12, no. 4: 942. https://doi.org/10.3390/w12040942




