Fluid Structure Interaction of 2D Objects through a Coupled KBC-Free Surface Model
Abstract
:1. Introduction
2. Numerical Model
2.1. Lattice Boltzmann Method
The Smagorinsky Subgrid Model
2.2. The KBC Model
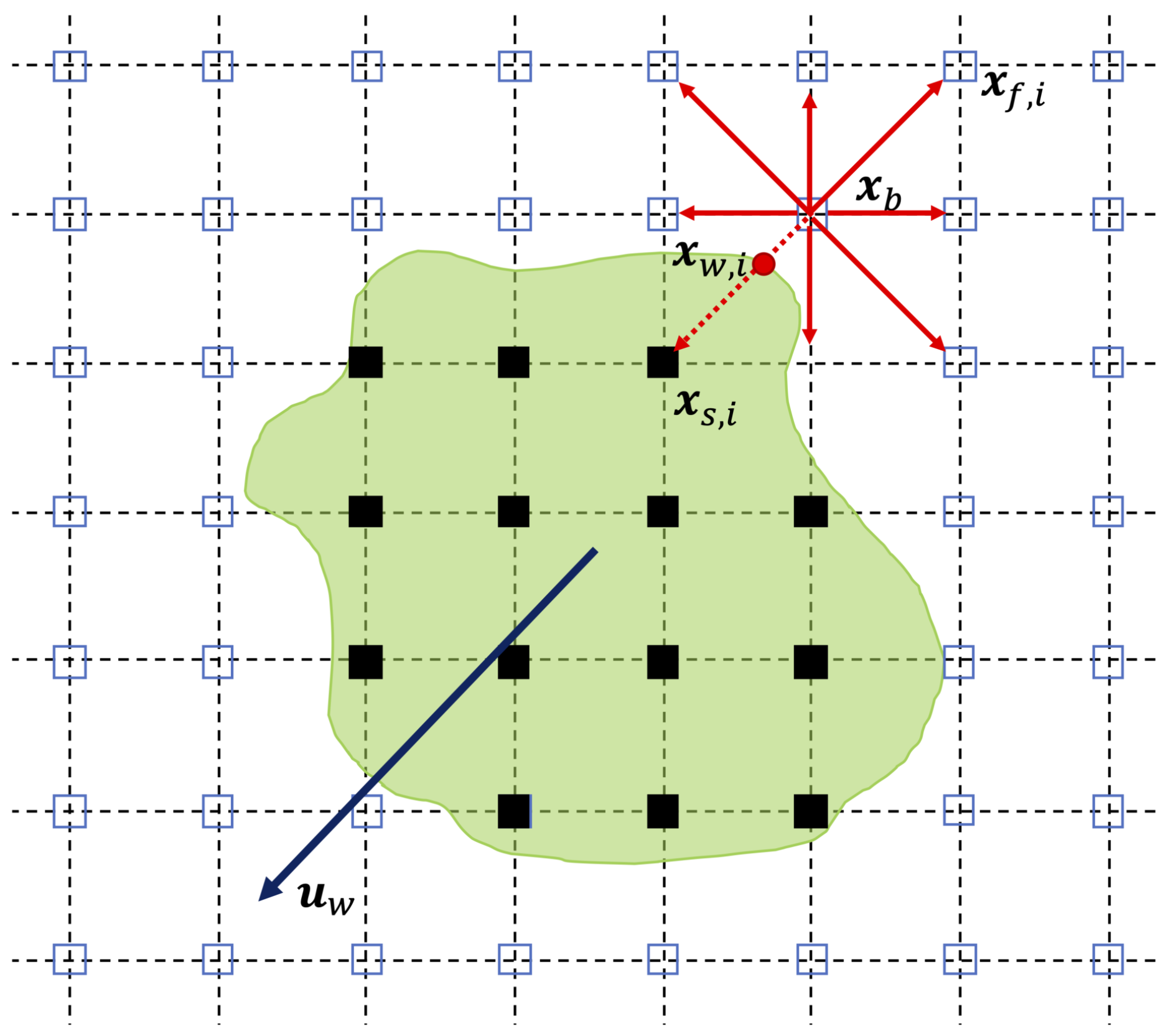
2.3. Fluid Structure Interaction and Moving Boundary Treatment
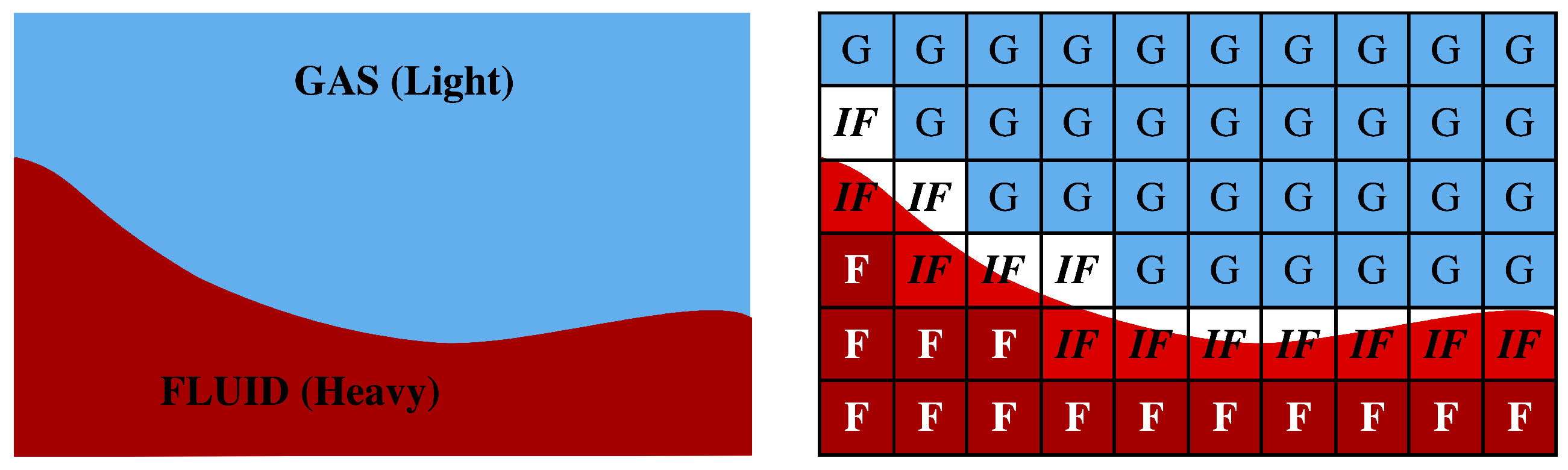
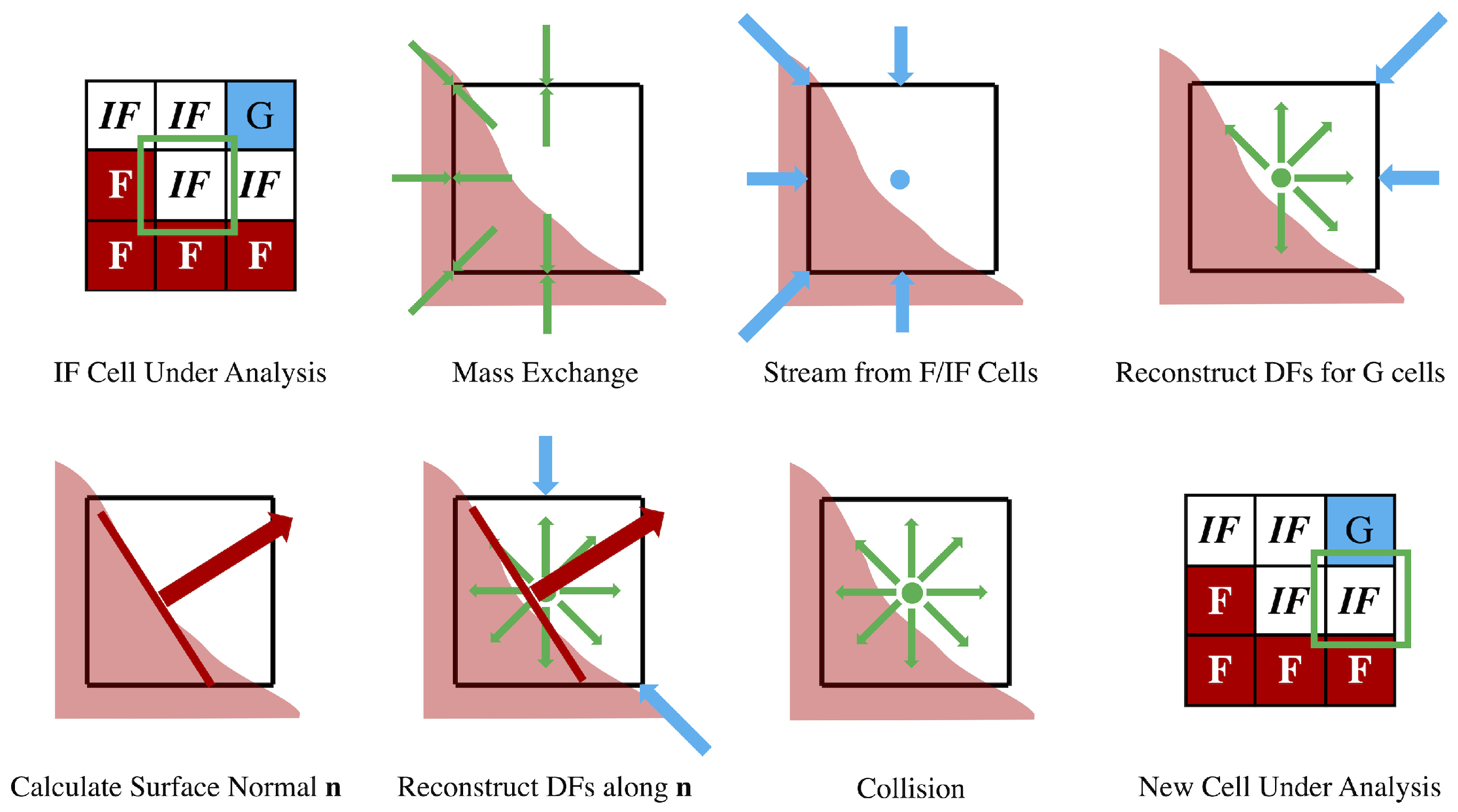
2.4. The Free-Surface Model
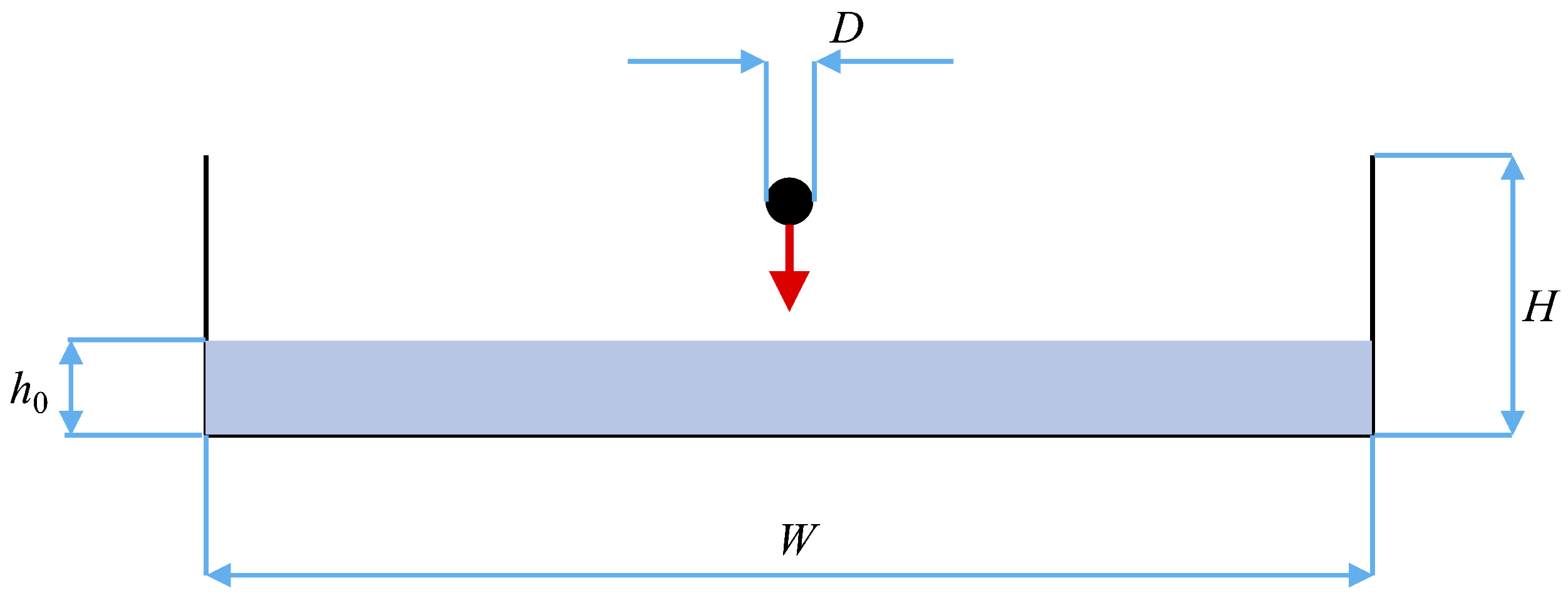
3. Model Validation
4. Results
5. Conclusions
Funding
Conflicts of Interest
References
- Faltinsen, O.M. Hydroelastic slamming. J. Mar. Sci. Technol. 2000, 5, 49–65. [Google Scholar] [CrossRef]
- Facci, A.L.; Panciroli, R.; Ubertini, S.; Porfiri, M. Assessment of PIV-based analysis of water entry problems through synthetic numerical datasets. J. Fluids Struct. 2015, 55, 484–500. [Google Scholar] [CrossRef] [Green Version]
- Panciroli, R.; Biscarini, C.; Falcucci, G.; Jannelli, E.; Ubertini, S. Live monitoring of the distributed strain field in impulsive events through fiber Bragg gratings. J. Fluids Struct. 2016, 61, 60–75. [Google Scholar] [CrossRef]
- Erturk, A.; Delporte, G. Underwater thrust and power generation using flexible piezoelectric composites: An experimental investigation toward self-powered swimmer-sensor platforms. Smart Mater. Struct. 2011, 20, 125013. [Google Scholar] [CrossRef]
- Batra, R.; Porfiri, M.; Spinello, D. Review of modeling electrostatically actuated microelectromechanical systems. Smart Mater. Struct. 2007, 16, R23. [Google Scholar] [CrossRef]
- De Tullio, M.; Cristallo, A.; Balaras, E.; Verzicco, R. Direct numerical simulation of the pulsatile flow through an aortic bileaflet mechanical heart valve. J. Fluid Mech. 2009, 622, 259–290. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Currao, G.M.; Han, F.; Neely, A.J.; Young, J.; Tian, F.B. An immersed boundary method for fluid–structure interaction with compressible multiphase flows. J. Comput. Phys. 2017, 346, 131–151. [Google Scholar] [CrossRef] [Green Version]
- Calderer, A.; Guo, X.; Shen, L.; Sotiropoulos, F. Fluid—Structure interaction simulation of floating structures interacting with complex, large-scale ocean waves and atmospheric turbulence with application to floating offshore wind turbines. J. Comput. Phys. 2018, 355, 144–175. [Google Scholar] [CrossRef]
- Ren, Z.; Wang, Z.; Stern, F.; Judge, C.; Ikeda-Gilbert, C. Vertical Water Entry of a Flexible Wedge into Calm Water: A Fluid-Structure Interaction Experiment. J. Ship Res. 2019, 63, 41–55. [Google Scholar] [CrossRef]
- Facci, A.L.; Falcucci, G.; Agresta, A.; Biscarini, C.; Jannelli, E.; Ubertini, S. Fluid Structure Interaction of Buoyant Bodies with Free Surface Flows: Computational Modelling and Experimental Validation. Water 2019, 11, 1048. [Google Scholar] [CrossRef] [Green Version]
- Panciroli, R.; Abrate, S.; Minak, G.; Zucchelli, A. Hydroelasticity in water-entry problems: Comparison between experimental and SPH results. Compos. Struct. 2012, 94, 532–539. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H.; Falahaty, H.; Shimizu, Y. An enhanced ISPH–SPH coupled method for simulation of incompressible fluid—Elastic structure interactions. Comput. Phys. Commun. 2018, 232, 139–164. [Google Scholar] [CrossRef]
- Owen, D.; Leonardi, C.; Feng, Y. An efficient framework for fluid–structure interaction using the lattice Boltzmann method and immersed moving boundaries. Int. J. Numer. Methods Eng. 2011, 87, 66–95. [Google Scholar] [CrossRef]
- De Rosis, A. Ground-induced lift enhancement in a tandem of symmetric flapping wings: Lattice Boltzmann-immersed boundary simulations. Comput. Struct. 2015, 153, 230–238. [Google Scholar] [CrossRef]
- Aureli, M.; Prince, C.; Porfiri, M.; Peterson, S.D. Energy harvesting from base excitation of ionic polymer metal composites in fluid environments. Smart Mater. Struct. 2009, 19, 015003. [Google Scholar] [CrossRef]
- Panciroli, R. Hydroelastic impacts of deformable wedges. In Dynamic Failure of Composite and Sandwich Structures; Springer: Dordrecht, The Netherlands, 2013; pp. 1–45. [Google Scholar]
- Panciroli, R.; Porfiri, M. Analysis of hydroelastic slamming through particle image velocimetry. J. Sound Vib. 2015, 347, 63–78. [Google Scholar] [CrossRef]
- Panciroli, R.; Ubertini, S.; Minak, G.; Jannelli, E. Experiments on the Dynamics of Flexible Cylindrical Shells Impacting on a Water Surface. Exp. Mech. 2015, 55, 1537–1550. [Google Scholar] [CrossRef]
- Panahi, R. Simulation of water-entry and water-exit problems using a moving mesh algorithm. J. Theor. Appl. Mech. 2012, 42, 79–92. [Google Scholar] [CrossRef] [Green Version]
- Cheon, J.S.; Jang, B.S.; Yim, K.H.; Lee, H.D.; Koo, B.Y.; Ju, H. A study on slamming pressure on a flat stiffened plate considering fluid–structure interaction. J. Mar. Sci. Technol. 2016, 21, 309–324. [Google Scholar] [CrossRef]
- Zhao, X.; Gao, Y.; Cao, F.; Wang, X. Numerical modeling of wave interactions with coastal structures by a constrained interpolation profile/immersed boundary method. Int. J. Numer. Methods Fluids 2016, 81, 265–283. [Google Scholar] [CrossRef]
- Falcucci, G.; Aureli, M.; Ubertini, S.; Porfiri, M. Transverse harmonic oscillations of laminae in viscous fluids: A lattice Boltzmann study. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 2456–2466. [Google Scholar] [CrossRef] [Green Version]
- De Rosis, A.; Falcucci, G.; Ubertini, S.; Ubertini, F.; Succi, S. Lattice Boltzmann analysis of fluid-structure interaction with moving boundaries. Commun. Comput. Phys. 2013, 13, 823–834. [Google Scholar] [CrossRef]
- De Rosis, A.; Falcucci, G.; Porfiri, M.; Ubertini, F.; Ubertini, S. Hydroelastic analysis of hull slamming coupling lattice Boltzmann and finite element methods. Comput. Struct. 2014, 138, 24–35. [Google Scholar] [CrossRef]
- De Rosis, A.; Falcucci, G.; Ubertini, S.; Ubertini, F. Aeroelastic study of flexible flapping wings by a coupled lattice Boltzmann-finite element approach with immersed boundary method. J. Fluids Struct. 2014, 49, 516–533. [Google Scholar] [CrossRef]
- Zarghami, A.; Falcucci, G.; Jannelli, E.; Succi, S.; Porfiri, M.; Ubertini, S. Lattice Boltzmann modeling of water entry problems. Int. J. Mod. Phys. C 2014, 25, 1441012. [Google Scholar] [CrossRef]
- Dorschner, B.; Chikatamarla, S.S.; Bösch, F.; Karlin, I.V. Grad’s approximation for moving and stationary walls in entropic lattice Boltzmann simulations. J. Comput. Phys. 2015, 295, 340–354. [Google Scholar] [CrossRef]
- Dorschner, B.; Chikatamarla, S.S.; Karlin, I.V. Entropic multirelaxation-time lattice Boltzmann method for moving and deforming geometries in three dimensions. Phys. Rev. E 2017, 95, 063306. [Google Scholar] [CrossRef] [Green Version]
- Di Ilio, G.; Dorschner, B.; Bella, G.; Succi, S.; Karlin, I.V. Simulation of turbulent flows with the entropic multirelaxation time lattice Boltzmann method on body-fitted meshes. J. Fluid Mech. 2018, 849, 35–56. [Google Scholar] [CrossRef]
- Karlin, I.V.; Bösch, F.; Chikatamarla, S. Gibbs’ principle for the lattice-kinetic theory of fluid dynamics. Phys. Rev. E 2014, 90, 031302. [Google Scholar] [CrossRef] [PubMed]
- Thuerey, N. Physically based Animation of Free Surface Flows with the Lattice Boltzmann Method. Ph.D. Thesis, University of Erlangen, Erlangen, Germany, 2007. [Google Scholar]
- Miao, G. Hydrodynamic Forces and Dynamic Responses of Circular Cylinders in Wave Zones. Ph.D. Thesis, Division of Marine Hydrodynamics, The Norwegian Institute of Technology, University of Trondheim, Trondheim, Norway, 1988. [Google Scholar]
- Zhu, X.; Faltinsen, O.M.; Hu, C. Water Entry and Exit of a Horizontal Circular Cylinder. J. Offshore Mech. Arct. Eng. 2006, 129, 253–264. [Google Scholar] [CrossRef]
- Sagaut, P. Toward advanced subgrid models for Lattice-Boltzmann-based Large-eddy simulation: Theoretical formulations. Comput. Math. Appl. 2010, 59, 2194–2199. [Google Scholar] [CrossRef] [Green Version]
- Guo, M.; Tang, X.; Su, Y.; Li, X.; Wang, F. Applications of Three-Dimensional LBM-LES Combined Model for Pump Intakes. Commun. Comput. Phys. 2018, 24, 104–122. [Google Scholar] [CrossRef] [Green Version]
- Benzi, R.; Succi, S.; Vergassola, M. The Lattice Boltzmann Equation: Theory and Applications. Phys. Rep. 1992, 222, 145–197. [Google Scholar] [CrossRef]
- Karlin, I.; Ferrante, A.; Öttinger, H. Perfect entropy functions of the Lattice Boltzmann method. Europhys. Lett. 1999, 47, 182–188. [Google Scholar] [CrossRef] [Green Version]
- Succi, S. The Lattice Boltzmann Equation: For Complex States of Flowing Matter; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Xie, C.; Zhang, J.; Bertola, V.; Wang, M. Lattice Boltzmann modeling for multiphase viscoplastic fluid flow. J. Non-Newton. Fluid Mech. 2016, 234, 118–128. [Google Scholar] [CrossRef]
- Di Ilio, G.; Chiappini, D.; Ubertini, S.; Bella, G.; Succi, S. Fluid flow around NACA 0012 airfoil at low-Reynolds numbers with hybrid lattice Boltzmann method. Comput. Fluids 2018, 166, 200–208. [Google Scholar] [CrossRef]
- Di Ilio, G.; Chiappini, D.; Ubertini, S.; Bella, G.; Succi, S. A moving-grid approach for fluid–structure interaction problems with hybrid lattice Boltzmann method. Comput. Phys. Commun. 2019, 234, 137–145. [Google Scholar] [CrossRef]
- Aidun, C.K.; Clausen, J.R. Lattice-Boltzmann method for complex flows. Ann. Rev. Fluid Mech. 2010, 42, 439–472. [Google Scholar] [CrossRef]
- Sbragaglia, M.; Benzi, R.; Biferale, L.; Succi, S.; Sugiyama, K.; Toschi, F. Generalized lattice Boltzmann method with multirange pseudopotential. Phys. Rev. E 2007, 75, 026702. [Google Scholar] [CrossRef] [Green Version]
- Fernandino, M.; Beronov, K.; Ytrehus, T. Large eddy simulation of turbulent open duct flow using a lattice Boltzmann approach. Math. Comput. Simul. 2009, 79, 1520–1526. [Google Scholar] [CrossRef]
- Bösch, F.; Chikatamarla, S.S.; Karlin, I.V. Entropic multirelaxation lattice Boltzmann models for turbulent flows. Phys. Rev. E 2015, 92, 043309. [Google Scholar] [CrossRef] [PubMed]
- Dorschner, B.; Frapolli, N.; Chikatamarla, S.S.; Karlin, I.V. Grid refinement for entropic lattice Boltzmann models. Phys. Rev. E 2016, 94, 053311. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dorschner, B.; Bösch, F.; Chikatamarla, S.S.; Boulouchos, K.; Karlin, I.V. Entropic multi-relaxation time lattice Boltzmann model for complex flows. J. Fluid Mech. 2016, 801, 623–651. [Google Scholar] [CrossRef]
- Kupershtokh, A.; Medvedev, D.; Karpov, D. On equations of state in a lattice Boltzmann method. Comput. Math. Appl. 2009, 58, 965–974. [Google Scholar] [CrossRef] [Green Version]
- Chikatamarla, S.S.; Ansumali, S.; Karlin, I.V. Grad’s approximation for missing data in lattice Boltzmann simulations. EPL Europhys. Lett. 2006, 74, 215. [Google Scholar] [CrossRef] [Green Version]
- Ginzburg, I.; Steiner, K. A free-surface lattice Boltzmann method for modelling the filling of expanding cavities by Bingham fluids. Philos. Trans. R. Soc. Lond. A 2002, 360, 453–466. [Google Scholar] [CrossRef]
- Thürey, N.; Rüde, U. Stable free surface flows with the lattice Boltzmann method on adaptively coarsened grids. Comput. Vis. Sci. 2009, 12, 247–263. [Google Scholar] [CrossRef]
- Körner, C.; Thies, M.; Hofmann, T.; Thürey, N.; Rüde, U. Lattice Boltzmann model for free surface flow for modeling foaming. J. Stat. Phys. 2005, 121, 179–196. [Google Scholar] [CrossRef]
- Janssen, C.; Krafczyk, M. A lattice Boltzmann approach for free-surface-flow simulations on non-uniform block-structured grids. Comput. Math. Appl. 2010, 59, 2215–2235. [Google Scholar] [CrossRef] [Green Version]
- Anderl, D.; Bogner, S.; Rauh, C.; Rüde, U.; Delgado, A. Free surface lattice Boltzmann with enhanced bubble model. Comput. Math. Appl. 2014, 67, 331–339. [Google Scholar] [CrossRef]
- Thürey, N.; Körner, C.; Rüde, U. Interactive Free Surface Fluids with the Lattice Boltzmann Method; Technical Report05-4; University of Erlangen-Nuremberg: Erlangen, Germany, 2005. [Google Scholar]






| 0.125 | 28.0 | 2.5 | 1.0 |
| Case | Re | ||
|---|---|---|---|
| 1 | 0.5124 | 64050 | 0.4628 |
| 2 | 0.6390 | 79875 | 0.5772 |
| 3 | 0.7600 | 95000 | 0.6865 |
| Simlation No. | ||||
|---|---|---|---|---|
| 1 | 50 | 11,200 × 1000 | 0.00440 | 366 |
| 2 | 50 | 11,200 × 1000 | 0.00044 | 3660 |
| 3 | 100 | 22,400 × 2000 | 0.00880 | 366 |
| 4 | 100 | 22,400 × 2000 | 0.00088 | 3660 |
| 5 | 150 | 33,600 × 3000 | 0.01320 | 366 |
| 6 | 150 | 33,600 × 3000 | 0.00132 | 3660 |
| 7 | 200 | 40,000 × 4000 | 0.01760 | 366 |
| 8 | 200 | 40,000 × 4000 | 0.00176 | 3660 |
| Simulation No. | |
|---|---|
| 1 | 0.25 |
| 2 | 0.50 |
| 3 | 1.00 |
| 4 | 2.00 |
| 5 | 4.00 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiappini, D. Fluid Structure Interaction of 2D Objects through a Coupled KBC-Free Surface Model. Water 2020, 12, 1212. https://doi.org/10.3390/w12041212
Chiappini D. Fluid Structure Interaction of 2D Objects through a Coupled KBC-Free Surface Model. Water. 2020; 12(4):1212. https://doi.org/10.3390/w12041212
Chicago/Turabian StyleChiappini, Daniele. 2020. "Fluid Structure Interaction of 2D Objects through a Coupled KBC-Free Surface Model" Water 12, no. 4: 1212. https://doi.org/10.3390/w12041212
APA StyleChiappini, D. (2020). Fluid Structure Interaction of 2D Objects through a Coupled KBC-Free Surface Model. Water, 12(4), 1212. https://doi.org/10.3390/w12041212





