Energy Dissipation and Hydraulics of Flow over Trapezoidal–Triangular Labyrinth Weirs
Abstract
1. Introduction
2. Materials and Methods
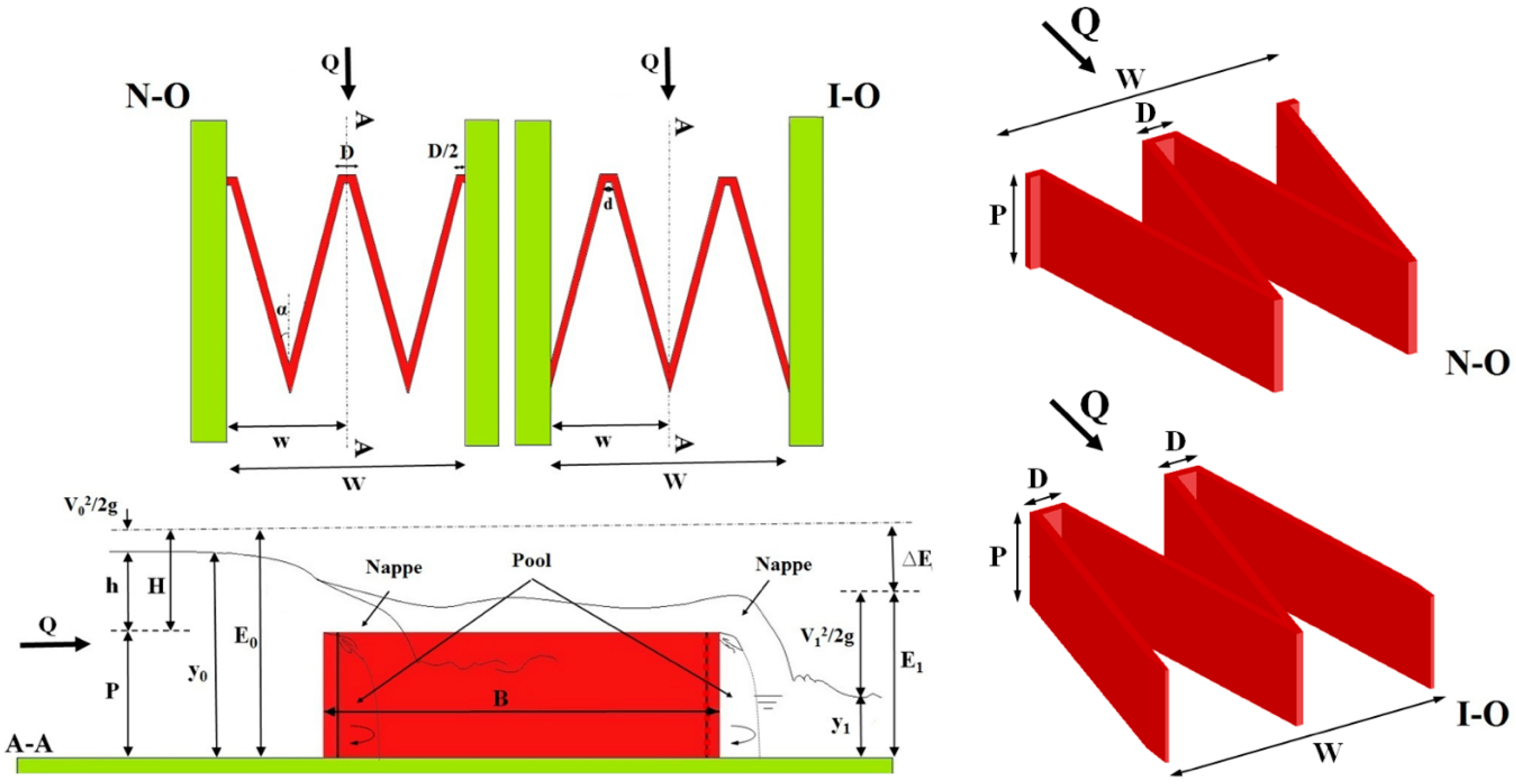
2.1. Effective Parameters in the Discharge Coefficient
2.2. Effective Parameters in the Energy Dissipation
2.3. Numerical Model
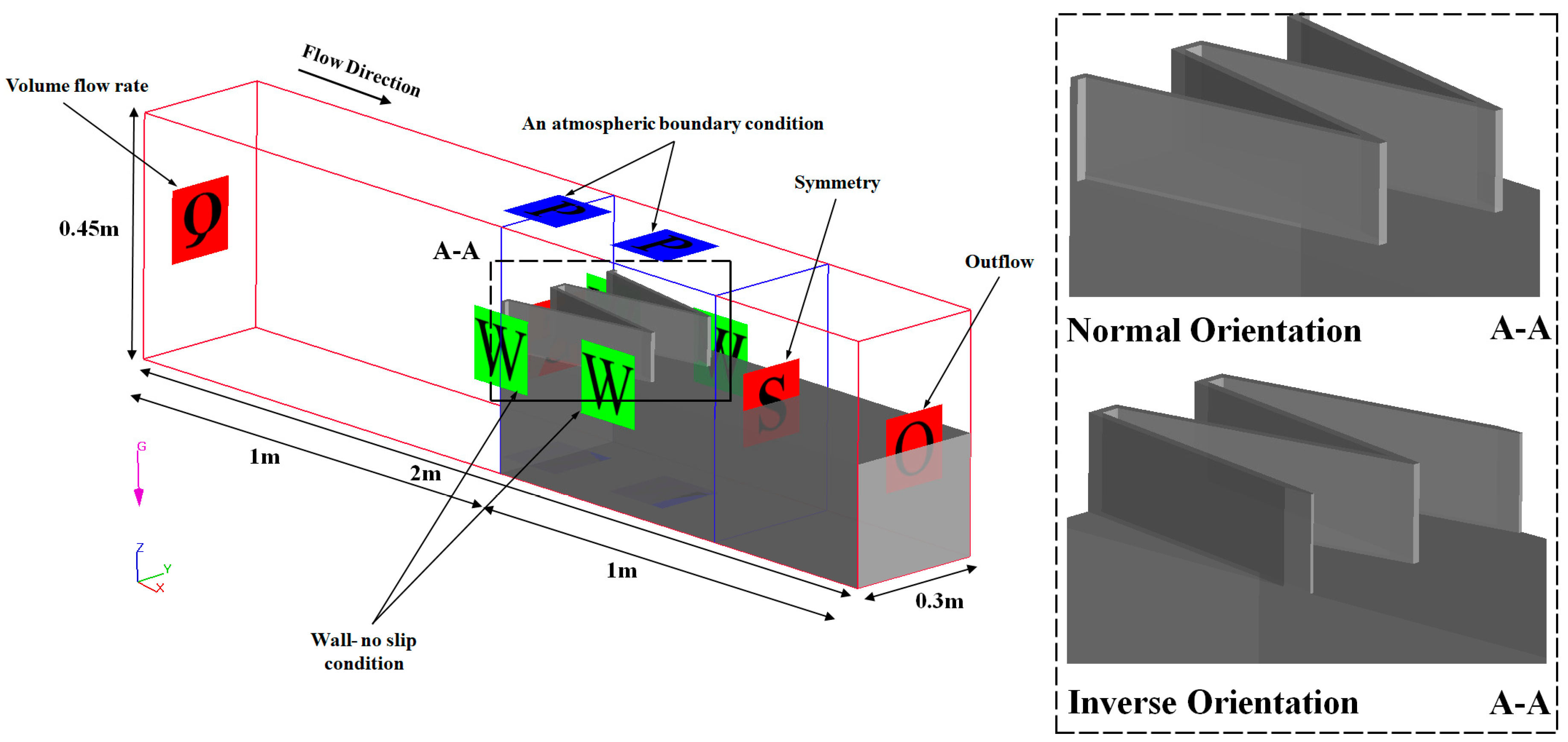
3. Case Study
Computational Mesh and Boundary Conditions
4. Results and Discussions
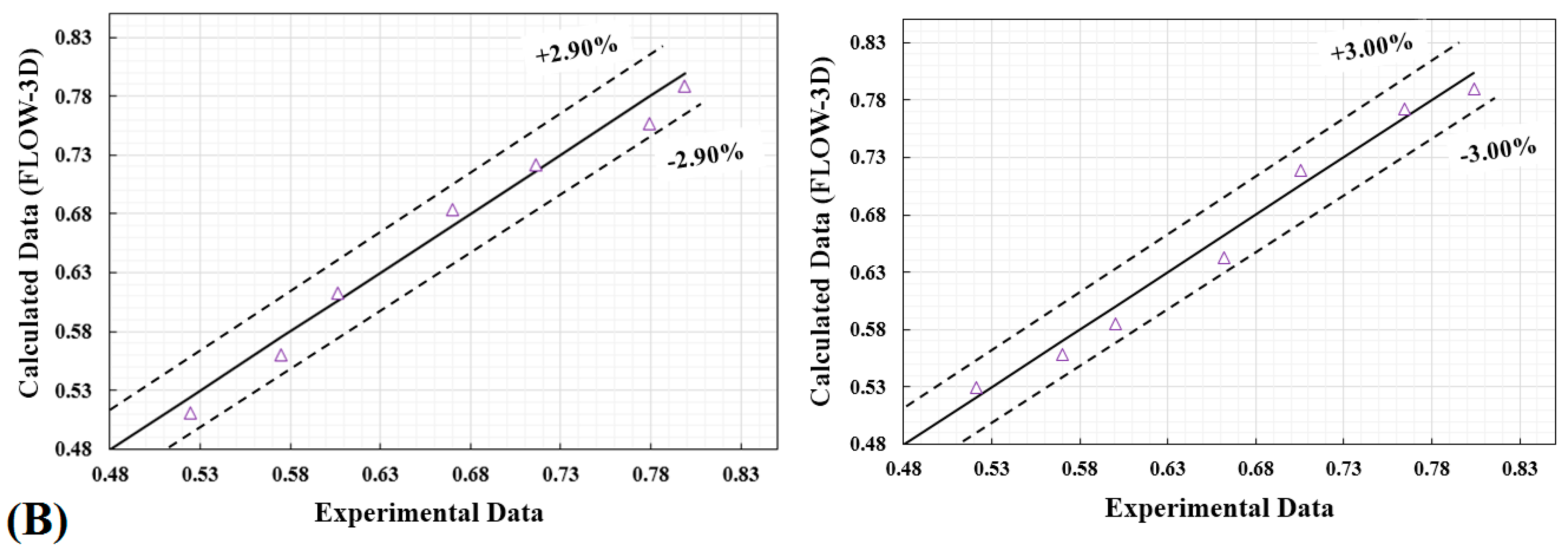
4.1. The Validity of the FLOW-3D Model
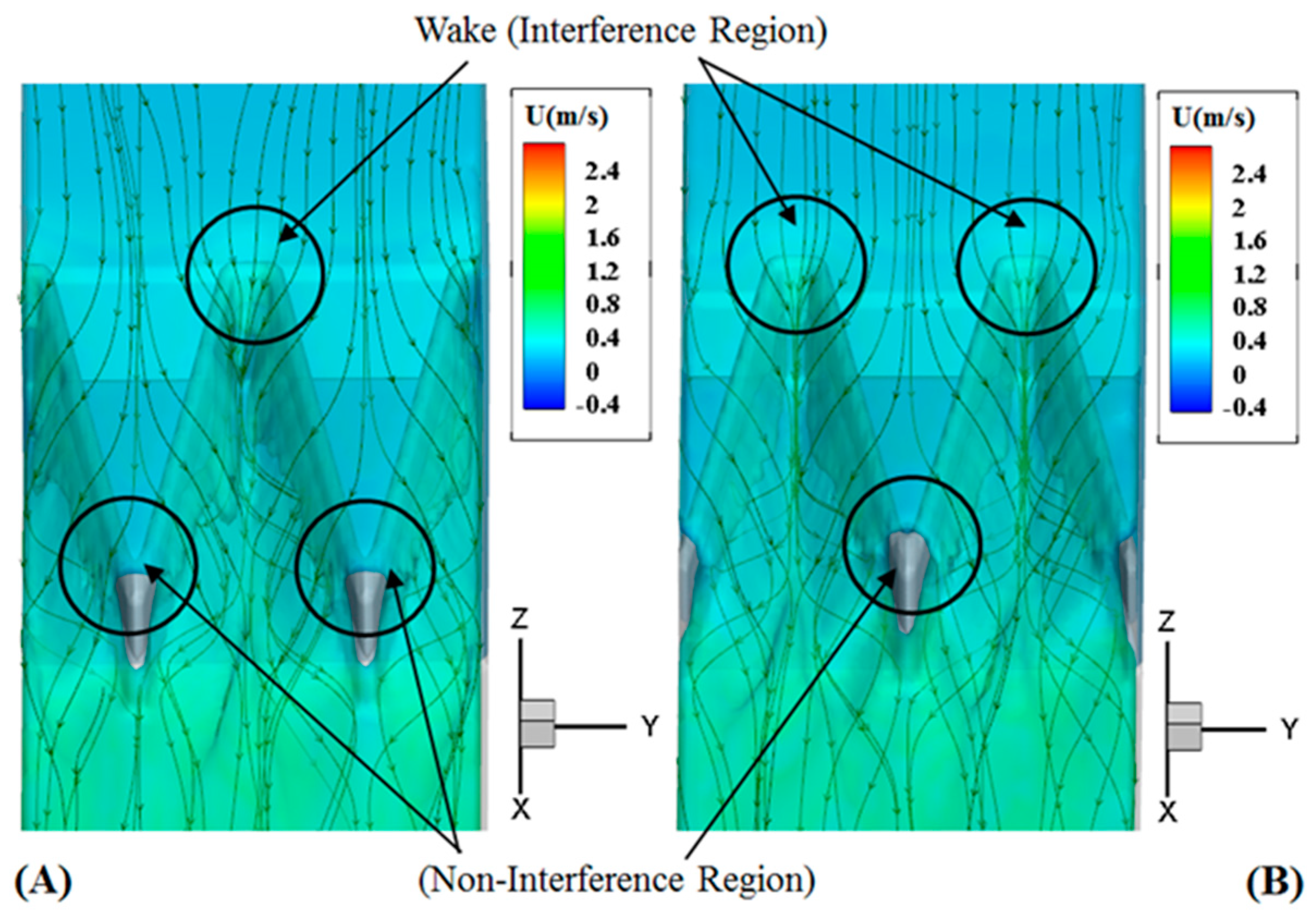
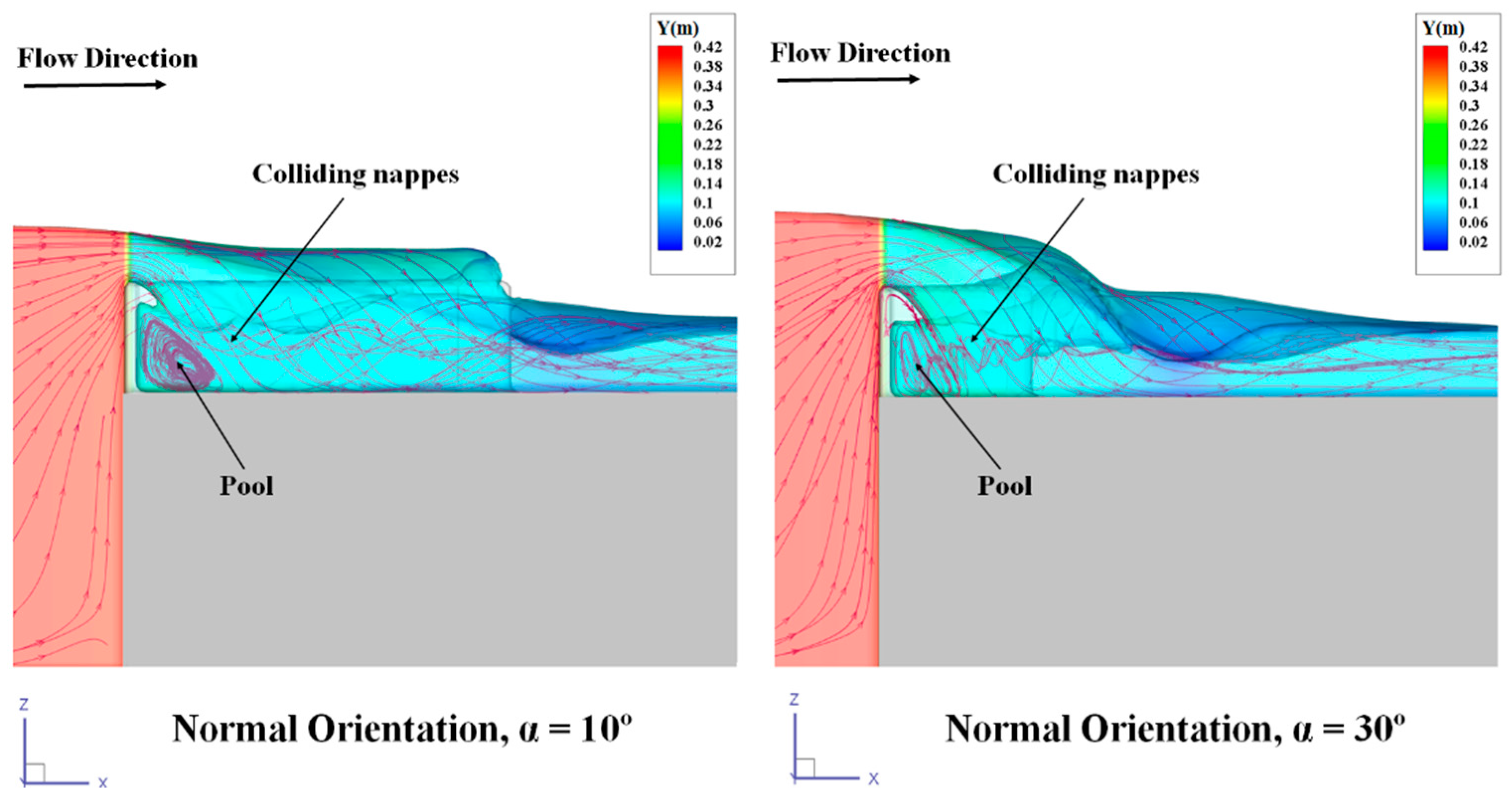
4.2. Hydraulics of Free Flow
4.3. Energy Charachterization and Flow Regime
5. Conclusions
- It can be concluded that the FLOW-3D software can accurately predict characteristics of flow over TTLW. In comparisons between the calculated and measured free surface profiles, appropriate mesh with 2,118,270 elements by relative error and RMSE of 3.05%, 0.43 cm and maximum aspect ratio 1.07, was selected for calculations. The maximum and minimum value MARE errors are 3% and 0.77%.
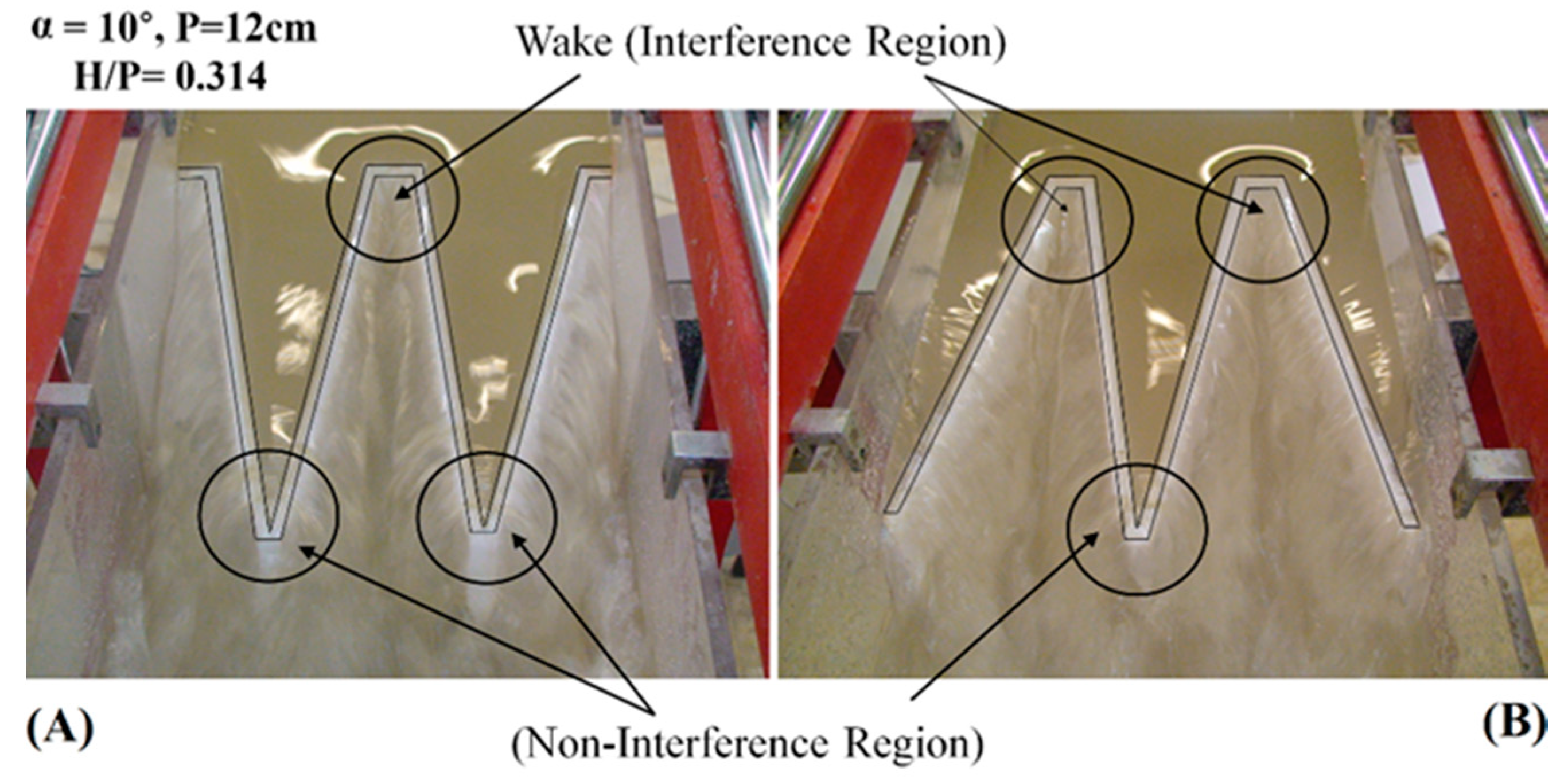
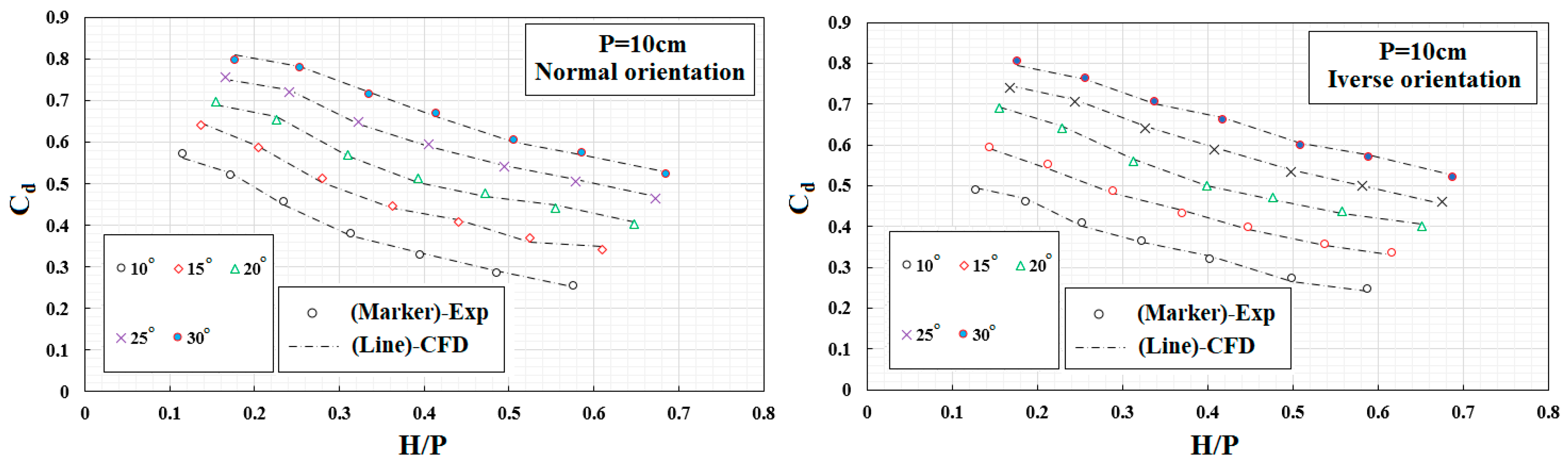
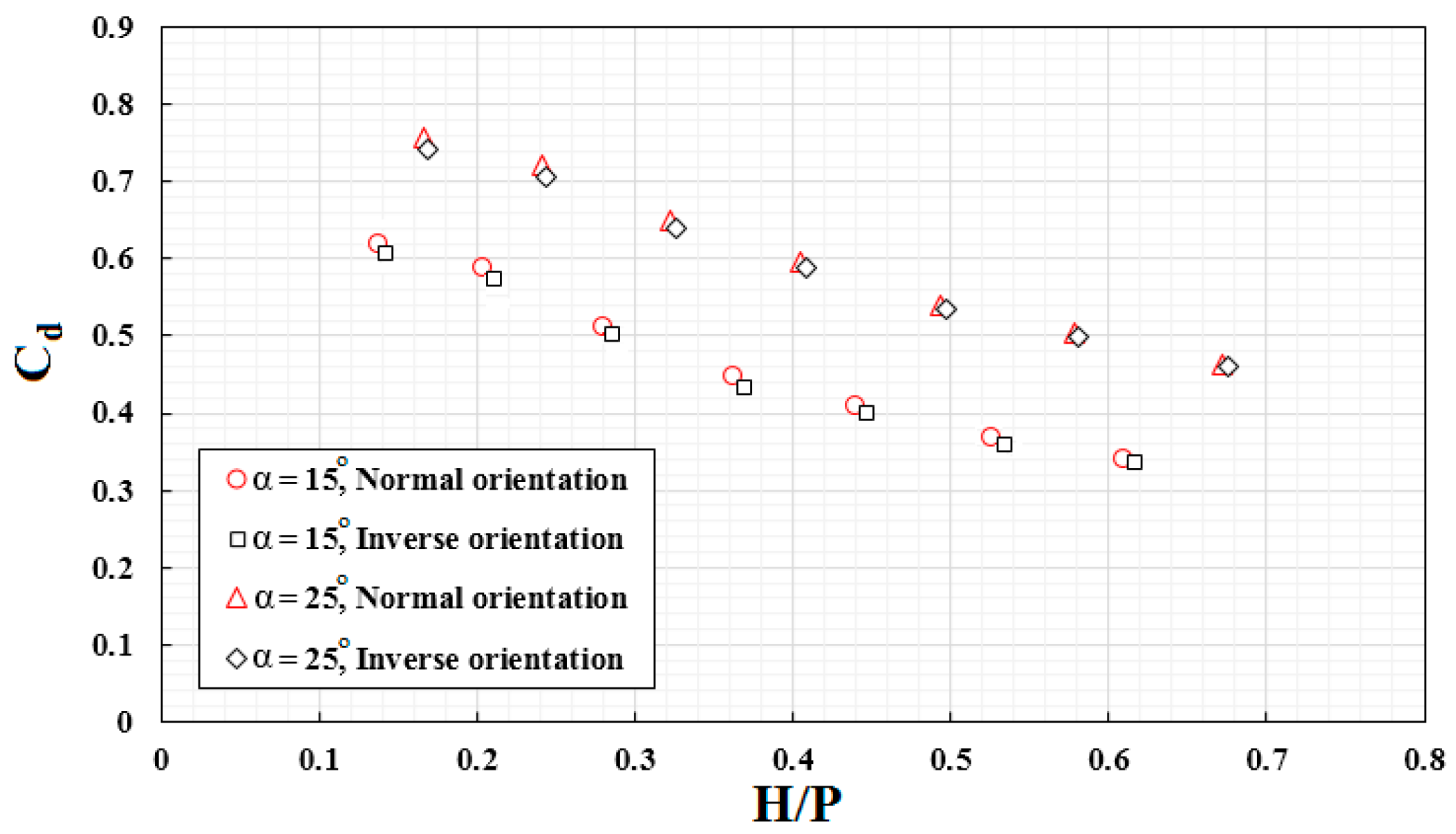
- In the high value of H/P due to the collision of the falling jets, the discharge coefficient decreases by decreasing the sidewall. While for the low of H/P, the collision of jets is not so severe, hence in high values for Cd. Also, by increasing the sidewall angle, the decrease of Cd with H/P increases. Increasing the weir heights decreases the discharge coefficient due to nappe interactions occurring when two or more nappes collide, and the nappe interaction increases as discharge increases.
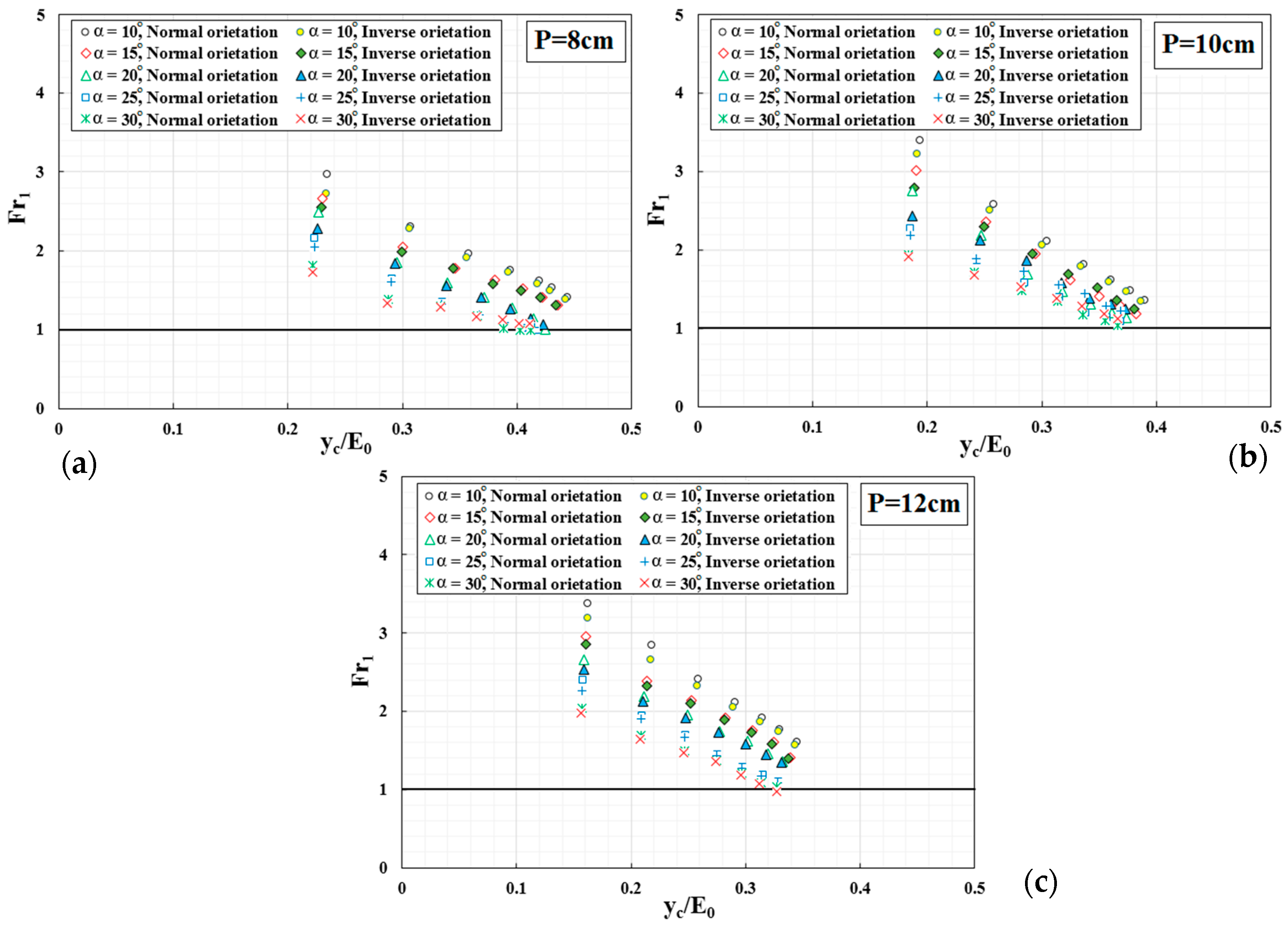
- In low discharge, hydraulics of flow over the TTLW has free flow conditions and for high discharge it has submerged conditions. In all models, the downstream Froude number is larger than one with an increase of relative critical depth yc/E0 at different weir heights.
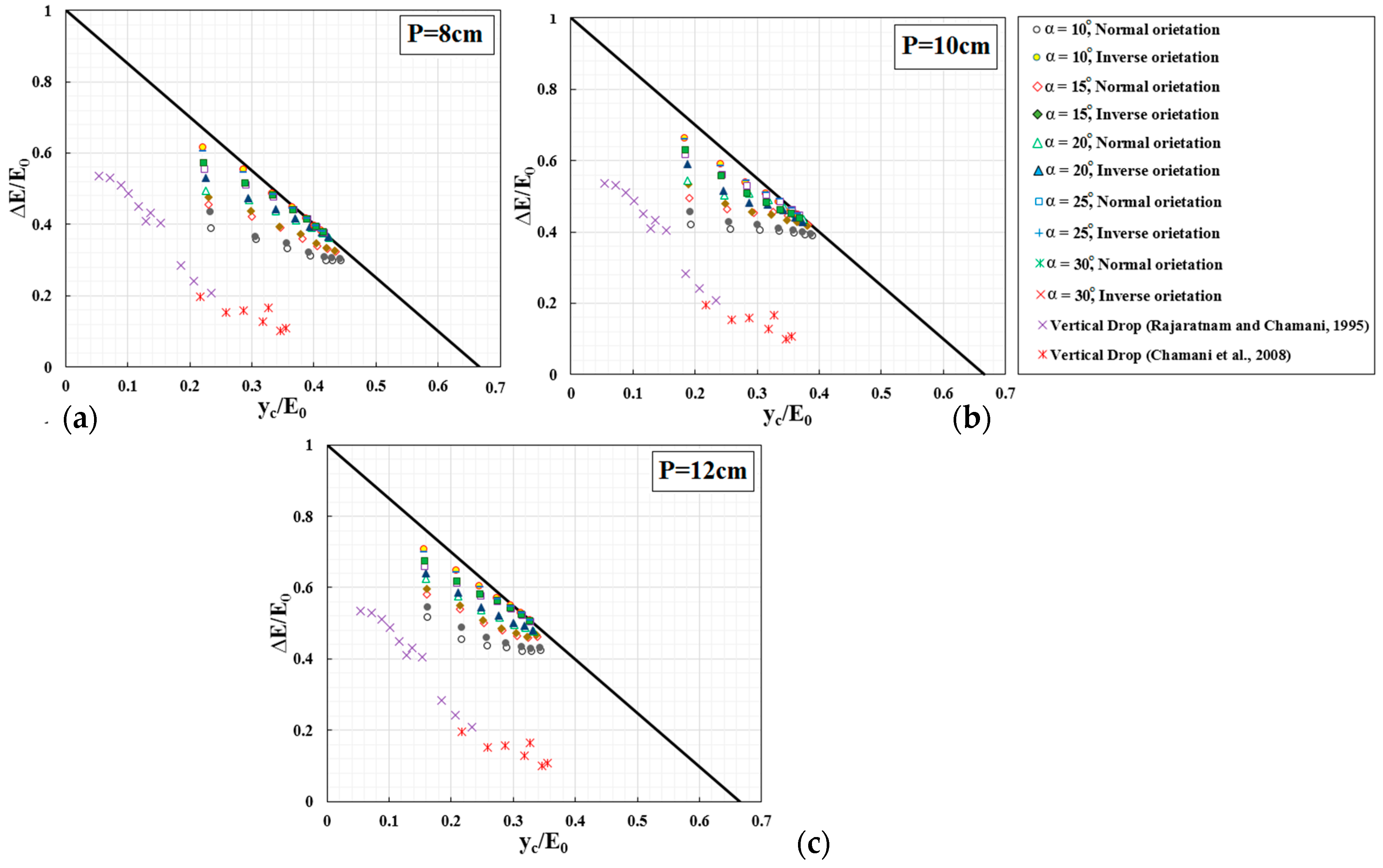
- TTLW approximately dissipates the maximum amount of energy and increases the sidewall angle, weir height, and relative critical depth yc/E0, it reduces more energy dissipation. Circulating flows behind the nappes enhances the turbulent mixing and dissipates a large portion of energy in the upstream apexes of TTLW. It must be noted that a weak hydraulic jump downstream of TTLW contributes to the more energy dissipation.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Falvey, H. Hydraulic Design of Labyrinth Weirs; American Society of Civil Engineers: Reston, VA, USA, 2003. [Google Scholar]
- Mayer, P.G. Bartletts Ferry Project, Labyrinth Weir Model Studies; Project No. E-20-610; Georgia Institute of Technology: Atlanta, GA, USA, 1980. [Google Scholar]
- Houston, K.L. Hydraulic Model Study of the UTE Dam Labyrinth Spillway; Report No. GR-82-7; U.S. Bureau of Reclamations: Denver, CO, USA, 1982.
- Lux, F.; Hinchliff, D.L. Design and construction of labyrinth spillways. In Proceedings of the 15th Congress ICOLD, Lausanne, Switzerland, 24–28 June 1985; Volume 4, pp. 249–274. [Google Scholar]
- Lux, F. Design and application of labyrinth weirs. In Design of Hydraulic Structures 89; Alberson, M.L., Kia, R.A., Eds.; Balkema/Rotterdam/Brookfield: Toronto, ON, Canada, 1989. [Google Scholar]
- Tullis, B.P.; Amanian, N.; Woldron, D. Design of labyrinth spillways. J. Hydraul. Eng. 1995, 121, 247–255. [Google Scholar] [CrossRef]
- Talor, G. The Performance of Labyrinth Weirs. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 1968. [Google Scholar]
- Hay, N.; Taylor, G. Performance and design of labyrinth weirs, American Society of Civil Engineering. J. Hydraul. Eng. 1970, 96, 2337–2357. [Google Scholar]
- Kumar, S.; Ahmad, Z.; Mansoor, T. A new approach to improve the discharging capacity of sharp crested triangular plan form weirs. J. Flow Meas. Instrum. 2011, 22, 175–180. [Google Scholar] [CrossRef]
- Crookston, B.M.; Tullis, B.P. Arced Labyrinth Weirs. J. Hydraul. Eng. 2012, 138, 555–562. [Google Scholar] [CrossRef]
- Carollo, G.F.; Ferro, V.; Pampalone, V. Experimental Investigation of the Outflow Process over a Triangular Labyrinth-Weir. ASCE J. Irrig. Drain. Eng. 2012, 138, 73–79. [Google Scholar] [CrossRef]
- Bilhan, O.; Emiroglu, M.E.; Miller, C.J. Experimental Investigation of Discharge Capacity of Labyrinth Weirs with and without Nappe Breakers. World J. Mech. 2016, 6, 207–221. [Google Scholar] [CrossRef][Green Version]
- Abbaspuor, B.; Haghiabi, A.H.; Maleki, A.; Poodeh, H.T. Experimental and numerical evaluation of discharge capacity of sharp-crested triangular plan form weirs. Int. J. Eng. Syst. Model. Simul. 2017, 9, 113–119. [Google Scholar] [CrossRef]
- Azimi, A.H.; Hakim, S.S. Hydraulics of flow over rectangular labyrinth weirs. Irrig. Sci. 2019, 37, 183–193. [Google Scholar] [CrossRef]
- Savage, B.M.; Crookston, B.M.; Paxson, G.S. Physical and numerical modeling of large headwater ratios for a 15 labyrinth spillway. J. Hydraul. Eng. 2016, 142, 04016046. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Joudi, A.R.; Ghahramanzadeh, A.; Ghaderi, A. Investigation of flow pressure distribution over a stepped spillway. Adv. Appl. Fluid Mech. 2016, 19, 811–822. [Google Scholar] [CrossRef]
- Ghaderi, A.; Daneshfaraz, R.; Dasineh, M. Evaluation and prediction of the scour depth of bridge foundations with HEC-RAS numerical model and empirical equations (Case Study: Bridge of Simineh Rood Miandoab, Iran). Eng. J. 2019, 23, 279–295. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Minaei, O.; Abraham, J.; Dadashi, S.; Ghaderi, A. 3-D Numerical simulation of water flow over a broad-crested weir with openings. ISH J. Hydraul. Eng. 2019, 25, 1–9. [Google Scholar] [CrossRef]
- Biscarini, C.; Di Francesco, S.; Ridolfi, E.; Manciola, P. On the Simulation of Floods in a Narrow Bending Valley: The Malpasset Dam Break Case Study. Water 2016, 8, 545. [Google Scholar] [CrossRef]
- Paxson, G.; Savage, B. Labyrinth Weirs: Comparison of Two Popular U.S.A Design Methods and Consideration of Non-Standard Approach Conditions and Geometries. In International Junior Researcher and Engineer Workshop on Hydraulic Structures; Report CH61/06, Div. of Civil Eng.; Matos, J., Chanson, H., Eds.; The University of Queensland: Brisbane, Australia, 2006. [Google Scholar]
- Daneshfaraz, R.; Ghahramanzadeh, A.; Ghaderi, A.; Joudi, A.R.; Abraham, J. Investigation of the Effect of Edge Shape on Characteristics of Flow under Vertical Gates. J. Am. Water Works Assoc. 2016, 108, 425–432. [Google Scholar] [CrossRef]
- Dabling, M.R.; Tullis, B.P. Modifying the downstream hydrograph with staged labyrinth weirs. J. Appl. Water Eng. Res. 2018, 6, 183–190. [Google Scholar] [CrossRef]
- Ghaderi, A.; Abbasi, S.; Abraham, J.; Azamathulla, H.M. Efficiency of Trapezoidal Labyrinth Shaped Stepped Spillways. Flow Meas. Instrum. 2020, 72, 101711. [Google Scholar] [CrossRef]
- Macián-Pérez, J.F.; García-Bartual, R.; Huber, B.; Bayon, A.; Vallés-Morán, F.J. Analysis of the Flow in a Typified USBR II Stilling Basin through a Numerical and Physical Modeling Approach. Water. 2020, 12, 227. [Google Scholar] [CrossRef]
- Sangsefidi, Y.; Mehraein, M.; Ghodsian, M. Numerical simulation of flow over labyrinth weirs. Sci. Iran. 2015, 22, 1779–1787. [Google Scholar]
- Shaghaghian, M.R.; Sharifi, M.T. Numerical modeling of sharp-crested triangular plan form weirs using FLUENT. Indian J. Sci. Technol. 2015, 8, 1–7. [Google Scholar] [CrossRef][Green Version]
- Carrillo, J.M.; Matos, J.; Lopes, R. Numerical modeling of free and submerged labyrinth weir flow for a large sidewall angle. Environ. Fluid Mech. 2019, 20, 1–18. [Google Scholar] [CrossRef]
- Norouzi, R.; Daneshfaraz, R.; Ghaderi, A. Investigation of discharge coefficient of trapezoidal labyrinth weirs using artificial neural networks and support vector machines. Appl. Water Sci. 2019, 9, 148. [Google Scholar] [CrossRef]
- Shafiei, S.; Najarchi, M.; Shabanlou, S. A novel approach using CFD and neuro-fuzzy-firefly algorithm in predicting labyrinth weir discharge coefficient. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 44. [Google Scholar] [CrossRef]
- Haghiabi, A.H.; Azamathulla, H.M.; Parsaie, A. Prediction of head loss on cascade weir using ANN and SVM. ISH J. Hydraul. Eng. 2017, 23, 102–110. [Google Scholar] [CrossRef]
- Mohammadzadeh-Habili, J.; Heidarpour, M.; Samiee, S. Study of energy dissipation and downstream flow regime of labyrinth weirs. Iran. J. Sci. Technol. Trans. Civil Eng. 2018, 42, 111–119. [Google Scholar] [CrossRef]
- Flow Science Inc. FLOW-3D V 11.2 User’s Manual; Flow Science Inc.: Santa Fe, NM, USA, 2016. [Google Scholar]
- Ghaderi, A.; Abbasi, S. CFD simulation of local scouring around airfoil-shaped bridge piers with and without collar. Sādhanā 2019, 44, 216. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Ghaderi, A. Numerical Investigation of Inverse Curvature Ogee Spillway. Civil Eng. J. 2017, 3, 1146–1156. [Google Scholar] [CrossRef]
- Zahabi, H.; Torabi, M.; Alamatian, E.; Bahiraei, M.; Goodarzi, M. Effects of Geometry and Hydraulic Characteristics of Shallow Reservoirs on Sediment Entrapment. Water 2018, 10, 1725. [Google Scholar] [CrossRef]
- Sangsefidi, Y.; MacVicar, B.; Ghodsian, M.; Mehraein, M.; Torabi, M.; Savage, B.M. Evaluation of flow characteristics in labyrinth weirs using response surface methodology. Flow Meas. Instrum. 2019, 69, 101617. [Google Scholar] [CrossRef]
- Ghaderi, A.; Dasineh, M.; Abbasi, S.; Abraham, J. Investigation of trapezoidal sharp-crested side weir discharge coefficients under subcritical flow regimes using CFD. Appl. Water Sci. 2020, 10, 31. [Google Scholar] [CrossRef]
- Ghaderi, A.; Dasineh, M.; Daneshfaraz, R.; Abraham, J. Reply to the discussion on paper: 3-D numerical simulation of water flow over a broad-crested weir with openings. ISH J. Hydraul. Eng. 2019, 1–9. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A.; Thangam, S.; Gatski, T.B.; Speziale, C.G. Development of turbulence models for shear flows by a double expansion technique. Phys. Fluids A Fluid Dyn. 1992, 4, 1510–1520. [Google Scholar] [CrossRef]
- Chero, E.; Torabi, M.; Zahabi, H.; Ghafoorisadatieh, A.; Bina, K. Numerical analysis of the circular settling tank. Drink. Water Eng. Sci. 2019, 12, 39–44. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. In Numerical Prediction of Flow, Heat Transfer, Turbulence and Combustion; Pergamon: Bergama, Turkey, 1983; pp. 96–116. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Johnson, M. Discharge Coefficient Scale Effects Analysis for Weirs. Ph.D. Thesis, Utah State University, Logan, UT, USA, 1996. [Google Scholar]
- Ghaderi, A.; Daneshfaraz, R.; Torabi, M.; Abraham, J.; Azamathulla, H.M. Experimental investigation on effective scouring parameters downstream from stepped spillways Water Supply. Water Supply 2020, in press. [Google Scholar] [CrossRef]
- Ackers, P.; White, W.R.; Perkins, J.A.; Harrison, A.J. Weirs and Flumes for Flow Measurements; Wiley: Chichester, UK, 1978; p. 327. [Google Scholar]
- Choufu, L.; Abbasi, S.; Pourshahbaz, H.; Taghvaei, P.; Tfwala, S. Investigation of flow, erosion, and sedimentation pattern around varied groynes under different hydraulic and geometric conditions: A numerical study. Water 2019, 11, 235. [Google Scholar] [CrossRef]
- Ghaderi, A.; Daneshfaraz, R.; Abbasi, S.; Abraham, J. Numerical analysis of the hydraulic characteristics of modified labyrinth weirs. Int. J. Energy Water Res. 2020, 1–12, in press. [Google Scholar] [CrossRef]
- Sicilian, J.M.; Hirt, C.W.; Harper, R.P. FLOW-3D. Computational Modeling Power for Scientists and Engineers; Report FSI-87-00-1; Flow Science: Los Alamos, NM, USA, 1987. [Google Scholar]
- Crookston, B.M. Labyrinth Weirs. Ph.D. Thesis, Utah State University, Logan, UT, USA, 2010. [Google Scholar]
- Rajaratnam, N.; Chamani, M.R. Energy loss at drops. J. Hydraul. Res. 1995, 33, 373–384. [Google Scholar] [CrossRef]
- Chamani, M.R.; Rajaratnam, N.; Beirami, M.K. Turbulent jet energy dissipation at vertical drops. J. Hydraul. Eng. 2008, 134, 1532–1535. [Google Scholar] [CrossRef]
- Ridolfi, E.; Di Francesco, S.; Pandolfo, C.; Berni, N.; Biscarini, C.; Manciola, P. Coping with extreme events: Effect of different reservoir operation strategies on flood inundation maps. Water 2019, 11, 982. [Google Scholar] [CrossRef]
- Manciola, P.; Di Francesco, S.; Biscarini, C. Flood Protection and Risk Management: The Case of Tescio River Basin; IAHS-AISH Publication: Capri, Italy, 2009; Volume 327, pp. 174–183. [Google Scholar]
- Di Francesco, S.; Biscarini, C.; Manciola, P. Characterization of a Flood Event through a Sediment Analysis: The Tescio River Case Study. Water 2016, 8, 308. [Google Scholar] [CrossRef]






| Models | Q (l/s) | α (°) | l (cm) | w (cm) | P (cm) | l/w | w/p | Fr0 |
|---|---|---|---|---|---|---|---|---|
| Range | 3–15 | 10–30 | 27–72 | 15 | 8–12 | 1.8–4.8 | 1.87–1.25 | 0.08–0.16 |
| Test No. | Turbulence Model | Coarser Cells Size (cm) | Finer Cells Size (cm) | Total Mesh Number | Computational Time (min) | * MAPE (%) | ** RMSE (cm) |
|---|---|---|---|---|---|---|---|
| T1 | k-ε (RNG) | 1.10 | 0.65 | 711,758 | 50 | 19.39 | 3.44 |
| T2 | k-ε (RNG) | 1.00 | 0.55 | 1,302,587 | 85 | 11.12 | 1.96 |
| T3 | k-ε (RNG) | 0.90 | 0.45 | 1,997,425 | 120 | 6.07 | 0.85 |
| T4 | k-ε (RNG) | 0.80 | 0.35 | 2,703,458 | 175 | 3.75 | 0.56 |
| T5 | k-ε (RNG) | 0.70 | 0.30 | 3,587,624 | 220 | 3.32 | 0.44 |
| Model | H/P | Cd-NO-Measured Values | Cd-NO-Computed Values | Cd-IO-Measured Values | Cd-IO-Computed Values | MARE (%)-NO | MARE (%)-IO |
|---|---|---|---|---|---|---|---|
| Trapezoidal–Triangular Labyrinth Weir (TTLW) | 0.176 | 0.799 | 0.789 | 0.804 | 0.790 | 1.29 | 1.70 |
| 0.256 | 0.779 | 0.757 | 0.764 | 0.772 | 2.87 | 1.10 | |
| 0.338 | 0.716 | 0.722 | 0.706 | 0.719 | 0.77 | 1.90 | |
| 0.417 | 0.670 | 0.684 | 0.662 | 0.642 | 2.02 | 3.00 | |
| 0.509 | 0.606 | 0.613 | 0.600 | 0.585 | 1.14 | 2.50 | |
| 0.589 | 0.575 | 0.560 | 0.570 | 0.559 | 2.55 | 2.00 | |
| 0.688 | 0.525 | 0.510 | 0.521 | 0.529 | 2.72 | 1.60 | |
| Mean | 1.91 | 1.97 | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghaderi, A.; Daneshfaraz, R.; Dasineh, M.; Di Francesco, S. Energy Dissipation and Hydraulics of Flow over Trapezoidal–Triangular Labyrinth Weirs. Water 2020, 12, 1992. https://doi.org/10.3390/w12071992
Ghaderi A, Daneshfaraz R, Dasineh M, Di Francesco S. Energy Dissipation and Hydraulics of Flow over Trapezoidal–Triangular Labyrinth Weirs. Water. 2020; 12(7):1992. https://doi.org/10.3390/w12071992
Chicago/Turabian StyleGhaderi, Amir, Rasoul Daneshfaraz, Mehdi Dasineh, and Silvia Di Francesco. 2020. "Energy Dissipation and Hydraulics of Flow over Trapezoidal–Triangular Labyrinth Weirs" Water 12, no. 7: 1992. https://doi.org/10.3390/w12071992
APA StyleGhaderi, A., Daneshfaraz, R., Dasineh, M., & Di Francesco, S. (2020). Energy Dissipation and Hydraulics of Flow over Trapezoidal–Triangular Labyrinth Weirs. Water, 12(7), 1992. https://doi.org/10.3390/w12071992







