Multi-Agent Simulation of Individuals’ Escape in the Urban Rainstorm Context Based on Dynamic Recognition-Primed Decision Model
Abstract
:1. Introduction
2. Materials and Methods
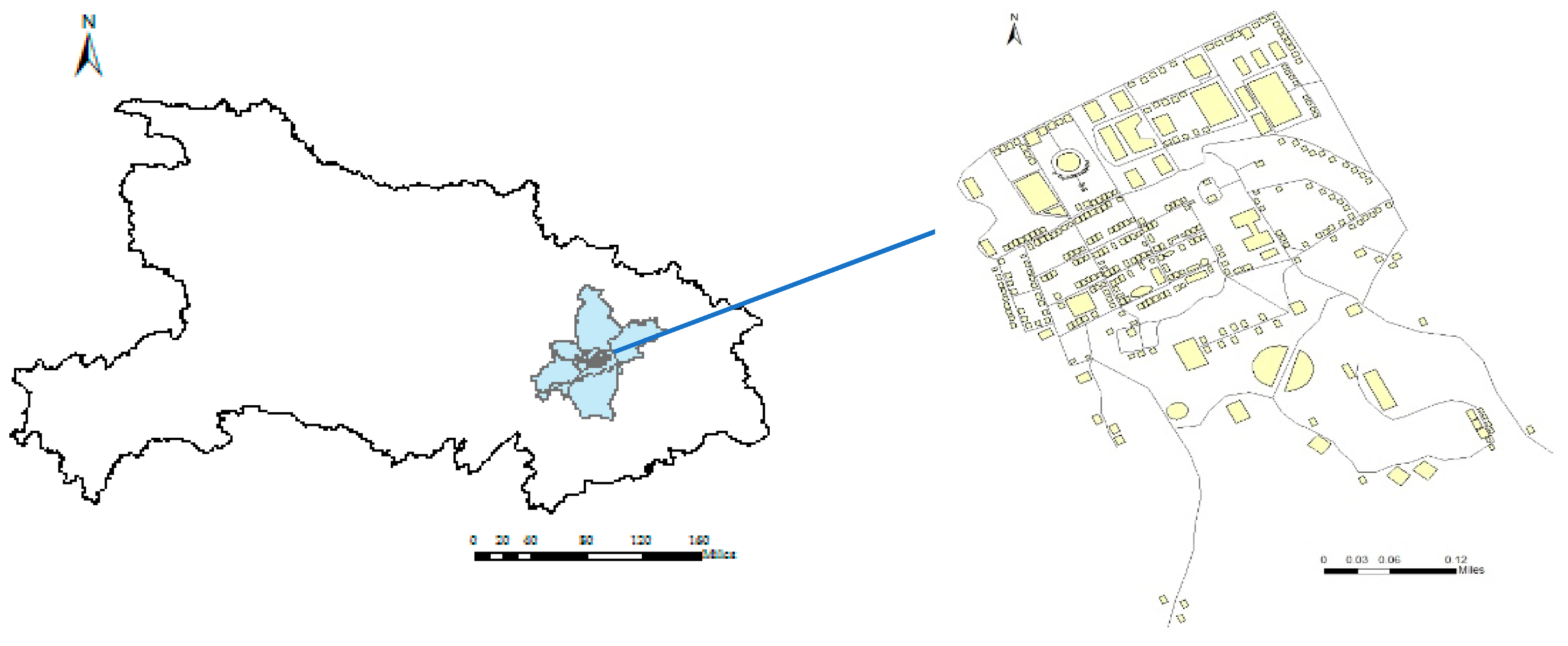
2.1. Study Area
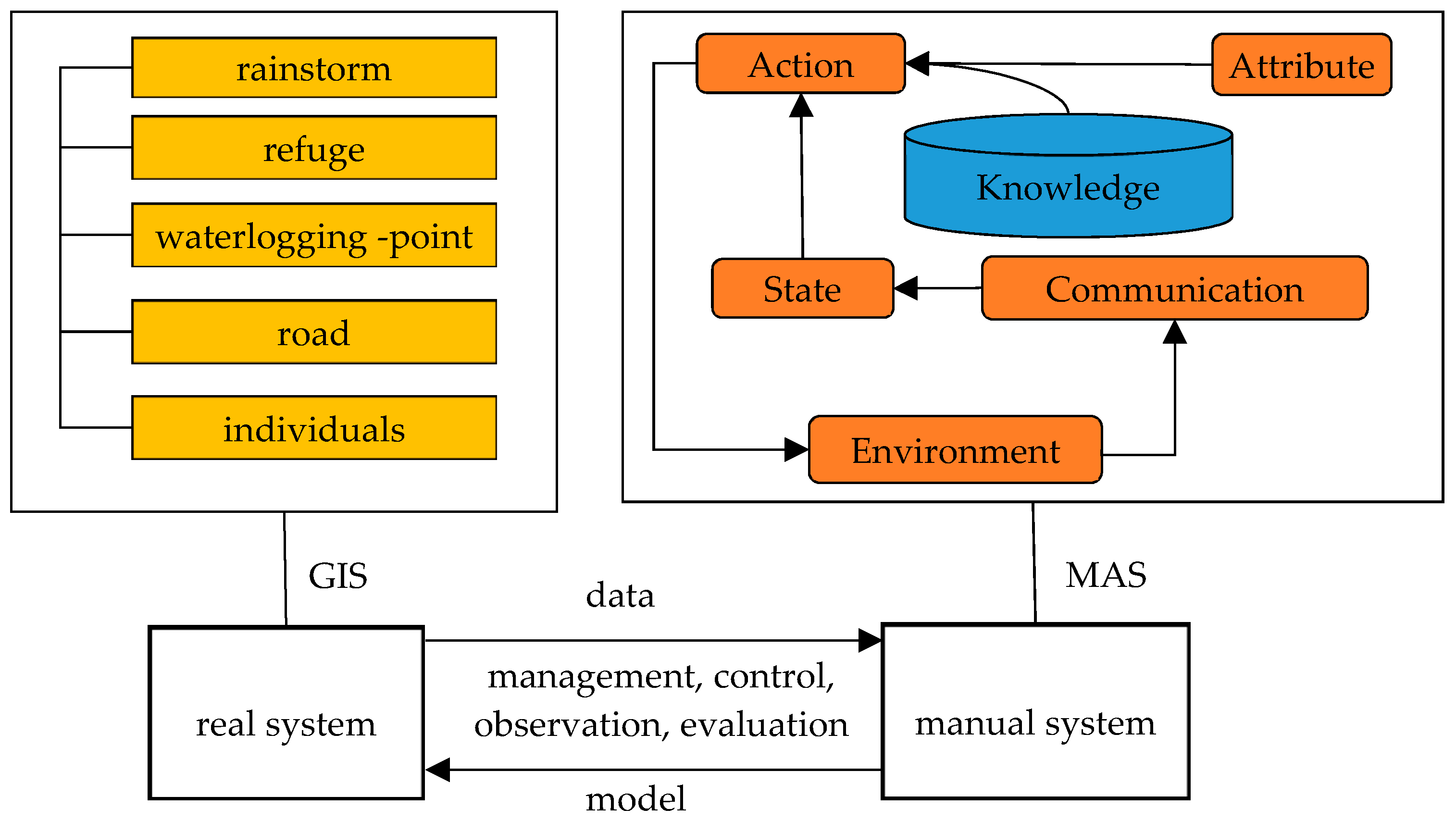
2.2. Framework of Multi-Agent Simulation
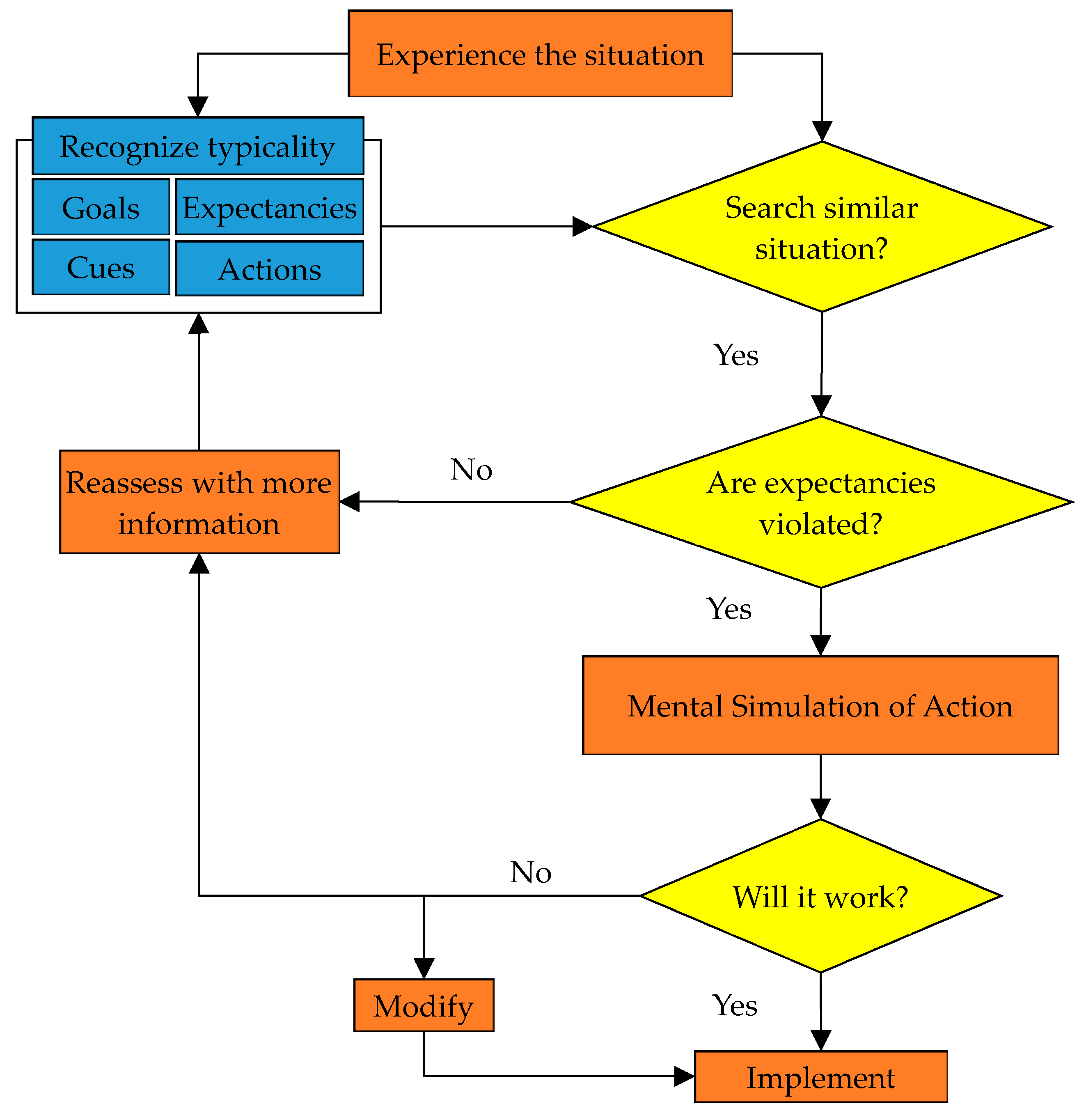
2.3. Recognition-Primed Decision Model
2.4. Dynamic Recognition-Primed Decision Model
2.5. Model of Individuals’ Escape in the Urban Rainstorm Context
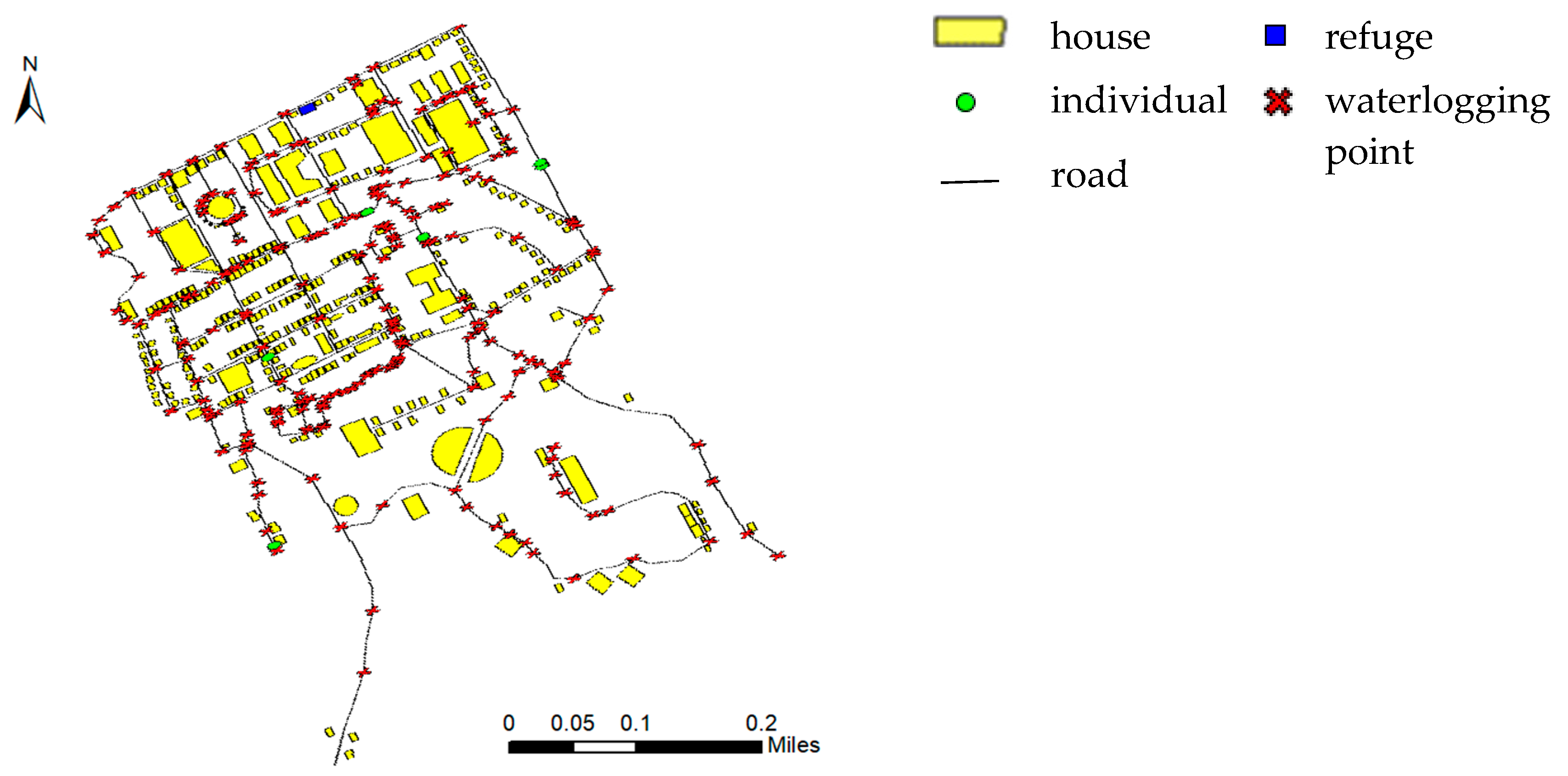
2.5.1. Agent Attributes
2.5.2. Agent Interaction Rule
3. Result and Discussion
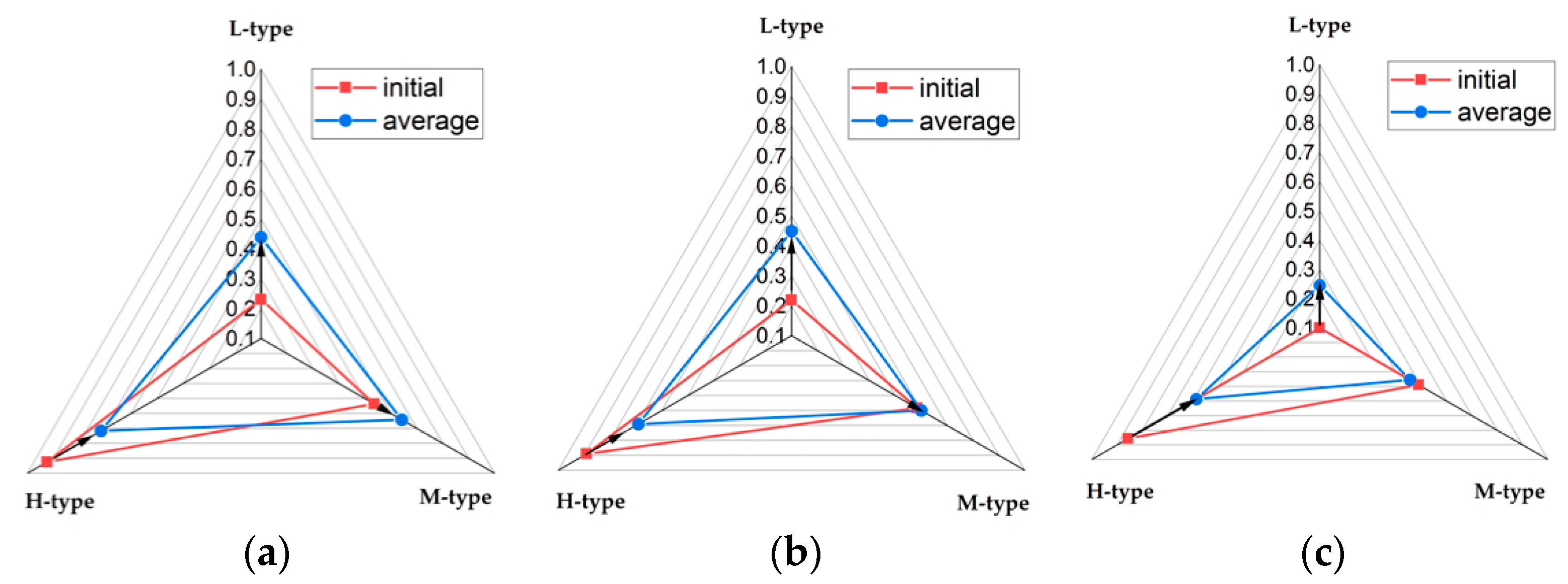
3.1. Individual’s Perception of Risk
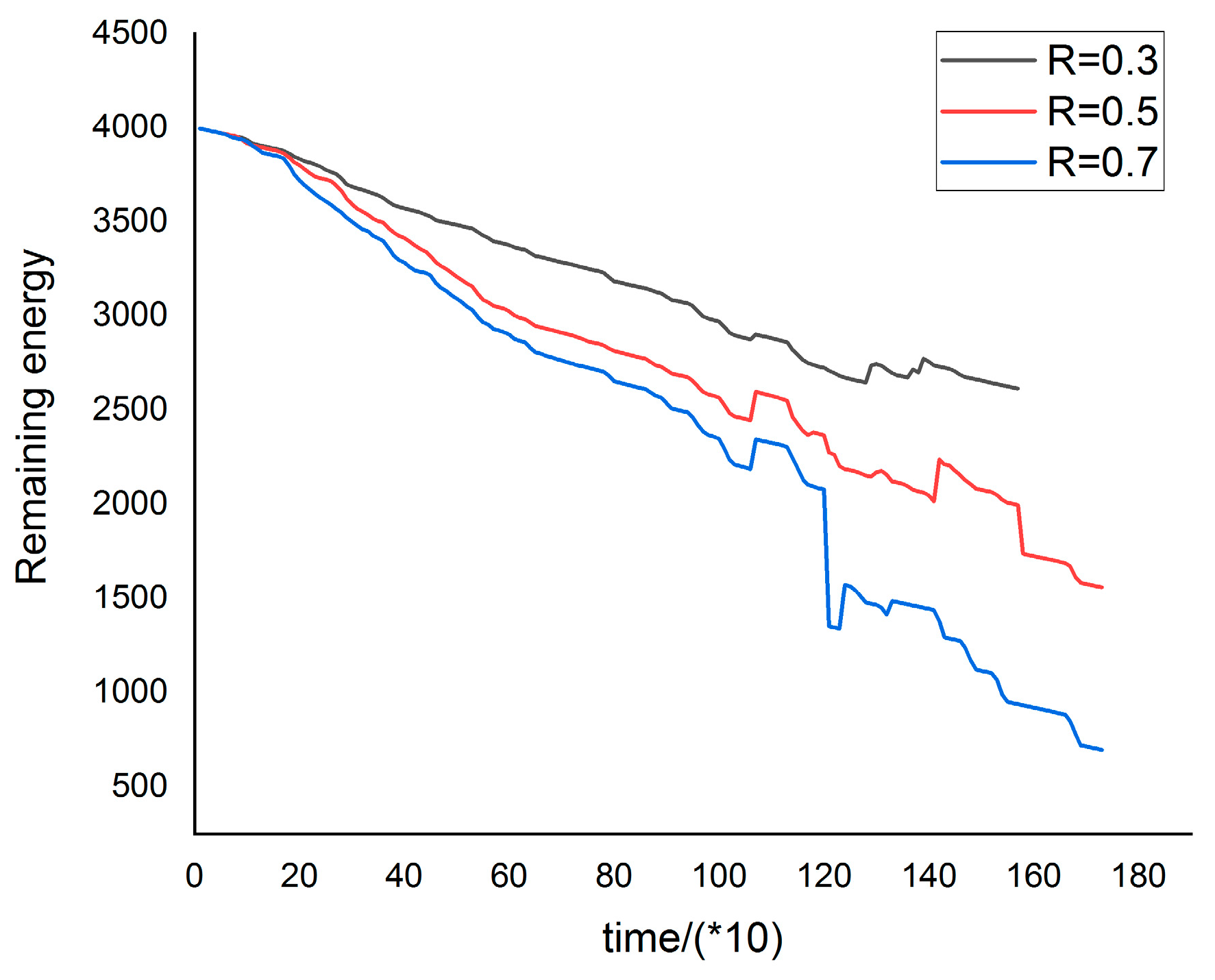
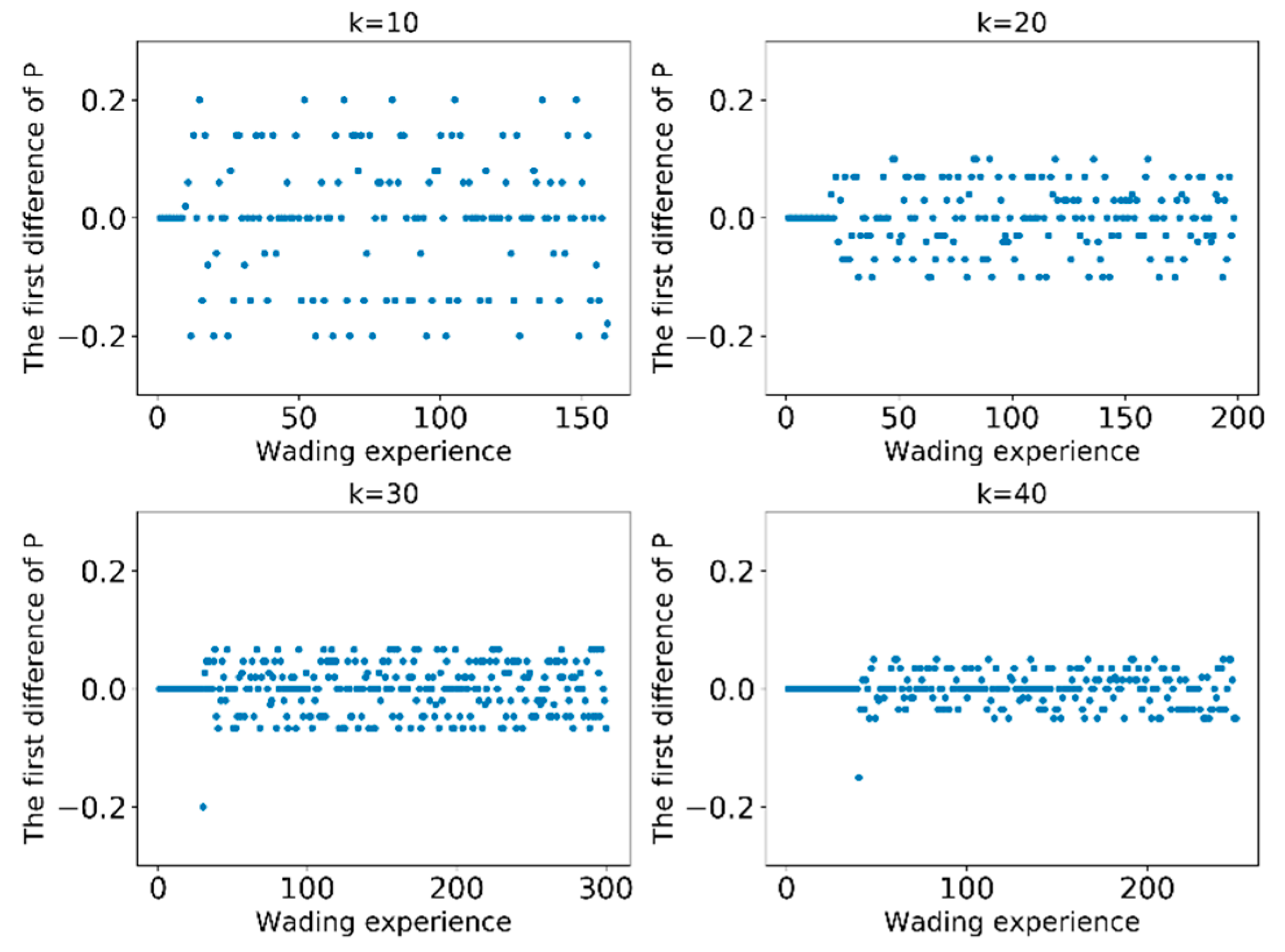
3.2. Influences of Individuals’ Experience Pool Size
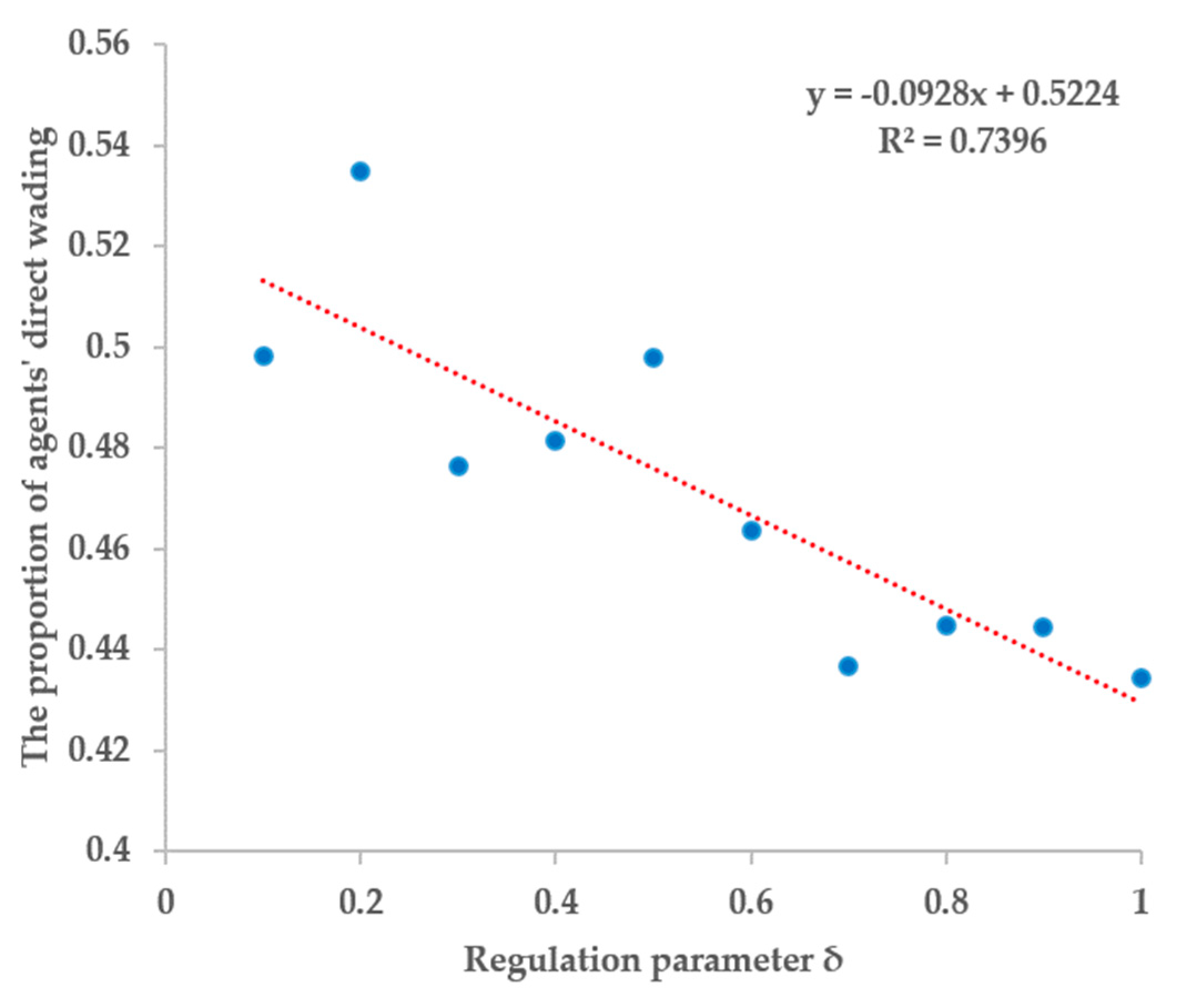
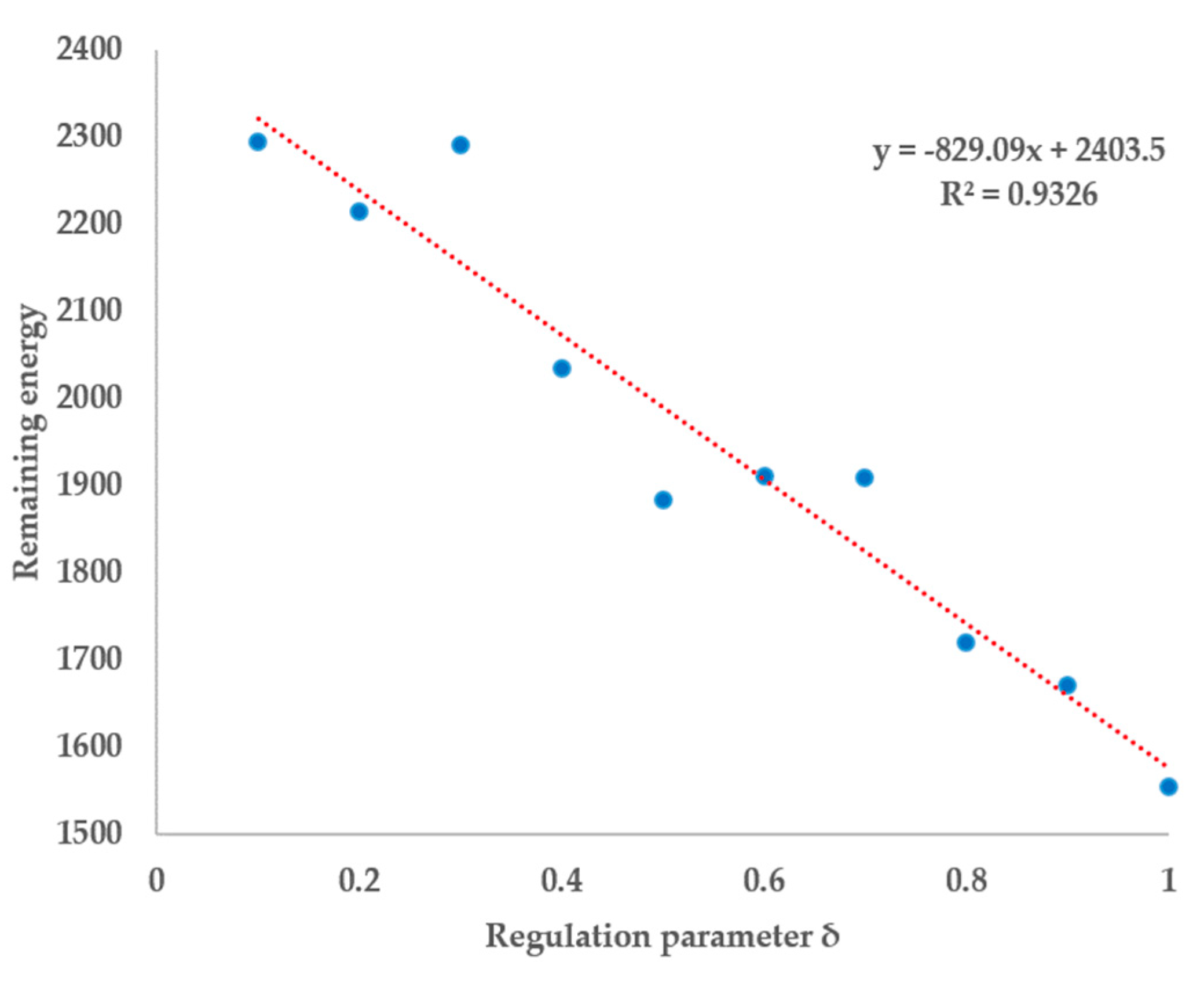
3.3. Influences of the Regulation Parameter on Individuals’ Behavior
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hegger, D.L.T.; Driessen, P.P.J.; Dieperink, C.; Wiering, M.; Raadgever, G.T.T.; van Rijswick, H.F.M.W. Assessing stability and dynamics in flood risk governance: An empirically illustrated research approach. Water Resour. Manag. 2014, 28, 4127–4142. [Google Scholar] [CrossRef]
- Shi, Y. Risk analysis of rainstorm waterlogging on residences in Shanghai based on scenario simulation. Nat. Hazards 2012, 62, 677–689. [Google Scholar] [CrossRef]
- Quan, R.S. Rainstorm waterlogging risk assessment in central urban area of Shanghai based on multiple scenario simulation. Nat. Hazards 2014, 73, 1569–1585. [Google Scholar] [CrossRef]
- Su, Y.; Zhao, F.; Tan, L. Whether a large disaster could change public concern and risk perception: A case study of the 7/21 extraordinary rainstorm disaster in Beijing in 2012. Nat. Hazards 2015, 78, 555–567. [Google Scholar] [CrossRef]
- Su, B.; Huang, H.; Li, Y. Integrated simulation method for waterlogging and traffic congestion under urban rainstorms. Nat. Hazards 2016, 81, 23–40. [Google Scholar] [CrossRef]
- Yin, Z.; Yin, J.; Xu, S.; Wen, J. Community-based scenario modelling and disaster risk assessment of urban rainstorm waterlogging. J. Geogr. Sci. 2011, 21, 274–284. [Google Scholar] [CrossRef]
- Hu, H.B. Rainstorm flash flood risk assessment using genetic programming: A case study of risk zoning in Beijing. Nat. Hazards 2016, 83, 485–500. [Google Scholar] [CrossRef]
- Chen, P.; Zhang, J.; Zhang, L.; Sun, Y. Evaluation of resident evacuations in urban rainstorm waterlogging disasters based on scenario simulation: Daoli district (Harbin, China) as an example. Int. J. Environ. Res. Public Health 2014, 11, 9964–9980. [Google Scholar] [CrossRef] [Green Version]
- Sugiura, K. Masahiro Arakawa Evaluation of Behavior of Evacuees on a Floor in a Disaster Situation Using Multi-agent Simulation and Mixed Reality Game: Effectiveness of the Field of Vision and Priority of Referred Objects. Comput. Technol. Appl. 2016, 7, 227–235. [Google Scholar]
- Lomnitz, C.; Castaños, H. Unplanned and Unforeseen Effects of Instabilities in the Nature-Society System as Possible Causes of Earthquake Disasters. Nat. Hazards 1995, 11, 45–56. [Google Scholar]
- Gao, L.; Durnota, B.; Ding, Y.; Dai, H. An agent-based simulation system for evaluating gridding urban management strategies. Knowl. Based Syst. 2012, 26, 174–184. [Google Scholar] [CrossRef]
- Chen, X.; Zhan, F.B. Agent-based modelling and simulation of urban evacuation: Relative effectiveness of simultaneous and staged evacuation strategies. J. Oper. Res. Soc. 2008, 59, 25–33. [Google Scholar] [CrossRef]
- Uno, K.; Kashiyama, K. Development of Simulation System for the Disaster Evacuation Based on Multi-Agent Model Using GIS. Tsinghua Sci. Technol. 2008, 13, 348–353. [Google Scholar] [CrossRef]
- Takahashi, T.; Tadokoro, S.; Ohta, M.; Ito, N. Agent Based Approach in Disaster Rescue Simulation-From Test-Bed of Multiagent System to Practical Application. In Robot Soccer World Cup; Springer: Berli/Heidelberg, Germany, 2002; pp. 102–111. [Google Scholar]
- Lai, W.Z.; Li, W.B.; Huang, Y.L.; Wang, W.X.; Xiao, D. Rainstorm flood building risk dynamic assessment conceptual model utilization agent based modeling. In Proceedings of the 2015 International Conference on Computer Science and Applications (CSA), Wuhan, China, 20–22 November 2015; pp. 191–195. [Google Scholar]
- Yu, J.; Zhang, C.; Wen, J.; Li, W.; Liu, R.; Xu, H. Integrating multi-agent evacuation simulation and multi-criteria evaluation for spatial allocation of urban emergency shelters. Int. J. Geogr. Inf. Sci. 2018, 32, 1884–1910. [Google Scholar] [CrossRef]
- Harris, D.; Beach, L.R.; Lipshitz, R. Why Classical Decision Theory is an Inappropriate Standard for Evaluating and Aiding Most Human Decision Making. Decis. Mak. Aviat. 2018, 85, 835–847. [Google Scholar]
- Abustan, M.S.; Rahman, N.A.; Gotoh, H.; Harada, E.; Talib, S.H.A. Numerical Simulation of Evacuation Process in Malaysia by Using Distinct-Element-Method Based Multi-Agent Model. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2016; Volume 136. [Google Scholar]
- Klein, G. Naturalistic Decision Making. Hum. Fact. J. Hum. Factors Ergon. Soc. 2008, 50, 456–460. [Google Scholar] [CrossRef] [Green Version]
- Fan, X.; Sun, S.; McNeese, M.; Yen, J. Extending the recognition-primed decision model to support human-agent collaboration. In Proceedings of the Fourth International Joint Conference on Autonomous Agents and Multiagent Systems (ACM), New York, NY, USA, 25–29 July 2005; pp. 945–952. [Google Scholar]
- Patrix, J.; Mouaddib, A.-I.; Gatepaille, S. Detection of Primitive Collective Behaviours in a Crowd Panic Simulation Based on Multi-Agent Approach. Int. J. Swarm Intell. Res. 2012, 3, 50–65. [Google Scholar] [CrossRef]
- Macal, C.M.; North, M.J. Tutorial on Agent-based Modeling and Simulation Agent-based Modeling and Simulation Initiative at Argonne National Laboratory View project Agent-Based Modeling and Simulation. In Proceedings of the Winter Simulation Conference, Orlando, FL, USA, 4 December 2005; p. 14. [Google Scholar]
- Linghu, B.; Chen, F.; Guo, X.; Li, W. A conceptual model for flood disaster risk assessment based on agent-based modeling. In Proceedings of the International Conference on Computer Sciences and Applications, Wuhan, China, 14–15 December 2013; pp. 369–373. [Google Scholar]
- Macal, C.M.; North, M.J. Tutorial on agent-based modeling and simulation part 2: How to model with agents. In Proceedings of the 38th conference on Winter simulation. Winter Simulation Conference, Monterey, CA, USA, 3–6 December 2006; pp. 73–83. [Google Scholar]
- Wang, F.Y.; Zeng, D.; Carley, K.M.; Mao, W. Social computing: From social informatics to social intelligence. IEEE Intell. Syst. 2007, 22, 79–83. [Google Scholar] [CrossRef]
- Wang, F.Y.; Wang, X.; Li, L.; Li, L. Steps toward Parallel Intelligence. IEEE/CAA J. Autom. Sin. 2016, 3, 345–348. [Google Scholar]
- Dawson, R.J.; Peppe, R.; Wang, M. An agent-based model for risk-based flood incident management. Nat. Hazards 2011, 59, 167–189. [Google Scholar] [CrossRef]
- Aven, T. The risk concept-historical and recent development trends. Reliab. Eng. Syst. Saf. 2012, 99, 33–44. [Google Scholar] [CrossRef]
- Dave, D.; Saffer, H. Alcohol demand and risk preference. J. Econ. Psychol. 2008, 29, 810–831. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Y.; Liu, R.; Barrett, D.; Gao, L.; Zhou, M.; Renzullo, L.; Emelyanova, I. A spatial assessment framework for evaluating flood risk under extreme climates. Sci. Total Environ. 2015, 538, 512–523. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Chen, Y.; Wu, J.; Gao, L.; Barrett, D.; Xu, T.; Li, X.; Li, L.; Huang, C.; Yu, J. Integrating Entropy-Based Naïve Bayes and GIS for Spatial Evaluation of Flood Hazard. Risk Anal. 2017, 37, 756–773. [Google Scholar] [CrossRef]
- Huang, Z.Y.; Peng, T.; Zhang, H.Y.; Yao, W.L. Study of risk and early warning index of rainstorm waterlogging in Wuhan City. IOP Conf. Ser. Earth Environ. Sci. 2017, 82. [Google Scholar] [CrossRef] [Green Version]
- Haer, T.; Botzen, W.J.W.; de Moel, H.; Aerts, J.C.J.H. Integrating Household Risk Mitigation Behavior in Flood Risk Analysis: An Agent-Based Model Approach. Risk Anal. 2017, 37, 1977–1992. [Google Scholar] [CrossRef] [Green Version]
- Li, B. The Classical Model of Decision Making Has Been Accepted as not providing an Accurate Account of How People Typically Make Decisions. Int. J. Bus. Manag. 2009, 3, 151–154. [Google Scholar] [CrossRef] [Green Version]
- Lipshitz, R.; Klein, G.; Orasanu, J.; Salas, E. Focus article: Taking stock of naturalistic decision making. J. Behav. Decis. Mak. 2001, 14, 331–352. [Google Scholar] [CrossRef]
- Klein, G.A.; Calderwood, R.; Clinton-Cirocco, A. Rapid Decision Making on the Fire Ground. Proc. Hum. Factors Soc. Annu. Meet. 1986, 30, 576–580. [Google Scholar] [CrossRef]
- Eisenberger, R. Decision Making in Action: Models and Methods, Klein, G.A., Orasanu, J., Calderwood, R., Zsambok, C.E. (eds). Norwood, NJ: Ablex, 1993, 480 pp. ISBN 0–89391–794–X (pb). J. Behav. Decis. Mak. 2007, 8, 218–219. [Google Scholar] [CrossRef]
- Klein, G. A naturalistic decision making perspective on studying intuitive decision making. J. Appl. Res. Mem. Cogn. 2015, 4, 164–168. [Google Scholar] [CrossRef] [Green Version]
- Ross, K.G.; Klein, G.A.; Thunholm, P.; Schmitt, J.F.; Baxter, H.C. The Recognition-Primed Decision Model; Army Combined Arms Center: Fort Leavenworth, KS, USA, 2004; pp. 6–10. [Google Scholar]
- Martin-Clouaire, R. Modelling Operational Decision-Making in Agriculture. Agric. Sci. 2017, 08, 527–544. [Google Scholar] [CrossRef] [Green Version]
- Ding, J.; Cai, J.; Guo, G.; Chen, C. An emergency decision-making method for urban rainstormwater-logging: A China study. Sustainability 2018, 10, 3453. [Google Scholar] [CrossRef] [Green Version]
- Raudkivi, A.J.; Lawgun, N. Synthesis of urban rainfall. Water Resour. Res. 1970, 6, 455–464. [Google Scholar] [CrossRef]
- Pan, X.; Han, C.S.; Dauber, K.; Law, K.H. A multi-agent based framework for the simulation of human and social behaviors during emergency evacuations. AI Soc. 2007, 22, 113–132. [Google Scholar] [CrossRef]
- Sugiura, K.; Arakawa, M.; Yokoi, N. Evaluation of the Behavior of Evacuees on Dynamic Floor Condition by Using Multi-agent Simulation. J. Electr. Eng. 2017, 5, 275–287. [Google Scholar]
- Gibbons, A. Becoming human. New fossils raise molecular questions. Science 2002, 295, 1217. [Google Scholar] [CrossRef]
- Arend, I.; Botella, J.; Contreras, M.J.; Hernández, J.M.; Santacreu, J. A betting dice test to study the interactive style of risk-taking behavior. Psychol. Rec. 2003, 53, 217–230. [Google Scholar] [CrossRef] [Green Version]
- Papagiannaki, K.; Kotroni, V.; Lagouvardos, K.; Bezes, A. Perspectives on Atmospheric Sciences; Springer: Berlin, Germany, 2017; pp. 217–223. [Google Scholar]
- Lilford, R.J.; Chilton, P.J. Does the internet limit or extend the human mind? Probably both. BMJ 2011, 343. [Google Scholar] [CrossRef]
- Gonzalez, C. Learning to make decisions in dynamic environments: Effects of time constraints and cognitive abilities. Hum. Fact. 2004, 46, 449–460. [Google Scholar] [CrossRef]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Sun, X.; Liu, X.; Wang, J. Multi-Agent Simulation of Individuals’ Escape in the Urban Rainstorm Context Based on Dynamic Recognition-Primed Decision Model. Water 2020, 12, 1190. https://doi.org/10.3390/w12041190
Yang Q, Sun X, Liu X, Wang J. Multi-Agent Simulation of Individuals’ Escape in the Urban Rainstorm Context Based on Dynamic Recognition-Primed Decision Model. Water. 2020; 12(4):1190. https://doi.org/10.3390/w12041190
Chicago/Turabian StyleYang, Qing, Xu Sun, Xingxing Liu, and Jinmei Wang. 2020. "Multi-Agent Simulation of Individuals’ Escape in the Urban Rainstorm Context Based on Dynamic Recognition-Primed Decision Model" Water 12, no. 4: 1190. https://doi.org/10.3390/w12041190



