Rainstorm Magnitude Likely Regulates Event Water Fraction and Its Transit Time in Mesoscale Mountainous Catchments: Implication for Modelling Parameterization
Abstract
:1. Introduction
2. Materials and Methods
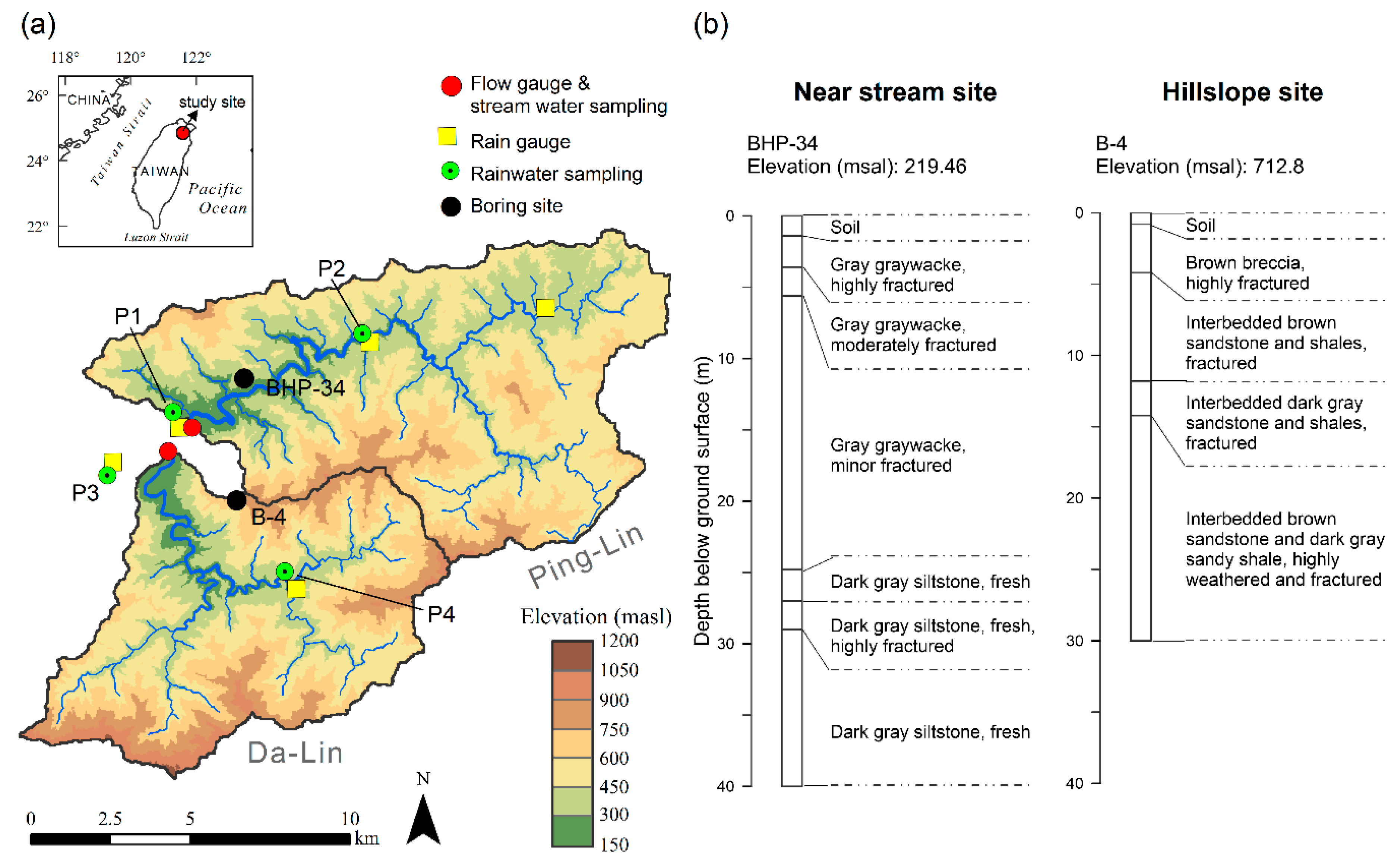
2.1. Study Site
2.2. Hydrometrics and Water Isotope Measurement
2.2.1. Hydrometrics
2.2.2. Water Isotope Measurement
2.3. Estimation of Mean Transit Time (MTTew) and Event Water Fraction (Few)
2.4. Parameter Calibration
2.5. Sensitivity Analysis
3. Results
3.1. Hydrometric and Tracer Dynamics among Typhoons
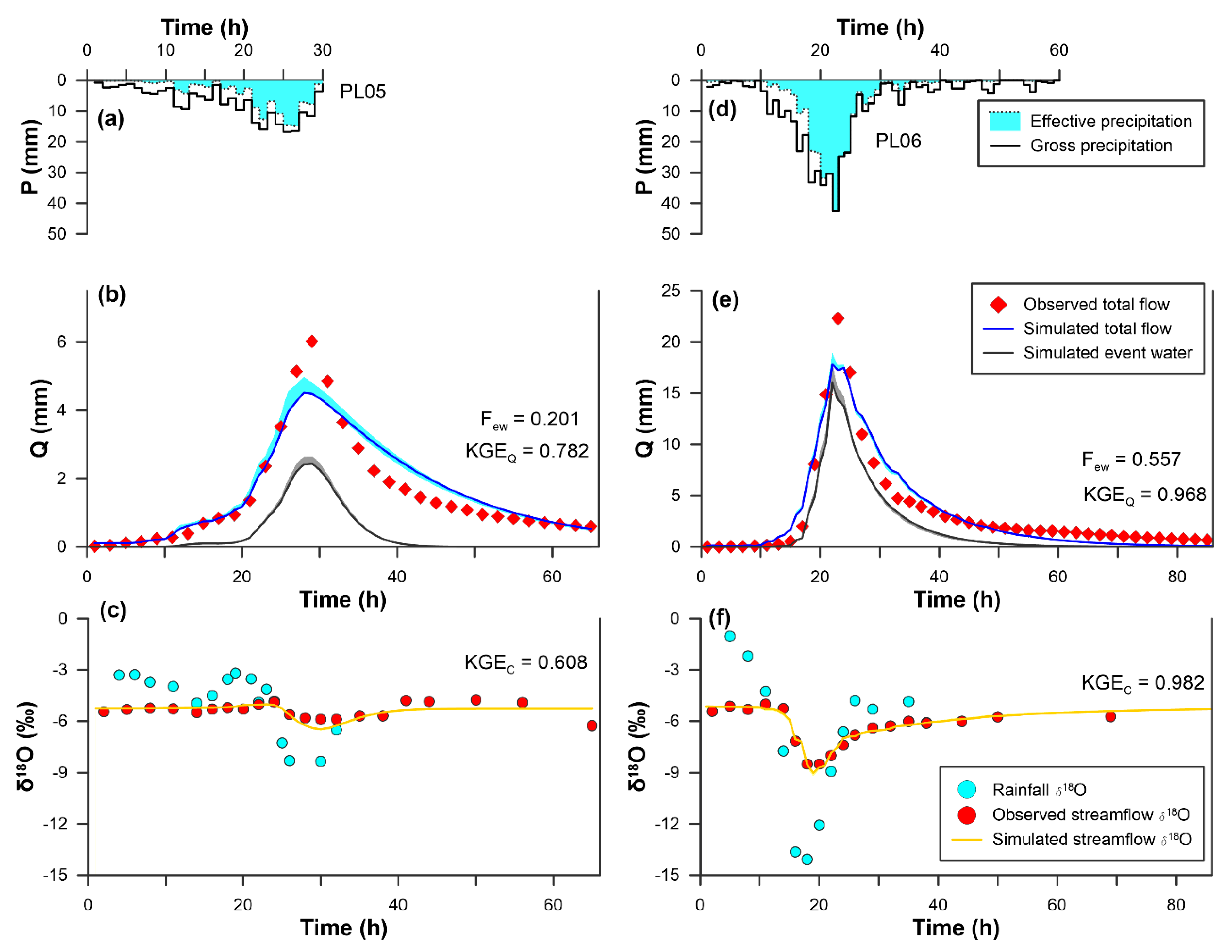
3.2. Simulation Performances and Estimations of MTTew and Few
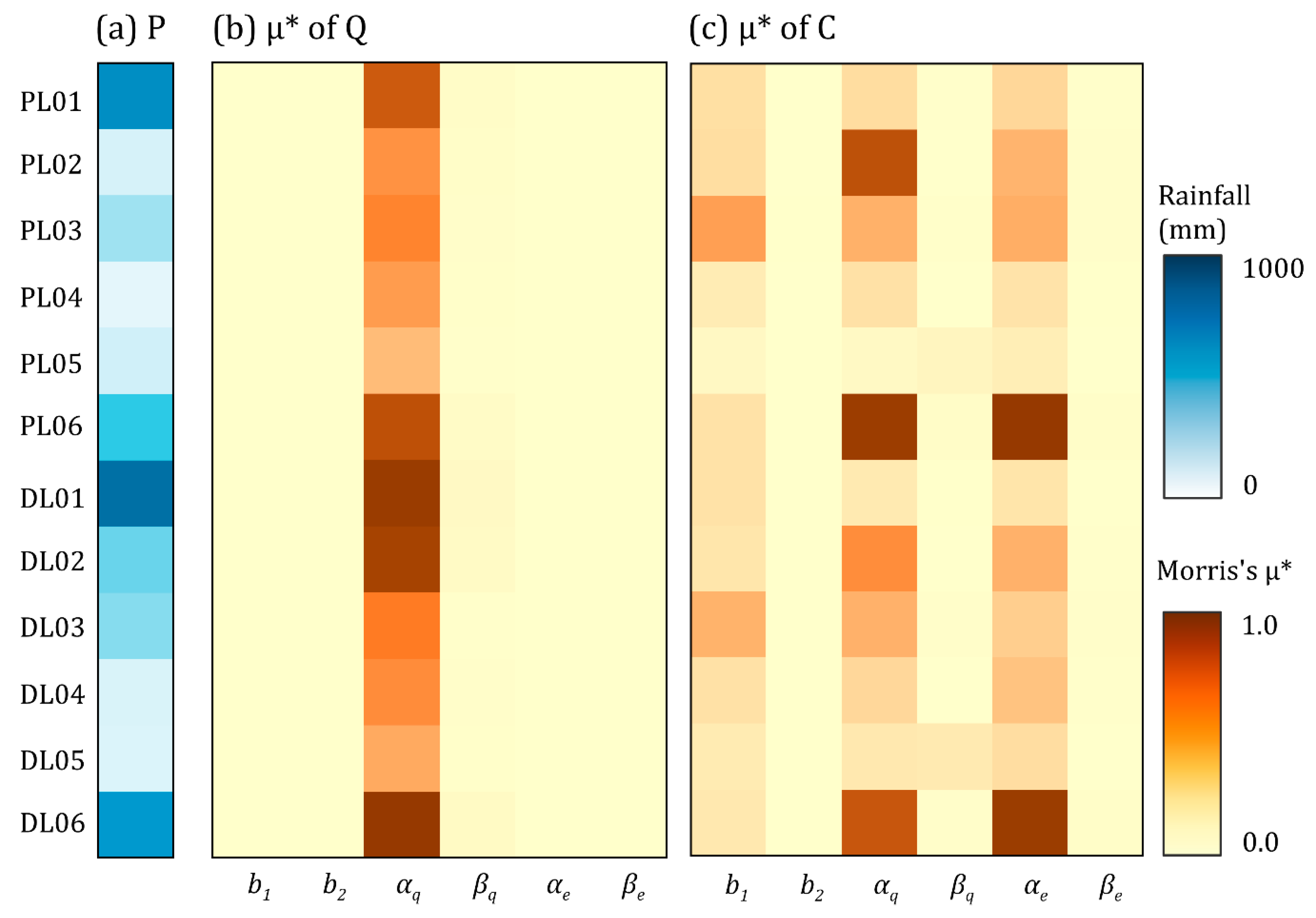
3.3. Parameter Sensitivity
4. Discussion
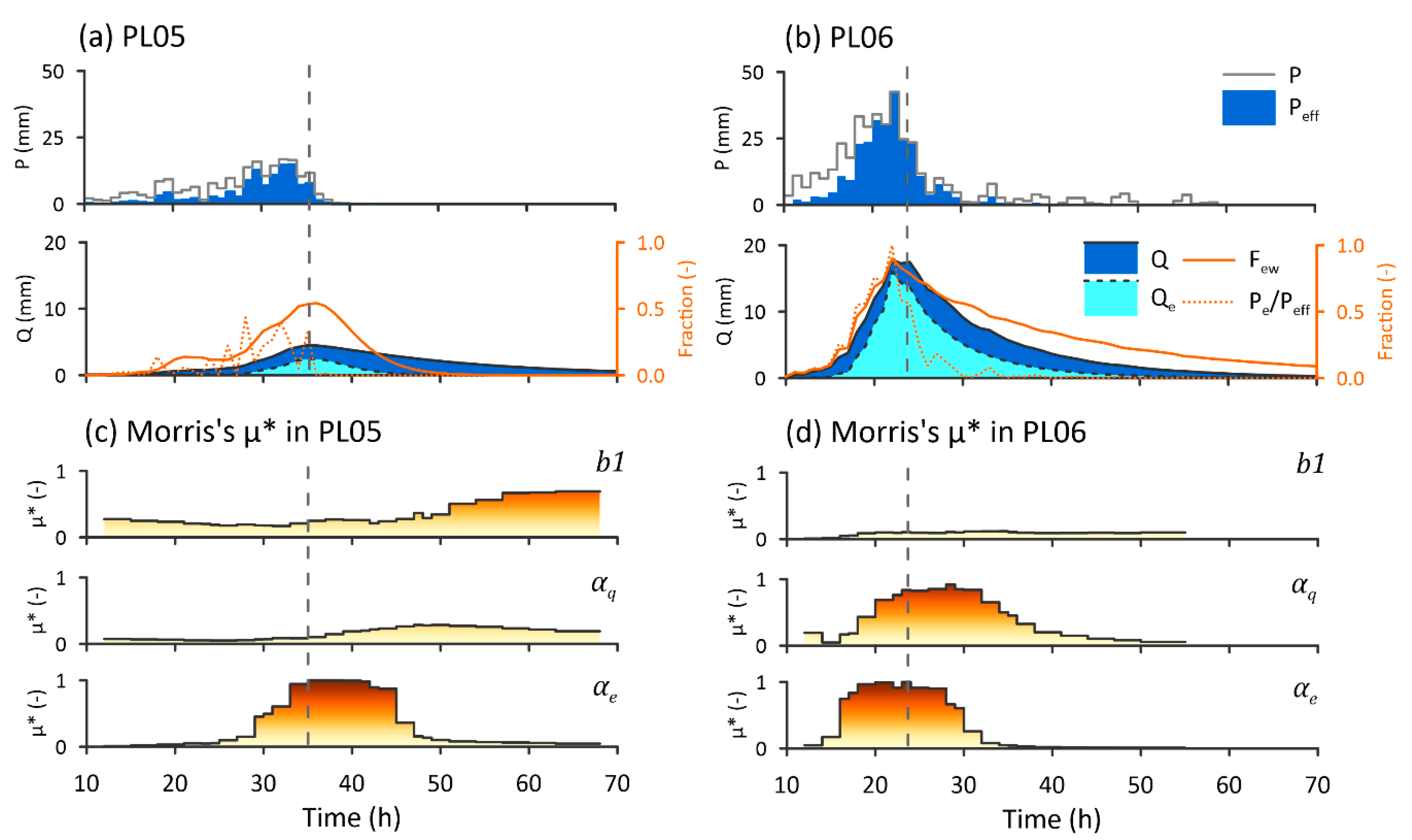
4.1. Rapid Response from Rainfall to Streamflow during Typhoons
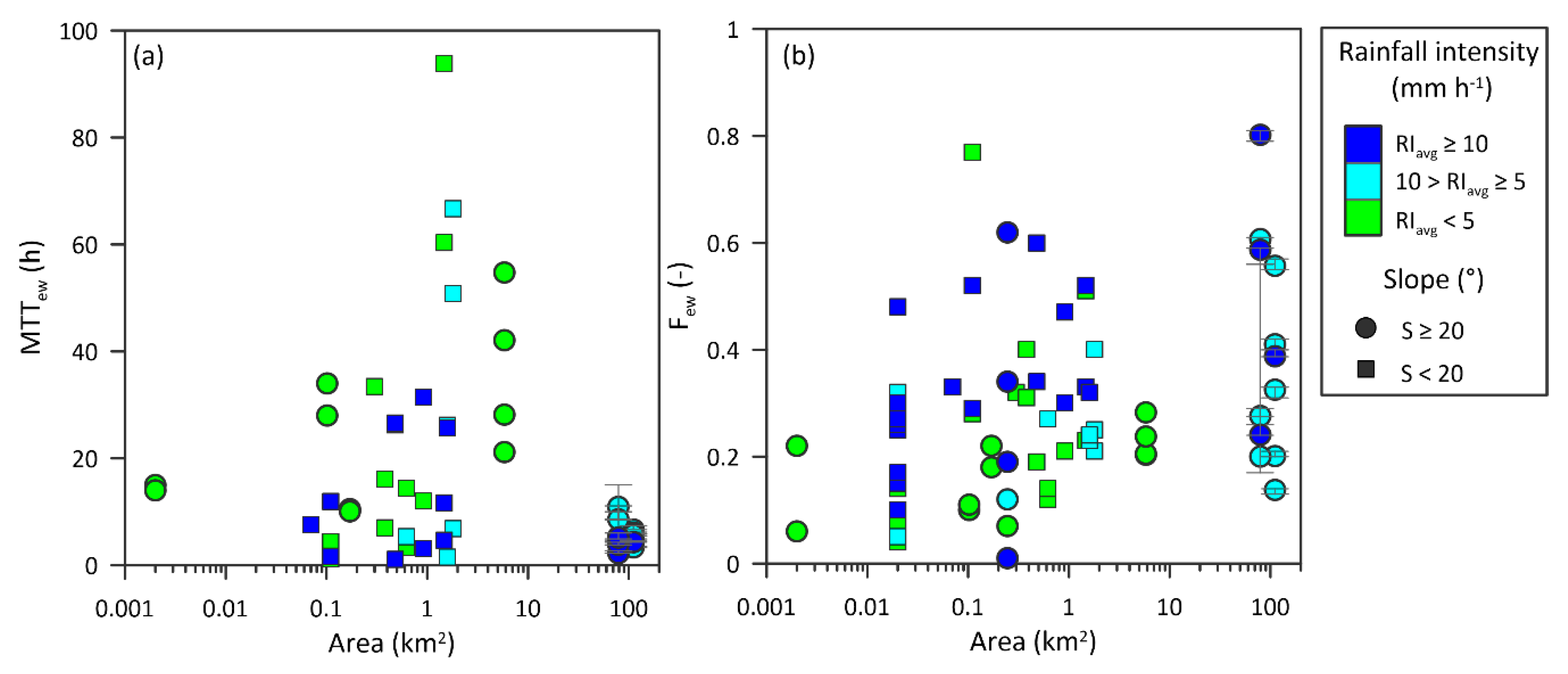
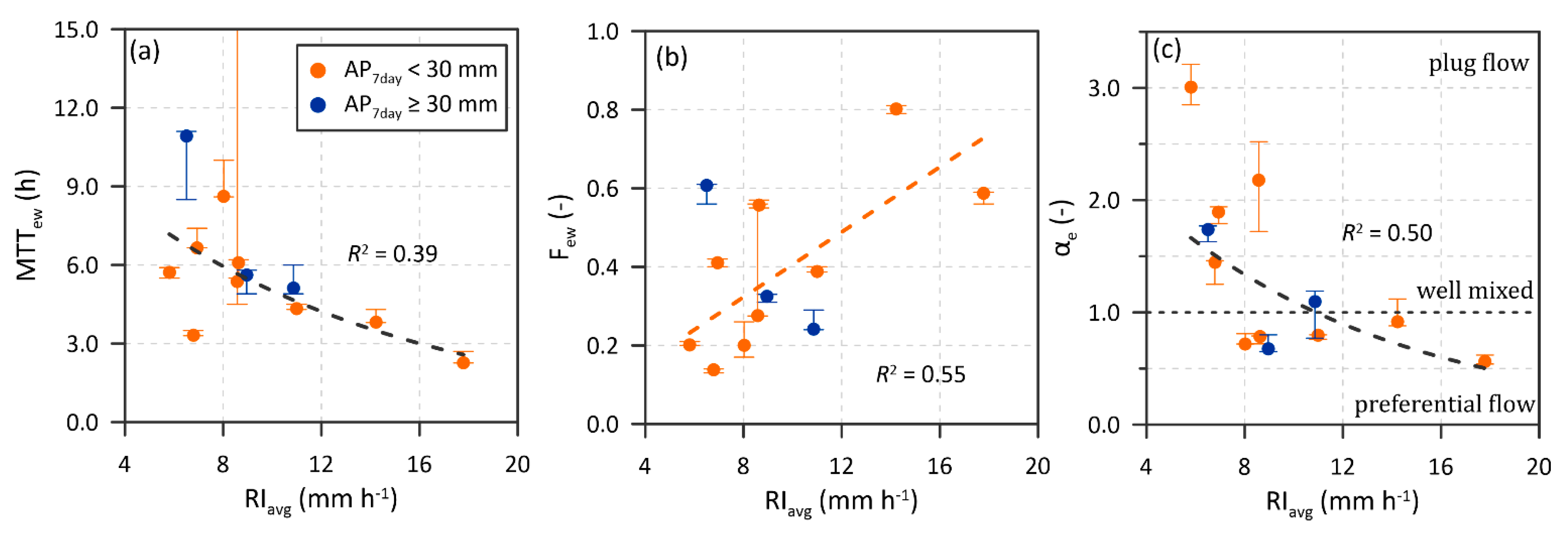
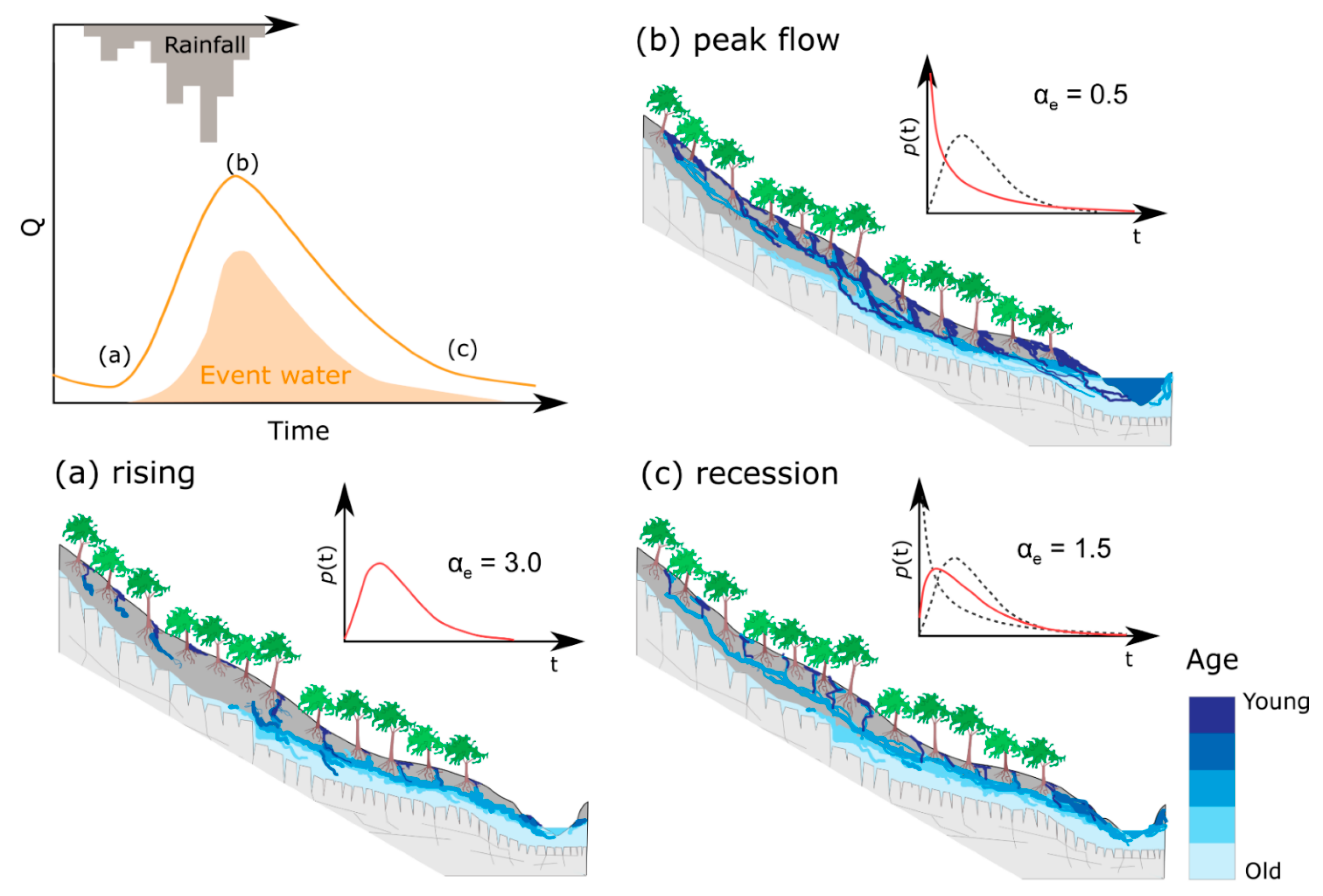
4.2. Rainfall Control on the Variability of MTTew, Few, and αe
4.3. Transition of Parameter Sensitivity during Typhoons
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stewart, M.; McDonnell, J.J. Modeling Base Flow Soil Water Residence Times from Deuterium Concentrations. Water Resour. Res. 1991, 27, 2681–2693. [Google Scholar] [CrossRef]
- Stark, C.; Stieglitz, M. The sting in a fractal tail. Nature 2000, 403, 493–495. [Google Scholar] [CrossRef] [PubMed]
- Maher, K.; Chamberlain, C.P. Hydrologic Regulation of Chemical Weathering and the Geologic Carbon Cycle. Science 2014, 343, 1502–1504. [Google Scholar] [CrossRef] [PubMed]
- Kirchner, J.W. A double paradox in catchment hydrology and geochemistry. Hydrol. Process. 2003, 17, 871–874. [Google Scholar] [CrossRef]
- Kirchner, J.W.; Feng, X.; Neal, C. Fractal stream chemistry and its implications for contaminant transport in catchments. Nature 2000, 403, 524–527. [Google Scholar] [CrossRef] [PubMed]
- Turner, J.; Albrechtsen, H.J.; Bonell, M.; Duguet, J.P.; Harris, B.; Meckenstock, R.; McGuire, K.; Moussa, R.; Peters, N.; Richnow, H.H.; et al. Future trends in transport and fate of diffuse contaminants in catchments, with special emphasis on stable isotope applications. Hydrol. Process. 2006, 20, 205–213. [Google Scholar] [CrossRef]
- Burns, D.A.; Vitvar, T.; McDonnell, J.J.; Hassett, J.; Duncan, J.; Kendall, C. Effects of suburban development on runoff generation in the Croton River basin, New York, USA. J. Hydrol. 2005, 311, 266–281. [Google Scholar] [CrossRef]
- Buttle, J.M.; Hazlett, P.; Murray, C.; Creed, I.F.; Jeffries, D.; Semkin, R. Prediction of groundwater characteristics in forested and harvested basins during spring snowmelt using a topographic index. Hydrol. Process. 2001, 15, 3389–3407. [Google Scholar] [CrossRef]
- McGuire, K.J.; McDonnell, J.J. A review and evaluation of catchment transit time modeling. J. Hydrol. 2006, 330, 543–563. [Google Scholar] [CrossRef]
- Harman, C. Time-variable transit time distributions and transport: Theory and application to storage-dependent transport of chloride in a watershed. Water Resour. Res. 2015, 51, 1–30. [Google Scholar] [CrossRef] [Green Version]
- Soulsby, C.; Birkel, C.; Geris, J.; Dick, J.; Tunaley, C.; Tetzlaff, D. Stream water age distributions controlled by storage dynamics and nonlinear hydrologic connectivity: Modeling with high-resolution isotope data. Water Resour. Res. 2015, 51, 7759–7776. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jasechko, S.; Kirchner, J.W.; Welker, J.M.; McDonnell, J.J. Substantial proportion of global streamflow less than three months old. Nat. Geosci. 2016, 9, 126–129. [Google Scholar] [CrossRef]
- McGuire, K.J.; McDonnell, J.J.; Weiler, M.; Kendall, C.; McGlynn, B.L.; Welker, J.M.; Seibert, J. The role of topography on catchment-scale water residence time. Water Resour. Res. 2005, 41, W05002. [Google Scholar] [CrossRef]
- Tetzlaff, D.; Seibert, J.; McGuire, K.J.; Laudon, H.; Burns, D.A.; Dunn, S.M.; Soulsby, C. How does landscape structure influence catchment transit time across different geomorphic provinces? Hydrol. Process. 2009, 23, 945–953. [Google Scholar] [CrossRef]
- Hale, V.C.; McDonnell, J.J. Effect of bedrock permeability on stream base flow mean transit time scaling relations: 1. A multiscale catchment intercomparison. Water Resour. Res. 2016, 52, 1358–1374. [Google Scholar] [CrossRef]
- Weiler, M.; McGlynn, B.L.; McGuire, K.J.; McDonnell, J.J. How does rainfall become runoff? A combined tracer and runoff transfer function approach. Water Resour. Res. 2003, 39, 315. [Google Scholar] [CrossRef] [Green Version]
- McDonnell, J.J.; McGuire, K.J.; Aggarwal, P.; Beven, K.J.; Biondi, D.; Frampton, A.; Dunn, S.; James, A.L.; Kirchner, J.W.; Kraft, P.; et al. How old is streamwater? Open questions in catchment transit time conceptualization, modelling and analysis. Hydrol. Process. 2010, 24, 1745–1754. [Google Scholar] [CrossRef] [Green Version]
- Botter, G. Catchment mixing processes and travel time distributions. Water Resour. Res. 2012, 48, W05545. [Google Scholar] [CrossRef]
- Herman, J.D.; Kollat, J.B.; Reed, P.M.; Wagener, T. From maps to movies: High-resolution time-varying sensitivity analysis for spatially distributed watershed models. Hydrol. Earth Syst. Sci. 2013, 17, 5109–5125. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.-C.; Milliman, J.D.; Lee, T.-Y.; Chen, Y.-C.; Lee, J.-F.; Liu, C.-C.; Lin, J.-C.; Kao, S.-J. Terrain attributes of earthquake- and rainstorm-induced landslides in orogenic mountain Belt, Taiwan. Earth Surf. Process. Landforms 2017, 42, 1549–1559. [Google Scholar] [CrossRef]
- Zehetner, F.; Vemuri, N.L.; Huh, C.-A.; Kao, S.-J.; Hsu, S.-C.; Huang, J.-C.; Chen, Z.-S. Soil and phosphorus redistribution along a steep tea plantation in the Feitsui reservoir catchment of northern Taiwan. Soil Sci. Plant Nutr. 2008, 54, 618–626. [Google Scholar] [CrossRef]
- Lin, T.-C.; Shaner, P.-J.L.; Wang, L.-J.; Shih, Y.-T.; Wang, C.-P.; Huang, G.-H.; Huang, J.-C. Effects of mountain tea plantations on nutrient cycling at upstream watersheds. Hydrol. Earth Syst. Sci. 2015, 19, 4493–4504. [Google Scholar] [CrossRef] [Green Version]
- Hrachowitz, M.; Soulsby, C.; Tetzlaff, D.; Malcolm, I.A.; Schoups, G. Gamma distribution models for transit time estimation in catchments: Physical interpretation of parameters and implications for time-variant transit time assessment. Water Resour. Res. 2010, 46, W10536. [Google Scholar] [CrossRef] [Green Version]
- Klaus, J.; McDonnell, J.J. Hydrograph separation using stable isotopes: Review and evaluation. J. Hydrol. 2013, 505, 47–64. [Google Scholar] [CrossRef]
- Segura, C.; James, A.L.; Lazzati, D.; Roulet, N.T. Scaling relationships for event water contributions and transit times in small-forested catchments in Eastern Quebec. Water Resour. Res. 2012, 48, W07502. [Google Scholar] [CrossRef]
- Huang, J.-C.; Yu, C.-K.; Lee, J.-Y.; Cheng, L.-W.; Lee, T.-Y.; Kao, S.-J. Linking typhoon tracks and spatialrainfall patterns for improving flood lead time predictions over a mesoscale mountainous watershed. Water Resour. Res. 2012, 48, W09540. [Google Scholar] [CrossRef]
- Jakeman, A.; Hornberger, G.M. How much complexity is warranted in a rainfall-runoff model? Water Resour. Res. 1993, 29, 2637–2649. [Google Scholar] [CrossRef]
- Maloszewski, P.; Rauert, W.; Trimborn, P.; Herrmann, A.; Rau, R. Isotope hydrological study of mean transit times in an alpine basin (Wimbachtal, Germany). J. Hydrol. 1992, 140, 343–360. [Google Scholar] [CrossRef]
- Lu, M.-C.; Chang, C.-T.; Lin, T.-C.; Wang, L.-J.; Wang, C.-P.; Hsu, T.-C.; Huang, J.-C. Modeling the terrestrial N processes in a small mountain catchment through INCA-N: A case study in Taiwan. Sci. Total. Environ. 2017, 593, 319–329. [Google Scholar] [CrossRef]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424, 264–277. [Google Scholar] [CrossRef]
- Madsen, H. Automatic calibration of a conceptual rainfall–runoff model using multiple objectives. J. Hydrol. 2000, 235, 276–288. [Google Scholar] [CrossRef]
- Morris, M.D. Factorial Sampling Plans for Preliminary Computational Experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Pianosi, F.; Beven, K.; Freer, J.; Hall, J.W.; Rougier, J.; Stephenson, D.B.; Wagener, T. Sensitivity analysis of environmental models: A systematic review with practical workflow. Environ. Model. Softw. 2016, 79, 214–232. [Google Scholar] [CrossRef]
- Herman, J.D.; Kollat, J.B.; Reed, P.M.; Wagener, T. Technical Note: Method of Morris effectively reduces the computational demands of global sensitivity analysis for distributed watershed models. Hydrol. Earth Syst. Sc. 2013, 17, 2893–2903. [Google Scholar] [CrossRef] [Green Version]
- Lyon, S.W.; Desilets, S.L.E.; Troch, P.A. Characterizing the response of a catchment to an extreme rainfall event using hydrometric and isotopic data. Water Resour. Res. 2008, 44, W06413. [Google Scholar] [CrossRef]
- McGuire, K.J.; McDonnell, J.J. Hydrological connectivity of hillslopes and streams: Characteristic time scales and nonlinearities. Water Resour. Res. 2010, 46, W10543. [Google Scholar] [CrossRef] [Green Version]
- Jencso, K.G.; McGlynn, B.L.; Gooseff, M.; Wondzell, S.M.; Bencala, K.E.; Marshall, L. Hydrologic connectivity between landscapes and streams: Transferring reach- and plot-scale understanding to the catchment scale. Water Resour. Res. 2009, 45, W04428. [Google Scholar] [CrossRef] [Green Version]
- Schellekens, J.; Scatena, F.; Bruijnzeel, L.; Van Dijk, A.; Groen, M.M.A.; Van Hogezand, R.J.P. Stormflow generation in a small rainforest catchment in the Luquillo Experimental Forest, Puerto Rico. Hydrol. Process. 2004, 18, 505–530. [Google Scholar] [CrossRef]
- Asano, Y.; Uchida, T. Flow path depth is the main controller of mean base flow transit times in a mountainous catchment. Water Resour. Res. 2012, 48, W03512. [Google Scholar] [CrossRef]
- Brown, V.A.; McDonnell, J.J.; Burns, D.A.; Kendall, C. The role of event water, a rapid shallow flow component, and catchment size in summer stormflow. J. Hydrol. 1999, 217, 171–190. [Google Scholar] [CrossRef]
- Kirchner, J.W. Quantifying new water fractions and transit time distributions using ensemble hydrograph separation: Theory and benchmark tests. Hydrol. Earth Syst. Sci. 2019, 23, 303–349. [Google Scholar] [CrossRef] [Green Version]
- Muñoz-Villers, L.E.; McDonnell, J.J. Runoff generation in a steep, tropical montane cloud forest catchment on permeable volcanic substrate Runoff generation in a steep, tropical montane cloud forest catchment on permeable volcanic substrate. Water Resour. Res. 2012, 48, W09528. [Google Scholar] [CrossRef] [Green Version]
- Gabrielli, C.P.; McDonnell, J.J.; Jarvis, W. The role of bedrock groundwater in rainfall–runoff response at hillslope and catchment scales. J. Hydrol. 2012, 450, 117–133. [Google Scholar] [CrossRef]
- Berghuijs, W.; Kirchner, J.W. The relationship between contrasting ages of groundwater and streamflow. Geophys. Res. Lett. 2017, 44, 8925–8935. [Google Scholar] [CrossRef] [Green Version]
- McDonnell, J.J. Where does water go when it rains? Moving beyond the variable source area concept of rainfall-runoff response. Hydrol. Process. 2003, 17, 1869–1875. [Google Scholar] [CrossRef]
- Lehmann, P.; Hinz, C.; McGrath, G.; Van Meerveld, I.; McDonnell, J.J. Rainfall threshold for hillslope outflow: An emergent property of flow pathway connectivity. Hydrol. Earth Syst. Sci. 2007, 11, 1047–1063. [Google Scholar] [CrossRef] [Green Version]
| Parameter | Description | Range |
|---|---|---|
| a1 | Weighting the precipitation | 0.005–0.1 |
| a2 | Exponentially weighting the precipitation backward in time | 1–15 |
| a3 | Initial antecedent precipitation index | 0–1 |
| αq | Shape parameter in runoff transfer function | 0.1–3.5 |
| βq | Scale parameter in runoff transfer function | 1–100 |
| b1 | Weighting the Peff | 0–100 |
| b2 | Exponentially weighting the Peff backward in time | 1–15 |
| αe | Shape parameter in event water transfer function | 0.1–3.5 |
| βe | Scale parameter in event water transfer function | 1–100 |
| Catchment Event | Typhoon | Date | P | D | RIavg | Pmax3h | Q | Qmax | Q/P | AP7day |
|---|---|---|---|---|---|---|---|---|---|---|
| (year/month/day) | (mm) | (h) | (mm h−1) | (mm) | (mm) | (mm) | (-) | (mm) | ||
| PL01 | Saola | 2012/7/31 | 699 | 78 | 9.0 | 116 | 440 | 20.9 | 0.63 | 73 |
| PL02 | Soulik | 2013/7/12 | 253 | 23 | 11.0 | 88 | 120 | 12.5 | 0.47 | 2 |
| PL03 | Trami | 2013/8/21 | 319 | 47 | 6.8 | 88 | 149 | 11.9 | 0.47 | 22 |
| PL04 | Matmo | 2014/7/22 | 236 | 34 | 6.9 | 54 | 135 | 6.7 | 0.57 | 0 |
| PL05 | Chan-hom | 2015/7/9 | 261 | 45 | 5.8 | 48 | 158 | 6.2 | 0.61 | 27 |
| PL06 | Soudelor | 2015/8/7 | 414 | 48 | 8.6 | 107 | 299 | 22.5 | 0.72 | 19 |
| Average | 364 | 46 | 8.0 | 84 | 217 | 13.5 | 0.58 | 24 | ||
| DL01 | Saola | 2012/7/31 | 934 | 86 | 10.9 | 121 | 621 | 27.0 | 0.66 | 135 |
| DL02 | Soulik | 2013/7/12 | 374 | 21 | 17.8 | 120 | 196 | 21.4 | 0.52 | 1 |
| DL03 | Trami | 2013/8/21 | 345 | 43 | 8.0 | 92 | 171 | 13.3 | 0.50 | 16 |
| DL04 | Matmo | 2014/7/22 | 249 | 29 | 8.6 | 55 | 178 | 9.2 | 0.71 | 6 |
| DL05 | Chan-hom | 2015/7/9 | 247 | 38 | 6.5 | 46 | 162 | 6.0 | 0.66 | 48 |
| DL06 | Soudelor | 2015/8/7 | 612 | 43 | 14.2 | 189 | 337 | 34.1 | 0.55 | 25 |
| Average | 460 | 43 | 11.0 | 104 | 278 | 18.5 | 0.60 | 39 |
| Catchment Event | Typhoon | Rainwater (‰) | Streamwater (‰) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| n | Average * | SE | Maximum | Minimum | n | Average * | SE | Maximum | Minimum | ||
| PL01 | Saola | 21 | −11.6 | 3.13 | −3.4 | −15.7 | 24 | −8.6 | 1.18 | −6.3 | −10.7 |
| PL02 | Soulik | 8 | −8.5 | 4.75 | 2.5 | −10.1 | 13 | −7.1 | 0.99 | −4.8 | −8.0 |
| PL03 | Trami | 11 | −14.1 | 4.18 | −5.7 | −18.1 | 15 | −8.5 | 0.94 | −6.5 | −10.0 |
| PL04 | Matmo | 10 | −10.4 | 3.15 | −6.4 | −16.0 | 13 | −7.1 | 1.00 | −5.1 | −7.8 |
| PL05 | Chan-hom | 16 | −5.3 | 1.76 | −3.2 | −8.3 | 21 | −5.6 | 0.41 | −4.8 | −6.3 |
| PL06 | Soudelor | 13 | −9.3 | 4.12 | −1.0 | −14.1 | 18 | −7.2 | 1.12 | −5.0 | −8.5 |
| DL01 | Saola | 21 | −11.2 | 3.13 | −3.4 | −15.7 | 24 | −8.8 | 0.94 | −7.0 | −11.0 |
| DL02 | Soulik | 8 | −8.0 | 4.75 | 2.5 | −10.1 | 12 | −6.9 | 0.60 | −5.4 | −7.6 |
| DL03 | Trami | 11 | −13.9 | 4.18 | −5.7 | −18.1 | 15 | −8.8 | 0.96 | −6.8 | −10.3 |
| DL04 | Matmo | 10 | −10.7 | 3.15 | −6.4 | −16.0 | 13 | −7.2 | 0.80 | −5.9 | −8.3 |
| DL05 | Chan-hom | 16 | −4.8 | 1.76 | −3.2 | −8.3 | 21 | −6.8 | 0.62 | −6.1 | −8.6 |
| DL06 | Soudelor | 13 | −9.1 | 4.12 | −1.0 | −14.1 | 18 | −7.5 | 0.97 | −5.7 | −8.7 |
| Catchment Event | αe | βe | Mean Transit Time of Event Water (MTTew) | Fraction of Event water (Few) | ||||
|---|---|---|---|---|---|---|---|---|
| PL01 | 0.68 | (0.65–0.80) | 8.3 | (6.2–8.4) | 5.6 | (4.9–5.8) | 0.33 | (0.31–0.33) |
| PL02 | 0.80 | (0.76–0.80) | 5.4 | (5.4–5.7) | 4.3 | (4.3–4.5) | 0.39 | (0.39–0.40) |
| PL03 | 1.45 | (1.25–1.46) | 2.3 | (2.3–2.8) | 3.3 | (3.3–3.5) | 0.14 | (0.13–0.14) |
| PL04 | 1.90 | (1.79–1.94) | 3.5 | (3.5–4.0) | 6.7 | (6.7–7.4) | 0.41 | (0.40–0.42) |
| PL05 | 3.01 | (2.85–3.21) | 1.9 | (1.7–2.0) | 5.7 | (5.5–5.9) | 0.20 | (0.20–0.21) |
| PL06 | 0.78 | (0.72–0.79) | 7.8 | (7.5–8.4) | 6.1 | (5.5–6.2) | 0.56 | (0.55–0.57) |
| DL01 | 1.10 | (0.77–1.19) | 4.7 | (4.3–7.6) | 5.1 | (4.9–6.0) | 0.24 | (0.24–0.29) |
| DL02 | 0.56 | (0.54–0.62) | 4.0 | (3.9–4.9) | 2.3 | (2.3–2.7) | 0.59 | (0.56–0.59) |
| DL03 | 0.72 | (0.72–0.81) | 12.0 | (11.8–13) | 8.6 | (8.6–10.0) | 0.20 | (0.17–0.26) |
| DL04 | 2.18 | (1.72–2.52) | 2.5 | (1.8–11.2) | 5.4 | (4.5–22.8) | 0.28 | (0.28–0.56) |
| DL05 | 1.74 | (1.63–1.77) | 6.3 | (5.2–6.3) | 10.9 | (8.5–11.1) | 0.61 | (0.56–0.61) |
| DL06 | 0.92 | (0.88–1.12) | 4.2 | (3.6–4.4) | 3.8 | (3.8–4.3) | 0.80 | (0.79–0.81) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.-Y.; Shih, Y.-T.; Lan, C.-Y.; Lee, T.-Y.; Peng, T.-R.; Lee, C.-T.; Huang, J.-C. Rainstorm Magnitude Likely Regulates Event Water Fraction and Its Transit Time in Mesoscale Mountainous Catchments: Implication for Modelling Parameterization. Water 2020, 12, 1169. https://doi.org/10.3390/w12041169
Lee J-Y, Shih Y-T, Lan C-Y, Lee T-Y, Peng T-R, Lee C-T, Huang J-C. Rainstorm Magnitude Likely Regulates Event Water Fraction and Its Transit Time in Mesoscale Mountainous Catchments: Implication for Modelling Parameterization. Water. 2020; 12(4):1169. https://doi.org/10.3390/w12041169
Chicago/Turabian StyleLee, Jun-Yi, Yu-Ting Shih, Chiao-Ying Lan, Tsung-Yu Lee, Tsung-Ren Peng, Cheing-Tung Lee, and Jr-Chuan Huang. 2020. "Rainstorm Magnitude Likely Regulates Event Water Fraction and Its Transit Time in Mesoscale Mountainous Catchments: Implication for Modelling Parameterization" Water 12, no. 4: 1169. https://doi.org/10.3390/w12041169
APA StyleLee, J.-Y., Shih, Y.-T., Lan, C.-Y., Lee, T.-Y., Peng, T.-R., Lee, C.-T., & Huang, J.-C. (2020). Rainstorm Magnitude Likely Regulates Event Water Fraction and Its Transit Time in Mesoscale Mountainous Catchments: Implication for Modelling Parameterization. Water, 12(4), 1169. https://doi.org/10.3390/w12041169








