Modeling Urban Flood Inundation and Recession Impacted by Manholes
Abstract
1. Introduction
2. Methods
2.1. Hydrodynamic Modeling Using SWMM
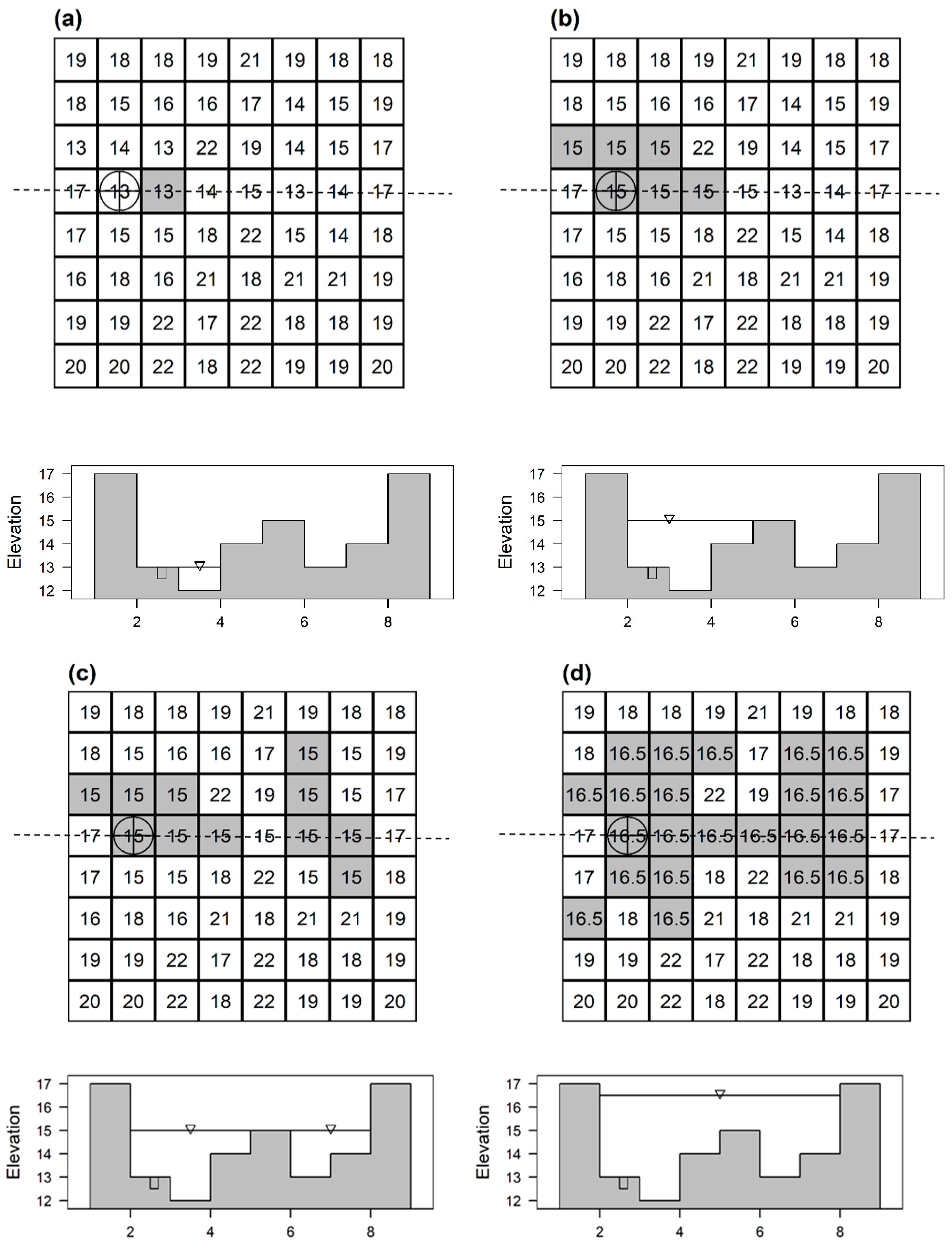
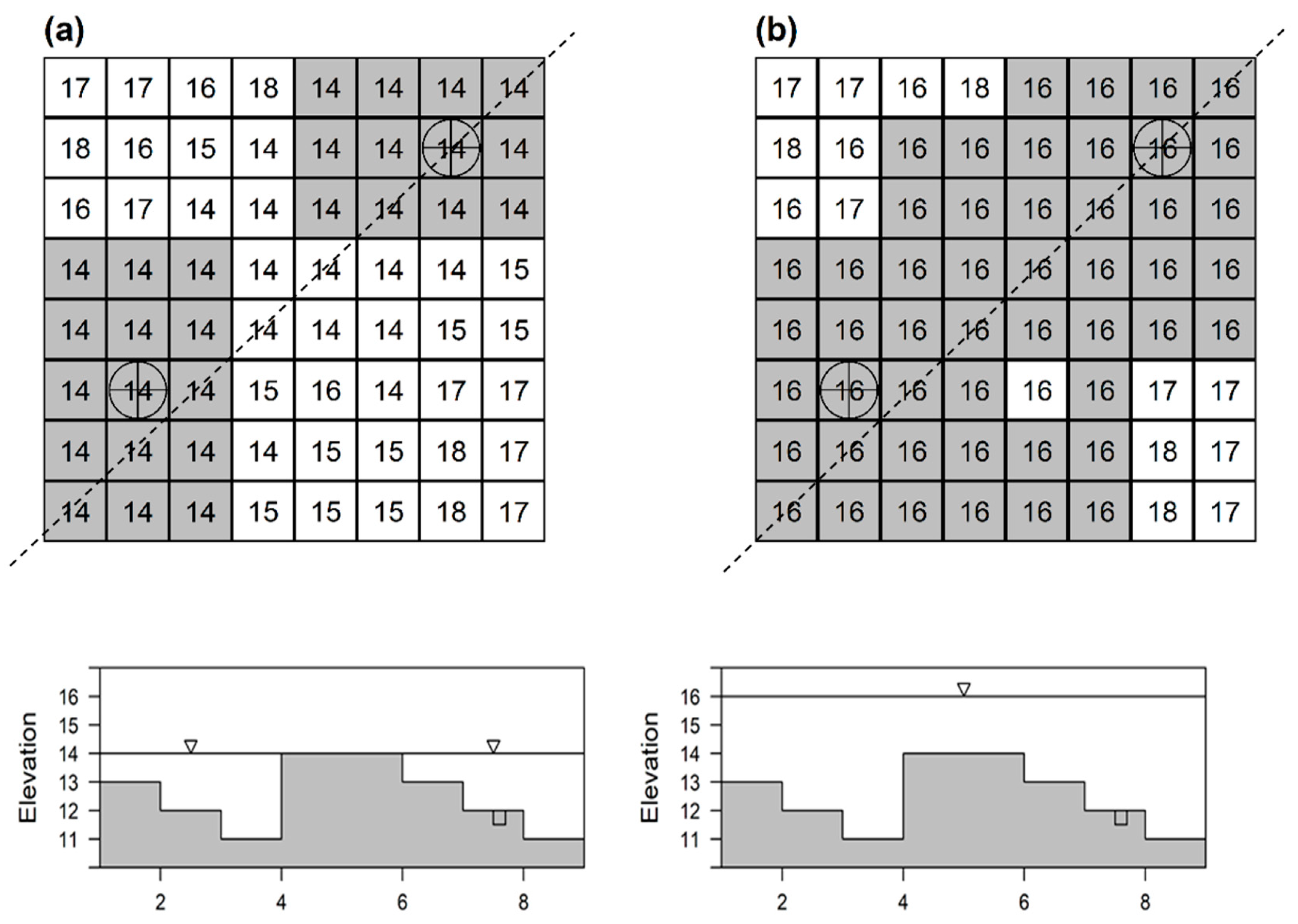
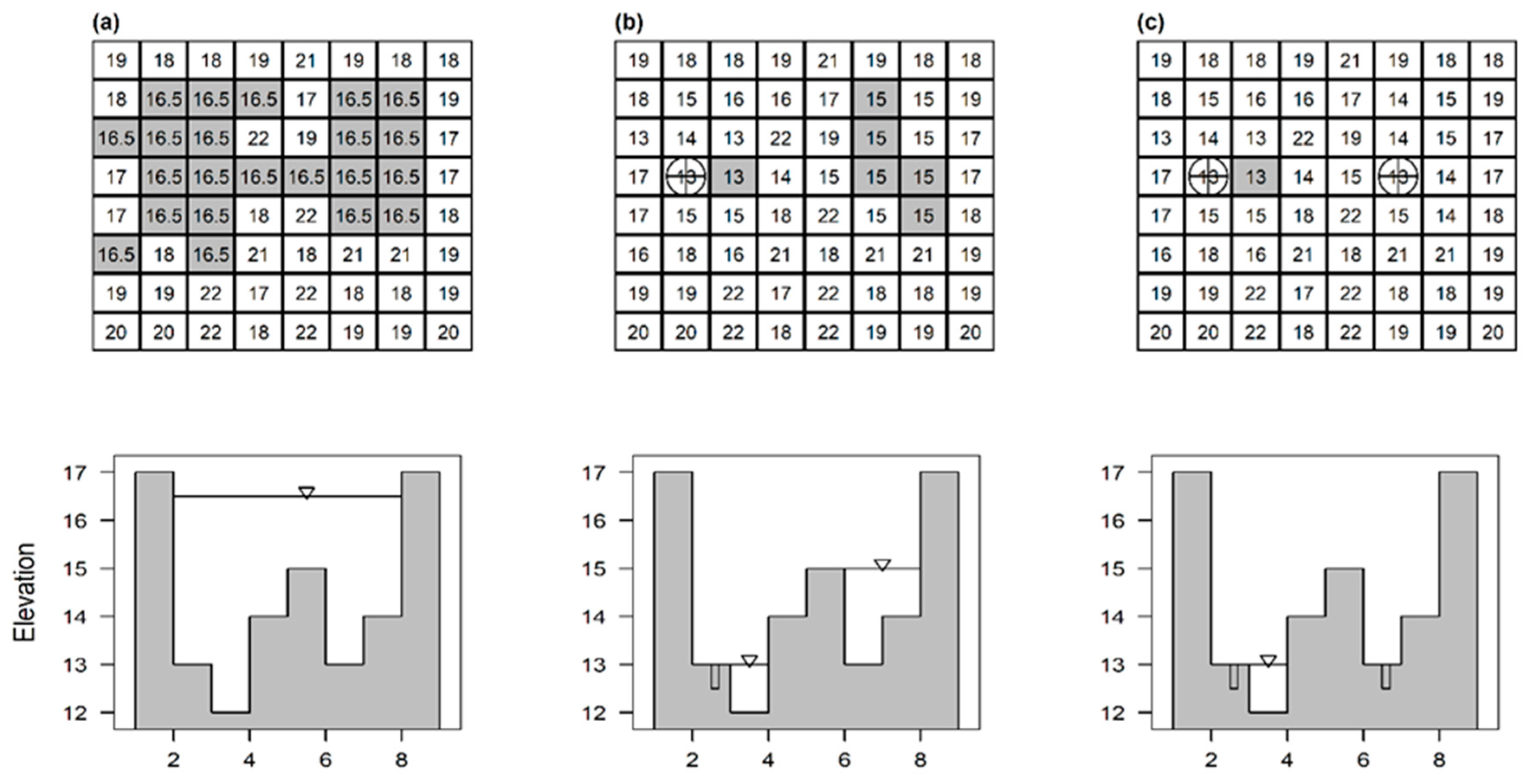
2.2. Manhole Overland Flow Inundation and Recession Modeling
2.2.1. Manhole Overland Flow Inundation Modeling
2.2.2. Recession Modeling Associated with Manholes
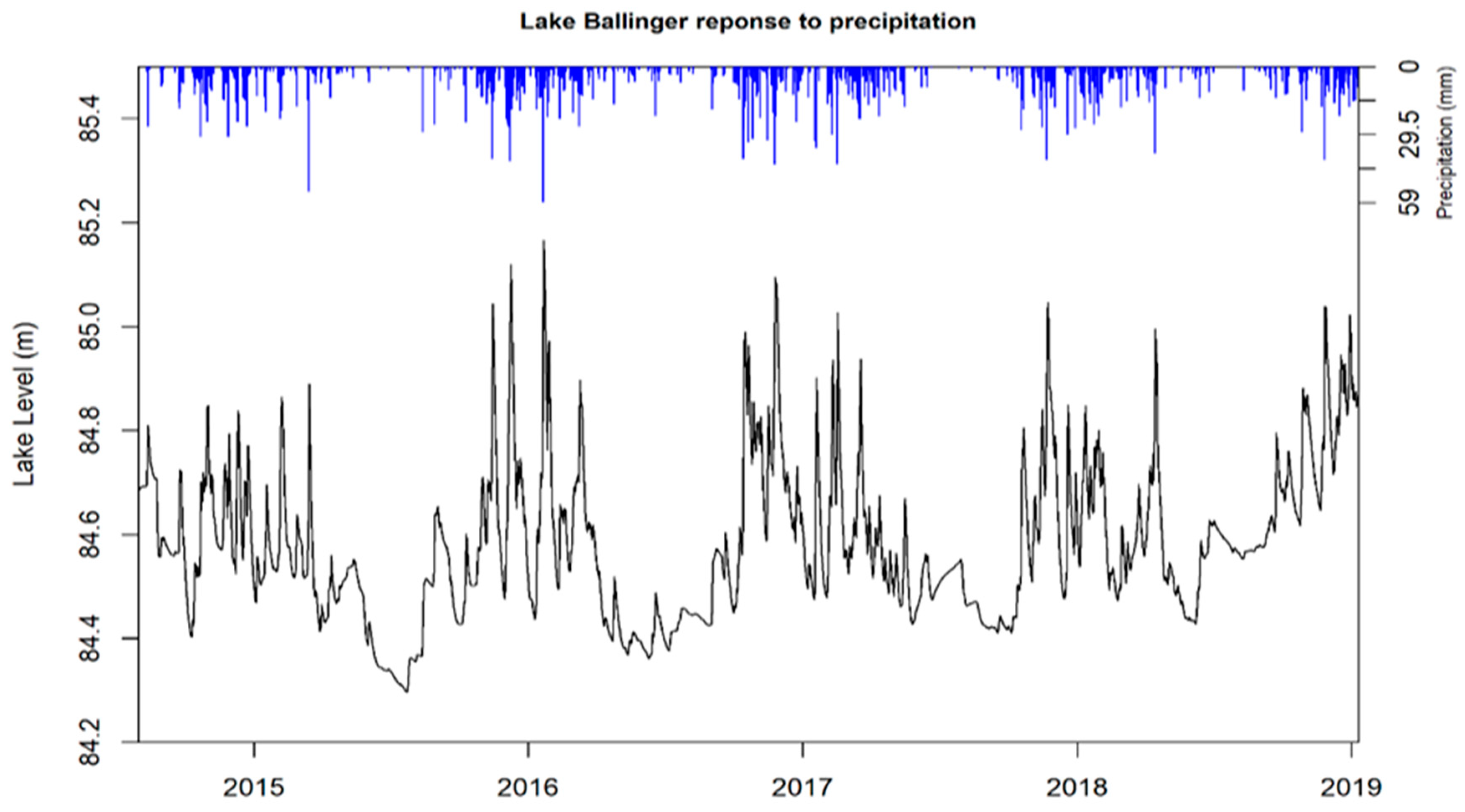
2.3. Study Site: The Hall Creek Watershed
2.3.1. Data
2.3.2. SWMM Model
2.4. Model Inundation Accuracy
3. Results and Discussion
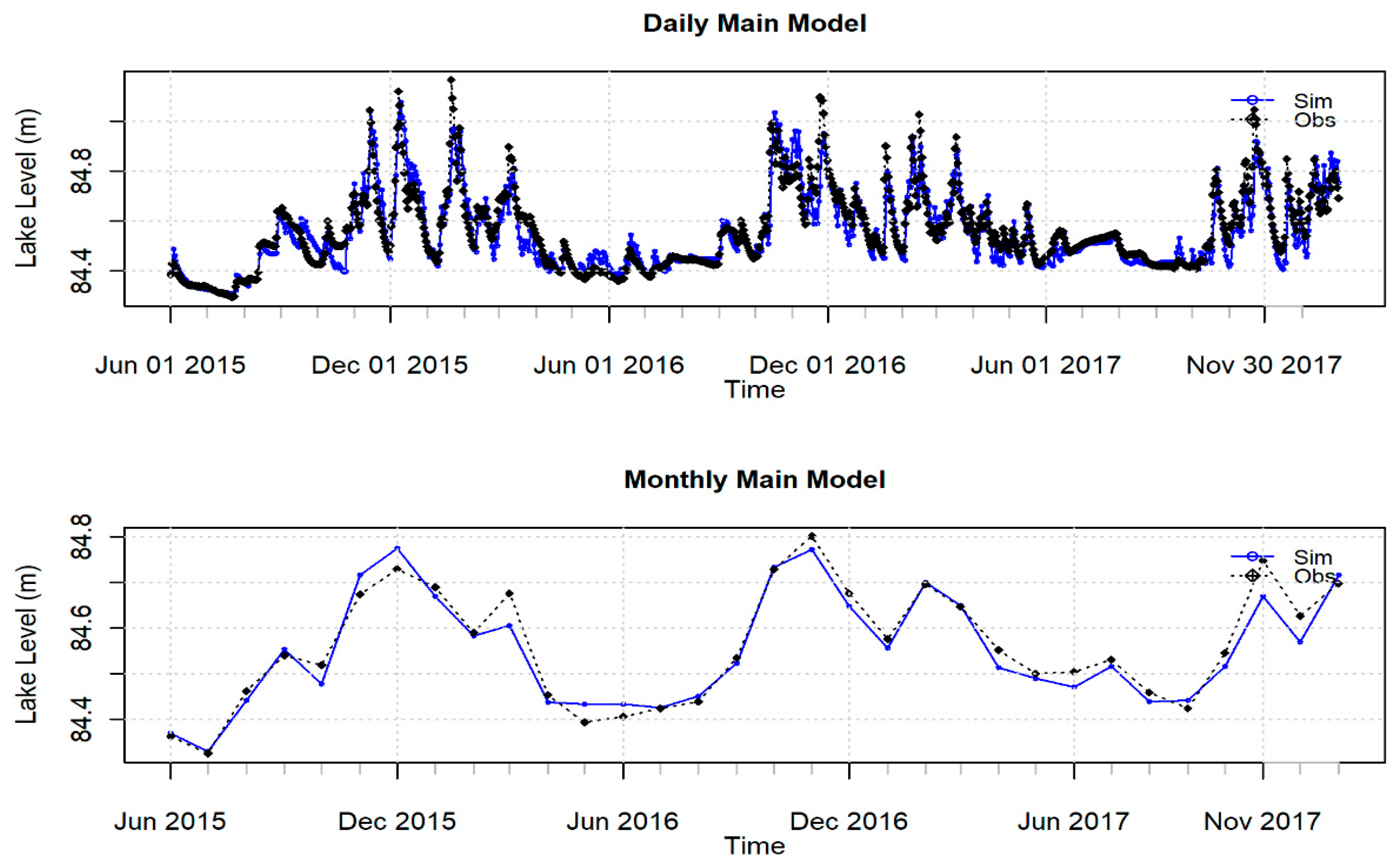
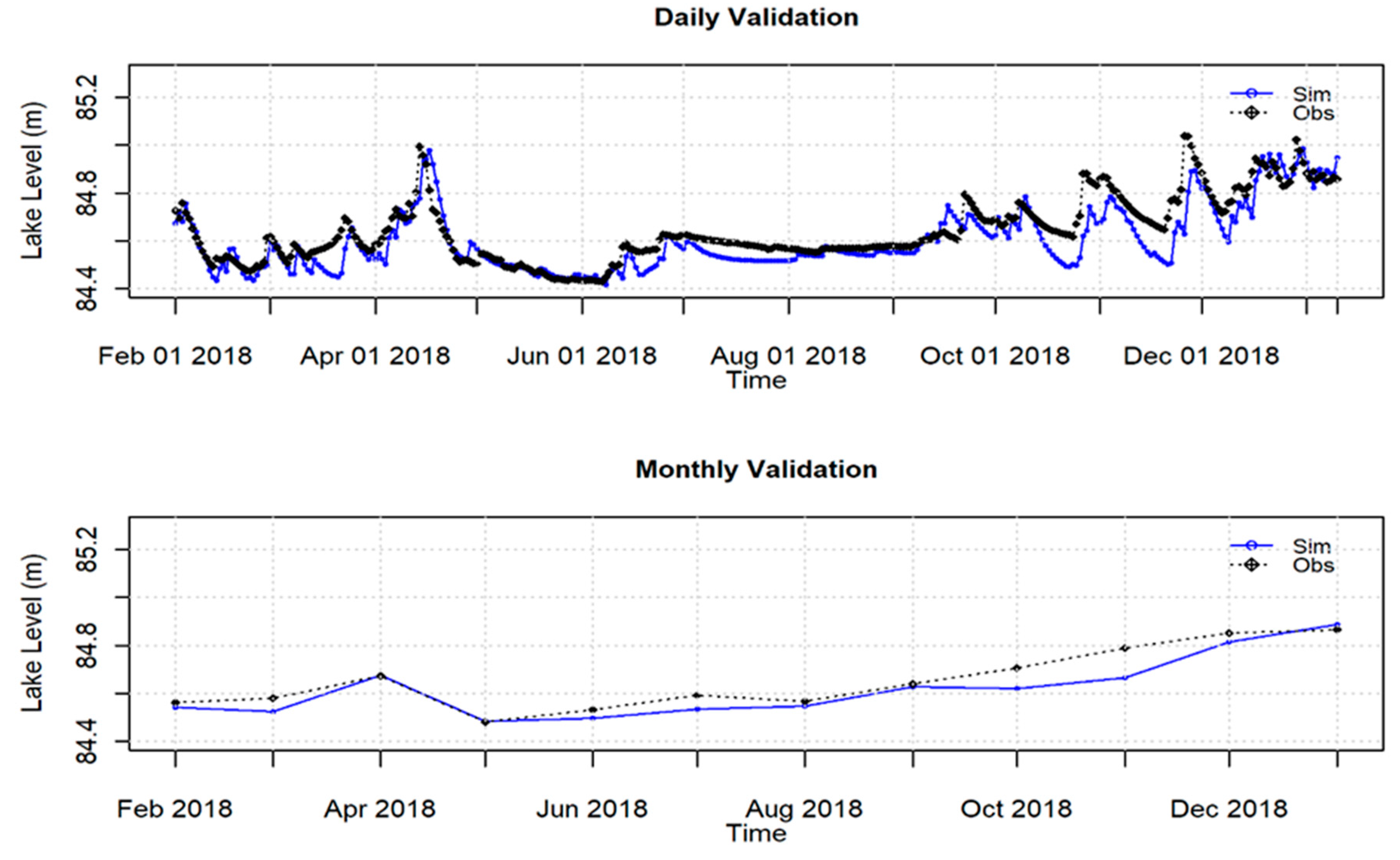
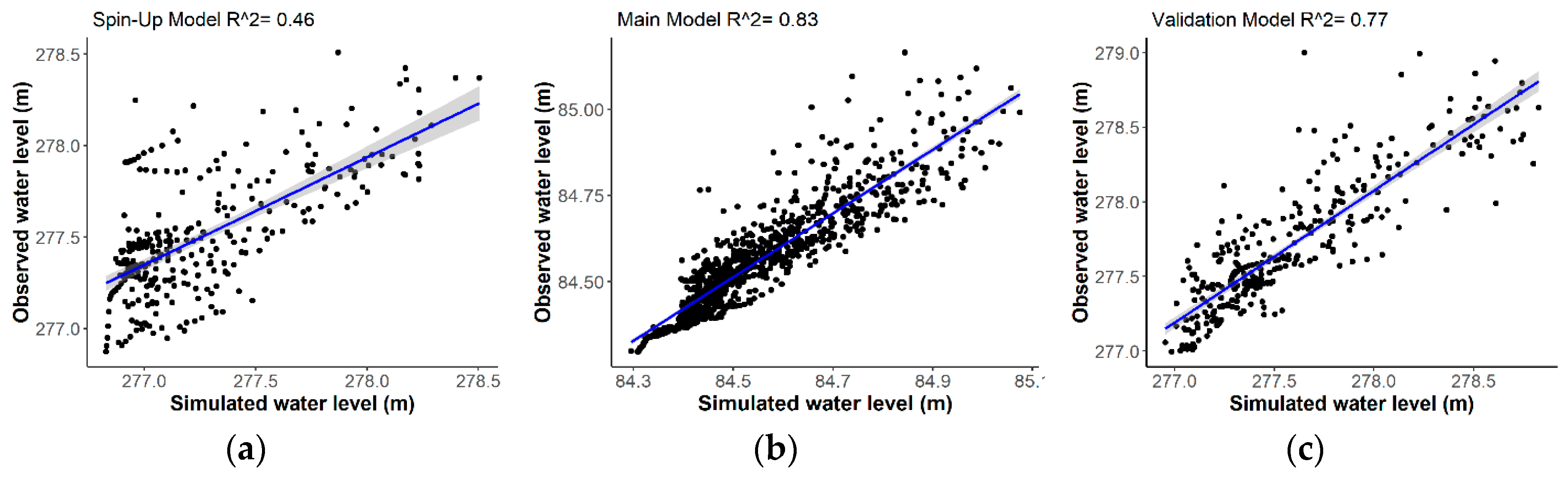
3.1. SWMM Model Calibration and Validation
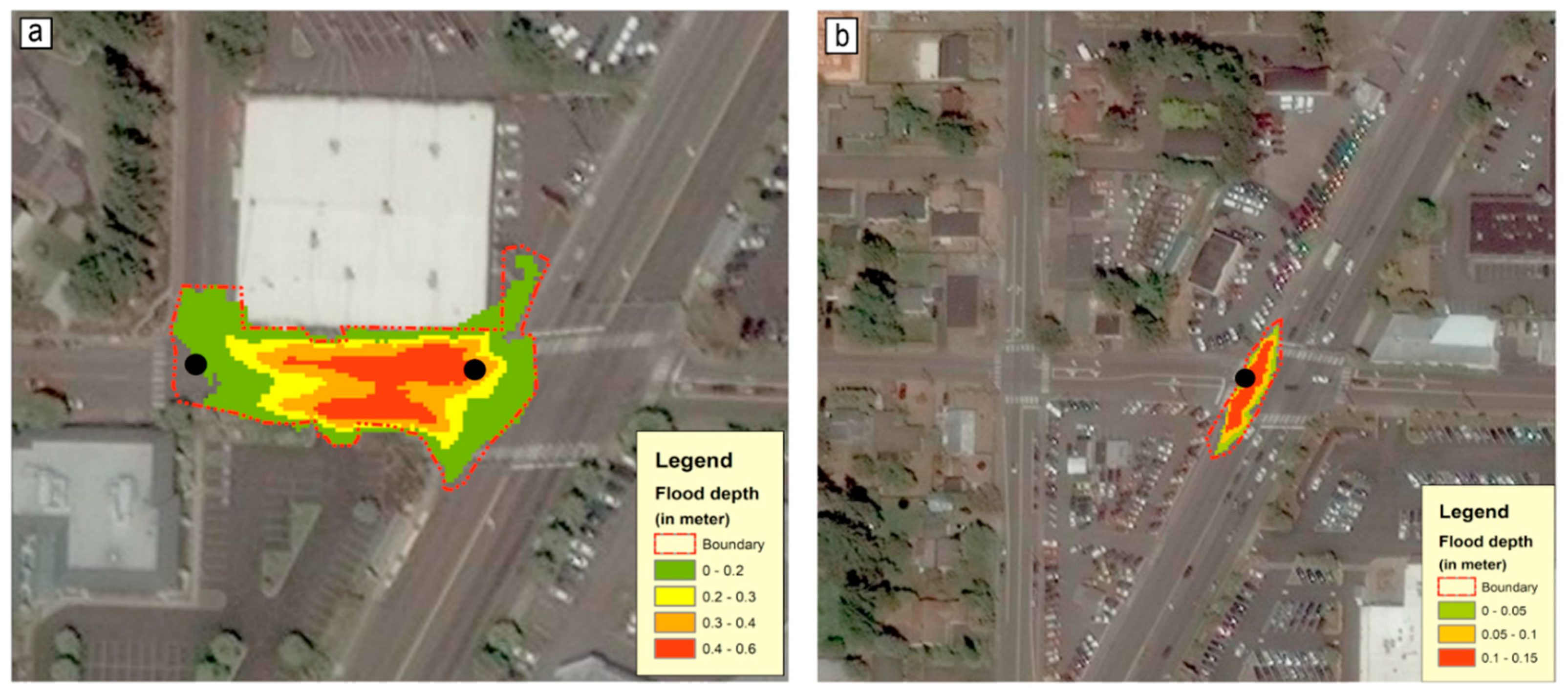
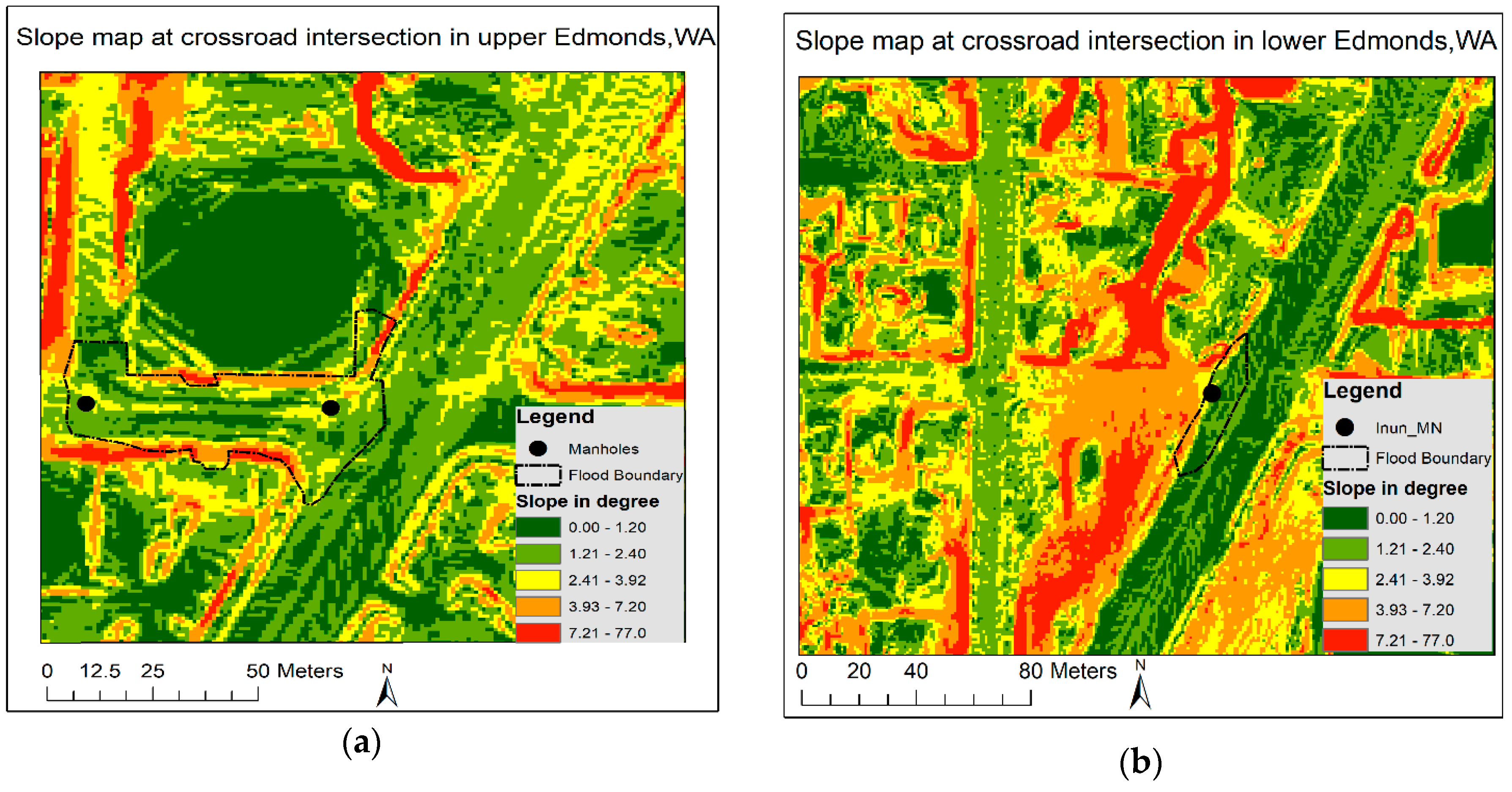
3.2. Flood Inundation and Recession
3.3. Model Inundation and Recession Accuracy
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wallemacq, P.; Herden, C.; House, R. The Human Cost of Natural Disasters 2015: A Global Perspective; Technical report; Centre for Research on the Epidemiology of Disasters: Brussels, Belgium, 2015. [Google Scholar]
- Stocker, T.F.; Qin, D.; Plattner, G.-K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M. Climate change 2013: The physical science basis. In Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013; Volume 1535. [Google Scholar]
- Technical Mapping Advisory Council (TMAC). Technical Mapping Advisory Council (TMAC) 2015 Annual Report Summary. Available online: https://www.fema.gov/media-library-data/1454954186441-34ff688ee1abc00873df80c4d323a4df/TMAC_2015_Annual_Report_Summary.pdf (accessed on 13 March 2020).
- Federal Emergency Management Agency (FEMA). Loss Dollars Paid by Calendar Year. Available online: https://www.fema.gov/loss-dollars-paid-calendar-year (accessed on 13 March 2020).
- European Environmental Agency (EEA). Mapping the impacts of natural hazards and technological accidents in Europe – an overview of the last decade. EEA Technical Report No13/2010. Available online: https://www.eea.europa.eu/publications/mapping-the-impacts-of-natural (accessed on 13 March 2020).
- Wang, W.; Li, H.Y.; Leung, L.R.; Yigzaw, W.; Zhao, J.; Lu, H.; Deng, Z.; Demisie, Y.; Blöschl, G. Nonlinear filtering effects of reservoirs on flood frequency curves at the regional scale. Water Resour. Res. 2017, 53, 8277–8292. [Google Scholar] [CrossRef]
- Ye, S.; Li, H.-Y.; Leung, L.R.; Guo, J.; Ran, Q.; Demissie, Y.; Sivapalan, M. Understanding flood seasonality and its temporal shifts within the contiguous United States. J. Hydrometeorol. 2017, 18, 1997–2009. [Google Scholar] [CrossRef]
- Milner, A.M.; Picken, J.L.; Klaar, M.J.; Robertson, A.L.; Clitherow, L.R.; Eagle, L.; Brown, L.E. River ecosystem resilience to extreme flood events. Ecol. Evol. 2018, 8, 8354–8363. [Google Scholar] [CrossRef] [PubMed]
- Scanlon, B.R.; Keese, K.E.; Flint, A.L.; Flint, L.E.; Gaye, C.B.; Edmunds, W.M.; Simmers, I. Global synthesis of groundwater recharge in semiarid and arid regions. Hydrol. Processes 2006, 20, 3335–3370. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, G.; Xu, Y.J. Impacts of the 2013 extreme flood in Northeast China on regional groundwater depth and quality. Water 2015, 7, 4575–4592. [Google Scholar] [CrossRef]
- Jasechko, S.; Birks, S.J.; Gleeson, T.; Wada, Y.; Fawcett, P.J.; Sharp, Z.D.; McDonnell, J.J.; Welker, J.M. The pronounced seasonality of global groundwater recharge. Water Resour. Res. 2014, 50, 8845–8867. [Google Scholar] [CrossRef]
- Cuthbert, M.O.; Taylor, R.G.; Favreau, G.; Todd, M.C.; Shamsudduha, M.; Villholth, K.G.; MacDonald, A.M.; Scanlon, B.R.; Kotchoni, D.V.; Vouillamoz, J.-M. Observed controls on resilience of groundwater to climate variability in sub-Saharan Africa. Nature 2019, 572, 230–234. [Google Scholar] [CrossRef]
- Dahlke, H.; Brown, A.; Orloff, S.; Putnam, D.; O’Geen, T. Managed winter flooding of alfalfa recharges groundwater with minimal crop damage. Calif. Agr. 2018, 72, 65–75. [Google Scholar] [CrossRef]
- GebreEgziabher, M. An Integrated Hydrogeological Study to Understand the Groundwater Flow Dynamics in Raya Valley Basin, Northern Ethiopia: Hydrochemistry, Isotope Hydrology and Flow Modeling Approaches. Master’s Thesis, Addis Ababa University, Addis Ababa, Ethiopia, 2011. [Google Scholar]
- Changnon, S.A., Jr. Recent studies of urban effects on precipitation in the United States. Bull. Am. Meteorol. Soc. 1969, 50, 411–421. [Google Scholar] [CrossRef]
- Arnbjerg-Nielsen, K.; Willems, P.; Olsson, J.; Beecham, S.; Pathirana, A.; Bülow Gregersen, I.; Madsen, H.; Nguyen, V.-T.-V. Impacts of climate change on rainfall extremes and urban drainage systems: A review. Water Sci. Technol. 2013, 68, 16–28. [Google Scholar] [CrossRef]
- Boyd, E.; Juhola, S. Adaptive climate change governance for urban resilience. Urban Stud. 2015, 52, 1234–1264. [Google Scholar] [CrossRef]
- Ford, A.; Barr, S.; Dawson, R.; Virgo, J.; Batty, M.; Hall, J. A multi-scale urban integrated assessment framework for climate change studies: A flooding application. Comput. Environ. Urban 2019, 75, 229–243. [Google Scholar] [CrossRef]
- Chen, J.; Hill, A.A.; Urbano, L.D. A GIS-based model for urban flood inundation. J. Hydrol. 2009, 373, 184–192. [Google Scholar] [CrossRef]
- Wang, R.-Q.; Mao, H.; Wang, Y.; Rae, C.; Shaw, W. Hyper-resolution monitoring of urban flooding with social media and crowdsourcing data. Comput. Geosci. 2018, 111, 139–147. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering, and Medicine. Framing the Challenge of Urban Flooding in the United States; National Academies Press: Washington, DC, USA, 2019. [Google Scholar]
- Jacobson, C.R. Identification and quantification of the hydrological impacts of imperviousness in urban catchments: A review. J. Environ. Manage. 2011, 92, 1438–1448. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Villarini, G.; Vecchi, G.A.; Smith, J.A. Urbanization exacerbated the rainfall and flooding caused by hurricane Harvey in Houston. Nature 2018, 563, 384–388. [Google Scholar] [CrossRef] [PubMed]
- Shuster, W.D.; Bonta, J.; Thurston, H.; Warnemuende, E.; Smith, D. Impacts of impervious surface on watershed hydrology: A review. Urban Water J. 2005, 2, 263–275. [Google Scholar] [CrossRef]
- Diakakis, M.; Deligiannakis, G.; Pallikarakis, A.; Skordoulis, M. Identifying elements that affect the probability of buildings to suffer flooding in urban areas using Google Street View. A case study from Athens metropolitan area in Greece. Int. J. Disaster Risk Reduct. 2017, 22, 1–9. [Google Scholar] [CrossRef]
- Golz, S.; Schinke, R.; Naumann, T. Assessing the effects of flood resilience technologies on building scale. Urban Water J. 2015, 12, 3043. [Google Scholar] [CrossRef]
- Hu, M.; Sayama, T.; Zhang, X.; Tanaka, K.; Takara, K.; Yang, H. Evaluation of low impact development approach for mitigating flood inundation at a watershed scale in China. J. Environ. Manage. 2017, 193, 430–438. [Google Scholar] [CrossRef]
- Brody, S.; Sebastian, A.; Blessing, R.; Bedient, P. Case study results from southeast Houston, Texas: Identifying the impacts of residential location on flood risk and loss. J. Flood Risk Manage. 2018, 11, S110–S120. [Google Scholar] [CrossRef]
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.F.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Modell. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Yu, D.; Coulthard, T.J. Evaluating the importance of catchment hydrological parameters for urban surface water flood modelling using a simple hydro-inundation model. J. Hydrol. 2015, 524, 385–400. [Google Scholar] [CrossRef]
- Courty, L.G.; Pedrozo-Acuña, A.; Bates, P.D. Itzï (version 17.1): An open-source, distributed GIS model for dynamic flood simulation. Geosci. Model. Dev. 2017, 10, 1835. [Google Scholar] [CrossRef]
- Rosenberg, E.A.; Keys, P.W.; Booth, D.B.; Hartley, D.; Burkey, J.; Steinemann, A.C.; Lettenmaier, D.P. Precipitation extremes and the impacts of climate change on stormwater infrastructure in Washington State. Clim. Change 2010, 102, 319–349. [Google Scholar] [CrossRef]
- Mishra, V.; Ganguly, A.R.; Nijssen, B.; Lettenmaier, D.P. Changes in observed climate extremes in global urban areas. Environ. Res. Lett. 2015, 10, 024005. [Google Scholar] [CrossRef]
- Muis, S.; Güneralp, B.; Jongman, B.; Aerts, J.C.; Ward, P.J. Flood risk and adaptation strategies under climate change and urban expansion: A probabilistic analysis using global data. Sci. Total Environ. 2015, 538, 445–457. [Google Scholar] [CrossRef]
- Zhao, G.; Xu, Z.; Pang, B.; Tu, T.; Xu, L.; Du, L. An enhanced inundation method for urban flood hazard mapping at the large catchment scale. J. Hydrol. 2019, 571, 873–882. [Google Scholar] [CrossRef]
- Zhao, T.; Shao, Q.; Zhang, Y. Deriving flood-mediated connectivity between river channels and floodplains: Data-driven approaches. Sci. Rep. 2017, 7, 43239. [Google Scholar] [CrossRef]
- Wang, X.; Kinsland, G.; Poudel, D.; Fenech, A. Urban flood prediction under heavy precipitation. J. Hydrol. 2019, 577, 123984. [Google Scholar] [CrossRef]
- Jamali, B.; Bach, P.M.; Cunningham, L.; Deletic, A. A Cellular Automata Fast Flood Evaluation (CA-ffé) Model. Water Resour. Res. 2019, 55, 4936–4953. [Google Scholar] [CrossRef]
- Zheng, X.; Maidment, D.R.; Tarboton, D.G.; Liu, Y.Y.; Passalacqua, P. GeoFlood: Large-Scale Flood Inundation Mapping Based on High-Resolution Terrain Analysis. Water Resour. Res. 2018, 54, 10013–10033. [Google Scholar] [CrossRef]
- Yang, T.-H.; Chen, Y.-C.; Chang, Y.-C.; Yang, S.-C.; Ho, J.-Y. Comparison of different grid cell ordering approaches in a simplified inundation model. Water 2015, 7, 438–454. [Google Scholar] [CrossRef]
- Meng, X.; Zhang, M.; Wen, J.; Du, S.; Xu, H.; Wang, L.; Yang, Y. A Simple GIS-Based Model for Urban Rainstorm Inundation Simulation. Sustainability 2019, 11, 2830. [Google Scholar] [CrossRef]
- Sörensen, J.; Mobini, S. Pluvial, urban flood mechanisms and characteristics–assessment based on insurance claims. J. Hydrol. 2017, 555, 51–67. [Google Scholar] [CrossRef]
- Leandro, J.; Martins, R. A methodology for linking 2D overland flow models with the sewer network model SWMM 5.1 based on dynamic link libraries. Water Sci. Technol. 2016, 73, 3017–3026. [Google Scholar] [CrossRef]
- Son, A.-L.; Kim, B.; Han, K.-Y. A simple and robust method for simultaneous consideration of overland and underground space in urban flood modeling. Water 2016, 8, 494. [Google Scholar] [CrossRef]
- Chang, T.-J.; Wang, C.-H.; Chen, A.S.; Djordjević, S. The effect of inclusion of inlets in dual drainage modelling. J. Hydrol. 2018, 559, 541–555. [Google Scholar] [CrossRef]
- Jang, J.-H.; Chang, T.-H.; Chen, W.-B. Effect of inlet modelling on surface drainage in coupled urban flood simulation. J. Hydrol. 2018, 562, 168–180. [Google Scholar] [CrossRef]
- Seyoum, S.D.; Vojinovic, Z.; Price, R.K.; Weesakul, S. Coupled 1D and noninertia 2D flood inundation model for simulation of urban flooding. J. Hydraul. Eng. 2012, 138, 23–34. [Google Scholar] [CrossRef]
- Chen, A.S.; Leandro, J.; Djordjević, S. Modelling sewer discharge via displacement of manhole covers during flood events using 1D/2D SIPSON/P-DWave dual drainage simulations. Urban Water J. 2016, 13, 830–840. [Google Scholar] [CrossRef]
- Rossman, L.A.; Huber, W. Storm water management model reference manual volume II–hydraulics. US Environ. Prot. Agency II (Mayo) 2017, 190. Available online: https://nepis.epa.gov/Exe/ZyPDF.cgi?Dockey=P100S9AS.pdf (accessed on 17 April 2020).
- Kessler, R. Stormwater strategies: Cities prepare aging infrastructure for climate change. Environ. Health Perspect. 2011, 119, 514–519. [Google Scholar] [CrossRef] [PubMed]
- Milly, P.C.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity is dead: Whither water management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef] [PubMed]
- Yan, H.; Sun, N.; Wigmosta, M.; Skaggs, R.; Hou, Z.; Leung, L.R. Next-generation intensity–duration–frequency curves to reduce errors in peak flood design. J. Hydrol. Eng. 2019, 24, 04019020. [Google Scholar] [CrossRef]
- Mullen, K.; Ardia, D.; Gil, D.L.; Windover, D.; Cline, J. DEoptim: An R package for global optimization by differential evolution. J. Stat. Softw. 2011, 40, 1–26. [Google Scholar] [CrossRef]
- Means, J.E.; Acker, S.A.; Harding, D.J.; Blair, J.B.; Lefsky, M.A.; Cohen, W.B.; Harmon, M.E.; McKee, W.A. Use of large-footprint scanning airborne lidar to estimate forest stand characteristics in the Western Cascades of Oregon. Remote Sens. Environ. 1999, 67, 298–308. [Google Scholar] [CrossRef]
- Leutnant, D.; Döring, A.; Uhl, M. swmmr-an R package to interface SWMM. Urban Water J. 2019, 16, 68–76. [Google Scholar] [CrossRef]
- Niazi, M.; Nietch, C.; Maghrebi, M.; Jackson, N.; Bennett, B.R.; Tryby, M.; Massoudieh, A. Storm water management model: Performance review and gap analysis. J. Sustain. Water Built Env. 2017, 3, 04017002. [Google Scholar] [CrossRef]
- Gray, J.E.; Pribil, M.J.; Van Metre, P.C.; Borrok, D.M.; Thapalia, A. Identification of contamination in a lake sediment core using Hg and Pb isotopic compositions, Lake Ballinger, Washington, WA, USA. J. Appl. Geochem. 2013, 29, 1–12. [Google Scholar] [CrossRef]
- Thapalia, A.; Borrok, D.M.; Van Metre, P.C.; Musgrove, M.; Landa, E.R. Zn and Cu isotopes as tracers of anthropogenic contamination in a sediment core from an urban lake. Environ. Sci. Technol. 2010, 44, 1544–1550. [Google Scholar] [CrossRef]
- Boyle, D.P.; Gupta, H.V.; Sorooshian, S. Toward improved calibration of hydrologic models: Combining the strengths of manual and automatic methods. Water Resour. Res. 2000, 36, 3663–3674. [Google Scholar] [CrossRef]
- Price, K.; Storn, R.M.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization; Springer Science & Business Media: Berlin, Germany, 2006. [Google Scholar]
- Ardia, D.; Mullen, K.; Peterson, B.; Ulrich, J. DEoptim’: Differential Evolution in ‘R’. Version 2.2-3. 2015. Available online: https://cran.r-project.org/web/packages/DEoptim/DEoptim.pdf (accessed on 4 April 2020).
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10(3), 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424, 264–277. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, A.S.; Fu, G.; Djordjević, S.; Zhang, C.; Savić, D.A. An integrated framework for high-resolution urban flood modelling considering multiple information sources and urban features. Environ. Modell Softw. 2018, 107, 85–95. [Google Scholar] [CrossRef]
- Wing, O.E.; Bates, P.D.; Sampson, C.C.; Smith, A.M.; Johnson, K.A.; Erickson, T.A. Validation of a 30 m resolution flood hazard model of the conterminous United States. Water Resour. Res. 2017, 53, 7968–7986. [Google Scholar] [CrossRef]
- Bates, P.D.; De Roo, A. A simple raster-based model for flood inundation simulation. J. Hydrol. 2000, 236, 54–77. [Google Scholar] [CrossRef]
- Bernini, A.; Franchini, M. A rapid model for delimiting flooded areas. Water Resour Manag. 2013, 27, 3825–3846. [Google Scholar] [CrossRef]
- Lhomme, J.; Sayers, P.; Gouldby, B.; Samuels, P.; Wills, M.; Mulet-Marti, J. Recent development and application of a rapid flood spreading method. In Proceedings of the FloodRisk 2008 Conference, Oxford, UK, 30 September–2 October 2008; Taylor and Francis Group: London, UK, 2008. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]


| Statistics | Ranges | Optimal Value |
|---|---|---|
| −∞ to 1 | 1 | |
| 0 to 100 | 0 | |
| 0 to 1 | 0 | |
| 0 to 1 | 1 |
| Flooded in Observed Boundary | Dry in Observed Boundary | |
|---|---|---|
| Flooded in FIRM | True flood (TP) | False flood (FP) |
| Dry in FIRM | False dry (FN) | True dry (TN) |
| Parameters | Lower–Upper Bound | Optimal Values |
|---|---|---|
| Impervious (%) | 25–90 | 70 |
| Width (m) | 150–300 | 152 |
| Roughness (−) | 0.01–0.03 | 0.012 |
| Depression Storage (mm) | 1.2–5.2 | 1.78 |
| Hydraulic Conductivity (mm/h) | 0.1–3 | 0.11 |
| Simulation | KGE | NSE | RSR | PBIAS | Performance Rating [71] | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Daily | Mon | Daily | Mon | Daily | Mon | Daily | Mon | Daily | Mon | |
| Spin Up | 0.64 | 0.61 | −0.31 | −1.15 | 1.14 | RSR | −0.10 | −0.10 | Unsat * | Unsat * |
| Calibration | 0.91 | 0.96 | 0.82 | 0.94 | 0.43 | 1.39 | 0.00 | 0.00 | V. good ^ | V. good ^ |
| Validation | 0.88 | 0.95 | 0.67 | 0.81 | 0.57 | 0.24 | 0.00 | 0.00 | Good | V. good ^ |
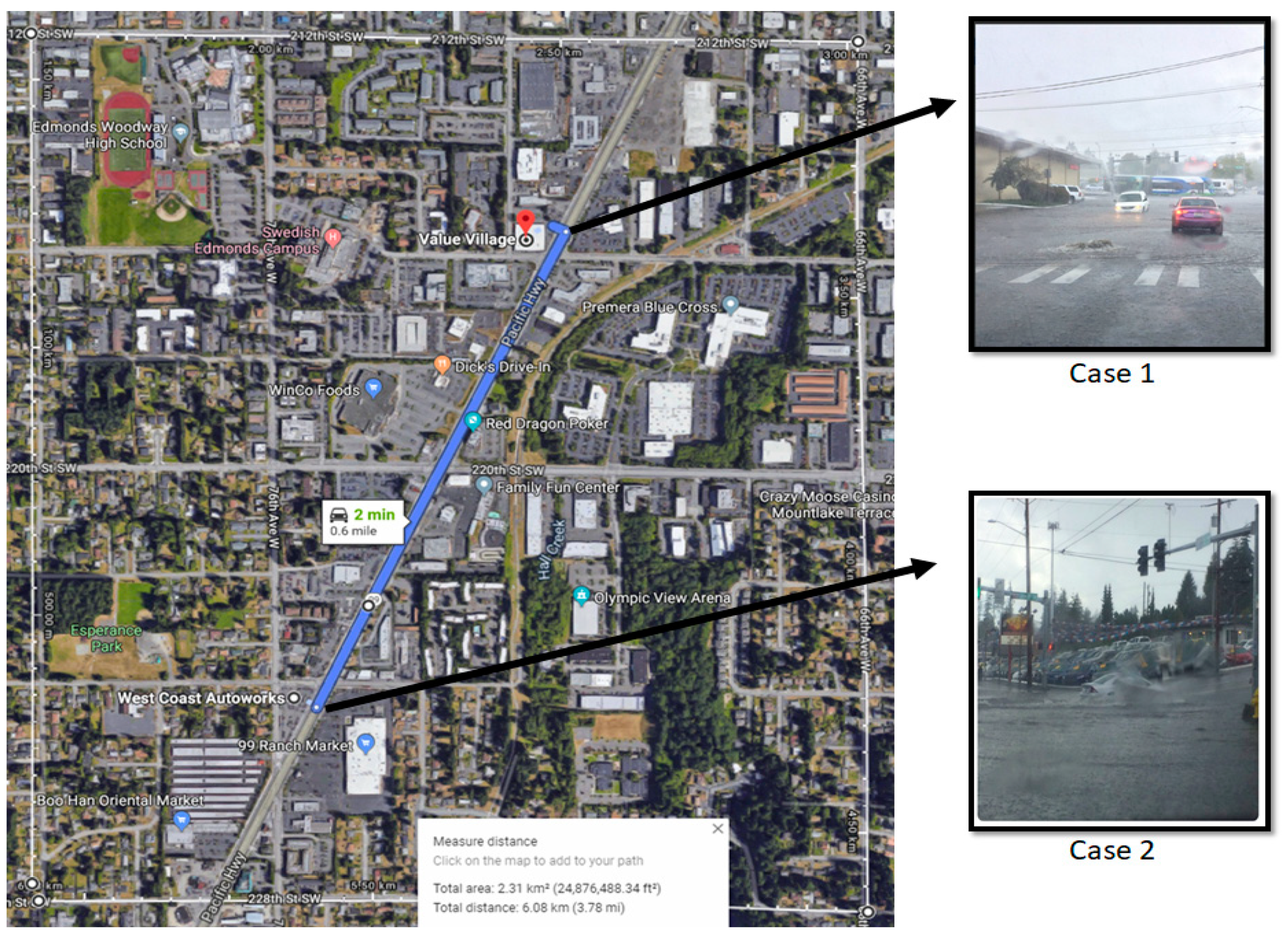
| Inundation Model Performance | Case 1 | Case 2 |
|---|---|---|
| True positive rate, TPR (%) | 89.04 | 71.31 |
| Positive predictive value, PPV (%) | 95.44 | 97.25 |
| Modified fit, MF (%) | 85.04 | 69.90 |
| Modified bias, MB (%) | −6.71 | −26.68 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
GebreEgziabher, M.; Demissie, Y. Modeling Urban Flood Inundation and Recession Impacted by Manholes. Water 2020, 12, 1160. https://doi.org/10.3390/w12041160
GebreEgziabher M, Demissie Y. Modeling Urban Flood Inundation and Recession Impacted by Manholes. Water. 2020; 12(4):1160. https://doi.org/10.3390/w12041160
Chicago/Turabian StyleGebreEgziabher, Merhawi, and Yonas Demissie. 2020. "Modeling Urban Flood Inundation and Recession Impacted by Manholes" Water 12, no. 4: 1160. https://doi.org/10.3390/w12041160
APA StyleGebreEgziabher, M., & Demissie, Y. (2020). Modeling Urban Flood Inundation and Recession Impacted by Manholes. Water, 12(4), 1160. https://doi.org/10.3390/w12041160





