Coupling SKS and SWMM to Solve the Inverse Problem Based on Artificial Tracer Tests in Karstic Aquifers
Abstract
:1. Introduction
2. Materials and Methods
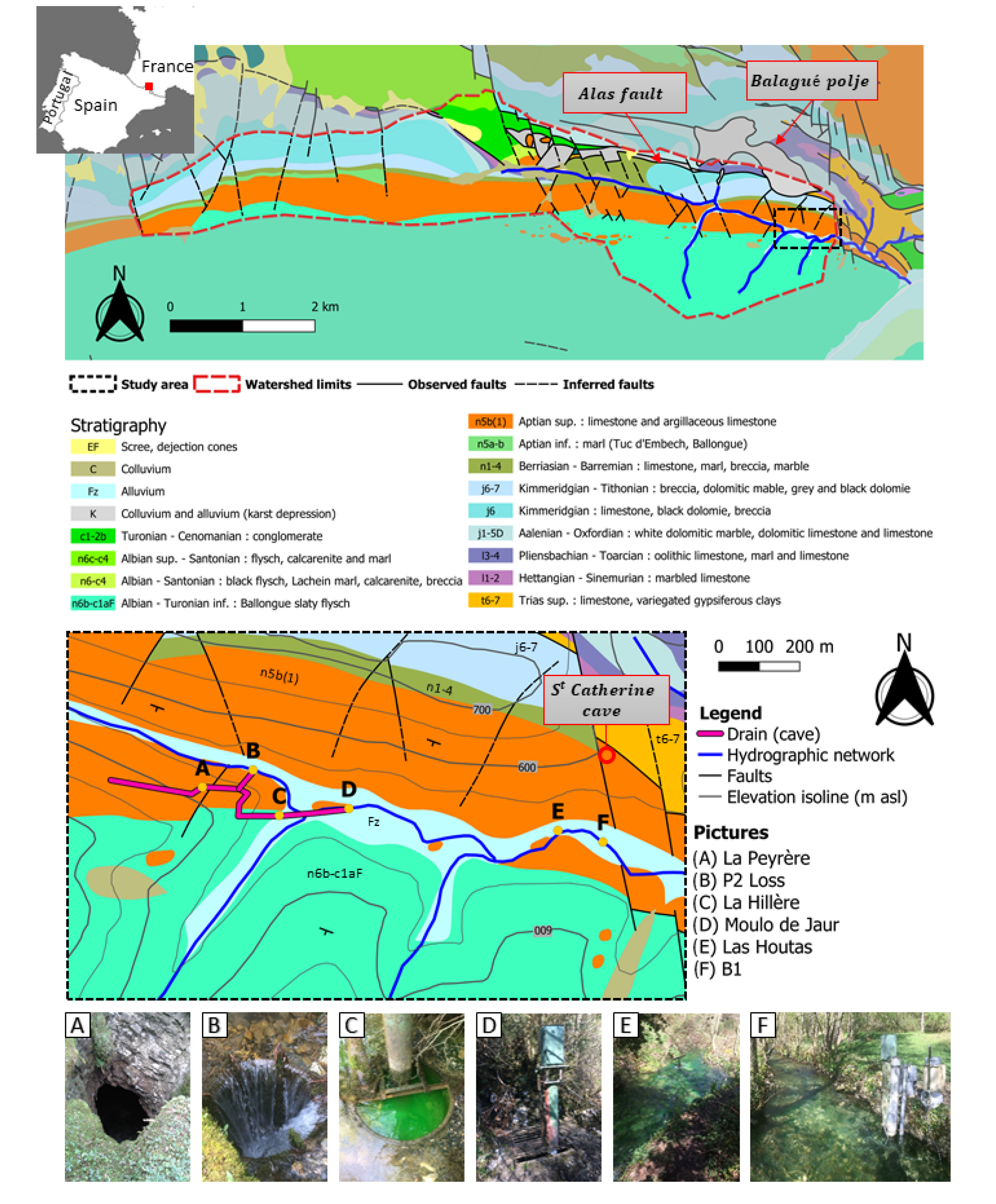
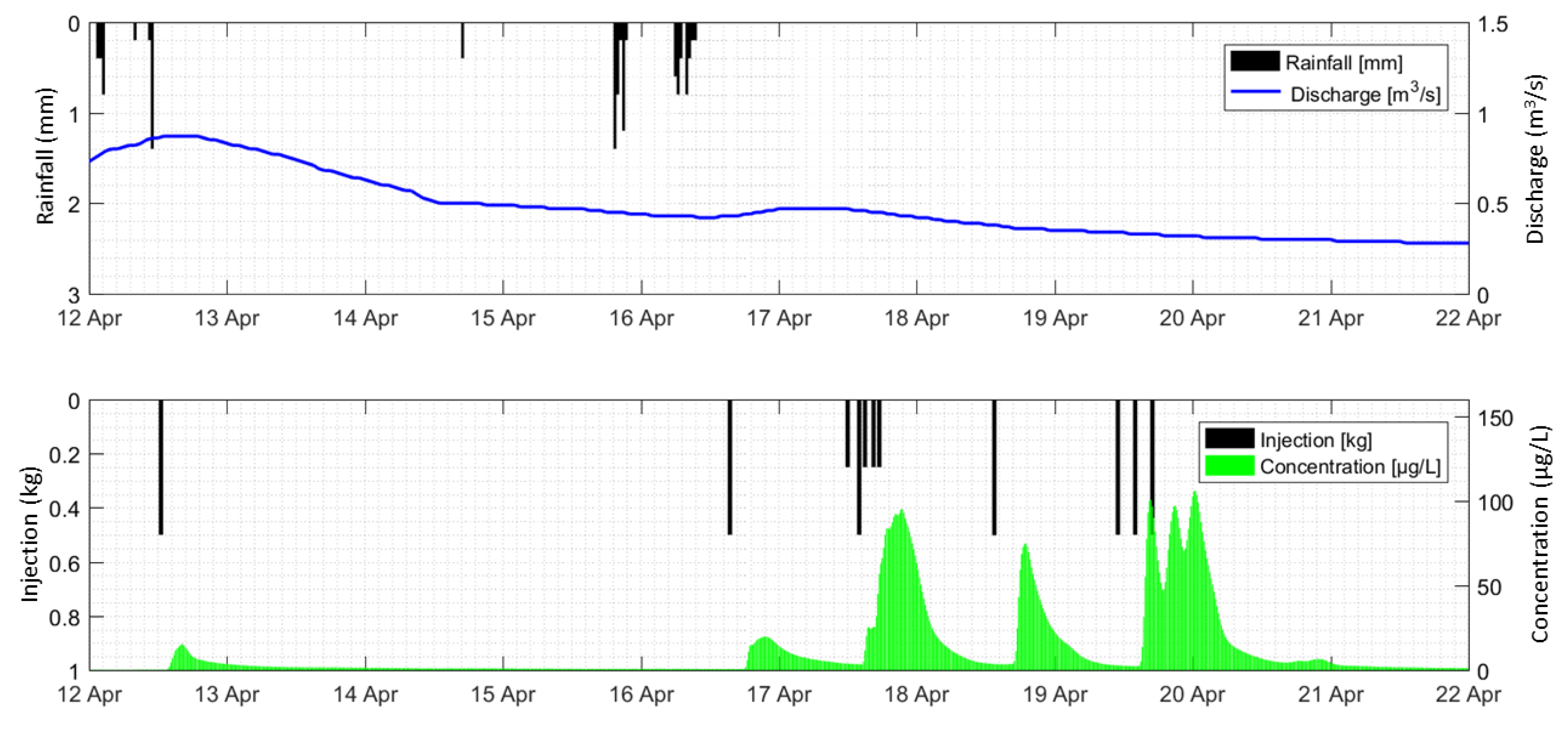
2.1. Study site and Field Data
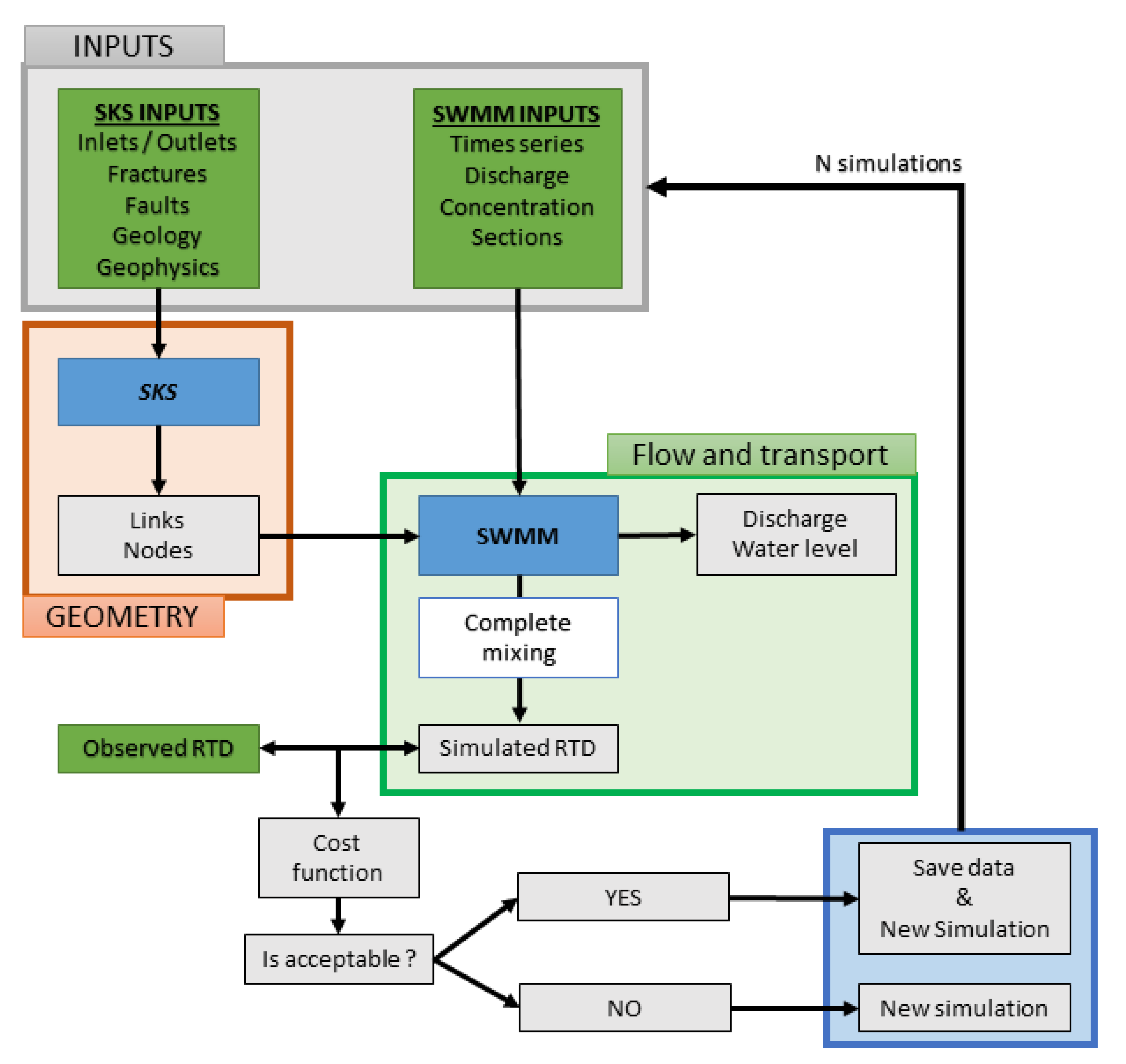
2.2. Modeling Approach
2.2.1. Conduit Network Simulation
- Building a geological model of the studied area. It covered about 1 km2. Only the two main geological formations were considered: the slaty flysch in the southern part of the area and the Jurassic to Cretaceous metamorphic limestones in the northern part of the area. The contact between these two formations is oriented in the west-east direction. The calcareous formation was numerically considered as a homogeneous formation affected by structural heterogeneities (faults and fractures). Then, bedding planes, inception horizons, or even foliation were not considered for implementation of geological constraints in conduit networks simulation with SKS. This constitutes a strong hypothesis but seems to be acceptable regarding the small extension of the simulation area. Moreover, slaty formations constituted a boundary condition for the development of the conduit networks.
- The structural heterogeneities (faults and fractures) over the area were considered in the SKS model. The main discontinuity direction was recognized from the satellite image, running 170° N to 10° N orientations [57,58,59] as well as the faults and fractures reported by the French geological survey (BRGM) in the BD_CHARM database [54]. The fracture model includes the main structures identified in the area and a set of stochastic fractures that is different for every simulation and generated following the statistical distributions derived from the field data. Besides, the observations made through speleological investigations [44] have been considered as conditional data in the conduit network simulations; thus, SKS reproduces this known conduit.
- The inlets and outlets can be identified and imposed in SKS. The inlets are composed of La Peyrère, P2 Loss, La Hillière and Moulo de Jaur. Moreover, some additional potential inlets can be randomly added over the area to ensure more physical realism and to allow potential feeding branches along with the solute transport to be considered. Then, Las Hountas, which is the perennial outlet of the Baget system, constitutes the only outlet of the synthetic conduits networks.
2.2.2. Flow Simulation
2.2.3. Solute Transport Modeling
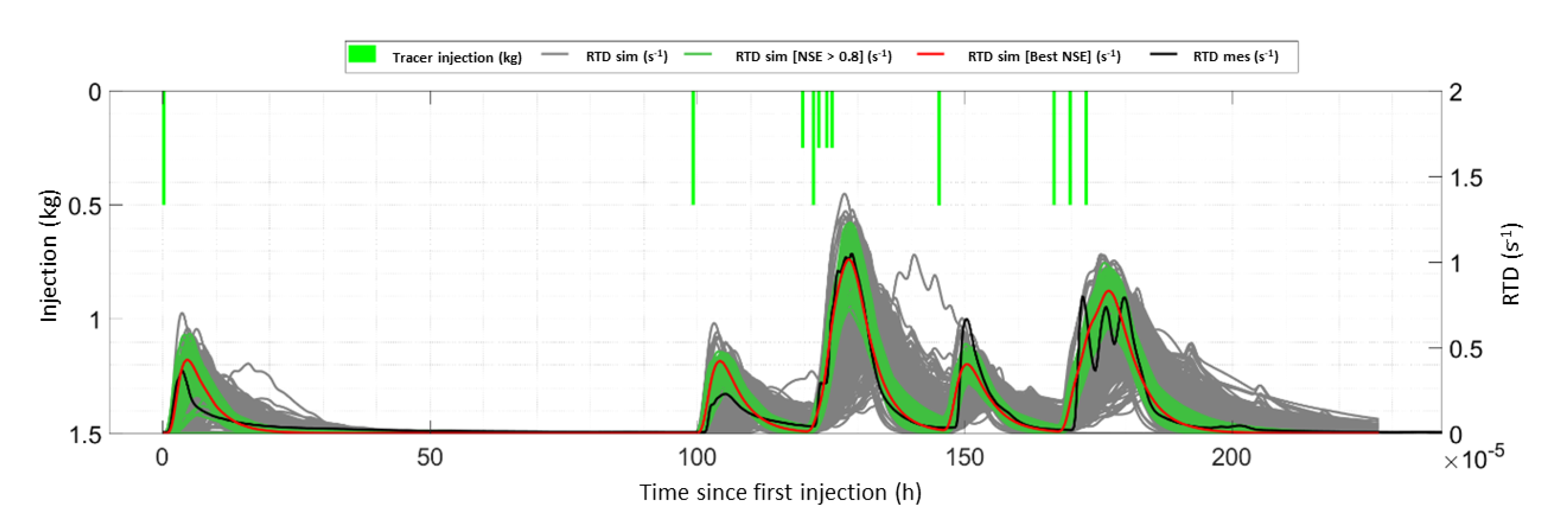
3. Results
3.1. Model Setup
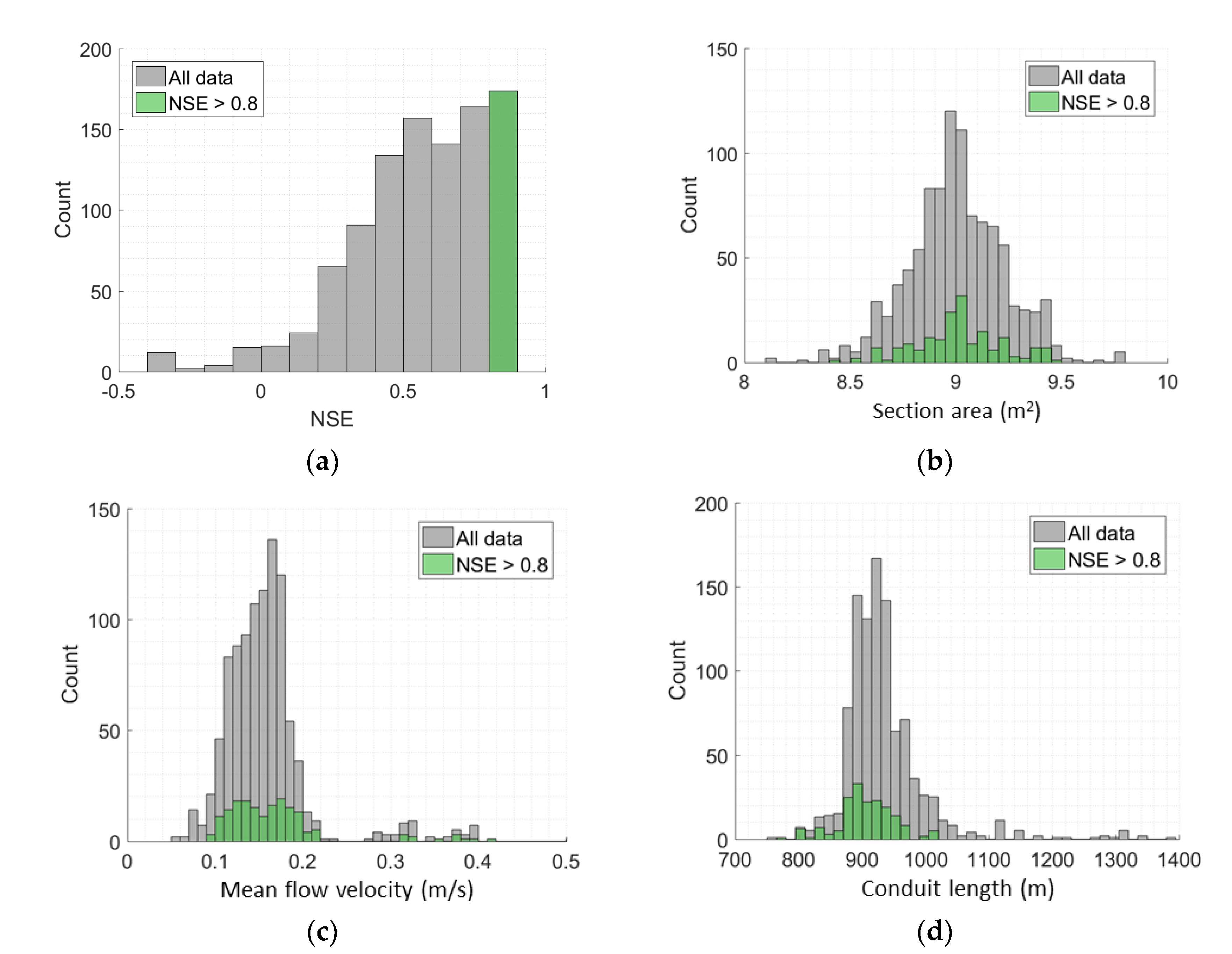
3.2. Statistical Analysis
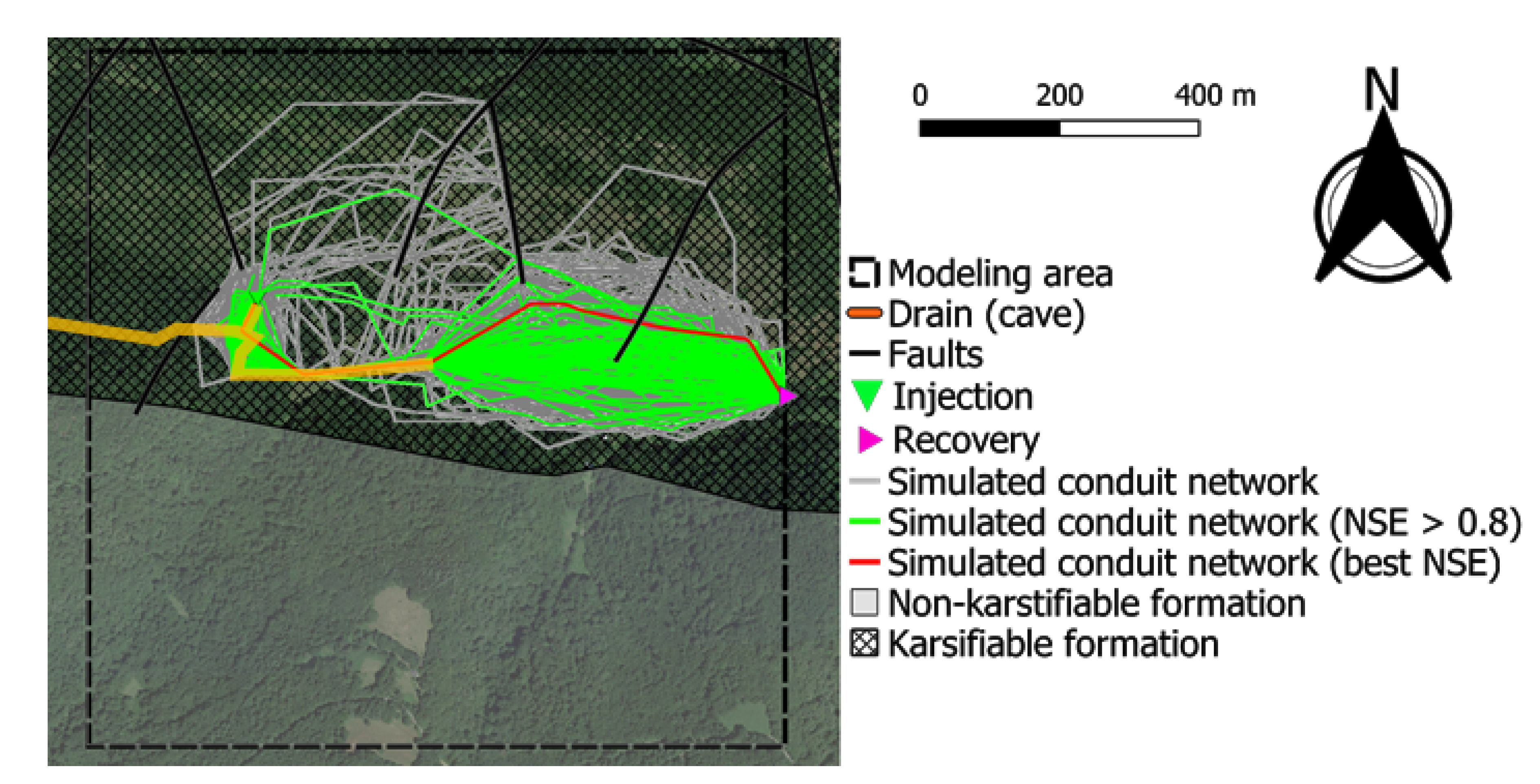
3.3. Conduit Geometry and Spatial Distribution of Flow
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Király, L. Rapport sur l’état actuel des connaissances dans le domaine des caractères physiques des roches karstiques. Hydrogeol. Karstic Terrains (Hydrogéol. Des Terrains Karstiques) Int. Union Geol. Sci. 1975, 3, 53–67. [Google Scholar]
- Palmer, A.N. Origin and morphology of limestone cave. Geol. Soc. Am. Bull. 1991, 103, 1–21. [Google Scholar] [CrossRef]
- Borghi, A.; Renard, P.; Cornaton, F. Can one identify karst conduit networks geometry and properties from hydraulic and tracer test data? Adv. Water Resour. 2016, 90, 99–115. [Google Scholar] [CrossRef] [Green Version]
- Ford, D.; Williams, P.D. Karst Hydrogeology and Geomorphology; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007; ISBN 978-0-470-84996-5. [Google Scholar]
- Chalikakis, K.; Plagnes, V.; Guerin, R.; Valois, R.; Bosch, F.P. Contribution of geophysical methods to karst-system exploration: An overview. Hydrogeol. J. 2011, 19, 1169–1180. [Google Scholar] [CrossRef]
- Field, M.S.; Pinsky, P.F. A two-region nonequilibrium model for solute transport in solution conduits in karstic aquifers. J. Contam. Hydrol. 2000, 44, 329–351. [Google Scholar] [CrossRef]
- Birk, S.; Geyer, T.; Liedl, R.; Sauter, M. Process-based interpretation of tracer tests in carbonate aquifers. Ground Water 2005, 43, 381–388. [Google Scholar] [CrossRef]
- Massei, N.; Wang, H.Q.; Field, M.S.; Dupont, J.P.; Bakalowicz, M.; Rodet, J. Interpreting tracer breakthrough tailing in a conduit-dominated karstic aquifer. Hydrogeol. J. 2006, 14, 849–858. [Google Scholar] [CrossRef]
- Goldscheider, N. A new quantitative interpretation of the long-tail and plateau-like breakthrough curves from tracer tests in the artesian karst aquifer of Stuttgart, Germany. Hydrogeol. J. 2008, 16, 1311–1317. [Google Scholar] [CrossRef] [Green Version]
- Labat, D.; Mangin, A. Transfer function approach for artificial tracer test interpretation in karstic systems. J. Hydrol. 2015, 529, 866–871. [Google Scholar] [CrossRef]
- Duran, L.; Fournier, M.; Massei, N.; Dupont, J.-P. Assessing the Nonlinearity of Karst Response Function under Variable Boundary Conditions. Ground Water 2016, 54, 46–54. [Google Scholar] [CrossRef]
- Ender, A.; Goeppert, N.; Goldscheider, N. Spatial resolution of transport parameters in a subtropical karst conduit system during dry and wet seasons. Hydrogeol. J. 2018, 26, 2241–2255. [Google Scholar] [CrossRef]
- Sivelle, V.; Labat, D. Short-term variations in tracer-test responses in a highly karstified watershed. Hydrogeol. J. 2019, 27, 2061–2075. [Google Scholar] [CrossRef]
- Morales, T.; Uriarte, J.A.; Olazar, M.; Antigüedad, I.; Angulo, B. Solute transport modelling in karst conduits with slow zones during different hydrologic conditions. J. Hydrol. 2010, 390, 182–189. [Google Scholar] [CrossRef]
- Dewaide, L.; Collon, P.; Poulain, A.; Rochez, G.; Hallet, V. Double-peaked breakthrough curves as a consequence of solute transport through underground lakes: A case study of the Furfooz karst system, Belgium. Hydrogeol. J. 2018, 26, 641–650. [Google Scholar] [CrossRef]
- Field, M.S.; Leij, F.J. Solute transport in solution conduits exhibiting multi-peaked breakthrough curves. J. Hydrol. 2012, 440–441, 26–35. [Google Scholar] [CrossRef]
- Vincenzi, V.; Riva, A.; Rossetti, S. Towards a better knowledge of Cansiglio karst system (Italy): Results of the first successful groundwater tracer test. Acta Carsologica 2011, 40. [Google Scholar] [CrossRef] [Green Version]
- Filippini, M.; Squarzoni, G.; De Waele, J.; Fiorucci, A.; Vigna, B.; Grillo, B.; Riva, A.; Rossetti, S.; Zini, L.; Casagrande, G.; et al. Differentiated spring behavior under changing hydrological conditions in an alpine karst aquifer. J. Hydrol. 2018, 556, 572–584. [Google Scholar] [CrossRef]
- Hauns, M.; Jeannin, P.-Y.; Atteia, O. Dispersion, retardation and scale effect in tracer breaktrough curves in karst conduits. J. Hydrol. 2001, 241, 177–193. [Google Scholar] [CrossRef]
- Mohammadi, Z.; Gharaat, M.J.; Field, M. The Effect of Hydraulic Gradient and Pattern of Conduit Systems on Tracing Tests: Bench-Scale Modeling. Groundwater 2018, 57, 110–125. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Chang, Y.; Wu, J.; Xue, X. Effects of flow rate variation on solute transport in a karst conduit with a pool. Environ. Earth Sci. 2019, 78, 237. [Google Scholar] [CrossRef]
- Thrailkill, J. Pipe Flow Models of a Kentucky Limestone Aquifer. Groundwater 1974, 12, 202–205. [Google Scholar] [CrossRef]
- Jeannin, P.-Y. Modeling flow in phreatic and epiphreatic karst conduits in the Hölloch cave (Muotatal, Switzerland). Water Resour. Res. 2001, 37, 191–200. [Google Scholar] [CrossRef]
- Gill, L.W.; Naughton, O.; Johnston, P.M. Modeling a network of turloughs in lowland karst. Water Resour. Res. 2013, 49, 3487–3503. [Google Scholar] [CrossRef]
- Schuler, P.; Duran, L.; McCormack, T.; Gill, L. Submarine and intertidal groundwater discharge through a complex multi-level karst conduit aquifer. Hydrogeol. J. 2018, 26, 2629–2647. [Google Scholar] [CrossRef] [Green Version]
- Shoemaker, W.B.; Kuniansky, E.L.; Birk, S.; Bauer, S.; Swain, E.D. Documentation of a Conduit Flow Process (CFP) for MODFLOW-2005; U.S. Geological Survey: Reston, VA, USA, 2008. [Google Scholar]
- Barenblatt, G.I.; Zheltov, I.P.; Kochina, I.N. Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks. J. Appl. Math. Mech. 1960, 24, 1286–1303. [Google Scholar] [CrossRef]
- Chang, Y.; Wu, J.; Jiang, G.; Liu, L.; Reimann, T.; Sauter, M. Modelling spring discharge and solute transport in conduits by coupling CFPv2 to an epikarst reservoir for a karst aquifer. J. Hydrol. 2019, 569, 587–599. [Google Scholar] [CrossRef]
- Xu, Z.; Hu, B.X.; Davis, H.; Cao, J. Simulating long term nitrate-N contamination processes in the Woodville Karst Plain using CFPv2 with UMT3D. J. Hydrol. 2015, 524, 72–88. [Google Scholar] [CrossRef]
- Xu, Z.; Hu, B.X.; Davis, H.; Kish, S. Numerical study of groundwater flow cycling controlled by seawater/freshwater interaction in a coastal karst aquifer through conduit network using CFPv2. J. Contam. Hydrol. 2015, 182, 131–145. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.; Hu, B.X. Development of a discrete-continuum VDFST-CFP numerical model for simulating seawater intrusion to a coastal karst aquifer with a conduit system. Water Resour. Res. 2017, 53, 688–711. [Google Scholar] [CrossRef]
- Assari, A.; Mohammadi, Z. Assessing flow paths in a karst aquifer based on multiple dye tracing tests using stochastic simulation and the MODFLOW-CFP code. Hydrogeol. J. 2017, 25, 1679–1702. [Google Scholar] [CrossRef]
- Gironás, J.; Roesner, L.A.; Rossman, L.A.; Davis, J. A new applications manual for the Storm Water Management Model (SWMM). Environ. Model. Softw. 2010, 25, 813–814. [Google Scholar] [CrossRef]
- Peterson, E.W.; Wicks, C.M. Assessing the importance of conduit geometry and physical parameters in karst systems using the storm water management model (SWMM). J. Hydrol. 2006, 329, 294–305. [Google Scholar] [CrossRef]
- Wu, Y.; Jiang, Y.; Yuan, D.; Li, L. Modeling hydrological responses of karst spring to storm events: Example of the Shuifang spring (Jinfo Mt., Chongqing, China). Environ. Geol. 2008, 55, 1545–1553. [Google Scholar] [CrossRef]
- Vuilleumier, C. Hydraulics and Sedimentary Processes in the Karst Aquifer of Milandre (Jura Mountains, Switzerland). Ph.D. Thesis, Université de Neuchâtel, Neuchâtel, Switzerland, 2017. [Google Scholar]
- Borghi, A.; Renard, P.; Jenni, S. A pseudo-genetic stochastic model to generate karstic networks. J. Hydrol. 2012, 414–415, 515–529. [Google Scholar] [CrossRef]
- Jourde, H.; Massei, N.; Mazzilli, N.; Binet, S.; Batiot-Guilhe, C.; Labat, D.; Steinmann, M.; Bailly-Comte, V.; Seidel, J.L.; Arfib, B.; et al. SNO KARST: A French Network of Observatories for the Multidisciplinary Study of Critical Zone Processes in Karst Watersheds and Aquifers. Vadose Zone J. 2018, 17, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Choukroune, P. Tectonic evolution of the Pyrenees. Annu. Rev. Earth Planet. Sci. 1992, 20, 143–158. [Google Scholar] [CrossRef]
- Angrand, P. Évolution 3D D’un Rétro-Bassin D’avant-Pays: Le Bassin Aquitain, France. Ph.D. Thesis, Université de Lorraine, Lorraine, France, 2017. [Google Scholar]
- Mangin, A. Contribution à L’étude Hydrodynamique des Aquifères Karstiques. Ph.D. Thesis, Université de Dijon, Dijon, France, 1975. [Google Scholar]
- Johnson, J.A.; Hall, C.A. The structural and sedimentary evolution of the Cretaceous North Pyrenean Basin, southern France. Geol. Soc. Am. Bull. 1989, 101, 231–247. [Google Scholar] [CrossRef]
- Genthon, P.; Bataille, A.; Fromant, A.; D’Hulst, D.; Bourges, F. Temperature as a marker for karstic waters hydrodynamics. Inferences from 1 year recording at La Peyrére cave (Ariège, France). J. Hydrol. 2005, 311, 157–171. [Google Scholar] [CrossRef]
- Brehier, F.; Horizon VerticalSaint Girons, France. Speleoglogic Investigations over the Baget Area. Personal Communication, 2019. [Google Scholar]
- Sivelle, V. Couplage D’approches Conceptuelles, Systémiques et Distribuées Pour L’interprétation de Traçages Artificiels en Domaine Karstiques. Implications Pour la Détermination de la Structure Interne des Aquifères Karstiques. Ph.D. Thesis, Université Paul Sabatier-Toulouse III, Touloue, France, 2019. [Google Scholar]
- Rousset, D.; Genthon, P.; Perroud, H.; Sénéchal, G. Detection and Characterization of Near Surface Small Karstic Cavities Using Integrated Geophysical Surveys; European Association of Geoscientists & Engineers: DB Houten, The Netherland, 1998. [Google Scholar]
- Bakalowicz, M.; Crochet, P.; D’Hulst, D.; Mangin, A.; Marsaud, B.; Ricard, J.; Rouch, R. High discharge pumping in a vertical cave, fundamental and applied results. Basic Appl. Hydrogeol. Res. Fr. Karstic Areas 1994, 65, 93–110. [Google Scholar]
- Schnegg, P.-A. An Inexpensive Field Fluorometer for Hydrogeological Tracer Tests with Three Tracers and Turbidity Measurement. Available online: https://doc.rero.ch/record/5068 (accessed on 15 April 2020).
- Sivelle, V.; Labat, D.; Duran, L.; Fournier, M.; Massei, N. Artificial Tracer Tests Interpretation Using Transfer Function Approach to Study the Norville Karst System. In Proceedings of the Eurokarst 2018, Besançon, France, 2–6 July 2018; Bertrand, C., Denimal, S., Steinmann, M., Renard, P., Eds.; Springer International Publishing: Heidelberg, Gemany, 2020; pp. 193–198. [Google Scholar]
- Wang, H.Q.; Crampon, N.; Huberson, S.; Garnier, J.M. A linear graphical method for determining hydrodispersive characteristics in tracer experiments with instantaneous injection. J. Hydrol. 1987, 95, 143–154. [Google Scholar] [CrossRef]
- Lauber, U.; Ufrecht, W.; Goldscheider, N. Spatially resolved information on karst conduit flow from in-cave dye tracing. Hydrol. Earth Syst. Sci. 2014, 18, 435–445. [Google Scholar] [CrossRef] [Green Version]
- Runkel, R.L. One-Dimensional Transport with Inflow and Storage (OTIS): A Solute Transport Model for Streams and Rivers; Water-Resources Investigations Report; Geological Survey (U.S.): Reston, VA, USA, 1998. [Google Scholar]
- Tinet, A.-J.; Collon, P.; Philippe, C.; Dewaide, L.; Hallet, V. OM-MADE: An open-source program to simulate one-dimensional solute transport in multiple exchanging conduits and storage zones. Comput. Geosci. 2019, 127, 23–35. [Google Scholar] [CrossRef]
- BRGM Geological Map at 1:50 000 (Bd-Charm-50), Department: Ariège (09, France). Available online: http://infoterre.brgm.fr/formulaire/telechargement-cartes-geologiques-departementales-150-000-bd-charm-50 (accessed on 30 December 2019).
- IGN BD ALTI® 25M—Orne. Available online: https://geo.data.gouv.fr/fr/datasets/22355590527b92116abf42a509b6defdbf4c0e33 (accessed on 5 April 2020).
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Debroas, E.-J. Géologie du bassin versant du Baget (Zone nord-pyrénéenne, Ariège, France): Nouvelles observations et conséquences. Strata 2009, 2, 1–93. [Google Scholar]
- Sisavath, S.; Mourzenko, V.; Genthon, P.; Thovert, J.-F.; Adler, P.M. Geometry, percolation and transport properties of fracture networks derived from line data. Geophys. J. Int. 2004, 157, 917–934. [Google Scholar] [CrossRef] [Green Version]
- Debroas, E.J. Modele de bassin triangulaire a l’intersection de decrochements divergents pour le fosse albo-cenomanien de la Ballongue (zone nord-pyreneenne, France). Bull. Soc. Géol. Fr. 1987, 3, 887–898. [Google Scholar] [CrossRef]
- Sethian, J.A. A fast marching level set method for monotonically advancing fronts. Proc. Natl. Acad. Sci. USA 1996, 93, 1591–1595. [Google Scholar] [CrossRef] [Green Version]
- Aryo, D. Dijkstra Algorithm. Available online: https://www.mathworks.com/matlabcentral/fileexchange/36140 (accessed on 21 June 2019).
- Sivelle, V.; Labat, D.; Mazzilli, N.; Massei, N.; Jourde, H. Dynamics of the Flow Exchanges between Matrix and Conduits in Karstified Watersheds at Multiple Temporal Scales. Water 2019, 11, 569. [Google Scholar] [CrossRef] [Green Version]
- Worthington, S.R.H.; Soley, R.W.N. Identifying turbulent flow in carbonate aquifers. J. Hydrol. 2017, 552, 70–80. [Google Scholar] [CrossRef]
- De Saint-Venant, A.; Barré, D.; Saint-Cyr, J. Théorie du Mouvement Non-Permanent des Eaux, Avec Application Aux Crues des Rivières et à L’introduction des Marées Dans Leur Lit; Académie des Sciences: Paris, France, 1871. [Google Scholar]
- Rossman, L.A. Storm Water Management Model User’s Manual, Version 5.0; National Risk Management Research Laboratory, Office of Research and Development, US Environmental Protection Agency: Cincinnati, OH, USA, 2010. [Google Scholar]
- Metcalf, E. Storm Water Management Model, Volume I-Final Report; University of Florida and Water Resources Engineers, Inc.: Washington, DC, USA, 1971. [Google Scholar]
- Goldscheider, N.; Meiman, J.; Pronk, M.; Smart, C. Tracer tests in karst hydrogeology and speleology. Int. J. Speleol. 2008, 37, 27–40. [Google Scholar] [CrossRef] [Green Version]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Pool, S.; Vis, M.; Seibert, J. Evaluating model performance: Towards a non-parametric variant of the Kling-Gupta efficiency. Hydrol. Sci. J. 2018, 63, 1941–1953. [Google Scholar] [CrossRef]
- Jouves, J.; Viseur, S.; Arfib, B.; Baudement, C.; Camus, H.; Collon, P.; Guglielmi, Y. Speleogenesis, geometry, and topology of caves: A quantitative study of 3D karst conduits. Geomorphology 2017, 298, 86–106. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.; Sirieix, C.; Riss, J.; Malaurent, P. A clustering approach applied to time-lapse ERT interpretation—Case study of Lascaux cave. J. Appl. Geophys. 2017, 144, 115–124. [Google Scholar] [CrossRef]
- Cheng, Q.; Chen, X.; Tao, M.; Binley, A. Characterization of karst structures using quasi-3D electrical resistivity tomography. Environ. Earth Sci. 2019, 78, 285. [Google Scholar] [CrossRef] [Green Version]
- Bermejo, L.; Ortega, A.I.; Guérin, R.; Benito-Calvo, A.; Pérez-González, A.; Parés, J.M.; Aracil, E.; de Bermúdez Castro, J.M.; Carbonell, E. 2D and 3D ERT imaging for identifying karst morphologies in the archaeological sites of Gran Dolina and Galería Complex (Sierra de Atapuerca, Burgos, Spain). Quat. Int. 2017, 433, 393–401. [Google Scholar] [CrossRef]
- Doerfliger, N.; Jeannin, P.-Y.; Zwahlen, F. Water vulnerability assessment in karst environments: A new method of defining protection areas using a multi-attribute approach and GIS tools (EPIK method). Environ. Geol. 1999, 39, 165–176. [Google Scholar] [CrossRef] [Green Version]
- Doerfliger, N.; Zwahlen, F. Practical Guide: Groundwater Vulnerability Mapping in Karstic Regions (EPIK); Agency for the Environment, Forests and Landscape (SAEFL): Bern, Switzerland, 1998; Volume 56. [Google Scholar]
- Ollivier, C.; Lecomte, Y.; Chalikakis, K.; Mazzilli, N.; Danquigny, C.; Emblanch, C. A QGIS Plugin Based on the PaPRIKa Method for Karst Aquifer Vulnerability Mapping. Groundwater 2019, 57, 201–204. [Google Scholar] [CrossRef]
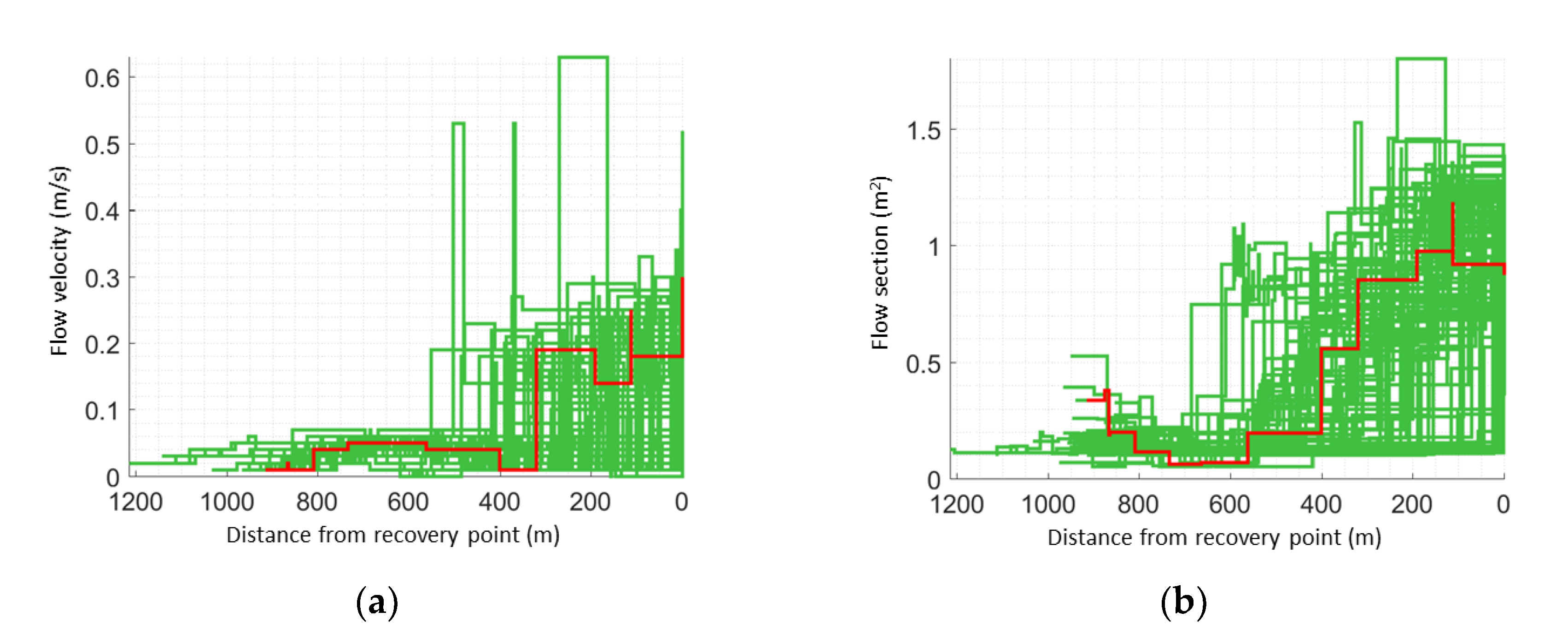
| Descriptive Statistics | Mean Flow Section Area (m2) | Mean Flow Velocity (m/s) | Transport Length (m) |
|---|---|---|---|
| Min | 8.42 | 0.09 | 772.7 |
| Max | 9.45 | 0.41 | 1007.0 |
| Mean | 9.01 | 0.16 | 905.5 |
| Standard Deviation | 0.20 | 0.06 | 43.1 |
| Variation Coefficient | 0.02 | 0.14 | 0.05 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sivelle, V.; Renard, P.; Labat, D. Coupling SKS and SWMM to Solve the Inverse Problem Based on Artificial Tracer Tests in Karstic Aquifers. Water 2020, 12, 1139. https://doi.org/10.3390/w12041139
Sivelle V, Renard P, Labat D. Coupling SKS and SWMM to Solve the Inverse Problem Based on Artificial Tracer Tests in Karstic Aquifers. Water. 2020; 12(4):1139. https://doi.org/10.3390/w12041139
Chicago/Turabian StyleSivelle, Vianney, Philippe Renard, and David Labat. 2020. "Coupling SKS and SWMM to Solve the Inverse Problem Based on Artificial Tracer Tests in Karstic Aquifers" Water 12, no. 4: 1139. https://doi.org/10.3390/w12041139
APA StyleSivelle, V., Renard, P., & Labat, D. (2020). Coupling SKS and SWMM to Solve the Inverse Problem Based on Artificial Tracer Tests in Karstic Aquifers. Water, 12(4), 1139. https://doi.org/10.3390/w12041139







