Uncertainty in Irrigation Return Flow Estimation: Comparing Conceptual and Physically-Based Parameterization Approaches
Abstract
:1. Introduction
2. Estimation of Irrigation Return Flow
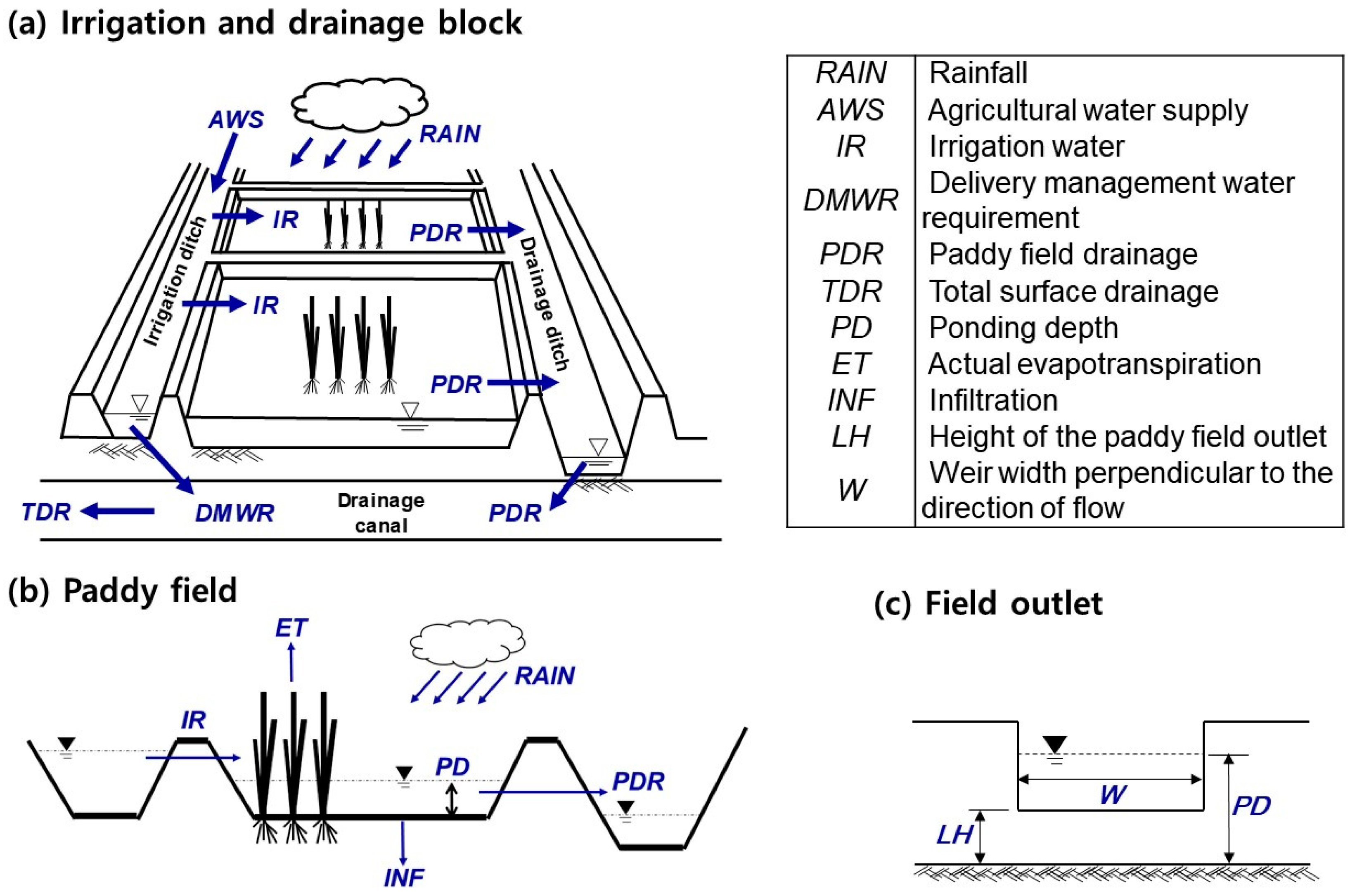
2.1. Mathematical Representation of Irrigation Return Flow
2.2. Paddy Drainage Model
2.2.1. Conceptual Parameter Approach
2.2.2. Physically-Based Approach
2.3. Estimation of Irrigation Return Flow from Paddy Drainage
- Water is not irrigated (zero ) within a rainfall event ().
- Surface runoff discharge () is always followed by irrigation water discharge ().
- Irrigation water ponded in a paddy plot is consumed by and first, and then water ponded by is used.
2.4. Parameter Value Range Selection Using Expert Knowledge
2.5. Evaluating Uncertainty and Accuracy
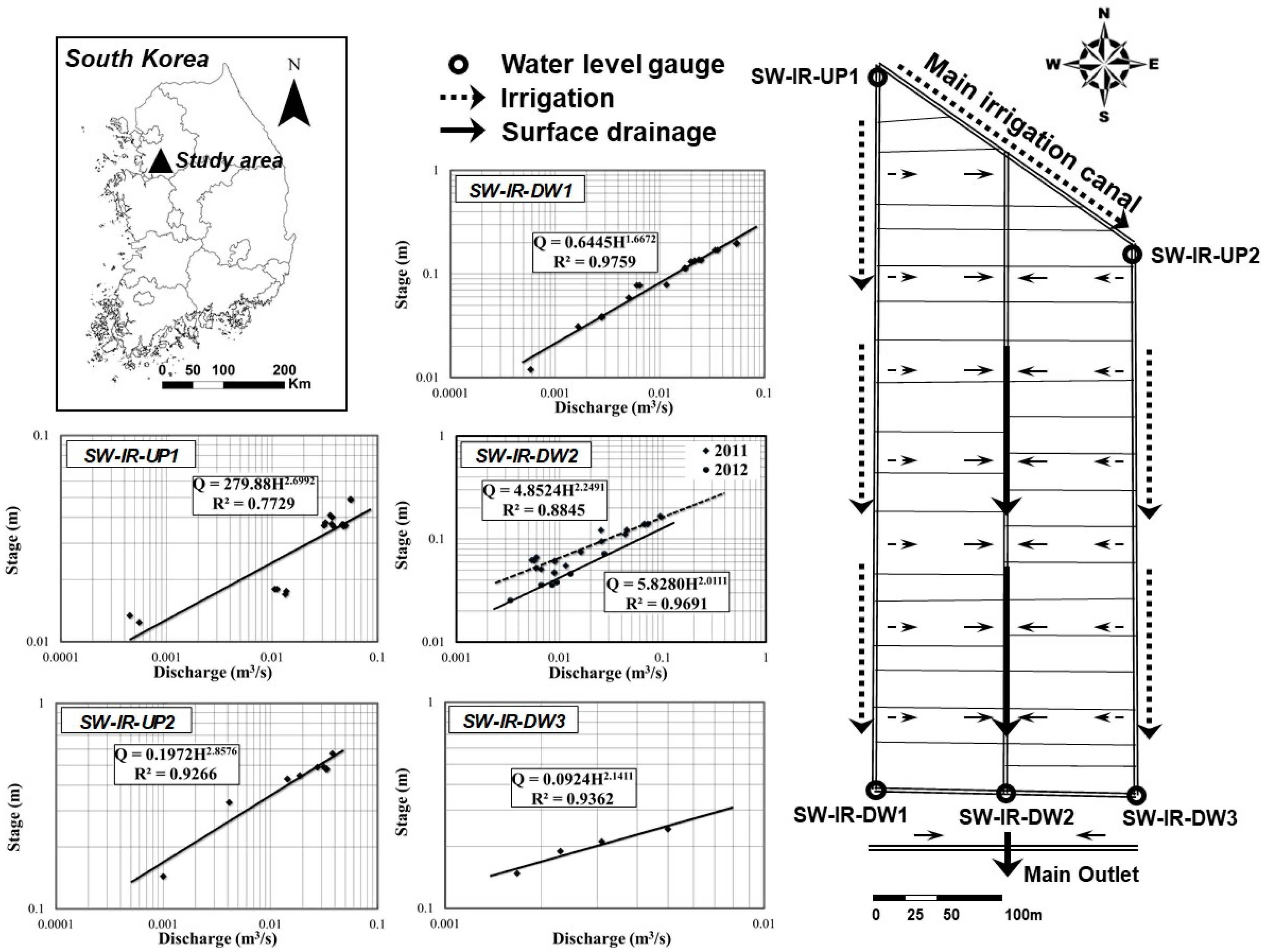
3. Study Area and Data
4. Results and Discussions
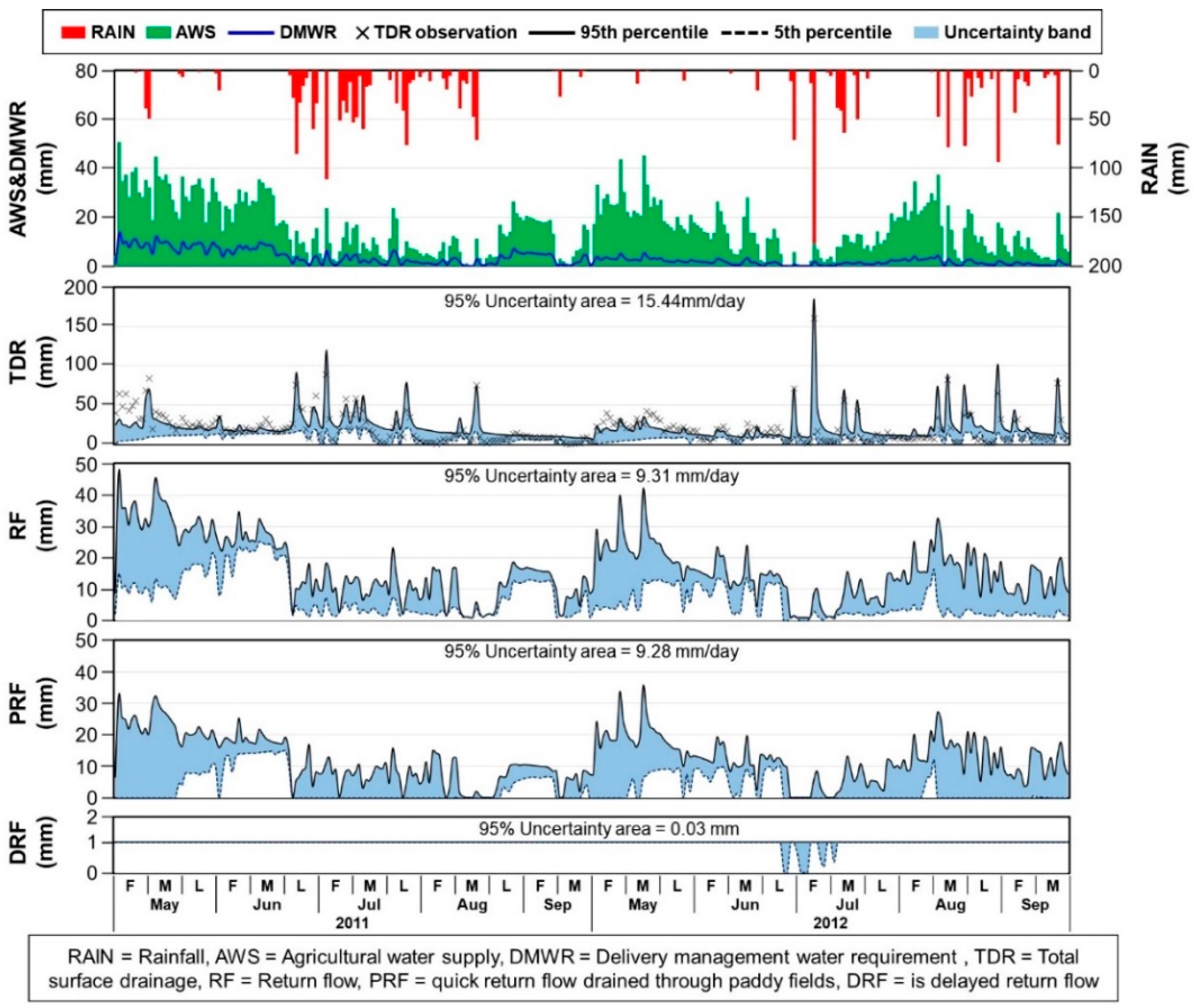
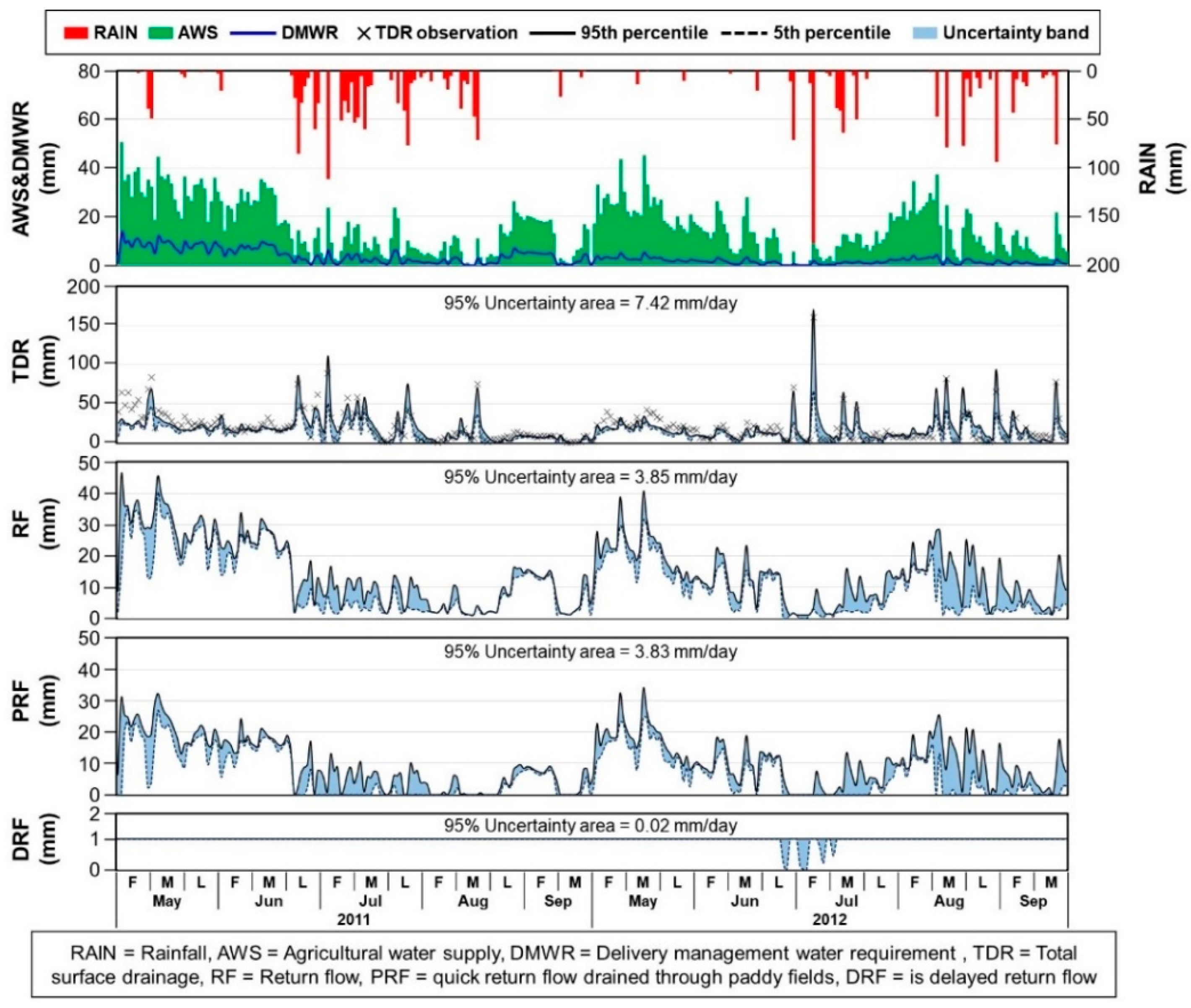
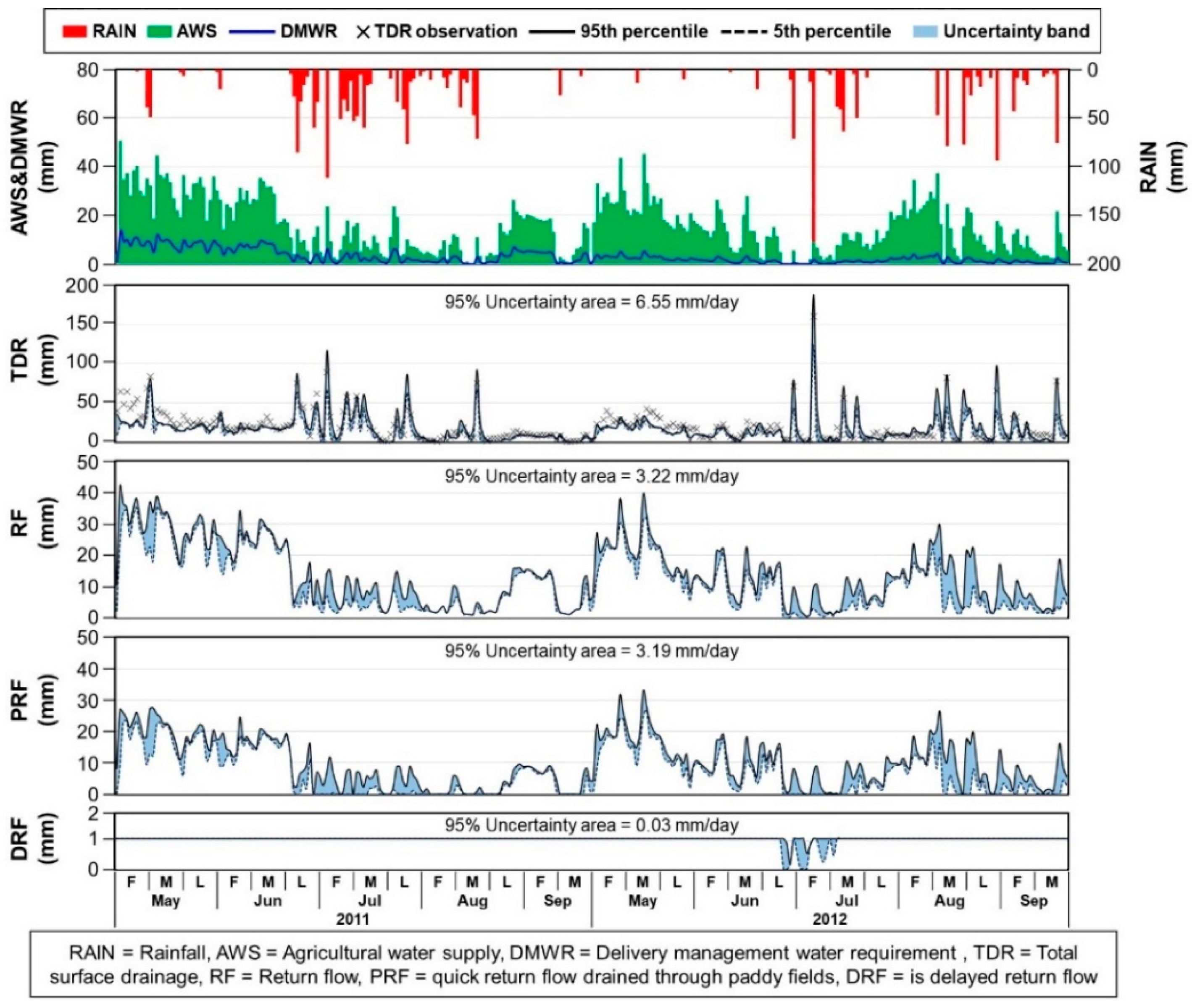
4.1. Uncertainty and Accuracy of Conceptual and Physically-Based Parameterization Approaches
4.2. Potential of Conceptual and Physically-Based Parameterization Approaches
5. Conclusions
- The results showed that the physically-based parameterization could effectively regulate the behavior of the RF model and thus produce smaller uncertainty compared to that of the conceptual approach, suggesting and confirming the potential of a physically-based approach as a way to effectively reduce modeling uncertainty without parameter calibration.
- When the value ranges of a conceptual parameter were naively (or simply) defined, the CON produced wide uncertainty in RF estimates.
- The conceptual parameter could be reasonably related to the physical and hydraulic characteristics of a study field, substantially reducing the size of uncertainty in RF estimates to as small as that of PHY.
- Narrow-CON and PHY reproduced at similar and acceptable accuracy, and the performance of the ensemble (Narrow-CON-Median and PHY-Median) was comparable to that of the calibrated approaches (CON-BestNSE and PHY-BestNSE).
Author Contributions
Funding
Conflicts of Interest
References
- Dewandel, B.; Gandolfi, J.-M.; de Condappa, D.; Ahmed, S. An efficient methodology for estimating irrigation return flow coefficients of irrigated crops at watershed and seasonal scale. Hydrol. Process. 2008, 22, 1700–1712. [Google Scholar] [CrossRef]
- Kang, M.; Park, S. Modeling water flows in a serial irrigation reservoir system considering irrigation return flows and reservoir operations. Agric. Water Manag. 2014, 143, 131–141. [Google Scholar] [CrossRef]
- Kim, H.K.; Jang, T.I.; Im, S.J.; Park, S.W. Estimation of irrigation return flow from paddy fields considering the soil moisture. Agric. Water Manag. 2009, 96, 875–882. [Google Scholar] [CrossRef]
- Song, J.-H.; Her, Y.; Park, J.; Lee, K.-D.; Kang, M.-S. Simulink implementation of a hydrologic model: A Tank model case study. Water 2017, 9, 639. [Google Scholar] [CrossRef] [Green Version]
- Song, J.-H.; Kang, M.S.; Song, I.; Jun, S.M. Water balance in irrigation reservoirs considering flood control and irrigation efficiency variation. J. Irrig. Drain. Eng. 2016, 142, 04016003. [Google Scholar] [CrossRef]
- Song, J.H.; Song, I.; Kim, J.-T.; Kang, M.S. Characteristics of irrigation return flow in a reservoir irrigated district. J. Korean Soc. Agric. Eng. 2015, 57, 69–78. [Google Scholar]
- Chien, C.-P.; Fang, W.-T. Modeling irrigation return flow for the return flow reuse system in paddy fields. Paddy Water Environ. 2012, 10, 187–196. [Google Scholar] [CrossRef]
- Song, J.-H.; Her, Y.; Jun, S.M.; Hwang, S.; Park, J.; Kang, M.-S. Lessons from assessing uncertainty in agricultural water supply estimation for sustainable rice production. Agronomy 2019, 9, 662. [Google Scholar] [CrossRef] [Green Version]
- Zulu, G.; Toyota, M.; Misawa, S. Characteristics of water reuse and its effects on paddy irrigation system water balance and the riceland ecosystem. Agric. Water Manag. 1996, 31, 269–283. [Google Scholar] [CrossRef]
- Grafton, R.Q.; Williams, J.; Perry, C.J.; Molle, F.; Ringler, C.; Steduto, P.; Udall, B.; Wheeler, S.A.; Wang, Y.; Garrick, D.; et al. The paradox of irrigation efficiency. Science 2018, 361, 748–750. [Google Scholar] [CrossRef] [Green Version]
- Tan, X.; Shao, D.; Gu, W. Improving water reuse in paddy field districts with cascaded on-farm ponds using hydrologic model simulations. Water Resour. Manag. 2018, 32, 1849–1865. [Google Scholar] [CrossRef]
- Choo, T.-H. A study on return flow ratio of irrigation for a paddy field in pumping station by water balance method. J. Korea Water Resour. Assoc. 2004, 37, 249–255. [Google Scholar] [CrossRef] [Green Version]
- Chung, S.-O.; Park, K.-J. Irrigation return flow measurements and analysis in a small size paddy area. J. Korea Water Resour. Assoc. 2004, 37, 517–526. [Google Scholar] [CrossRef]
- Kim, T.-C.; Lee, H.-C.; Moon, J.-P. Estimation of return flow rate of irrigation water in Daepyeong pumping district. J. Korean Soc. Agric. Eng. 2010, 52, 41–49. [Google Scholar]
- Kim, J.-S.; Oh, S.-Y.; Oh, K.-Y.; Cho, J.-W. Delivery management water requirement for irrigation ditches associated with large-sized paddy plots in Korea. Paddy Water Environ. 2005, 3, 57–62. [Google Scholar] [CrossRef]
- Im, S. Modeling Irrigation Return Flow from Paddy Fields on Agricultural Watersheds; Seoul National University: Seoul, Korea, 2000. [Google Scholar]
- Song, J.-H. Hydrologic Analysis System with Multi-Objective Optimization for Agricultural Watersheds; Seoul National University: Seoul, Korea, 2017. [Google Scholar]
- Chang, Y.-C.; Kan, C.-E.; Lin, G.-F.; Chiu, C.-L.; Lee, Y.-C. Potential benefits of increased application of water to paddy fields in Taiwan. Hydrol. Process. 2001, 15, 1515–1524. [Google Scholar] [CrossRef]
- Chen, R.-S.; Yang, K.-H. Terraced paddy field rainfall-runoff mechanism and simulation using a revised tank model. Paddy Water Environ. 2011, 9, 237–247. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.-K.; Chen, R.-S.; Yang, T.-Y. Application of a tank model to assess the flood-control function of a terraced paddy field. Hydrol. Sci. J. 2014, 59, 1020–1031. [Google Scholar] [CrossRef] [Green Version]
- Yoshinaga, I.; Miura, A.; Hitomi, T.; Hamada, K.; Shiratani, E. Runoff nitrogen from a large sized paddy field during a crop period. Agric. Water Manag. 2007, 87, 217–222. [Google Scholar] [CrossRef]
- Jang, T.I.; Kim, H.K.; Im, S.J.; Park, S.W. Simulations of storm hydrographs in a mixed-landuse watershed using a modified TR-20 model. Agric. Water Manag. 2010, 97, 201–207. [Google Scholar] [CrossRef]
- Kang, M.S.; Koo, J.H.; Chun, J.A.; Her, Y.G.; Park, S.W.; Yoo, K. Design of drainage culverts considering critical storm duration. Biosyst. Eng. 2009, 104, 425–434. [Google Scholar] [CrossRef]
- Odhiambo, L.O.; Murty, V.V.N. Modeling water balance components in relation to field layout in lowland paddy fields. I. Model development. Agric. Water Manag. 1996, 30, 185–199. [Google Scholar] [CrossRef]
- Wu, R.-S.; Sue, W.-R.; Chien, C.-B.; Chen, C.-H.; Chang, J.-S.; Lin, K.-M. A simulation model for investigating the effects of rice paddy fields on the runoff system. Math. Comput. Model. 2001, 33, 649–658. [Google Scholar] [CrossRef]
- Gharari, S.; Shafiei, M.; Hrachowitz, M.; Kumar, R.; Fenicia, F.; Gupta, H.V.; Savenije, H.H.G. A constraint-based search algorithm for parameter identification of environmental models. Hydrol. Earth Syst. Sci. 2014, 18, 4861–4870. [Google Scholar] [CrossRef] [Green Version]
- Gharari, S.; Hrachowitz, M.; Fenicia, F.; Gao, H.; Savenije, H.H.G. Using expert knowledge to increase realism in environmental system models can dramatically reduce the need for calibration. Hydrol. Earth Syst. Sci. 2015, 18, 4839–4859. [Google Scholar] [CrossRef] [Green Version]
- Hrachowitz, M.; Fovet, O.; Ruiz, L.; Euser, T.; Gharari, S.; Nijzink, R.; Freer, J.; Savenije, H.H.G.; Gascuel-Odoux, C. Process consistency in models: The importance of system signatures, expert knowledge, and process complexity. Water Resour. Res. 2014, 50, 7445–7469. [Google Scholar] [CrossRef] [Green Version]
- Song, J.-H.; Her, Y.; Hwang, S.; Park, J.; Yoon, K.-S.; Kang, M.S. Evaluating the applicability of drainage routing schemes for paddy fields. J. Irrig. Drain. Eng. 2020, in press. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998. [Google Scholar]
- Song, J.-H.; Kang, M.-S.; Song, I.; Hwang, S.-H.; Park, J.; Ahn, J.-H. Surface drainage simulation model for irrigation districts composed of paddy and protected cultivation. J. Korean Soc. Agric. Eng. 2013, 55, 63–73. [Google Scholar]
- Yoo, S.-H.; Choi, J.-Y.; Lee, S.-H.; Oh, Y.-G.; Yun, D.K. Climate change impacts on water storage requirements of an agricultural reservoir considering changes in land use and rice growing season in Korea. Agric. Water Manag. 2013, 117, 43–54. [Google Scholar]
- Nash, J.E. The form of the instantaneous unit hydrograph. IAHS Publ. 1957, 3, 114–121. [Google Scholar]
- Purcell, P.J. Physical Analog of the Linear Reservoir. J. Hydrol. Eng. 2006, 11, 184–187. [Google Scholar] [CrossRef]
- Song, J.-H.; Her, Y.; Park, J.; Kang, M.-S. Exploring parsimonious daily rainfall-runoff model structure using the hyperbolic tangent function and Tank model. J. Hydrol. 2019, 574, 574–587. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Kang, M.S.; Park, S.W.; Lee, J.J.; Yoo, K.H. Applying SWAT for TMDL programs to a small watershed containing rice paddy fields. Agric. Water Manag. 2006, 79, 72–92. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Oudin, L.; Andréassian, V.; Mathevet, T.; Perrin, C.; Michel, C. Dynamic averaging of rainfall-runoff model simulations from complementary model parameterizations. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Toward improved calibration of hydrologic models: Multiple and noncommensurable measures of information. Water Resour. Res. 1998, 34, 751–763. [Google Scholar] [CrossRef]
- Beven, K.J. Rainfall-Runoff Modelling: The Primer; John Wiley & Sons: Chichester, UK, 2001; ISBN 1-119-95101-1. [Google Scholar]
- Vinogradov, Y.B.; Semenova, O.M.; Vinogradova, T.A. An approach to the scaling problem in hydrological modelling: The deterministic modelling hydrological system. Hydrol. Process. 2011, 25, 1055–1073. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- Efstratiadis, A.; Koutsoyiannis, D. One decade of multi-objective calibration approaches in hydrological modelling: A review. Hydrol. Sci. J. 2010, 55, 58–78. [Google Scholar] [CrossRef] [Green Version]
- Khu, S.T.; Madsen, H. Multiobjective calibration with Pareto preference ordering: An application to rainfall-runoff model calibration. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]

| Parameter | P.S. | T.S. | Growing and Harvesting Season (10-days) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |||
| 0.78 | 0.78 | 0.78 | 0.97 | 1.07 | 1.16 | 1.28 | 1.45 | 1.5 | 1.58 | 1.46 | 1.45 | 1.25 | 1.01 | 1.01 | 1.01 | 1.01 | |
| (mm) | 66.1 | 80.9 | 74 | 57.3 | 34.6 | 72.9 | 67.2 | 57.7 | 63.4 | 67.2 | 66.1 | 66.1 | 66.1 | 66.1 | 66.1 | 66.1 | 66.1 |
| Schemes | CON | PHY |
|---|---|---|
| Description | Conceptual based parameter approach | Physically-based parameter approach |
| Routing scheme | Linear reservoir with threshold scheme | Broad-crested weir equation |
| Calibration parameter | , , | |
| Simulation time step | Daily | Hourly |
| Scheme | Parameter | Definition | Min. | Max. |
|---|---|---|---|---|
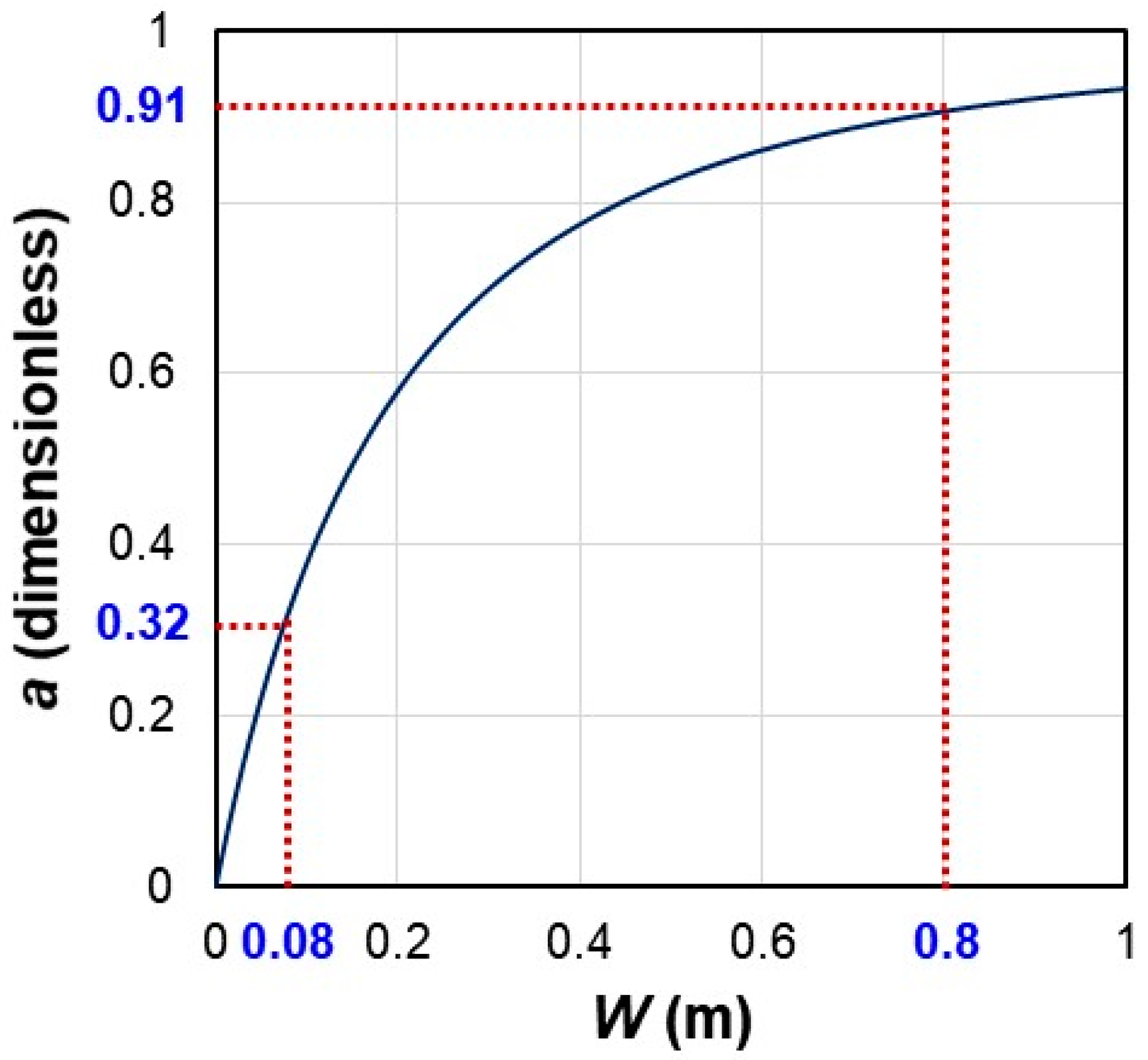
| Wide-CON | Drainage capacity of a paddy outlet (dimensionless) | 0.08 | 1 | |
| Narrow-CON | Drainage capacity of a paddy outlet (dimensionless) | 0.32 | 0.91 | |
| PHY | Weir width perpendicular to the direction of flow (m) | 0.08 | 0.8 | |
| PHY | Parameter representing the overall flow condition (dimensionless) | 1.7 | 2.0 | |
| PHY | Area of a unit paddy field (m2) | 1800 | 5900 |
| Performance Measures | CON | CON | Narrow-CON | PHY | PHY | |
|---|---|---|---|---|---|---|
| = 1 | Best NSE a | Median b | Best NSE a | Median b | ||
| 0.79 | 0.84 | 0.83 | 0.86 | 0.86 | ||
| 0.69 | 0.84 | 0.83 | 0.85 | 0.83 | ||
| −0.05 | 0.44 | 0.56 | 0.56 | 0.46 | ||
| (%) | 3 | 3 | 6 | 2 | 5 | |
| (%) | 2011 | 86 | 85 | 83 | 84 | 84 |
| 2012 | 79 | 77 | 75 | 76 | 77 | |
| Entire period | 82 | 81 | 80 | 80 | 81 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J.-H.; Her, Y.; Hwang, S.; Kang, M.-S. Uncertainty in Irrigation Return Flow Estimation: Comparing Conceptual and Physically-Based Parameterization Approaches. Water 2020, 12, 1125. https://doi.org/10.3390/w12041125
Song J-H, Her Y, Hwang S, Kang M-S. Uncertainty in Irrigation Return Flow Estimation: Comparing Conceptual and Physically-Based Parameterization Approaches. Water. 2020; 12(4):1125. https://doi.org/10.3390/w12041125
Chicago/Turabian StyleSong, Jung-Hun, Younggu Her, Soonho Hwang, and Moon-Seong Kang. 2020. "Uncertainty in Irrigation Return Flow Estimation: Comparing Conceptual and Physically-Based Parameterization Approaches" Water 12, no. 4: 1125. https://doi.org/10.3390/w12041125
APA StyleSong, J.-H., Her, Y., Hwang, S., & Kang, M.-S. (2020). Uncertainty in Irrigation Return Flow Estimation: Comparing Conceptual and Physically-Based Parameterization Approaches. Water, 12(4), 1125. https://doi.org/10.3390/w12041125






