Spatial Diagnosis of Rain Gauges’ Distribution and Flood Impacts: Case Study in Itaperuna, Rio de Janeiro—Brazil
Abstract
:1. Introduction
2. Materials and Methods
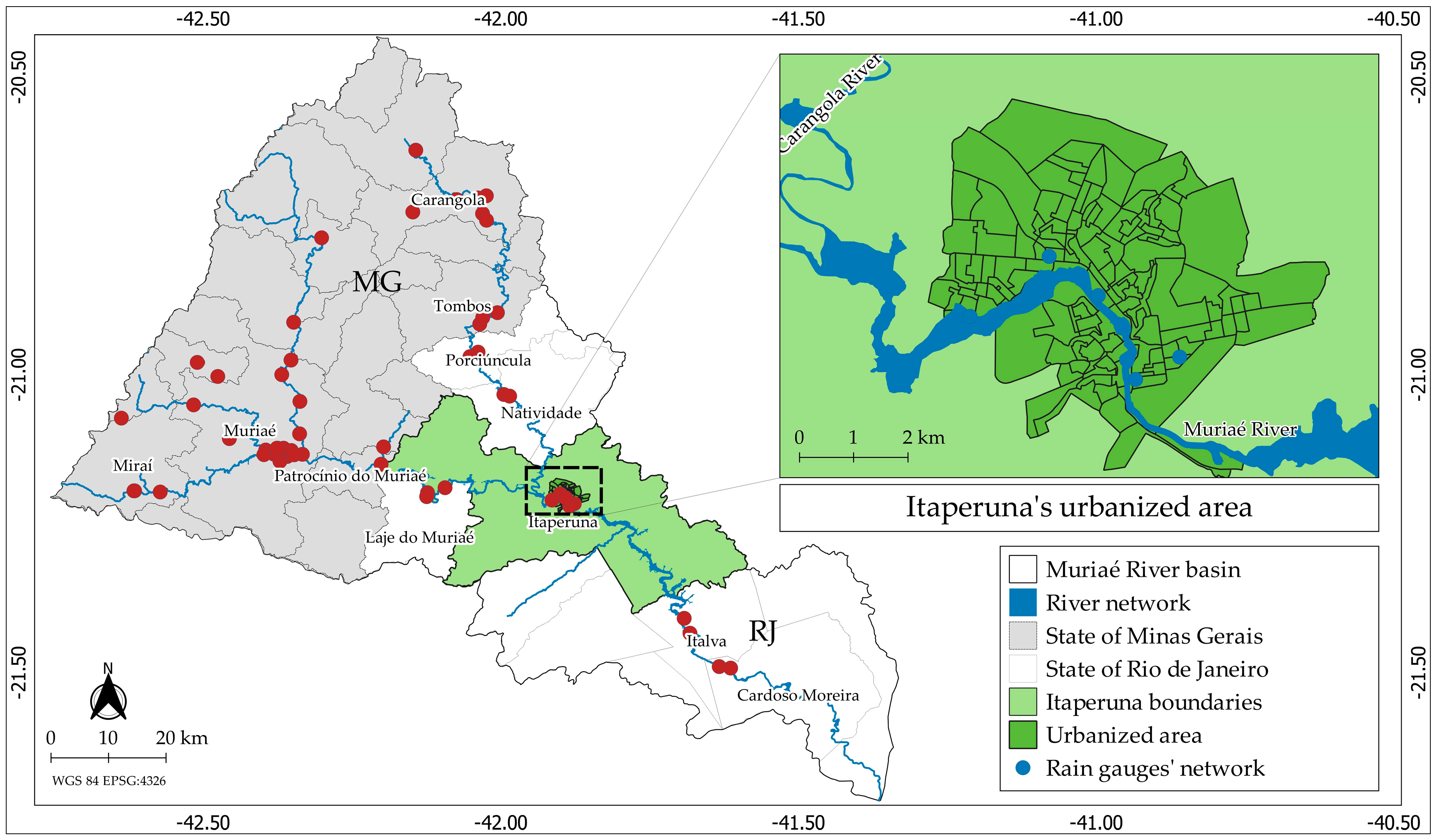
2.1. Study Context Area: Municipality of Itaperuna, Rio de Janeiro–Brazil
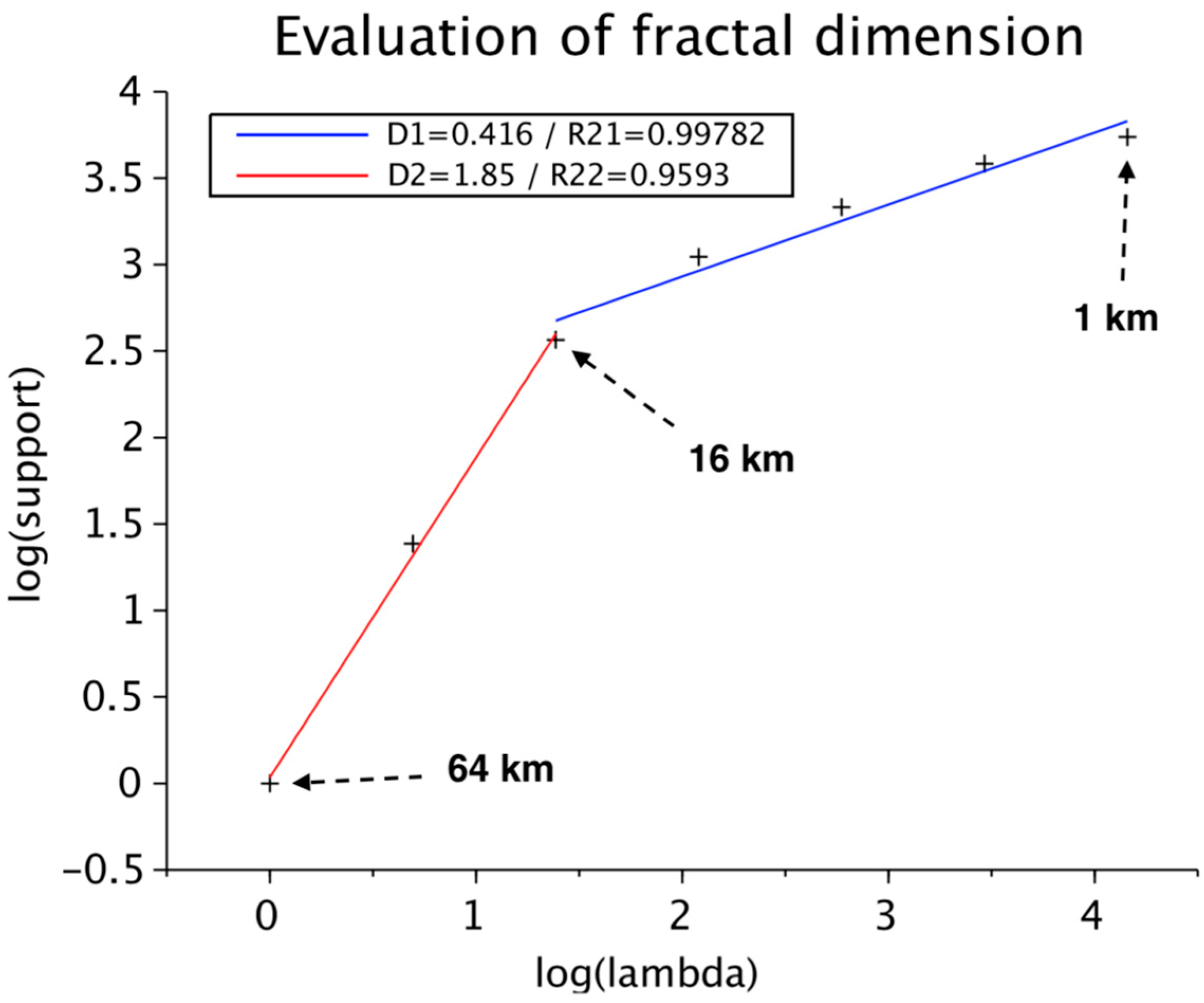
2.2. Fractal Analysis of the Rain Gauge Network Distribution
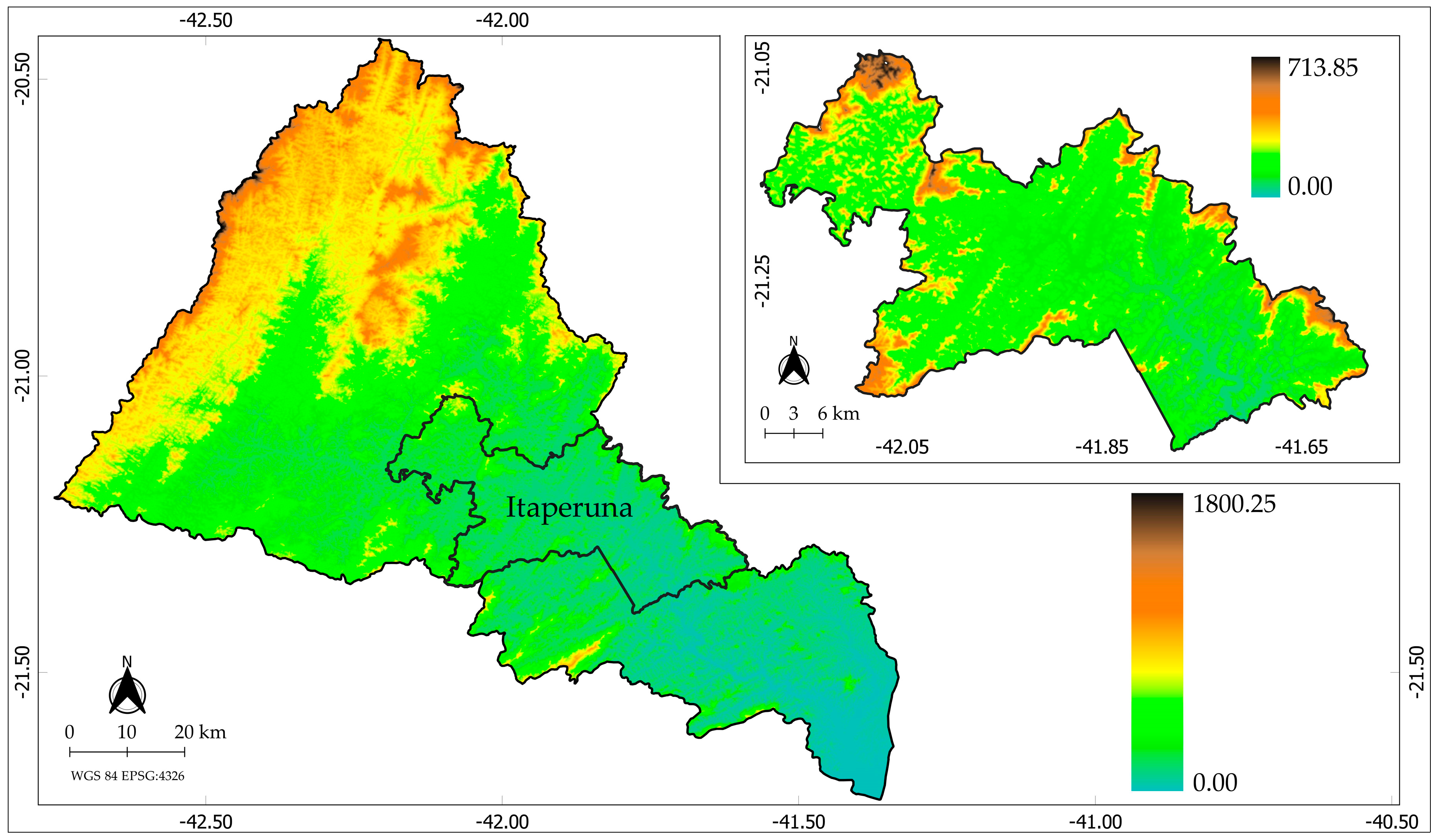
2.3. Physical-Environmental Characterization and Topography
2.4. Flood Susceptibility Maps
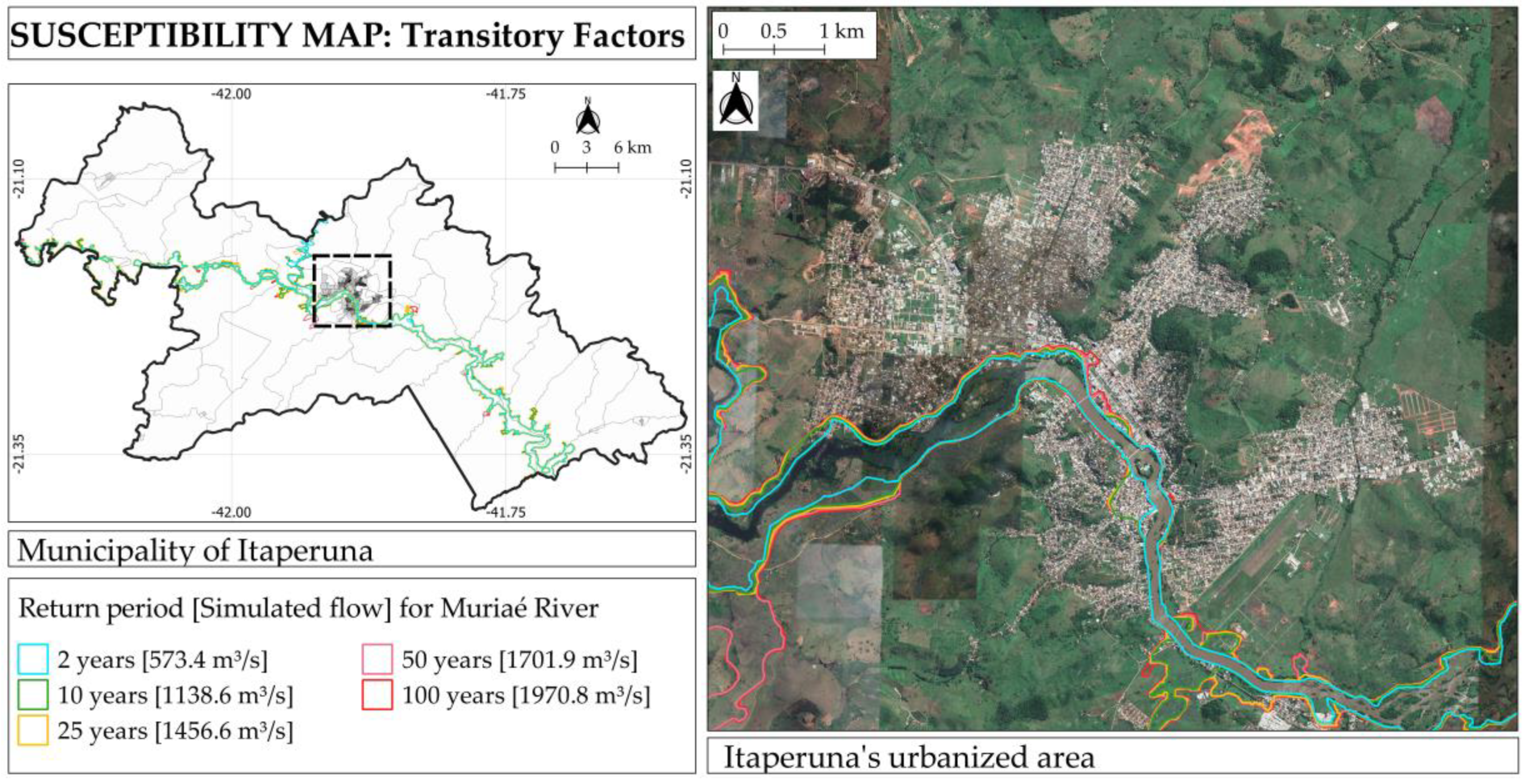
2.4.1. Flood Susceptibility Map Based on Transitory Factors
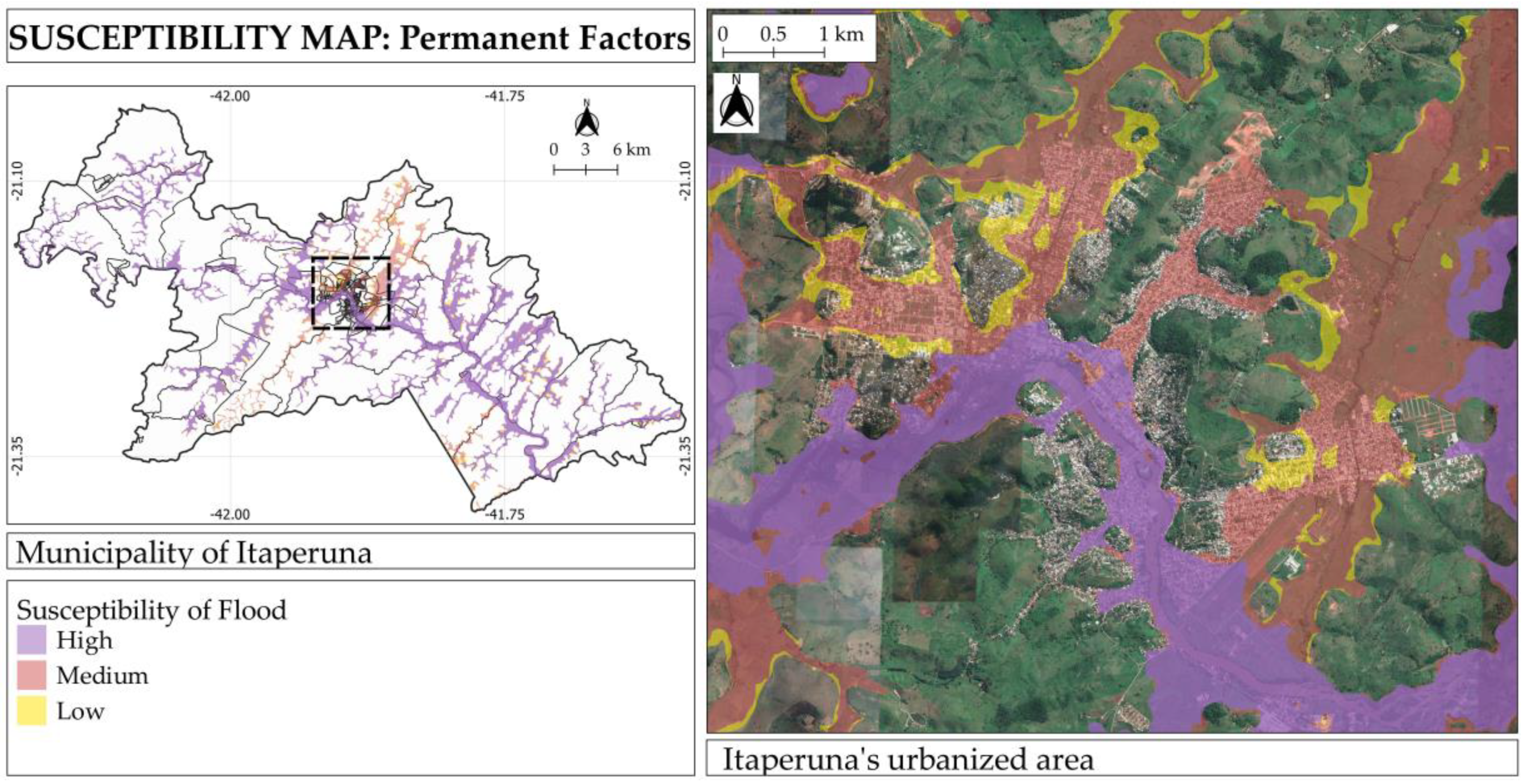
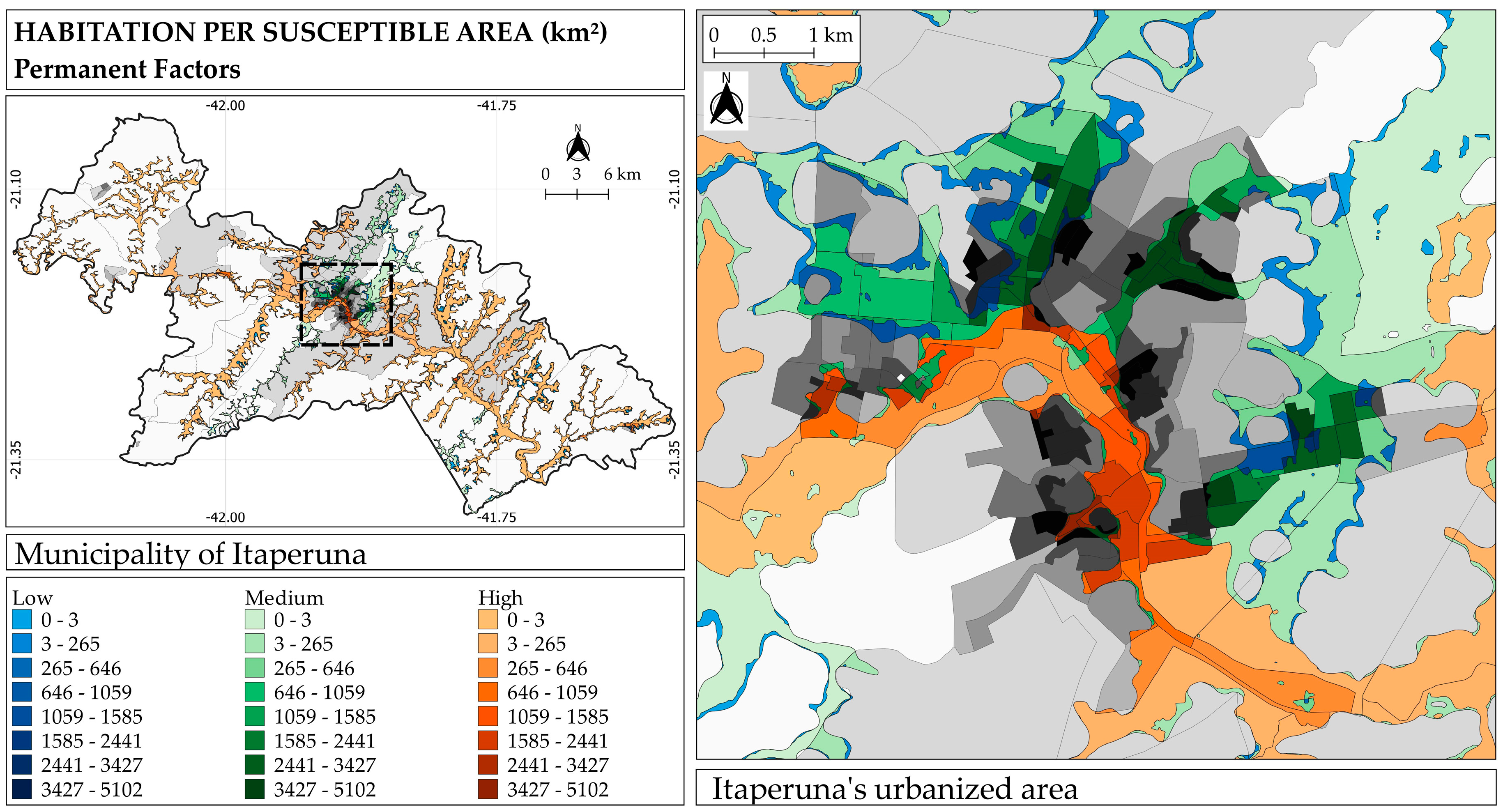
2.4.2. Flood Susceptibility Map Based on Permanent Factors
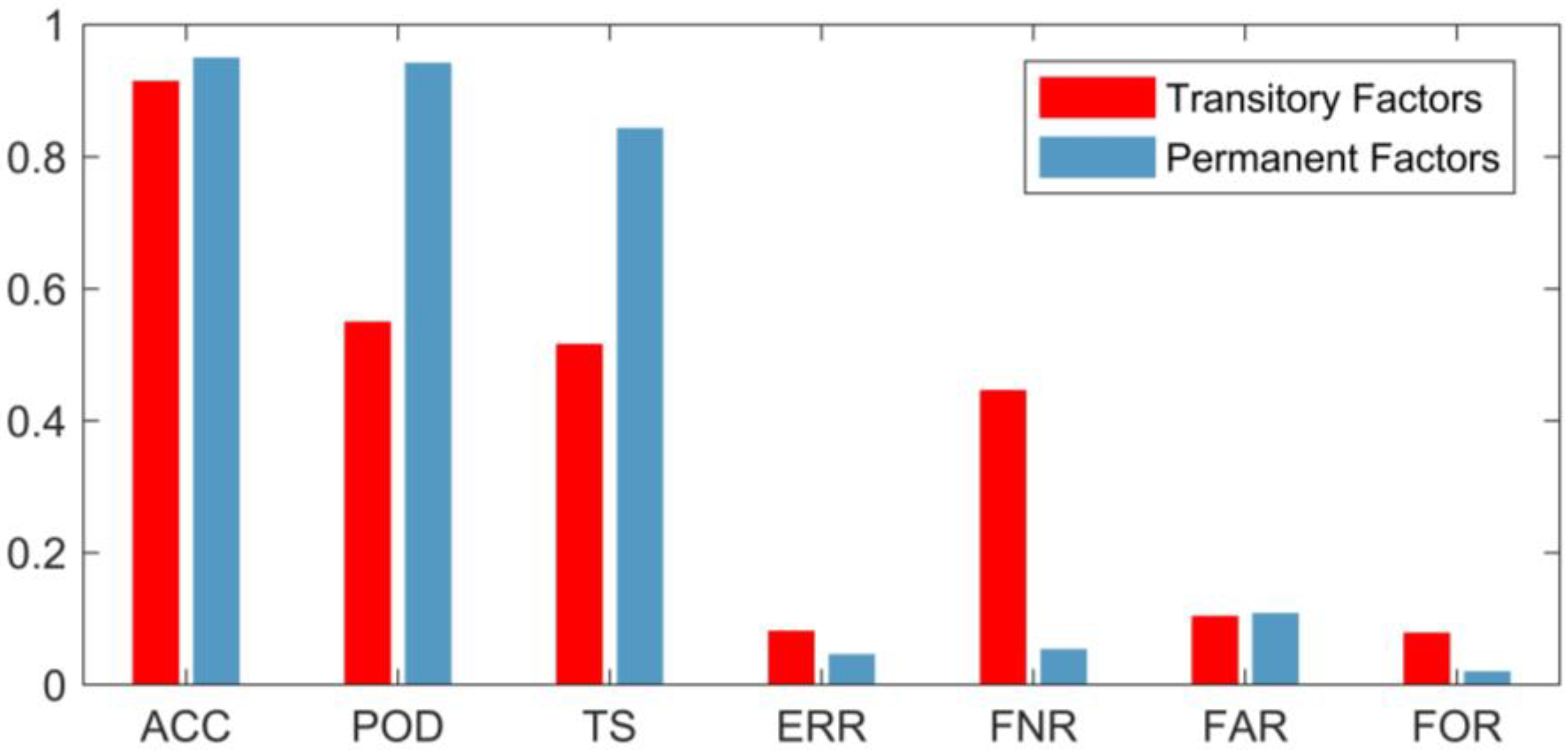
2.4.3. Maps Validation: Cross-Tabulation Method
- The accuracy (ACC) measures the percentage of the assertiveness (correct forecasts, TP + TN) over the total:
- The Probability of Detection (POD), Recall (REC), or True Positive Rate (TPR) indicates the ratio between the events occurred that were predicted by the model (TP) and the total of positive observations (TP + FN):
- The Threat Score (TS) or Critical Success Index (CSI) measures the ratio between the number of events predicted correctly (TP) and the total events and false alarms (TP + FN + FP). The TS highlights the importance of correct predictions of the events that have occurred, where the correct rejections have less relevance and are disregarded from the calculations. This index is a great indicator of the forecasts of extreme events (as floods), and it can be calculated as:
- The Error Rate (ERR) or Misclassification Rate measures the percentage of errors (FN + FP) over the total:
- The Miss Rate or False Negative Rate (FNR) measures the ratio between the number of unannounced events (FN) and the total of positive observations (TP + FN):
- The False Alarm Ratio (FAR) or False Discovery Rate (FDR) measures the relationship between false warnings (FP) and the total warnings (TP + FP):
- The False Omission Rate (FOR) indicates the ratio between the unannounced events (FN) and the total of non-predictions (FN + TN):
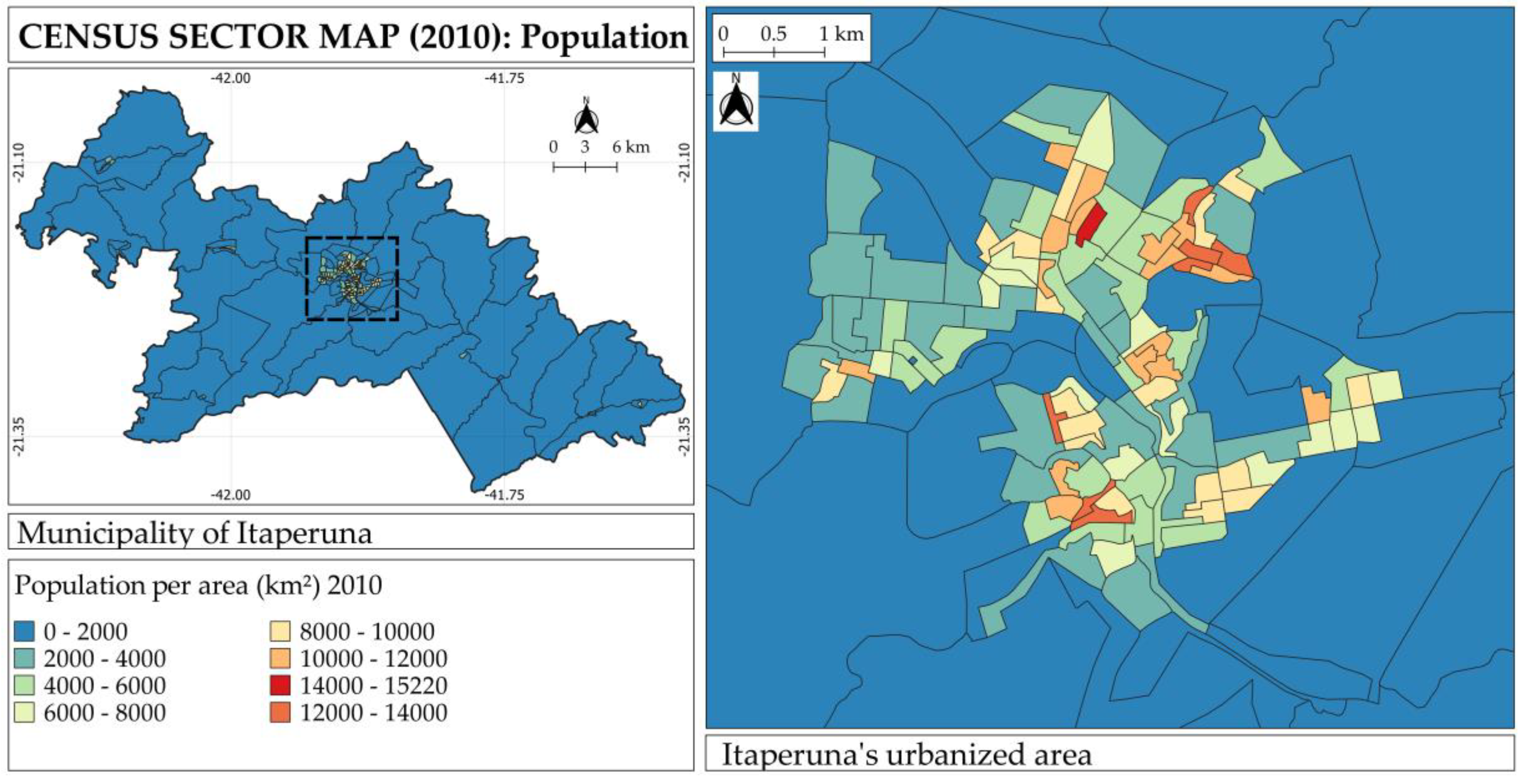
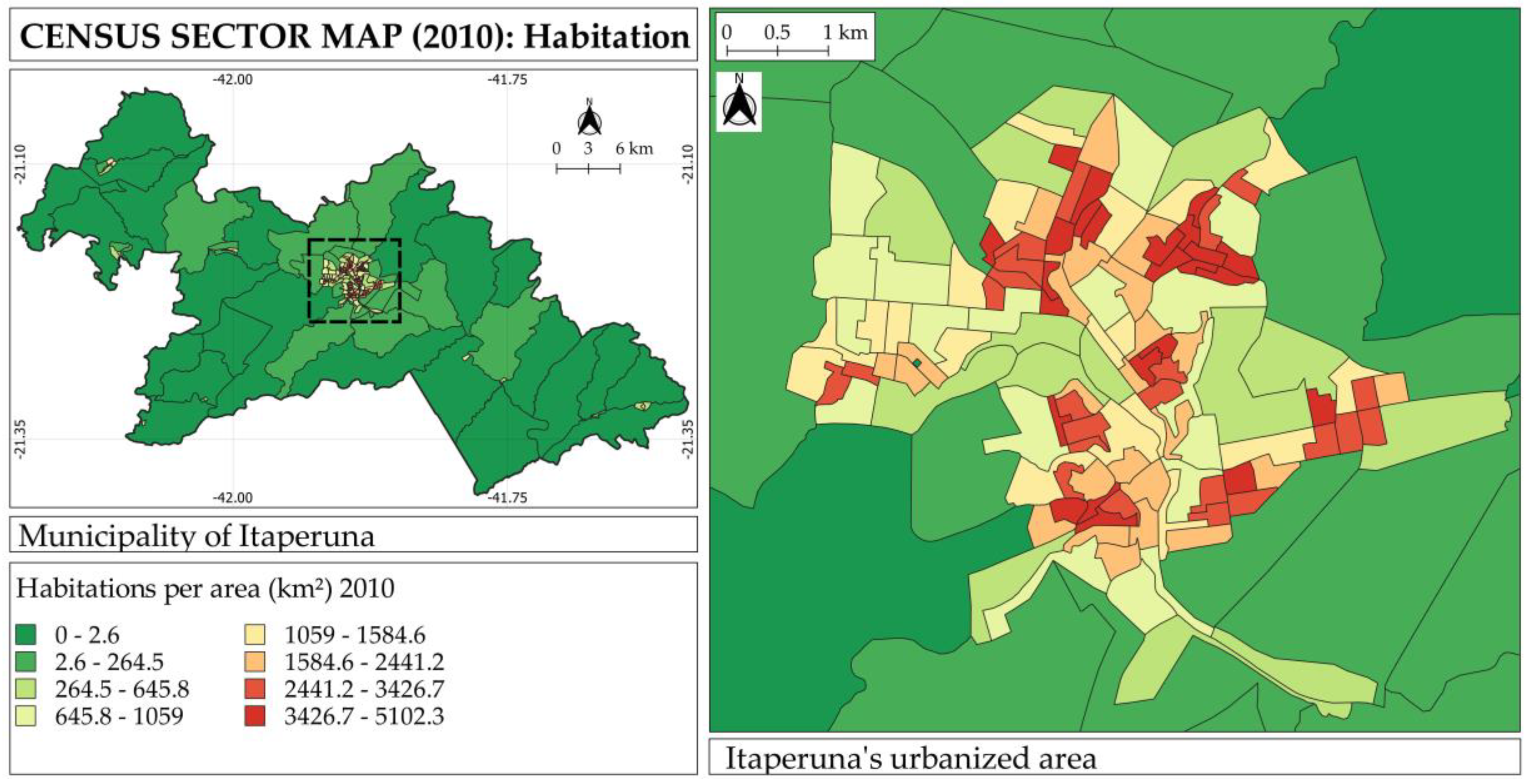
2.5. Census Sector Maps
3. Results
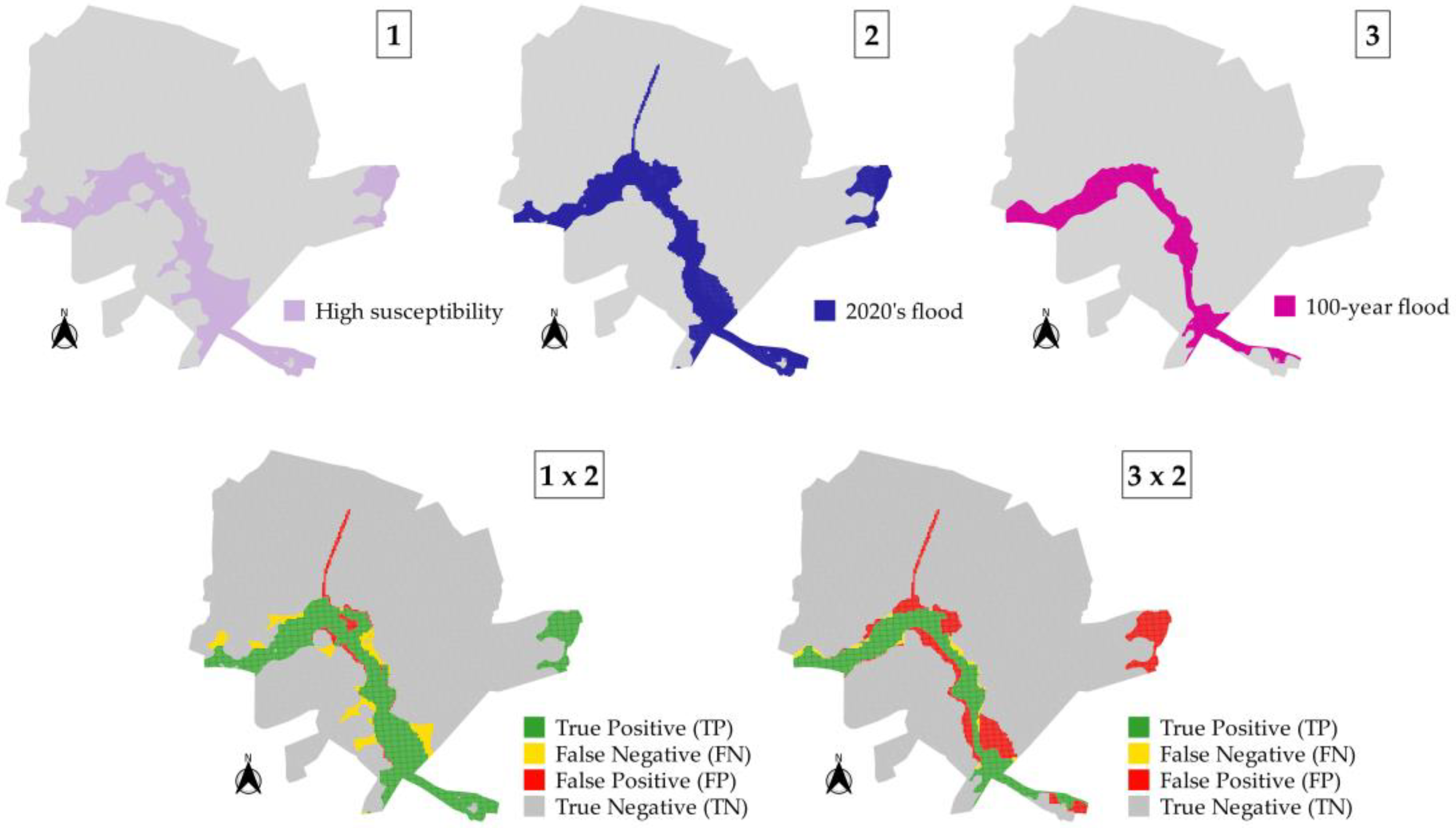
- The flood susceptibility areas corresponding to return periods of 2, 10, and 25 years were restricted to the areas of the smallest riverbed;
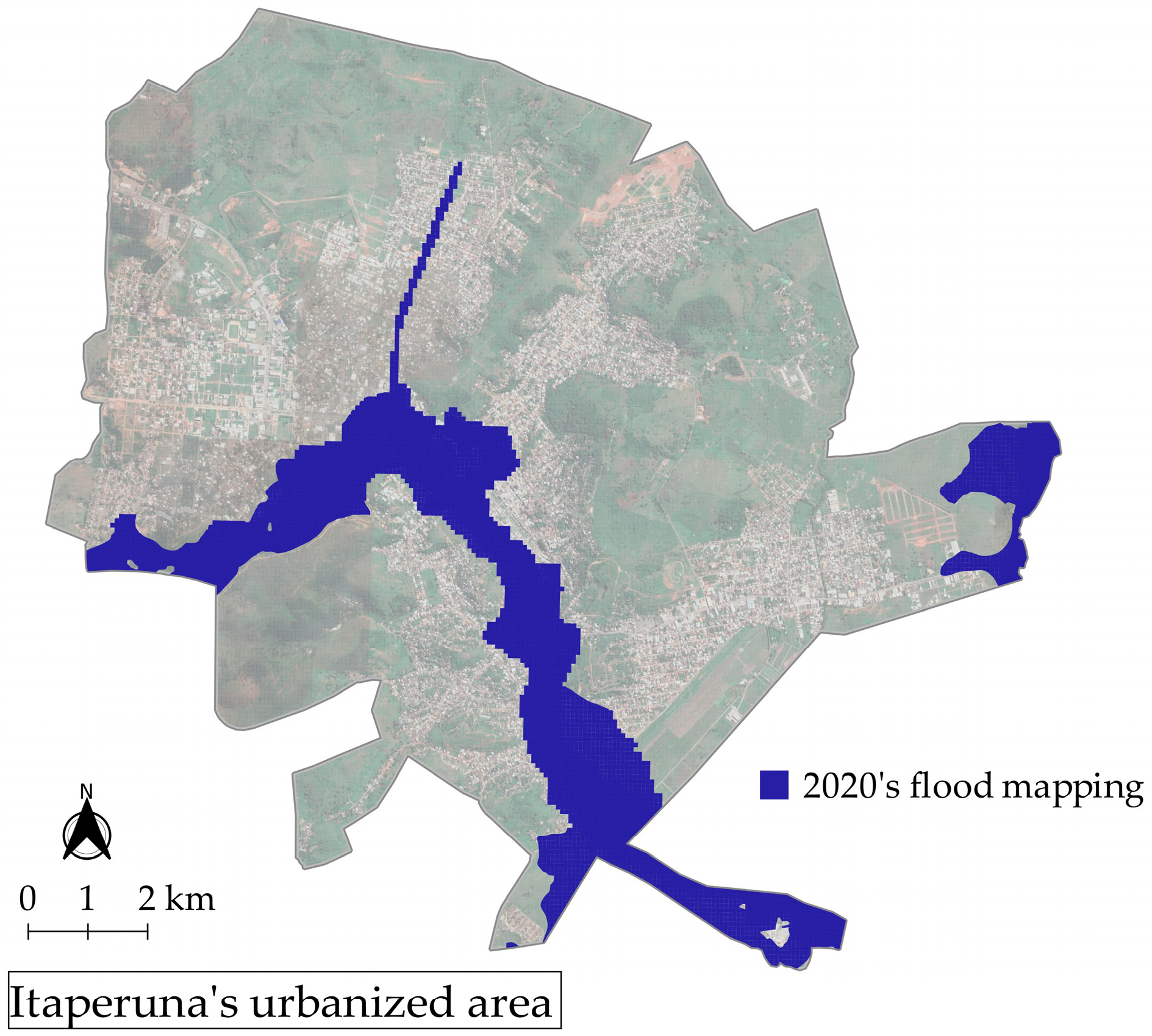
- The flood susceptibility areas corresponding to return periods of 50 and 100 years extended to areas of uninhabited floodplains (lower-left corner of the flood susceptibility map displayed in Figure 12);
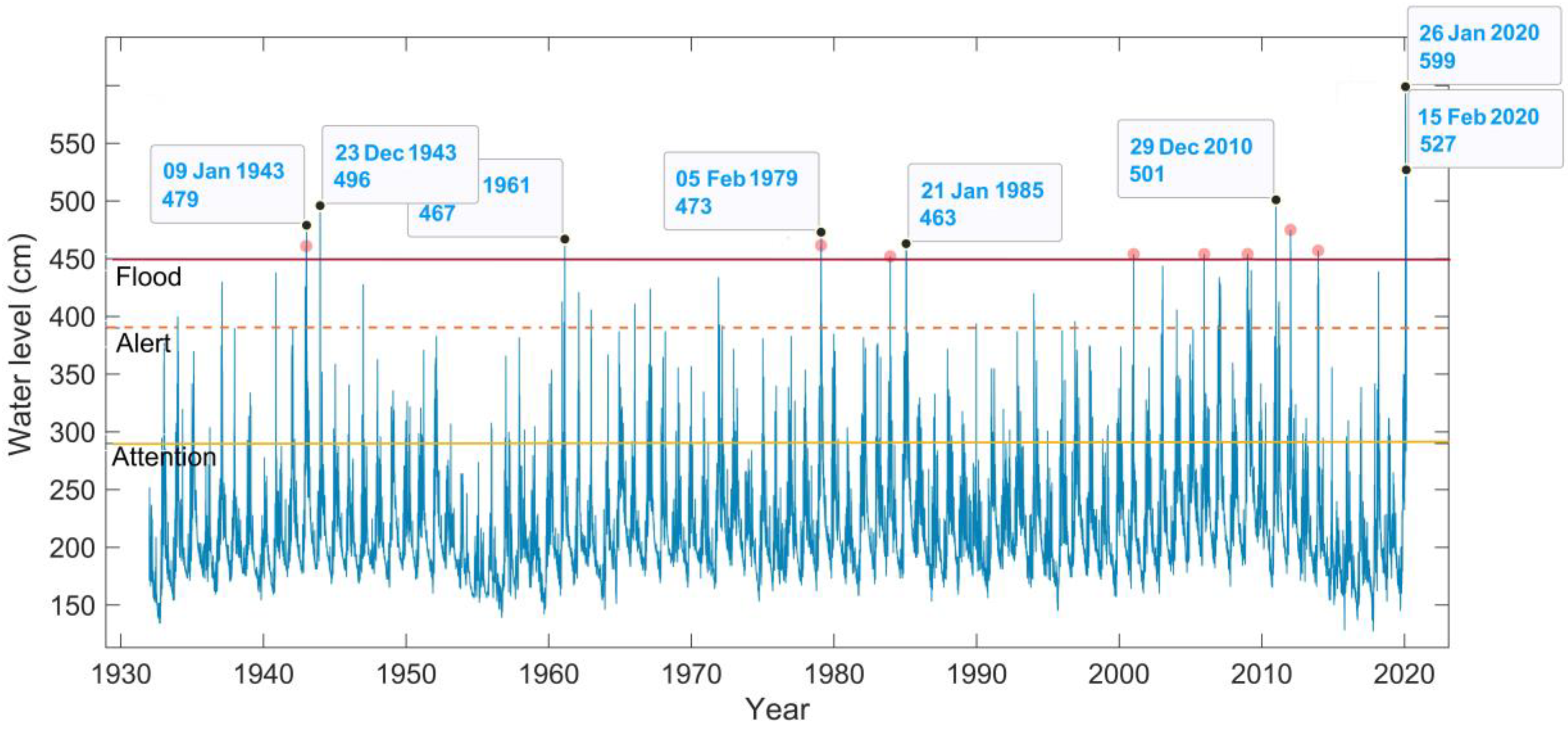
- Local (1), which is out of the susceptible areas (considering all analyzed return periods) estimated by the map, has been affected by five major floods in the last 12 years (2008, 2010, 2012, and twice in 2020);
- Local (2) has been affected by many floods over the years, where Figure 12 illustrates 1979, 2008, and 2020’s floods in this located area;
- Locals (3), (4), and (5), which are also out of the susceptible areas (considering all analyzed return periods), have been affected by at least four floods in the last 12 years (2008, 2012, and twice in 2020).
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schmitt, T.G.; Thomas, M.; Ettrich, N. Analysis and modeling of flooding in urban drainage systems. J. Hydrol. 2004, 299, 300–311. [Google Scholar] [CrossRef]
- Da Hora, S.B.; Gomes, R.L. Mapeamento e avaliação do risco a inundação do Rio Cachoeira em trecho da área urbana do Município de Itabuna/BA. Soc. Nat. 2009, 21, 57–75. [Google Scholar] [CrossRef]
- Furusho, C.; Andrieu, H.; Chancibault, K. Analysis of the hydrological behaviour of an urbanizing basin. Hydrol. Process. 2014, 28, 1809–1819. [Google Scholar] [CrossRef]
- Salvadore, E.; Bronders, J.; Batelaan, O. Hydrological modelling of urbanized catchemnts: A review and future directions. J. Hydrol. 2015, 529, 62–81. [Google Scholar] [CrossRef]
- Dougherty, M.; Dymond, R.L.; Grizzard, T.J., Jr.; Godrej, A.N.; Zipper, C.E.; Randolph, J. Quantifying long- term hydrologic response in an urbanizing basin. J. Hydrol. Eng. 2006, 12, 33–41. [Google Scholar] [CrossRef] [Green Version]
- Sheng, J.; Wilson, J.P. Watershed urbanization and changing flood behavior across the Los Angeles metropolitan region. Nat. Hazards 2009, 48, 41–57. [Google Scholar] [CrossRef]
- Du, J.; Qian, L.; Rui, H.; Zuo, T.; Zheng, D.; Zu, Y.; Xu, C. Assessing the effects of urbanization on annual runoff and flood events using an integrated hydrological modeling system for Qinhuai River basin, China. J. Hydrol. 2012, 464–465, 127–139. [Google Scholar] [CrossRef]
- Suria, S.; Mudgal, B.V. Impact of urbanization on flooding: The Thirusoolam sub watershed A case study. J. Hydrol. 2012, 412–413, 210–219. [Google Scholar] [CrossRef]
- Azizi, M.M. The Provision of Urban Infrastructure in Iran: An Empirical Evaluation. Urban. Stud. 1995, 32, 507–522. [Google Scholar] [CrossRef]
- Amis, P.; Kumar, S. Urban economic growth, infrastructure and poverty in India: Lessons from Visakhapatnam. Environ. Urban. 2000, 12, 185–196. [Google Scholar] [CrossRef]
- Ogun, T.P. Infrastructure and Poverty Reduction: Implications for Urban Development in Nigeria. Urban Forum 2010, 21, 249–266. [Google Scholar] [CrossRef] [Green Version]
- Qin, H.; Su, Q.; Khu, S.; Tang, N. Water Quality Changes during Rapid Urbanization in the Shenzhen River Catchment: An Integrated View of Socio-Economic and Infrastructure Development. Sustainability 2014, 6, 7433–7451. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Zhou, H.; Zhang, H.; Du, G.; Zhou, J. Urban flood risk warning under rapid urbanization. Environ. Res. 2015, 139, 3–10. [Google Scholar] [CrossRef] [PubMed]
- IBGE—Instituto Brasileiro de Geografia e Estatística. Agência IBGE Notícias. Available online: https://agenciadenoticias.ibge.gov.br/agencia-sala-de-imprensa/2013-agencia-de-noticias/releases/25278-ibge-divulga-as-estimativas-da-populacao-dos-municipios-para-2019 (accessed on 2 November 2019).
- Carneiro, P.R.F.; Miguez, M.G. Controle de Inundações em Bacias Hidrográficas Metropolitanas; Annablume: São Paulo, Brazil, 2011. [Google Scholar]
- Rezende, O.M. Manejo De Águas Pluviais: Uso De Paisagens Multifuncionais Em Drenagem Urbana Para Controle Das Inundações; Specialization course in urban engineering; Universidade Federal do Rio de Janeiro: Rio de Janeiro, Brazil, 2010. [Google Scholar]
- Kellens, W.; Terpstra, T.; De Maeyer, P. Perception and communication of flood risks: A systematic review of empirical research. Risk Anal. 2013, 33, 24–39. [Google Scholar] [CrossRef] [Green Version]
- Loucks, D.P. Debates—Perspectives on socio-hydrology: Simulating hydrologic-human interactions. Water Resour. Res. 2015, 51, 4789–4794. [Google Scholar] [CrossRef]
- Houston, D.; Cheung, W.; Basolo, V.; Feldmand, D.; Matthew, R.; Sanders, B.F.; Karlin, B.; Schubert, J.E.; Goodrich, K.A.; Contreras, G.; et al. The Influence of Hazard Maps and Trust of Flood Controls on Coastal Flood Spatial Awareness and Risk Perception. Environ. Behav. 2017, 51, 347–375. [Google Scholar] [CrossRef]
- Bertilsson, L.; Wiklund, K.; Tebaldi, I.M.; Rezende, O.M.; Veról, A.P.; Miguez, M.G. Urban flood resilience—A multi-criteria index to integrate flood resilience into urban planning. J. Hydrol. 2019, 573, 970–982. [Google Scholar] [CrossRef]
- Grossi, P.; Kunreuther, H.C. Catastrophe Modeling: A New Approach of Managing Risk; Springer: New York, NY, USA, 2005. [Google Scholar]
- IDSR International Strategy for Disaster Reduction UN. United Nations Documents Related to Disaster Reduction 2000–2007: Advance copy; UN: Geneva, Switzerland, 2007. [Google Scholar]
- Silva, A.P.M.; Barbosa, A.A. Validação da função mancha de inundação do SPRING. In Proceedings of the Anais XIII Simpósio Brasileiro de Sensoriamento Remoto, Florianópolis, Brazil, 21–26 April 2007; INPE: São José dos Campos, Brazil, 2007; pp. 5499–5505. [Google Scholar]
- Faulkner, H.; Ball, D. Environmental hazards and risk communication. Environ. Hazards 2007, 7, 71–78. [Google Scholar] [CrossRef]
- Newell, B.R.; Rakow, T.; Yechiam, E.; Sambur, M. Rare disaster information can increase risk-taking. Nat. Clim. Chang. 2016, 6, 158–161. [Google Scholar] [CrossRef]
- Kim, N.W.; Lee, J.-Y.; Park, D.-H.; Kim, T.-W. Evaluation of Future Flood Risk According to RCP Scenarios Using a Regional Flood Frequency Analysis for Ungauged Watersheds. Water 2019, 11, 992. [Google Scholar] [CrossRef] [Green Version]
- Lim, C.-H.; Kim, S.H.; Chun, J.A.; Kafatos, M.C.; Lee, W.-K. Assessment of Agricultural Drought Considering the Hydrological Cycle and Crop Phenology in the Korean Peninsula. Water 2019, 11, 1105. [Google Scholar] [CrossRef] [Green Version]
- Narbondo, S.; Gorgoglione, A.; Crisci, M.; Chreties, C. Enhancing Physical Similarity Approach to Predict Runoff in Ungauged Watersheds in Sub-Tropical Regions. Water 2020, 12, 528. [Google Scholar] [CrossRef] [Green Version]
- IBGE Instituto Brasileiro de Geografia e Estatística. Portal IBGE Cidades. Available online: https://cidades.ibge.gov.br/brasil/rj/itaperuna/panorama (accessed on 26 October 2019).
- Paz, I.; Tchiguirinskaia, I.; Schertzer, D. Rain gauge networks’ limitations and the implications to hydrological modelling highlighted with a X-band radar. J. Hydrol. 2020, 583, 124615. [Google Scholar] [CrossRef]
- Lovejoy, S.; Schertzer, D. Generalized scale-invariance in the atmosphere and fractal models of rain. Water Resour. Res. 1985, 21, 1233–1250. [Google Scholar] [CrossRef] [Green Version]
- Nikora, V. Fractal structures of river plan forms. Water Resour. Res. 1991, 27, 1327–1333. [Google Scholar] [CrossRef]
- Gires, A.; Tchiguirinskaia, I.; Schertzer, D.; Ochoa-Rodriguez, S.; Willems, P.; Ichiba, A.; Wang, L.-P.; Pina, R.; Van Assel, J.; Bruni, G.; et al. Fractal analysis of urban catchments and their representation in semi-distributed models: Imperviousness and sewer system. Hydrol. Earth Syst. Sci. 2017, 21, 2361–2375. [Google Scholar] [CrossRef] [Green Version]
- Paz, I.S.R. Quantifying the Rain Heterogeneity by X-Band Radar Measurements for Improving Flood Forecasting. Ph.D. Thesis, Université Paris-Est, Champs-sur-Marne, France, 2018. [Google Scholar]
- Versini, P.-A.; Gires, A.; Tchiguirinskaia, I.; Schertzer, D. Fractal analysis of green roof spatial implementation in European cities. Urban For. Urban Green. 2020, 49, 126629. [Google Scholar] [CrossRef]
- Rangel, M.P. Eleições Municipais E Infraestrutura Urbana. O caso Itaperuna-RJ. Master’s Thesis, Universidade Candido Mendes, Campos dos Goytacazes RJ, Brazil, 2010. [Google Scholar]
- Prefeitura Municipal de Itaperuna. PMASI—Plano Municipal de Assistência Social de Itaperuna 2016–2019; Secretaria Municipal de Ação Social Habitação e Trabalho: Itaperuna, Brazil, 2016. [Google Scholar]
- Santos, R.J.F. A Segregação Sócio-Espacial Na Cidade De Itaperuna (RJ). Master’s Thesis, Universidade Federal Fluminense, Campos dos Goytacazes RJ, Brazil, 2018. [Google Scholar]
- CPRM—Companhia de Pesquisa Recursos Minerais. Bacia do Rio Muriaé. Available online: https://www.cprm.gov.br/sace/index_bacias_monitoradas.php?getbacia=bmuriae# (accessed on 26 October 2019).
- CEIVAP—Comitê de Integração da Bacia Hidrográfica do Rio Paraíba do Sul. Plano de recursos hídricos da Bacia Paraíba do Sul Resumo. Available online: http://www.ceivap.org.br/downloads/cadernos/Caderno%206%20-%20Muriae.pdf (accessed on 26 October 2019).
- Diniz, D. O desenvolver de um município: Itaperuna, RJ.; Damadá Artes Gráficas: Itaperuna, Brazil, 1985. [Google Scholar]
- Blog do Marcelo Lessa ATENÇÃO!!! As águas voltam a subir em Itaperuna!!! Available online: http://marcelolessasjuba.blogspot.com/2012_01_08_archive.html (accessed on 17 February 2020).
- Blog Alan Gonçalves Imagens aéreas da enchente que atingiu Itaperuna em fevereiro de 2020. Available online: https://blogalangoncalvesoficial.blogspot.com/2020/02/imagens-aereas-da-enchente-que-atingiu.html (accessed on 17 February 2020).
- ANA—Agência Nacional de Águas. Sistema Hidro Telemetria. Available online: http://www.snirh.gov.br/hidrotelemetria/Mapa.aspx (accessed on 10 March 2020).
- Pussiareli, N. Itaperuna Enchente 2020. Available online: https://youtu.be/VVoW-mwu3Io (accessed on 10 March 2020).
- Mandelbrot, B.B. Intermittent turbulence in self-similar cascades: Divergence of high moments and dimension of the carrier. J. Fluid Mech. 1974, 62, 331–358. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. How long is the coast of Britain. Science 1967, 156, 636–638. [Google Scholar] [CrossRef] [Green Version]
- Mandelbrot, B.B. Fractals: Form, Chance and Dimension; Freeman: San Francisco, CA, USA, 1977. [Google Scholar]
- Mandelbrot, B.B.; Pignoni, R. The Fractal Geometry of Nature; Freeman: New York, NY, USA, 1983. [Google Scholar]
- Feder, J. Fractals (Physics of Solids and Liquids); Plennum: New York, NY, USA, 1988. [Google Scholar]
- Hentschel, H.; Procaccia, I. The infinite number of generalized dimensions of fractals and strange attractors. Physical D 1983, 8, 435–444. [Google Scholar] [CrossRef]
- Lovejoy, S.; Schertzer, D.; Tsonis, A.A. Functional box-counting and multiple elliptical dimensions in rain. Science 1987, 235, 1036–1038. [Google Scholar] [CrossRef]
- Oliveira, O.O. Diagnóstico ambiental do município de Itaperuna/RJ a partir do mapeamento geológico-geotécnico e do uso de técnicas de geoprocessamento. Master’s Thesis, Universidade Estadual do Norte Fluminense Darcy Ribeiro, Campos dos Goytacazes RJ, Brazil, 2006. [Google Scholar]
- Campos, P.C.O. Avaliação do efeito da variação da umidade no comportamento mecanístico em um trecho homogêneo da Estrada de Ferro Carajás. Master’s Thesis, Instituto Militar de Engenharia, Rio de Janeiro RJ, Brazil, 2019. [Google Scholar] [CrossRef]
- Campos, P.C.O.; Silva, B.-H.A.; Marques, M.E.S. Caracterização geotécnica dos solos de subleito ferroviário: Investigações de campo e laboratoriais. Rev. Ibero-Am. De Ciências Ambient. 2019, 10, 178–193. [Google Scholar] [CrossRef]
- EMBRAPA—Empresa Brasileira de Pesquisa Agropecuária. Sistema Brasileiro de Classificação de Solos; Empresa Brasileira de Agropecuária CNPS, Serviço de Produção de Informação: Brasília, Brazil, 2006. [Google Scholar]
- Martorano, L.G.; Rossiello, R.O.P.; Meneguelli, N.A.; Lumbreras, J.F.; Valle, L.S.S.; Motta, P.E.F.; Rebello, E.R.G.; Said, U.P.; Martins, G.S. Aspectos climáticos do noroeste fluminense; EMBRAPA Solos: Rio de Janeiro, Brazil, 2003. [Google Scholar]
- Duarte, B.P.; Heilbron, M.; Gontijo-Pascutti, A.H.F.; Silva, T.M.; Valladares, C.S.; Almeida, J.C.H.; Tupinambá, M.; Nogueira, J.R.; Valeriano, C.; Silva, L.G.E.; et al. Geologia e RecursosMinerais da Folha Itaperuna; CPRM: Belo Horizonte, Brazil, 2012. [Google Scholar]
- INPE Instituto Nacional de Pesquisas Espaciais. TOPODATA Banco de Dados Geomorfométricos do Brasil. Available online: www.dsr.inpe.br/topodata/ (accessed on 16 November 2019).
- Lumbreras, J.F. Relações solo-paisagem no noroeste do estado do Rio de Janeiro: Subsídios ao planejamento de uso sustentável em áreas de relevo acidentado do bioma Mata Atlântica. Ph.D. Thesis, Universidade Federal do Rio de Janeiro, Brazil, 2008. [Google Scholar]
- CENSIPAM Centro Gestor e Operacional do Sistema de Proteção da Amazônia. Mapas de manchas de inundação ajudam no planejamento urbano e no ressarcimento de danos. Available online: http://www.sipam.gov.br/mapas-de-risco-ajudam-no-planejamento-urbano-e-no-ressarcimento-de-danos (accessed on 1 November 2019).
- CPRM—Companhia de Pesquisa Recursos Minerais. Cartas de Suscetibilidade a Movimentos Gravitacionais de Massa e Inundações—1:25000. Available online: http://www.cprm.gov.br/publique/Gestao-Territorial/Prevencao-de-Desastres/Cartas-de-Suscetibilidade-a-Movimentos-Gravitacionais-de-Massa-e-Inundacoes-5379.html (accessed on 14 March 2020).
- Cooke, R.U.; Doornkamp, J.C. Geomorphology in Environmental Management; Claredon Press: Oxford, UK, 1990. [Google Scholar]
- ANA—Agência Nacional de Águas. Estudos Auxiliares para a Gestão de Risco de Inundações—Bacia do Rio Paraíba do Sul. Available online: http://gripbsul.ana.gov.br/SisprecR05.html (accessed on 10 March 2020).
- HEC (Hydrologic Engineering Center). Hydrologic Modeling System (HEC) User’s Manual; US Army Corps of Engineers: Washington, DC, USA, 2006.
- HEC (Hydrologic Engineering Center). HEC-RAS River Analysis Sytem User’s Manual; Version 1.0.; U.S. Army Corps of Engineers Hydrologic Engineering Center: Davis, CA, USA, 1995.
- Horritt, M.S.; Bates, P.D. Evaluation of 1D and 2D numerical models for predicting riverflood inundation. J. Hydrol. 2002, 268, 87–99. [Google Scholar] [CrossRef]
- Pappenberger, F.; Beven, K.; Horritt, M.; Blazkova, S. Uncertainty in the calibration of effective roughness parameters in HEC-RAS using inundation and downstream level observations. J. Hydrol. 2005, 302, 46–69. [Google Scholar] [CrossRef]
- Salimi, S.; Ghanbarpour, M.R.; Solaimani, K.; Ahamadi, M Z. Flood plain mapping using hydraulic simulation model in GIS. J. Appl. Sci. 2008, 8, 660–665. [Google Scholar] [CrossRef] [Green Version]
- Koutroulis, A.G.; Tsanis, I.K. A method for estimating flash flood peak discharge in a poorly gauged basin: Case study for the 13–14 January 1994 flood, Giofiros basin, Crete, Greece. J. Hydrol. 2010, 385, 150–164. [Google Scholar] [CrossRef]
- Pinar, E.; Paydas, K.; Seckin, G.; Akilli, H.; Sahin, B.; Cobaner, M.; Kocaman, S.; Atakan Akar, M. Artificial neural network approaches for prediction of backwater through arched bridge constrictions. Adv. Eng. Softw. 2010, 41, 627–635. [Google Scholar] [CrossRef]
- Quirogaa, V.M.; Kurea, S.; Udoa, K.; Manoa, A. Application of 2D numerical simulation for the analysis of the February 2014 Bolivian Amazonia flood: Application of the new HEC-RAS version 5. Rev. Iberoam. Del. Agua. 2016, 3, 25–33. [Google Scholar] [CrossRef] [Green Version]
- Patel, D.P.; Ramirez, J.A.; Srivastava, P.K.; Bray, M.; Han, D. Assessment of flood inundation mapping of Surat city by coupled 1D/2D hydrodynamic modeling: A case application of the new HEC-RAS 5. Nat. Hazards 2017, 89, 93–130. [Google Scholar] [CrossRef]
- ANA—Agência Nacional de Águas. Previsão de Eventos Críticos na Bacia do Rio Paraíba do Sul. R32 Caracterização das Cheias e das Planícies de Inundação dos Rios Pomba e Muriaé para o SIEMEC; 1069-ANA-RPS-RT-021; Brasília, DF, Brazil: ENGECORPS, 2011; 55p. [Google Scholar]
- HEC (Hydrologic Engineering Center). Hydrologic Modeling System HEC-HMS, Technical Reference Manual; U.S. Army Corps of Engineers: Davis, CA, USA, 2000. [Google Scholar]
- HEC (Hydrologic Engineering Center). Hydrologic Modeling System (HEC-HMS) Applications Guide: Version 3.1.0; U.S. Army Corps of Engineers: Davis, CA, USA, 2008.
- Bründl, M.; Romang, H.E.; Bischof, N.; Rheinberger, C.M. The risk concept and its application in natural hazard risk management in Switzerland. Nat. Hazards Earth Syst. Sci. 2009, 9, 801–813. [Google Scholar] [CrossRef]
- Röthlisberger, V.; Zischg, A.; Keiler, M. Spatiotemporal aspects of flood exposure in Switzerland. E3s Web Conf. 2016, 7, 8008. [Google Scholar] [CrossRef] [Green Version]
- Lindner, E.A.; Gomig, K.; Kobiyama, M. Sensoriamento remoto aplicado à caracterização morfométrica e classificação do uso do solo na bacia rio do Peixe/SC. In Proceedings of the Simpósio Brasileiro de Sensoriamento Remoto, Florianópolis, Brazil, 21–26 April 2007; INPE: São José dos Campos, Brazil, 2007; pp. 3405–3412. [Google Scholar]
- Rennó, C.D.; Nobre, A.D.; Cuartas, L.A.; Soares, J.V.; Hodnett, M.G.; Tomasella, J.; Waterloo, M.J. HAND, a new terrain descriptor using SRTM-DEM: Mapping terra-firme rainforest environments in Amazonia. Remote Sens. Environ. 2008, 112, 3469–3481. [Google Scholar] [CrossRef]
- de Oliveira, G.G.; Guasselli, L.A.; Saldanha, D.L. Influência de variáveis morfométricas e da distribuição das chuvas na previsão de enchentes em São Sebastião do Caí, RS. Rev. De Geogr. 2010, 3, 140–155. [Google Scholar]
- Schumm, S.A. Evolution of drainage systems and slopes in badlands of Perth Amboy. Geol. Soc. Am. Bull. 1956, 67, 597–646. [Google Scholar] [CrossRef]
- Horton, R.E. Erosional development of streams and their drainage basins: Hydrophysical approach to quantitative morphology. Geol. Soc. Am. Bull. 1945, 56, 275–370. [Google Scholar] [CrossRef] [Green Version]
- Müller, V.C. A Quantitative Geomorphology Study of Drainage Basin Characteristics in the Clinch Mountain Area, Virginia and Tennessee; Department of Geology, Columbia University: New York, NY, USA, 1953. [Google Scholar]
- Schumm, S.A. Sinuosity of alluvial rivers on the great plains. Geol. Soc. Am. Bull. 1963, 74, 1089–1100. [Google Scholar] [CrossRef]
- Bajabaa, S.; Masoud, M.; Al-Amri, N. Flash flood hazard mapping based on quantitative hydrology, geomorphology and GIS techniques (case study of Wadi Al Lith, Saudi Arabia). Arab. J. Geosci. 2014, 7, 2469–2481. [Google Scholar] [CrossRef]
- Pires, E.G.; Borma, L.S. Utilização do modelo HAND para o mapeamento de bacias hidrográficas em ambiente de Cerrado. In Proceedings of the Simpósio Brasileiro de Sensoriamento Remoto, Foz do Iguaçu, PR, Brazil, 13–18 April 2013; INPE: São José dos Campos, Brazil, 2013; pp. 5568–5575. [Google Scholar]
- Goodman, L.A.; Kruskal, W.H. Measures of Association for Cross Classifications. J. Am. Stat. Assoc. 1954, 49, 732–764. [Google Scholar] [CrossRef]
- Cohen, J. A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- IBGE Instituto Brasileiro de Geografia e Estatística. Censo 2010. Available online: https://censo2010.ibge.gov.br (accessed on 16 November 2019).
- Nepal, S. Evaluating upstream-downstream linkages of hydrological dynamics in the Himalayan region. Ph.D. Thesis, Friedrich Schiller University of Jena, Jena, Germany, 2012. [Google Scholar]
- Nepal, S.; Flügel, W.-A.; Shrestha, A.B. Upstream-downstream linkages of hydrological processes in the Himalayan region. Ecol. Process. 2014, 3, 19. [Google Scholar] [CrossRef] [Green Version]
- Tabari, M.M.R. Prediction of River Runoff Using Fuzzy Theory and Direct Search Optimization Algorithm Coupled Model. Arab. J. Sci. Eng. 2017, 41, 4039–4051. [Google Scholar] [CrossRef]
- Tanaka, T.; Tachikawa, Y.; Ichikawa, Y.; Yorozu, K. Impact assessment of upstream flooding on extreme flood frequency analysis by incorporating a flood-inundation model for flood risk assessment. J. Hydrol. 2017, 554, 370–382. [Google Scholar] [CrossRef]
- ANA—Agência Nacional de Águas. Elaboração de Estudos Para Concepção de um Sistema de Previsão de Eventos Críticos na Bacia do Rio Paraíba do Sul e de um Sistema de Intervenções Estruturais Para Mitigação dos Efeitos de Cheias nas Bacias dos Rios Muriaé e Pomba e Investigações de Campo Correlatas; 1069-ANA-RPS-RT-017; Tomo, I., Ed.; R05—Estudos e modelagem de cheias, previsão de vazões e estudos relacionados; Brasília, DF, Brazil: ENGECORPS, 2012; Volume 1, p. 153. [Google Scholar]
- COPPETEC. Laboratório de Hidrologia e Estudos de Meio Ambiente. Plano Estadual de Recursos Hídricos do Estado do Rio de Janeiro. Available online: Agevap.org.br/downloads/Diagnostico-Rede-Quali-quantitativa.pdf (accessed on 11 March 2020).
- Salviano, M.F. Modelagem hidrológica da bacia do rio Muriaé com TOPMODEL, telemetria e sensoriamento remoto. Master’s Thesis, Instituto de Astronomia, Geofísica e Ciências Atmosféricas, São Paulo—SP, Brazil, 2019. [Google Scholar]
- de Oliveira, M.N.; Martins, C.A.; da Silva, R.M. Rio de Janeiro’s Flash Flood Warning System. In Proceedings of the Sustainable Urban Communities towards a Nearly Zero Impact Built Environment, Proceedings of the SBE16 Brazil & Portugal, Vitória, Brazil, 7–9 September 2016; Available online: http//hdl.handle.net/1822/56568 (accessed on 15 January 2020).
- INEA Instituto Estadual de Ambiente. Monitoramento Hidrometeorológico. Available online: http://www.inea.rj.gov.br/ar-agua-e-solo/monitoramento-hidrometeorologico/ (accessed on 21 February 2020).
- Gires, A.; Abbes, J.-B.; da Silva Rocha Paz, I.; Tchiguirinskaia, I.; Schertzer, D. Multifractal characterization of a simulated surface flow: A case study with Multi-Hydro in Jouy-en-Josas, France. J. Hydrol. 2018, 558, 482–495. [Google Scholar] [CrossRef] [Green Version]
- Lovejoy, S.; Schertzer, D.; Ladoy, P. Fractal characterization of inhomogeneous geophysical measuring networks. Nature 1986, 319, 43–44. [Google Scholar] [CrossRef]
- Tessier, Y.; Lovejoy, S.; Schertzer, D. Multifractal analysis and simulation of the global meteorological network. J. Appl. Meteorol. 1994, 33, 1572–1586. [Google Scholar] [CrossRef] [Green Version]
- Mazzarella, A.; Tranfaglia, G. Fractal characterization of geophysical measuring networks and its implication for an optimal location of additional stations: An application to a rain-gauge network. Appl. Clim. 2000, 65, 157–163. [Google Scholar] [CrossRef]
- Capecchi, V.; Crisci, A.; Melani, S.; Morabito, M.; Politi, P. Fractal characterization of rain-gauge networks and precipitations: An application in Central Italy. Theor. Appl. Climatol. 2012, 107, 541–546. [Google Scholar] [CrossRef] [Green Version]
- Schilling, W. Rainfall data for urban hydrology: What do we need? Atmos. Res. 1991, 27, 5–21. [Google Scholar] [CrossRef]
- Berne, A.; Delrieu, G.; Creutin, J.-D.; Obled, C. Temporal and spatial resolution of rainfall measurements required for urban hydrology. J. Hydrol. 2004, 299, 166–179. [Google Scholar] [CrossRef]
- Einfalt, T.; Arnbjerg-Nielsen, K.; Golz, C.; Jensen, N.-E.; Quirmbach, M.; Vaes, G.; Vieux, B. Towards a roadmap for use of radar rainfall data in urban drainage. J. Hydrol. 2004, 299, 186–202. [Google Scholar] [CrossRef]
- Ochoa-Rodriguez, S.; Wang, L.-P.; Gires, A.; Pina, R.; Reinoso-Rondinel, R.; Bruni, G.; Ichiba, A.; Gaitan, S.; Cristiano, E.; van Assel, J.; et al. Impact of spatial and temporal resolution of rainfall inputs on urban hydrodynamic modelling outputs: A multi-catchment investigation. J. Hydrol. 2015, 531, 389–407. [Google Scholar] [CrossRef]
- Paz, I.; Willinger, B.; Gires, A.; Ichiba, A.; Monier, L.; Zobrist, C.; Tisserand, B.; Tchiguirinskaia, I.; Schertzer, D. Multifractal Comparison of Reflectivity and Polarimetric Rainfall Data from C-and X-Band Radars and Respective Hydrological Responses of a Complex Catchment Model. Water 2018, 10, 269. [Google Scholar] [CrossRef] [Green Version]
- Paz, I.; Willinger, B.; Gires, A.; Alves de Souza, B.; Monier, L.; Cardinal, H.; Tisserand, B.; Tchiguirinskaia, I.; Schertzer, D. Small-scale rainfall variability impacts analyzed by fully-distributed model using C-band and X-band radar data. Water 2019, 11, 1273. [Google Scholar] [CrossRef] [Green Version]
- Villarini, G.; Mandapaka, P.V.; Krajewski, W.F.; Moore, R.J. Rainfall and sampling uncertainties: A rain gauge perspective. J. Geophys. Res. Atmos. 2008, 113, D11102. [Google Scholar] [CrossRef]
- Peleg, N.; Ben-Asher, M.; Morin, E. Radar subpixel-scale rainfall variability and uncertainty: Lesson learned from observations of a dense rain-gauge network. Hydrol. Earth Syst. Sci. 2013, 17, 2195–2208. [Google Scholar] [CrossRef] [Green Version]
- O’Donnell, T.; Canedo, P. The reliability of conceptual basin model calibration. In Hydrological Forecasting, Proceedings of the Oxford Symposium, Oxford, UK, April 1980; IAHS Publisher: Oxford, UK, 1980; Volume 129, pp. 263–269. [Google Scholar]



| Morphometric Indexes\HAND Model | High Susceptibility | Medium Susceptibility | Low Susceptibility |
|---|---|---|---|
| High Susceptibility | High | High | Medium |
| Medium Susceptibility | High | Medium | Low |
| Low Susceptibility | Medium | Low | Low |
| Predicted 1 | Observations 2 | Row Total | |
|---|---|---|---|
| Positive | Negative | ||
| Positive | TP 3 | FP 5 | TP + FP |
| Negative | FN 4 | TN 6 | FN + TN |
| Column Total | TP + FN | FP + TN | |
| Predicted | Observations | Row Total | |
|---|---|---|---|
| Positive | Negative | ||
| Positive | 2493 | 296 | 2789 |
| Negative | 2024 | 23,042 | 25,066 |
| Column Total | 4517 | 23,338 | |
| Predicted | Observations | Row Total | |
|---|---|---|---|
| Positive | Negative | ||
| Positive | 7294 | 905 | 8199 |
| Negative | 432 | 19,224 | 19,656 |
| Column Total | 7726 | 20,129 | |
| Census Type | High Susceptibility | Medium Susceptibility | Low Susceptibility |
|---|---|---|---|
| Population | 17,042 | 42,013 | 47,055 |
| Habitation | 5874 | 14,705 | 16,661 |
| Itaperuna’s Zones | Census Type | High Susceptibility | Medium Susceptibility | Low Susceptibility |
|---|---|---|---|---|
| ZRBD | Population | 6638 | 17,873 | 19,031 |
| Habitation | 2238 | 5884 | 6290 | |
| ZRMD | Population | 3687 | 13,909 | 16,879 |
| Habitation | 1257 | 4669 | 5668 | |
| ZC | Population | 1341 | 1750 | 1750 |
| Habitation | 520 | 674 | 674 | |
| ZROR | Population | 336 | 625 | 649 |
| Habitation | 114 | 213 | 221 | |
| ZDI | Population | 11 | 14 | 14 |
| Habitation | 4 | 5 | 5 | |
| ZEDE | Population | 7 | 11 | 18 |
| Habitation | 2 | 4 | 6 | |
| ZEIS | Population | 0 | 496 | 505 |
| Habitation | 0 | 152 | 155 | |
| Rural/District | Population | 5023 | 7336 | 8209 |
| Habitation | 1739 | 3104 | 3642 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campos, P.C.d.O.; Paz, I. Spatial Diagnosis of Rain Gauges’ Distribution and Flood Impacts: Case Study in Itaperuna, Rio de Janeiro—Brazil. Water 2020, 12, 1120. https://doi.org/10.3390/w12041120
Campos PCdO, Paz I. Spatial Diagnosis of Rain Gauges’ Distribution and Flood Impacts: Case Study in Itaperuna, Rio de Janeiro—Brazil. Water. 2020; 12(4):1120. https://doi.org/10.3390/w12041120
Chicago/Turabian StyleCampos, Priscila Celebrini de Oliveira, and Igor Paz. 2020. "Spatial Diagnosis of Rain Gauges’ Distribution and Flood Impacts: Case Study in Itaperuna, Rio de Janeiro—Brazil" Water 12, no. 4: 1120. https://doi.org/10.3390/w12041120






