Numerical Investigation of a High-Speed Electrical Submersible Pump with Different End Clearances
Abstract
:1. Introduction
2. Numerical Methods
2.1. Geometry Model
2.2. Mesh and Turbulence Model
2.3. Turbulence Model and Boundary Conditions
3. Results and Discussion
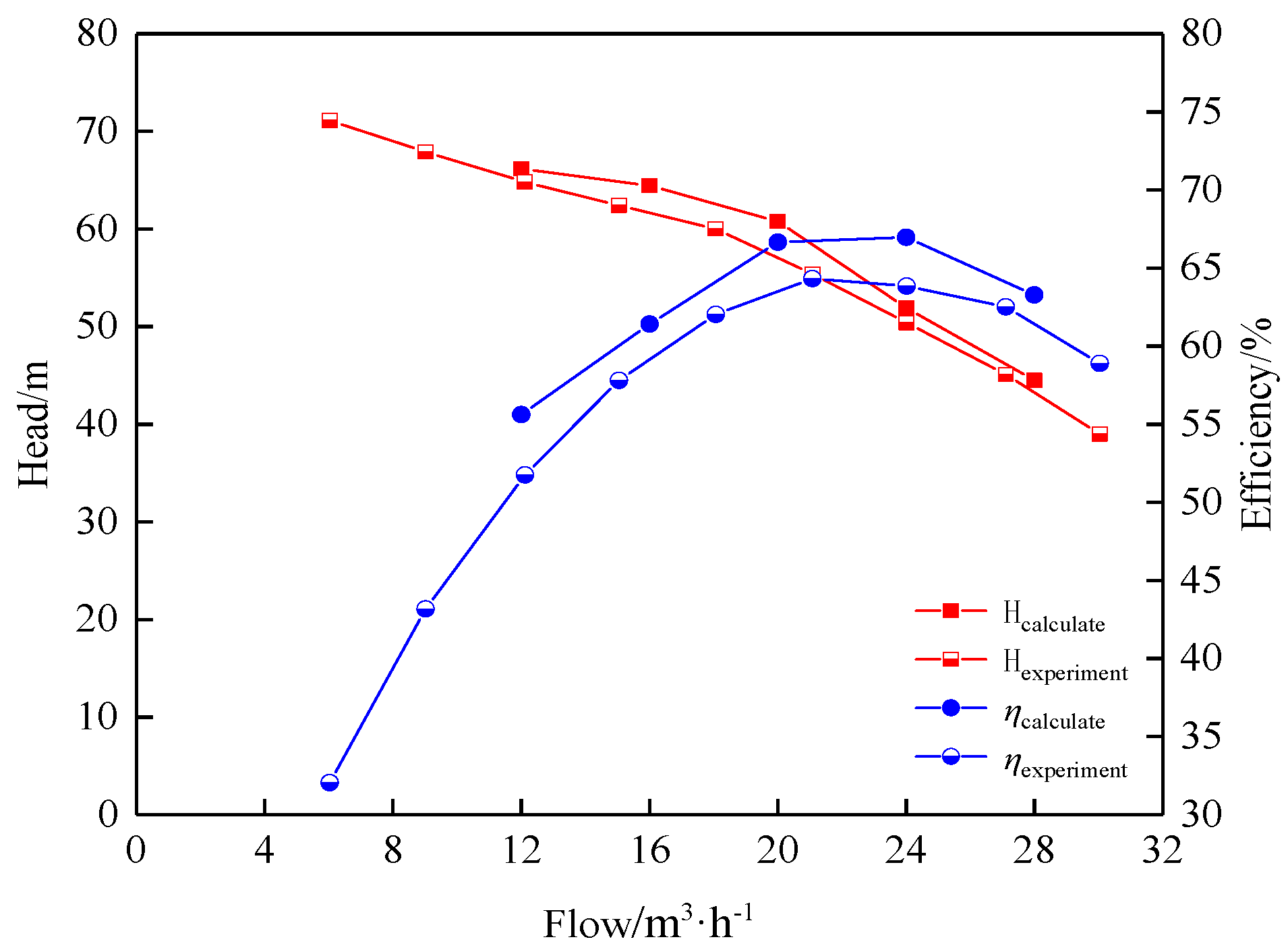
3.1. Pump Performance Verification
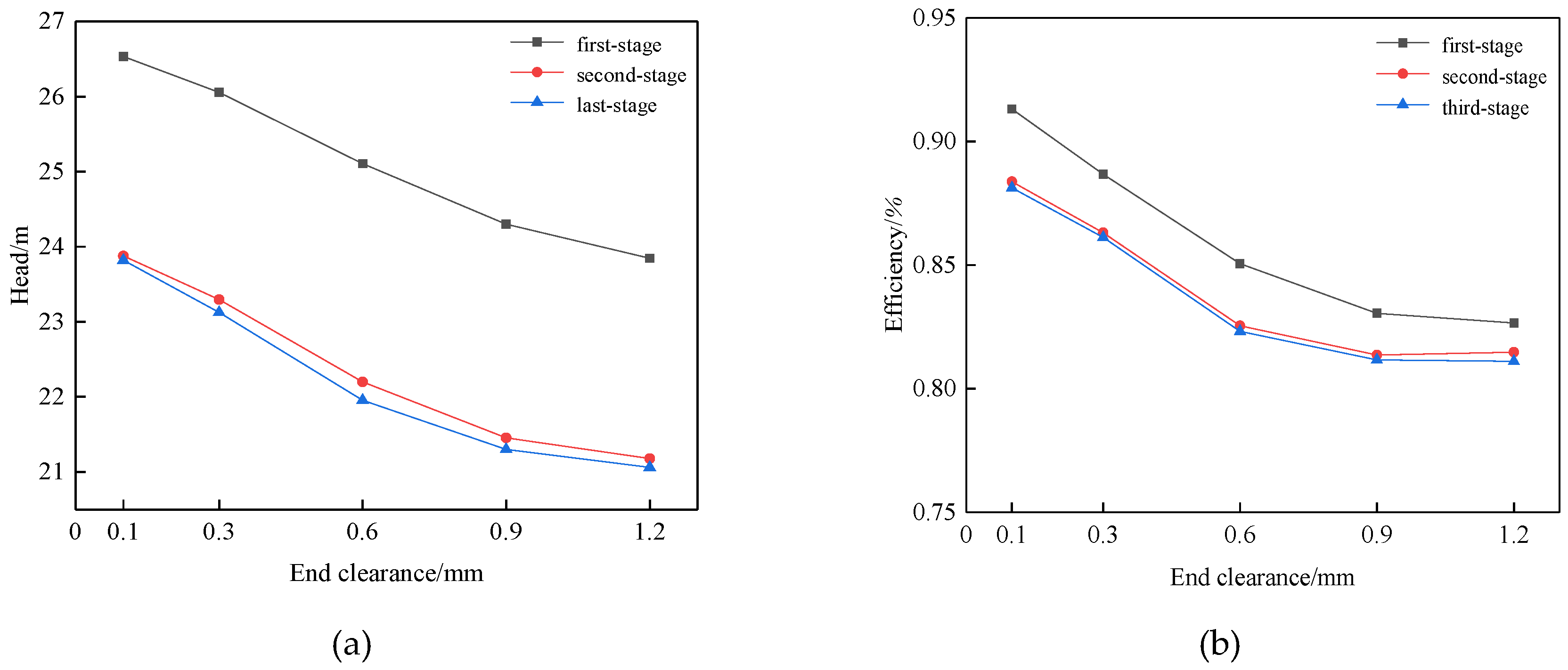
3.2. Performance Analysis
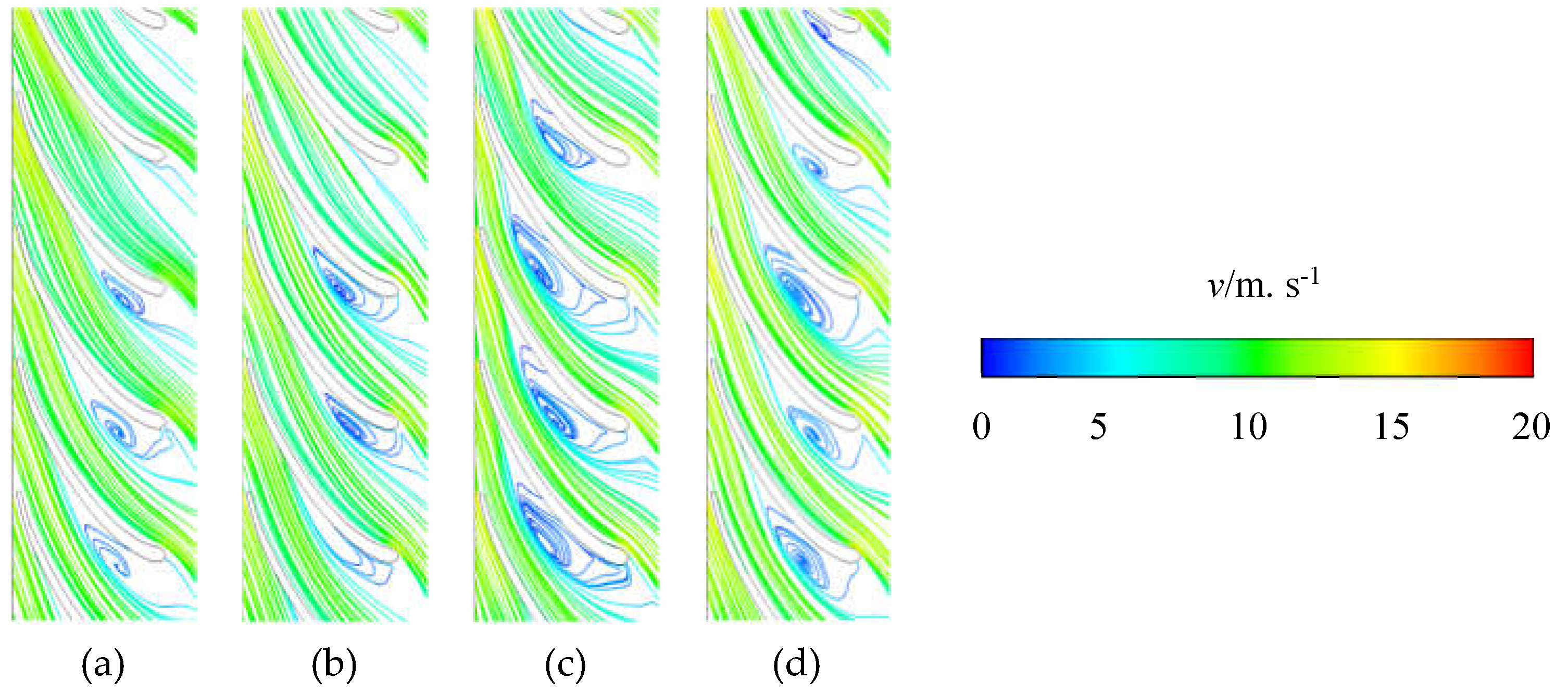
3.3. Flow Field Analysis
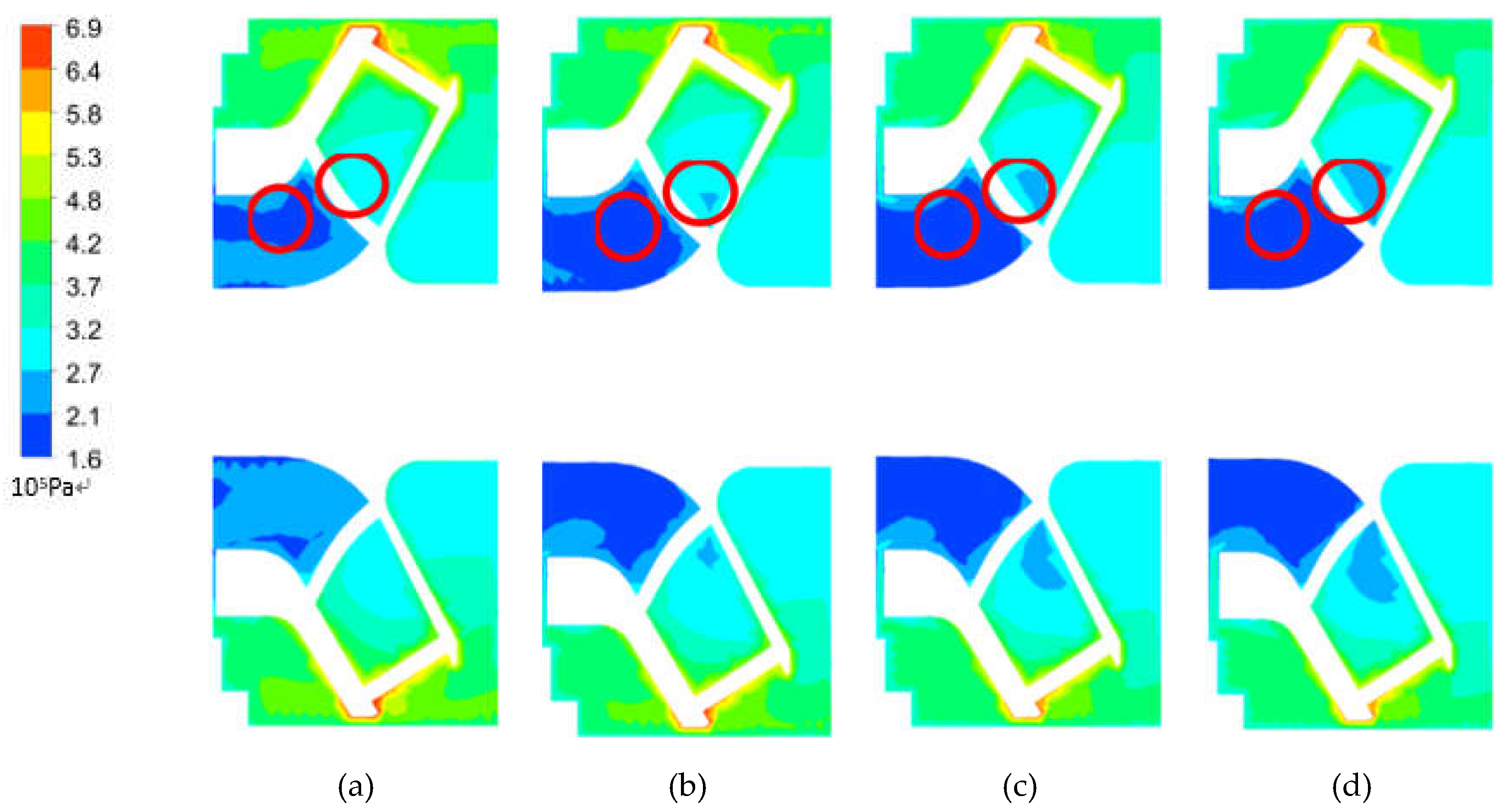
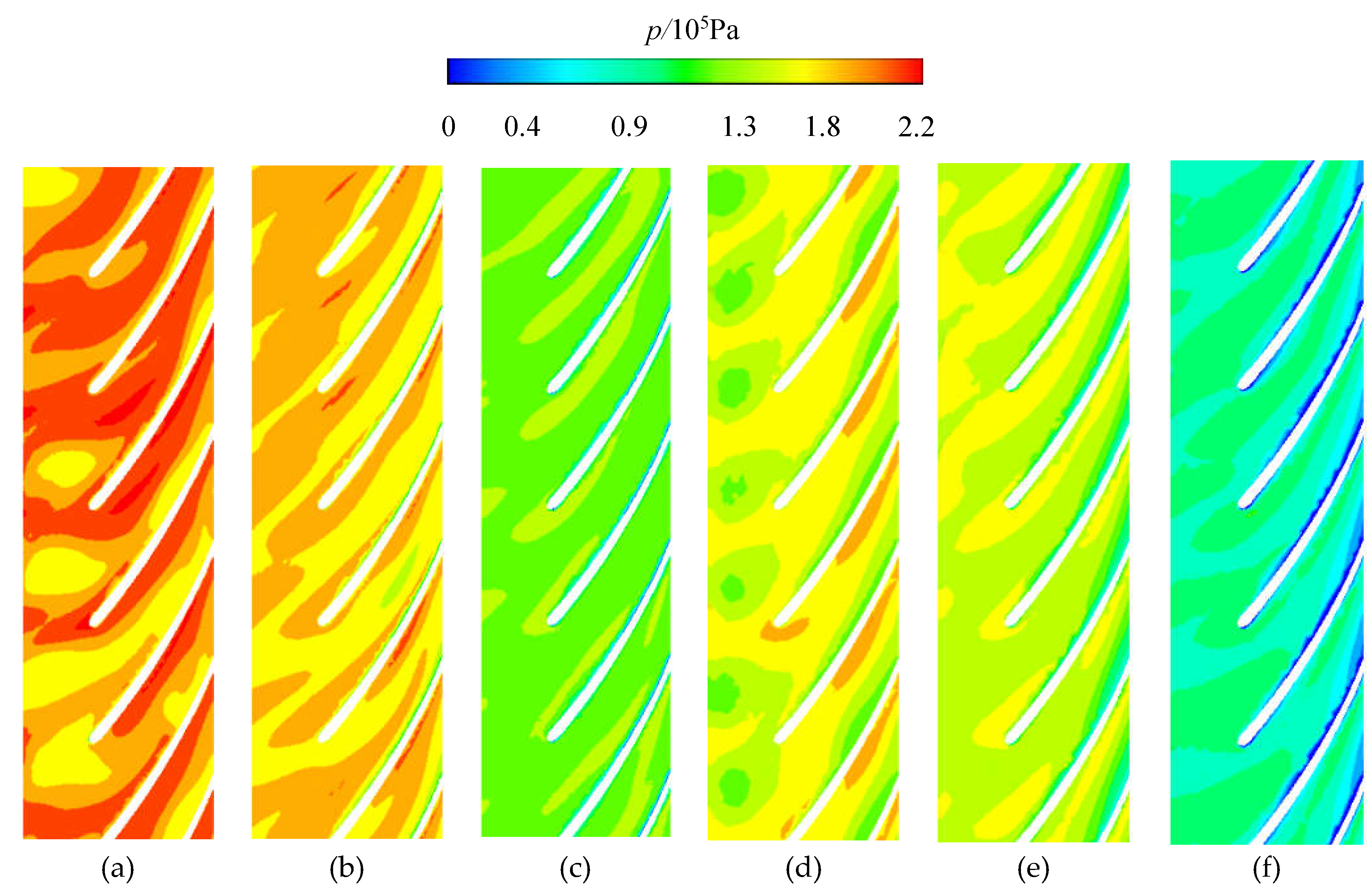
3.3.1. Influence of End Clearance on the Performance of Impellers
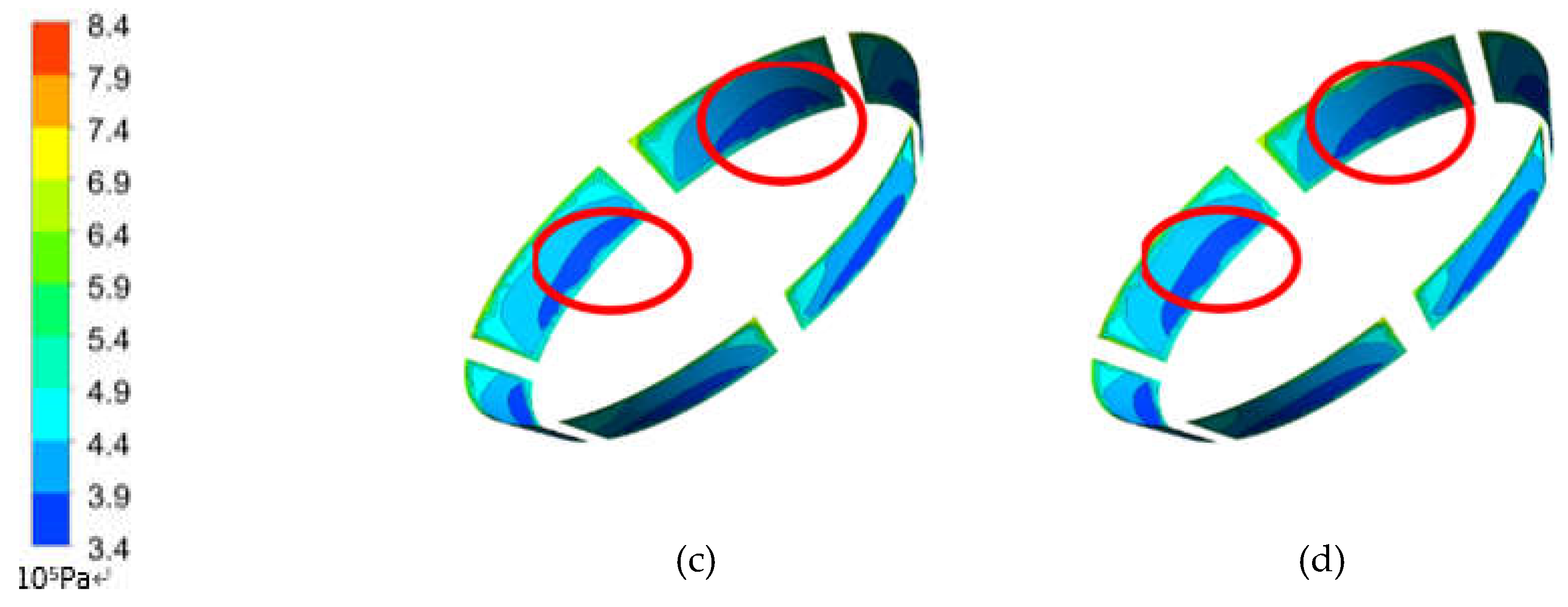
3.3.2. Influence of End Clearance on the Performance of the Diffuser
4. Conclusions
- (1)
- The results illustrate that as the increase of internal leakage caused by the end clearance, the turbulence flow occurred in the impeller and the diffuser. Meanwhile, the turbulence intensity was aggravated when the end clearance increased. The diminution of the actual flow caused by the end clearance also gave rise to the free pre-whirl and aggravated energy loss.
- (2)
- It was found that the end clearance caused a decrease of ESP performance within the full flow range, and in the small flow conditions the drop was even more serious. The effect of the end clearance was especially serious in small flow conditions.
- (3)
- According to the CFD results, the suitable installation clearance was 0.1 mm~0.6 mm with the different diameters of the sand in the medium. When the clearance exceeded 0.9 mm, the ESP performance dropped rapidly. The results of this study may lay the foundation for further improving the design and operating reliability for high-speed ESP.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Q | flow rate |
| Qd | design flow rate |
| H | head |
| pout | total pressure at impeller outlet |
| pin | total pressure at impeller inlet |
| ρ | liquid density |
| M | torque |
| ω | angular velocity |
| Hideal | ideal head |
| cu1 | circumferential component of the flow velocity at the impeller inlet |
| cu2 | circumferential component of the flow velocity at the impeller outlet |
| u1 | the peripheral speed at impeller inlet |
| u2 | the peripheral speed at impeller outlet |
| g | gravity acceleration |
| P | hydraulic power |
| Pim | power consumed by impeller |
| H’ | single-stage head |
| p2 | the pressure at diffuser outlet |
| p1 | the pressure at diffuser inlet |
| ηst | The efficiency of single-stage pump |
| ηd | the efficiency of the diffuser |
| v | velocity |
References
- Romero, O.J.; Hupp, A. Subsea electrical submersible pump significance in petroleum offshore production. J. Energy Resour. Technol. 2014, 136, 012902. [Google Scholar] [CrossRef]
- Bai, L.; Zhou, L.; Han, C.; Zhu, Y.; Shi, W. Numerical study of pressure fluctuation and unsteady flow in a centrifugal pump. Processes 2019, 7, 354. [Google Scholar] [CrossRef] [Green Version]
- Tournerie, B.; Danos, J.C.; Frene, J. Three-Dimensional Modeling of THD Lubrication in Face Seals. Tribol. Trans. 2002, 45, 284–293. [Google Scholar] [CrossRef]
- Jiang, X.; Li, W.; Zhou, L.; Li, W.; Wang, C. Transient response analysis of cantilever multistage centrifugal pump based on multi-source excitation. J. Low Freq. Noise Vib. Act. Control 2019, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Fabrizio, S.; Alessandro, R. Steadily loaded journal bearings: Quasi-3D mass-energy-conserving analysis. Tribol. Int. 2009, 42, 448–460. [Google Scholar]
- Yang, J.; Liu, J.; Liu, X.; Xie, T. Numerical Study of Pressure Pulsation of Centrifugal Pumps with the Compressible Mode. J. Therm. Sci. 2019, 28, 106–114. [Google Scholar] [CrossRef]
- Zhou, L.; Deshpande, K.; Zhang, X.; Agarwal, R. Process simulation of Chemical Looping Combustion using ASPEN Plus for a mixture of biomass and coal with various oxygen carriers. Energy 2020, 195, 116955. [Google Scholar] [CrossRef]
- Li, X.; Jiang, Z.; Zhu, Z.; Si, Q.; Li, Y. Entropy generation analysis for the cavitating head-drop characteristic of a centrifugal pump. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 4637–4646. [Google Scholar] [CrossRef]
- Zhou, L.; Bai, L.; Shi, W.; Li, W.; Wang, C.; Ye, D. Numerical analysis and performance experiment of electric submersible pump with different diffuser vanes number. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 89. [Google Scholar] [CrossRef]
- Mohammadzaheri, M.; Tafreshi, R.; Khan, Z.; Franchek, M.; Grigoriadis, K. An intelligent approach to optimize multiphase subsea oil fields lifted by electrical submersible pumps. J. Comput. Sci. 2016, 15, 50–59. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, X.; Shen, Q. Research on dynamic modeling and simulation of axial-flow pumping system based on RBF neural network. Neuro Comput. 2016, 186, 200–206. [Google Scholar] [CrossRef]
- Noon, A.A.; Kim, M.H. Erosion wear on centrifugal pump casing due to slurry flow. Wear 2016, 364, 103–111. [Google Scholar] [CrossRef]
- Bai, L.; Zhou, L.; Jiang, X.; Pang, Q.; Ye, D. Vibration in a Multistage Centrifugal Pump under Varied Conditions. Shock Vib. 2019, 2019, 2057031. [Google Scholar] [CrossRef]
- Stel, H.; Sirino, T.; Ponce, F.J.; Chiva, S.; Morales, R.E. Numerical investigation of the flow in a multistage electric submersible pump. J. Pet. Sci. Eng. 2015, 136, 41–54. [Google Scholar] [CrossRef]
- Shi, Y.; Zhu, H.; Zhang, J.; Zhang, J.; Zhao, J. Experiment and numerical study of a new generation three-stage multiphase pump. J. Pet. Sci. Eng. 2018, 169, 471–484. [Google Scholar] [CrossRef]
- Shi, W.; Zhou, L.; Lu, W.; Xu, L.; Li, W. Numerical simulation and experimental study of different stages deep-well centrifugal pump. J. Comput. Theor. Nanosci. 2013, 10, 2897–2901. [Google Scholar] [CrossRef]
- Pang, Q.; Jiang, X.; Zhu, J.; Wu, G.; Wang, X.; Wang, L. Influences of radial clearance between impeller and diffuser on flow field in side chambers of multistage centrifugal pump. J. Drain. Irrig. Mach. Eng. 2019, 37, 580–586. [Google Scholar]
- Li, W.; Zhang, Y.; Sun, B.; Shi, W.; Xu, R. Rotor radial force and pressure fluctuation of the mixed flow pump under different flow conditions. J. Drain. Irrig. Mach. Eng. 2019, 37, 277–283. [Google Scholar]
- Hsu, Y.; Brennen, C.E. Effect of swirl on rotor dynamic forces caused by front shroud pump leakage. J. Fluids Eng. 2002, 124, 1005–1010. [Google Scholar] [CrossRef]
- San Andres, L.; Lu, X.; Jie, Z. On the Leakage and Rotor Dynamic Force Coefficients of Pump Annula Seals Operating with Air/Oil Mixtures: Measurements and Predictions. In Asia Turbomachinery & Pump Symposia; Turbomachinery Laboratory, Texas A&M Engineering Experiment Station: College Station, TX, USA, 2018. [Google Scholar]
- Gao, X.; Shi, W.; Zhou, L.; Zhang, D.; Zhang, Q. Computational fluid dynamics and experimental study of inter-stage seal clearance on submersible well pump. Adv. Mech. Eng. 2016, 8, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Ma, R.; Devenport, W.J. Tip gap effects on the unsteady behavior of a tip leakage vortex. AIAA J. 2007, 45, 1713–1724. [Google Scholar] [CrossRef]
- Tamm, A.; Stoffel, B. The influences of gap clearance and surface roughness on leakage loss and disc friction of centrifugal pumps. In Proceedings of the ASME 2002 Fluids Engineering Division Summer Meeting, Montreal, QC, Canada, 14–18 July 2002; pp. 14–18. [Google Scholar]
- Schleer, M.; Abhari, R.S. Clearance effects on the evolution of the flow in the vanless diffuser of a centrifugal compressor at part load conditions. ASME J. Turbomach. 2008, 130, 031009. [Google Scholar] [CrossRef]
- Black, H.F. Effects of fluid-filled clearance spaces on centrifugal pump and submerged motor vibrations. In Proceedings of the 8th Turbomachinery Symposium; Texas A&M University, Gas Turbine Laboratories: College Station, TX, USA, 1979. [Google Scholar]
- Schlatter, P.; Örlü, R. Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 2010, 659, 116–126. [Google Scholar] [CrossRef]
- Zhou, L.; Bai, L.; Li, W.; Shi, W.; Wang, C. PIV validation of different turbulence models used for numerical simulation of a centrifugal pump diffuser. Eng. Comput. 2018, 35, 2–17. [Google Scholar] [CrossRef]
- Pavesi, G.; Cavazzini, G.; Ardizzon, G. Numerical Simulation of a Pump–Turbine Transient Load Following Process in Pump Mode. J. Fluids Eng. 2018, 140, 021114. [Google Scholar] [CrossRef]
- Posa, A.; Lippolis, A.; Balaras, E. Large-eddy simulation of a mixed-flow pump at off-design conditions. J. Fluids Eng. 2015, 137, 101302. [Google Scholar] [CrossRef]
- Li, B.; Li, X.; Jia, X.; Chen, F.; Fang, H. The Role of Blade Sinusoidal Tubercle Trailing Edge in a Centrifugal Pump with Low Specific Speed. Processes 2019, 7, 625. [Google Scholar] [CrossRef] [Green Version]
- Shim, H.S.; Kim, K.Y.; Choi, Y.S. Three-objective optimization of a centrifugal pump to reduce flow recirculation and cavitation. J. Fluids Eng. 2018, 140, 091202. [Google Scholar] [CrossRef]
- Liu, H.; Wang, K.; Yuan, S.; Tan, M.; Wang, Y.; Dong, L. Multicondition optimization and experimental measurements of a double-blade centrifugal pump impeller. J. Fluids Eng. 2013, 135, 011103. [Google Scholar] [CrossRef] [Green Version]
- Yan, P.; Chu, N.; Wu, D.; Cao, L.; Yang, S.; Wu, P. Computational fluid dynamics-based pump redesign to improve efficiency and decrease unsteady radial forces. J. Fluids Eng. 2017, 139, 011101. [Google Scholar] [CrossRef]
- Muggli, F.A.; Holbein, P.; Dupont, P. CFD calculation of a mixed flow pump characteristic from shutoff to maximum flow. J. Fluids Eng. 2002, 124, 798–802. [Google Scholar] [CrossRef]
- He, X.; Jiao, W.; Wang, C.; Cao, W. Influence of surface roughness on the pump performance based on Computational Fluid Dynamics. IEEE Access 2019, 7, 105331–105341. [Google Scholar] [CrossRef]
- Laín, S.; García, M.; Quintero, B.; Orrego, S. CFD Numerical simulations of Francis turbines. Rev. Fac. de Ing. Univ. de Antioq. 2010, 51, 24–33. [Google Scholar]
- Garcia, M.; Laín, S.; Orrego, S.; Barbosa, J.; Quintero, B. Hydraulic and rotor-dynamic interaction for performance evaluation on a Francis turbine. Int. J. Interact. Des. Manuf. 2017, 11, 623–632. [Google Scholar] [CrossRef]
- Sotoudeh, N.; Maddahian, R.; Cervantes, M.J. Investigation of Rotating Vortex Rope formation during load variation in a Francis turbine draft tube. Renew. Energy 2020, 151, 238–254. [Google Scholar] [CrossRef]
- Borkowski, D.; Węgiel, M.; Ocłoń, P.; Węgiel, T. CFD model and experimental verification of water turbine integrated with electrical generator. Energy 2019, 185, 875–883. [Google Scholar] [CrossRef]
- Bouhal, T.; Rajad, O.; Kousksou, T.; Arid, A.; El Rhafiki, T.; Jamil, A.; Benbassou, A. CFD performance enhancement of a low cut-in speed current Vertical Tidal Turbine through the nested hybridization of Savonius and Darrieus. Energy Convers. Manag. 2018, 169, 266–278. [Google Scholar]
- Zhu, Y.; Tang, S.; Quan, L.; Jiang, W.; Zhou, L. Extraction method for signal effective component based on extreme-point symmetric mode decomposition and Kullback-Leibler divergence. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 100. [Google Scholar] [CrossRef]
- Tang, S.; Yuan, S.; Zhu, Y. Deep learning-based intelligent fault diagnosis methods towards rotating machinery. IEEE Access 2020, 8, 9335–9346. [Google Scholar] [CrossRef]
- Zhou, L.; Shi, W.; Lu, W.; Hu, B.; Wu, S. Numerical investigations and performance experiments of a deep-well centrifugal pump with different diffusers. ASME J. Fluids Eng. 2012, 134, 071102. [Google Scholar] [CrossRef]
- Patil, A.; Sundar, S.; Delgado, A.; Gamboa, J. CFD based evaluation of conventional electrical submersible pump for high-speed application. J. Pet. Sci. Eng. 2019, 182, 106287. [Google Scholar] [CrossRef]
- Li, W.; Li, E.; Ji, L.; Zhou, L.; Shi, W.; Zhu, Y. Mechanism and propagation characteristics of rotating stall in a mixed-flow pump. Renew. Energy 2020, 153, 74–92. [Google Scholar] [CrossRef]
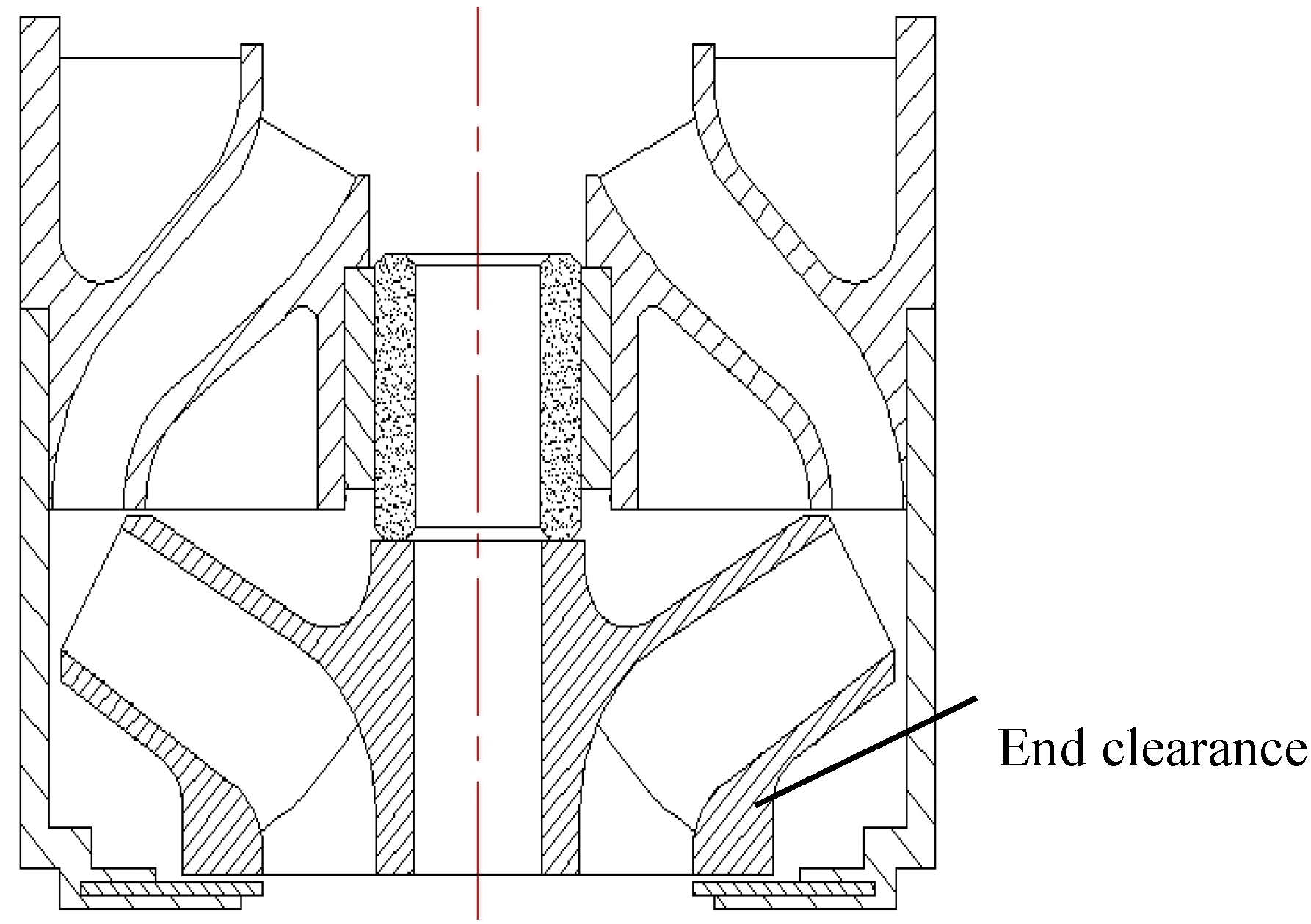

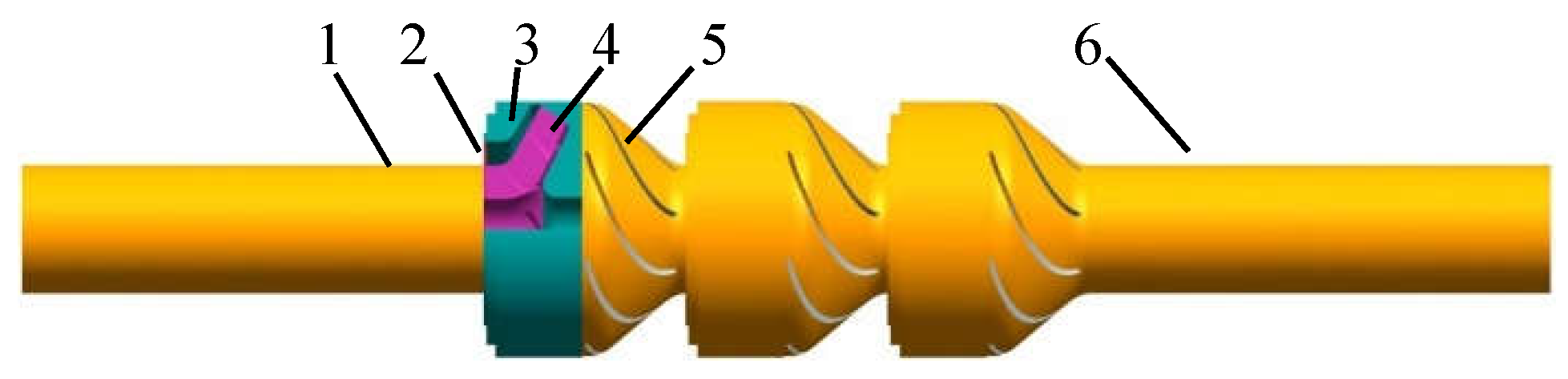



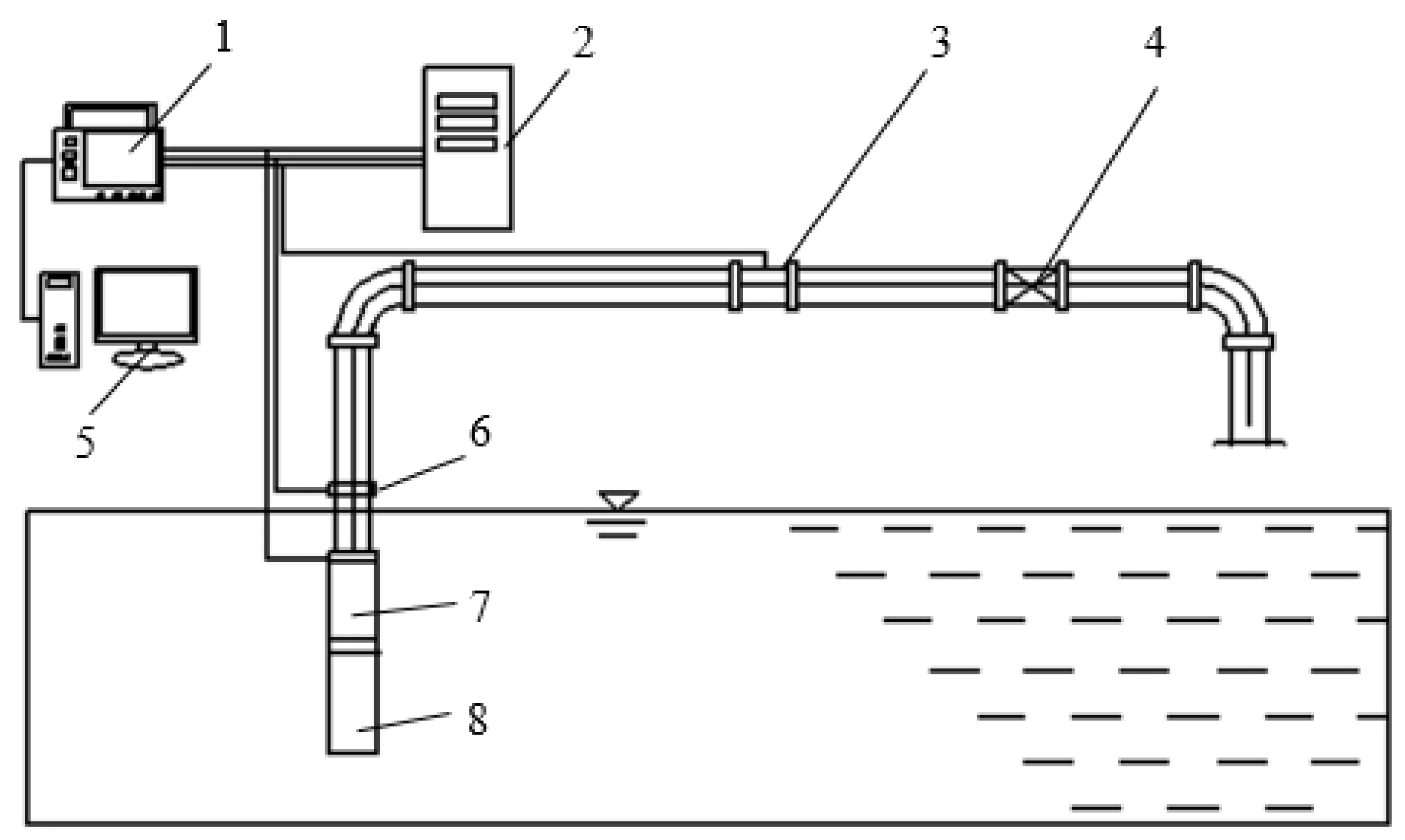




| Blade wrap angle of impeller | 85° | Impeller inlet diameter | 40 mm |
| Inlet setting angle of impeller | 44° | Impeller outlet width | 6 mm |
| Outlet setting angle of impeller | 25° | Hub diameter | 19 mm |
| Blade number of impeller | 6 | Impeller outlet diameter | 77 mm |
| Blade number of diffuser | 7 | Blade wrap angle of diffuser | 75° |
| Inlet setting angle of diffuser | 15° | Outlet setting angle of diffuser | 88° |
| Scheme No. | Grid Number | Head (m) | Efficiency (%) |
|---|---|---|---|
| Scheme 1 | 1120764 | 57.55 | 69.64 |
| Scheme 2 | 1543478 | 58.91 | 70.02 |
| Scheme 3 | 2610407 | 60.77 | 71.65 |
| Scheme 4 | 3241243 | 60.79 | 71.33 |
| Flow Rate | Turbulence Model | Standard k-ε | RNG k-ε | Standard k-ω | SST k-ω | Test Data |
|---|---|---|---|---|---|---|
| 20 m3/h | Efficiency (%) | 66.65 | 67.35 | 66.72 | 66.91 | 64.73 |
| Head(m) | 60.77 | 62.1 | 61.35 | 61.51 | 57.26 | |
| 16 m3/h | Efficiency (%) | 61.41 | 62.82 | 62.09 | 61.95 | 58.47 |
| Head(m) | 64.45 | 66.20 | 65.41 | 64.70 | 61.55 | |
| 12 m3/h | Efficiency (%) | 55.61 | 56.31 | 56.08 | 55.44 | 52.15 |
| Head(m) | 67.15 | 67.59 | 67.26 | 66.81 | 64.92 |
| Location | Boundary Condition Types | Settings |
|---|---|---|
| Inlet | Pressure inlet | 101,325 Pa, 5% turbulence intensity |
| Outlet | Mass flow outlet, | Equal to the operating flow rate |
| Wall | Nonslip wall | Surface roughness 0.01 mm |
| Impellers | Rotating | 6000 r/min |
| Diffusers | Stationary | 0 r/min |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, L.; Wang, W.; Hang, J.; Shi, W.; Yan, H.; Zhu, Y. Numerical Investigation of a High-Speed Electrical Submersible Pump with Different End Clearances. Water 2020, 12, 1116. https://doi.org/10.3390/w12041116
Zhou L, Wang W, Hang J, Shi W, Yan H, Zhu Y. Numerical Investigation of a High-Speed Electrical Submersible Pump with Different End Clearances. Water. 2020; 12(4):1116. https://doi.org/10.3390/w12041116
Chicago/Turabian StyleZhou, Ling, Wanhong Wang, Jianwei Hang, Weidong Shi, Hao Yan, and Yong Zhu. 2020. "Numerical Investigation of a High-Speed Electrical Submersible Pump with Different End Clearances" Water 12, no. 4: 1116. https://doi.org/10.3390/w12041116





