Dam Breach Size Comparison for Flood Simulations. A HEC-RAS Based, GIS Approach for Drăcșani Lake, Sitna River, Romania
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Chosen Area for Dam Breach Flood Simulations
2.3. Data Aquisition
2.3.1. Generating the Digital Elevation Model
2.3.2. Hydrological Data
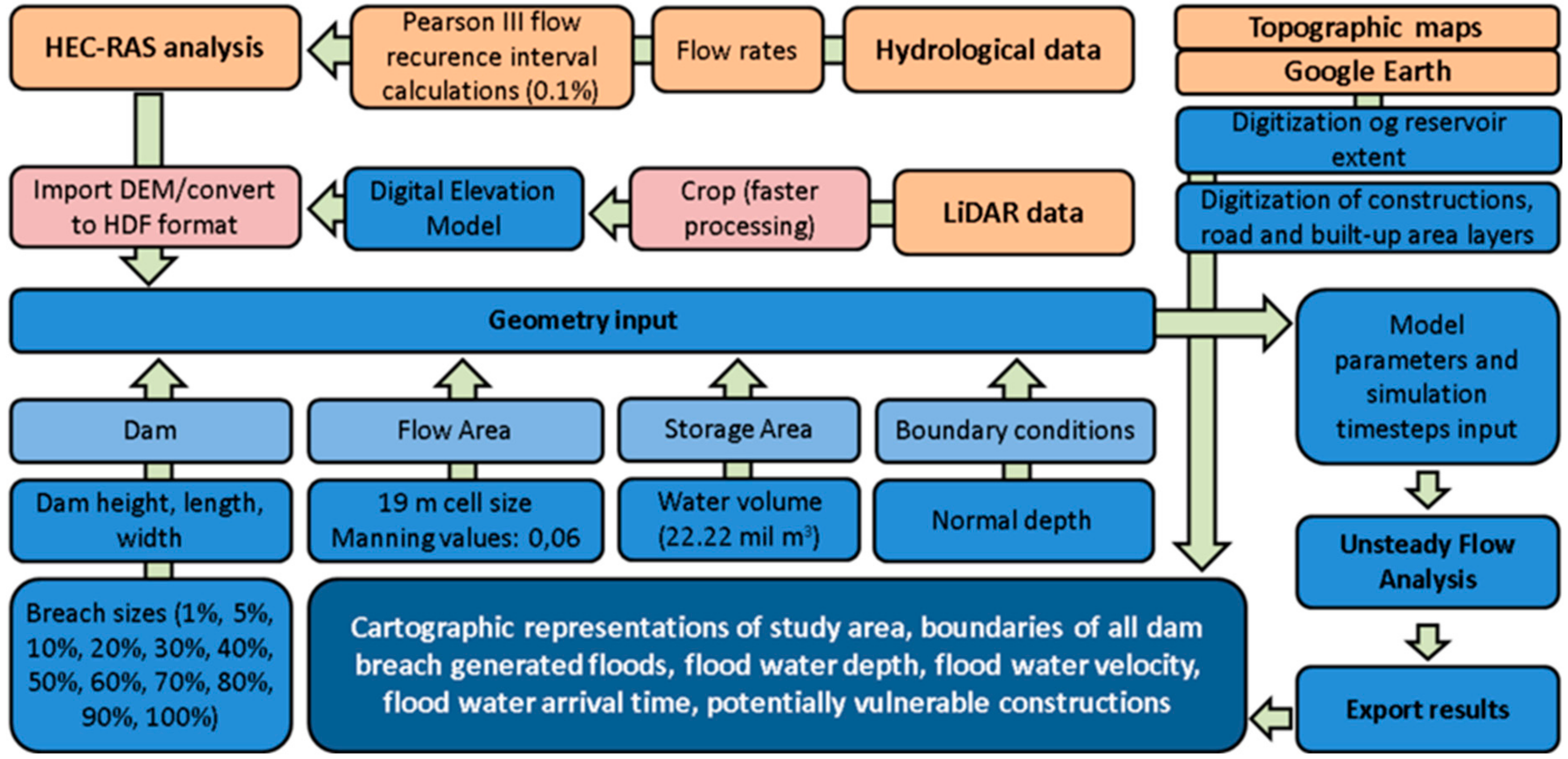
2.4. Dam Breach Hydraulic Model
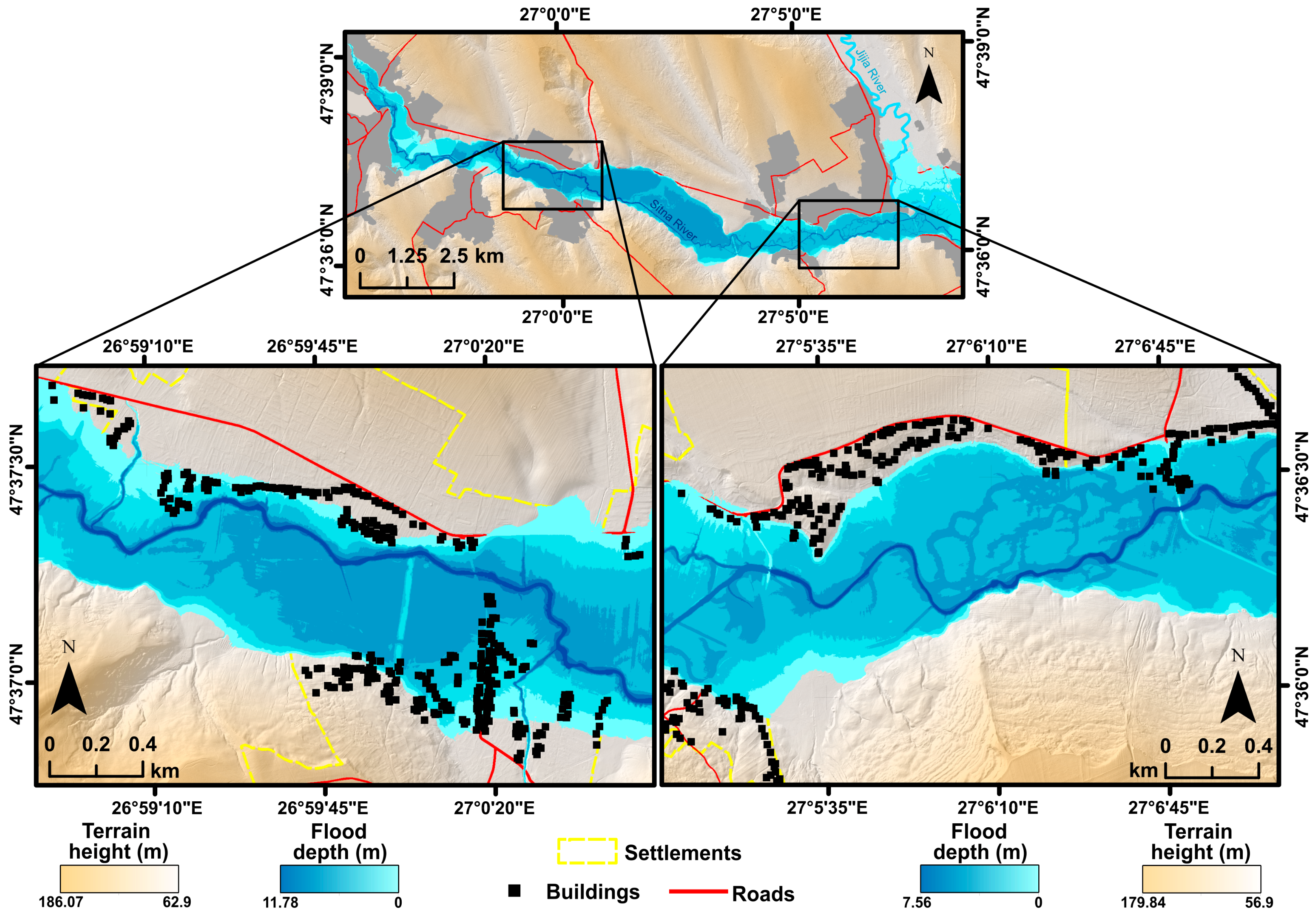
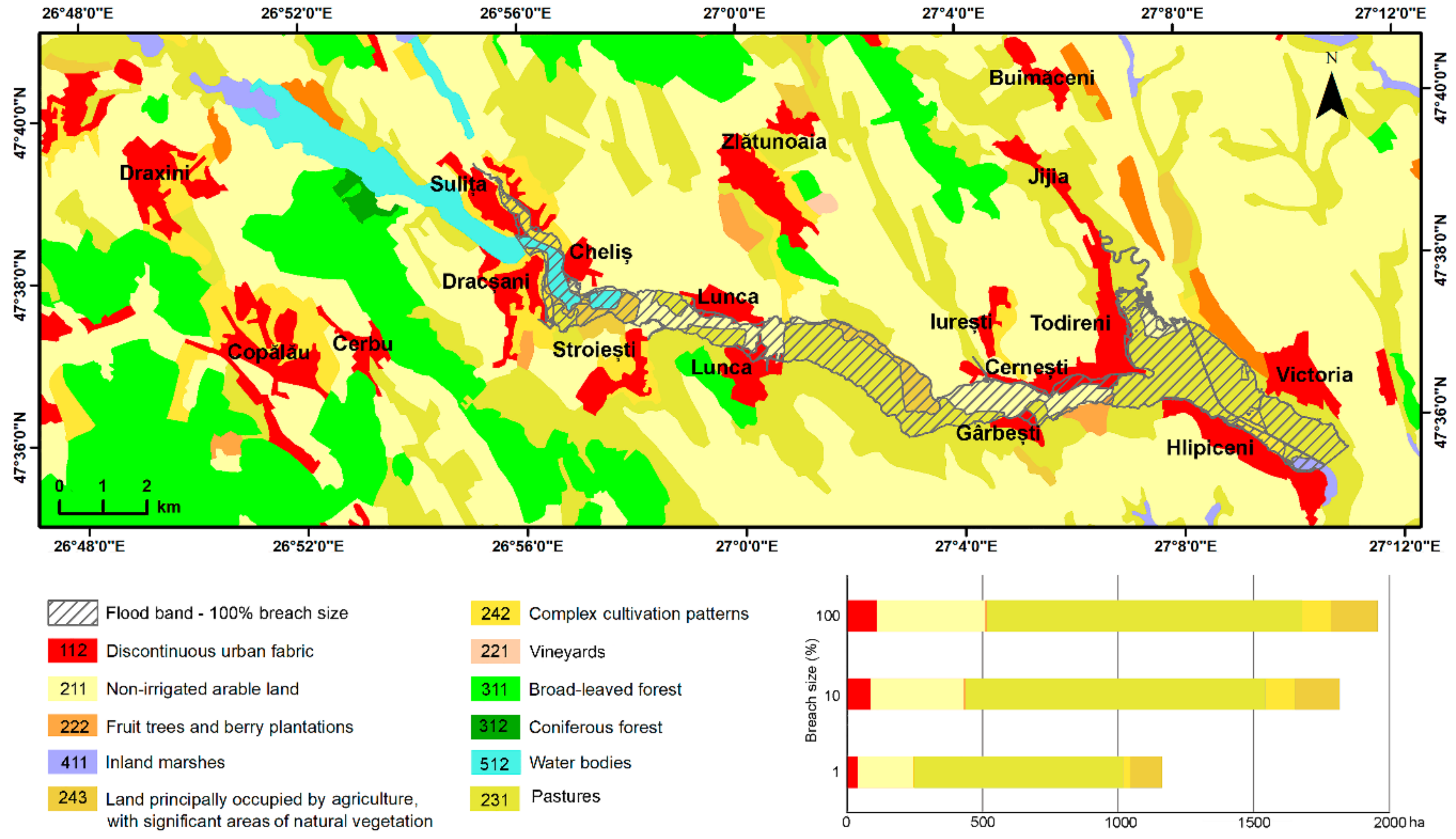
3. Results
4. Discussion
4.1. General Discussion
4.2. Backwater Discussion
4.3. Temporal Aspects
- The first class (the 1% scenario) corresponded to a delay of 7 h and 50 min. It posed little to no risk to the local population. Additionally, the flood extent would be limited enough, that it would only reach a reduced number of buildings.
- Second class was comprised of the 5% and 10% simulations, with an average delay of 6 h and 15 min. This was still considered to have low risk, during which warnings could reach the population early enough, that potential casualties would be completely preventable.
- The last, and most dangerous class, grouped the 20% to 100% scenarios, with an estimated delay ranging from 2 h and 30 min (100% breach) to 3 h and 30 min (20% breach), posing significantly less warning time, in addition to the high flow rate values, which would cause considerably more potential damages and casualties.
4.4. Flood Mitigation Aspects
4.5. Validation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Singh, V.P. Dam Breach Modeling Technology; Springer Science & Business Media: Dordrecht, The Netherlands, 1996; p. 242. [Google Scholar]
- Kérisel, J. The history of geotechnical engineering up until 1700. In Proceedings of the 11th International Conference on Soil Mechanics and Geotechnical Engineering, San Francisco, CA, USA, 12–16 August 1985; pp. 3–93. [Google Scholar]
- International Commission on Large Dams. Available online: https://www.icold-cigb.org/ (accessed on 10 December 2019).
- Wang, B.; Wu, C.; Song, J.; Liu, W.; Peng, Y.; Chen, Y.; Liu, X. Empirical and semi-analytical models for predicting peak outflows caused by embankment dam failures. J. Hydrol. 2018, 562, 692–702. [Google Scholar] [CrossRef]
- Zhang, L.; Xu, Y.; Jia, J.S. Analysis of earth dam failures: A database approach. Georisk 2009, 3, 184–189. [Google Scholar] [CrossRef] [Green Version]
- Zhong, Q.M.; Chen, S.S.; Deng, Z.; Mei, S.A. Prediction of Overtopping-Induced Breach Process of Cohesive Dams. J. Geotech. Geoenviron. Eng. 2019, 145, 1–9. [Google Scholar] [CrossRef]
- Sharma, R.P.; Kumar, A. Case Histories of Earthen Dam Failures. In Proceedings of the Seventh International Conferences on Case Histories in Geotechnical Engineering, Chicago, IL, Chicago, 29 April–5 May 2013; Missouri University of Science and Technology: Rolla, MO, USA; pp. 1–7. [Google Scholar]
- Foster, M.; Fell, R.; Spannagle, M. The statistics of embankment dam failures and accidents. Can. Geotech. J. 2000, 37, 1000–1024. [Google Scholar] [CrossRef]
- Albu, L.M.; Enea, A.; Stoleriu, C.C.; Iosub, M.; Romanescu, G.; Huțanu, E. Evaluation of the propagation time of a theorethical flood wave in the case of the breaking of Catamarasti Dam, Botosani (Romania). In Proceedings of the International Scientific Conference Geobalcanica 2018, Ohrid, North Macedonia, 12–13 May 2018; pp. 497–504. [Google Scholar] [CrossRef]
- Peter, S.J.; Siviglia, A.; Nagel, J.; Marelli, S.; Boes, R.M.; Vetsch, D.; Sudret, B. Development of Probabilistic Dam Breach Model Using Bayesian Inference. Water Resour. Res. 2018, 54, 4376–4400. [Google Scholar] [CrossRef] [Green Version]
- Shoda, D.; Kawamoto, O.; Yoshisako, H.; Inoue, K. Prediction of inundation areas due to failure in small earthfill dam using numerical analysis. Jpn. Agric. Res. Q. 2015, 49, 97–102. [Google Scholar] [CrossRef] [Green Version]
- Drobot, R.; Dinu, C.; Draghia, A.; Adler, M.J.; Corbus, C.; Matreata, M. Simplified approach for flood estimation and propagation. In Proceedings of the 2014 IEEE International Conference on Automation, Quality and Testing, Robotics, Cluj-Napoca, Romania, 22–24 May 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Moglen, G.E.; Hood, K.; Hromadka, T.V. Examination of Multiple Predictive Approaches for Estimating Dam Breach Peak Discharges. J. Hydrol. Eng. 2018, 24, 1–11. [Google Scholar] [CrossRef]
- Ministerul Apelor și Pădurilor. Available online: http://apepaduri.gov.ro/situatia-barajelor-din-romania-la-finele-anului-2018/ (accessed on 7 February 2020).
- Romanescu, G.; Sandu, I.; Stoleriu, C.C.; Sandu, I.G. Water resources in Romania and their quality in the main lacustrine basins. Rev. Chim. (Buchar.) 2014, 65, 344–349. [Google Scholar]
- Prăvălie, R.; Piticar, A.; Roșca, B.; Sfîcă, L.; Bandoc, G.; Tiscovschi, A.; Patriche, C. Spatio-temporal changes of the climatic water balance in Romania as a response to precipitation and reference evapotranspiration trends during 1961–2013. Catena 2019, 172, 295–312. [Google Scholar] [CrossRef]
- Sandu, I.; Pescaru, V.I.; Poiana, I.; Geicu, A.; Candea, I.; Tastea, D. The Climate of Romania; Romanian Academy Publishing: Bucharest, Romania, 2008. (In Romanian) [Google Scholar]
- Iosub, M.; Minea, I.; Chelariu, O.E.; Ursu, A. Assessment of flash flood susceptibility potential in Moldavian Plain (Romania). J. Flood Risk Manag. 2020. [Google Scholar] [CrossRef]
- Romanescu, G.; Romanescu, A.M.; Romanescu, G. History of Building the Main Dams and Reservoirs. In Proceedings of the 2nd International Conference on Water Resources and Wetlands, Tulcea, Romania, 11–13 September 2014; pp. 11–13. [Google Scholar]
- The Romanian Register of Big Dams. Available online: http://www.baraje.ro/rrmb/rrmb_idx.html (accessed on 10 December 2019).
- Government Emergency Ordinance No. 244/2000 Regarding the Safety of the Dams; Republished; Approved by the Law No. 466/2001; The Government of Romania: Bucharest, Romania, 2001.
- Enea, A. Metode şi Tehnici Moderne de Cuantificare a Vulnerabilităţii la Inundaţii în Bazinul Hidrografic Tazlău. Ph.D. Thesis, Alexandru Ioan Cuza University of Iași, Iași, Romania, 2017. (In Romanian). [Google Scholar]
- Eleutério, J. Flood Risk Analysis: Impact of Uncertainty in Hazard Modeling and Vulnerability Assessments on Damage Estimations. Ph.D. Thesis, Université de Strasbourg, Strasbourg, France, 2012. [Google Scholar]
- Kreis, N. Modélisation des Crues des Rivières de Moyenne Montagne Pour la Gestion Intégrée du Risque D’inondation: Application à la Vallée de la Thur (Haut-Rhin). Ph.D. Thesis, Centre d’Ecologie Végétale et d’Hydrologie, Ecole Nationale du Génie de l’eau et de l’Environnement de Strasbourg, Strasbourg, France, 2004. [Google Scholar]
- Papa, M.N.; Sarno, L.; Vitiello, F.S.; Medina, V. Application of the 2D depth-averaged model, FLATModel, to pumiceous debris flows in the Amalfi Coast. Water 2018, 10, 1159. [Google Scholar] [CrossRef] [Green Version]
- Ciervo, F.; Papa, M.N.; Medina, V.; Bateman, A. Simulation of flash floods in ungauged basins using post-event surveys and numerical modelling. J. Flood Risk Manag. 2015, 8, 343–355. [Google Scholar] [CrossRef]
- García-Navarro, P.; Murillo, J.; Fernández-Pato, J.; Echeverribar, I.; Morales-Hernandez, M. The shallow water equations and their application to realistic cases. Environ. Fluid Mech. 2019, 19, 1235–1252. [Google Scholar] [CrossRef] [Green Version]
- Woodhead, S. Evaluation of Inundation Models—Limits Capabilities of Models; FLOOD Site Consortium: Wallingford, UK, 2007; p. 34. [Google Scholar]
- Mihu-Pintilie, A.; Cîmpianu, C.I.; Stoleriu, C.C.; Pérez, M.N.; Paveluc, L.E. Using High-Density LiDAR Data and 2D Streamflow Hydraulic Modeling to Improve Urban Flood Hazard Maps: A HEC-RAS Multi-Scenario Approach. Water 2019, 11, 1832. [Google Scholar] [CrossRef] [Green Version]
- Pappenberg, F.; Beven, K.; Horitt, M.; Blazkova, S. Uncertainty in the calibration of effective roughness parameter in HEC-RAS using inundation and downstream level observation. J. Hydrol. 2005, 302, 46–69. [Google Scholar] [CrossRef]
- Horrit, M.S.; Bates, P.D. Evaluation of 1D and 2D numerical models for predicting river flood inundation. J. Hydrol. 2002, 268, 87–99. [Google Scholar] [CrossRef]
- Farooq, M.; Shafique, M.; Khattak, M.S. Flood hazard assessment and mapping of River Swat using HEC-RAS 2D model and high-resolution 12-m TanDEM-X DEM (WorldDEM). Nat. Hazards 2019, 97, 477–492. [Google Scholar] [CrossRef]
- Zeleňáková, M.; Fijko, R.; Labant, S.; Weiss, E.; Markovič, G.; Weiss, R. Flood risk modelling of the Slatvinec stream in Kružlov village, Slovakia. J. Clean. Prod. 2019, 212, 109–118. [Google Scholar] [CrossRef]
- Hardesty, S.; Shen, X.; Nikolopoulos, E.; Anagnostou, E. A numerical framework for evaluating flood inundation hazard under different dam operation scenarios—A case study in Naugatuck river. Water 2018, 10, 1798. [Google Scholar] [CrossRef] [Green Version]
- Khosravi, K.; Rostaminejad, M.; Cooper, J.R.; Mao, L.; Melesse, A.M. Dam break analysis and flood inundation mapping: The case study of Sefid-Roud Dam, Iran. In Extreme Hydrology and Climate Variability; Melesse, A., Abtew, W., Senay, G., Eds.; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar] [CrossRef]
- Stoleriu, C.C.; Urzică, A.; Mihu-Pintilie, A. Improving flood risk map accuracy using high-density LiDAR data and the HEC-RAS river analysis system: A case study from north-eastern Romania. J. Flood Risk Manag. 2019, 13, e12572. [Google Scholar] [CrossRef]
- Romanian Limnogeographical Association; Vartolomei, F. Date Privind Amenajarile Hidrotehnice din Bazinul Prut. Water Resour. from Rom. Vulnerability to Press. Man’s Act. 2010, pp. 202–208. Available online: https://www.limnology.ro/water2010/Proceedings/26.pdf (accessed on 20 November 2019). (In Romanian).
- Lahovari, G.I.; Brătianu, C.I.; Tocilescu, G. Marele Dictionar al României; Stab. Grafic. J.V. Socecu: Bucharest, Romania, 1900; Volume 3. (In Romanian) [Google Scholar]
- Enea, A.; Urzică, A.; Breabăn, I.G. Remote sensing, GIS and HEC-RAS techniques, applied for flood extent validation, based on landsat imagery, lidar and hydrological data. Case study: Bașeu river, Romania. J. Environ. Prot. Ecol. 2018, 19, 1091–1101. [Google Scholar]
- Maftei, C.; Papatheodorou, K. Flash flood prone area assessment using geomorphological and hydraulic model. J. Environ. Prot. Ecol. 2015, 16, 63–73. [Google Scholar]
- Sonmez, O.; Demir, I.H.; Demir, F.; Dobrucali, E. Determination of flood inundation areas and assessment of flood hazard costs in urban settlements: A case study of Agva. J. Environ. Prot. Ecol. 2017, 18, 509–523. [Google Scholar]
- Olaru, L.; Shram, M. Analiza palinologica a sedimentelor lacului Sulita-Dracsani (Botoșani). Comunicări Bot. 1969, 10, 103–110. (In Romanian) [Google Scholar]
- Planul de Management al Riscului la Inundații. Administratia Bazinala a Apelor Prut-Barlad. 2016, p. 232. Available online: http://www.rowater.ro/daprut/EPRI (accessed on 12 October 2019).
- Chen, B.; Krajewski, W.F.; Goska, R.; Young, N. Using LiDAR surveys to document floods: A case study of the 2008 Iowa flood. J. Hydrol. 2017, 553, 338–349. [Google Scholar] [CrossRef]
- Croke, J.; Todd, P.; Thompson, C.; Watson, F.; Denham, R.; Khanal, G. The use of multi temporal LiDAR to assess basin-scale erosion and deposition following the catastrophic January 2011 Lockyer flood, SE Queensland, Australia. Geomorphology 2013, 184, 111–126. [Google Scholar] [CrossRef]
- Leitão, J.P.; de Sousa, L.M. Towards the optimal fusion of high-resolution Digital Elevation Models for detailed urban flood assessment. J. Hydrol. 2018, 561, 651–661. [Google Scholar] [CrossRef]
- Tschiedel, A.F.; Paiva, R.C.D. Uncertainty assessment in hydrodynamic modeling of floods generated by dam break. RBRH 2018, 23, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Quiroga, V.M.; Kure, S.; Udo, K.; Mano, A. Application of 2D numerical simulation for the analysis of the February 2014 Bolivian Amazonia flood: Application of the new HEC-RAS version 5. Ribagua 2016, 3, 25–33. [Google Scholar] [CrossRef] [Green Version]
- Chen, A.S.; Evans, B.; Djordjević, S.; Savić, D.A. A coarse-grid approach to representing building blockage effects in 2D urban flood modelling. J. Hydrol. 2012, 426, 1–16. [Google Scholar] [CrossRef] [Green Version]
- County Emergency Plan. 2006. Available online: http://www.botosani.eu.org/urgenta/plan_jud_2006.pdf (accessed on 20 September 2019). (In Romanian).
- Kreiser, Z.; Killough, B.; Rizvi, S.R. Water Across Synthetic Aperture Radar Data (WASARD): SAR Water Body Classification for the Open Data Cube. In Proceedings of the IGARSS 2018–2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; p. 440. [Google Scholar] [CrossRef]
- Álvarez, M.; Puertas, J.; Peña, E.; Bermúdez, M. Two-dimensional dam-break flood analysis in data-scarce regions: The case study of Chipembe dam, Mozambique. Water 2017, 9, 432. [Google Scholar] [CrossRef] [Green Version]
- Sarno, L.; Carravetta, A.; Martino, R.; Tai, Y.C. Pressure coefficient in dam-break flows of dry granular matter. J. Hydraul. Eng. 2013, 139, 1126–1133. [Google Scholar] [CrossRef]
- Sarno, L.; Papa, M.N.; Martino, R. Dam-break flows of dry granular materials on gentle slopes. In Proceedings of the 5th International Conference on Debris-Flow Hazards Mitigation: Mechanics, Prediction and Assessment, Padua, Italy, 14–17 June 2011; pp. 503–512. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S.S. One-dimensional modeling of dam-break flow over movable beds. J. Hydraul. Eng. 2007, 133, 48–58. [Google Scholar] [CrossRef]
- USACE HEC-RAS. HEC-RAS River Analysis System, 2D Modeling User’s Manual Version 5.0; US Army Corps of Engineers California USA: Davis, CA, USA, 2016. [Google Scholar]
- Yakti, B.P.; Adityawan, M.B.; Farid, M.; Suryadi, Y.; Nugroho, J.; Hadihardaja, I.K. 2D modeling of flood propagation due to the failure of way Ela natural dam. MATEC Web Conf. 2018, 17, 03009. [Google Scholar] [CrossRef] [Green Version]
- Cannata, M.; Marzocchi, R. Two-dimensional dam break flooding simulation: A GIS-embedded approach. Nat. Hazards 2012, 61, 1143–1159. [Google Scholar] [CrossRef]
- Wang, L.; Liang, Q.; Kesserwani, G.; Hall, J. A 2D shallow flow model for practical dam-break simulations. J. Hydraul. Res. 2011, 49, 307–316. [Google Scholar] [CrossRef]
- Vozinaki, A.K.; Morianou, G.G.; Alexakis, D.D.; Tsanis, I.K. Comparing 1D and combined 1D/2D hydraulic simulations using high-resolution topographic data: A case study of the Koiliaris basin, Greece. Hydrol. Sci. J. 2017, 62, 642–656. [Google Scholar] [CrossRef]
- Brunner, G.W.; Piper, S.S.; Jensen, M.R.; Chacon, B. Combined 1D and 2D Hydraulic Modeling within HEC-RAS. World Environ. Water Resour. Congr. 2015, 2015, 1432–1443. [Google Scholar] [CrossRef]
- Yu, D.; Lane, S.N. Urban fluvial flood modelling using a two-dimensional diffusion-wave treatment, part 1: Mesh resolution effects. Hydrol. Process. 2006, 20, 1541–1565. [Google Scholar] [CrossRef]
- Betsholtz, A.; Nordlöf, B. Potentials and Limitations of 1D, 2D and Coupled 1D-2D Flood Modelling in HEC-RAS. Master’s Thesis, Lund University, Lund, Sweden, 2017. [Google Scholar]
- Annunziato, A.; Andredakis, I.; Probst, P. Impact of Flood by a Possible Failure of the Mosul Dam; EUR 27923 EN; Publications Office of the European Union: Brussels, Belgium, 2016. [Google Scholar] [CrossRef]
- Wahl, T. Prediction of Embankment Dam Breach Parameters. A Literature Review and Needs Assessment. U.S Department of the Interior, Bureau of Reclamation, Dam Safety Office U.S.; 1998; p. 67. Available online: https://www.nrc.gov/docs/ML0901/ML090150051.pdf (accessed on 7 February 2020).
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill Book Co.: New York, NY, USA, 1959; p. 680. [Google Scholar]
- Singh, K.; Snorrason, A. Sensitivity of Outflow Peaks and Flood Stages to the Selection of Dam Breach Parameters and Simulation Models; SWS Contract Report, 288; Illinois Department of Energy and Natural Resources, State Water Survey Division, Eds.; Surface Water Section at the University of Illinois: Champaign, IL, USA, 1982; p. 182. [Google Scholar]
- Singh, V.P.; Scarlatos, P.D. Analysis of Gradual Earth-Dam Failure. J. Hydraul. Eng. 1988, 114, 21–42. [Google Scholar] [CrossRef]
- Romanescu, G.; Stoleriu, C.C. An inter-basin backwater overflow (the Buhai Brook and the Ezer reservoir on the Jijia River, Romania). Hydrol. Process. 2014, 28, 3118–3131. [Google Scholar] [CrossRef]
- Gharbi, M.; Soualmia, A.; Dartus, D.; Masbernat, L. Comparison of 1D and 2D Hydraulic Models for Floods Simulation on the Medjerda Riverin Tunisia. J. Mater. Environ. Sci. 2016, 7, 3017–3026. [Google Scholar]
- Dimitriadis, P.; Tegos, A.; Oikonomou, A.; Pagana, V.; Koukouvinos, A.; Mamassis, N.; Koutsoyiannis, D.; Efstratiadis, A. Comparative evaluation of 1D and quasi-2D hydraulic models based on benchmark and real-world applications for uncertainty assessment in flood mapping. J. Hydrol. 2016, 534, 478–492. [Google Scholar] [CrossRef]
- Rubiu, F. Flood Risk Assessment in the Vicinity of Kartena Town Using HEC-RAS 1D-2D Models. Master’s Thesis, Aleksandras Stulginskis University, Akademija, Lithuania, 2018. [Google Scholar]
- Patel, D.P.; Ramirez, J.A.; Srivastava, P.K.; Bray, M.; Han, D. Assessment of flood inundation mapping of Surat city by coupled 1D/2D hydrodynamic modeling: A case application of the new HEC-RAS 5. Nat. Hazards 2017, 89, 93–130. [Google Scholar] [CrossRef]



| Relief Ratio | Drainage Density | Form Factor | Circularity Ratio | Elongation Ratio |
|---|---|---|---|---|
| 5.28 | 1.31 | 0.21 | 0.14 | 0.52 |
| Breach Size | NFB | TFA (ha) | MWD (m) | MWV (m/s) | FPT(h) | RET (min) | AWV (m/s) |
|---|---|---|---|---|---|---|---|
| 1% | 36 | 1179.70 | 8.44 | 8.78 | 10 h 13 min | 54 h | 0.35 |
| 5% | 214 | 1876.74 | 9.95 | 8.80 | 7 h 59 min | 32 h | 0.57 |
| 10% | 233 | 1903.52 | 9.97 | 8.82 | 7 h 48 min | 23 h | 0.59 |
| 20% | 235 | 1908.71 | 10.01 | 8.83 | 5 h 41 min | 20 h | 0.60 |
| 30% | 238 | 1909.71 | 10.02 | 8.84 | 5 h 37 min | 14 h | 0.62 |
| 40% | 240 | 1913.38 | 10.05 | 9.19 | 5 h 32 min | 11 h | 0.62 |
| 50% | 241 | 1918.36 | 10.06 | 9.28 | 5 h 26 min | 8 h 15 min | 0.63 |
| 60% | 241 | 1921.03 | 10.07 | 10.13 | 5 h 21 min | 7 h 15 min | 0.63 |
| 70% | 242 | 1922.40 | 10.07 | 11.65 | 5 h 20 min | 6 h 30 min | 0.63 |
| 80% | 242 | 1926.84 | 10.08 | 12.91 | 5 h 19 min | 5 h 30 min | 0.63 |
| 90% | 242 | 1929.75 | 10.10 | 13.55 | 5 h 19 min | 4 h 15 min | 0.63 |
| 100% | 376 | 2068.34 | 11.76 | 21.78 | 5 h 18 min | 3 h 15 min | 0.68 |
| CLC Code | Flooded Areas (ha) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1% | 5% | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% | 100% | |
| 112 1 | 40.3 | 85.8 | 87.2 | 86.3 | 87.7 | 82.9 | 85.3 | 86.9 | 87.2 | 87.1 | 86.4 | 110.6 |
| 211 2 | 204.7 | 339.8 | 343.9 | 340.5 | 347.1 | 329.0 | 337.6 | 343.1 | 344.4 | 343.9 | 341.6 | 398.7 |
| 221 3 | - | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| 222 4 | 3.6 | 5.3 | 5.3 | 5.3 | 5.3 | 5.3 | 5.3 | 5.3 | 5.3 | 5.3 | 5.3 | 6.5 |
| 231 5 | 771.1 | 1095.8 | 1106.3 | 1094.0 | 1107.0 | 1092.1 | 1093.3 | 1099.0 | 1101.4 | 1100.6 | 1096.7 | 1163.3 |
| 242 6 | 25.5 | 108.1 | 110.0 | 109.4 | 107.7 | 94.7 | 108.4 | 109.6 | 109.4 | 109.5 | 109.0 | 105.8 |
| 243 7 | 117.3 | 164.5 | 164.6 | 164.7 | 165.3 | 164.8 | 164.2 | 164.9 | 165.0 | 165.0 | 164.8 | 173.2 |
| Study Results (10% Breach Size) | 2D Unsteady (10% Breach Flow Rate) | Correlation | |
|---|---|---|---|
| Area (m2) | 20,683,352.5 | 20,403,841.6 | 98.70% |
| Official 0.1% flood extent | 2D Unsteady flow—0.1% recurrence | Correlation | |
| Area (m2) | 9,466,001.6 | 8,537,745.3 | 90.20% |
| Study results (50% breach size) | Full momentum (50% breach size) | Correlation | |
| Area (m2) | 19,183,623.66 | 17,987,918.28 | 93.80% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albu, L.-M.; Enea, A.; Iosub, M.; Breabăn, I.-G. Dam Breach Size Comparison for Flood Simulations. A HEC-RAS Based, GIS Approach for Drăcșani Lake, Sitna River, Romania. Water 2020, 12, 1090. https://doi.org/10.3390/w12041090
Albu L-M, Enea A, Iosub M, Breabăn I-G. Dam Breach Size Comparison for Flood Simulations. A HEC-RAS Based, GIS Approach for Drăcșani Lake, Sitna River, Romania. Water. 2020; 12(4):1090. https://doi.org/10.3390/w12041090
Chicago/Turabian StyleAlbu, Liviu-Marian, Andrei Enea, Marina Iosub, and Iuliana-Gabriela Breabăn. 2020. "Dam Breach Size Comparison for Flood Simulations. A HEC-RAS Based, GIS Approach for Drăcșani Lake, Sitna River, Romania" Water 12, no. 4: 1090. https://doi.org/10.3390/w12041090






