The Response of Groundwater Level to Climate Change and Human Activities in Baotou City, China
Abstract
:1. Introduction
2. Materials and Methods
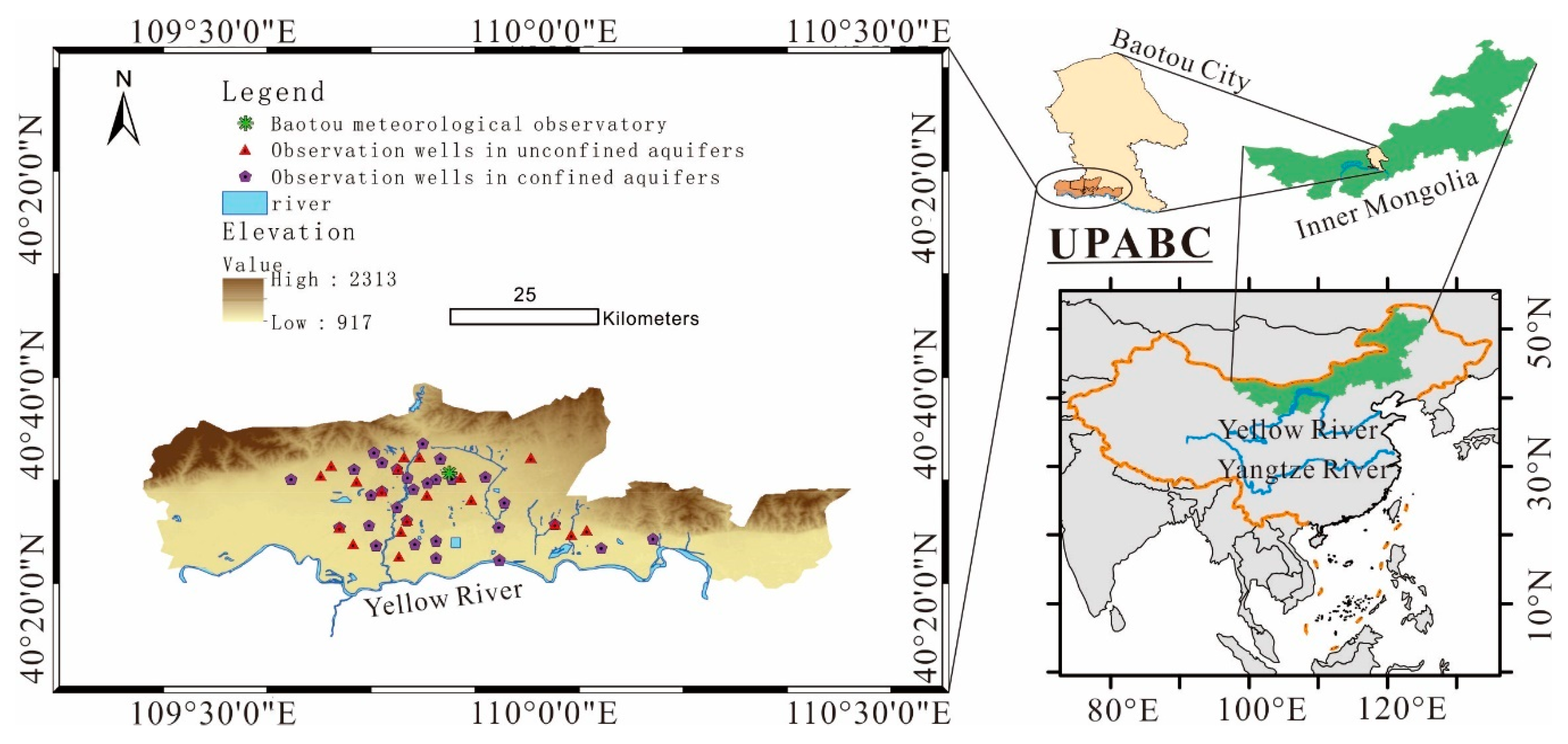
2.1. Study Area
2.2. Data
2.2.1. Hydrological and Climate Data
2.2.2. Groundwater Table Data
2.3. Statistical Analysis
2.3.1. Trend-Free Pre-Whitening (TFPW)-Mann–Kendall Test
2.3.2. Pearson Correlation Coefficient
2.3.3. Cross Wavelet Transform (XWT)
2.3.4. Wavelet Transform Coherence (WTC)
3. Results
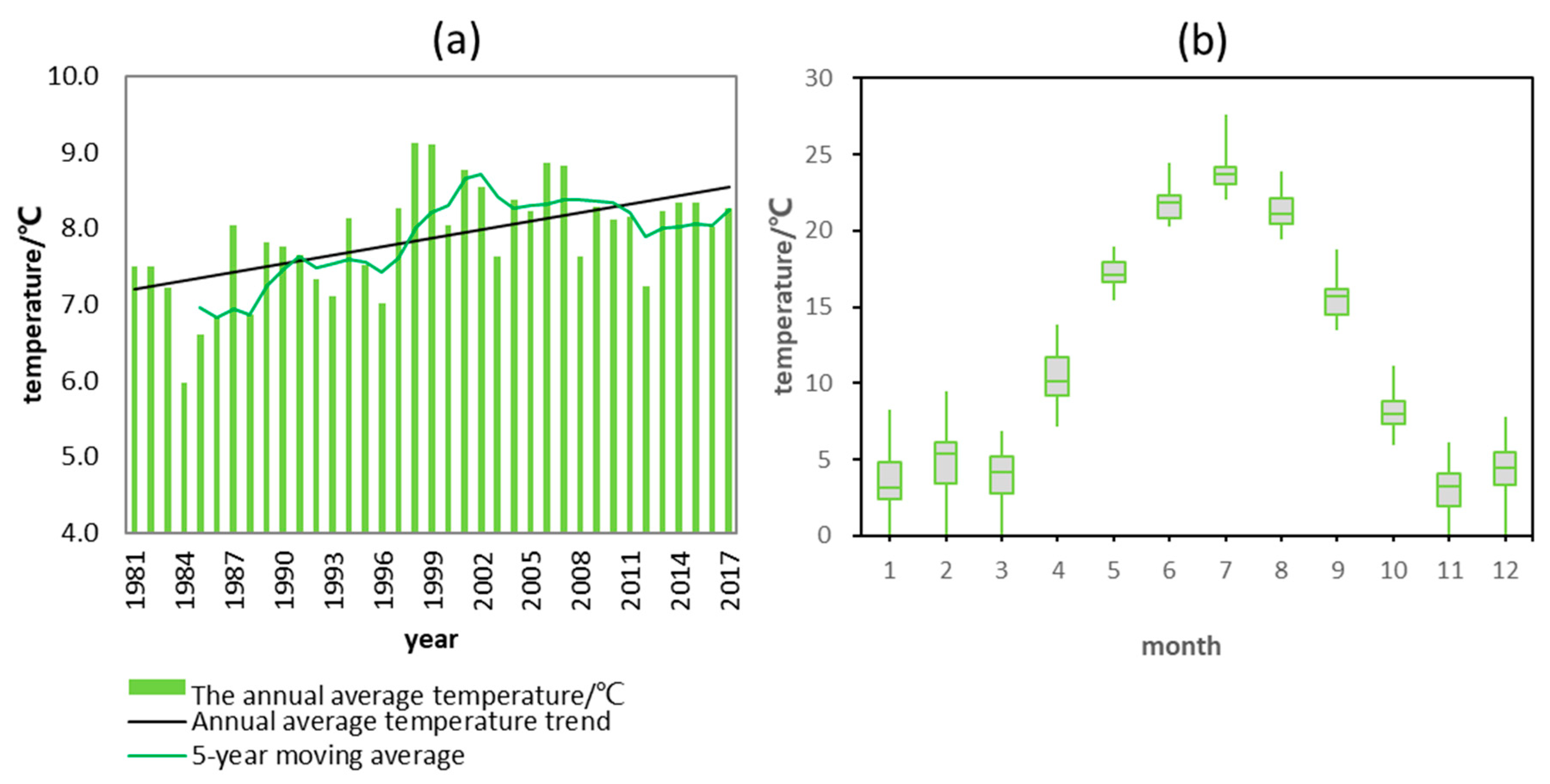
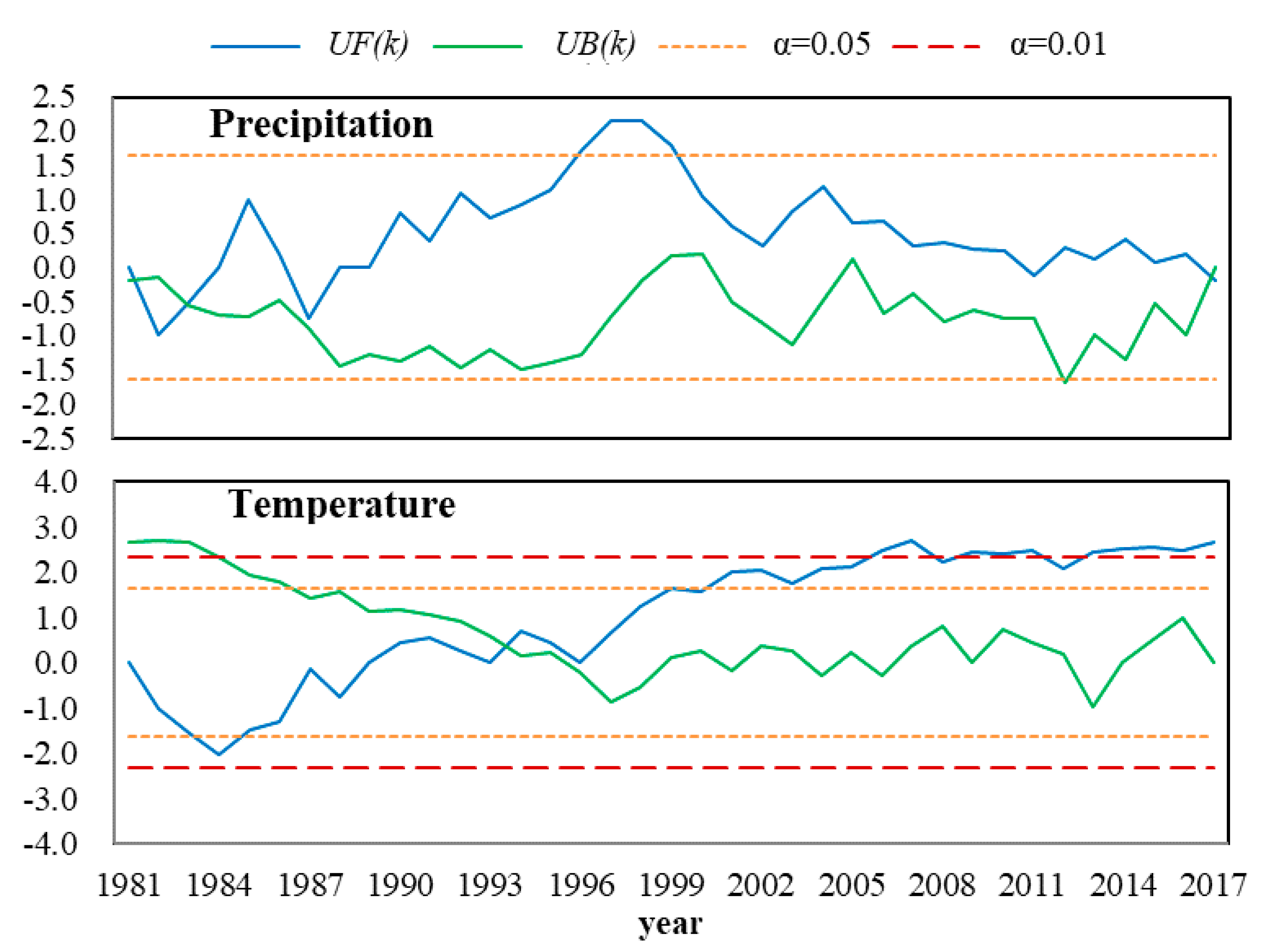
3.1. Climate Change
3.2. Human Groundwater Demand and Pumping
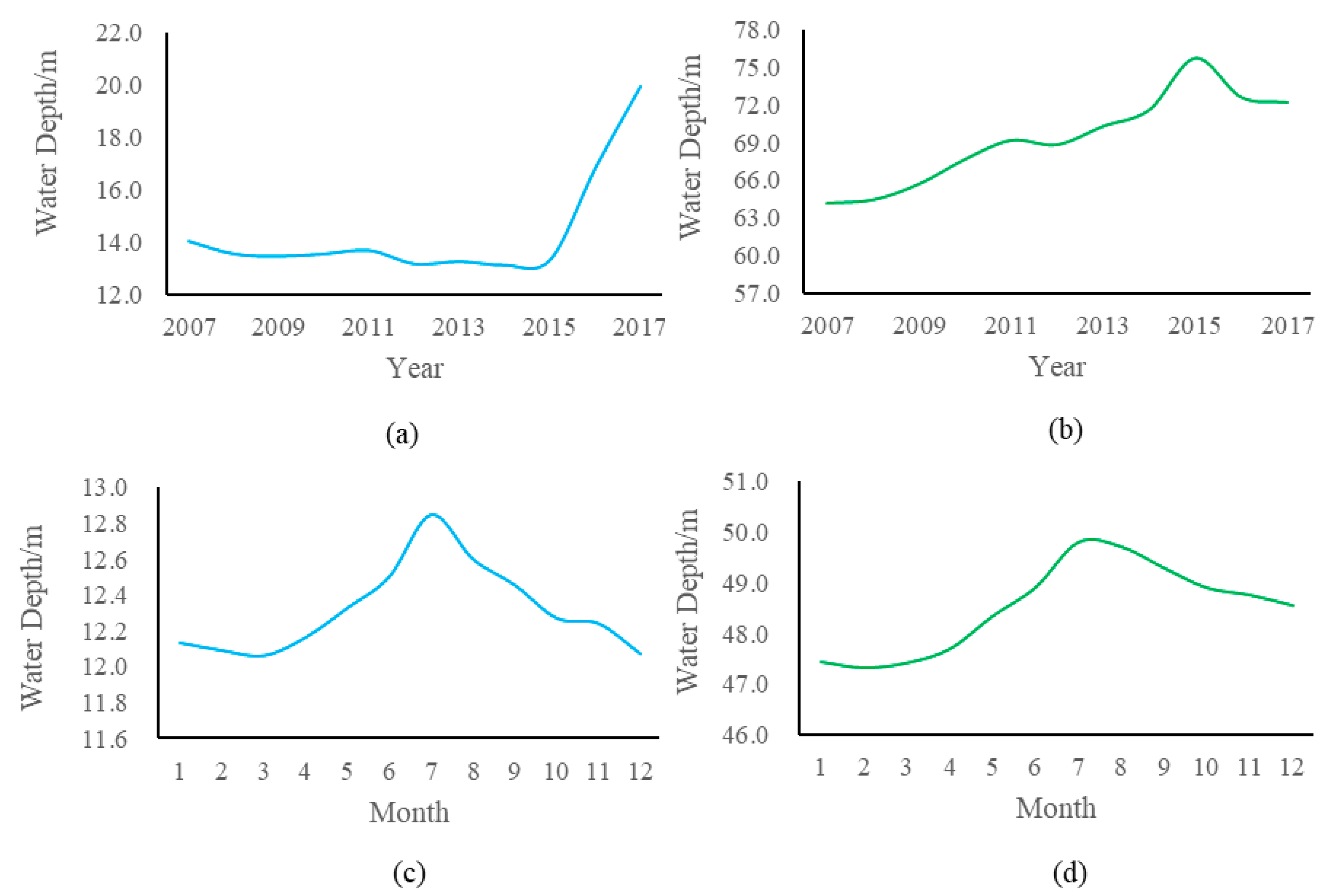
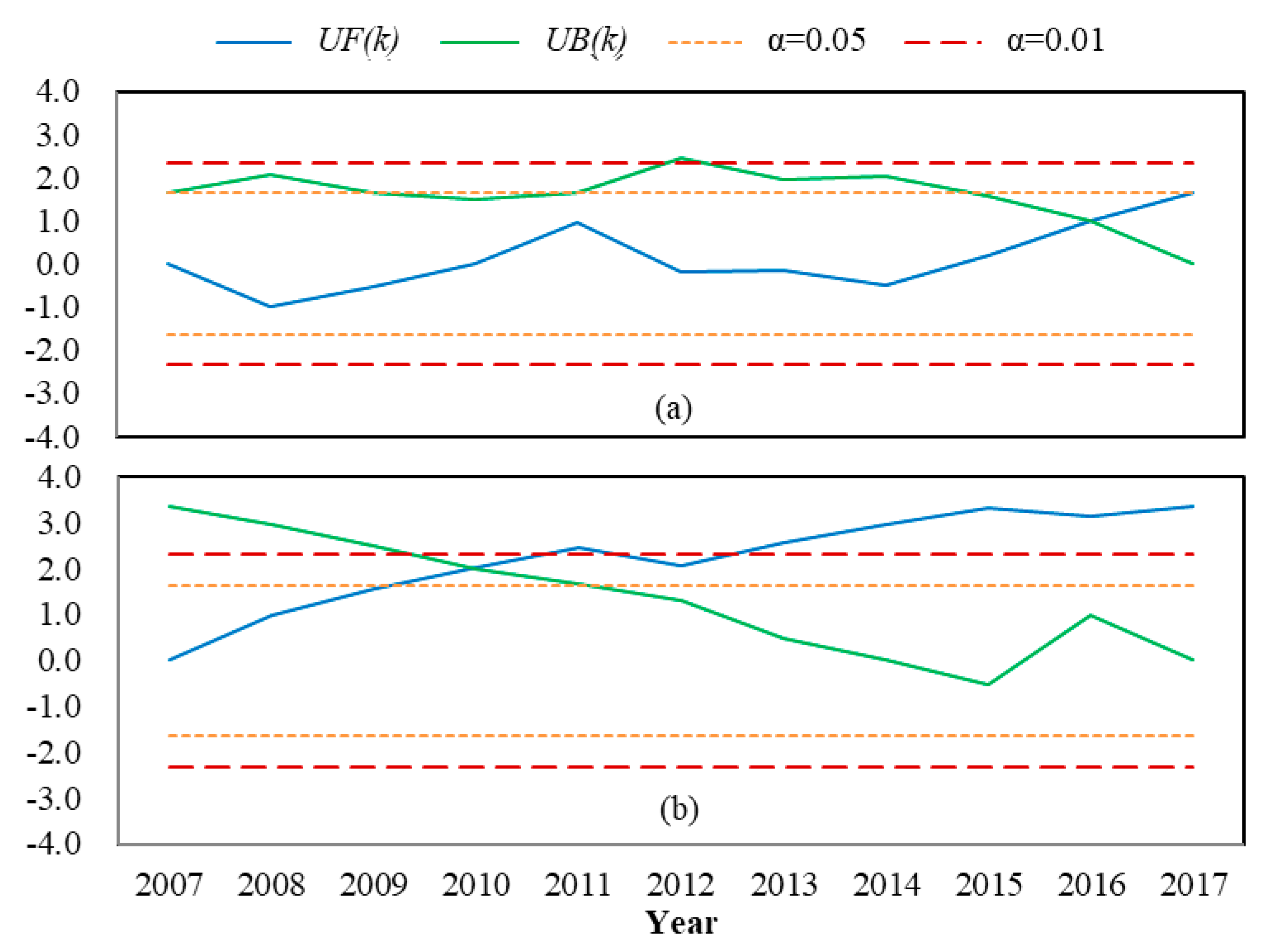
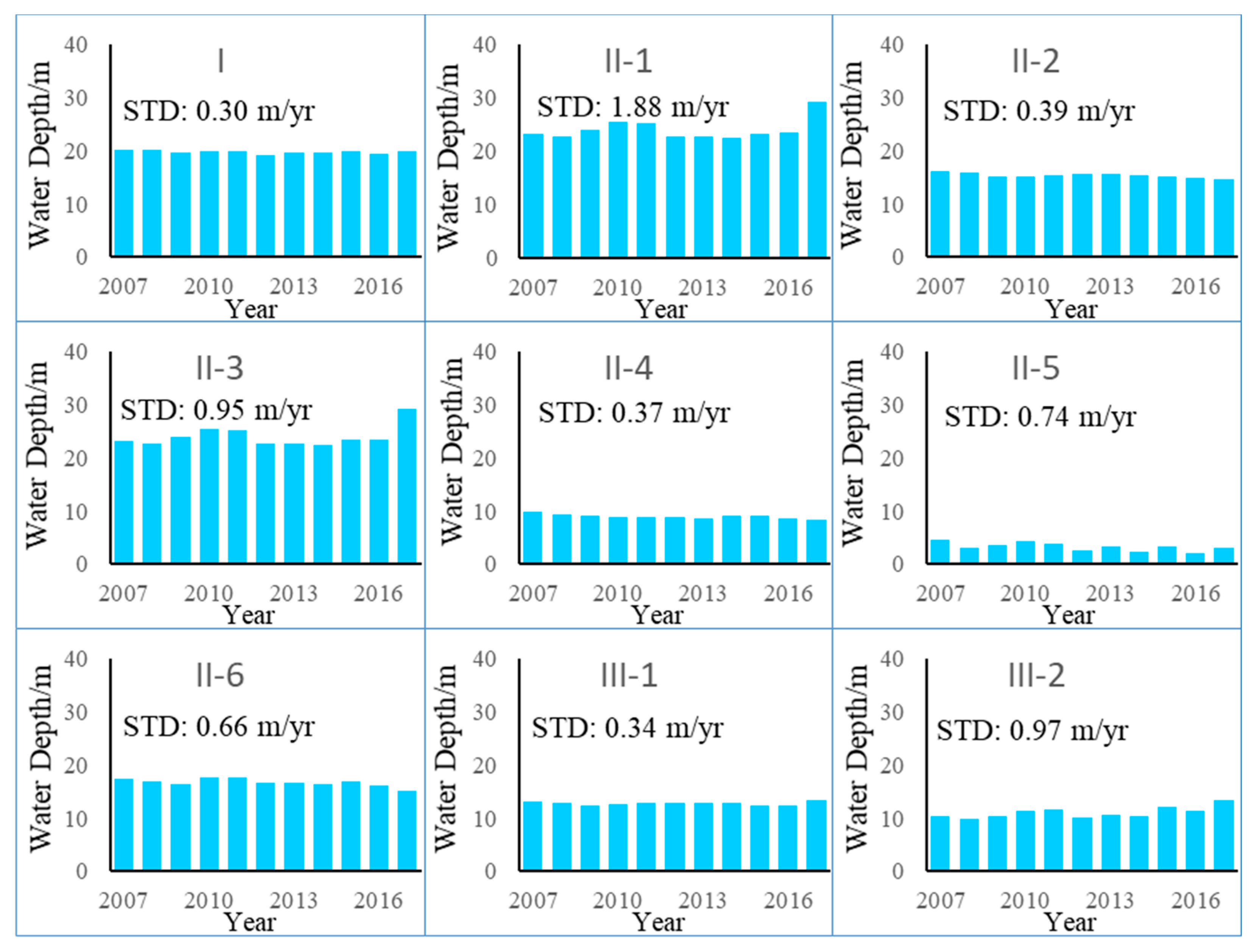
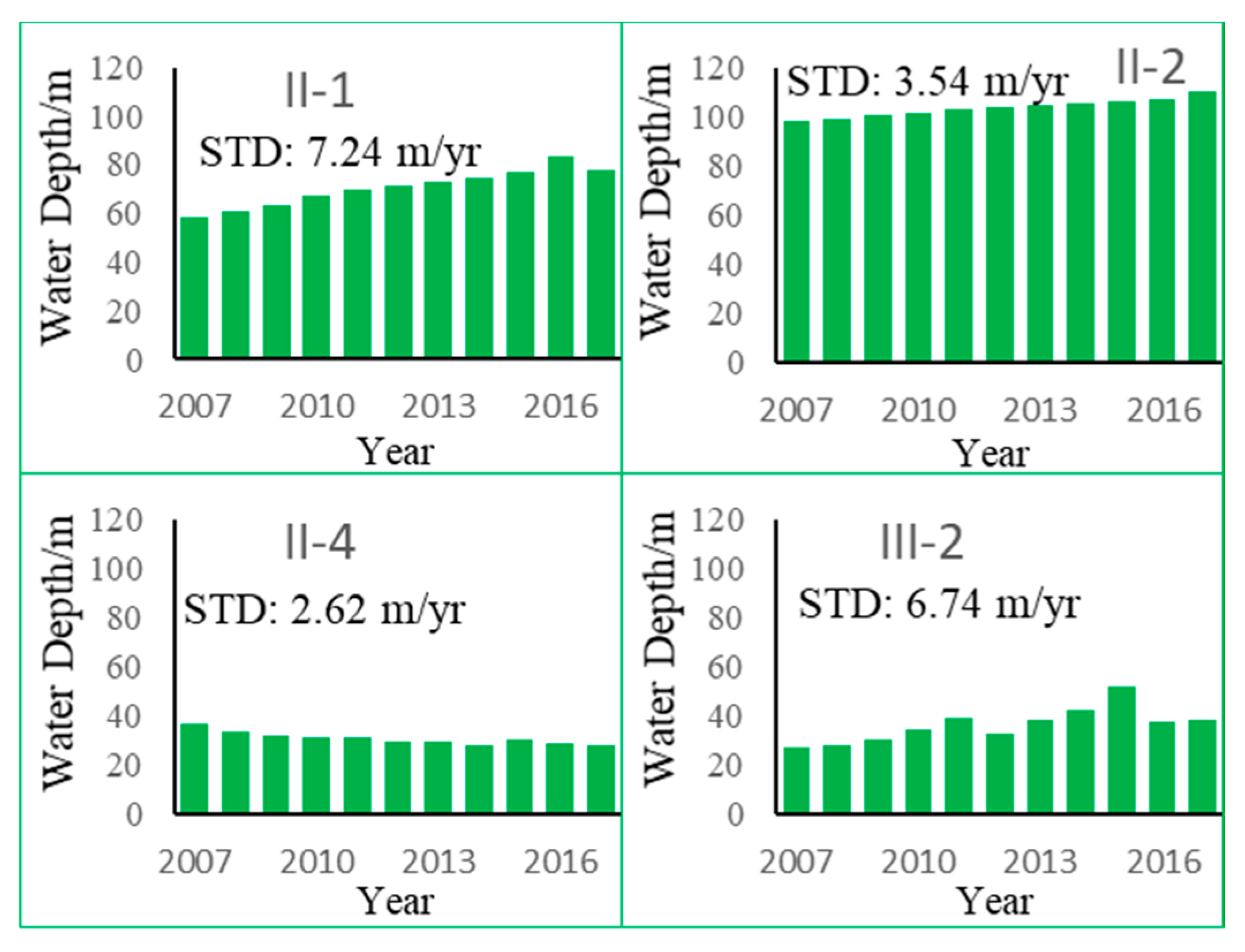
3.3. Temporal and Spatial Variation of Groundwater Depth
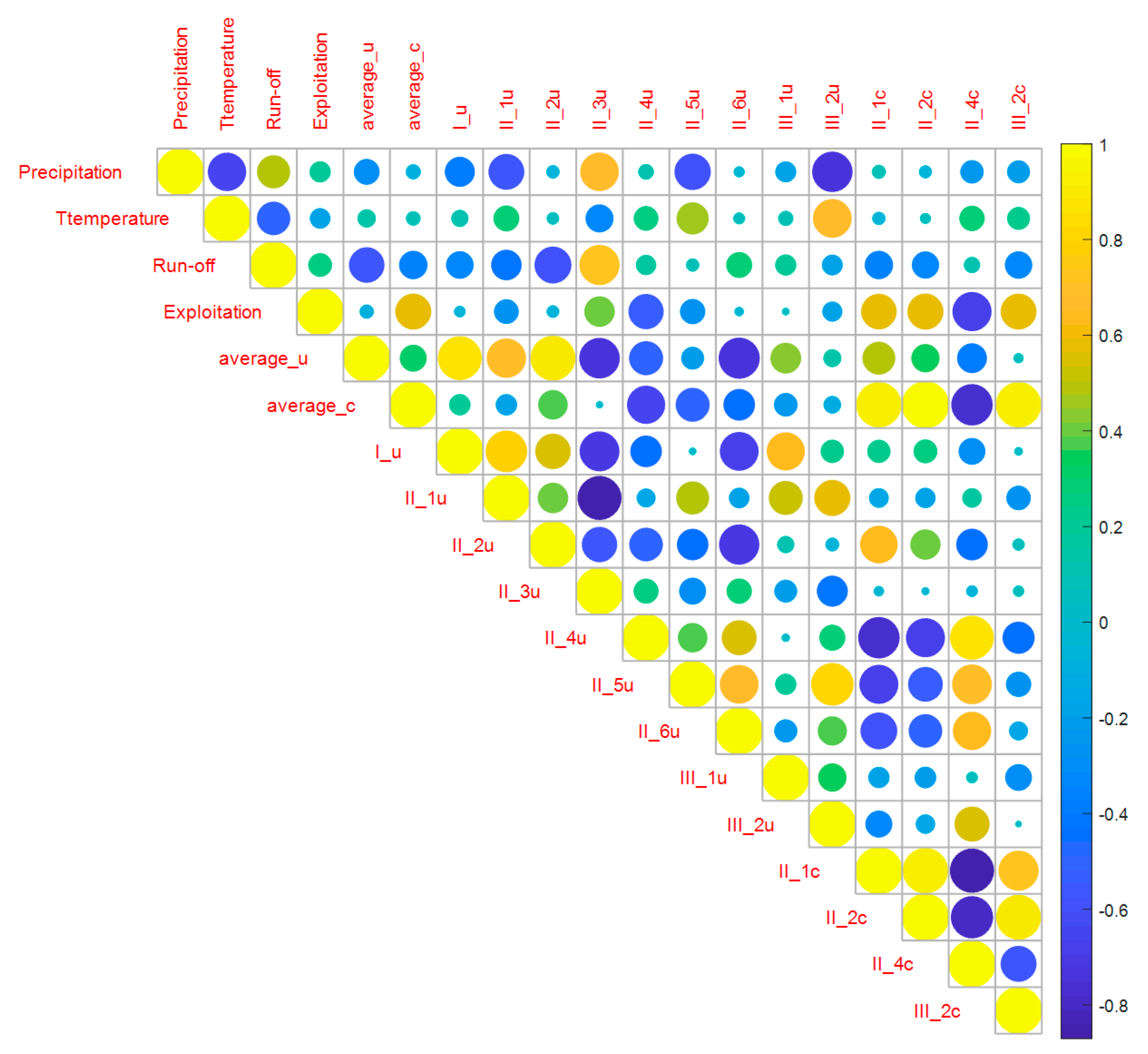
3.4. Driving Factors of Groundwater Depth Changes
4. Discussion
4.1. Drivers of Change in and Sustainability of the Groundwater System
4.2. Comparison with Other Studies in Groundwater Level Drivers
4.3. Key Lessons, Limitations, and Prospects
5. Conclusions
- (1)
- The annual precipitation changed slowly, the overall trend showed an increasing trend, and the possible abrupt change points of the annual precipitation sequence appeared in 1984. Moreover, the overall trend of temperature was increasing, and the regional climate was warming; possible abrupt change points of the annual average temperature sequence appeared in 1993. Furthermore, groundwater consumption increased, with the majority used for agricultural consumption.
- (2)
- The groundwater depth of both unconfined and confined water was increasing, and there were slight differences in groundwater changes in different hydrogeological zones. There was no abrupt change point in unconfined water depth from 2007–2017, and the abrupt change point in confined water depth occurred in 2011.
- (3)
- The biggest impact on groundwater depth was precipitation and mining volume. The lag time of groundwater depth response to precipitation was about 9–14 months, and agricultural water had the biggest impact on groundwater depth. In the future, agricultural water-saving facilities should be promoted in similar areas, and multiple sources of water should be used instead of groundwater for agricultural irrigation.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Giordano, M. Global Groundwater? Issues and Solutions. Annu. Rev. Environ. Resour. 2009, 34, 153–178. [Google Scholar] [CrossRef]
- Döll, P.; Hoffmann-Dobrev, H.; Portmann, F.; Siebert, S.; Eicker, A.; Rodell, M.; Strassberg, G.; Scanlon, B.R. Impact of water withdrawals from groundwater and surface water on continental water storage variations. J. Geodyn. 2012, 59, 143–156. [Google Scholar] [CrossRef]
- Castellazzi, P.; Martel, R.; Galloway, D.; Longuevergne, L.; Rivera, A. Assessing Groundwater Depletion and Dynamics Using GRACE and InSAR: Potential and Limitations. Ground Water 2016, 54, 768–780. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Çelik, R. Temporal changes in the groundwater level in the Upper Tigris Basin, Turkey, determined by a GIS technique. J. Afr. Earth Sci. 2015, 107, 134–143. [Google Scholar] [CrossRef]
- Narany, T.S.; Aris, A.Z.; Sefie, A.; Keesstra, S. Detecting and predicting the impact of land use changes on groundwater quality, a case study in Northern Kelantan, Malaysia. Sci. Total. Environ. 2017, 599, 844–853. [Google Scholar] [CrossRef]
- Rahmani, S.E.A.; Chibane, B.; Boucefiène, A. Groundwater recharge estimation in semi-arid zone: A study case from the region of Djelfa (Algeria). Appl. Water Sci. 2016, 7, 2255–2265. [Google Scholar] [CrossRef] [Green Version]
- Scanlon, B.R.; Keese, K.E.; Flint, A.L.; Flint, L.E.; Gaye, C.B.; Edmunds, W.M.; Simmers, I. Global synthesis of groundwater recharge in semiarid and arid regions. Hydrol. Process. 2006, 20, 3335–3370. [Google Scholar] [CrossRef]
- Huang, X.; Deng, H.; Zheng, C.; Cao, G. Hydrogeochemical signatures and evolution of groundwater impacted by the Bayan Obo tailing pond in northwest China. Sci. Total. Environ. 2016, 543, 357–372. [Google Scholar] [CrossRef]
- Kumar, C.P. Climate Change and Its Impact on Groundwater Resources. Research Inventy: International. J. Eng. Sci. 2012, 1, 43–60. [Google Scholar]
- Arnell, N.W. Relative effects of multi-decadal climatic variability and changes in the mean and variability of climate due to global warming: Future streamflows in Britain. J. Hydrol. 2003, 270, 195–213. [Google Scholar] [CrossRef]
- Crosbie, R.S.; McCallum, J.L.; Walker, G.R.; Chiew, F.H.S. Modelling climate-change impacts on groundwater recharge in the Murray-Darling Basin, Australia. Hydrogeol. J. 2010, 18, 1639–1656. [Google Scholar] [CrossRef]
- Mileham, L.; Taylor, R.; Todd, M.; Tindimugaya, C.; Thompson, J. The impact of climate change on groundwater recharge and runoff in a humid, equatorial catchment: Sensitivity of projections to rainfall intensity. Hydrol. Sci. J. 2009, 54, 727–738. [Google Scholar] [CrossRef] [Green Version]
- Gurdak, J.S.; Hanson, R.; Green, T.R. Effects of Climate Variability and Change on Groundwater Resources of the United States. In Fact Sheet; US Geological Survey: Reston, VA, USA, 2009. [Google Scholar]
- Green, T.R. Linking Climate Change and Groundwater. In Integrated Groundwater Management: Concepts, Approaches and Challenges; Jakeman, A.J., Barreteau, O., Hunt, R.J., Rinaudo, J., Ross, A., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 97–141. [Google Scholar]
- Liao, C.; Zhuang, Q. 2017 Regents of the University of Colorado Quantifying the Role of Permafrost Distribution in Groundwater and Surface Water Interactions Using a Three-Dimensional Hydrological Model. Arctic Antarct. Alp. Res. 2017, 49, 81–100. [Google Scholar] [CrossRef]
- Macdonald, A.; Calow, R.; Macdonald, D.M.J.; Darling, W.G.; Dochartaigh, B.É.Ó. What impact will climate change have on rural groundwater supplies in Africa? Hydrol. Sci. J. 2009, 54, 690–703. [Google Scholar] [CrossRef] [Green Version]
- Green, T.R.; Taniguchi, M.; Kooi, H.; Gurdak, J.J.; Allen, D.M.; Hiscock, K.M.; Treidel, H.; Aureli, A. Beneath the surface of global change: Impacts of climate change on groundwater. J. Hydrol. 2011, 405, 532–560. [Google Scholar] [CrossRef] [Green Version]
- Huang, T.; Jahan, C.S.; Edmunds, W.M. Soil profile evolution following land-use change: Implications for groundwater quantity and quality. Hydrol. Process. 2012, 27, 1238–1252. [Google Scholar] [CrossRef]
- Salem, G.S.A.; Kazama, S.; Shahid, S.; Dey, N.C. Impacts of climate change on groundwater level and irrigation cost in a groundwater dependent irrigated region. Agric. Water Manag. 2018, 208, 33–42. [Google Scholar] [CrossRef]
- Shahid, S.; Hazarika, M.K. Groundwater Drought in the Northwestern Districts of Bangladesh. Water Resour. Manag. 2009, 24, 1989–2006. [Google Scholar] [CrossRef]
- Taylor, R.G.; Scanlon, B.; Döll, P.; Rodell, M.; Van Beek, R.; Wada, Y.; Longuevergne, L.; Leblanc, M.; Famiglietti, J.; Edmunds, M.; et al. Ground water and climate change. Nat. Clim. Chang. 2012, 3, 322–329. [Google Scholar] [CrossRef] [Green Version]
- Duvert, C.; Jourde, H.; Raiber, M.; Cox, M.E. Correlation and spectral analyses to assess the response of a shallow aquifer to low and high frequency rainfall fluctuations. J. Hydrol. 2015, 527, 894–907. [Google Scholar] [CrossRef]
- Hocking, M.; Kelly, B.F. Groundwater recharge and time lag measurement through Vertosols using impulse response functions. J. Hydrol. 2016, 535, 22–35. [Google Scholar] [CrossRef]
- Sophocleous, M. Interactions between groundwater and surface water: The state of the science. Hydrogeol. J. 2002, 10, 52–67. [Google Scholar] [CrossRef]
- Hu, B.X.; Xu, Z. Numerical Simulation of Groundwater Flow and Solute Transport in a Karst Aquifer with Conduits. In Groundwater—Contaminant and Resource Management; IntechOpen: London, UK, 2016. [Google Scholar]
- Hughes, J.; Petrone, K.C.; Silberstein, R.P. Drought, groundwater storage and stream flow decline in southwestern Australia. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Tallaksen, L.M.; Hisdal, H.; Van Lanen, H.A. Space–time modelling of catchment scale drought characteristics. J. Hydrol. 2009, 375, 363–372. [Google Scholar] [CrossRef]
- Castle, S.L.; Thomas, B.; Reager, J.T.; Rodell, M.; Swenson, S.C.; Famiglietti, J. Groundwater depletion during drought threatens future water security of the Colorado River Basin. Geophys. Res. Lett. 2014, 41, 5904–5911. [Google Scholar] [CrossRef] [Green Version]
- Rodell, M.; Velicogna, I.; Famiglietti, J. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef] [Green Version]
- Naumburg, E.; Mata-González, R.; Hunter, R.G.; McLendon, T.; Martin, D.W. Phreatophytic Vegetation and Groundwater Fluctuations: A Review of Current Research and Application of Ecosystem Response Modeling with an Emphasis on Great Basin Vegetation. Environ. Manag. 2005, 35, 726–740. [Google Scholar] [CrossRef]
- Newman, B.D.; Wilcox, B.P.; Archer, S.R.; Breshears, D.D.; Dahm, C.N.; Duffy, C.J.; McDowell, N.G.; Phillips, F.M.; Scanlon, B.R.; Vivoni, E.R. Ecohydrology of water-limited environments: A scientific vision. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Lite, S.; Stromberg, J. Surface water and ground-water thresholds for maintaining Populus–Salix forests, San Pedro River, Arizona. Boil. Conserv. 2005, 125, 153–167. [Google Scholar] [CrossRef]
- Orellana, F.; Verma, P.; Ii, S.P.L.; Daly, E. Monitoring and modeling water-vegetation interactions in groundwater-dependent ecosystems. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef]
- Minh, H.V.T.; Ngoc, D.; Ngan, H.; Van Men, H.; Van, T.; Tran Van, T. Assessment of Groundwater Level and Quality: A Case Study in O Mon and Binh Thuy Districts, Can Tho City, Vietnam. Naresuan Univ. Eng. J. 2016, 11, 25–33. [Google Scholar] [CrossRef]
- Soylu, M.E.; Lenters, J.D.; Istanbulluoglu, E.; Ii, S.P.L. On evapotranspiration and shallow groundwater fluctuations: A Fourier-based improvement to the White method. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef] [Green Version]
- Cui, Y.; Shao, J. The Role of Ground Water in Arid/Semiarid Ecosystems, Northwest China. Ground Water 2005, 43, 471–477. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Guo, Z.; Lu, Y.; Yan, D.; Liao, Z.; Liu, H.; Cui, Y. Pixel-Level Spatiotemporal Analyses of Vegetation Fractional Coverage Variation and Its Influential Factors in a Desert Steppe: A Case Study in Inner Mongolia, China. Water 2017, 9, 478. [Google Scholar] [CrossRef]
- Jones, P.; Osborn, T.J.; Briffa, K.R. The Evolution of Climate over the Last Millennium. Science 2001, 292, 662–667. [Google Scholar] [CrossRef] [Green Version]
- Pau, S.; Wolkovich, E.M.; Cook, B.I.; Davies, T.J.; Kraft, N.J.; Bolmgren, K.; Betancourt, J.L.; Cleland, E.E. Predicting phenology by integrating ecology, evolution and climate science. Glob. Chang. Boil. 2011, 17, 3633–3643. [Google Scholar] [CrossRef]
- Hamed, K.; Rao, A.R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Cavadias, G. Power of the Mann–Kendall and Spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Sarr, M.A.; Gachon, P.; Seidou, O.; Bryant, C.R.; Ndione, J.A.; Comby, J. Inconsistent linear trends in Senegalese rainfall indices from 1950 to 2007. Hydrol. Sci. J. 2015, 60, 1538–1549. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, B.; Xin, C.; Lan, T. Effects of trend-free pre-whitening methods on trend detection in Mann-Kendall test of runoff series. J. Hydroelectr. Eng. 2016, 35, 56–69. [Google Scholar] [CrossRef]
- Chen, Z.; Jiang, W.; Wang, W.; Deng, Y.; He, B.; Jia, K. The Impact of Precipitation Deficit and Urbanization on Variations in Water Storage in the Beijing-Tianjin-Hebei Urban Agglomeration. Remote. Sens. 2017, 10, 4. [Google Scholar] [CrossRef] [Green Version]
- Jarrah, A.M.; Khanna, N. Some results on vanishing moments of wavelet packets, convolution and cross-correlation of wavelets. Arab. J. Math. Sci. 2019, 25, 169–179. [Google Scholar] [CrossRef]
- Huang, L.; Hao, H.; Li, X.; Li, J. Source identification of microseismic events in underground mines with interferometric imaging and cross wavelet transform. Tunn. Undergr. Space Technol. 2018, 71, 318–328. [Google Scholar] [CrossRef]
- Huang, H.B.; Huang, X.R.; Yang, M.L.; Lim, T.C.; Ding, W.P. Identification of vehicle interior noise sources based on wavelet transform and partial coherence analysis. Mech. Syst. Signal Process. 2018, 109, 247–267. [Google Scholar] [CrossRef]
- Cui, Y.; Wei, Y.; Guo, Z.; Liao, Z.; Long, Y. Response of Groundwater Level to Variation of Precipitation Factors in Ecologically Fragile Grassland Areas. Water Sav. Irrig. 2017, 60–64. [Google Scholar]
- Cui, T.; Raiber, M.; Pagendam, D.; Gilfedder, M.; Rassam, D. Response of groundwater level and surface-water/groundwater interaction to climate variability: Clarence-Moreton Basin, Australia. Hydrogeol. J. 2017, 26, 593–614. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Jing, J.; Sun, J. Response of groundwater to climate change under extreme climate conditions in North China Plain. J. Earth Sci. 2014, 25, 612–618. [Google Scholar] [CrossRef]
- Liao, Z.; Long, Y.; Liu, H.; Song, Y.; Guo, Z.; Wei, Y. Influence of Climate Change and Human Activities on Groundwater Level in Baotou City. Arid Zone Res. 2014, 31, 138–143. [Google Scholar]
- Qi, P.; Zhang, G.; Xu, Y.J.; Wang, L.; Ding, C.; Cheng, C. Assessing the Influence of Precipitation on Shallow Groundwater Table Response Using a Combination of Singular Value Decomposition and Cross-Wavelet Approaches. Water 2018, 10, 598. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Lu, Y.; Zheng, C.; Zhang, X.; Zhou, B.; Wu, J. Seasonal and Inter-Annual Variability of Groundwater and Their Responses to Climate Change and Human Activities in Arid and Desert Areas: A Case Study in Yaoba Oasis, Northwest China. Water 2020, 12, 303. [Google Scholar] [CrossRef] [Green Version]
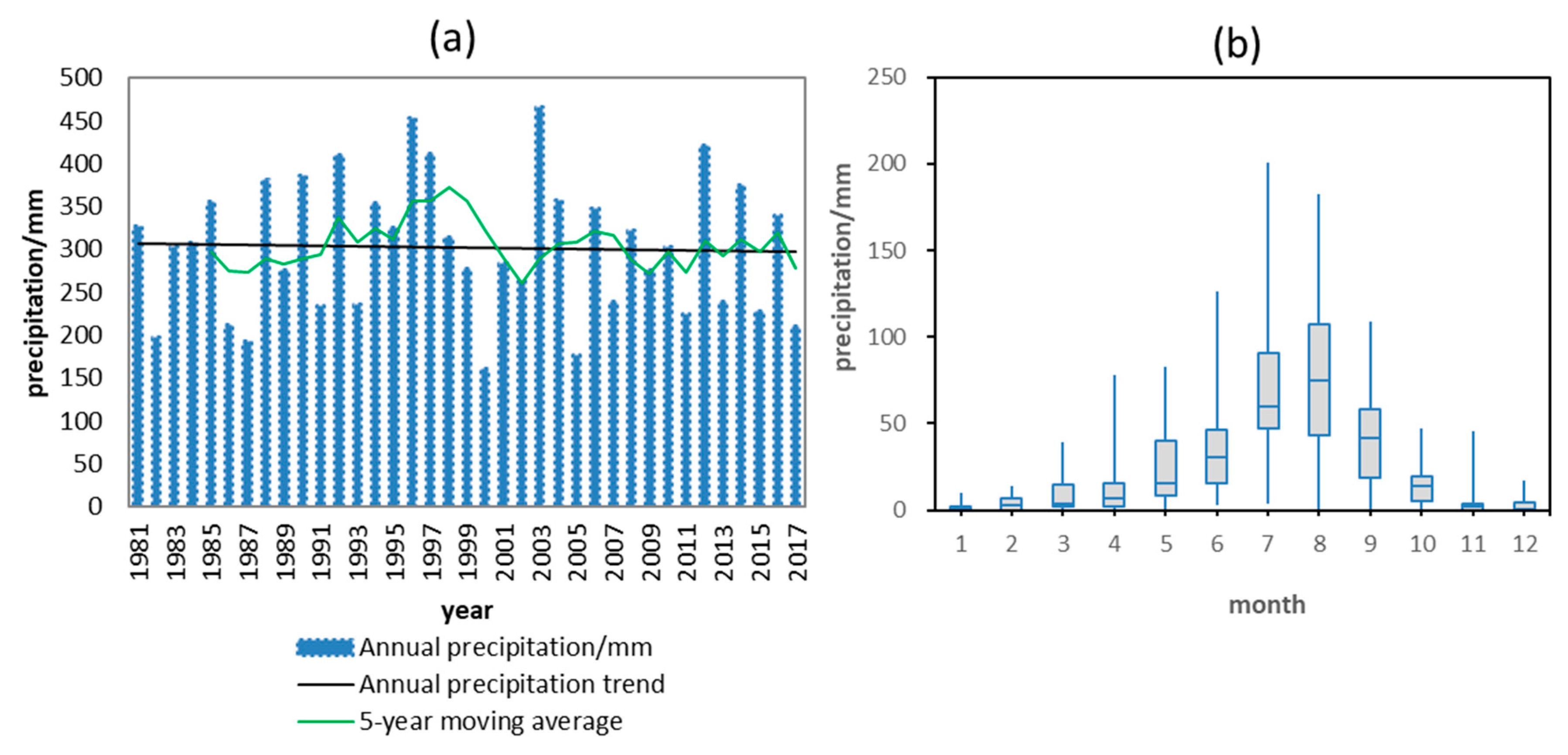

| Climatic Factor | Value | |
|---|---|---|
| Precipitation (mm) | Average | 305.90 |
| Max | 465.20 | |
| Min | 161.20 | |
| Evaporation (mm) | Average | 2273.80 |
| Max | 2793.20 | |
| Min | 1960.00 | |
| Temperature (°C) | Average | 7.80 |
| Max | 39.20 | |
| Min | −31.40 | |
| Sunshine (h) | Average | 2873.06 |
| Max | 3167.00 | |
| Min | 2576.70 | |
| Wind speed (m/s) | Average | 9.75 |
| Max | 21.30 | |
| Min | 4.10 | |
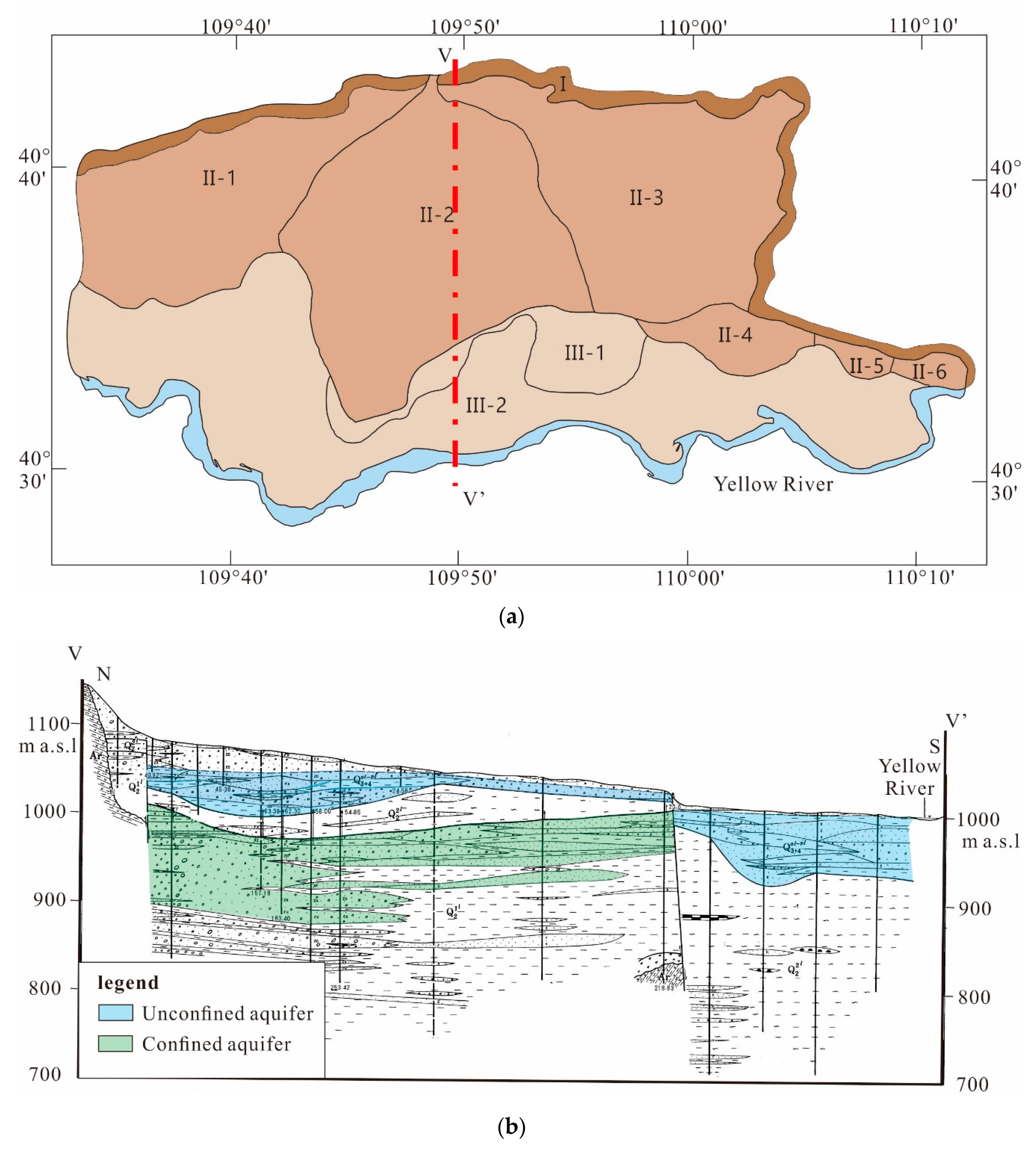
| Hydrogeological Area CODE | Unconfined Aquifer | Confined Aquifer | ||||
|---|---|---|---|---|---|---|
| Depth/m | Thickness/m | Lithology | Depth/m | Thickness/m | Lithology | |
| I | Low mountain hills hydrological address area | |||||
| I | 3–10 | 5–20 | Gneiss-based | – | – | – |
| II | Piedmont Plain hydrogeological area | |||||
| II-1 | 3–40 | 10–25 | The lithology of the upper and middle layers is gravel and pebble layer, mixed with medium-fine sand and cohesive soil, the particle size is poorly sorted, and the lower part is coarse sand and medium-fine sand. | 70–110 | 20–50 | Most of them are gravel, and the edges are coarse, medium, or fine sand. |
| II-2 | 3–40 | 5–30 | The area is dominated by gravel, with coarse sand, medium-fine sand, and fine sand distributed on the western and southwestern edges. | 90–110 | 20–70 | The area is mainly composed of gravel and sand eggs, and the lower and edges are medium-coarse sand and medium-fine sand. |
| II-3 | 3–30 | 2–8 | Mainly medium-coarse sand, medium-fine sand, and fine sand. | 50–70 | 10–30 | The main lithology is gravel. |
| II-4 | 10–30 | 5–20 | The southern edge is medium-coarse sand and medium-fine sand, and the rest are all gravel layers. | 20–40 | 70–90 | The north is mostly gravel, while the south is mainly medium-thick and medium-fine sand. |
| II-5 | 10–30 | 15–20 | The entire sector is composed of coarse-grained gravel. | – | – | – |
| II-6 | 5–30 | 25 | The entire fan-shaped ground is composed of coarse-grained gravel. | – | – | – |
| III | Hydrogeological area of the Yellow River Alluvial Plain | |||||
| III-1 | 3–5 | 30–50 | Some are gravel or gravel sand, and the remaining sections are mainly medium-fine sand and silty sand, followed by silt. | – | – | – |
| III-2 | 1–3 | 10–40 | Some areas are medium-coarse sand and medium-fine sand, and other areas are fine sand and fine sand. | 0–3 | 10–20 | Medium coarse sand, medium-fine sand, or silt. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Y.; Liao, Z.; Wei, Y.; Xu, X.; Song, Y.; Liu, H. The Response of Groundwater Level to Climate Change and Human Activities in Baotou City, China. Water 2020, 12, 1078. https://doi.org/10.3390/w12041078
Cui Y, Liao Z, Wei Y, Xu X, Song Y, Liu H. The Response of Groundwater Level to Climate Change and Human Activities in Baotou City, China. Water. 2020; 12(4):1078. https://doi.org/10.3390/w12041078
Chicago/Turabian StyleCui, Yingjie, Zilong Liao, Yongfu Wei, Xiaomin Xu, Yifan Song, and Huiwen Liu. 2020. "The Response of Groundwater Level to Climate Change and Human Activities in Baotou City, China" Water 12, no. 4: 1078. https://doi.org/10.3390/w12041078





