Evaluation of the Influence of Farming Practices and Land Use on Groundwater Resources in a Coastal Multi-Aquifer System in Puck Region (Northern Poland)
Abstract
1. Introduction
- Coupling of groundwater model with SWAT hydrological model to obtain detailed information on groundwater recharge rate and nitrate loads leached from soil. SWAT has already been used in a number of studies on the hydrological balance and nutrient transport in the Baltic region [38,39,40,41,42,43], including the Puck Bay region [44,45]. However, there has been no attempt to apply SWAT-MODFLOW coupling on the Polish Baltic coast.
- Evaluation of the time variability of the groundwater recharge rate and SGD rate and the associated nitrate loads under different land use scenarios. While the impact of crop type and land use on water and nutrient fluxes has been extensively studied for different watersheds using SWAT, there have been no such investigations in the context of submarine groundwater discharge. In this work, we evaluate 10 scenarios, corresponding to six types of crops and four types of land use.
2. Materials and Methods
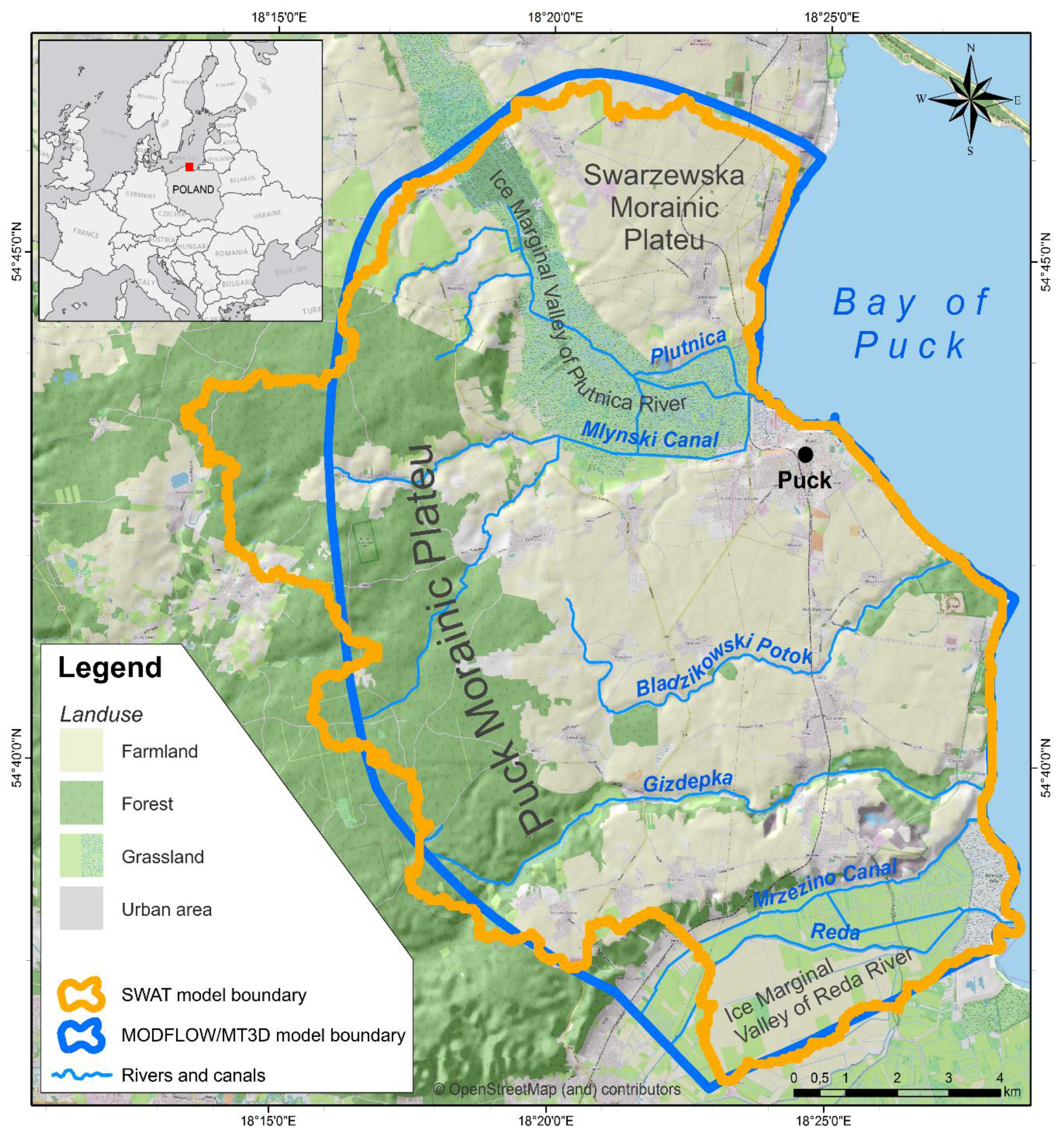
2.1. Study Area
2.2. SWAT Model
2.3. Groundwater Flow Model
2.4. Nitrate Transport Model
2.5. Scenarios for Transient Flow Simulations
3. Results and Discussion
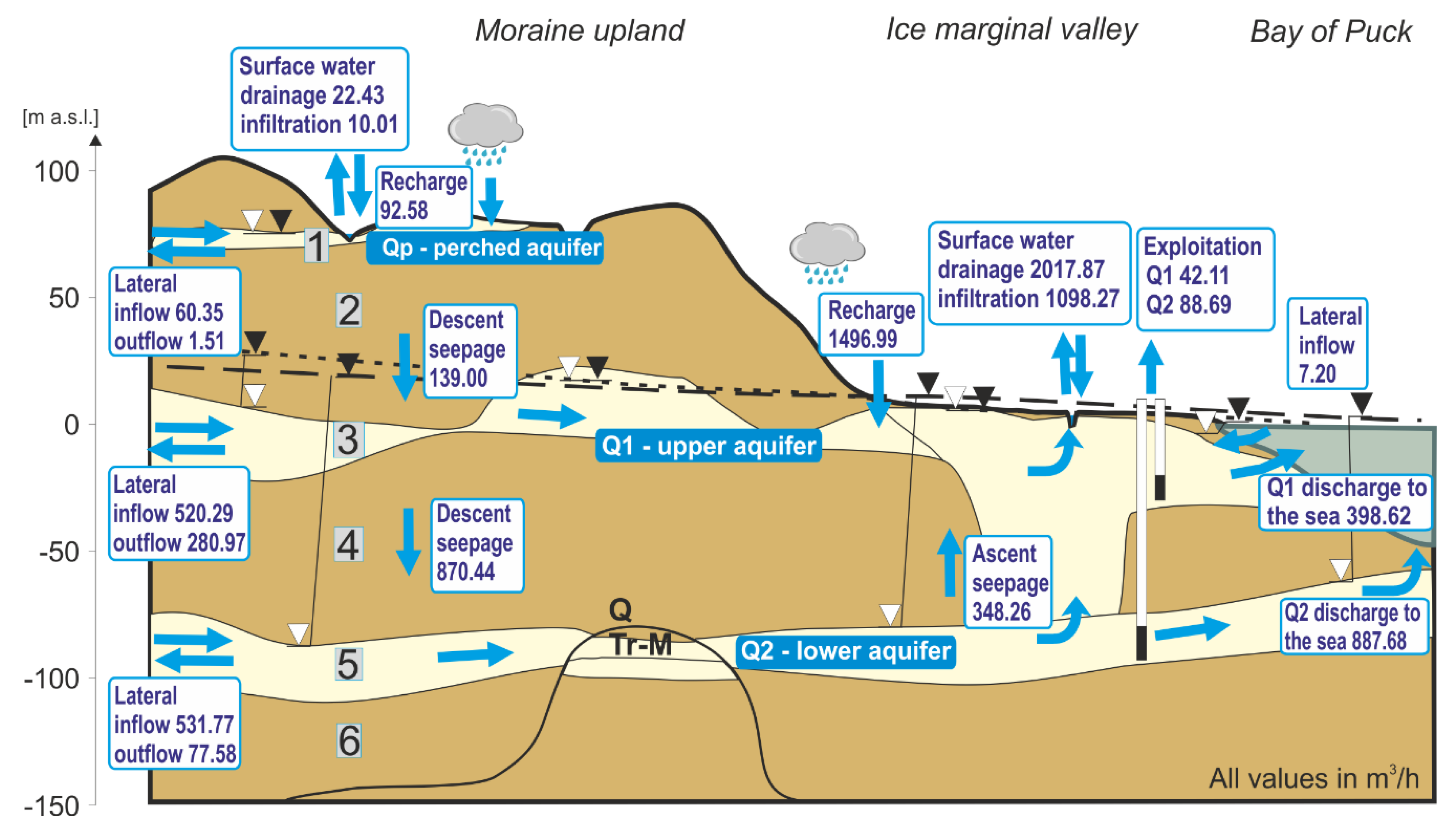
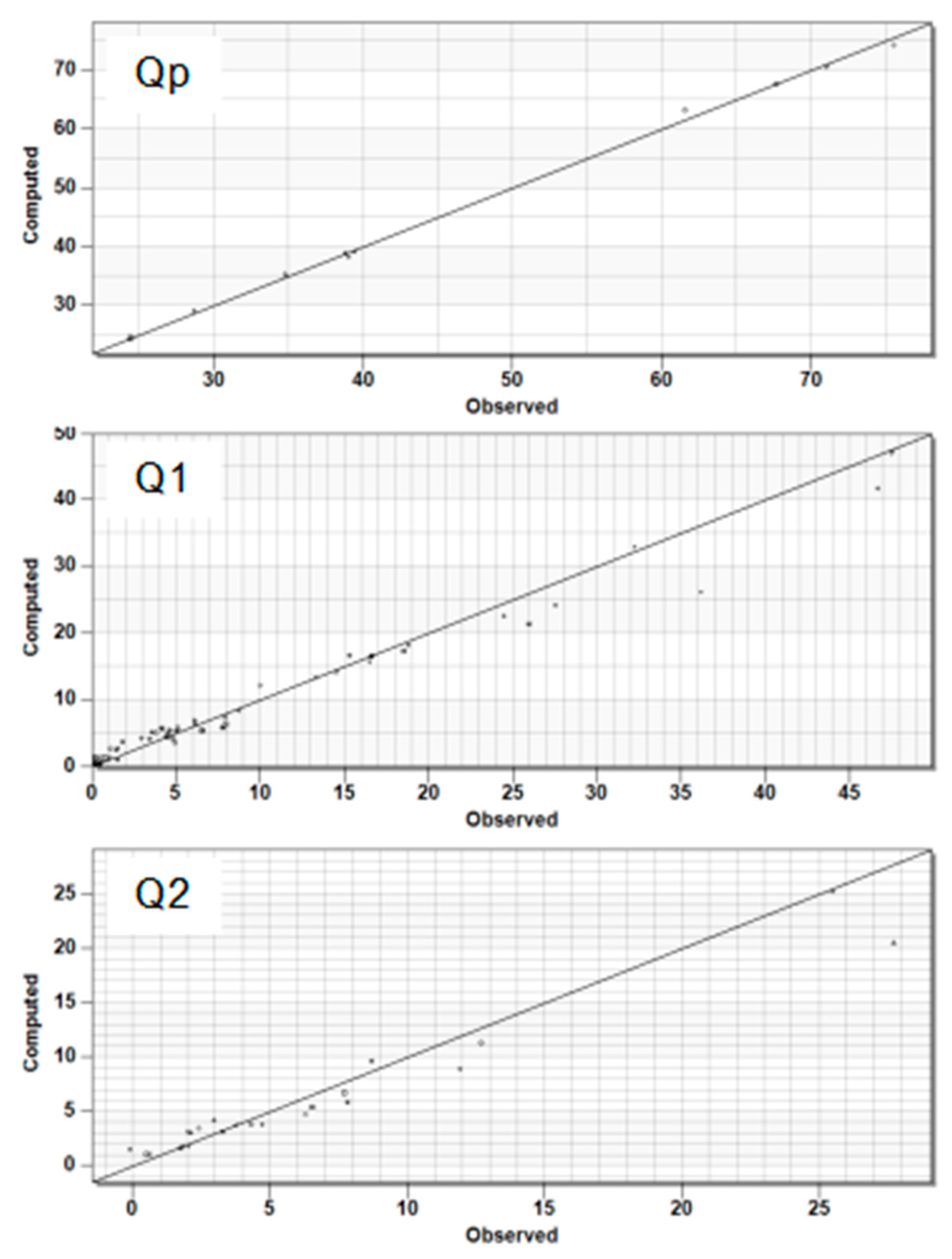
3.1. Steady-State Flow Simulation
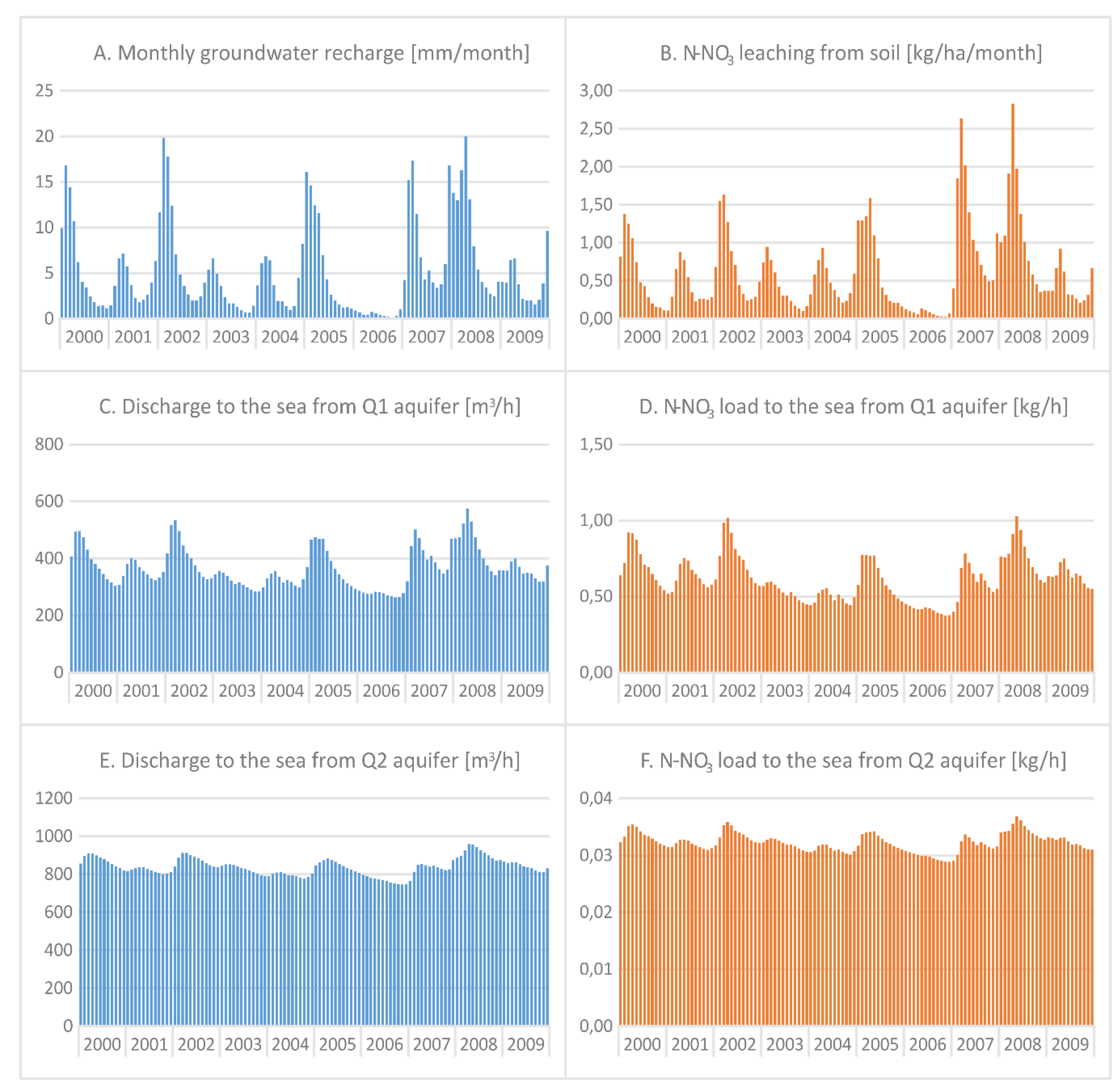
3.2. Transient Simulations of Flow and Nitrogen Transport
4. Conclusions
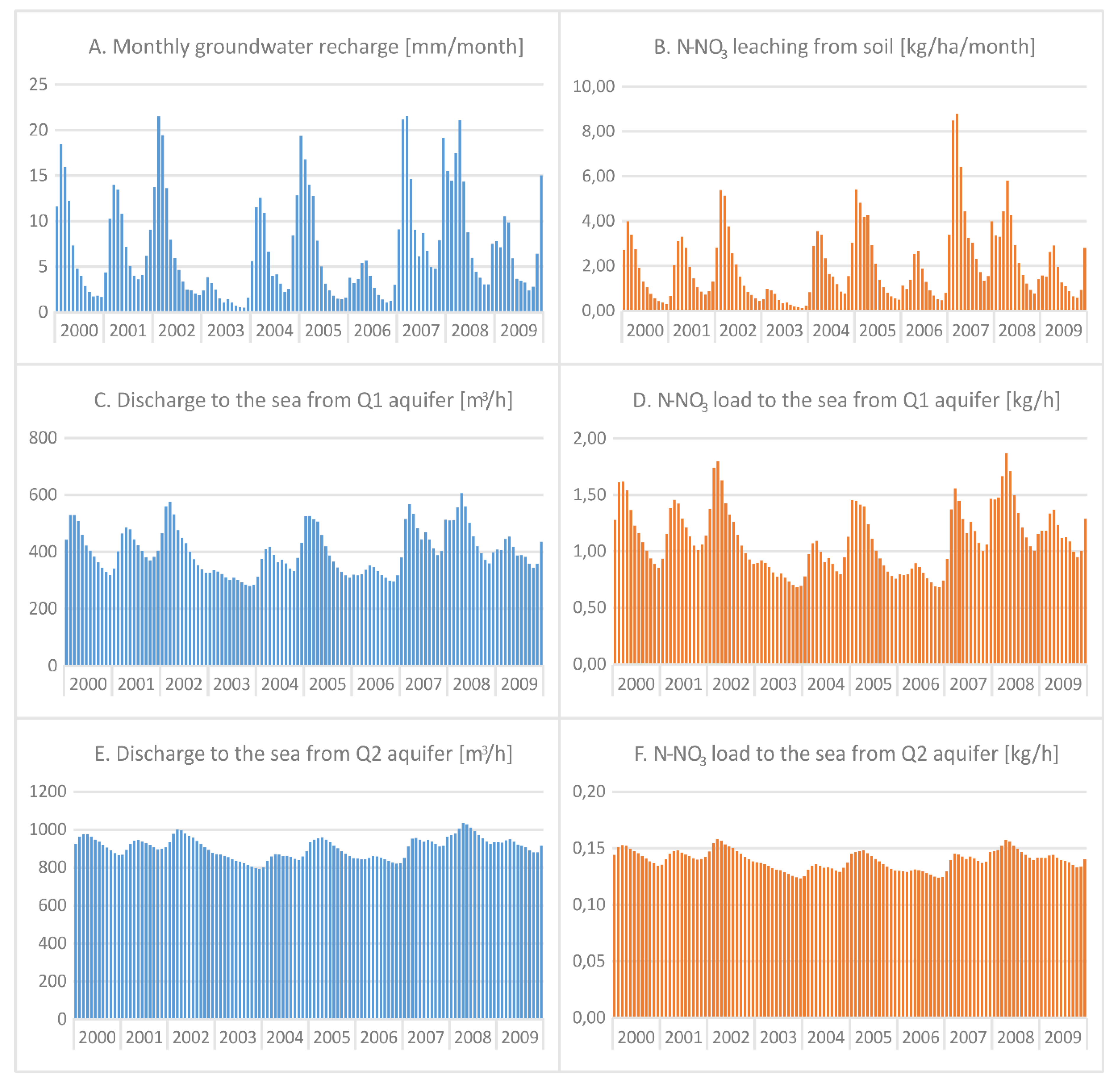
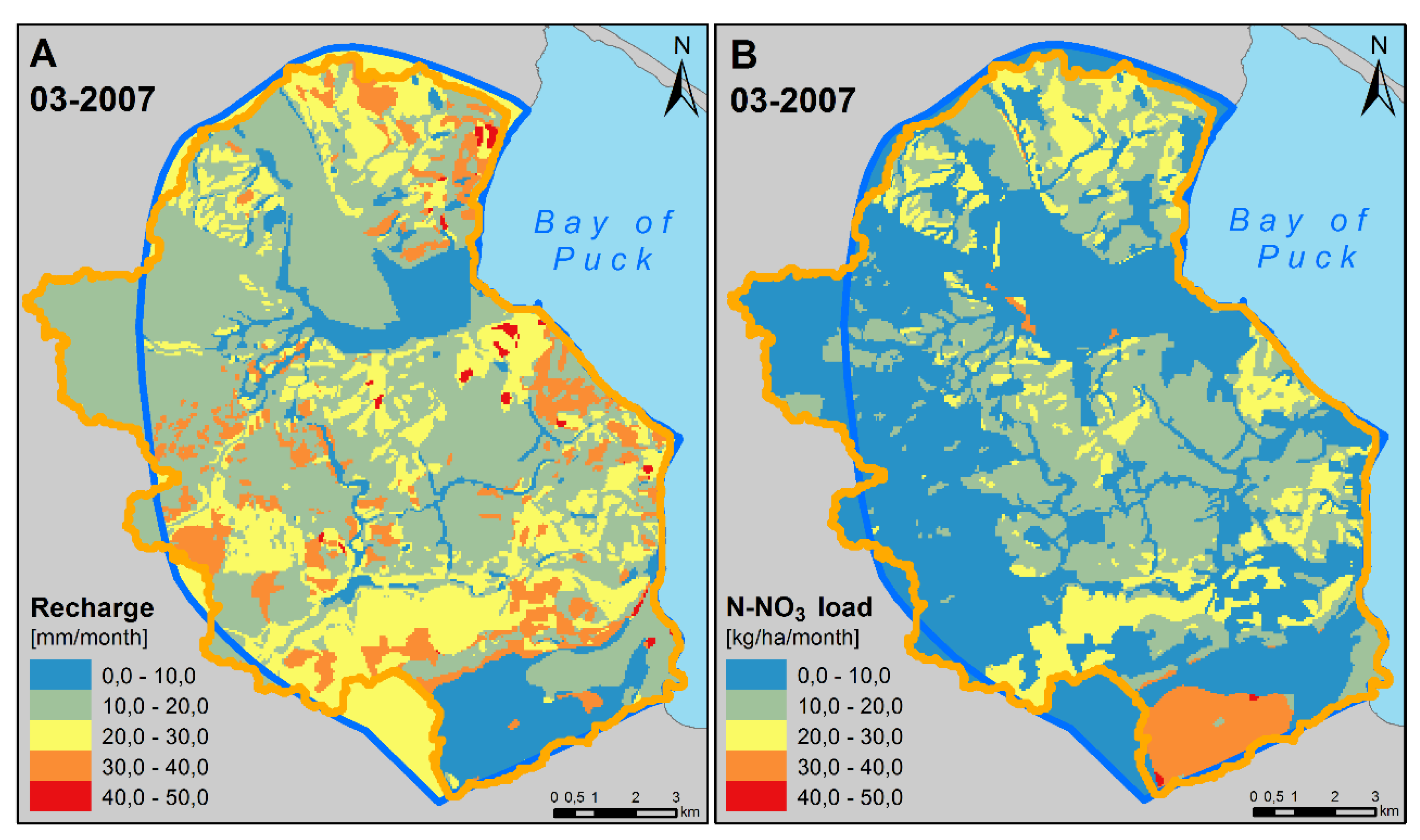
- Groundwater recharge, SGD, and the corresponding nitrate loads show a distinct time variable pattern, with maximum recharge rates and NO3 leaching in late winter/early spring.
- The average values of recharge and SGD fluxes are influenced more significantly by crop type grown on farmlands than by the changes in land use. The maximum relative difference between the 10 y average of SGD flux between different scenarios did not exceed 12%. In contrast, nitrate leaching from soil and nitrate transport via SGD shows a larger variability, strongly depending on crop type and land use.
- The lowest N-NO3 load in SGD occurred for the hypothetical scenario with all land converted to grassland, and it was three times smaller than the largest load, corresponding to converting all land to growing crops.
Author Contributions
Funding
Conflicts of Interest
References
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute: College Station, TX, USA, 2011. [Google Scholar]
- Harbaugh, A.W. MODFLOW-2005, the US Geological Survey Modular Ground-Water Model: The Ground-Water Flow Process; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2005; pp. A6–A16.
- Zheng, C.; Wang, P.P. MT3DMS: A Modular Three-Dimensional Multispecies Transport Model for Simulation of Advection, Dispersion, and Chemical Reactions of Contaminants in Groundwater Systems; Documentation and User’s Guide; Alabama University: Tuscaloosa, AL, USA, 1999. [Google Scholar]
- Perkins, S.P.; Sophocleous, M. Development of a comprehensive watershed model applied to study stream yield under drought conditions. Groundwater 1999, 37, 418–426. [Google Scholar] [CrossRef]
- Sophocleous, M.A.; Koelliker, J.K.; Govindaraju, R.S.; Birdie, T.; Ramireddygari, S.R.; Perkins, S.P. Integrated numerical modeling for basin-wide water management: The case of the Rattlesnake Creek basin in south-central Kansas. J. Hydrol. 1999, 214, 179–196. [Google Scholar] [CrossRef]
- Conan, C.; Bouraoui, F.; Turpin, N.; de Marsily, G.; Bidoglio, G. Modeling flow and nitrate fate at catchment scale in Brittany (France). J. Environ. Qual. 2003, 32, 2026–2032. [Google Scholar] [CrossRef] [PubMed]
- Galbiati, L.; Bouraoui, F.; Elorza, F.J.; Bidoglio, G. Modeling diffuse pollution loading into a Mediterranean lagoon: Development and application of an integrated surface–subsurface model tool. Ecol. Model. 2006, 193, 4–18. [Google Scholar] [CrossRef]
- Kim, N.W.; Chung, I.M.; Won, Y.S.; Arnold, J.G. Development and application of the integrated SWAT–MODFLOW model. J. Hydrol. 2008, 356, 1–16. [Google Scholar] [CrossRef]
- Chung, I.M.; Kim, N.W.; Lee, J.; Sophocleous, M. Assessing distributed groundwater recharge rate using integrated surface water-groundwater modelling: Application to Mihocheon watershed, South Korea. Hydrogeol. J. 2010, 18, 1253–1264. [Google Scholar] [CrossRef]
- Lin, H.T.; Ke, K.Y.; Tan, Y.C.; Wu, S.C.; Hsu, G.; Chen, P.C.; Fang, S.T. Estimating pumping rates and identifying potential recharge zones for groundwater management in multi-aquifers system. Water Resour. Manag. 2013, 27, 3293–3306. [Google Scholar] [CrossRef]
- Pisinaras, V.; Petalas, C.; Tsihrintzis, V.A.; Karatzas, G.P. Integrated modeling as a decision-aiding tool for groundwater management in a Mediterranean agricultural watershed. Hydrol. Process. 2013, 27, 1973–1987. [Google Scholar] [CrossRef]
- Ke, K.Y. Application of an integrated surface water-groundwater model to multi-aquifers modeling in Choushui River alluvial fan, Taiwan. Hydrol. Process. 2014, 28, 1409–1421. [Google Scholar] [CrossRef]
- Guzman, J.A.; Moriasi, D.N.; Gowda, P.H.; Steiner, J.L.; Starks, P.J.; Arnold, J.G.; Srinivasan, R. A model integration framework for linking SWAT and MODFLOW. Environ. Model. Softw. 2015, 73, 103–116. [Google Scholar] [CrossRef]
- Pulido-Velazquez, M.; Peña-Haro, S.; García-Prats, A.; Mocholi-Almudever, A.F.; Henríquez-Dole, L.; Macian-Sorribes, H.; Lopez-Nicolas, A. Integrated assessment of the impact of climate and land use changes on groundwater quantity and quality in the Mancha Oriental system (Spain). Hydrol. Earth Syst. Sci. 2015, 19, 1677–1693. [Google Scholar] [CrossRef]
- Bailey, R.T.; Wible, T.C.; Arabi, M.; Records, R.M.; Ditty, J. Assessing regional-scale spatio-temporal patterns of groundwater–surface water interactions using a coupled SWAT-MODFLOW model. Hydrol. Process. 2016, 30, 4420–4433. [Google Scholar] [CrossRef]
- Ehtiat, M.; Mousavi, S.J.; Vaghefi, S.A.; Ghaheri, A. Analysis of recharge conceptualization in inverse groundwater modelling. Hydrol. Sci. J. 2016, 61, 2789–2801. [Google Scholar] [CrossRef]
- Ehtiat, M.; Mousavi, S.J.; Srinivasan, R. Groundwater modeling under variable operating conditions using SWAT, MODFLOW and MT3DMS: A catchment scale approach to water resources management. Water Resour. Manag. 2018, 32, 1631–1649. [Google Scholar] [CrossRef]
- Aliyari, F.; Bailey, R.T.; Tasdighi, A.; Dozier, A.; Arabi, M.; Zeiler, K. Coupled SWAT-MODFLOW model for large-scale mixed agro-urban river basins. Environ. Model. Softw. 2019, 115, 200–210. [Google Scholar] [CrossRef]
- Chunn, D.; Faramarzi, M.; Smerdon, B.; Alessi, D.S. Application of an Integrated SWAT–MODFLOW Model to Evaluate Potential Impacts of Climate Change and Water Withdrawals on Groundwater–Surface Water Interactions in West-Central Alberta. Water 2019, 11, 110. [Google Scholar] [CrossRef]
- Gao, F.; Feng, G.; Han, M.; Dash, P.; Jenkins, J.; Liu, C. Assessment of Surface Water Resources in the Big Sunflower River Watershed Using Coupled SWAT–MODFLOW Model. Water 2019, 11, 528. [Google Scholar] [CrossRef]
- Semiromi, M.T.; Koch, M. Analysis of spatio-temporal variability of surface–groundwater interactions in the Gharehsoo river basin, Iran, using a coupled SWAT-MODFLOW model. Environ. Earth Sci. 2019, 78, 201. [Google Scholar] [CrossRef]
- Wei, X.; Bailey, R.T. Assessment of System Responses in Intensively Irrigated Stream–Aquifer Systems Using SWAT-MODFLOW. Water 2019, 11, 1576. [Google Scholar] [CrossRef]
- Wei, X.; Bailey, R.T.; Records, R.M.; Wible, T.C.; Arabi, M. Comprehensive simulation of nitrate transport in coupled surface-subsurface hydrologic systems using the linked SWAT-MODFLOW-RT3D model. Environ. Model. Softw. 2019, 122, 104242. [Google Scholar] [CrossRef]
- Welch, E.M.; Dulai, H.; El-Kadi, A.; Shuler, C. Submarine groundwater discharge and stream baseflow sustain pesticide and nutrient fluxes in Faga’alu Bay, American Samoa. Front. Environ. Sci. 2019, 7, 162. [Google Scholar] [CrossRef]
- Kim, G.; Swarzenski, P.W. Submarine groundwater discharge (SGD) and associated nutrient fluxes to the coastal ocean. In Carbon and Nutrient Fluxes in Continental Margins; Springer: Berlin/Heidelberg, Germany, 2010; pp. 529–538. [Google Scholar]
- Kotwicki, L.; Grzelak, K.; Czub, M.; Dellwig, O.; Gentz, T.; Szymczycha, B.; Böttcher, M.E. Submarine groundwater discharge to the Baltic coastal zone: Impacts on the meiofaunal community. J. Mar. Syst. 2014, 129, 118–126. [Google Scholar] [CrossRef]
- Lipka, M.; Böttcher, M.E.; Wu, Z.; Sültenfuß, J.; Jenner, A.K.; Westphal, J.; Dellwig, O.; Escher, P.; Schmiedinger, I.; Winde, V.; et al. Ferruginous groundwaters as a source of P, Fe, and DIC for coastal waters of the southern Baltic Sea:(Isotope) hydrobiogeochemistry and the role of an iron curtain. In E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2018; Volume 54, p. 00019. [Google Scholar]
- Kłostowska, Ż.; Szymczycha, B.; Lengier, M.; Zarzeczańska, D.; Dzierzbicka-Głowacka, L. Hydrogeochemistry and magnitude of SGD in the Bay of Puck, southern Baltic Sea. Oceanologia 2019. [Google Scholar] [CrossRef]
- Jiao, J.; Post, V. Coastal Hydrogeology; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Wojciechowska, E.; Nawrot, N.; Matej-Łukowicz, K.; Gajewska, M.; Obarska-Pempkowiak, H. Seasonal changes of the concentrations of mineral forms of nitrogen and phosphorus in watercourses in the agricultural catchment area (Bay of Puck, Baltic Sea, Poland). Water Supply 2019, 19, 986–994. [Google Scholar] [CrossRef]
- Wojciechowska, E.; Pietrzak, S.; Matej-Łukowicz, K.; Nawrot, N.; Zima, P.; Kalinowska, D.; Wielgat, P.; Obarska-Pempkowiak, H.; Gajewska, M.; Dembska, G.; et al. Nutrient loss from three small-size watersheds in the southern Baltic Sea in relation to agricultural practices and policy. J. Environ. Manag. 2019, 252, 109637. [Google Scholar] [CrossRef]
- Szymczycha, B.; Kłostowska, Ż.; Lengier, M.; Dzierzbicka-Głowacka, L. Significance of nutrient fluxes via submarine groundwater discharge in the Bay of Puck, southern Baltic Sea. Oceanologia 2020. [Google Scholar] [CrossRef]
- Dzierzbicka-Głowacka, L.; Janecki, M.; Dybowski, D.; Szymczycha, B.; Obarska-Pempkowiak, H.; Wojciechowska, E.; Zima, P.; Pietrzak, S.; Pazikowska-Sapota, G.; Jaworska-Szulc, B.; et al. A new approach for investigating the impact of pesticides and nutrient flux from agricultural holdings and land-use structures on the coastal waters of the Baltic Sea. Pol. J. Environ. Stud. 2019, 28, 2531–2539. [Google Scholar] [CrossRef]
- Dybowski, D.; Jakacki, J.; Janecki, M.; Nowicki, A.; Rak, D.; Dzierzbicka-Glowacka, L. High-Resolution Ecosystem Model of the Puck Bay (Southern Baltic Sea)—Hydrodynamic Component Evaluation. Water 2019, 11, 2057. [Google Scholar] [CrossRef]
- Piekarek-Jankowska, H. Zatoka Pucka jako obszar drenażu wód podziemnych (The Bay of Puck as A Groundwater Drainage Area); University of Gdańsk: Gdańsk, Poland, 1994; p. 104. (In Polish) [Google Scholar]
- Kryza, J.; Kryza, H. Analityczna i modelowa ocena bezpośredniego dopływu podziemnego do Bałtyku na terytorium Polski. Geologos 2006, 10, 153–165. [Google Scholar]
- Jaworska-Szulc, B. Groundwater flow modelling of multi-aquifer systems for regional resources evaluation: The Gdansk hydogeological system, Poland. Hydrogeol. J. 2009, 17, 1521–1542. [Google Scholar] [CrossRef]
- Piniewski, M.; Szcześniak, M.; Kardel, I.; Berezowski, T.; Okruszko, T.; Srinivasan, R.; Vikhamar Schuler, D.; Kundzewicz, Z.W. Hydrological modelling of the Vistula and Odra river basins using SWAT. Hydrol. Sci. J. 2017, 62, 1266–1289. [Google Scholar] [CrossRef]
- Thodsen, H.; Farkas, C.; Chormanski, J.; Trolle, D.; Blicher-Mathiesen, G.; Grant, R.; Engebretsen, A.; Kardel, I.; Andersen, H.E. Modelling nutrient load changes from fertilizer application scenarios in six catchments around the Baltic Sea. Agriculture 2017, 7, 41. [Google Scholar] [CrossRef]
- Tamm, O.; Maasikamäe, S.; Padari, A.; Tamm, T. Modelling the effects of land use and climate change on the water resources in the eastern Baltic Sea region using the SWAT model. Catena 2018, 167, 78–89. [Google Scholar] [CrossRef]
- Trolle, D.; Nielsen, A.; Andersen, H.E.; Thodsen, H.; Olesen, J.E.; Børgesen, C.D.; Refsgaard, J.C.; Sonnenborg, T.O.; Karlsson, I.B.; Christensen, J.P.; et al. Effects of changes in land use and climate on aquatic ecosystems: Coupling of models and decomposition of uncertainties. Sci. Total Environ. 2019, 657, 627–633. [Google Scholar] [CrossRef]
- Olesen, J.E.; Børgesen, C.D.; Hashemi, F.; Jabloun, M.; Bar-Michalczyk, D.; Wachniew, P.; Zurek, A.J.; Bartosova, A.; Bosshard, T.; Hansen, A.L.; et al. Nitrate leaching losses from two Baltic Sea catchments under scenarios of changes in land use, land management and climate. Ambio 2019, 48, 1252–1263. [Google Scholar] [CrossRef]
- Terskii, P.; Kuleshov, A.; Chalov, S.; Terskaia, A.; Pluntke, T.; Karthe, D. Assessment of Water Balance for Russian Subcatchment of Western Dvina River Using SWAT Model. Front. Earth Sci. 2019, 7, 241. [Google Scholar] [CrossRef]
- Marcinkowski, P.; Piniewski, M.; Kardel, I.; Gielczewski, M.; Okruszko, T. Modelling of discharge, nitrate and phosphate loads from the Reda catchment to the Puck Lagoon using SWAT. Annals of Warsaw University of Life Sciences-SGGW. Land Reclam. 2013, 45, 2. [Google Scholar]
- Piniewski, M.; Kardel, I.; Giełczewski, M.; Marcinkowski, P.; Okruszko, T. Climate change and agricultural development: Adapting Polish agriculture to reduce future nutrient loads in a coastal watershed. Ambio 2014, 43, 644–660. [Google Scholar] [CrossRef]
- Jereczek-Korzeniowska, K.; Jegliński, W. The Late Glacial and holocene development of valley network in the puck morainic plateau. Geologija 2011, 53, 10–14. [Google Scholar] [CrossRef][Green Version]
- Dzierzbicka-Głowacka, L.; Pietrzak, S.; Dybowski, D.; Białoskórski, M.; Marcinkowski, T.; Rossa, L.; Urbaniak, M.; Majewska, Z.; Juszkowska, D.; Nawalany, P.; et al. Impact of agricultural farms on the environment of the Puck Commune: Integrated agriculture calculator—CalcGosPuck. PeerJ 2019, 7, e6478. [Google Scholar]
- Zawadzki, S. Gleboznawstwo [Soil Science]; Państwowe Wydawnictwa Rolnicze i Leśne: Warszawa, Poland, 1999. [Google Scholar]
- Duda, R.; Winid, B.; Zdechlik, R.; Stępień, M. Metodyka Wyboru Optymalnej Metody Wyznaczania Zasięgu Stref Ochronnych Ujęć Zwykłych Wód Podziemnych z Uwzględnieniem Warunków Hydrogeologicznych Obszaru RZGW w Krakowie [Methodology of Selecting the Optimal Method of the Wellhead Protection Area Delineation Taking into Account the Hydrogeological Conditions in Areas Administered by the Regional Water Management Board in Cracow]; Akademia Górniczo-Hutnicza: Kraków, Poland, 2013; ISBN 9788388927294. (In Polish) [Google Scholar]
- Jaworska-Szulc, B. Formowanie się zasobów wód podziemnych w młodoglacjalnym, wielopoziomowym systemie wodonośnym na przykładzie Pojezierza Kaszubskiego. [Formation of Groundwater Resources in the Young Glacial Multiaquifer System, of the Kashubian Lake District]; GUT (Gdańsk University of Technology) Publishing House Monograph: Gdańsk, Poland, 2015. [Google Scholar]
- Czyżyk, F.; Steinhoff-Wrześniewska, A. Zróżnicowanie ewapotranspiracji niektórych gatunków roślin uprawnych w warunkach różnego nawożenia [Variability of evapotranspiration of some crop species under different fertilizing schemes]. Woda-Środowisko-Obszary Wiejskie 2017, 17, s25–s36. [Google Scholar]
- Bogdanowicz, R.; Cysewski, A. Przestrzenna i czasowa zmienność transportu zanieczyszczeń w wybranych ciekach Nadmorskiego Parku Krajobrazowego [Spatial and temporal variability of pollutants transport in selected streams of Nadmorski Park Krajobrazowy]. In Wody na obszarach chronionych; Pociask-Karteczka, J., Partyka, J., Eds.; Instytut Geografii i Gospodarki Przestrzennej UJ, Ojcowski Park Narodowy, Komisja Hydrologiczna PTG: Kraków, Poland, 2008; pp. 91–100. [Google Scholar]
- Stachy, J. Atlas hydrologiczny Polski [Hydrological atlas of Poland] Volume 1; IMGW, Wydawnictwa Geologiczne: Warszawa, Poland, 1987; T 1. [Google Scholar]
- Orzeł, S.; Forgiel, M.; Ochał, W.; Socha, J. Nadziemna biomasa i roczna produkcja drzewostanów sosnowych Puszczy Niepołomickiej [Above-ground biomass and yearly production of pine stands in Puszcza Niepołomicka]. Sylwan 2006, 150, 16–32. [Google Scholar]
- Wejherowo Forest Administration (Wejherowo, Poland). Personal communication.
- Jadczyszyn, T.; Kowalczyk, J.; Lipiński, W. Zalecenia nawozowe dla roślin uprawy polowej i trwałych użytków zielonych [Recommendations for fertilizing crops and perennial grasslands]. In Materiały szkoleniowe; Nr 95; IUNG-PIB: Puławy, Poland, 2010; p. 24. [Google Scholar]
- Niswonger, R.G.; Panday, S.; Ibaraki, M. MODFLOW-NWT, a Newton formulation for MODFLOW-2005. Us Geol. Surv. Tech. Methods 2011, 6, 44. [Google Scholar]
- Aquaveo.com. Available online: https://www.aquaveo.com/software/gms-groundwater-modeling-system-introduction (accessed on 6 April 2020).
- Winston, R.B. ModelMuse: A Graphical User Interface for MODFLOW-2005 and PHAST; US Geological Survey: Reston, VA, USA, 2009; p. 52.
- Bakker, M.; Post, V.; Langevin, C.D.; Hughes, J.D.; White, J.T.; Starn, J.J.; Fienen, M.N. Scripting MODFLOW model development using Python and FloPy. Groundwater 2016, 54, 733–739. [Google Scholar] [CrossRef]
- Papadopulos, S.S.; Larson, S.P. Aquifer storage of heated water: II. Numerical simulation of field results. Groundwater 1978, 16, 242–248. [Google Scholar] [CrossRef]
- Sykes, J.F.; Pahawa, S.B.; Ward, D.S.; Lantz, D.S. The Validation of SWENT, a Geosphere Transport Model; W: Scientific Computing, red. R. Stapleman i in; IMAES/North Holland: Amsterdam, The Netherlands, 1983; pp. 351–361. [Google Scholar]
- Molenat, J.; Gascuel-Odoux, C.H. Modelling flow and nitrate transport in groundwater for the prediction of water travel times and of consequences of land use evolution on water quality. Hydrol. Process. 2002, 16, 479–492. [Google Scholar] [CrossRef]
- Almasri, M.N.; Kaluarachchi, J.J. Modeling nitrate contamination of groundwater in agricultural watersheds. J. Hydrol. 2007, 343, 211–229. [Google Scholar] [CrossRef]
- Florida Onsite Sewage Nitrogen Reduction Strategies Study. Literature Review of Nitrogen Fate and Transport Modeling. TaskD.2. Final Report; Florida Department of Health, Division of Environmental Health: Tallahassee, FL, USA, 2010. [Google Scholar]
- Psarropoulou, E.T.; Karatzas, G.P. Pollution of nitrates–contaminant transport in heterogeneous porous media: A case study of the coastal aquifer of Corinth, Greece. Glob. Nest J. 2014, 16, 9–23. [Google Scholar]
- Lidzbarski, M. Identyfikacja systemu krążenia wód podziemnych w procesie ustalania zasobów odnawialnych na przykładzie zlewni Redy i Zagórskiej Strugi. [Identification of groundwater circulation system during assessment renewable resources for example of the Reda and Zagórska Struga catchment.]. Prz. Geol. 2015, 63, 893–900. [Google Scholar]
- Ilnicki, P. Polskie Rolnictwo a Ochrona Środowiska [Polish agriculture and environmental protection]; Wydawnictwo Akademia Rolnicza Poznań: Poznań, Poland, 2004. [Google Scholar]
- Potrykus, D.; Gumuła-Kawęcka, A.; Jaworska-Szulc, B.; Pruszkowska-Caceres, M.; Szymkiewicz, A. Assessing groundwater vulnerability to pollution in the Puck region (denudation moraine upland) using vertical seepage method. E3S Web. Conf. 2018, 44, 00147. [Google Scholar] [CrossRef]
- Szymkiewicz, A.; Gumuła-Kawęcka, A.; Potrykus, D.; Jaworska-Szulc, B.; Pruszkowska-Caceres, M.; Gorczewska-Langner, W. Estimation of conservative contaminant travel time through vadose zone based on transient and steady flow approaches. Water 2018, 10, 1417. [Google Scholar] [CrossRef]
- Szymkiewicz, A.; Savard, J.; Jaworska-Szulc, B. Numerical Analysis of Recharge Rates and Contaminant Travel Time in Layered Unsaturated Soils. Water 2019, 11, 545. [Google Scholar] [CrossRef]

| Output Type | Unit | Model Values | Reference Values |
|---|---|---|---|
| Groundwater recharge (a) | mm/y | 36 to 146 (d) | 19 to 186 [49,50] |
| Evapotranspiration, including REVAP (a) | mm/y | 459 (c) | 450 to 495 [51] |
| Total runoff (b) | mm/y | 162 (c) | 47 to 268 [52] |
| Surface runoff / total runoff ratio (b) | - | 0.55 (c) | 0.5 [53] |
| Forest biomass production (a) | t/ha/y | 6.1 to 8.5 (d) | 6.5 to 7.5 [54,55] |
| Yield: Winter wheat (b) | t/ha/y | 5.9 to 7.3 (d) | 5.5 [47] |
| Yield: Canola (b) | t/ha/y | 2.6 to 3.4 (d) | 3.4 [47] |
| Yield: Silage corn (b) | t/ha/y | 9.2 to 10.3 (d) | 13.5 [47] |
| Yield: Hay (b) | t/ha/y | 4.7 to 7.0 (d) | 4.0 to 10.0 [56] |
| Layer No. | Type | Hydraulic Conductivity [m/s] | |
|---|---|---|---|
| MIN | MAX | ||
| 1 | aquifer (Qp) | 5.56 × 10−5 | 1.39 × 10−4 |
| 2 | aquitard | 1.25 × 10−9 | 2.50 × 10−8 |
| 3 | aquifer (Q1) | 1.94 × 10−5 | 4.72 × 10−4 |
| 4 | aquitard | 7.78 × 10−9 | 1.94 × 10−8 |
| 5 | aquifer (Q2) | 8.33 × 10−5 | 5.56 × 10−4 |
| 6 | aquitard | 7.78 × 10−9 | 7.78 × 10−9 |
| Scenario | Recharge [mm/y] | N-NO3 Leaching from Soil [kg/ha/y] | Discharge to Puck Bay [m3/h] | N-NO3 Load to Puck Bay [kg/h] | ||
|---|---|---|---|---|---|---|
| Q1 | Q2 | Q1 | Q2 | |||
| S1 (baseline) | 73 | 19.7 | 386 | 875 | 0.95 | 0.10 |
| S2 (winter wheat) | 62 | 7.4 | 367 | 839 | 0.62 | 0.03 |
| S3 (silage corn | 84 | 23.9 | 403 | 906 | 1.12 | 0.14 |
| S4 (canola) | 75 | 30.5 | 389 | 881 | 1.22 | 0.15 |
| S5 (summer cereals) | 73 | 12.7 | 384 | 872 | 0.79 | 0.07 |
| S6 (potatoes) | 90 | 26.0 | 414 | 927 | 1.21 | 0.17 |
| S7 (peas) | 92 | 19.5 | 417 | 933 | 1.02 | 0.12 |
| S8 (only farmland) | 79 | 33.9 | 391 | 881 | 1.75 | 0.14 |
| S9 (only grassland) | 85 | 3.4 | 398 | 897 | 0.59 | 0.03 |
| S10 (only forest) | 71 | 14.7 | 379 | 858 | 1.19 | 0.04 |
| Layer | N-NO3 in SGD Flux in Numerical Simulations [mg/dm3] | N-NO3 Measured in Groundwater in Coastal Area [mg/dm3] |
|---|---|---|
| Upper aquifer (Q1) | 1.48–5.03 | <0.02–20.78 |
| Lower aquifer (Q2) | 0.03–0.38 | <0.02–0.23 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szymkiewicz, A.; Potrykus, D.; Jaworska-Szulc, B.; Gumuła-Kawęcka, A.; Pruszkowska-Caceres, M.; Dzierzbicka-Głowacka, L. Evaluation of the Influence of Farming Practices and Land Use on Groundwater Resources in a Coastal Multi-Aquifer System in Puck Region (Northern Poland). Water 2020, 12, 1042. https://doi.org/10.3390/w12041042
Szymkiewicz A, Potrykus D, Jaworska-Szulc B, Gumuła-Kawęcka A, Pruszkowska-Caceres M, Dzierzbicka-Głowacka L. Evaluation of the Influence of Farming Practices and Land Use on Groundwater Resources in a Coastal Multi-Aquifer System in Puck Region (Northern Poland). Water. 2020; 12(4):1042. https://doi.org/10.3390/w12041042
Chicago/Turabian StyleSzymkiewicz, Adam, Dawid Potrykus, Beata Jaworska-Szulc, Anna Gumuła-Kawęcka, Małgorzata Pruszkowska-Caceres, and Lidia Dzierzbicka-Głowacka. 2020. "Evaluation of the Influence of Farming Practices and Land Use on Groundwater Resources in a Coastal Multi-Aquifer System in Puck Region (Northern Poland)" Water 12, no. 4: 1042. https://doi.org/10.3390/w12041042
APA StyleSzymkiewicz, A., Potrykus, D., Jaworska-Szulc, B., Gumuła-Kawęcka, A., Pruszkowska-Caceres, M., & Dzierzbicka-Głowacka, L. (2020). Evaluation of the Influence of Farming Practices and Land Use on Groundwater Resources in a Coastal Multi-Aquifer System in Puck Region (Northern Poland). Water, 12(4), 1042. https://doi.org/10.3390/w12041042





