Groundwater Circulation in Fractured and Karstic Aquifers of the Umbria-Marche Apennine

Abstract

The Umbria-Marche Apennine has a large number of springs that drain water stored in carbonate formations. Spring groundwater constitutes a crucial freshwater resource for many countries, regions, and cities around the world. This study aimed to understand the hydrological mechanisms behind groundwater circulation and their relationship to the structural and stratigraphic settings of specific aquifers. Recession analysis and time series analysis were applied to the daily discharge of six springs monitored over eight years. Both analyses indicated the presence of two types of aquifers: aquifer with unimodal behavior and aquifer with bimodal behavior. The first are characterized by two hydrodynamic sub-regimes, in which fracture networks control the baseflow and conduit networks control the quickflow. In contrast, other springs present only one hydrodynamic sub-regime related to fracture network drainage. Time series analysis confirms the results of recession analysis, showing a large memory effect and a large response time, implying the dominance of the baseflow sub-regime. These results indicate that the Maiolica Formation is characterized by a high degree of fracturation and slight karstification, which control infiltration and percolation, whereas the Calcare Massiccio Formation regulates groundwater circulation in the deeper zones of the aquifer, characterized by a high degree of karstification through moderately developed conduit networks.

1. Introduction

To construct a distributive model of groundwater circulation in a carbonate aquifer, the definition of realistic hydraulic and geometric parameters is essential [1,2,3]. Carbonate aquifers differ from other types of hydrogeological systems in their complex behavior, stemming from strong spatial heterogeneity and temporal variation [4]. This heterogeneity is linked to the hydraulic properties of the through media, such as low-permeability of rock matrix or high permeability of conduit networks, especially when karstified. However, in most cases, spring discharge time series data can be obtained and used to perform an analysis of hydrograph recession curves, which are an often-used method in the interpretation of the characteristics and flow attributes of an aquifer [5,6,7].

Some hydrograph analytical techniques are based on the analysis of slow hydrograph recession segments using the Maillet and Boussinesq equations [8,9]. Therein, deviations from the calculated exponential trends may indicate the presence of hydraulic anisotropies and, therefore, highlight the close relationship between spring hydrographs and hydro-structural geometry [10,11,12,13].

Other authors proposed characterizing the recession process by employing different mathematical functions. Drogue [14] described the whole recession process by using one single hyperbolic formula, where the recession coefficient, α, is not equivalent to the coefficient used by Maillet [9]. In contrast, Mangin [10] distinguished two processes that influence recession curves: discharge from the non-saturated zone with a non-linear flood recession and discharge from the saturated zone with a linear baseflow recession. Kovács et al. [12] showed that the recession coefficient allows for obtaining important information about aquifer hydraulic parameters and conduit network characteristics. One main advantage of recession curve analysis is that a set of empirical, quantitative parameters attributed to drainage mechanisms can be calculated [15].

Analysis of individual recession periods sometimes generates inconsistences related to the complexity of groundwater circulation and the processes acting on the system [16]. Therefore, a master recession curve (MRC) is commonly used for simultaneously analyzing a set of hydrograph recessions at a particular catchment [17,18,19,20,21,22].

Malík and Vojtková [23] performed a recession curve analysis to evaluate the karstification degree and the hydrodynamic behavior of an aquifer. With given recession coefficients and initial discharge values, both runoff and partial runoff segments (sub-regimes) can be fully described. In karst hydrogeology, the term “sub-regime” refers to the changing conditions of a groundwater system, its characteristic behavior, or the controlling of natural processes, which usually occur in a regular pattern [24].

Apart from recession analysis, univariate and bivariate analyses can also be performed on spring hydrographs. Valuable indirect information regarding karst systems can be obtained by performing a time series analysis [25]. Mangin [26] developed a specific methodology for studying the input-output relationships in karst aquifers, as well as for performing auto-correlation (univariate analysis) and cross-correlation (bivariate analysis). This methodology was based on a systemic approach and was applied and elaborated further by several authors [27,28,29,30]. In karst hydrogeology, auto-correlation functions (ACF) of spring discharge (Q) are generally used to assess the interdependence of spring discharge and evaluate the so-called “memory effect” [31], whereas the cross-correlation function (CCF) is widely used to analyze the linear relationship between input (rainfall or snowmelt, P) and output (Q).

A hydrogeological study of aquifer spring provides key information for the sustainable management of water resources exploitable by different end-users (e.g., hydrogeologists, hydraulic engineers, well drillers, environmental decision-makers).

The present work aims to characterize the behavior and groundwater circulation of the Umbria-Marche carbonate aquifers (northern Apennines) on a regional scale. MRCs were constructed and used (i) to define the mechanisms controlling flow path distribution within carbonate hydro-structures, (ii) to discretize the possible sub-regimes, and (iii) to define the karstification degree of each carbonate complex analyzed. The statistical methods applied to the time series gave information about the characteristics of the carbonate systems under study. Particular emphasis was given to the hydro-geological interpretation of the functions and their relationships with the structural setting in this portion of the Apennine ridge.

2. Materials and Methods

2.1. Study Area

The Apenninic chain of Central Italy is a mountain range characterized by the presence of extensive outcrops of thick Mesozoic limestone sequences. The study area includes a large sector that starts at the M. Cucco anticline and terminates at the M. Pennino anticline. The outcropping geological formations are mainly composed of calcareous and marly lithotypes (from Triassic to Cretaceous in age) belonging to the Umbria-Marche Succession [32,33]. From a structural point of view, the Umbria-Marche Apennines can be considered a typical thin-skinned thrust belt in which a hierarchy of multiple, superimposed detachments occurred over a main, basal detachment at the level of Triassic evaporites that act as an aquiclude. The Apenninic arch has a vergency towards ENE [34,35] and is characterized by SW dipping thrust and by fault systems with a N-S and E-W strike.

The evaporitic level is overlaid by the Mesozoic carbonatic sequence consisting of three superimposed aquifers of different permeabilities controlled mainly by fissures, joints, and karst conduits (see the hydrogeological map in Figure 1) [36,37,38,39,40,41]. Starting from the bottom, these aquifers are the basal aquifer of the Massiccio Complex, the middle aquifer of Maiolica Complex and the upper aquifer of the Scaglia Complex. The Calcare Massiccio aquifer, with a thickness ranging between 700 and 900 m, represents the most important hydrogeological complex in the Umbria-Marche limestone ridge. It is characterized by a regional flow through highly-developed fissures and karst conduits. The Maiolica aquifer is separated from the basal aquifer by a sequence (from 100 to 350 m thick) of Upper Jurassic and calcareous marls (Calcari ad Aptici, Diasprini, Posidonia, Rosso Ammonitico Fms.) that act as an aquiclude. This sequence can be substituted locally by the very thin (20–100 m) Bugarone Calcareous Fm., which transforms it into an aquitard from a hydrological point of view. The Maiolica Complex is rather thick (200–400 m) and is constituted of more limited karstification but a high degree of fracturation. This aquifer is overlain by the Marne a Fucoidi Fm., a low permeability formation that acts as a regional aquiclude [36].

Finally, the Marne a Fucoidi Fm. is overlain by the Scaglia aquifer complex, which consists of alternating limestone and marly limestone layers with chert nodules and ribbons [16]. This complex is characterized by a high fracturation degree and a significant thickness (200–400 m), which affords it high storage capacity of infiltration water. Above, the aquifer is capped by a low permeability clayey-marly-calcareous sequence (Scaglia Variegata, Scaglia Cinerea, Bisciaro and Schlier Fms), usually enclosing an independent aquifer [42]. Eighty percent of the groundwater resource of the Umbria-Marche hydrogeological domain surfaces at liner springs [36], i.e., when a stream or river is directly fed by groundwater of saturated hydrogeological system.

The outcropping area of hydrogeological complexes playing an active role in groundwater recharge, thanks to their high capability of infiltration [43]. The extension of recharge area of each spring has been defined on lithological and structural geological data and compared with the literature data [44,45,46,47,48]. Recharge area of Scirca spring has been localized using multi-tracer tests from the karstic conduits [44] and correspond to specific lithological and geological structures [46]. The Vaccara, Boschetto, and Capo d’Acqua recharge areas have been calculated in the water balance of the Mountains of Gualdo [47]. Finally, the recharge area of the Bagnara spring corresponds to the outcrop of the core structure; this interpretation seems to be confirmed by the hydrochemical characteristics of the water (calcium bicarbonate with few increases of sulphates), which would indicate a fed due to the deep aquifer of Mt Pennino [48].

The area under study, about 220 km², includes the following main reliefs: Mt. Cucco (1566 m a.s.l.), Mt. Maggio (1362 m a.s.l.), Mt. Serrasanta (1423 m a.s.l.), Mt. Penna (1432 m a.s.l.), Mt. Burella (1095 m a.s.l.), and Mt. Pennino (1572 m a.s.l.). Each relief represents a distinct hydrostructure with internal aquifer systems connected to one or more springs in their recharge areas (

Table 1. General characteristics of the carbonate complexes and their related catchment areas (geographic coordinates are expressed in WGS84 UTM Zone 33N).

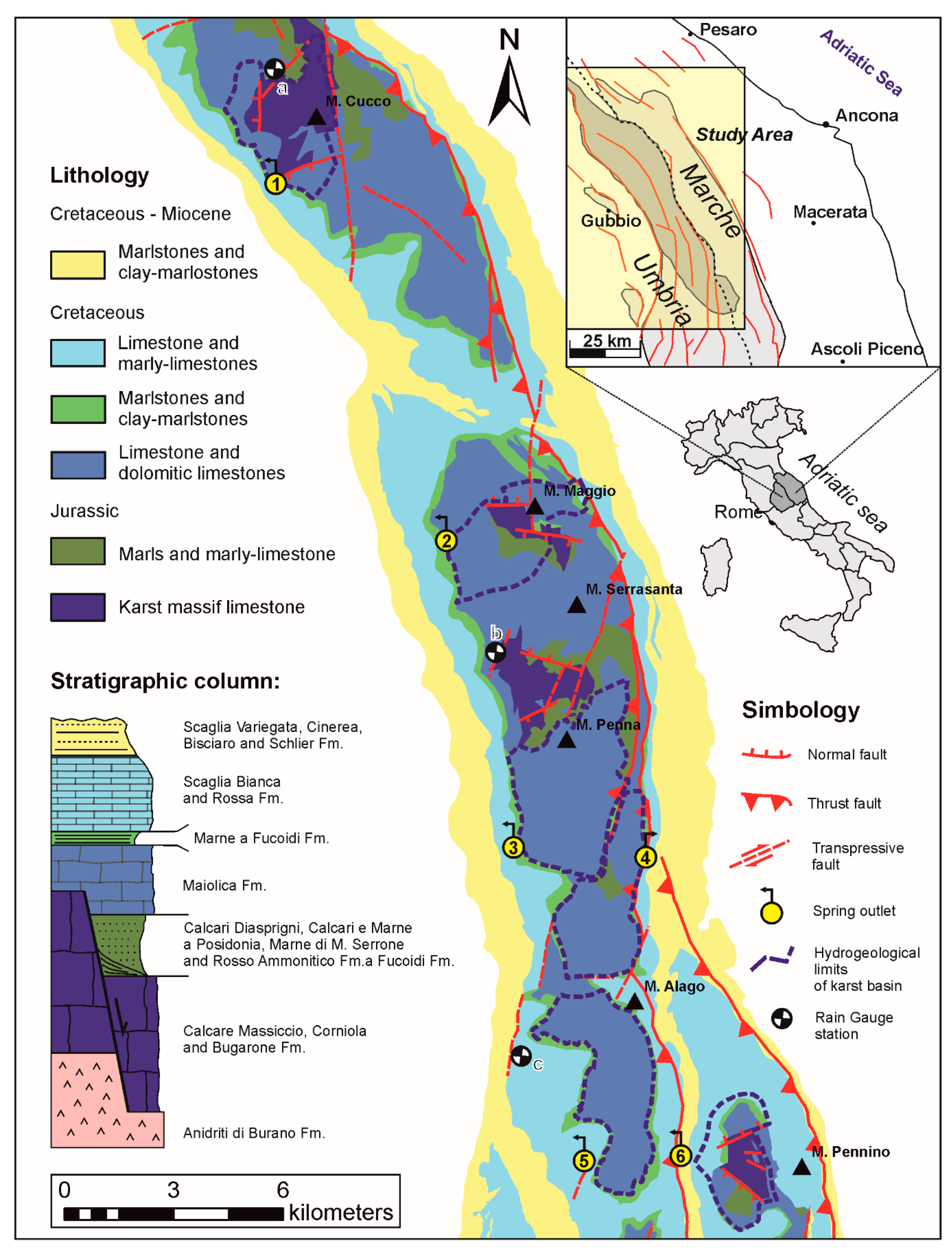
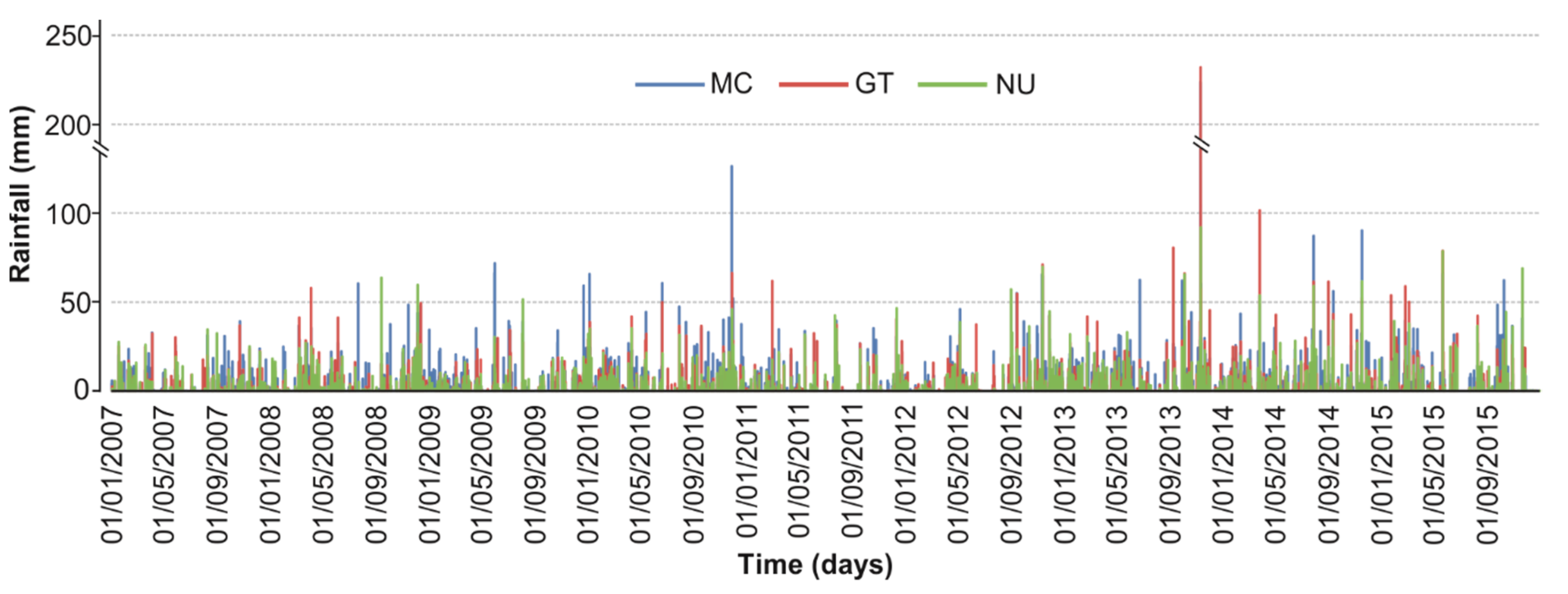
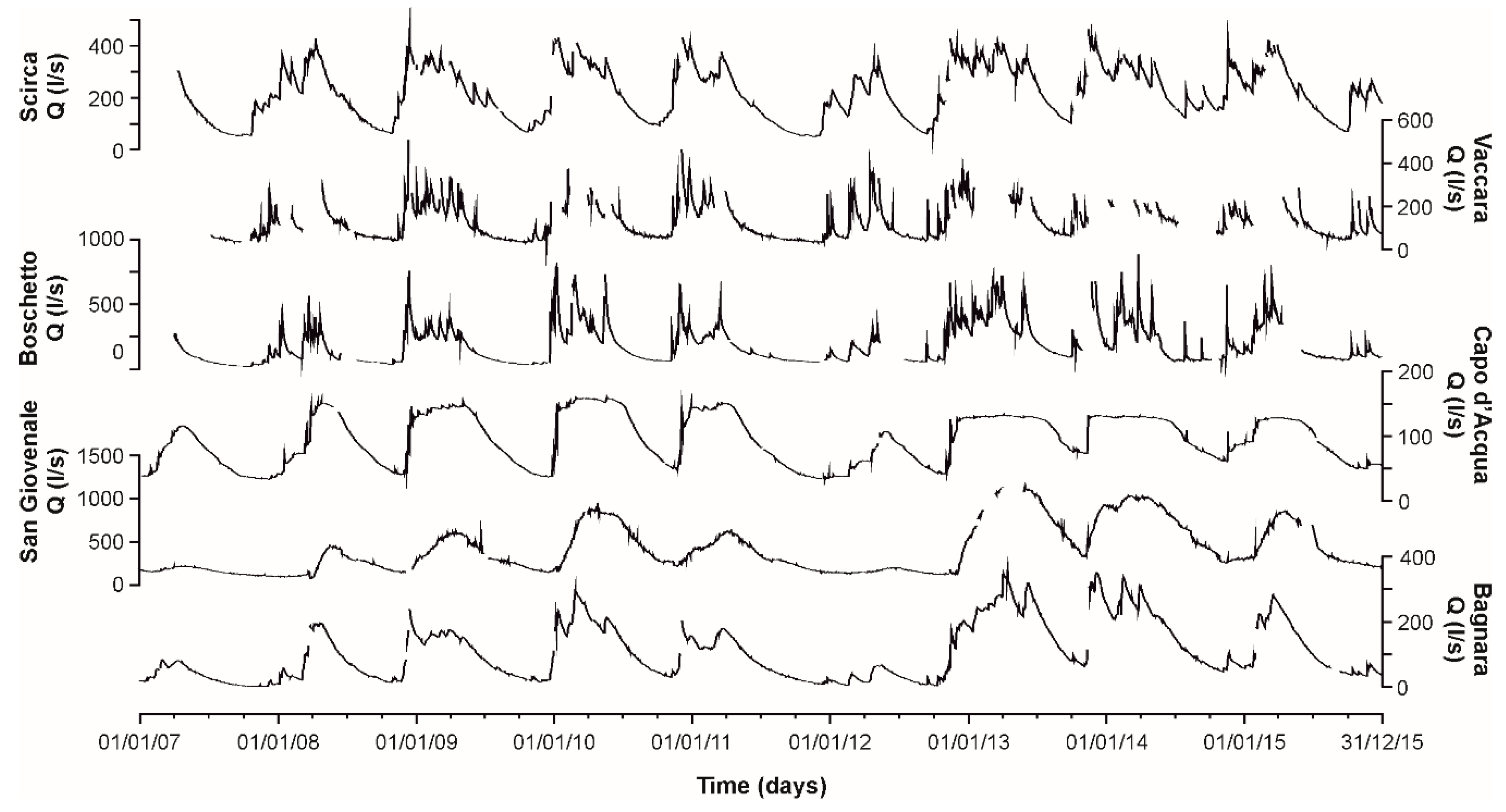
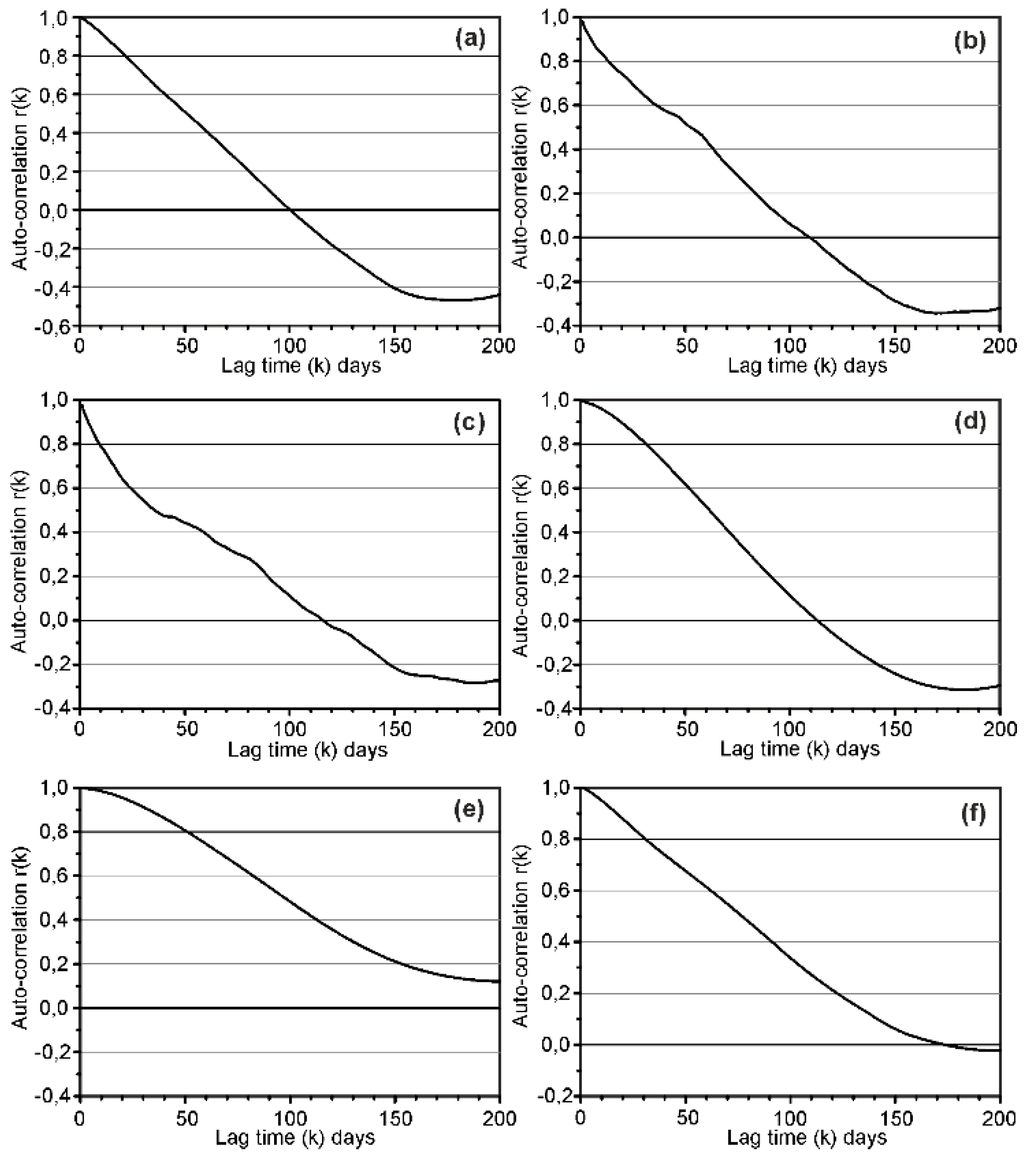
Hydro- Structures	Spring	Latitude	Longitude	Spring Altitude (m a.s.l.)	Recharge Area (km2)
Mt Cucco	Scirca	323,040.1821	4,774,571.7434	575	8.0
Mt Maggio	Vaccara	325,711.2678	4,774,969.1254	468	6.2
Mt Penna	Boschetto	324,530.5164	4,782,340.2809	538	11.5
Mt Penna	Capo d’Acqua	316,236.3956	4,802,705.2176	570	7.4
Mt Burella	San Giovenale	301,037.8923	4,823,140.7066	480	10.5
Mt Pennino	Bagnara	321,608.1134	4,783,863.2012	630	4.9

).

2.2. Data Acquisition

The rainfall data (mm) has been collected by automated rain gauges provided by the Hydrographic Service of Umbria Region; in particular, only three rain gauge stations located within the study area were considered (

Table 2. Location and characteristics of rain gauge station (geographic coordinate system is expressed in WGS84 UTM Zone 33).

Rain Gauge Station	Gauge Station Code	Latitude	Longitude	Monitored Period	Station Altitude (m a.s.l.)
Mt Cucco	MT-13015	316,280.8388	4,805,532.5274	2007–2015	1116
Gualdo Tadino	GT-27422	321,232.2980	4,789,176.7740	2007–2015	563
Nocera Umbra	NU-12907	320,698.8825	4,775,721.4408	2007–2015	542

) and the data were collected over eight years (from 01 January 2007 to 31 December 2015). Snowfall was recorded by only the MC station (located at 1116 m a.s.l.); therefore, the available dataset was not enough to cover the entire study area.

The UM area has a typical subcontinental climate characterized by a dry and warm summer and a wet period during autumn, winter, and spring. The monthly rainfall reaches a maximum during November and a minimum in July and August. In the more elevated zones (above 1000 m a.s.l.), the precipitation can present as snow during winter (mainly in January–February), with a thickness of a few decimeters, which can have a significant effect on groundwater aquifer recharge (Figure 2).

The discharge of six carbonate springs (Scirca, Vaccara, Boschetto, Capo d’Acqua, San Giovenale, and Bagnara) of the Umbria-Marche Apennines monitored by ARPA Umbria (www.arpa.umbria.it), with an acquisition time interval of one day, was analyzed. All springs treated were captured for potable purposes and were measured by eight channel electromagnetic and ultrasound systems. The monitoring systems recorded the minimum, mean, and maximum value each hour, and the dataset was computed at the end of the day and transmitted as daily mean. Figure 3 shows a subset of about eight years of the available data. Due to a lack of continuity in data recording, some gaps are present in the time series. The statistical analyses of dataset quality are presented in

Table 3. General characteristics of the time-series of the analyzed aquifer springs.

Spring	Monitored Period	No. of All Data	No. Miss Data	Time-Series Lag (%)
Scirca	2007–2015	3186	107	3.4
Vaccara	2007–2015	3097	754	24.3
Boschetto	2007–2015	3194	246	7.7
Capo d’Acqua	2007–2015	3232	55	1.7
San Giovenale	2007–2015	2107	180	5.8
Bagnara	2007–2015	3240	47	1.5

.

2.3. Recession Analysis

Recession analysis focuses on the recession curve, which is the portion of the hydrograph immediately following a stream peak (and rainfall event), when flow diminishes. In this study, the Maillet exponential equation was used (Equation (1)) because it generates good fits for analyzing hydrograph recession curves and accurately describes recession over long time periods [12,13,49]:

$$Q_t=Q_0\times e^{-{\alpha }_{i}t}$$

(1)

where Q_t is the discharge at time t and Q₀ is the discharge at time t = 0. Specifically, the modified Maillet equation was used, which can be expressed by a sum of several exponential components that represent the presence of possible sub-regimes [13,18,50,51,52]:

$$Q_t={{\displaystyle \sum }}_{i=1}^n{Q}_{0i}\times e^{-{\alpha }_{i}t}$$

(2)

where i represents the media i in the aquifer, Q_0i represents the discharge of media i at t = 0, and n represents the number of sub-regimes or flow components. A karst aquifer can always be divided into different sub-regimes based on the different hydraulic conductivities of the media that comprise it [52,53,54]. Therefore, the modified Maillet equation can be written as:

$$Q_t=Q_q\times e^{-{\alpha }_{q}t}+Q_b\times e^{-{\alpha }_{b}t}$$

(3)

where Q_q and Q_b are the initial discharges, and α_q and α_b are the recession coefficients of the quickflow and baseflow, respectively.

Analyzing the hydrographs of each aquifer system (Figure 3) has shown that the recession curves do not exhibit the same trends within the time series analyzed, making it impossible to use a single interpolating curve to characterize all aquifer systems. Therefore, a procedure for dividing the curve into single segments with different slopes was needed. The Master Recession Curve methodology enables one to work simultaneously with numerous recession periods, making the influence exerted by precipitation negligible and obtaining realistic parameters of each aquifer system. Hence, MRCs were calculated using the freeware software RC 4.0 of the HydroOffice [21], applying the manual method tool to create a graphical analysis and to divide curves into different segments having homogeneous trends, thereby enabling separate analysis. The conceptual model applied is that of a linear reservoir [8,9], which follows Maillet’s exponential recession function shown above.

2.4. Time-Series Analysis

The ACF evaluates a time series by quantifying the linear dependency of successive values over a specified time period (lag time) [55]. It can be written as follows [28,50]:

For k > 0,

$$C\left(k\right)=\frac{1}{n}{\displaystyle \sum }_{t=1}^{n-k}\left(x_t-\overline{x}\right)\left(x_{t+k}-\overline{x}\right)$$

(4)

$$r\left(k\right)=\frac{C\left(k\right)}{C\left(0\right)}$$

(5)

where r(k) is the auto-correlation function, C(k) is the correlogram, k is the time lag (k = 0 to m), n is the length of the time series, x_t is the value of the studied variable at time t, and m is the cutting point [56]. The cutting point determines the interval within which the analysis is conducted. The correlogram reflects the “memory effect” of a system [26,50,57,58], i.e., the time needed for the system to “forget” its initial conditions, and corresponds to the lag time required for the ACF to reach 0.2 [54,55,59]. The CCF is used to examine the dependence of output series y (discharge) on the input series x (precipitation) and can be calculated using the following equation [27]:

For k > 0,

$$C_{xy}\left(k\right)=\frac{1}{n}{\displaystyle \sum }_{t=1}^{n-k}\left(x_t-\overline{x}\right)\left(y_{t+k}-\overline{y}\right)$$

(6)

$$r_{xy}\left(k\right)=\frac{C_{xy\left(k\right)}}{{\sigma }_x{\sigma }_y}$$

(7)

where k is the time lag, n is the length of the time series, x_t and y_t are input and output time series, respectively, r_xy (k) is the cross-correlation function, σ_x and σ_y are the standard deviations of the time series, and C_xy (k) is the cross-correlogram [56].

Both of ACF and CCF analyses are performed using correlograms. A steep slope in the correlogram means a fast response of the aquifer to a rainfall event and indicates a higher karstification degree. In particular, CCF analysis can provide strong support for the identification of the main rainfall contribution and the travel time through the main infiltration pathways [60]. The results can be compared using recession coefficients estimated by hydrograph analysis.

3. Results

3.1. Discharge Time Series Description

Monitoring in the field has provided the time series of daily average discharge of six springs covering about eight years, from 2007 to 2015. The hydrographs in Figure 3 show that the springs are reactive, i.e., that the discharges vary after rainfall events throughout the year. However, the response of each spring reflects the spatial distribution of permeability in each respective aquifer and their hydrogeological characteristics [61]. The amplitude of the discharge variations depends both on the size of the recharge area and on the porosity and heterogeneity characteristics of the carbonate reservoir.

The Scirca spring is located in the SW limb of the Mt. Cucco anticline, at 575 m a.s.l. The spring’s catchment area is about 8 km² and its discharge averages 214.9 l/s [44]. The time-series of the Scirca spring is rather continuous and the hydrograph passes from quick- to baseflow conditions, with the corresponding rapid decrease in water level, generally in early summer.

The waters of the Vaccara spring, set at an elevation of 468 m a.s.l, drains the SW limb of Mt. Maggio. The spring has a large recharge area of 6.2 km² and a mean discharge of about 119 l/s. The time-series is rather incomplete (24% of data is missing). The gaps in data are due to instrumental errors. The spring’s hydrograph shows a very fast response to recharge events and rather clear passages from quick- to baseflow during dry periods.

The hydrograph for Boschetto spring was very similar to that of Vaccara spring, exhibiting clear differences between baseflow and quickflow regimes. This spring is located on Mt. Penna at 538 m a.s.l. and has a mean discharge of about 185 l/s, which is about 65 l/s more than the Vaccara spring. This difference can be explained by Boschetto spring’s larger recharge area (about 11.5 km²).

The Capo d’Acqua spring is located on the same hydrostructure as Boschetto spring but drains the other side of the relief (NE limb of Mt. Penna). This spring has an average discharge of 94.2 l/s and does not show a clear passage from quickflow to baseflow regimes because of a significant lag in discharge response following infiltration. The estimated catchment area is about 7.4 km².

The San Giovenale spring drains the greatest amount of water of all other carbonate systems in this study, with an average discharge of 394.7 l/s. The estimated recharge area is about 10.5 km² and the karst system shows the same behavior as the Capo d’Acqua spring. Differences between quick- and baseflow regimes are not observable and the decrease in water level is very slight and delayed. The high average discharge of the San Giovenale spring cannot be explained by the size of the recharge area. Most likely, this carbonate system is supplied by non-negligible groundwater flows from the Colfiorito plain [43].

The hydrograph of Bagnara spring shows characteristics intermediate between those of the Scirca, Vaccara and Boschetto springs, and those of the San Giovenale and Capo d’Acqua springs. This karst aquifer shows a fast response to infiltration in a quickflow regime and a slight decrease in discharge during the baseflow regime. This behavior indicates a very marked spatial heterogeneity in porosity along the aquifer.

Thus, the Scirca, Vaccara, Boschetto, and Bagnara springs show a quick response to a rainfall event characterized by steep peaks followed by rapid decreases in water level. This behavior is characteristic of all karst systems with a well-developed network of fractures and conduits. The San Giovenale and Capo d’Acqua springs, on the other hand, show a delayed response to rainfall events, with a slow decrease in discharge over time. This behavior is typical of a poorly-developed karst systems, where groundwater circulation occurs through the matrix and fracture networks.

3.2. MRCs Analysis

Recession curve analysis was performed on hydrographs from six aquifer springs located in the Umbria-Marche Apennines. Different shapes of a spring’s recession curve are attributable to drainage from different components of the groundwater system, reflecting karstification degree [15]. The karstification of soluble rock can be considered the most important geological phenomenon influencing the hydraulic behavior of carbonate aquifers. The presence of different lithologies in the catchment area can highlight these hydraulic differences [62].

The Master Recession Curve methodology was used to work simultaneously with numerous recession periods (Figure 4), making the influence exerted by precipitation negligible and allowing to obtain an average value representative of the entire recharge area [16].

Changes in the slope of the recession curve have been attributed to aquifer heterogeneity [63,64], whereas recession curves that can be expressed by one exponent represent homogeneous conductivity and storage properties. The discharge of the aquifer can be considered approximately constant and specific for each aquifer-spring system when the changes of hydraulic conditions (transmissivity, water table area) are not appreciable during the emptying associate with the recession limb of the hydrograph [65]. Therefore, recession analysis using the MRC methodology has allowed to identify two groups with different hydraulic behavior: aquifers with unimodal behavior (having one sub-regime) and aquifers with bimodal behavior (having two sub-regimes). All the aquifer springs analyzed have a good fit with the exponential equation of Maillet [9], indicating that the more appropriate conceptual model is that of a linear reservoir [8,9].

A recession curve analysis was conducted on records from eight years, resulting in about seven intervals (individual recessional discharge sets). These partial recession curve records were assembled to create a master recession curve of each spring (Figure 4 and Figure 5).

Table 4. Characteristics of recession curves of springs with bimodal behavior and their related sub-regimes (baseflow or quickflow).

Spring	No. of Recession Segments	Qb1 (l/s)	αb (d−1)	tb (day)	Qq2 (l/s)	αq (d−1)	tq (day)
Scirca	8	180	0.0060	225	220	0.025	150
Vaccara	7	90	0.0053	200	220	0.080	60
Boschetto	7	180	0.0065	200	650	0.100	50
Bagnara	6	120	0.0085	300	180	0.015	200

¹ b = baseflow; ² q = quickflow.

and

Table 5. Recession curve characteristics of aquifer springs with unimodal behavior.

Spring	No. of Recession Segments	Q (l/s)	α (d−1)	tr (day)
Capo d’acqua	4	145	0.0074	200
San Giovenale	6	380	0.0115	200

present the recession coefficients, discharge range, duration of sub-regime of measured recession curves, and the number of assembled individual recessional discharge successions used to create an MRC of each spring.

For the Scirca, Vaccara, Boschetto, and Bagnara springs, the results showed a significant degree of curve separation in two segments, characterized by different recession constants (Figure 4). Indeed, the values of the recession coefficients of quickflow sub-regimes (α_q) are rather high, ranging from 0.015 d⁻¹ (Bagnara spring) to 0.1 d⁻¹ (Boschetto spring). This may be caused by the change of hydraulic or geometric characteristics of the aquifer during the depletion process [65]. According to Amit et al. [11], the exponential term with the largest slope represents a rapid depletion of flow channels with the highest hydraulic conductivity.

The transition from quickflow to baseflow occurs after 150 and 180 days in the Scirca and Bagnara (Figure 4a,d) springs, indicating that fast drainage is the dominant component for most of the years. In contrast, the baseflow sub-regime is the dominant component of Vaccara and Boschetto springs, with a sub-regime transition occurring after about 30 and 50 days in Boschetto and Vaccara springs (Figure 4b,c), respectively. The parameters of these springs reflect the structural properties of their aquifers, such as karstification degree, fracture networks, and conduit networks.

The Capo d’Acqua and San Giovenale springs present a unimodal behavior because their MRCs can be expressed by one exponent (Figure 5). This means that their aquifer systems are characterized by homogeneous conductivity and storage properties. However, these two springs differ in their recession coefficients. Capo d’Acqua spring has a recession coefficient of 0.0074 d⁻¹, a value with the same order of magnitude as baseflow recession coefficients of the previously described springs with bimodal behavior. An exponential term with a small slope corresponds to slow depletion of a flow network with low hydraulic conductivity [11]. The recession coefficient of San Giovenale spring (0.0115 d⁻¹), on the other hand, is very similar to quickflow components of aquifer springs with bimodal behavior.

The recession period estimated by the MRC method is 200 days for both carbonate systems (

Table 6. Time series analysis parameters: system memory effect, maximum discharge/rainfall cross-correlation coefficient, and time lag for maximum cross-correlation coefficient (Q discharge).

Aquifer Spring	Memory Effect (days)	Cross-Correlation Coef.	Time LagSS (days)
Scirca	80	0.24	13
Vaccara	90	0.18	2
Boschetto	89	0.27	2
Capo d’Acqua	90	0.18	74
San Giovenale	150	0.18	119
Bagnara	121	0.20	39

). The difference between the two aquifers is in their dominant components (quickflow vs. baseflow sub-regimes). Capo d’Acqua spring is dominated by a baseflow sub-regime, where drainage is controlled by matrix and fracture network porosity, while San Giovenale spring has a quickflow-dominated sub-regime, characterized by a fast drop in water level controlled by fracture and conduit networks.

3.3. Time-Series Analysis: Autocorrelation and Cross-Correlation

3.3.1. Autocorrelation Function (ACF)

The autocorrelation function treatment quantifies the linear dependency of successive values over a specific time period and reflects the memory of the system [61]. The values estimated using this method are shown in Table 6. The daily time series correlograms for each spring are shown in Figure 6. The correlogram of the Scirca spring shows a rapid and regular ACF slope that reaches r_k = 0.2 after 80 days. The shape of the autocorrelation functions and the high memory effect implies a significant storage capacity, probably linked to a well-developed fracture network.

The ACF of the Vaccara spring further confirms its bimodal behavior. First, it displays a rapid decrease in the first days (10 days), comportment associated with a quickflow sub-regime; then, its slope levels out, reaching r_k = 0.2 at a much slower rate after 90 days, a response characteristic of a baseflow sub-regime. In the case of the Boschetto spring, the decrease in the autocorrelation function is uneven and marked by two discrete components. The first drops quickly, within about 20 days, while the second decreases more slowly and reaches r_k = 0.2 at 89 days, indicating a strong duality of these karst systems. The Bagnara spring shows a very slight decrease in ACF with no steps. The estimated memory effect is high, with a value of about 121 days, indicating a higher storage capacity and high filtration potential of this aquifer systems. The correlogram of Capo d’Acqua spring discharge displays a regular decrease in the slope of the ACF, reaching r_k = 0.2 with the same time lag as the other systems seen thus far (90 days). This suggests the prevalence of the baseflow component, probably due to a fractured matrix. The ACF for the flow rates at San Giovenale spring diminishes very slowly when the time lag increases. This karst system shows a memory effect of 150 days, presenting great inertia and indicating that the aquifer has a large storage capacity, which is drained very slowly.

3.3.2. Cross-Correlation Function (CCF)

The delays between inputs and outputs of various springs are useful information in the regional study of a carbonate aquifer because they give an estimate of the variation in pressure pulse transfer times and of particle travel times through the aquifer [29]. The delays are also significant in the modeling of the aquifer and indicate the karstification degree of a karst system.

The wet and dry periods, which induce high and low flow periods in the spring discharge series, appear more difficult to define in the rainfall time-series [66]. The lowest values of the rainfall cause the most intense droughts in the spring discharge series, as shown for example by the period included between June 2011 and March 2012.

Rainfall data of different rain gauge stations were used in relation to correspondent hydrostructure and proximity to them. Therefore, the MC station has been used for the Scirca spring, the GT station has been used for the Vaccara, Boschetto, and Capo d’Acqua springs, and the NU station has been used for the San Giovenale and Bagnara springs.

The CCFs between the rainfall and discharge time series of each spring are shown in Figure 7, while the relative parameters (maximum cross-correlation coefficients and their related time lag) of the time-series analysis are listed in Table 6. The cross-correlograms show rather low r_xy(k) values (between 0.18 to 0.27). This indicates that the precipitation signal is significantly reduced between its entry into the system and the time when it reaches the water table via the unsaturated zone [29].

Cross-correlograms of the Boschetto, Scirca, and Vaccara springs are each characterized by a sharp peak (0.27, 0.24, and 0.18, respectively) that diminishes rather rapidly in the first days, reflecting a short response time (2 days for Boschetto and Vaccara springs and 13 days for Scirca spring). Subsequently, the CCFs gradually decrease with a gentle slope for about 50 days. This shape indicates the duality of the aquifers, with the sharp peaks indicating a transmissive function and the slight decreases indicating a capacitive function [61].

Cross-correlation functions of the Capo d’Acqua, San Giovenale and Bagnara springs show much more regular unimodal trends than the previously described springs. In fact, CCFs decrease rather slowly with a gentle slope. They have barely perceptible mean response delays, with cross-correlation coefficients ranging between 0.18 to 0.20. This behavior corresponds to that of a barely karstified system, similar to a porous medium in which there is no quickflow.

The response times of these carbonate systems are 39 days for the Bagnara spring, 74 days for the Capo d’Acqua spring, and 119 days for the San Giovenale spring. These results indicate a gradual emptying of the hydric system with a large storage capacity that regulates the input flow (baseflow sub-regime).

Finally, in the CCFs of both the Boschetto and Bagnara springs, a series of peaks were observed after the initial peak (64, 142, and 201 days for the Boschetto spring, 68, 145, and 232 days for the Bagnara spring). It appears that these may have been caused by one or more additional flow components within the aquifers. An explanation for this behavior must be sought in the slight control exercised by the system on the input function. Moreover, further limitations in the rainfall-discharge relationship exist, since spring discharge can depend on the rainfall of the previous year [60].

4. Discussion

The recession coefficient is one of the most important parameters for understanding aquifer characteristics. In this study, the Master Recession Curve method was applied to recession periods that are mainly controlled by the rate of decline in the water table [67]. Different recession coefficients reflect flow regimes with different hydraulic conductivities [5]. Therefore, the recession coefficient is always used to identify the structural properties (matrix, fractures, and conduit networks) and the karstification degree of a karst aquifer [23,52,53,54,68,69].

Applying the MRC method to the six springs allowed to define two main structural types of the karst systems in question (aquifer heterogeneity): systems with a unimodal behavior (characterized by a single flow component, α_b) and systems with a bimodal behavior (characterized by two flow components, α_q and α_b). The number of flow phases depends mainly on the degree of karstification [70].

The recession analysis (illustrated in the equation in Figure 8) exposed different groups of aquifer systems. Bimodal aquifers have mean recession coefficient values during the quickflow sub-regime of about an order of magnitude higher than recession coefficients estimated during baseflow conditions. The MRCs displayed values between 5.3 × 10⁻³ (α_b of Vaccara spring) and 0.1 day⁻¹ (α_q of Boschetto spring). This is in agreement with Mangin [10] and Amit et al. [11] and confirms the presence of two types of flow (fast and slow), as verified by the two main slopes exhibited by the recession curves. The exponential term with the largest slope, αq, represents a fast depletion (quickflow sub-regime) of flow channels with high transfer capacity, while the largest α-value likely reflects extensive fracturing and intrakarst connectivity [11].

The Capo d’Acqua and San Giovenale springs (unimodal aquifer systems) present only one type of flow, which, however, have very different magnitudes. In fact, the Capo d’Acqua spring was characterized by an exponential term with a small slope, about 7.4 × 10⁻³ day⁻¹ (analogous to bimodal aquifers during baseflow conditions), whereas the San Giovenale spring showed a depletion coefficient of 1.15 × 10⁻² day⁻¹, which is the lowest value, but bears the same magnitude as bimodal aquifers under a quickflow sub-regime. Therefore, the drainage of the Capo d’Acqua spring occurs as a diffusive flow in low hydraulic conductivity conditions, most likely controlled by a dense fracture network in the rock matrix. In contrast, the discharge of the San Giovenale spring occurs in intermediate flow conditions (diffusive-turbulent) through a well-developed fracture network with the possible presence of karst conduits of a limited extent.

The analysis emphasizes the role played by the structural geological setting, revealing a net demarcation of the dominantly calcareous cores of anticlines, surrounded by the impermeable Marne a Fucoidi belt and containing variably extensive basal aquifers in line with Mastrorillo and Pettita [71].

A summary of the equations describing discharge and the relative karstification degree estimated using a 10-degree scale in accordance with Malìk and Vojtková [23] for the six analyzed springs is shown in

Table 7. Karstification degrees of spring recharge areas according to recession curve parameters, after [15,23].

Spring	Characteristics of Recession Curve Parameters	Karstification Degree
Scirca	αb > 0.0043 αc < 0.060	3.7
Vaccara	αb = 0.0041 to 0.018 αc = 0.055 to 0.16	4.0
Boschetto	αb = 0.0041 to 0.018 αc = 0.055 to 0.16	4.0
Bagnara	αb > 0.0043 αc < 0.060	3.7
Capo d’Acqua	α > 0.007	2.3
San Giovenale	α > 0.007	2.3

. The Boschetto and Bagnara springs showed a karstification degree of 4.0, a value only slightly higher than those of the Scirca and Vaccara springs, both of which showed a karstification degree of 3.7. These aquifer springs are characterized by aquifers with irregularly developed fissure networks dominated by open micro-fissures, which are probably associated with shallow infiltration zones (upper portion of the aquifer) mainly characterized by drainage of the Maiolica Complex. In addition, the presence of karst conduits of a limited extention in the basal portion of the aquifer linked to drainage of the Massiccio Complex, where karstic processes are very common, is very likely. In extreme cases, even short-term turbulent flow might occur in this type of rock environment. From a geological point of view, these aquifers are characterized by a hydraulic connection between the Massiccio Complex and the overlying Maiolica Complex (Figure 8). Moreover, in the Mt Pennino hydrostructures, the hydraulic continuity between Scaglia aquifer complex and the below basal aquifer is not excluded [48].

The Capo d’Acqua and San Giovenale springs showed a single exponential flow component with values of recession coefficients (α > 0.007) associated with a karstification degree of 2.3 (much lower than carbonate aquifers with the duality of discharge). Malík and Vojtková [23] described the karst systems with this karstification degree as characterized by a recharge area with tectonic faults filled with crushed material with higher permeability and lower buffering capability in relation to discharge. As shown in Figure 7, the water discharged by the Capo d’Acqua and San Giovenale springs is drained only by the Maiolica Complex. These aquifers are confined below by an aquiclude of Upper Jurassic and calcareous marls. The Maiolica complex, as well as the basal aquifer, can be characterized as a less developed karst network. Additionally, the Capo d’Acqua and San Giovenale systems are characterized by shallow aquifers, where drainage is controlled almost exclusively by fracture networks.

Hence, in terms of regional hydrogeology, the Umbria-Marche carbonate domain generally has deeper groundwater flowing through hydrogeological complexes consisting of the Calcare Massiccio, Corniola, and Maiolica formations [72]. Furthermore, the structural, geological, and geomorphological conditions have favored the emplacement of a drainage network transversal to the axes of the carbonate ridges [73].

Employing the daily time series data of each spring, an interpretation of auto-correlation and cross-correlation functions proved to be a valuable tool in the study of these aquifer systems, although individual analysis has not shown the same results, because the two hydrodynamic systems (bimodal and unimodal) were not recognized in some cases. The auto-correlation functions (Figure 6) display regular correlogram curves in most cases. Only the Vaccara and Boschetto springs present sharp drop offs in their ACFs in the first 10–20 days, followed by components with much gentler slopes, with a decorrelation time of about 90 days. This confirms the bimodal behavior in the springs indicated by recession analysis. Such behavior points to the existence of an appreciable quickflow component in the initial days, linked to karst conduits that quickly drain the aquifer after a rainfall event, and a dominant baseflow sub-regime in the later days, controlled by the emptying of fracture networks. This complex and heterogeneous framework suggests that, when a rainfall event occurs, rainwater reaches the springs through different flowpaths in both unsaturated and saturated zones. Once rainwater reaches the saturated zones, the hydraulic head raises instantaneously and causes a rapid discharge increase [74].

In contrast, univariate analysis of the Scirca and Bagnara springs does not reflect the duality of aquifer systems indicated by recession analysis. The auto-correlation functions show regular, very gentle slopes with a decorrelation time of 80 days for the Scirca spring and 121 days for the Bagnara spring. The memory effect is therefore rather high for both systems, in which the baseflow component should dominate [75]. The explanation for this is probably that the karst features are mainly located in the unsaturated zone [44].

The correlograms of the San Giovenale and Capo d’Acqua springs, on the other hand, are in agreement with the recession analysis, presenting one flow hydrodynamic component (unimodal behavior). The time lag of the Capo d’Acqua spring has a similar value to those seen thus far, about 90 days. Considering the small recharge area and the limited thickness of the Capo d’Acqua aquifer, the aquifer system is characterized only by a flow component under baseflow conditions and is associated with a low karstification degree. The auto-correlation function of the San Giovenale spring presents the highest memory effect of all aquifer systems analyzed, reaching r_k = 0.2 after about 150 days. This great inertia indicates a low karstification degree and, consequently, the large storage capacity of the system. From a hydrogeological point of view, the aquifer is characterized by a large recharge area (10.5 km²) and a rather limited thickness (Figure 7d), due to drainage that occurs only into the Maiolica complex.

The analysis of cross-correlation functions produced approximately the same results as those of recession analysis, and partially the same as those of the auto-correlation analysis, although the coefficients estimated between spring discharges and rainfall events were rather low (0.18–0.27). In fact, the CCFs of Scirca, Vaccara, and Boschetto springs indicated a bimodal character, showing a discrete peak with a delay of a few days. This can be interpreted as a rapid response of the aquifer to a rainfall occurrence.

In contrast, the CCFs of the Capo d’Acqua, San Giovenale, and Bagnara springs show a long impulsional response, which exceeds 200 days, with a rather high delay ranging from 39 days (Bagnara spring) to 119 days (San Giovenale spring). This indicates a powerful memory of the systems and the dominance of baseflow at the expense of quickflow.

5. Conclusions

In order to define the characteristics of groundwater circulation in carbonate hydrostructures of the Umbria-Marche Apennine, the discharge time-series from 1 January of 2007 to 31 December of 2015 (eight years) of six aquifer springs were analyzed, using different methodologies (MRC “master recession curve” analysis, ACF “auto-correlation function” analysis, and CCF “cross-correlation analysis”). The carbonate aquifers analyzed simulated drainage under linear reservoir conditions, where discharge followed the exponential form of the modified Maillet equation, although not all systems showed the same structural properties. In fact, two types of aquifers were observed: a carbonate aquifer with bimodal behavior and a carbonate aquifer with unimodal functionality. These substantial differences can be attributed to the different structural and geological settings of individual hydrostructures, which control the different components of groundwater systems [5].

In the hydrostructures, springs represent the “spill-over” of the deep regional flow. The recharge areas of springs and deep flow are separated by dynamic groundwater divides, which move horizontally as the water table falls or rises [76].

Specifically, the discharges of the Scirca, Vaccara, Boschetto, and Bagnara springs were characterized by two hydrodynamic sub-regimes (bimodal behavior), where the fracture networks and micro-fissures (rock matrix) controlled the slow drainage (baseflow sub-regime) with an αb of about 10⁻³, and the conduit networks controlled the fast drainage (quickflow sub-regime) with an αq of one order of magnitude lower than that of the matrix. This reflects the karstification degree (3.7–4, according to the classification of Malík and Vojtková [23]), where conduit networks of limited extent were characterized by rare interconnected systems and surrounded by a fractured rock mass with irregularly developed and moderately opened fissures. These carbonate aquifers were defined by the hydrostratigraphic contact between the Maiolica Complex and the Massiccio Complex. The Capo d’Acqua and San Giovenale springs, on the other hand, presented unimodal behavior, showing a single exponential flow component with values of recession coefficients lower than other, previously seen aquifer systems. This is explained by groundwater circulation that happens only within the Maiolica complex, where the karst is scarcely developed, and water moves through fracture networks [77].

When the recession coefficient increased with time, a more rapid decrease of discharge was found and little available water could be supplied. This is what happened during the quickflow components of the aquifer with bimodal behavior (Scirca, Vaccara, Boschetto, and Bagnara springs). In contrast, when the recession coefficient decreased continuously with time, the decrease of the discharge was slower than the exponential recession, and the aquifer provided more available water during long dry periods [78]. This is represented by the aquifer with unimodal behavior (San Giovenale and Capo d’Acqua spring) and by a baseflow component of the aquifer with bimodal behavior.

Both auto-correlation and cross-correlation functions showed approximately the same results as the recession analysis. Bimodal aquifers showed a steep slope and a short lag time (2–13 days) followed by a gentle slope, whereas unimodal aquifers showed a somewhat uniform decrease with high delay times. In addition, both the CCF and the ACF indicate a large memory effect (over 80 days) and large response time (over 100 days), implying the dominance of the baseflow sub-regime. This suggests great inertia, showing how the aquifers filter the information given by rainfall events very well. Consequently, the analyzed aquifer systems highlight large storage capacity (very important for the water management) and the attenuation character.

Taking into consideration the results achieved, it can be concluded that the structural and hydrogeological setting influences the structural properties of aquifers and, consequently, the groundwater circulation within the Apenninic carbonate sequence. The hydrostructures contained within the Maiolica Complex present a high fracturation degree and a slightly karstified rock mass, which exerts the dominant influence over infiltration and percolation. Here, groundwater circulation occurs within fracture networks and discharge is dominated by baseflow sub-regimes (probably with a Darcian flow), resulting in unimodal functionality. The aquifers contained within the Massiccio Complex, on the other hand, have a higher karstification degree, which controls water circulation characterized by different flow components. This complex is affected by moderately developed conduit networks, especially in the deeper aquifer zones, which results in a quickflow sub-regime and, therefore, dual behavior.

Due to these specific characteristics, fractured and karst aquifers are of increasing interest because they represent a significant percentage of the world’s water supply. Aquifers are extremely vulnerable to the various sources of pollution; hence, the exploitation, maintenance of water quality, and the protection of fractured and karst aquifers are of vital importance. Therefore, the knowledge of recession coefficient is very helpful in water management.