Predicting River Embankment Failure Caused by Toe Scour Considering 1D and 2D Hydraulic Models: A Case Study of Da-An River, Taiwan
Abstract
:1. Introduction
2. Bend Scour Simulation Model
2.1. WASH1D Model
2.2. SFM2D Model
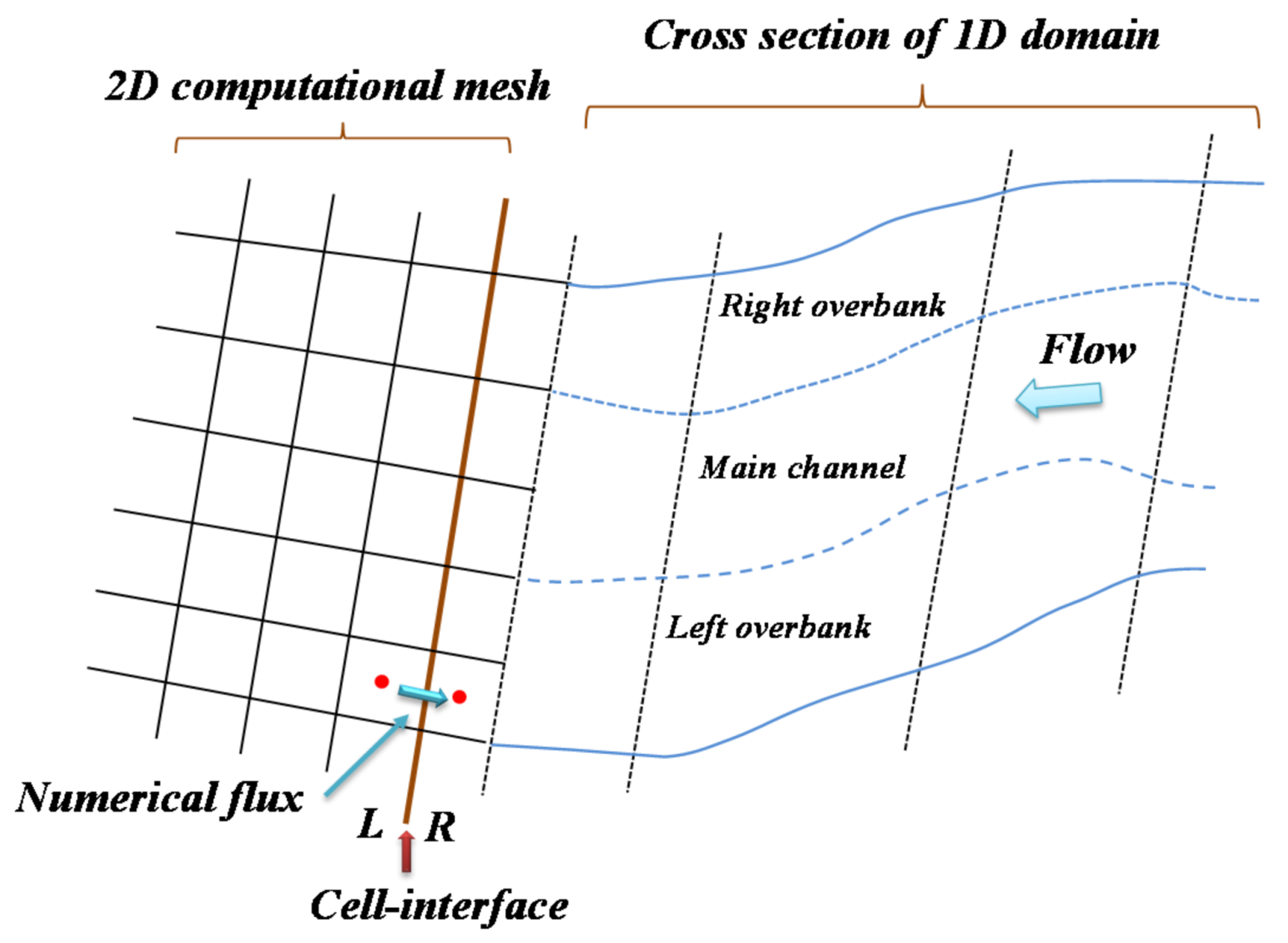
2.3. Boundary Connection of 1D and 2D Models
- When the inflow at the connection boundary is subcritical, the unknown unit width discharge has to be given. The three unknown variables (, , and ) can be solved simultaneously from the following three equations [36,37]:in which the unit width discharge could be given from the simulated results of the WASH1D model. Thus, the value of at the flow distribution in 2D computation cells can be achieved from the following equation calculations:where K is the conveyance, and the variables with subscript c, ol, and or denote the values at the main channel, left overbank, and right overbank, respectively.
- When the outflow at the connection boundary is subcritical, the unknown water depth should be given. Thus, other two unknown variables ( and ) can be obtained from the following two relationships:in which water depth is obtained from the 1D simulated results (e.g., ).
- When the inflow at the connection boundary is supercritical, all three unknown variables (i.e., , and ) should be given from measured data. However, as the field data are not available, one can use the relation () and employ Equations (11) and (12) to achieve variables and .
- When outflow at the connection boundary is supercritical, the transmissive boundary conditions are specified as follows:
2.4. Empirical Equation for Bend Scour Prediction
3. Bend Scour Simulation Results and Discussions
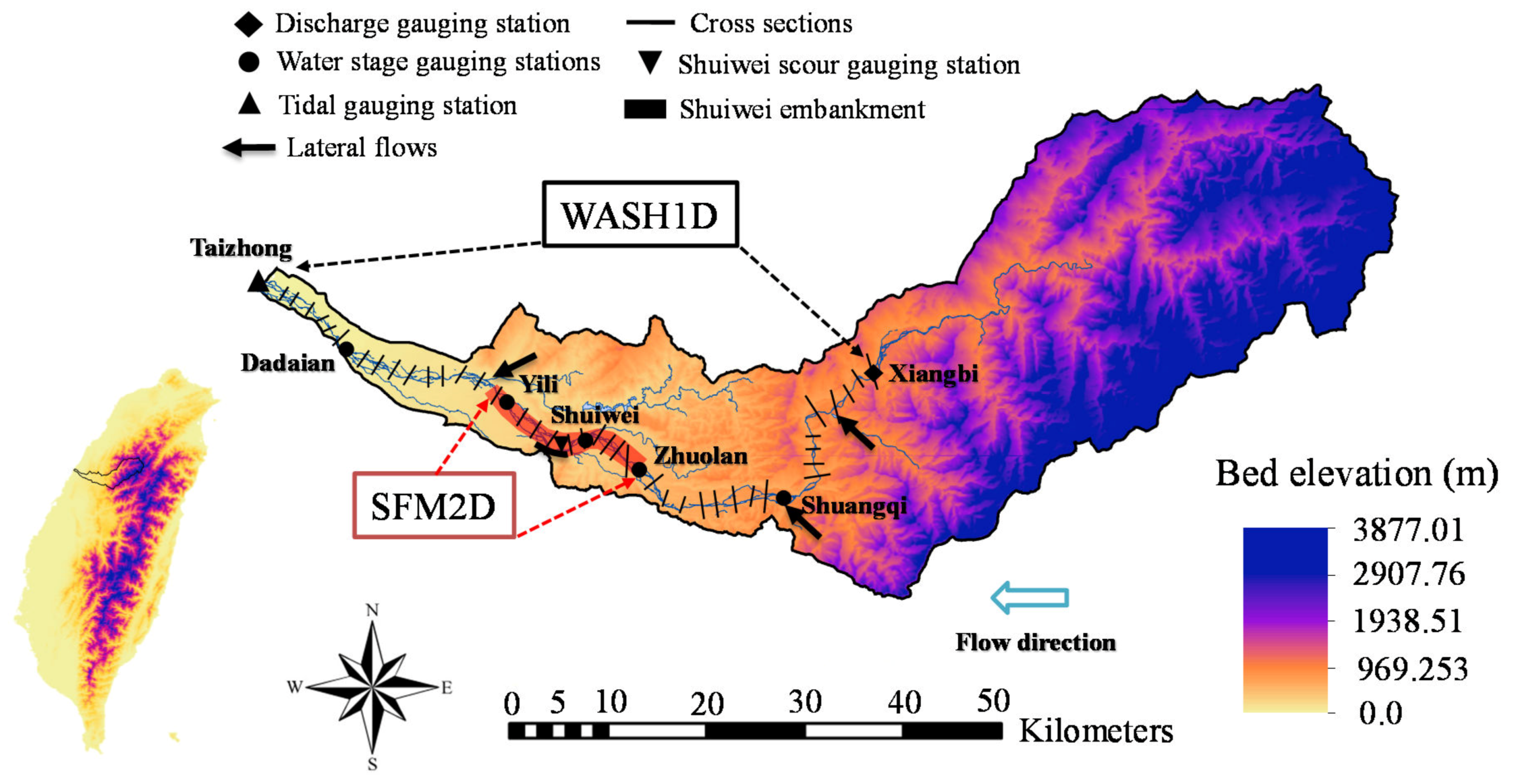
3.1. Study Site, Field Data, and Model Setup
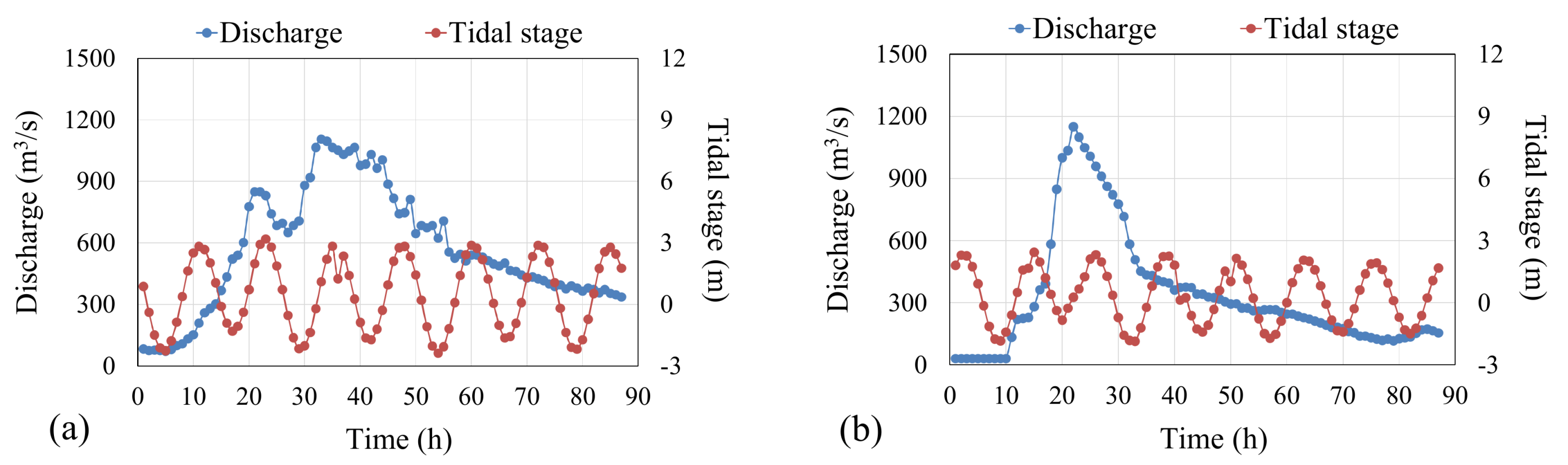
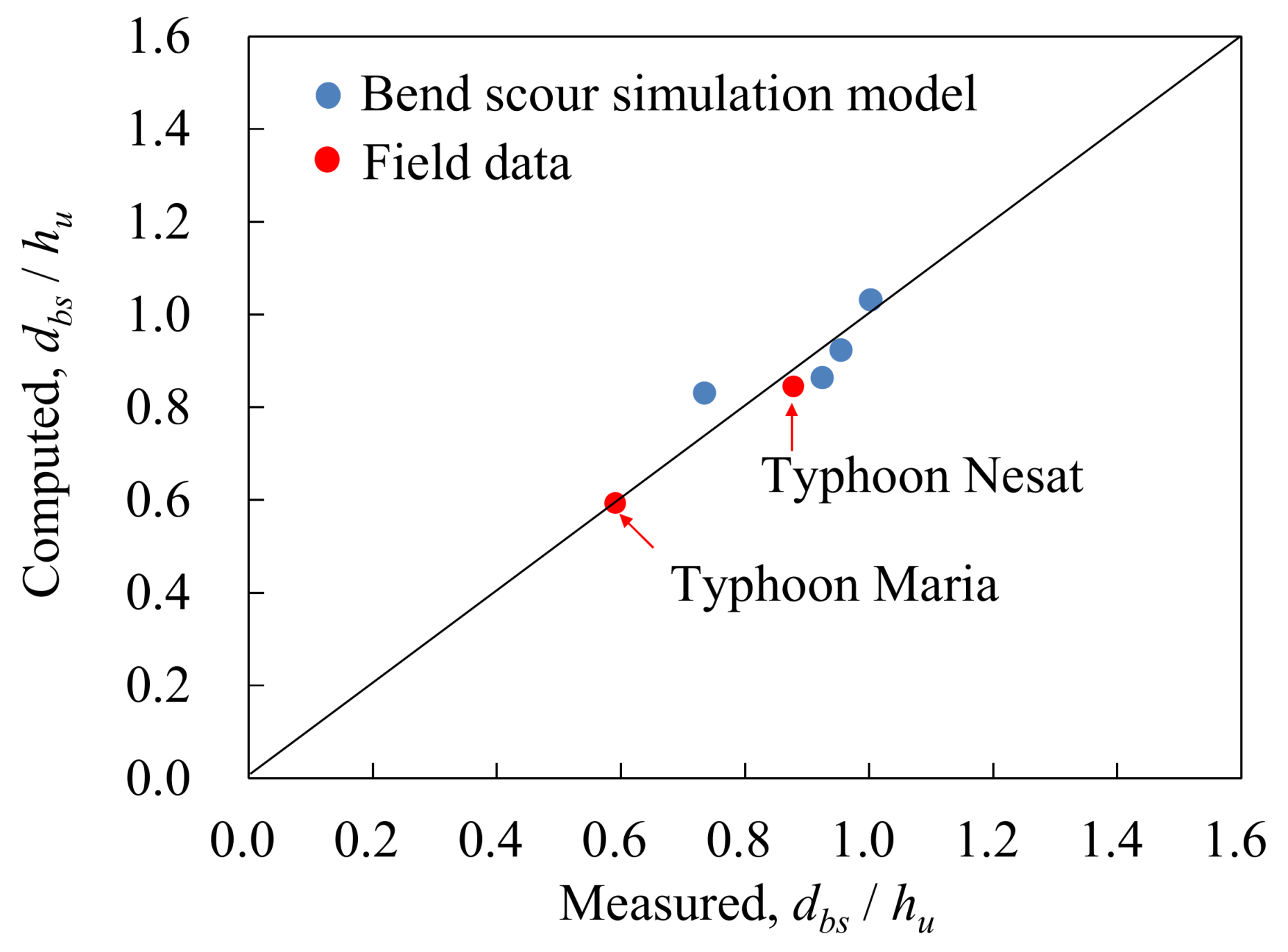
3.2. Performance Verification of WASH1D Model
3.3. Performance Verification of SFM2D Model
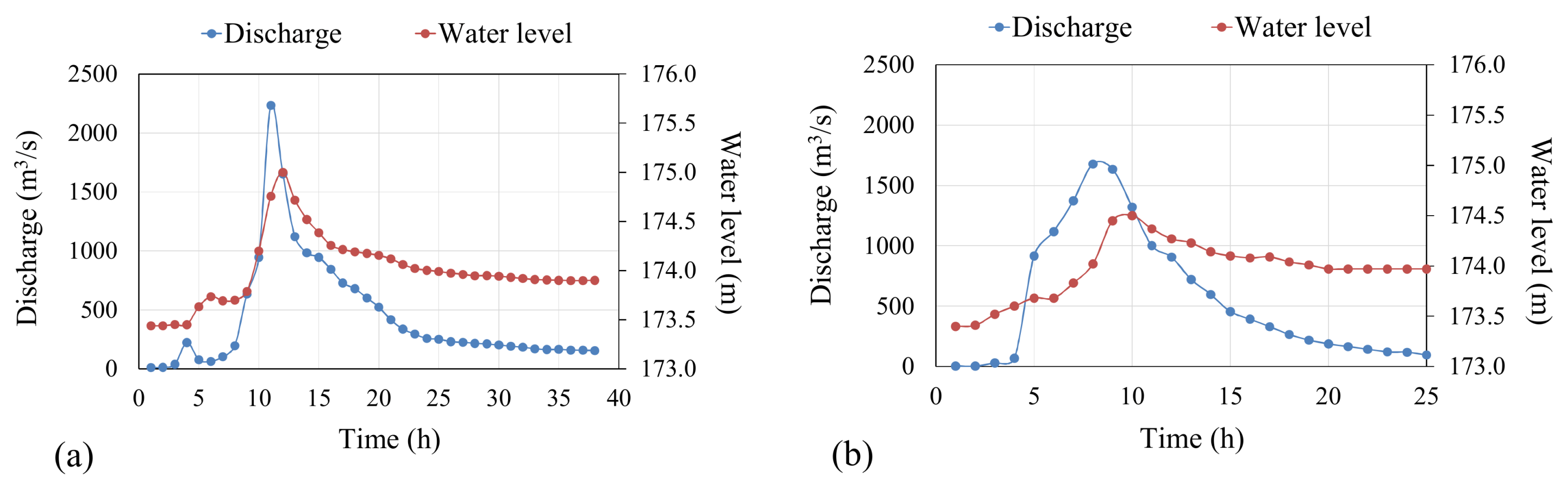
3.4. Comparisons of WASH1D and SFM2D Models for Scour Prediction
- WASH1D-CS approach, which is constructed using cross-sectional bed-elevation data.
- WASH1D-HR approach, formed using high-resolution bed-elevation data. The high-resolution DEM was used to recreate the cross-sectional topography for the WASH1D model.
- SFM2D model based on high-resolution bed-elevation data.
4. Model Application for River Embankment Failure Assessment
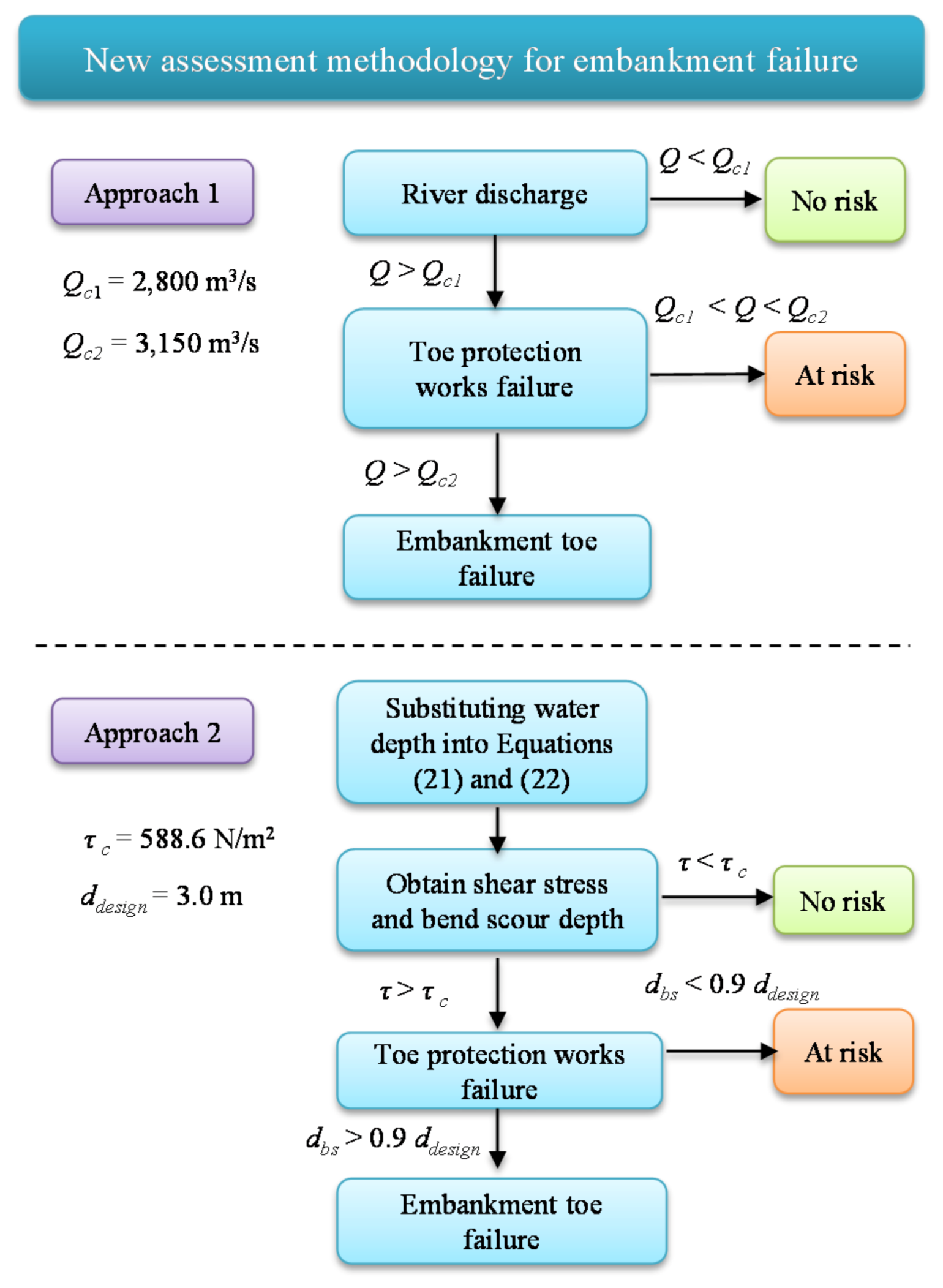
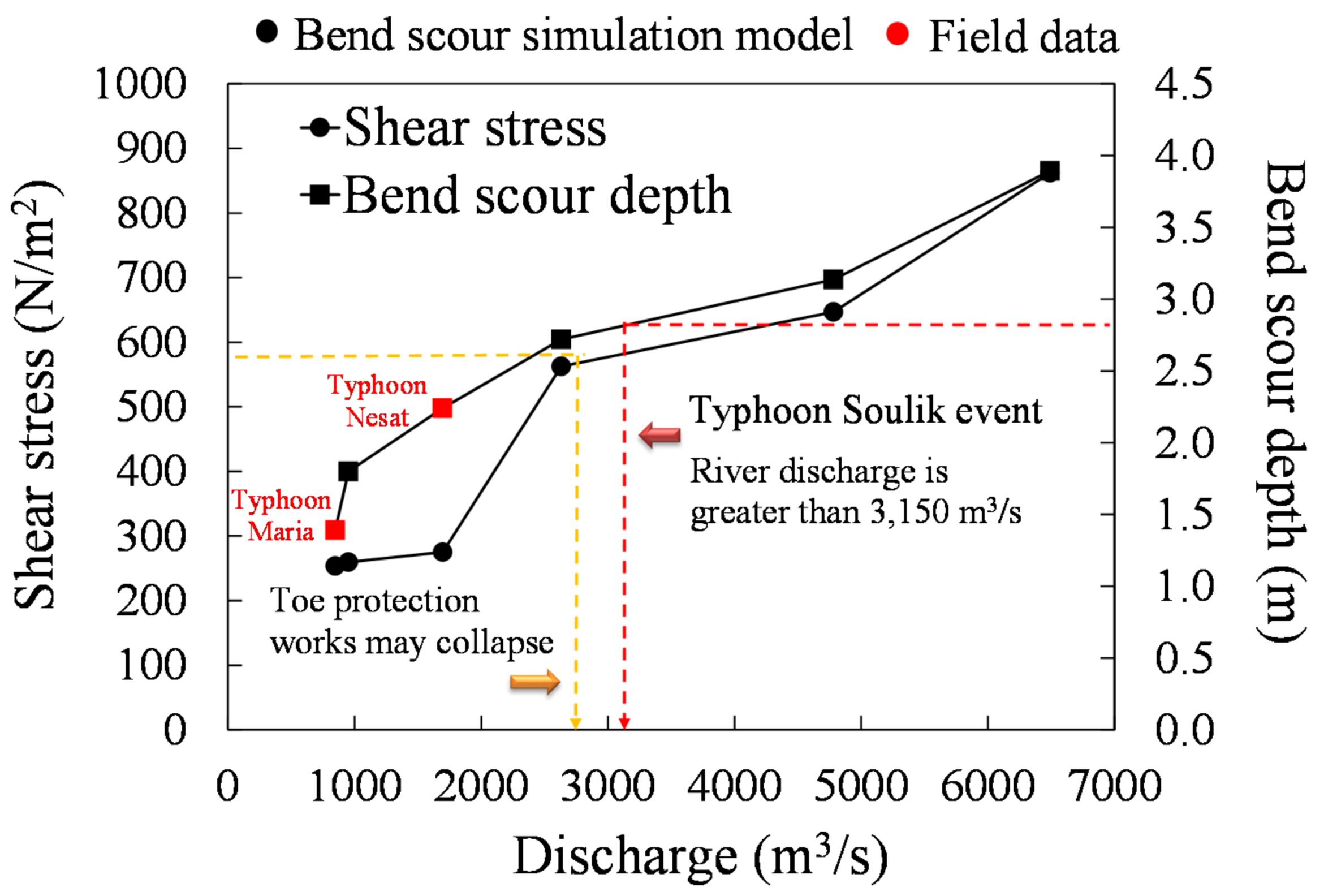
4.1. New Assessment Methodology: Approach 1
4.2. New Assessment Methodology: Approach 2
- Combine Equations (21) and (22) with water depth values to estimate the shear stress and bend scour depth.
- The estimated shear stress can then be compared with the critical value.
- If the estimated shear stress is larger than the critical value of 588.6 N/m2, the riverbank toe protection works may fail.
- The estimated bend scour depth can be compared with the designed value. If the estimated bend scour depth is larger than the designed value, the riverbank may fail.
5. Conclusions
- The integrations of WASH1D, SFM2D, and bend scouring computation equations create a bend scour simulation model. The applications of the integrated model indicated that the model was able to successfully resolve the temporal process of bend scour caused by typhoon-induce floods.
- Based on high-resolution bed-elevation data, three approaches (namely WASH1D-CS, WASH1D-HR, and SFM2D) were presented and compared. The results demonstrate that the SFM2D model produces reasonable scour predictions with acceptable accuracy for water level and bend scour depth.
- A new methodology for assessing embankment failure is proposed. The novel aspects of the proposed methodology include the consideration of toe protections and two new predictive equations. The former is implemented to enhance the reliability of riverbank failure assessments. The latter provides more specific deterministic results.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ojha, C.; Singh, V.; Adrian, D. Influence of porosity on piping models of levee failure. J. Geotech. Geoenviron. Eng. 2001, 127, 1071–1074. [Google Scholar] [CrossRef]
- Vrijling, J.K.; Schweckendiek, T.; Kanning, W. Safety standards of flood defenses. In Proceedings of the 3rd International Symposium on Geotechnical Safety and Risk, Munich, Germany, 2–3 June 2011. [Google Scholar]
- Dos Santos, R.N.C.; Caldeira, L.M.M.S.; Serra, J.P.B. FMEA of a tailings dam. Georisk 2012, 6, 89–104. [Google Scholar] [CrossRef]
- Zhang, L.M.; Xu, Y.; Liu, Y.; Peng, M. Assessment of flood risks in Pearl River Delta due to levee breaching. Georisk 2013, 7, 122–133. [Google Scholar] [CrossRef]
- Langendoen, E.J.; Simon, A. Modeling the evolution of incised streams. II: Streambank erosion. J. Hydraul. Eng. 2008, 134, 905–915. [Google Scholar] [CrossRef]
- Hossain, M.B.; Sakai, T.; Hossain, M.Z. River embankment and bank failure: A study on geotechnical, characteristics and stability analysis. Am. J. Environ. Sci. 2011, 7, 102–107. [Google Scholar] [CrossRef]
- Polemio, M.; Lollino, P. Failure of infrastructure embankments induced by flooding and seepage: A neglected source of hazard. Nat. Hazards Earth Syst. Sci. 2011, 11, 3383–3396. [Google Scholar] [CrossRef] [Green Version]
- Midgley, T.L.; Fox, G.A.; Heeren, D.M. Evaluation of the bank stability and toe erosion model (BSTEM) for predicting lateral retreat on composite streambanks. Geomorphology 2012, 145–146, 107–114. [Google Scholar] [CrossRef] [Green Version]
- Huang, W.C.; Weng, M.C.; Chen, R.K. Levee failure mechanisms during the extreme rainfall event: A case study in Southern Taiwan. Nat. Hazards 2014, 70, 1287–1307. [Google Scholar] [CrossRef] [Green Version]
- Huang, W.C.; Yu, H.W.; Weng, M.C. Levee reliability analyses for various flood return periods—A case study in southern Taiwan. Nat. Hazards Earth Syst. Sci. 2015, 15, 919–930. [Google Scholar] [CrossRef]
- Hossain, A.T.M.S.; Haque, S.A. Influence of short term rainfall on the Jamuna river west bank protection flood embankment stability at Bahuka, Sirajgonj, Bangladesh—A Case Study. IOSR J. Environ. Sci. Toxicol. Food Technol. (IOSR-JESTFT) 2019, 13, 60–68. [Google Scholar]
- Faeh, R. Numerical modeling of breach erosion of river embankments. J. Hydraul. Eng. 2007, 133, 1000–1009. [Google Scholar] [CrossRef]
- Jia, D.D.; Shao, X.; Wang, H.; Zhou, G. Three-dimensional modeling of bank erosion and morphological changes in the Shishou bend of the middle Yangtze River. Adv. Water Resour. 2010, 33, 348–360. [Google Scholar] [CrossRef]
- Mizutani, H.; Nakagawa, H.; Yoden, T.; Kawaike, K.; Zhang, H. Numerical modelling of river embankment failure due to overtopping flow considering infiltration effects. J. Hydraul. Res. 2013, 51, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Lai, Y.G. Modeling stream bank erosion: Practical stream results and future needs. Water 2017, 9, 950. [Google Scholar] [CrossRef] [Green Version]
- Rousseau, Y.Y.; De Wiel, M.J.V.; Biron, P.M. Simulating bank erosion over an extended natural sinuous river reach using a universal slope stability algorithm coupled with a morphodynamic model. Geomorphology 2017, 295, 690–704. [Google Scholar] [CrossRef] [Green Version]
- Stecca, G.; Measures, R.; Hicks, D.M. A framework for the analysis of noncohesive bank erosion algorithms in morphodynamic modeling. Water Resour. Res. 2017, 53, 6663–6686. [Google Scholar] [CrossRef]
- Lin, C. Study on Related Countermeasures of Scour Vulnerable Levees along Cho-Shui River; Fourth River Management Office, Water Resources Agency, Ministry of Economic Affairs: Changhua County, Taiwan, 2007. [Google Scholar]
- Guo, W.D.; Hong, J.H.; Chen, C.H.; Su, C.C.; Lai, J.S. A simplified simulation method for flood-induced bend scour—A case study near the Shuideliaw embankment on the Cho-Shui River. Water 2017, 9, 324. [Google Scholar] [CrossRef] [Green Version]
- Yeh, G.T.; Shih, D.S.; Cheng, J.R. An integrated media, integrated processes watershed model. Comput. Fluids 2011, 45, 2–13. [Google Scholar] [CrossRef]
- Hong, J.H. Real-time Monitoring for Embankment Scour along River Bends; Water Resources Planning Institute, Water Resources Agency, Ministry of Economic Affairs: Taichung, Taiwan, 2018. [Google Scholar]
- Melville, B.W.; Coleman, S.E. Bridge Scour; Water Resources Publications: Highlands Ranch, CO, USA, 2000. [Google Scholar]
- Shih, D.S.; Yeh, G.T. Using a characteristic-based particle tracking method to solve one-dimensional fully dynamic wave flow. Comput. Geosci. 2018, 22, 439–449. [Google Scholar] [CrossRef]
- Yu, L.; Chua, L.H.C.; Shih, D.S. An ensemble approach for typhoon runoff simulation with perturbed rainfall forecasts in Taiwan. In Proceedings of the 11th International Conference on Hydroinformatics, New York, NY, USA, 17–21 August 2014. [Google Scholar]
- Basri, H.; Sidek, L.M.; Shih, D.S.; Lloyd, H.C.; Azad, W.H.; Abdul Razad, A.Z. One dimensional shallow water equation streamflow modeling using WASH123D model. Int. J. Eng. Technol. 2018, 7, 880–884. [Google Scholar] [CrossRef] [Green Version]
- Shih, D.S.; Hsu, T.W.; Chang, K.C.; Juan, H.L. Implementing coastal inundation data with an integrated wind wave model and hydrological watershed simulations. Terr. Atmos. Ocean. Sci. 2012, 23, 513–525. [Google Scholar] [CrossRef] [Green Version]
- Yang, T.H.; Chen, Y.C.; Chang, Y.C.; Yang, S.C.; Ho, J.Y. Comparison of different grid cell ordering approaches in a simplified inundation model. Water 2015, 7, 438–454. [Google Scholar] [CrossRef] [Green Version]
- Liu, P.C.; Shih, D.S.; Chou, C.Y.; Chen, C.H.; Wang, Y.C. Development of a parallel computing watershed model for flood forecasts. Procedia Eng. 2016, 154, 1043–1049. [Google Scholar] [CrossRef] [Green Version]
- Lai, J.S.; Guo, W.D.; Lin, G.F.; Tan, Y.C. A well-balanced upstream flux-splitting finite-volume scheme for shallow-water flow simulations with irregular bed topography. Int. J. Numer. Methods Fluids 2010, 62, 927–944. [Google Scholar] [CrossRef]
- Guo, W.D.; Lai, J.S.; Lin, G.F.; Lee, F.Z.; Tan, Y.C. Finite volume multi-stage scheme for advection-diffusion modeling in shallow water flow. J. Mech. 2011, 27, 415–430. [Google Scholar] [CrossRef]
- Miglio, E.; Perotto, S.; Saleri, F. Model coupling techniques for free surface flow problems: Part I. Nonlin. Anal. 2005, 63, 1885–1896. [Google Scholar] [CrossRef]
- Finaud-Guyot, P.; Delenne, C.; Guinot, V.; Llovel, C. 1D-2D coupling for river flow modelling. Comptes Rendus Mécanique 2011, 339, 226–234. [Google Scholar] [CrossRef] [Green Version]
- Bladé, E.; Gómez-Valentín, M.; Dolz, J.; Aragón-Hernández, J.L.; Corestein, G.; Sánchez-Juny, M. Integration of 1D and 2D finite volume schemes for computations of water flow in natural channels. Adv. Water Resour. 2012, 42, 17–29. [Google Scholar] [CrossRef]
- Yin, J.; Yu, D.; Yin, Z.; Wang, J.; Xu, S. Multiple scenario analyses of Huangpu River flooding using a 1D/2D coupled flood inundation model. Nat. Hazards 2013, 66, 577–589. [Google Scholar] [CrossRef]
- Morales-Hernández, M.; Petaccia, G.; Brufau, P.; García-Navarro, P. Conservative 1D–2D coupled numerical strategies applied to river flooding: The Tiber (Rome). Appl. Math. Modell. 2016, 40, 2087–2105. [Google Scholar] [CrossRef]
- Anastasiou, K.; Chan, C.T. Solution of the 2D shallow water equations using the finite volume method on unstructured triangular meshes. Int. J. Numer. Methods Fluids 1997, 24, 1225–1245. [Google Scholar] [CrossRef]
- Guo, W.D.; Lai, J.S.; Lin, G.F. Hybrid flux-splitting finite-volume scheme for the shallow water flow simulations with source terms. J. Mech. 2007, 23, 399–414. [Google Scholar] [CrossRef]
- Galay, V.J.; Yaremko, E.K.; Quazi, M.E. River Bed Scour and Construction of Stone Riprap Protection in Sediment. Transport. Gravel Bed Rivers; John Wiley and Sons, Ltd.: New York, NY, USA, 1987. [Google Scholar]
- Thorne, C.R. Bank Processes on the Red River between Index, Arkansas and Shreveport, Louisiana; Final Report to the US Army European Research Office, contract number DAJA45-88-C-0018; Department of Geography, Queen Mary College: London, UK, 1988. [Google Scholar]
- USA Army Corps of Engineering (USACE). Hydraulic Design of Flood Control. Channels; Engineering Manual 1110-2-1601; Department of the Army, Corps of Engineers, Office of the Chief of Engineers: Washington, DC, USA, 1994. [Google Scholar]
- Lin, G.H.; Lin, C. Research in Foundation Erosion of Hazard. Potential Levees in Jhuoshuei River; Fourth River Management Office, Water Resources Agency, Ministry of Economic Affairs: Changhua County, Taiwan, 2013. [Google Scholar]
- Lu, J.Y. Field Study of Short-Term Riverbed General Scour for Typhoon-induced Floods; Water Resources Planning Institute, Water Resources Agency, Ministry of Economic Affairs: Taichung, Taiwan, 2014. [Google Scholar]
- Su, C.C.; Lu, J.Y. Comparison of sediment load and riverbed scour during floods for gravel-bed and sand-bed reaches of intermittent rivers: Case study. J. Hydraul. Eng. 2016, 142, 05016001. [Google Scholar] [CrossRef]
- Yi, R.; Wang, R.Y. Applied Hydrology; National Compilation Committee: Taipei, Taiwan, 1988. [Google Scholar]
- Xia, H.M. Establishment of Flood-Warning System for Yen-Shui Creek Basin; Water Resources Office, Water Resources Agency, Ministry of Economic Affairs: Taipei, Taiwan, 2000. [Google Scholar]
- Su, C.C.; Hong, J.H.; Guo, W.D.; Wang, H.W. Internet of things for bend scour disaster warning system-a case study near Shuiwei Embankment in Daann River. J. Chin. Inst. Civ. Hydraul. Eng. 2019, 31, 301–314. [Google Scholar]
- Yang, J.C. Study of Revetment Safety Monitoring and Analysis Modeling in Urban Area Drainage Systems; Water Resources Planning Institute, Water Resources Agency, Ministry of Economic Affairs: Taichung, Taiwan, 2014. [Google Scholar]


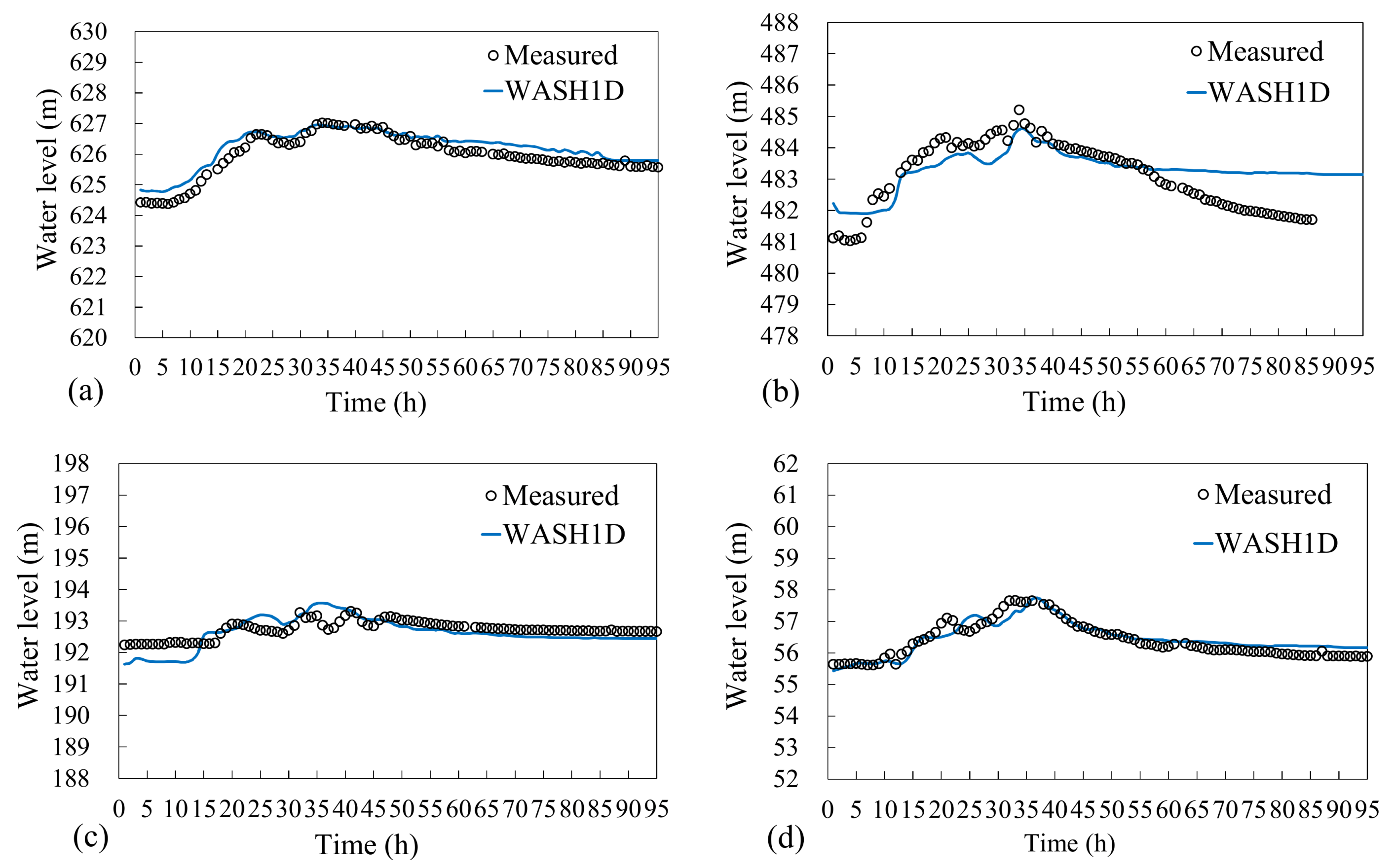

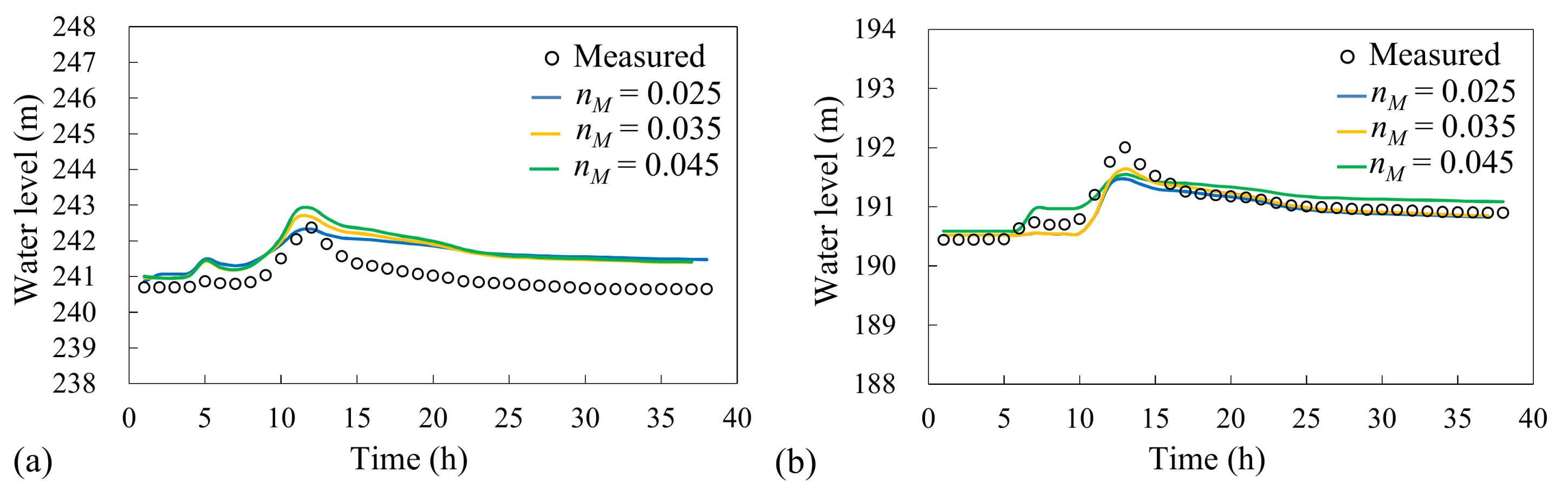





| Flood Events | tp (h) | S0(%) | σg | Rc (m) |
|---|---|---|---|---|
| Typhoon Nesat | 1.5 | 1.09 | 3.28 | 489 |
| Typhoon Maria | 3.0 | 1.09 | 3.28 | 434 |
| Events | Stations | Three Criteria | ||
|---|---|---|---|---|
| Ehp (%) | ETp (%) | R2 | ||
| Typhoon Saola (July 2012) | Xiangbi | 1.64 | 2.94 | 0.97 |
| Shuangqi | 15.07 | 2.94 | 0.76 | |
| Yili | 13.82 | 12.1 | 0.80 | |
| Dadaian | 3.07 | 12.1 | 0.93 | |
| Typhoon Soulik (July 2013) | Xiangbi | 18.24 | 0 | 0.97 |
| Shuangqi | 16.19 | 14.3 | 0.78 | |
| Yili | 14.59 | 0 | 0.75 | |
| Dadaian | 17.91 | 23.8 | 0.93 | |
| Stations | Three Criteria | ||
|---|---|---|---|
| Ehp (%) | ETp (%) | R2 | |
| Yili | 18.18 | 0 | 0.92 |
| Shuiwei scour | 2.41 | 0 | 0.82 |
| Computational Mesh | CPU Time (h) | Ehp (%) | |
|---|---|---|---|
| Yili | Shuiwei Scour | ||
| Coarse mesh (1230 elements and 1364 nodes) | 0.46 | 57.65 | 34.13 |
| Fine mesh (7465 elements and 7910 nodes) | 1.85 | 18.18 | 2.41 |
| Events | Approaches | Three Criteria | ||
|---|---|---|---|---|
| Ehp (%) | ETp (%) | R2 | ||
| Typhoon Nesat (July 2017) | WASH1D-CS | 108.42 | 0 | 0.88 |
| WASH1D-HR | 57.67 | 0 | 0.85 | |
| SFM2D | 20.81 | 0 | 0.91 | |
| Typhoon Maria (July 2018) | WASH1D-CS | 56.81 | 8.33 | 0.89 |
| WASH1D-HR | 26.67 | 8.33 | 0.88 | |
| SFM2D | 12.73 | 8.33 | 0.96 | |
| Events | Edbs by Different Approaches | ||
|---|---|---|---|
| WASH1D-CS | WASH1D-HR | SFM2D | |
| Typhoon Nesat (July 2017) | 0.142 | 0.104 | 0.080 |
| Typhoon Maria (July 2018) | 2.022 | 2.096 | 1.097 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, C.-H.; Chen, H.; Guo, W.-D.; Yeh, S.-H.; Chen, W.-B.; Liu, C.-H.; Lee, S.-C. Predicting River Embankment Failure Caused by Toe Scour Considering 1D and 2D Hydraulic Models: A Case Study of Da-An River, Taiwan. Water 2020, 12, 1026. https://doi.org/10.3390/w12041026
Chang C-H, Chen H, Guo W-D, Yeh S-H, Chen W-B, Liu C-H, Lee S-C. Predicting River Embankment Failure Caused by Toe Scour Considering 1D and 2D Hydraulic Models: A Case Study of Da-An River, Taiwan. Water. 2020; 12(4):1026. https://doi.org/10.3390/w12041026
Chicago/Turabian StyleChang, Chih-Hsin, Hongey Chen, Wen-Dar Guo, Sen-Hai Yeh, Wei-Bo Chen, Che-Hsin Liu, and Shih-Chiang Lee. 2020. "Predicting River Embankment Failure Caused by Toe Scour Considering 1D and 2D Hydraulic Models: A Case Study of Da-An River, Taiwan" Water 12, no. 4: 1026. https://doi.org/10.3390/w12041026





