Water Network Partitioning into District Metered Areas: A State-Of-The-Art Review
Abstract
:1. Introduction
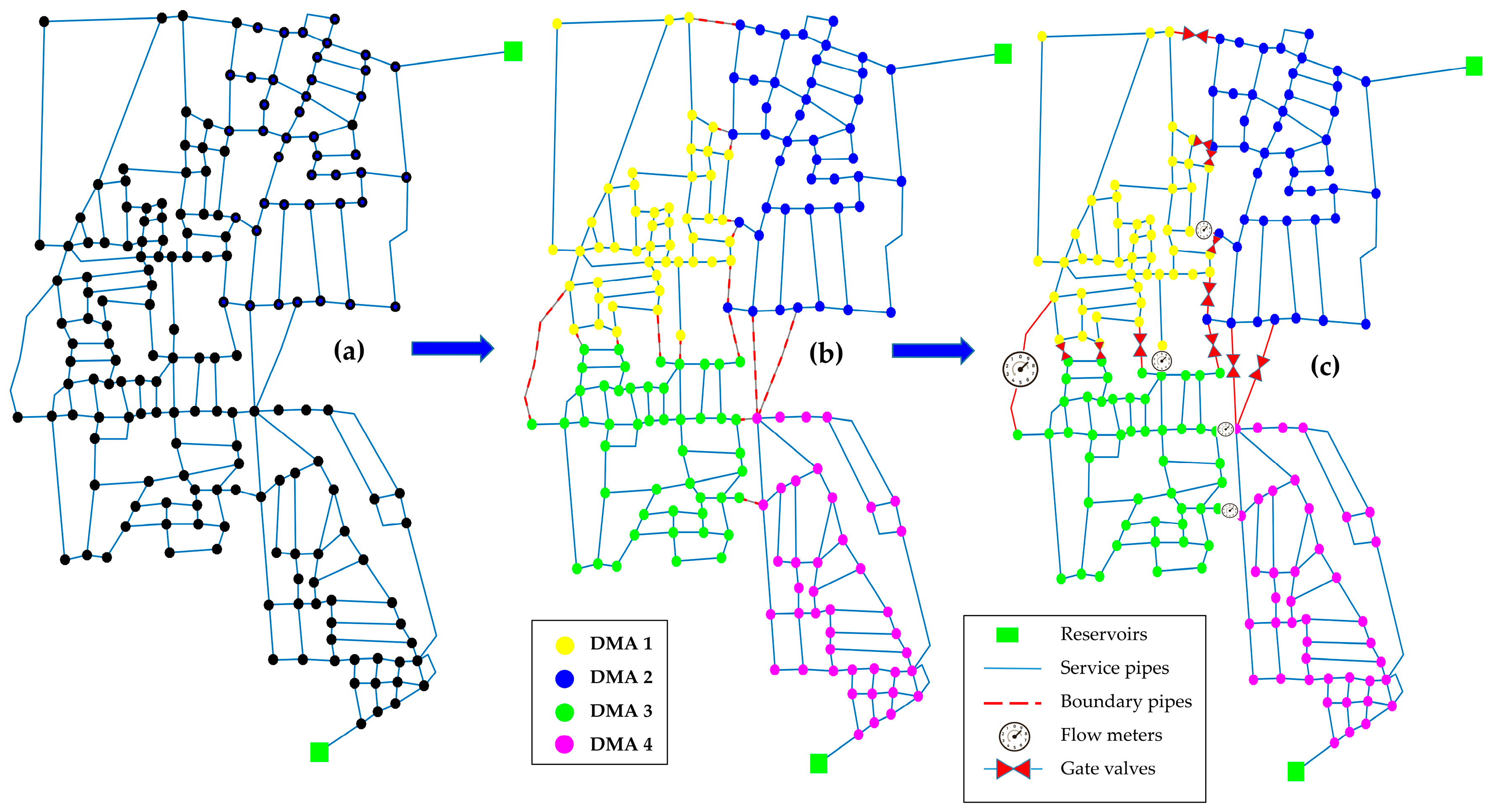
2. Principles of District Metered Areas
- Maximum percentage of leakage allowed by the water utility;
- Topography and number of properties per DMA;
- Characteristics and topological taxonomy of WDNs;
- Variations in nodal elevation, water demand, and pressure;
- The number of flow meters and gate valves; and
- Water quality considerations.
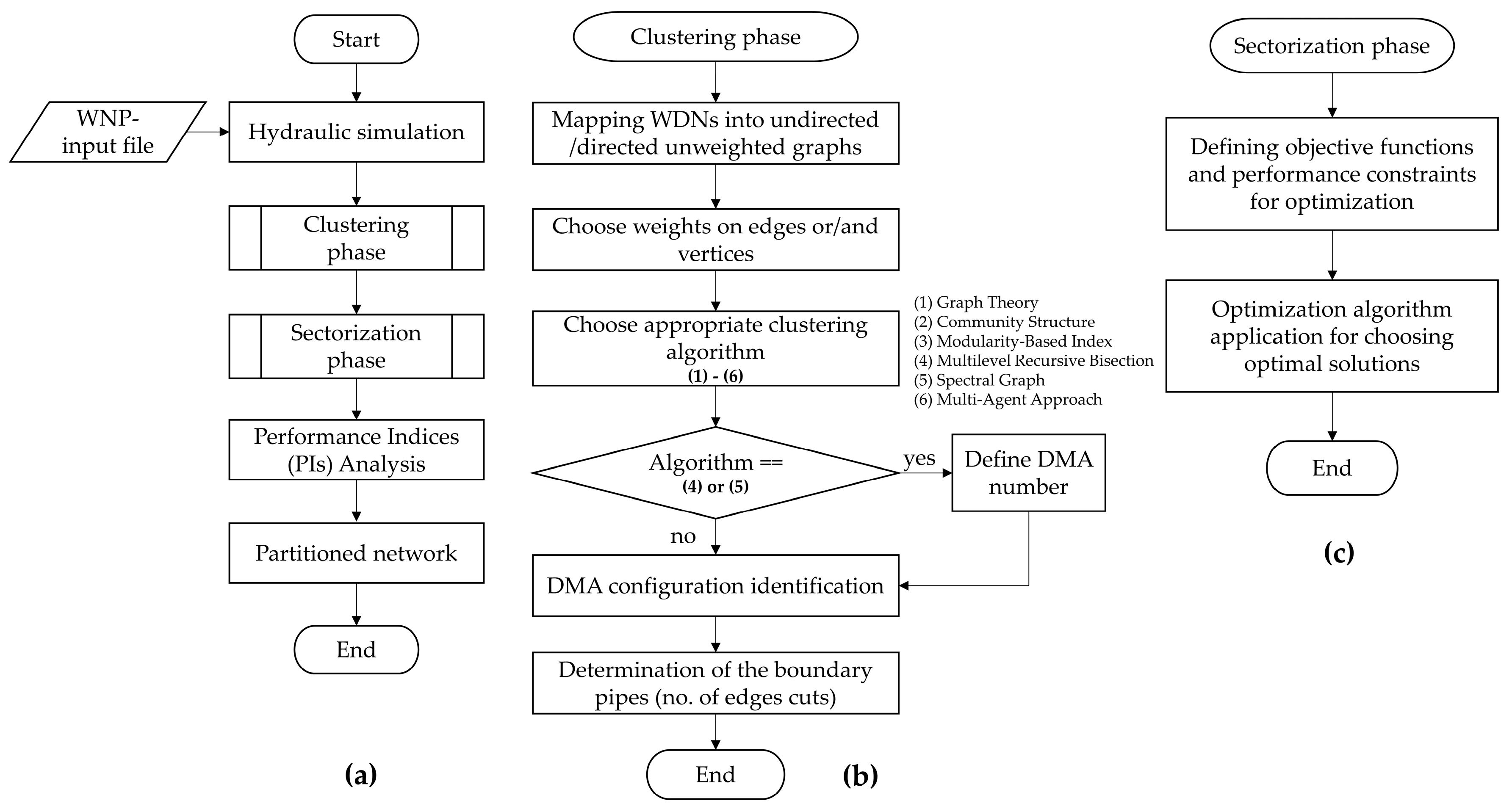
3. Clustering to Create Feasible DMAs
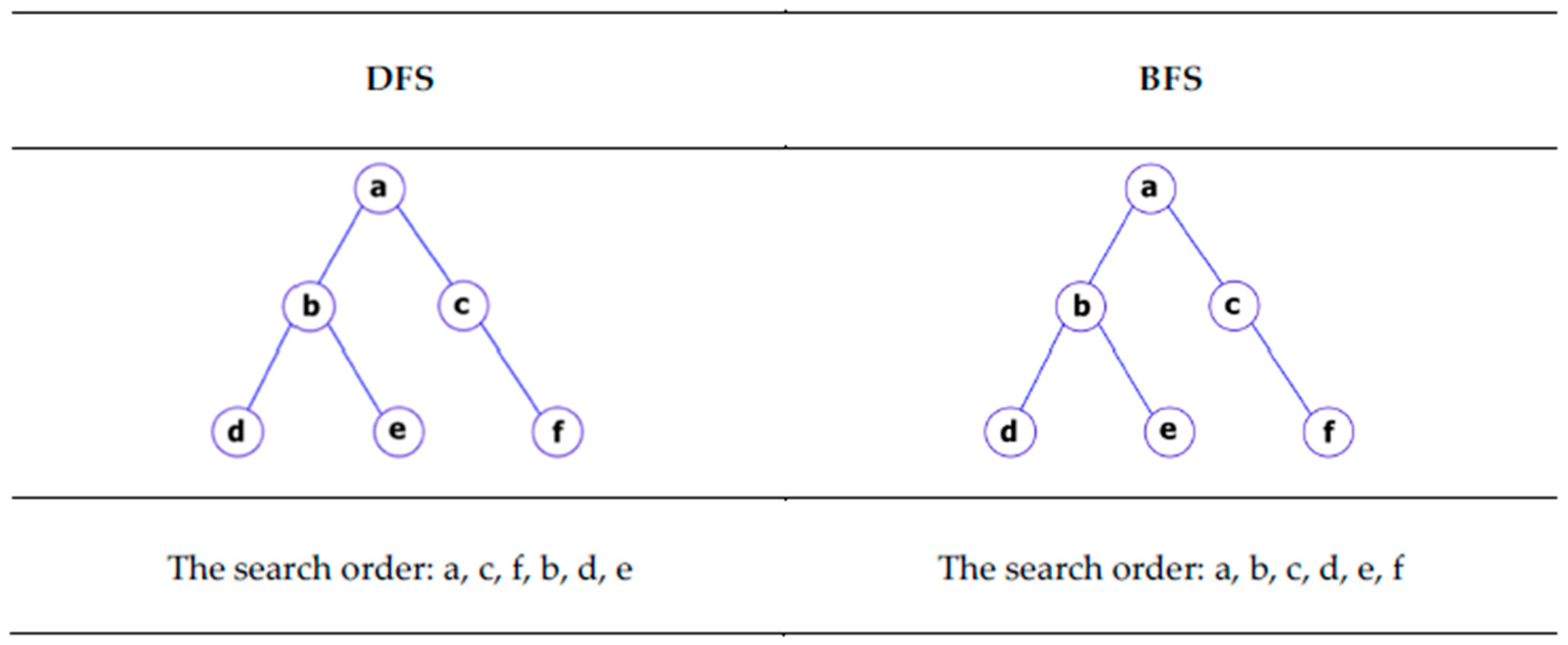
3.1. Graph Theory
3.2. Community Structure Algorithm
3.3. Modularity-Based Algorithm
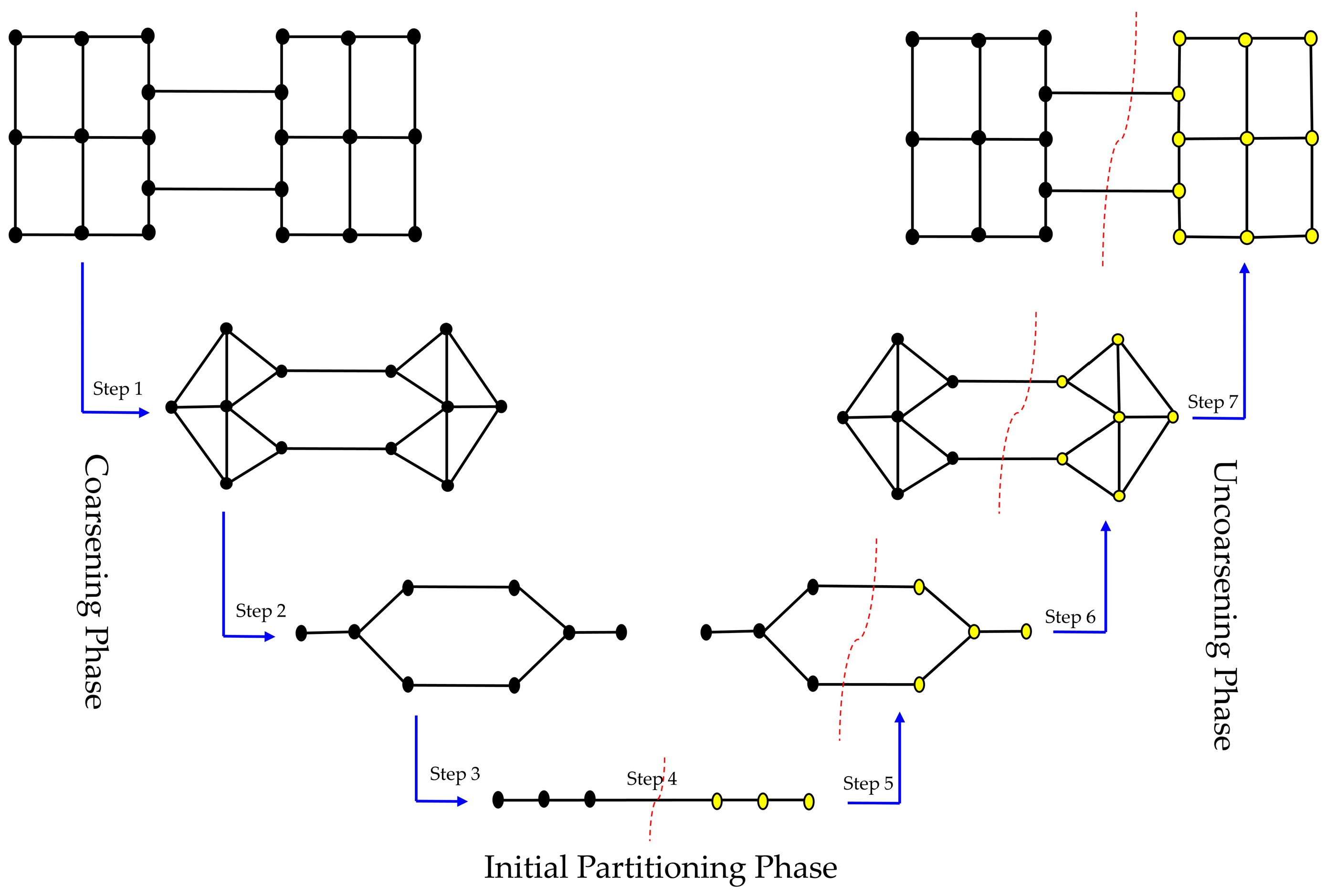
3.4. Multilevel Graph Partitioning
3.5. Spectral Graph Algorithms
- is symmetric and positive-semidefinite with eigenvalues for all .
- Every row sum and column sum of equals zero.
- The smallest eigenvalue of equals zero.
- has non-negative and the number of connected components in the graph equals the algebraic multiplicity of .
- intracluster edges:, and
- intercluster edges:.
3.6. Multi-Agent Approach
- Each agent has an imperfect standard or may lack the capacity for problem solving, and therefore has a somewhat limited and unbalanced perspective;
- There is no global information;
- Data is decentralized; and
- Computation is asynchronous.
4. Sectorization to Locate Flow Meters and Valves
4.1. Single-Objective Optimization Approach
4.2. Multiple-Objective Optimization Approach
4.3. Iterative Approach
4.4. Adaptive Sectorization for Dynamic DMAs
5. Performance Assessment of Water Network Partitioning
6. Discussion and Future Work
- Clustering is the crucial phase for WNP. Several algorithms and software tools were developed to deal with the large-scale networks that are burdensome to tackle manually. Various engineering aspects were embedded as weights to modulate WDN characteristics. More extensions of the existing graph clustering algorithms to weighted networks would be of great interest, as well as novel methods for clustering directed graphs.
- While there were many different approaches for the identification of DMAs in water networks, few studies tackled to determine the optimal number of DMAs for a given network. It is an open question and requires a decision-making procedure utilizing various network performance quantification metrics.
- In the sectorization phase, it still lacks how to assess the pump and tank operations in the partitioned network. Moreover, an approach to consider the consequences of device placements to the leakage, energy use, and post-damage restoration should be studied quantitatively in this phase.
- A demand-driven analysis (DDA) is generally used for WNP under the normal working condition at peak hour demand. In DDA, the supplied demand is assumed to be independent of pressure and this approach is valid when the pressure is above the minimum pressure requirement. In reality, a WDN works more likely as a pressure-driven analysis (PDA), in which the nodal consumption depends on the nodal pressure. Therefore, in pressure-deficient conditions (e.g., pipe failures, fire-fighting, unexpected water demand increase), a PDA should be applied for the novel dynamic WNP that adapts flexibly under the abnormal operating conditions.
- Last but not least, a WDN is supplied by single or multiple sources, with different elevations, divergent intended pressure in each zone. It also can be expanded or replaced according to urban planning needs. Further research should address the change of network’s topology, controlling hydraulic uniformity in each zone as well as improving system resilience. Future research needs to be conducted to improve the abovementioned limits and eventually to provide optimal DMA layouts for efficient network operation and management.
Author Contributions
Funding
Conflicts of Interest
References
- Lifshitz, R.; Ostfeld, A. Clustering for Analysis of Water Distribution Systems. J. Water Resour. Plan. Manag. 2018, 144, 04018016. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Di Mauro, A. Water Supply Network District Metering: Theory and Case Study; CISM Courses and Lectures; Springer: Wien, Austria; New York, NY, USA, 2013. [Google Scholar]
- Saldarriaga, J.; Bohorquez, J.; Celeita, D.; Vega, L.; Paez, D.; Savic, D.; Dandy, G.; Filion, Y.; Grayman, W.; Kapelan, Z. Battle of the Water Networks District Metered Areas. J. Water Resour. Plan. Manag. 2019, 145, 04019002. [Google Scholar] [CrossRef]
- Morrison, J.; Tooms, S.; Rogers, D. DMA Management Guidance Notes; IWA Publishing: London, UK, 2007. [Google Scholar]
- UK Water Industry Research Limited. A Manual of DMA Practice; UK Water Industry Research Limited: London, UK, 1999. [Google Scholar]
- Di Nardo, A.; Di Natale, M.; Santonastaso, G.F.; Tzatchkov, V.G.; Alcocer-Yamanaka, V.H. Water Network Sectorization Based on Graph Theory and Energy Performance Indices. J. Water Resour. Plan. Manag. 2014, 140, 620–629. [Google Scholar] [CrossRef]
- Ilaya-Ayza, A.; Martins, C.; Campbell, E.; Izquierdo, J. Implementation of DMAs in Intermittent Water Supply Networks Based on Equity Criteria. Water 2017, 9, 851. [Google Scholar] [CrossRef] [Green Version]
- Ciaponi, C.; Creaco, E.; Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Musmarra, D.; Santonastaso, G. Reducing Impacts of Contamination in Water Distribution Networks: A Combined Strategy Based on Network Partitioning and Installation of Water Quality Sensors. Water 2019, 11, 1315. [Google Scholar] [CrossRef] [Green Version]
- Scarpa, F.; Lobba, A.; Becciu, G. Elementary DMA Design of Looped Water Distribution Networks with Multiple Sources. J. Water Resour. Plan. Manag. 2016, 142, 04016011. [Google Scholar] [CrossRef] [Green Version]
- Grayman, W.M.; Murray, R.; Savic, D.A. Effects of Redesign of Water Systems for Security and Water Quality Factors. In World Environmental and Water Resources Congress 2009; American Society of Civil Engineers: Kansas City, MO, USA, 2009; pp. 1–11. [Google Scholar] [CrossRef]
- Farley, M. Leakage Management and Control: A Best Practice Training Manual; No. WHO/SDE/WSH/01.1; World Health Organization: Geneva, Switzerland, 2001. [Google Scholar]
- Puust, R.; Kapelan, Z.; Savic, D.A.; Koppel, T. A Review of Methods for Leakage Management in Pipe Networks. Urban Water J. 2010, 7, 25–45. [Google Scholar] [CrossRef]
- Beuken, R.H.S.; Lavooij, C.S.W.; Bosch, A.; Schaap, P.G. Low Leakage in the Netherlands Confirmed. In Water Distribution Systems Analysis Symposium 2006; American Society of Civil Engineers: Cincinnati, OH, USA, 2008; pp. 1–8. [Google Scholar] [CrossRef]
- Lambert, A.O. International Report: Water Losses Management and Techniques. Water Sci. Technol. Water Supply 2002, 2, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Lambert, A. Relationships between pressure, bursts and infrastructure life-an international perspective. In Proceedings of the Water UK Annual Leakage Conference, Coventry, UK, 18 October 2012. [Google Scholar]
- Giugni, M.; Fontana, N.; Portolano, D.; Romanelli, D. A DMA design for “Napoli Est” water distribution system. In Proceedings of the 13th IWRA World Water Congress, Montpellier, France, 1–4 September 2008. [Google Scholar]
- Di Nardo, A.; Di Natale, M.; Santonastaso, G.F.; Venticinque, S. An Automated Tool for Smart Water Network Partitioning. Water Resour. Manag. 2013, 27, 4493–4508. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Musmarra, D.; Santonastaso, G.F.; Tuccinardi, F.P.; Zaccone, G. Software for Partitioning and Protecting a Water Supply Network. Civ. Eng. Environ. Syst. 2016, 33, 55–69. [Google Scholar] [CrossRef]
- Diao, K.; Zhou, Y.; Rauch, W. Automated Creation of District Metered Area Boundaries in Water Distribution Systems. J. Water Resour. Plan. Manag. 2013, 139, 184–190. [Google Scholar] [CrossRef]
- Savić, D.; Ferrari, G. Design and Performance of District Metering Areas in Water Distribution Systems. Procedia Eng. 2014, 89, 1136–1143. [Google Scholar] [CrossRef] [Green Version]
- Rajeswaran, A.; Narasimhan, S.; Narasimhan, S. A Graph Partitioning Algorithm for Leak Detection in Water Distribution Networks. Comput. Chem. Eng. 2018, 108, 11–23. [Google Scholar] [CrossRef] [Green Version]
- Kunkel, G. Committee Report: Applying worldwide BMPs in water loss control. J. Am. Water Work. Assoc. 2003, 95, 65–79. [Google Scholar]
- Gomes, R.; Sá Marques, A.; Sousa, J. Estimation of the Benefits Yielded by Pressure Management in Water Distribution Systems. Urban Water J. 2011, 8, 65–77. [Google Scholar] [CrossRef]
- Huang, P.; Zhu, N.; Hou, D.; Chen, J.; Xiao, Y.; Yu, J.; Zhang, G.; Zhang, H. Real-Time Burst Detection in District Metering Areas in Water Distribution System Based on Patterns of Water Demand with Supervised Learning. Water 2018, 10, 1765. [Google Scholar] [CrossRef] [Green Version]
- Ferrari, G.; Savic, D. Economic Performance of DMAs in Water Distribution Systems. Procedia Eng. 2015, 119, 189–195. [Google Scholar] [CrossRef] [Green Version]
- Lifshitz, R.; Ostfeld, A. District Metering Areas and Pressure Reducing Valves Trade-Off in Water Distribution System Leakage Management. In Proceedings of the WDSA/CCWI Joint Conference Proceedings, Kingston, ON, Canada, 23–25 July 2018; Volume 1. [Google Scholar]
- Marchi, A.; Salomons, E.; Ostfeld, A.; Kapelan, Z.; Simpson, A.R.; Zecchin, A.C.; Maier, H.R.; Wu, Z.Y.; Elsayed, S.M.; Song, Y.; et al. Battle of the Water Networks II. J. Water Resour. Plan. Manag. 2014, 140, 04014009. [Google Scholar] [CrossRef] [Green Version]
- Di Nardo, A.; Di Natale, M.; Musmarra, D.; Santonastaso, G.F.; Tzatchkov, V.; Alcocer-Yamanaka, V.H. Dual-Use Value of Network Partitioning for Water System Management and Protection from Malicious Contamination. J. Hydroinform. 2015, 17, 361–376. [Google Scholar] [CrossRef]
- UKWIR. Effect of District Meter Areas on Water Quality; UK Water Industry Research Limited: London, UK, 2000. [Google Scholar]
- WRc. The Effects of System Operation on Water Quality in Distribution; WRc: Swindon, UK, 2000. [Google Scholar]
- Armand, H.; Stoianov, I.; Graham, N. Impact of Network Sectorisation on Water Quality Management. J. Hydroinform. 2018, 20, 424–439. [Google Scholar] [CrossRef] [Green Version]
- Javier Martínez-Solano, F.; Iglesias-Rey, P.L.; Mora Meliá, D.; Ribelles-Aguilar, J.V. Combining Skeletonization, Setpoint Curves, and Heuristic Algorithms to Define District Metering Areas in the Battle of Water Networks District Metering Areas. J. Water Resour. Plan. Manag. 2018, 144, 04018023. [Google Scholar] [CrossRef]
- Salomons, E.; Skulovich, O.; Ostfeld, A. Battle of Water Networks DMAs: Multistage Design Approach. J. Water Resour. Plan. Manag. 2017, 143, 04017059. [Google Scholar] [CrossRef]
- Campbell, E.; Ayala-Cabrera, D.; Izquierdo, J.; Pérez-García, R.; Tavera, M. Water Supply Network Sectorization Based on Social Networks Community Detection Algorithms. Procedia Eng. 2014, 89, 1208–1215. [Google Scholar] [CrossRef] [Green Version]
- Giudicianni, C.; Di Nardo, A.; Di Natale, M.; Greco, R.; Santonastaso, G.; Scala, A. Topological Taxonomy of Water Distribution Networks. Water 2018, 10, 444. [Google Scholar] [CrossRef] [Green Version]
- Giudicianni, C.; Herrera, M.; di Nardo, A.; Adeyeye, K. Automatic Multiscale Approach for Water Networks Partitioning into Dynamic District Metered Areas. Water Resour. Manag. 2020. [Google Scholar] [CrossRef] [Green Version]
- Sela Perelman, L.; Allen, M.; Preis, A.; Iqbal, M.; Whittle, A.J. Automated Sub-Zoning of Water Distribution Systems. Environ. Model. Softw. 2015, 65, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Tzatchkov, V.G.; Alcocer-Yamanaka, V.H.; Bourguett Ortíz, V. Graph Theory Based Algorithms for Water Distribution Network Sectorization Projects. In Water Distribution Systems Analysis Symposium 2006; American Society of Civil Engineers: Cincinnati, OH, USA, 2008; pp. 1–15. [Google Scholar] [CrossRef]
- Perelman, L.; Ostfeld, A. Topological Clustering for Water Distribution Systems Analysis. Environ. Model. Softw. 2011, 26, 969–972. [Google Scholar] [CrossRef]
- Ciaponi, C.; Murari, E.; Todeschini, S. Modularity-Based Procedure for Partitioning Water Distribution Systems into Independent Districts. Water Resour. Manag. 2016, 30, 2021–2036. [Google Scholar] [CrossRef]
- Giustolisi, O.; Ridolfi, L. New Modularity-Based Approach to Segmentation of Water Distribution Networks. J. Hydraul. Eng. 2014, 140, 04014049. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, Z.Y.; Zhao, M.; Qi, J.; Huang, Y.; Zhao, H. Automatic Partitioning of Water Distribution Networks Using Multiscale Community Detection and Multiobjective Optimization. J. Water Resour. Plan. Manag. 2017, 143, 04017057. [Google Scholar] [CrossRef]
- Brentan, B.M.; Campbell, E.; Meirelles, G.L.; Luvizotto, E.; Izquierdo, J. Social Network Community Detection for DMA Creation: Criteria Analysis through Multilevel Optimization. Math. Probl. Eng. 2017, 2017, 1–12. [Google Scholar] [CrossRef]
- Brentan, B.; Campbell, E.; Goulart, T.; Manzi, D.; Meirelles, G.; Herrera, M.; Izquierdo, J.; Luvizotto, E. Social Network Community Detection and Hybrid Optimization for Dividing Water Supply into District Metered Areas. J. Water Resour. Plan. Manag. 2018, 144, 04018020. [Google Scholar] [CrossRef] [Green Version]
- Sempewo, J.; Pathirana, A.; Vairavamoorthy, K. Spatial Analysis Tool for Development of Leakage Control Zones from the Analogy of Distributed Computing. In Water Distribution Systems Analysis 2008; American Society of Civil Engineers: Kruger National Park, South Africa, 2009; pp. 1–15. [Google Scholar] [CrossRef] [Green Version]
- Alvisi, S. A New Procedure for Optimal Design of District Metered Areas Based on the Multilevel Balancing and Refinement Algorithm. Water Resour. Manag. 2015, 29, 4397–4409. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Greco, R.; Santonastaso, G.F. Weighted Spectral Clustering for Water Distribution Network Partitioning. Appl. Netw. Sci. 2017, 2, 19. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Han, R. Spectral Clustering and Multicriteria Decision for Design of District Metered Areas. J. Water Resour. Plan. Manag. 2018, 144, 04018013. [Google Scholar] [CrossRef]
- Di Nardo, A.; Giudicianni, C.; Greco, R.; Herrera, M.; Santonastaso, G. Applications of Graph Spectral Techniques to Water Distribution Network Management. Water 2018, 10, 45. [Google Scholar] [CrossRef] [Green Version]
- Herrera, M.; Izquierdo, J.; Pérez-García, R.; Ayala-Cabrera, D. Water Supply Clusters by Multi-Agent Based Approach. In Water Distribution Systems Analysis 2010; American Society of Civil Engineers: Tucson, AZ, USA, 2011; pp. 861–869. [Google Scholar] [CrossRef]
- Hajebi, S.; Barrett, S.; Clarke, A.; Clarke, S. Multi-agent simulation to support water distribution network partitioning. In Proceedings of the Modelling and Simulation 2013-European Simulation and Modelling Conference, ESM 2013, (Fernández), Lancaster, UK, 23–25 October 2013; pp. 163–168. [Google Scholar]
- Herrera, M.; Izquierdo, J.; Pérez-García, R.; Montalvo, I. Multi-Agent Adaptive Boosting on Semi-Supervised Water Supply Clusters. Adv. Eng. Softw. 2012, 50, 131–136. [Google Scholar] [CrossRef]
- Schaeffer, S.E. Graph Clustering. Comput. Sci. Rev. 2007, 1, 27–64. [Google Scholar] [CrossRef]
- Song, S.; Zhao, J. Survey of Graph Clustering Algorithms Using Amazon Reviews. In Proceedings of the 17th International Conference on World Wide Web, Beijing, China, 21–25 April 2008. [Google Scholar]
- Tarjan, R. Depth-first search and linear graph algorithms. SIAM J. Comput. 1972, 1, 146–160. [Google Scholar] [CrossRef]
- Pohl, I.S. Bi-Directional and Heuristic Search in Path Problems. Ph.D. Thesis, Stanford Linear Accelerator Center, Stanford University, Stanford, CA, USA, 1969. [Google Scholar]
- Di Battista, G.; Eades, P.; Tamassia, R.; Tollis, I.G. Graph Drawing: Algorithms for the Visualization of Graphs; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Campbell, E.; Izquierdo, J.; Montalvo, I.; Ilaya-Ayza, A.; Pérez-García, R.; Tavera, M. A Flexible Methodology to Sectorize Water Supply Networks Based on Social Network Theory Concepts and Multi-Objective Optimization. J. Hydroinform. 2016, 18, 62–76. [Google Scholar] [CrossRef] [Green Version]
- Campbell, E.; Izquierdo, J.; Montalvo, I.; Pérez-García, R. A Novel Water Supply Network Sectorization Methodology Based on a Complete Economic Analysis, Including Uncertainties. Water 2016, 8, 179. [Google Scholar] [CrossRef] [Green Version]
- Alvisi, S.; Franchini, M. A Heuristic Procedure for the Automatic Creation of District Metered Areas in Water Distribution Systems. Urban Water J. 2014, 11, 137–159. [Google Scholar] [CrossRef]
- Gomes, R.; Marques, A.S.; Sousa, J. Decision Support System to Divide a Large Network into Suitable District Metered Areas. Water Sci. Technol. 2012, 65, 1667–1675. [Google Scholar] [CrossRef]
- Borgwardt, K.M.; Kriegel, H. Shortest-Path Kernels on Graphs. In Proceedings of the Fifth IEEE International Conference on Data Mining (ICDM’05), Houston, TX, USA, 27–30 November 2005; pp. 74–81. [Google Scholar] [CrossRef] [Green Version]
- Newman, M.E.J.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [Green Version]
- Clauset, A.; Newman, M.E.J.; Moore, C. Finding Community Structure in Very Large Networks. Phys. Rev. E 2004, 70, 066111. [Google Scholar] [CrossRef] [Green Version]
- Fortunato, S.; Barthelemy, M. Resolution Limit in Community Detection. Proc. Natl. Acad. Sci. USA 2007, 104, 36–41. [Google Scholar] [CrossRef] [Green Version]
- Giustolisi, O.; Ridolfi, L. A Novel Infrastructure Modularity Index for the Segmentation of Water Distribution Networks. Water Resour. Res. 2014, 50, 7648–7661. [Google Scholar] [CrossRef]
- Laucelli, D.B.; Simone, A.; Berardi, L.; Giustolisi, O. Optimal Design of District Metering Areas for the Reduction of Leakages. J. Water Resour. Plan. Manag. 2017, 143, 04017017. [Google Scholar] [CrossRef]
- Simone, A.; Giustolisi, O.; Laucelli, D.B. A Proposal of Optimal Sampling Design Using a Modularity Strategy: Optimal Sampling Design. Water Resour. Res. 2016, 52, 6171–6185. [Google Scholar] [CrossRef] [Green Version]
- Fortunato, S. Community Detection in Graphs. Phys. Rep. 2010, 486, 75–174. [Google Scholar] [CrossRef] [Green Version]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Greco, R.; Santonastaso, G.F. Water Distribution Network Clustering: Graph Partitioning or Spectral Algorithms? In Complex Networks & Their Applications VI; Cherifi, C., Cherifi, H., Karsai, M., Musolesi, M., Eds.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Liu, H.; Zhao, M.; Zhang, C.; Fu, G. Comparing Topological Partitioning Methods for District Metered Areas in the Water Distribution Network. Water 2018, 10, 368. [Google Scholar] [CrossRef] [Green Version]
- Karypis, G.; Kumar, V. Multilevelk-Way Partitioning Scheme for Irregular Graphs. J. Parallel Distrib. Comput. 1998, 48, 96–129. [Google Scholar] [CrossRef] [Green Version]
- Creaco, E.; Cunha, M.; Franchini, M. Using Heuristic Techniques to Account for Engineering Aspects in Modularity-Based Water Distribution Network Partitioning Algorithm. J. Water Resour. Plan. Manag. 2019, 145, 04019062. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A Fast Elitist Non-Dominated Sorting Genetic Algorithm for Multi-Objective Optimization: NSGA-II. In Parallel Problem Solving from Nature PPSN VI; Schoenauer, M., Deb, K., Rudolph, G., Yao, X., Lutton, E., Merelo, J.J., Schwefel, H.-P., Eds.; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1917, pp. 849–858. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Santonastaso, G.; Tzatchkov, V.; Varela, J. Economic and Energy Criteria for District Meter Areas Design of Water Distribution Networks. Water 2017, 9, 463. [Google Scholar] [CrossRef] [Green Version]
- Yazdani, A.; Jeffrey, P. Robustness and vulnerability analysis of water distribution networks using graph theoretic and complex network principles. In Water Distribution Systems Analysis 2010, Proceedings of the 12th International Conference, WDSA 2010, Tucson, AZ, USA, 12–15 September 2010; American Society of Civil Engineers: Reston, VA, USA, 2010; pp. 933–945. [Google Scholar] [CrossRef]
- Yazdani, A.; Jeffrey, P. Complex network analysis of water distribution systems. Chaos Interdiscip. J. Nonlinear Sci. 2011, 21. [Google Scholar] [CrossRef] [Green Version]
- Von Luxburg, U. A tutorial on spectral clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Mohar, B.; Alavi, Y.; Chartrand, G.; Oellermann, O.R. The Laplacian spectrum of graphs. In Graph Theory, Combinatorics, and Applications; Wiley: Hoboken, NJ, USA, 1991; pp. 871–898. [Google Scholar]
- Shi, J.; Malik, J. Normalized Cuts and Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 888–905. [Google Scholar] [CrossRef] [Green Version]
- Zevnik, J.; Kramar Fijavž, M.; Kozelj, D. Generalized Normalized Cut and Spanning Trees for Water Distribution Network Partitioning. J. Water Resour. Plan. Manag. 2019, 145, 04019041. [Google Scholar] [CrossRef]
- Bonacich, P. Power and centrality: A family of measures. Am. J. Sociol. 1987, 92, 1170–1182. [Google Scholar] [CrossRef]
- Freeman, L.C. A set of measures of centrality based on betweenness. Sociometry 1977, 40, 35–41. [Google Scholar] [CrossRef]
- Zevnik, J.; Kozelj, D. Partition of Water Distribution Networks into District Metered Areas Using a Graph Theoretical Approach. In Proceedings of the 13th International Conference on Hydroinformatics, Palermo, Italy, 1–6 July 2018; pp. 2408–2417. [Google Scholar] [CrossRef]
- Herrera, M.; Canu, S.; Karatzoglou, A.; Perez-García, R.; Izquierdo, J. An approach to water supply clusters by semi-supervised learning. In Modelling for Environment’s Sake: Proceedings of the 5th Biennial Conference of the International Environmental Modelling and Software Society, IEMSs 2010, Ottawa, ON, Canada, 5–8 July 2010; International Environmental Modelling and Software Society: Ottawa, ON, Canada, 2010; Volume 3, pp. 1925–1932. [Google Scholar]
- Zhu, X.; Kandola, J.; Lafferty, J.; Ghahramani, Z. Graph Kernels by Spectral Transforms. In Semi-Supervised Learning; MIT Press: Cambridge, MA, USA, 2006; pp. 277–291. [Google Scholar]
- Scholkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Giudicianni, C.; Herrera, M.; di Nardo, A.; Carravetta, A.; Ramos, H.M.; Adeyeye, K. Zero-Net Energy Management for the Monitoring and Control of Dynamically-Partitioned Smart Water Systems. J. Clean. Prod. 2020, 252, 119745. [Google Scholar] [CrossRef]
- Sycara, K.P. Multiagent Systems. AI Mag. 1998, 19, 79. [Google Scholar] [CrossRef]
- Izquierdo, J.; Herrera, M.; Montalvo, I.; Pérez-García, R. Agent-based division of water distribution systems into district metered areas. In Proceedings of the 4th International Conference on Software and Data Technologies, Sofia, Bulgaria, 26–29 July 2009; SciTePress-Science and and Technology Publications: Sofia, Bulgaria, 2009; pp. 83–90. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Santonastaso, G.F.; Tzatchkov, V.G.; Alcocer-Yamanaka, V.H. Water Network Sectorization Based on a Genetic Algorithm and Minimum Dissipated Power Paths. Water Sci. Technol. Water Supply 2013, 13, 951–957. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Greco, R.; Santonastaso, G.F. Ant Algorithm for Smart Water Network Partitioning. Procedia Eng. 2014, 70, 525–534. [Google Scholar] [CrossRef] [Green Version]
- Ferrari, G.; Savic, D.; Becciu, G. Graph-Theoretic Approach and Sound Engineering Principles for Design of District Metered Areas. J. Water Resour. Plan. Manag. 2014, 140, 04014036. [Google Scholar] [CrossRef] [Green Version]
- Gilbert, D.; Abraham, E.; Montalvo, I.; Piller, O. Iterative multistage method for a large water network sectorization into DMAs under multiple design objectives. J. Water Resour. Plan. Manag. 2017, 143, 04017067. [Google Scholar] [CrossRef] [Green Version]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Musmarra, D.; Santonastaso, G.F.; Simone, A. Water Distribution System Clustering and Partitioning Based on Social Network Algorithms. Procedia Eng. 2015, 119, 196–205. [Google Scholar] [CrossRef] [Green Version]
- Di Nardo, A.; Di Natale, M. A Heuristic Design Support Methodology Based on Graph Theory for District Metering of Water Supply Networks. Eng. Optim. 2011, 43, 193–211. [Google Scholar] [CrossRef]
- Shao, Y.; Yao, H.; Zhang, T.; Chu, S.; Optimal, X. An Improved Genetic Algorithm for Optimal Layout of Flow Meters and Valves in Water Network Partitioning. Water 2019, 11, 1087. [Google Scholar] [CrossRef] [Green Version]
- Todini, E. Looped Water Distribution Networks Design Using a Resilience Index Based Heuristic Approach. Urban Water 2000, 2, 115–122. [Google Scholar] [CrossRef]
- Gomes, R.; Marques, A.S.A.; Sousa, J. District Metered Areas Design Under Different Decision Makers’ Options: Cost Analysis. Water Resour. Manag. 2013, 27, 4527–4543. [Google Scholar] [CrossRef]
- Creaco, E.; Haidar, H. Multiobjective Optimization of Control Valve Installation and DMA Creation for Reducing Leakage in Water Distribution Networks. J. Water Resour. Plan. Manag. 2019, 145, 04019046. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Holland, J.H. Genetic algorithms and machine learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Gomes, R.; Sá Marques, A.; Sousa, J. Identification of the Optimal Entry Points at District Metered Areas and Implementation of Pressure Management. Urban Water J. 2012, 9, 365–384. [Google Scholar] [CrossRef]
- Zhang, K.; Yan, H.; Zeng, H.; Xin, K.; Tao, T. A Practical Multi-Objective Optimization Sectorization Method for Water Distribution Network. Sci. Total Environ. 2019, 656, 1401–1412. [Google Scholar] [CrossRef]
- De Paola, F.; Fontana, N.; Galdiero, E.; Giugni, M.; Savic, D.; Uberti, G.S. degli. Automatic Multi-Objective Sectorization of a Water Distribution Network. Procedia Eng. 2014, 89, 1200–1207. [Google Scholar] [CrossRef] [Green Version]
- Hajebi, S.; Temate, S.; Barrett, S.; Clarke, A.; Clarke, S. Water Distribution Network Sectorisation Using Structural Graph Partitioning and Multi-Objective Optimization. Procedia Eng. 2014, 89, 1144–1151. [Google Scholar] [CrossRef] [Green Version]
- Gallagher, J.; Styles, D.; McNabola, A.; Williams, A.P. Life Cycle Environmental Balance and Greenhouse Gas Mitigation Potential of Micro-Hydropower Energy Recovery in the Water Industry. J. Clean. Prod. 2015, 99, 152–159. [Google Scholar] [CrossRef]
- Galdiero, E.; De Paola, F.; Fontana, N.; Giugni, M.; Savic, D. Decision Support System for the Optimal Design of District Metered Areas. J. Hydroinform. 2016, 18, 49–61. [Google Scholar] [CrossRef] [Green Version]
- Hadka, D.; Reed, P. Borg: An Auto-Adaptive Many-Objective Evolutionary Computing Framework. Evol. Comput. 2013, 21, 231–259. [Google Scholar] [CrossRef] [PubMed]
- Montalvo, I.; Izquierdo, J.; Pérez-García, R.; Herrera, M. Water Distribution System Computer-Aided Design by Agent Swarm Optimization: Water Distribution System Computer-Aided Design by Agent Swarm Optimization. Comput. Aided Civ. Infrastruct. Eng. 2014, 29, 433–448. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Moosavian, N.; Kasaee Roodsari, B. Soccer League Competition Algorithm: A Novel Meta-Heuristic Algorithm for Optimal Design of Water Distribution Networks. Swarm Evol. Comput. 2014, 17, 14–24. [Google Scholar] [CrossRef]
- Wright, R.; Stoianov, I.; Parpas, P.; Henderson, K.; King, J. Adaptive Water Distribution Networks with Dynamically Reconfigurable Topology. J. Hydroinform. 2014, 16, 1280–1301. [Google Scholar] [CrossRef]
- Perelman, L.S.; Allen, M.; Preis, A.; Iqbal, M.; Whittle, A.J. Flexible Reconfiguration of Existing Urban Water Infrastructure Systems. Environ. Sci. Technol. 2015, 49, 13378–13384. [Google Scholar] [CrossRef] [Green Version]
- Di Nardo, A.; Cavallo, A.; Di Natale, M.; Greco, R.; Santonastaso, G.F. Dynamic Control of Water Distribution System Based on Network Partitioning. Procedia Eng. 2016, 154, 1275–1282. [Google Scholar] [CrossRef] [Green Version]
- Santonastaso, G.F.; Di Nardo, A.; Creaco, E. Dual Topology for Partitioning of Water Distribution Networks Considering Actual Valve Locations. Urban Water J. 2019, 16, 469–479. [Google Scholar] [CrossRef]
- Herrera, M.; Abraham, E.; Stoianov, I. A Graph-Theoretic Framework for Assessing the Resilience of Sectorised Water Distribution Networks. Water Resour. Manag. 2016, 30, 1685–1699. [Google Scholar] [CrossRef] [Green Version]
- Eppstein, D. Finding the k shortest paths. SIAM J. Comput. 1998, 28, 652–673. [Google Scholar] [CrossRef] [Green Version]
- Di Nardo, A.; Di Natale, M.; Santonastaso, G.F.; Tzatchkov, V.G.; Alcocer-Yamanaka, V.H. Performance Indices for Water Network Partitioning and Sectorization. Water Sci. Technol. Water Supply 2015, 15, 499–509. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Guida, M.; Musmarra, D. Water Network Protection from Intentional Contamination by Sectorization. Water Resour. Manag. 2013, 27, 1837–1850. [Google Scholar] [CrossRef]
- Alvisi, S.; Franchini, M. A Procedure for the Design of District Metered Areas in Water Distribution Systems. Procedia Eng. 2014, 70, 41–50. [Google Scholar] [CrossRef] [Green Version]
- Araque, D.; Saldarriaga, J.G. Water Distribution Network Operational Optimization by Maximizing the Pressure Uniformity at Service Nodes. In Impacts of Global Climate Change; American Society of Civil Engineers: Anchorage, AK, USA, 2005; pp. 1–10. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Gargano, R.; Giudicianni, C.; Greco, R.; Santonastaso, G.F. Performance of Partitioned Water Distribution Networks under Spatial-Temporal Variability of Water Demand. Environ. Model. Softw. 2018, 101, 128–136. [Google Scholar] [CrossRef]



| Advantages | Disadvantages |
|---|---|
| Improved burst detection and leakage identification | Reduced resilience to failures |
| Advantaged subarea management and reduced NRW | Reduced operational flexibility |
| Improved subarea pressure control | Potential negative impact on water quality |
| Improved protection against contamination | Security issues in peripheral areas and emergency cases |
| Reduced maintenance and repair costs | High initial investment cost |
| Characterized demand curve, especially at night | Reduced hydraulic redundancy |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khoa Bui, X.; S. Marlim, M.; Kang, D. Water Network Partitioning into District Metered Areas: A State-Of-The-Art Review. Water 2020, 12, 1002. https://doi.org/10.3390/w12041002
Khoa Bui X, S. Marlim M, Kang D. Water Network Partitioning into District Metered Areas: A State-Of-The-Art Review. Water. 2020; 12(4):1002. https://doi.org/10.3390/w12041002
Chicago/Turabian StyleKhoa Bui, Xuan, Malvin S. Marlim, and Doosun Kang. 2020. "Water Network Partitioning into District Metered Areas: A State-Of-The-Art Review" Water 12, no. 4: 1002. https://doi.org/10.3390/w12041002
APA StyleKhoa Bui, X., S. Marlim, M., & Kang, D. (2020). Water Network Partitioning into District Metered Areas: A State-Of-The-Art Review. Water, 12(4), 1002. https://doi.org/10.3390/w12041002





