Microphysical Characteristics of Winter Precipitation in Eastern China from 2014 to 2019
Abstract
1. Introduction
2. Data and Method
2.1. Data Sources
2.2. Quality Control
2.3. Calculation of Integral Parameters
2.4. Classification of Precipitation Types
3. Results
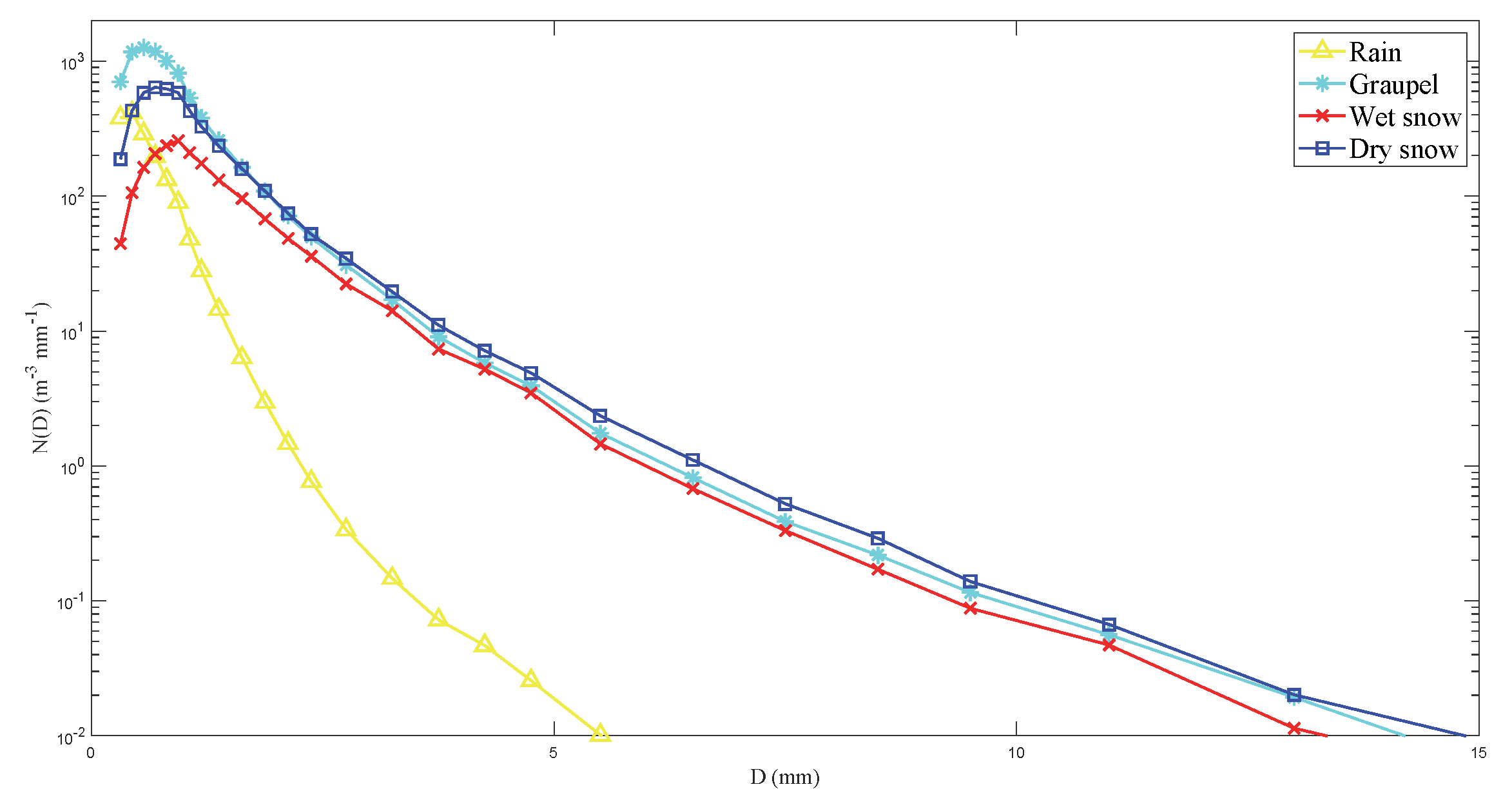
3.1. The PSD of Different Types of Precipitation
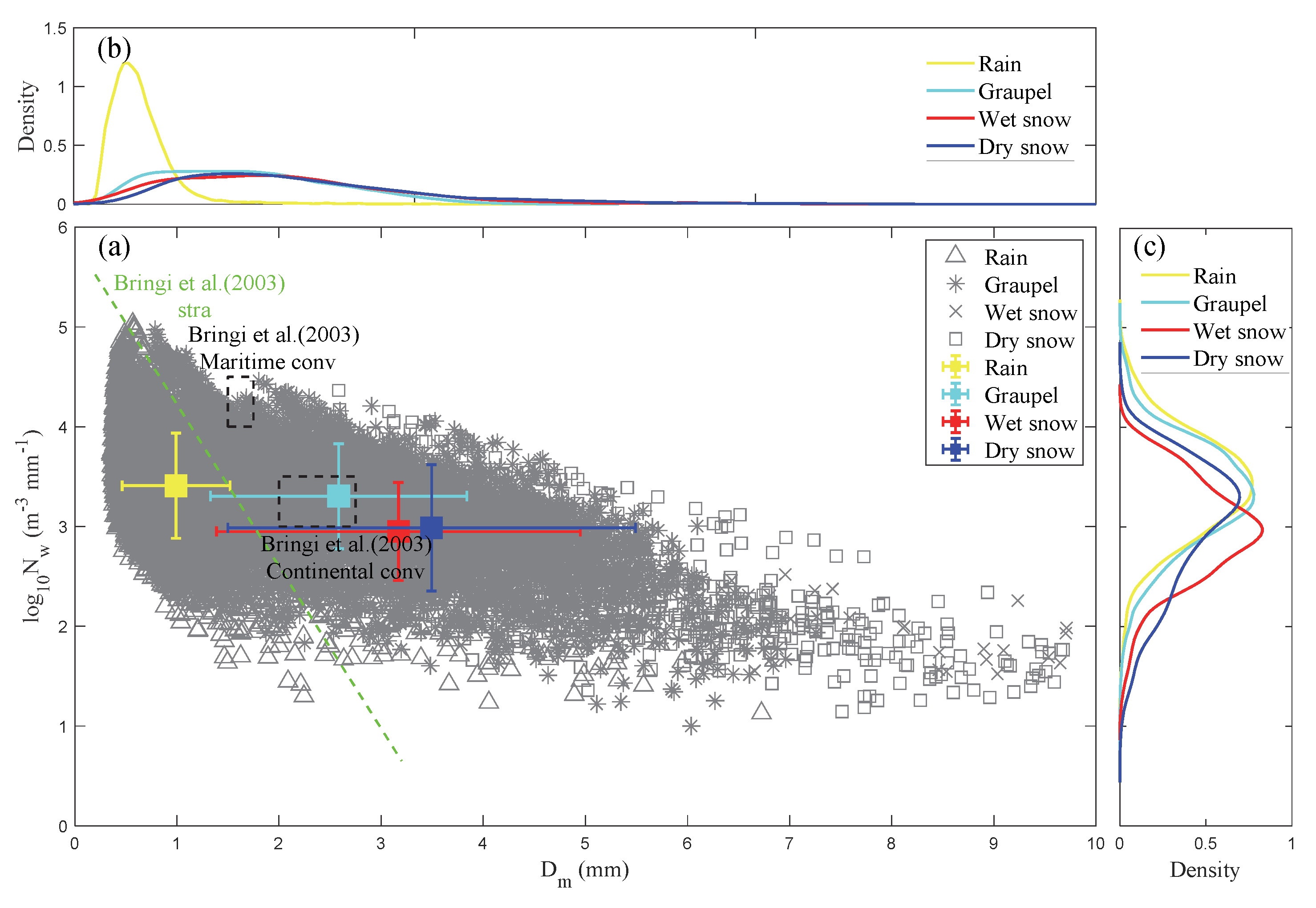
3.2. The log10Nw-Dm Distributions of Different Types of Precipitation
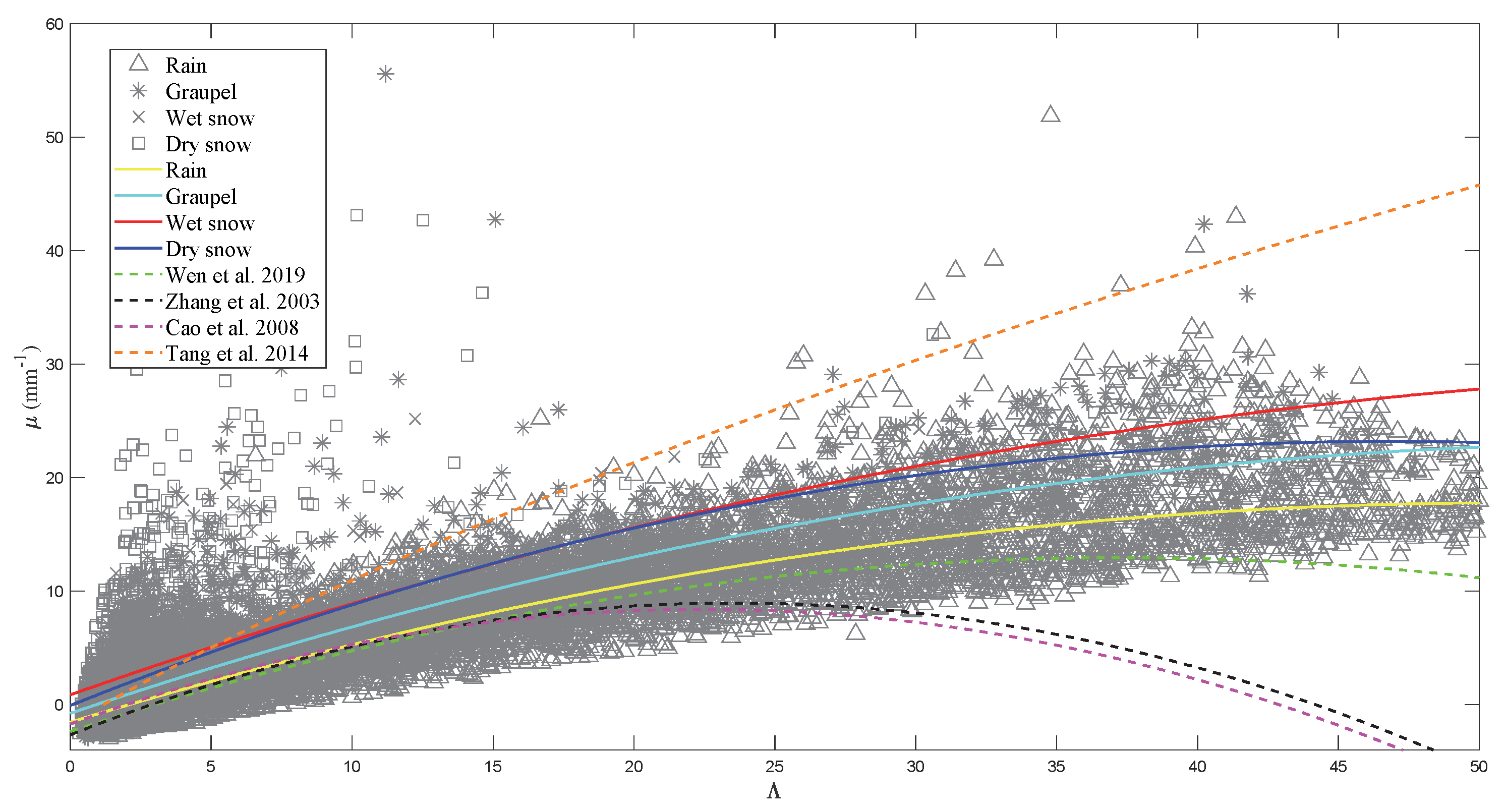
3.3. The μ–Λ Relationships among Different Types of Precipitation
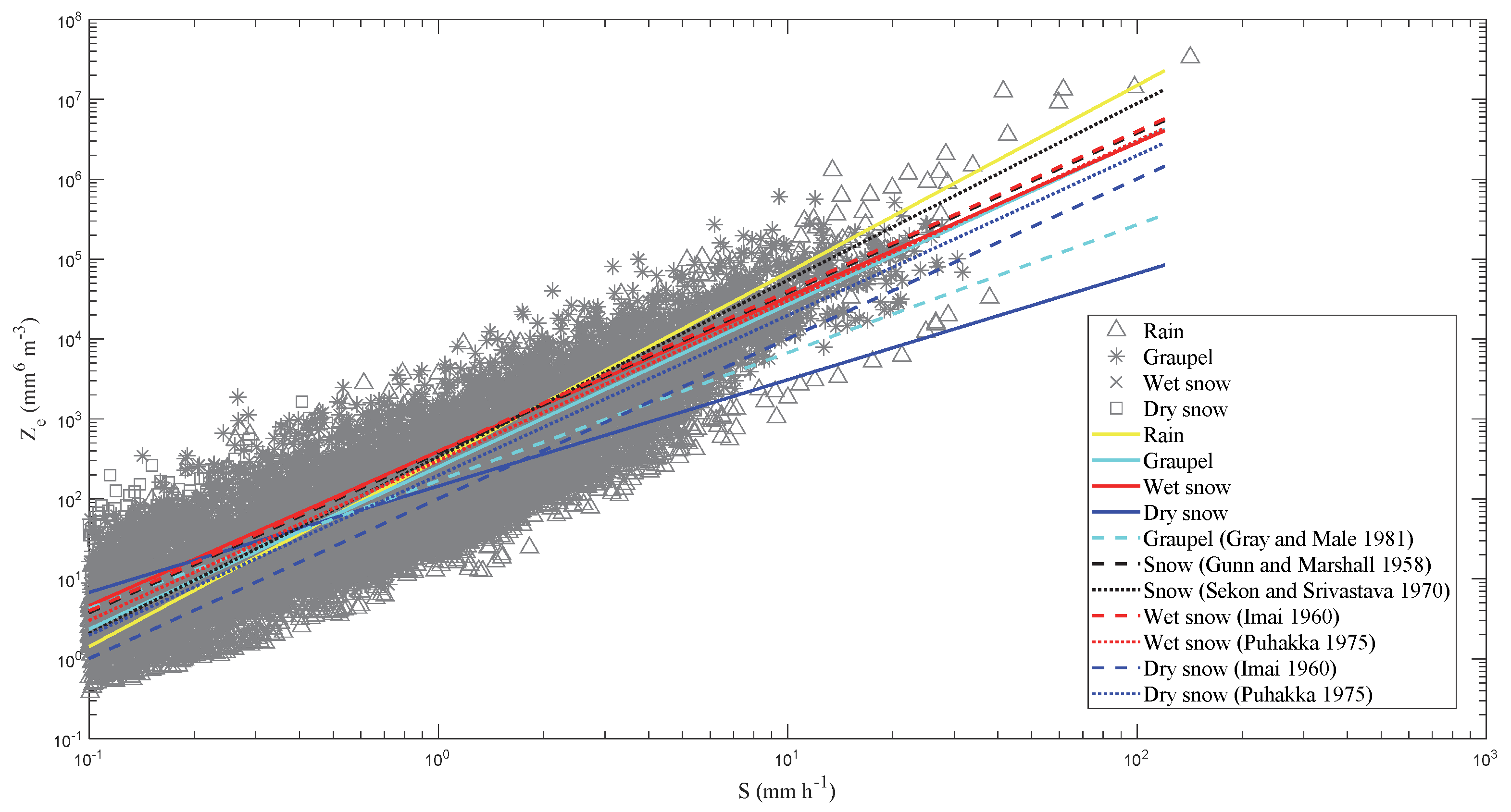
3.4. The Ze–S Relationships among Different Types of Precipitation
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Boudala, F.S.; Isaac, G.A. Parameterization of visibility in snow: Application in numerical weather prediction models. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Rasmussen, R.; Dixon, M.; Vasiloff, S.; Hage, F.; Knight, S.; Vivekanandan, J.; Xu, M. Snow Nowcasting Using a Real-Time Correlation of Radar Reflectivity with Snow Gauge Accumulation. J. Appl. Meteorol. 2003, 42, 20–36. [Google Scholar] [CrossRef]
- Notaroš, B.; Bringi, V.; Kleinkort, C.; Kennedy, P.; Huang, G.-J.; Thurai, M.; Newman, A.; Bang, W.; Lee, G. Accurate Characterization of Winter Precipitation Using Multi-Angle Snowflake Camera, Visual Hull, Advanced Scattering Methods and Polarimetric Radar. Atmosphere 2016, 7, 81. [Google Scholar] [CrossRef]
- Hongyan, L.; Hongbin, C.; Hengchi, L.; Yuxia, W. Relationship between rain rate and radar reflectivity based on the raindrop distribution data in Beijing during 2004. Acta Meteorol. Sin. 2008, 66, 125–129. [Google Scholar] [CrossRef]
- Holt, A.R.; Cummings, R.J.; Upton, G.J.G.; Bradford, W.J. Rain rates, drop size information, and precipitation type, obtained from one-way differential propagation phase and attenuation along a microwave link. Radio Sci. 2008, 43, 1–18. [Google Scholar] [CrossRef]
- Angulo-Martínez, M.; Beguería, S.; Latorre, B.; Fernández-Raga, M. Comparison of precipitation measurements by OTT Parsivel2 and Thies LPM optical disdrometers. Hydrol. Earth Syst. Sci. 2018, 22, 2811–2837. [Google Scholar] [CrossRef]
- Garrett, T.J.; Yuter, S.E. Observed influence of riming, temperature, and turbulence on the fallspeed of solid precipitation. Geophys. Res. Lett. 2014, 41, 6515–6522. [Google Scholar] [CrossRef]
- Praz, C.; Roulet, Y.-A.; Berne, A. Solid hydrometeor classification and riming degree estimation from pictures collected with a Multi-Angle Snowflake Camera. Atmos. Meas. Tech. 2017, 10, 1335–1357. [Google Scholar] [CrossRef]
- Woods, C.P.; Stoelinga, M.T.; Locatelli, J.D. The IMPROVE-1 storm of 1-2 February 2001. Part III: Sensitivity of a mesoscale model simulation to the representation of snow particle types and testing of a bulk microphysical scheme with snow habit prediction. J. Atmos. Sci. 2007, 64, 3927–3948. [Google Scholar] [CrossRef]
- Jia, X.; Liu, Y.; Ding, D.; Ma, X.; Chen, Y.; Bi, K.; Tian, P.; Lu, C.; Quan, J. Combining disdrometer, microscopic photography, and cloud radar to study distributions of hydrometeor types, size and fall velocity. Atmos. Res. 2019, 228, 176–185. [Google Scholar] [CrossRef]
- Yuter, S.E.; Kingsmill, D.E.; Nance, L.B.; Martin, L.-M. Observations of Precipitation Size and Fall Speed Characteristics within Coexisting Rain and Wet Snow. J. Appl. Meteorol. Climatol. 2006, 45, 1450–1464. [Google Scholar] [CrossRef]
- Garrett, T.J.; Yuter, S.E.; Fallgatter, C.; Shkurko, K.; Rhodes, S.R.; Endries, J.L. Orientations and aspect ratios of falling snow. Geophys. Res. Lett. 2015, 42, 4617–4622. [Google Scholar] [CrossRef]
- Angulo-Martínez, M.; López-Vicente, M.; Vicente Serrano, S.M.; Beguería, S. Mapping rainfall erosivity at a regional scale: A comparison of interpolation methods in the ebro basin (ne spain). Hydrol. Earth Syst. Sci. 2009, 13, 1907–1920. [Google Scholar] [CrossRef]
- Nanko, K.; Moskalski, S.M.; Torres, R. Rainfall erosivity–intensity relationships for normal rainfall events and a tropical cyclone on the US southeast coast. J. Hydrol. 2016, 534, 440–450. [Google Scholar] [CrossRef]
- Vaezi, A.R.; Abbasi, M.; Bussi, G.; Keesstra, S. Modeling sediment yield in semi-arid pasture micro-catchments, NW Iran. Land Degrad. Dev. 2017, 28, 1274–1286. [Google Scholar] [CrossRef]
- Barthazy, E.; Göke, S.; Schefold, R.; Högi, D. An optical array instrument for shape and fall velocity measurements of hydrometeors. J. Atmos. Ocean. Technol. 2004, 21, 1400–1416. [Google Scholar] [CrossRef]
- Zhang, G.; Luchs, S.; Ryzhkov, A.; Xue, M.; Ryzhkova, L.; Cao, Q. Winter Precipitation Microphysics Characterized by Polarimetric Radar and Video Disdrometer Observations in Central Oklahoma. J. Appl. Meteorol. Climatol. 2011, 50, 1558–1570. [Google Scholar] [CrossRef]
- Sekhon, R.S.; Srivastava, R.C. Snow size spectra and radar reflectivity. J. Atmos. Sci. 1970, 27, 299–307. [Google Scholar] [CrossRef]
- Fujiyoshi, Y.; Endoh, T.; Yamada, T.; Tsuboki, K.; Tachibana, Y.; Wakahama, G. Determination of a Z-R relationship for snowfall using a radar and high sensitivity snow gauges. J. Appl. Meteorol. 1990, 29, 147–152. [Google Scholar] [CrossRef]
- Kubo, M.; Sougen, A.; Muramoto, K.; Fujiyoshi, Y. ZR relation for snowfall using small Doppler radar and high sensitive snow gauges. In Proceedings of the ICCAS-SICE, Fukuoka, Japan, 18–21 August 2009. [Google Scholar]
- Huang, G.-J.; Bringi, V.N.; Cifelli, R.; Hudak, D.; Petersen, W.A. A methodology to derive radar reflectivity–liquid equivalent snow rate relations using C-band radar and a 2D video disdrometer. J. Atmos. Ocean. Technol. 2010, 27, 637–651. [Google Scholar] [CrossRef]
- Newman, A.J.; Kucera, P.A.; Bliven, L.F. Presenting the Snowflake Video Imager (SVI). J. Atmos. Ocean. Technol. 2009, 26, 167–179. [Google Scholar] [CrossRef]
- Battaglia, A.; Rustemeier, E.; Tokay, A.; Blahak, U.; Simmer, C. PARSIVEL Snow Observations: A Critical Assessment. J. Atmos. Ocean. Technol. 2010, 27, 333–344. [Google Scholar] [CrossRef]
- Yin, D.; Sun, Y. Climatic Characteristics of Low-temperature Freezing and Snow Calamities in Nanjing in Recent 50 Years. J. Catastrophol. 2011, 26. [Google Scholar] [CrossRef]
- Ghada, W.; Buras, A.; Lüpke, M.; Schunk, C.; Menzel, A. Rain Microstructure Parameters Vary with Large-Scale Weather Conditions in Lausanne, Switzerland. Remote Sens. 2018, 10, 811. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, L. Statistical characteristics of raindrop size distribution in the Tibetan Plateau and southern China. Adv. Atmos. Sci. 2017, 34, 727–736. [Google Scholar] [CrossRef]
- Chen, B.; Yang, J.; Pu, J. Statistical Characteristics of Raindrop Size Distribution in the Meiyu Season Observed in Eastern China. J. Meteorol. Soc. Jpn. Ser. II 2013, 91, 215–227. [Google Scholar] [CrossRef]
- Bringi, V.N.; Chandrasekar, V.; Hubbert, J. Raindrop Size Distribution in Different Climatic Regimes from Disdrometer and Dual-Polarized Radar Analysis. J. Atmos. Sci. 2003, 60, 354–365. [Google Scholar] [CrossRef]
- Zhang, A.; Hu, J.; Chen, S.; Hu, D.; Liang, Z.; Huang, C.; Xiao, L.; Min, C.; Li, H. Statistical Characteristics of Raindrop Size Distribution in the Monsoon Season Observed in Southern China. Remote Sens. 2019, 11, 432. [Google Scholar] [CrossRef]
- Chen, B.; Hu, Z.; Liu, L.; Zhang, G. Raindrop Size Distribution Measurements at 4500 m on the Tibetan Plateau During TIPEX-III. J. Geophys. Res. Atmos. 2017, 122. [Google Scholar] [CrossRef]
- Jaffrain, J.; Berne, A. Experimental quantification of the sampling uncertainty associated with measurements from PARSIVEL disdrometers. J. Hydrometeorol. 2011, 12, 352–370. [Google Scholar] [CrossRef]
- Niu, S.; Jia, X.; Sang, J.; Liu, X.; Lu, C.; Liu, Y. Distributions of Raindrop Sizes and Fall Velocities in a Semiarid Plateau Climate: Convective versus Stratiform Rains. J. Appl. Meteorol. Climatol. 2010, 49, 632–645. [Google Scholar] [CrossRef]
- Seela, B.K.; Janapati, J.; Lin, P.-L.; Wang, P.K.; Lee, M.-T. Raindrop Size Distribution Characteristics of Summer and Winter Season Rainfall over North Taiwan. J. Geophys. Res. Atmos. 2018, 123. [Google Scholar] [CrossRef]
- Balaji Kumar, S.; Jayalakshmi, J.; Pay-Liam, L.; Krishna, R.K.; Ryuichi, S.; Pao, K.W. A Comparison Study of Summer Season Raindrop Size Distribution between Palau and Taiwan, Two Islands in Western Pacific. J. Geophys. Res. Atmos. 2017, 122. [Google Scholar] [CrossRef]
- Wang, M.; Zhao, K.; Xue, M.; Zhang, G.; Liu, S.; Wen, L.; Chen, G. Precipitation microphysics characteristics of a Typhoon Matmo (2014) rainband after landfall over eastern China based on polarimetric radar observations. J. Geophys. Res. Atmos. 2016, 121, 12–415. [Google Scholar] [CrossRef]
- Locatelli, J.D.; Hobbs, P.V. Fall speeds and masses of solid precipitation particles. J. Geophys. Res. 1974, 79, 2185–2197. [Google Scholar] [CrossRef]
- Smith, P.L. Equivalent radar reflectivity factors for snow and ice particles. J. Clim. Appl. Meteorol. 1984, 23, 1258–1260. [Google Scholar] [CrossRef]
- Atlas, D.; Srivastava, R.C.; Sekhon, R.S. Doppler characteristics of precipitation at vertical incidence. Rev. Geophys. Space Phys. 1973, 11, 1–35. [Google Scholar] [CrossRef]
- Barthazy, E.; Schefold, R. Fall velocity of snowflakes of different riming degree and crystal types. Atmos. Res. 2006, 82, 391–398. [Google Scholar] [CrossRef]
- Schefold, R.; Baschek, B.; Wüest, M.; Barthazy, E. Fall velocity and axial ratio of snowflakes. In Proceedings of the Second European Conference on Radar Meteorology (ERAD) in conjunction with COST 717 mid-term seminar, Netherlands, 18–22 November 2002; pp. 84–89. [Google Scholar]
- Schmitt, C.G.; Heymsfield, A.J. The Dimensional Characteristics of Ice Crystal Aggregates from Fractal Geometry. J. Atmos. Sci. 2010, 67, 1605–1616. [Google Scholar] [CrossRef]
- Löffler-Mang, M.; Joss, J. An Optical Disdrometer for Measuring Size and Velocity of Hydrometeors. J. Atmos. Ocean. Technol. 2000, 17, 130–139. [Google Scholar] [CrossRef]
- Gonzalez, S.; Bech, J.; Udina, M.; Codina, B.; Paci, A.; Trapero, L. Decoupling between Precipitation Processes and Mountain Wave Induced Circulations Observed with a Vertically Pointing K-Band Doppler Radar. Remote Sens. 2019, 11, 1034. [Google Scholar] [CrossRef]
- Wen, L.; Zhao, K.; Wang, M.; Zhang, G. Seasonal Variations of Observed Raindrop Size Distribution in East China. Adv. Atmos. Sci. 2019, 36, 346–362. [Google Scholar] [CrossRef]
- D’Adderio, L.P.; Vulpiani, G.; Porcù, F.; Tokay, A.; Meneghini, R. Comparison of GPM Core Observatory and Ground-Based Radar Retrieval of Mass-Weighted Mean Raindrop Diameter at Midlatitude. J. Hydrometeorol. 2018, 19, 1583–1598. [Google Scholar] [CrossRef]
- Berne, A.; Schleiss, M. Retrieval of the rain drop size distribution using telecommunication dual-polarization microwave links. In Proceedings of the 34th Conference on Radar Meteorology, Williamsburg, VA, USA, 5–9 October 2009. [Google Scholar]
- Chwala, C.; Kunstmann, H. Commercial microwave link networks for rainfall observation: Assessment of the current status and future challenges. Wiley Interdiscip. Rev. Water 2019, 6. [Google Scholar] [CrossRef]
- Rose, C.R.; Chandrasekar, V. A systems approach to GPM dual-frequency retrieval. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1816–1826. [Google Scholar] [CrossRef]
- Vivekanandan, J.; Zhang, G.; Brandes, E. Polarimetric Radar Estimators Based on a Constrained Gamma Drop Size Distribution Model. J. Appl. Meteorol. 2004, 43, 217–230. [Google Scholar] [CrossRef]
- Rincon, R.F.; Lang, R.H. Microwave link dual-wavelength measurements of path-average attenuation for the estimation of drop size distributions and rainfall. IEEE Trans. Geosci. Remote Sens. 2002, 40, 760–770. [Google Scholar] [CrossRef]
- Jacques, T.; Stephane, O.; Blackb, R.A.; Amayencc, P.; Doud, X. The Concept of “Normalized” Distribution to Describe Raindrop Spectra: A Tool for Cloud Physics and Cloud Remote Sensing. J. Appl. Meteorl. 2001, 40, 1118–1140. [Google Scholar] [CrossRef]
- Cao, Q.; Zhang, G.; Brandes, E.; Schuur, T.; Ryzhkov, A.; Ikeda, K. Analysis of Video Disdrometer and Polarimetric Radar Data to Characterize Rain Microphysics in Oklahoma. J. Appl. Meteorol. Climatol. 2008, 47, 2238–2255. [Google Scholar] [CrossRef]
- Tang, Q.; Xiao, H.; Guo, C.; Feng, L. Characteristics of the raindrop size distributions and their retrieved polarimetric radar parameters in northern and southern China. Atmos. Res. 2014, 135, 59–75. [Google Scholar] [CrossRef]
- Zhang, G.; Vivekanandan, J.; Brandes, E.A. The Shape–Slope Relation in Observed Gamma Raindrop Size Distributions: Statistical Error or Useful Information? J. Atmos. Ocean. Technol. 2003, 20, 1106–1119. [Google Scholar] [CrossRef]
- Yu, M.; Guangheng, N.; Chandrasekar, V.; Fuqiang, T.; Haonan, C. Statistical characteristics of raindrop size distribution during rainy seasons in Beijing urban area and implications for radar rainfall estimation. Hydrol. Earth Syst. Sci. 2019, 23, 4153–4170. [Google Scholar] [CrossRef]
- Imai, J. Raindrop size distributions and the Z–R relationship. In Proceedings of the Eighth Weather Radar Conference, San Francisco, CA, USA, 11–14 April 1960; pp. 321–326. [Google Scholar]
- Puhakka. On the dependence of the Z–R relation on the temperature in snowfall. In Proceedings of the 16th Conference on Radar Meteorology, Houston, TX, USA, 22–24 April 1975; pp. 504–507.
- Gunn, K.L.S.; Marshall, J.S. The distribution with size of aggregate snowflakes. J. Meteorol. 1957, 15, 452–461. [Google Scholar] [CrossRef]
- Gray, D.M.; Male, D.H. Handbook of Snow: Principles, Processes, Management and Use; Pergamon Press: Oxford, UK, 1981; Volume 776, p. 776. [Google Scholar]
- Mallet, C.; Barthes, L. Estimation of Gamma Raindrop Size Distribution Parameters: Statistical Fluctuations and Estimation Errors. J. Atmos. Ocean. Technol. 2009, 26, 1572–1584. [Google Scholar] [CrossRef]
- Löffler-Mang, M.; Blahak, U. Estimation of the Equivalent Radar Reflectivity Factor from Measured Snow Size Spectra. J. Appl. Meteorol. 2001, 40, 843–849. [Google Scholar] [CrossRef]
- Garrett, T.J.; Fallgatter, C.; Shkurko, K.; Howlett, D. Fall speed measurement and high-resolution multi-angle photography of hydrometeors in free fall. Atmos. Meas. Tech. 2012, 5, 2625–2633. [Google Scholar] [CrossRef]
- Xichuan, L.; Taichang, G.; Lei, L. A video precipitation sensor for imaging and velocimetry of hydrometeors. Atmos. Meas. Tech. 2014, 7, 2037–2046. [Google Scholar] [CrossRef]
| Year | Date | Historical Weather Observation | Ground Temperature (°C) | Precipitation Time |
|---|---|---|---|---|
| 2014 | 0205 | Sleet/Small to moderate rain | 2~3 | 02:30~23:59 |
| 0207 | Sleet/Light snow | −3~2 | 00:00~19:30 | |
| 0212 | Sleet/Moderate snow | 0~4 | 20:30~23:59 | |
| 0213 | Sleet/Cloudy | −1~4 | 00:00~08:00 | |
| 0218 | Heavy snow/Light to moderate snow | −3~2 | 08:00~23:00 | |
| 2015 | 0305 | Sleet/Overcast | 2~5 | 13:00~16:00 |
| 2016 | 0111 | Small rain/Sleet | 0~6 | 00:00~23:59 |
| 0120 | Sleet/Moderate to heavy snow | 0~4 | 19:30~23:59 | |
| 0121 | Light snow/Light snow | −1~1 | 00:00~07:30 | |
| 0122 | Light to moderate snow/Light snow | −5~2 | 09:30~16:00 | |
| 0130 | Sleet/Overcast | −1~4 | 08:30~10:00 | |
| 2017 | 0208 | Light snow/Overcast | −2~2 | 00:00~23:30 |
| 2018 | 0104 | Snowstorm/Moderate snow | −1~1 | 00:00~06:00/15:30~23:59 |
| 0107 | Light rain/Sleet | −1~4 | 00:30~14:00 | |
| 0124 | Overcast/Heavy snow | −1~3 | 16:30~23:59 | |
| 0125 | Heavy snow to Snowstorm/Moderate snow | −3~0 | 00:00~23:59 | |
| 0126 | Overcast/Light snow | −3~−1 | 00:00~03:00 | |
| 0127 | Heavy snow to Snowstorm/Heavy snow | −2~−1 | 06:00~23:59 | |
| 0128 | Light snow/Overcast | −7~−1 | 00:00~14:30 | |
| 1208 | Overcast/Light snow | 0~2 | No precipitation | |
| 1230 | Light snow/Light snow | −2~1 | 12:00~23:00 | |
| 2019 | 0109 | Heavy snow/Sleet | 0~2 | 02:00~23:00 |
| 0130 | Light rain/Sleet | 1~8 | 00:00~08:30/17:30~23:59 | |
| 0131 | Light snow/Overcast | −3~4 | 00:00~08:00 | |
| 0207 | Light rain/Moderate rain | 0~4 | 00:00~09:00/23:00~23:59 | |
| 0208 | Light snow/Moderate snow | −1~2 | 00:00~05:30/18:00~23:59 | |
| 0209 | Overcast/Overcast | −1~1 | 00:00~05:00/13:30~22:00 | |
| 0210 | Light snow/Overcast | −2~1 | 06:00~17:00 | |
| 0221 | Light rain/Sleet | 2~7 | 00:00~02:00/16:30~23:59 | |
| 0222 | Sleet/Overcast | −1~6 | 00:00~13:00 |
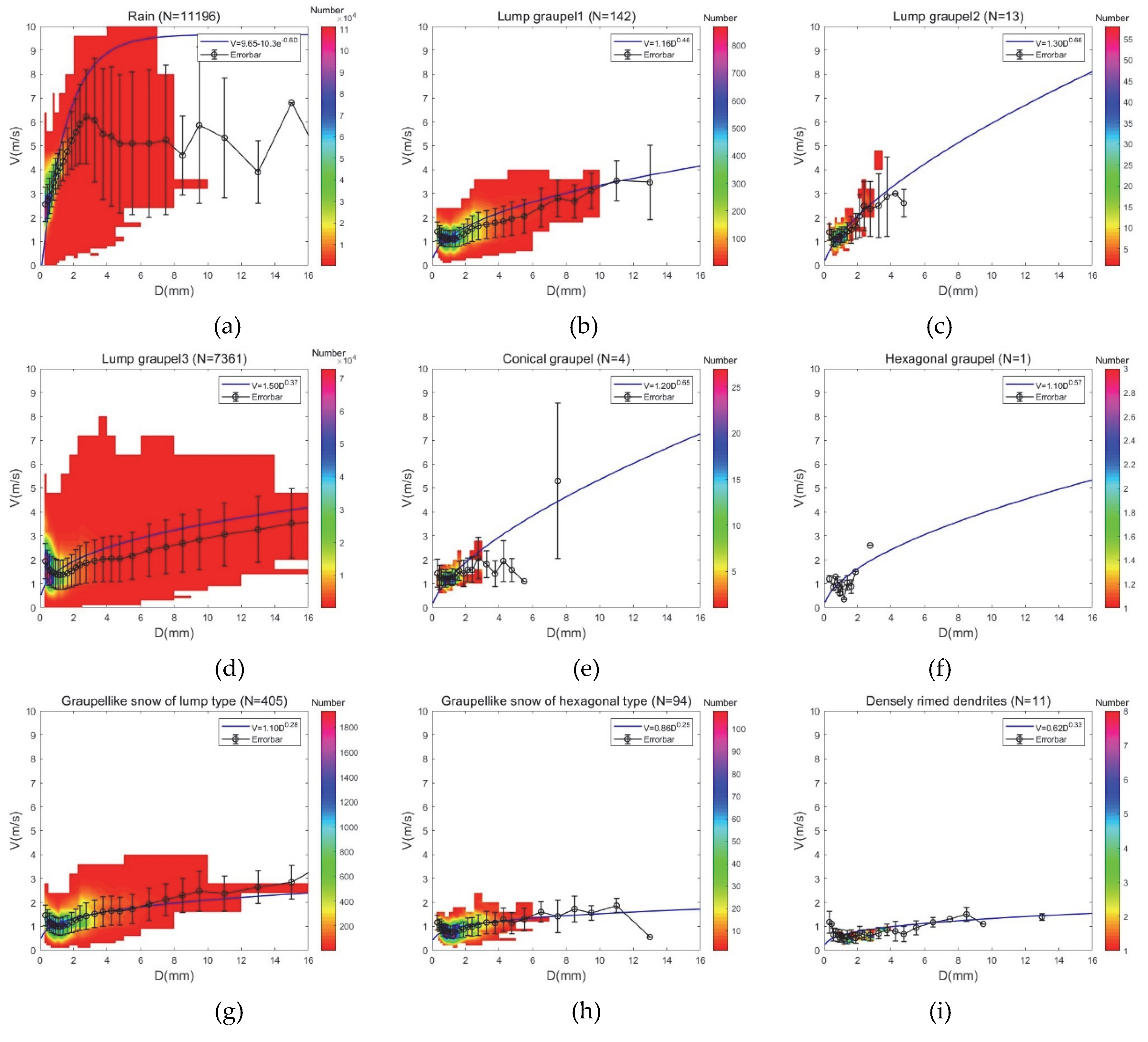
| Categories | Precipitation Type | V-D | M-D | N | Sum |
|---|---|---|---|---|---|
| Rain | Rain | V = 9.65 − 10.3exp(−0.6D) | M = π/6D3.0 | 11196 | 11196 |
| Graupel | Lump graupel 1 | V = 1.16D0.46 | M = 0.042D3.0 | 142 | 7521 |
| Lump graupel 2 | V = 1.30D0.66 | M = 0.078D2.8 | 13 | ||
| Lump graupel 3 | V = 1.50D0.37 | M = 0.140D2.7 | 7361 | ||
| Conical graupel | V = 1.20D0.65 | M = 0.073D2.6 | 4 | ||
| Hexagonal graupel | V = 1.10D0.57 | M = 0.044D2.9 | 1 | ||
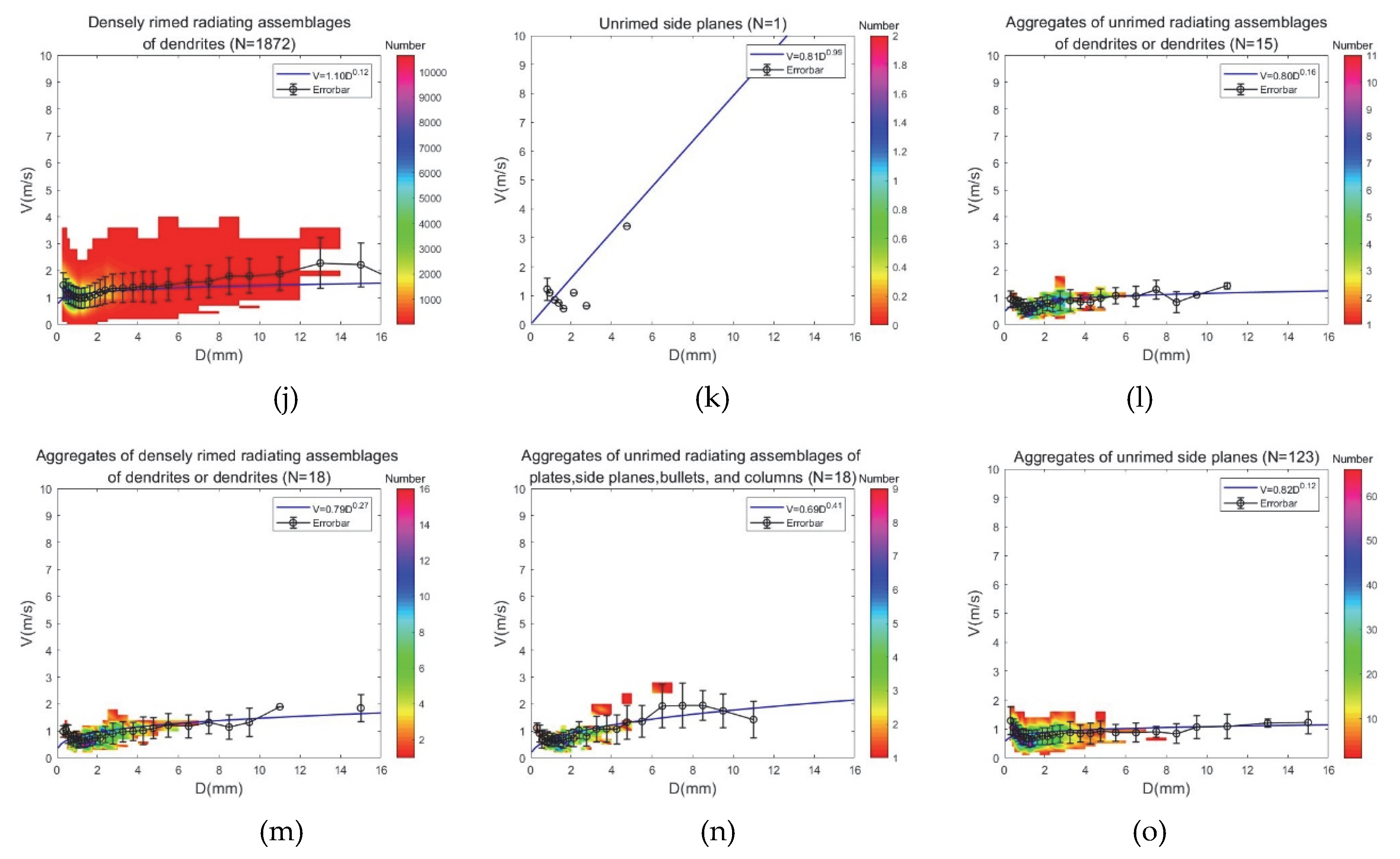
| Snow | Graupellike snow of lump type | V = 1.10D0.28 | M = 0.059D2.1 | 405 | 2557 |
| Graupellike snow of hexagonal type | V = 0.86D0.25 | M = 0.021D2.4 | 94 | ||
| Densely rimed dendrites | V = 0.62D0.33 | M = 0.015D2.3 | 11 | ||
| Densely rimed radiating assemblages | V = 1.10D0.12 | M = 0.039D2.1 | 1872 | ||
| Unrimed side planes | V = 0.81D0.99 | - | 1 | ||
| Aggregates of unrimed radiating assemblages | V = 0.80D0.16 | M = 0.073D1.4 | 15 | ||
| Aggregates of densely rimed radiating assemblages of dendrites or dendrites | V = 0.79D0.27 | M = 0.037D1.9 | 18 | ||
| Aggregates of unrimed radiating assemblages of plates, side planes, bullets, and columns | V = 0.69D0.41 | M = 0.037D1.9 | 18 | ||
| Aggregates of unrimed side planes | V = 0.82D0.12 | M = 0.040D1.4 | 123 |
| Precipitation Type | Peak Diameter (mm) | Skewness | Kurtosis |
|---|---|---|---|
| Rain | 0.437 | 2.32 | 4.12 |
| Graupel | 0.562 | 1.52 | 0.77 |
| Wet snow | 0.937 | 1.23 | 0.06 |
| Dry snow | 0.687 | 1.34 | 0.24 |
| Precipitation Type | log10N0 (mm−1-μ m−3) | μ | Λ (mm−1) | log10Nw (mm−1 m−3) | Dm (mm) | S (mm h−1) | Ze (dBZ) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ME | SD | ME | SD | ME | SD | ME | SD | ME | SD | ME | SD | ME | SD | |
| Rain | 7.86 | 4.47 | 7.58 | 6.35 | 15.53 | 12.43 | 3.41 | 0.53 | 0.99 | 0.53 | 0.73 | 2.55 | 9.58 | 11.01 |
| Graupel | 4.22 | 2.72 | 2.90 | 4.98 | 4.53 | 6.71 | 3.30 | 0.53 | 2.58 | 1.25 | 2.07 | 2.93 | 23.40 | 13.87 |
| Wet snow | 3.59 | 2.38 | 4.79 | 4.49 | 4.37 | 4.87 | 2.95 | 0.49 | 3.17 | 1.78 | 0.16 | 0.20 | 6.83 | 9.89 |
| Dry snow | 2.90 | 2.64 | 4.10 | 5.38 | 3.21 | 3.59 | 2.99 | 0.63 | 3.49 | 2.00 | 0.27 | 0.40 | 9.67 | 8.89 |
| Precipitation Type | Site | Time | μ-Λ |
|---|---|---|---|
| Rain | Nanjing, East China | Winter from Feb 2014 to Feb 2019 | μ = −0.0074Λ2 + 0.7564Λ − 1.5520 |
| Graupel | μ = −0.0073Λ2 + 0.8340Λ − 0.7664 | ||
| Wet snow | μ = −0.0066Λ2 + 0.8688Λ + 0.8648 | ||
| Dry snow | μ = −0.0106Λ2 + 0.9936Λ − 0.0820 | ||
| Winter rain (Wen et al. [44]) | Nanjing, East China | 2014 to 2016 | μ = −0.0110Λ2 + 0.8210Λ − 2.3700 |
| Rain (Zhang et al. [54]) | Florida, America | Summer of 1998 | μ = −0.0210Λ2 + 0.9880Λ − 2.6690 |
| Rain (Cao et al. [52]) | Oklahoma, America | 2005 to 2007 | μ = −0.0201Λ2 + 0.9020Λ − 1.7180 |
| Rain (Tang et al. [53]) | Beijing, North China | Jul to Oct 2008 | Λ = 0.0075μ2 + 0.7230μ + 1.1721 |
| Precipitation Type | Ze–S |
|---|---|
| Rain | Ze = 311S2.34 |
| Graupel | Ze = 252S2.03 |
| Wet snow | Ze = 394S1.93 |
| Dry snow | Ze = 145S1.33 |
| Graupel (Gray and Male [59]) | Ze = 170S1.60 |
| Snow (Gunn and Marshall [58]) | Ze = 378S2.00 |
| Wet snow (Imai 1960 [56]) | Ze = 397S2.00 |
| Dry snow (Imai 1960 [56]) | Ze = 101S2.00 |
| Snow (Sekon and Srivastava [18]) | Ze = 337S2.21 |
| Wet snow (Puhakka [57] ) | Ze = 302S2.00 |
| Dry snow (Puhakka [57]) | Ze = 198S2.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pu, K.; Liu, X.; He, H.; Sun, Y.; Hu, S.; Wu, Y. Microphysical Characteristics of Winter Precipitation in Eastern China from 2014 to 2019. Water 2020, 12, 920. https://doi.org/10.3390/w12030920
Pu K, Liu X, He H, Sun Y, Hu S, Wu Y. Microphysical Characteristics of Winter Precipitation in Eastern China from 2014 to 2019. Water. 2020; 12(3):920. https://doi.org/10.3390/w12030920
Chicago/Turabian StylePu, Kang, Xichuan Liu, Hongbing He, Yu Sun, Shuai Hu, and Yi Wu. 2020. "Microphysical Characteristics of Winter Precipitation in Eastern China from 2014 to 2019" Water 12, no. 3: 920. https://doi.org/10.3390/w12030920
APA StylePu, K., Liu, X., He, H., Sun, Y., Hu, S., & Wu, Y. (2020). Microphysical Characteristics of Winter Precipitation in Eastern China from 2014 to 2019. Water, 12(3), 920. https://doi.org/10.3390/w12030920





