Pipeline Scour Rates Prediction-Based Model Utilizing a Multilayer Perceptron-Colliding Body Algorithm
Abstract
1. Introduction
Background
2. Material and Methods
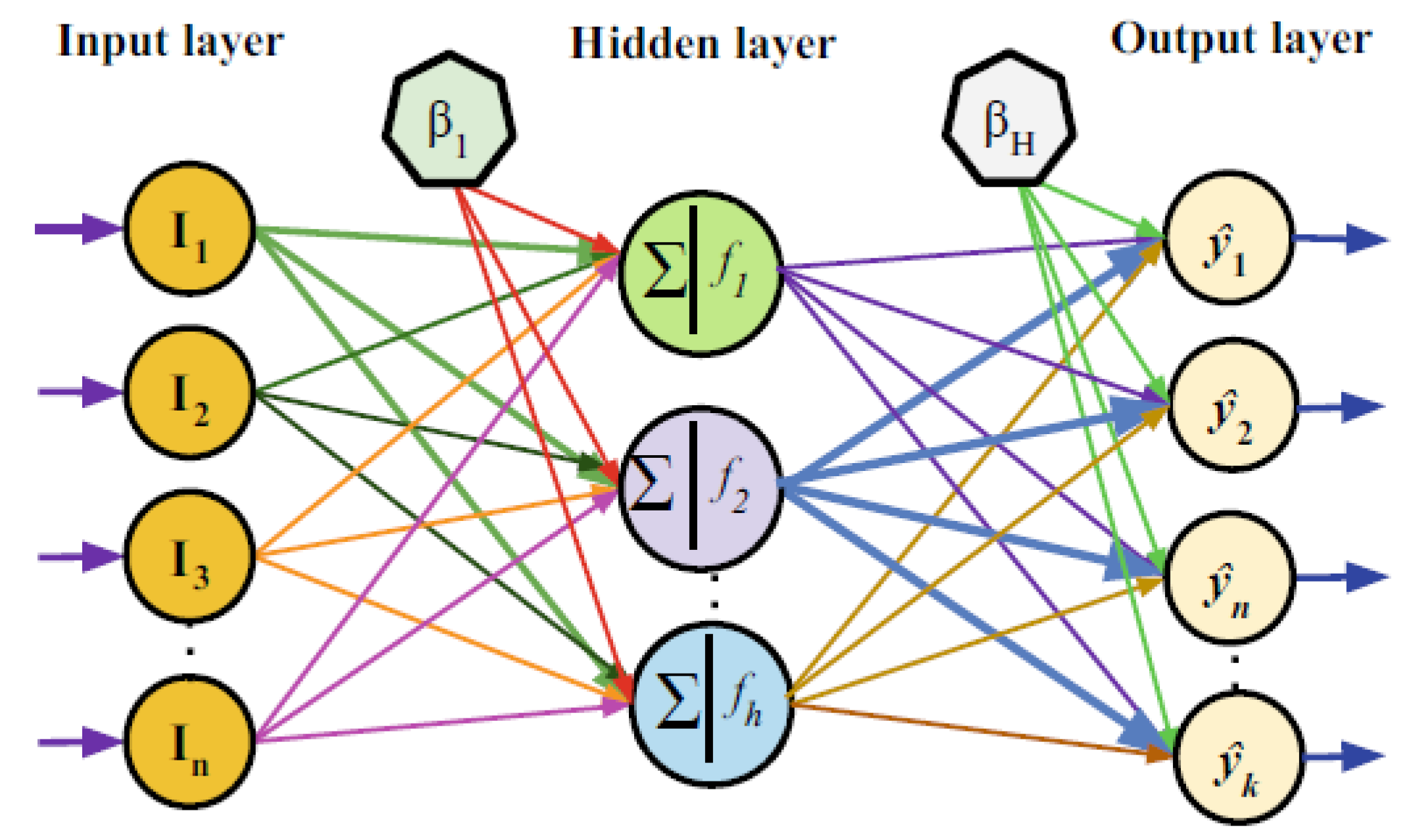
2.1. Multilayer Perceptron (MLP)
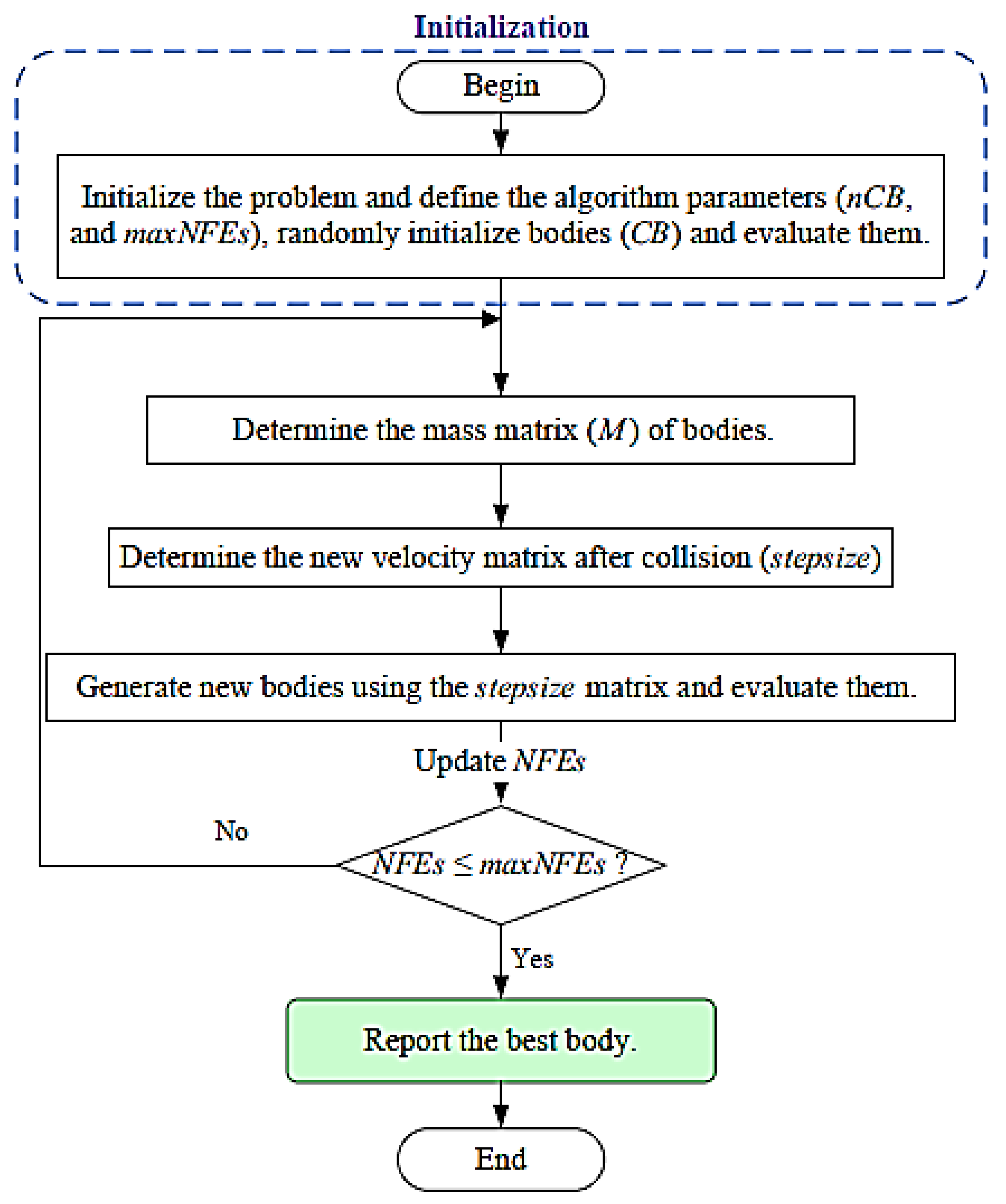
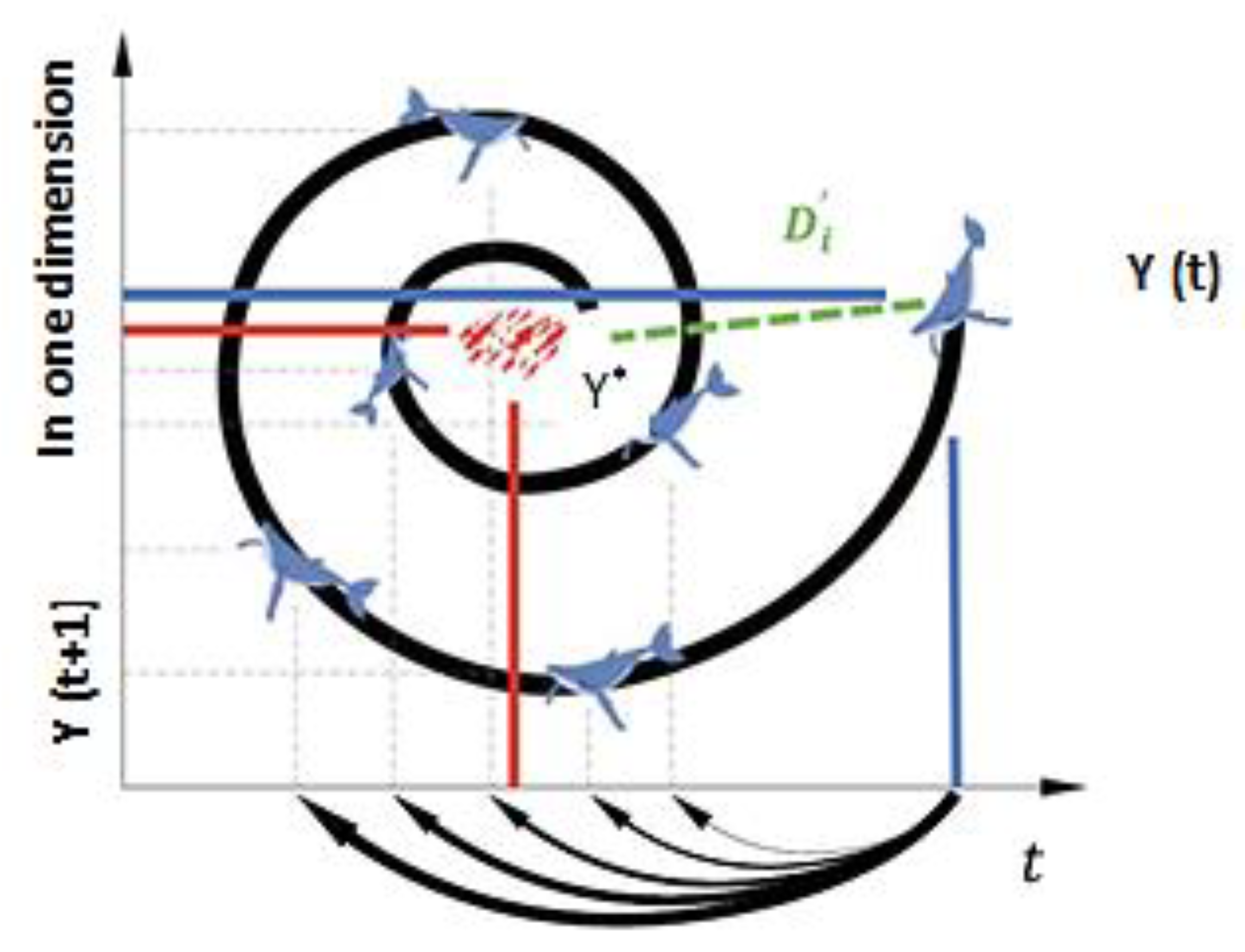
2.2. Colliding Body Optimization
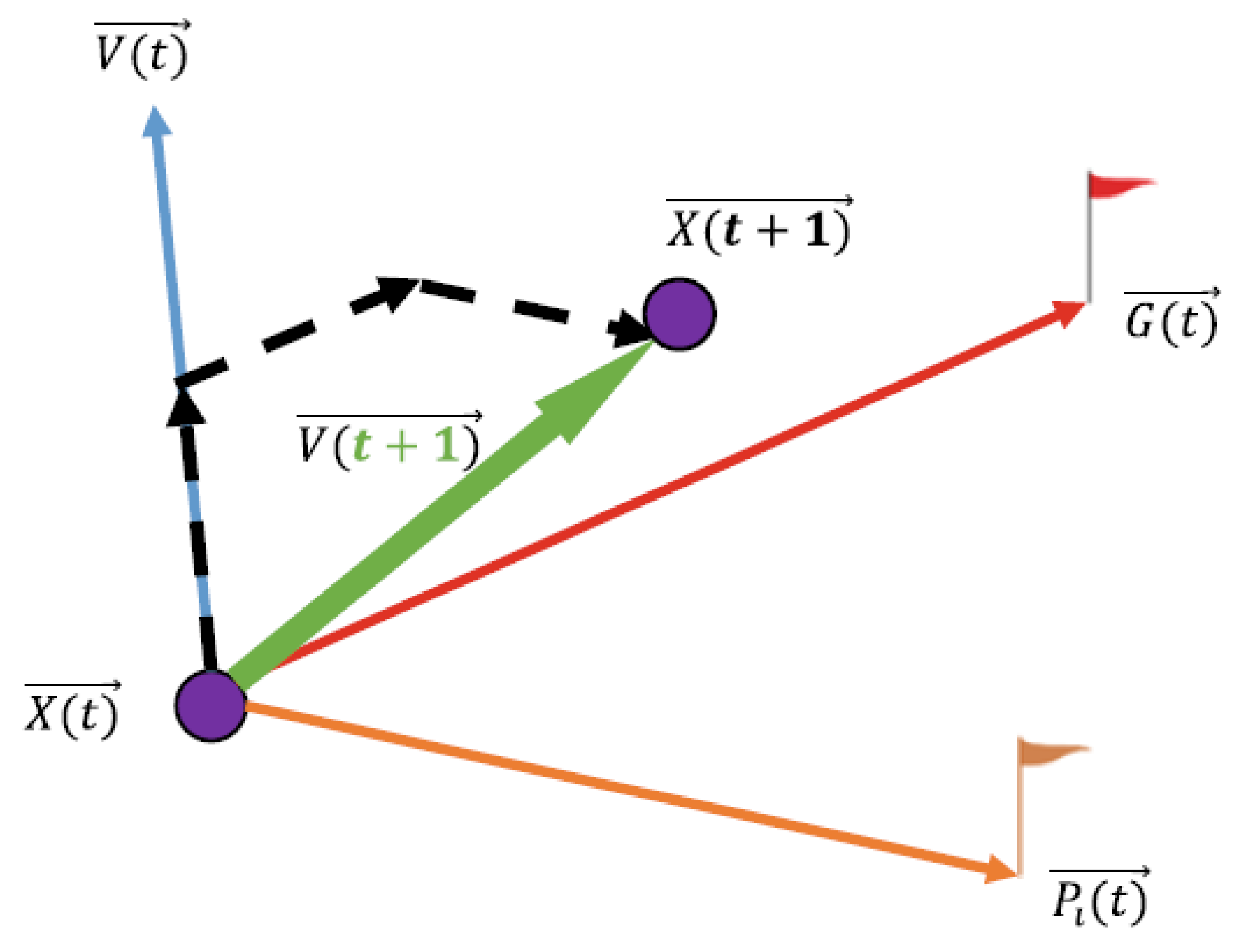
2.3. Particle Swarm Optimization (PSO)
2.4. Whale Algorithm (WA)
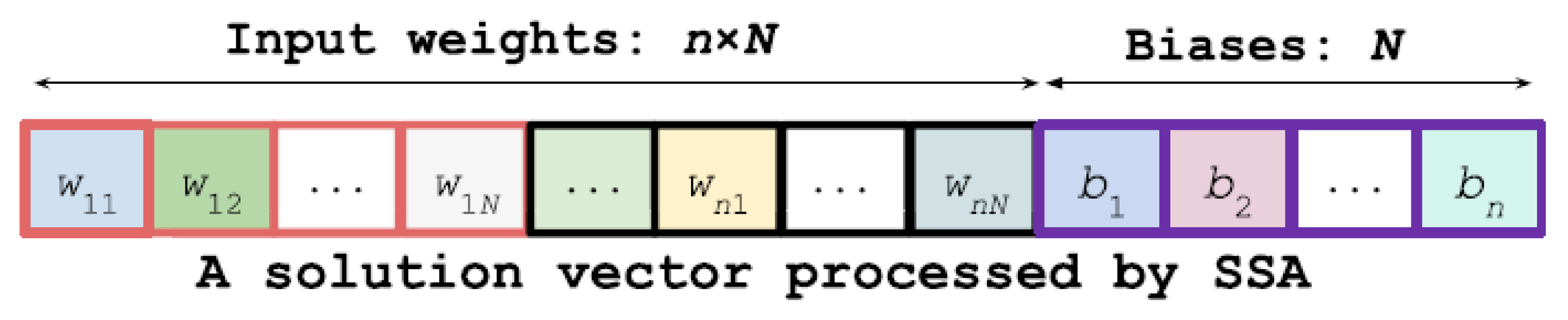
2.5. Optimization Algorithms for Training MLPs
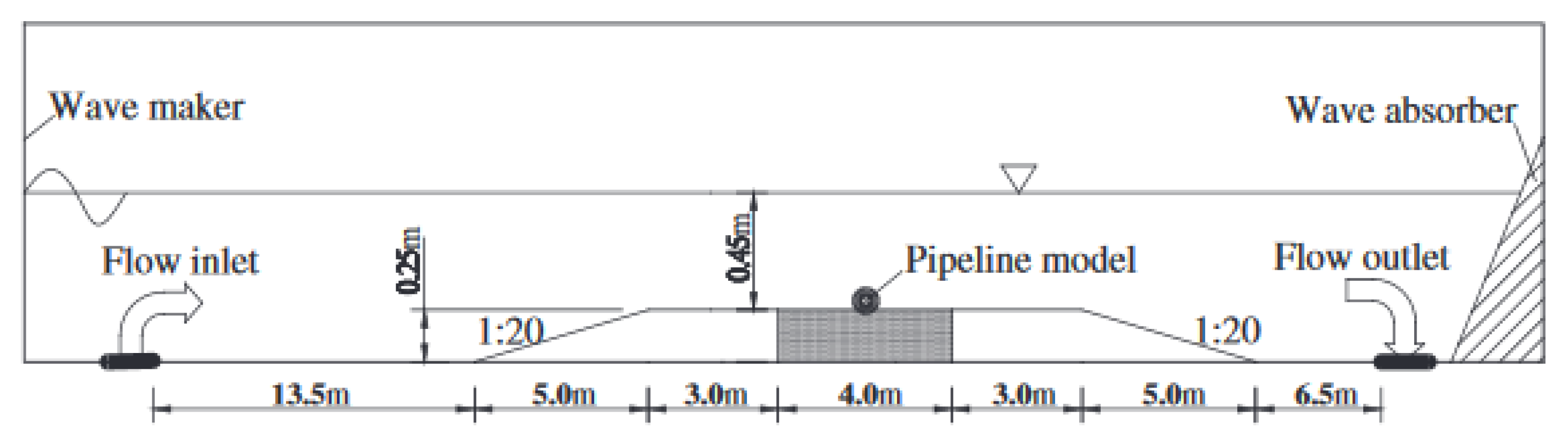
3. Datasets
4. Discussion and Results
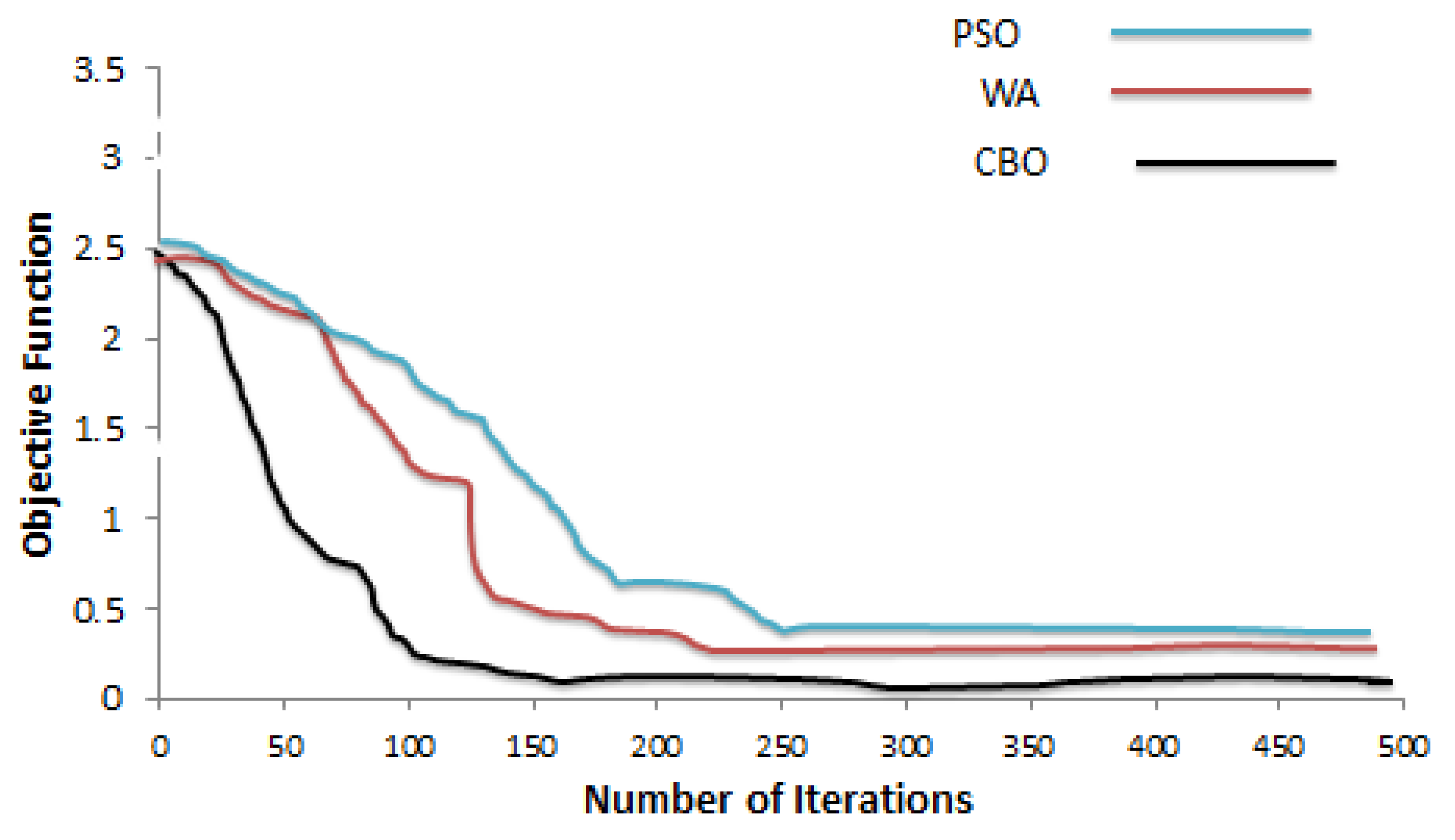
4.1. The Selection of Optimization Algorithm Parameters
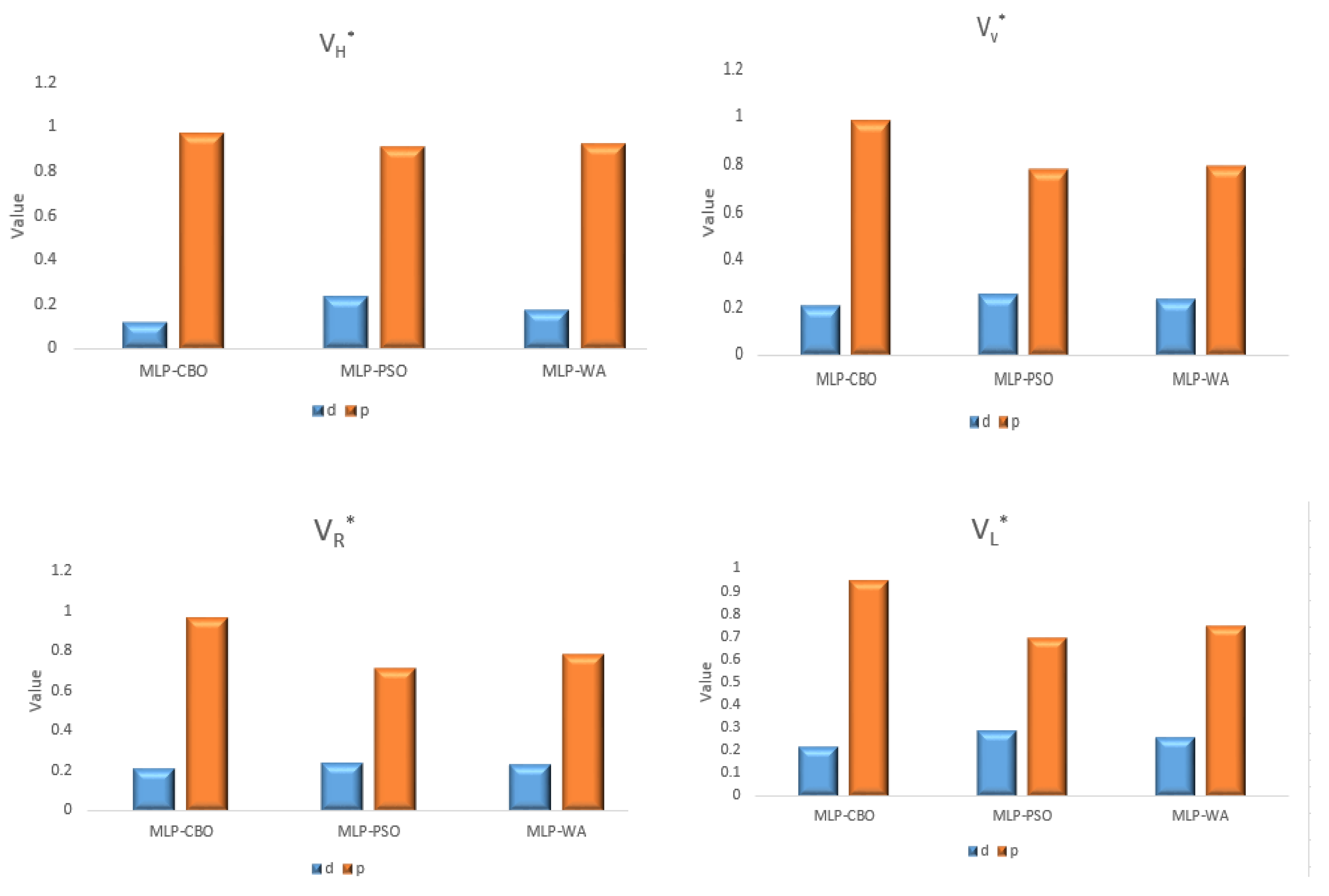
4.2. The Statistical Results for Different Soft Computing Models
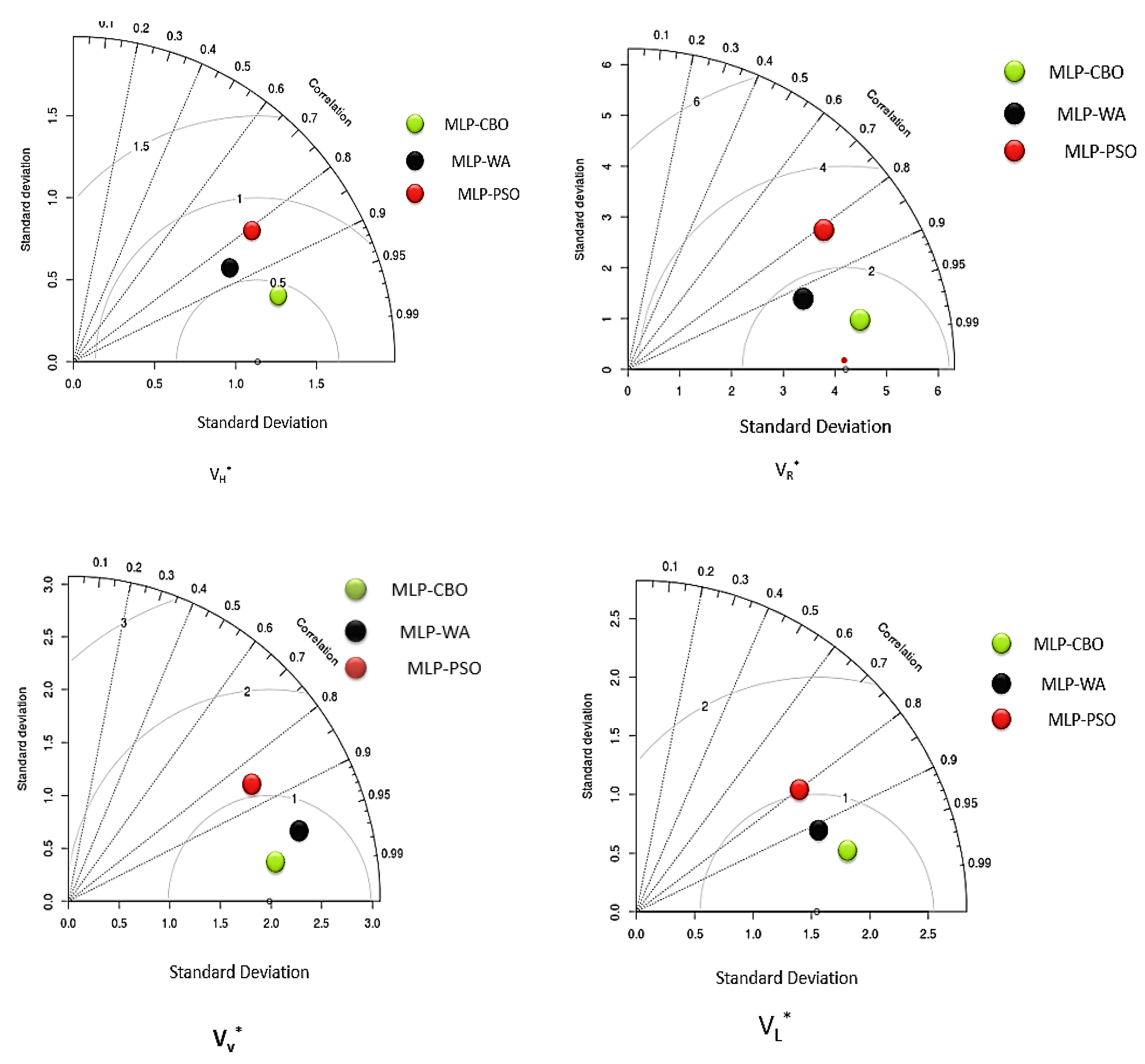
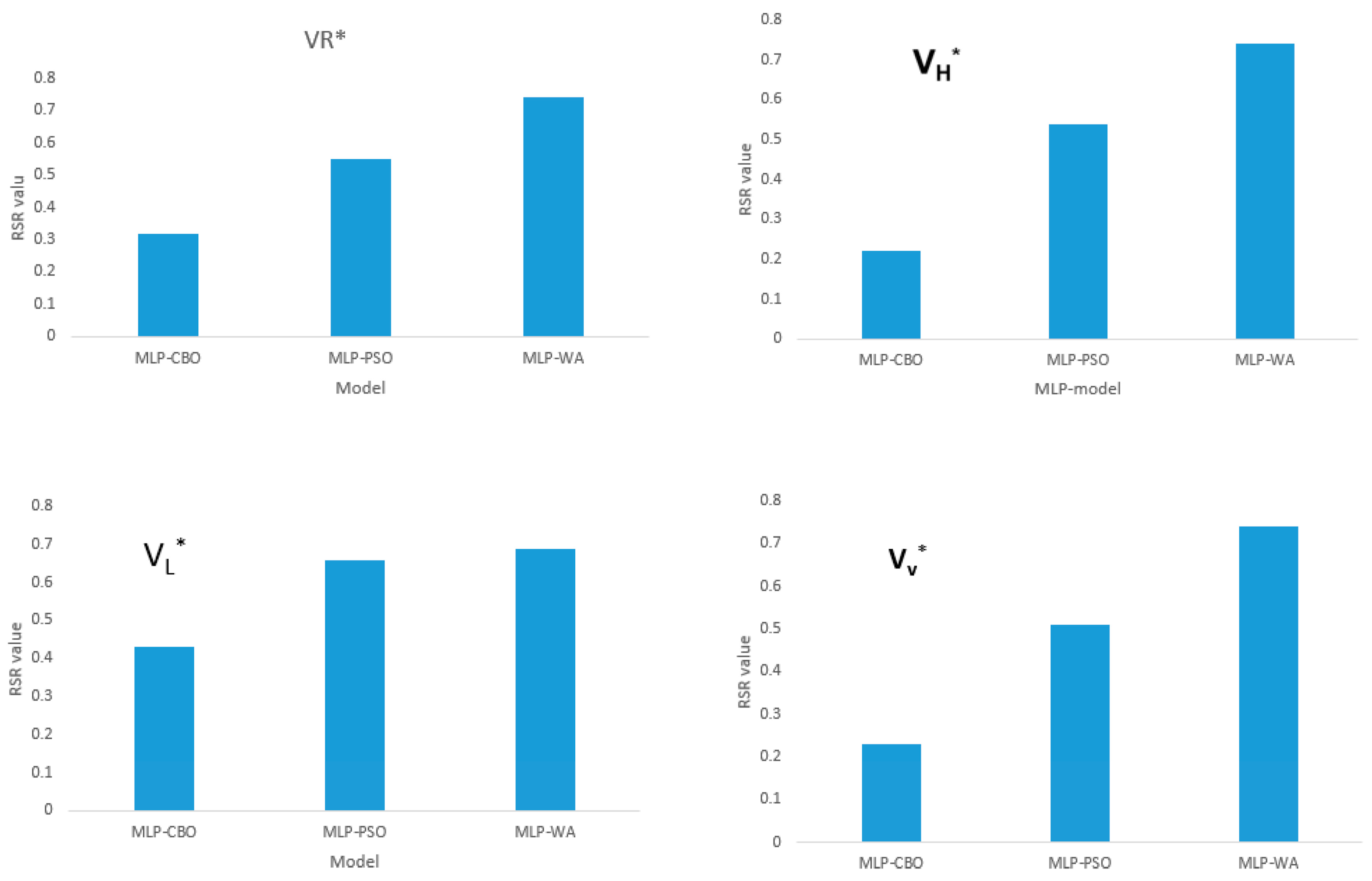
4.3. Comparison of Soft Computing Models
4.4. Comparison Analysis
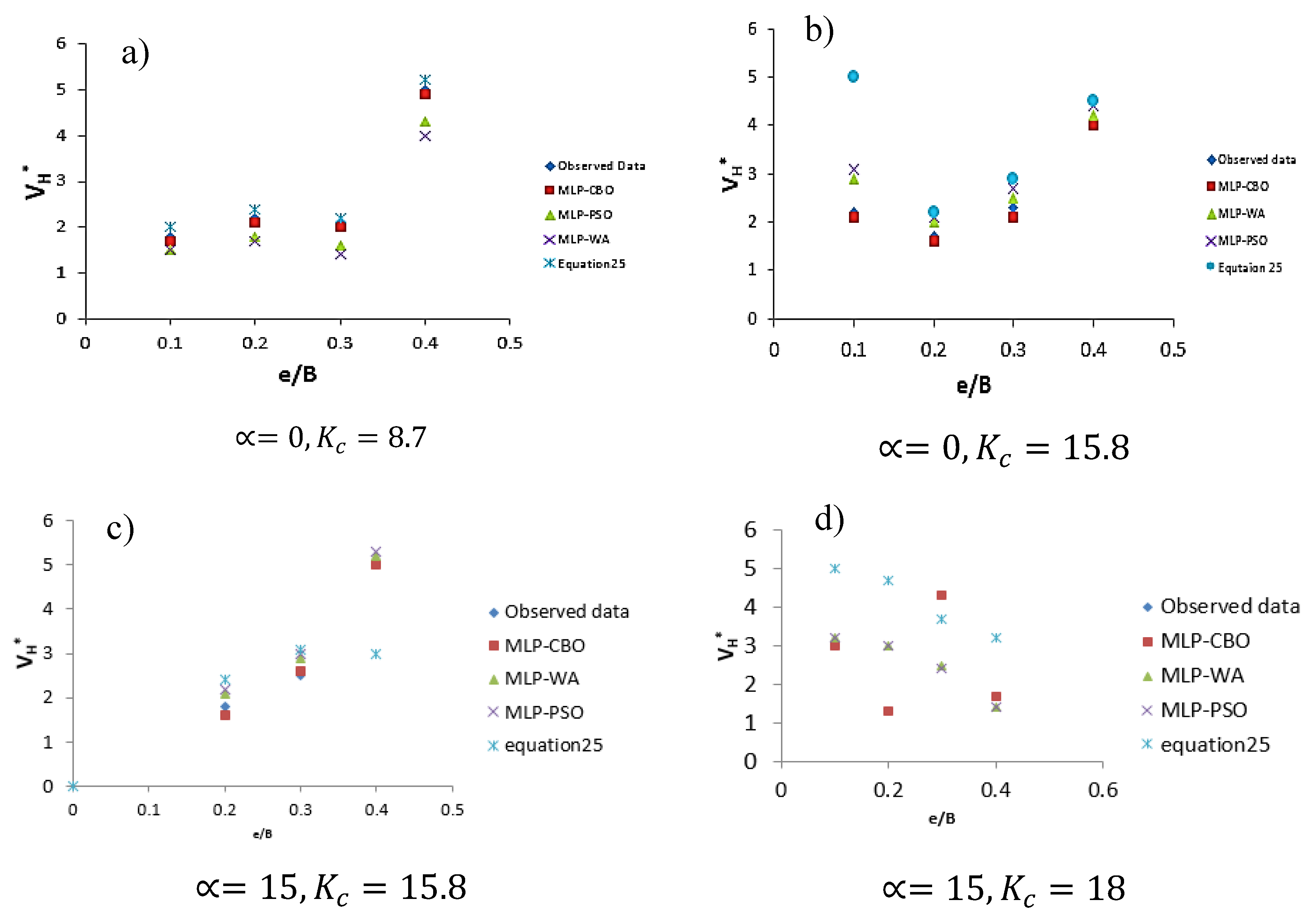
4.5. Parametric Analysis
- 1
- At the beginning, the fitness g (b) and the uncertainty ranges for the parameters are determined, where mean square error has been chosen as the objective function.
- 2
- The Latin hypercube is performed in the range of [bmin, bmax], which is initially set to [bj, abs_mean, bj, abs_max]; the corresponding fitness functions are evaluated and the sensitivity matrix J and the parameters covariance matrix C are calculated.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ANFIS | Adaptive Neuro Fuzzy Interface System |
| ANN | Artificial Neural Network |
| BA | Bat Algorithm |
| CBO | Colliding Bodies’ Optimization |
| FFA | Firefly Algorithm |
| FS | Free Spans |
| GA | Genetic Algorithm |
| GP | Genetic Programming |
| MLP | Multilayer Perceptron |
| MLP-CBO | Multilayer Perceptron-Colliding Bodies’ Optimization |
| MLP-PSO | Multilayer Perceptron-Particle Swarm Optimization |
| MLP-WA | Multilayer Perceptron-Whale Algorithm |
| PL | Pipe Line |
| PSO | Particle Swarm Optimization |
| SA | Shark Algorithm |
| WA | Whale Algorithm |
References
- Parsaie, A.; Haghiabi, A.H.; Moradinejad, A. Prediction of Scour Depth below River Pipeline Using Support Vector Machine. KSCE J. Civ. Eng. 2019, 23, 2503–2513. [Google Scholar] [CrossRef]
- Peng, Z.; Zou, Q.-P.; Lin, P. A Partial Cell Technique for Modeling the Morphological Change and Scour. Coast. Eng. 2018, 131, 88–105. [Google Scholar] [CrossRef]
- Mawat, M.J.; Khudier, A.S.; Hashim, S.J. Evaluation Study of Free Spanning Subjected to Hydrodynamic Loads. J. Univ. Babylon 2018, 26, 227–237. [Google Scholar]
- Najafzadeh, M.; Shiri, J.; Rezaie-Balf, M. New Expression-Based Models to Estimate Scour Depth at Clear Water Conditions in Rectangular Channels. Mar. Georesour. Geotechnol. 2017, 36, 227–235. [Google Scholar] [CrossRef]
- Jamei, M.; Ahmadianfar, I. Prediction of Scour Depth at Piers with Debris Accumulation Effects Using Linear Genetic Programming. Mar. Georesour. Geotechnol. 2019, 1–12. [Google Scholar] [CrossRef]
- Sharafati, A.; Yasa, R.; Azamathulla, H.M. Assessment of Stochastic Approaches in Prediction of Wave-Induced Pipeline Scour Depth. J. Pipeline Syst. Eng. Pract. 2018, 9. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Kargar, A.R. Gene-Expression Programming, Evolutionary Polynomial Regression, and Model Tree to Evaluate Local Scour Depth at Culvert Outlets. J. Pipeline Syst. Eng. Pract. 2019, 10. [Google Scholar] [CrossRef]
- Dang, N.M.; Tran Anh, D.; Dang, T.D. ANN Optimized by PSO and Firefly Algorithms for Predicting Scour Depths around Bridge Piers. Eng. Comput. 2019. [Google Scholar] [CrossRef]
- Moradi, F.; Bonakdari, H.; Kisi, O.; Ebtehaj, I.; Shiri, J.; Gharabaghi, B. Abutment Scour Depth Modeling Using Neuro-Fuzzy-Embedded Techniques. Mar. Georesour. Geotechnol. 2018, 37, 190–200. [Google Scholar] [CrossRef]
- Niazkar, M.; Afzali, S.H. Developing a New Accuracy-Improved Model for Estimating Scour Depth around Piers Using a Hybrid Method. Iran. J. Sci. Technol. Trans. Civ. Eng. 2018, 43, 179–189. [Google Scholar] [CrossRef]
- Eghbalzadeh, A.; Hayati, M.; Rezaei, A.; Javan, M. Prediction of Equilibrium Scour Depth in Uniform Non-Cohesive Sediments Downstream of an Apron Using Computational Intelligence. Eur. J. Environ. Civ. Eng. 2016, 22, 28–41. [Google Scholar] [CrossRef]
- Sreedhara, B.M.; Rao, M.; Mandal, S. Application of an Evolutionary Technique (PSO–SVM) and ANFIS in Clear-Water Scour Depth Prediction around Bridge Piers. Neural Comput. Appl. 2018, 31, 7335–7349. [Google Scholar] [CrossRef]
- Hassanzadeh, Y.; Jafari-Bavil-Olyaei, A.; Aalami, M.-T.; Kardan, N. Experimental and Numerical Investigation of Bridge Pier Scour Estimation Using ANFIS and Teaching-Learning-Based Optimization Methods. Eng. Comput. 2018, 35, 1103–1120. [Google Scholar] [CrossRef]
- Aamir, M.; Ahmad, Z. Estimation of Maximum Scour Depth Downstream of an Apron under Submerged Wall Jets. J. Hydroinform. 2019, 21, 523–540. [Google Scholar] [CrossRef]
- Azamathulla, H.M.D.; Ghani, A.A. ANFIS-Based Approach for Predicting the Scour Depth at Culvert Outlets. J. Pipeline Syst. Eng. Pract. 2011, 2, 35–40. [Google Scholar] [CrossRef]
- Haghiabi, A.H. Closure to “Prediction of River Pipeline Scour Depth Using Multivariate Adaptive Regression Splines” by Amir Hamzeh Haghiabi. J. Pipeline Syst. Eng. Pract. 2019, 10. [Google Scholar] [CrossRef]
- Ahmad, N.; Bihs, H.; Myrhaug, D.; Kamath, A.; Arntsen, Ø.A. Numerical Modeling of Breaking Wave Induced Seawall Scour. Coast. Eng. 2019, 150, 108–120. [Google Scholar] [CrossRef]
- Cheng, L.; Yeow, K.; Zhang, Z.; Teng, B. Three-Dimensional Scour below Offshore Pipelines in Steady Currents. Coast. Eng. 2009, 56, 577–590. [Google Scholar] [CrossRef]
- Ehteram, M.; El-Shafie, A.H.; Hin, L.S.; Othman, F.; Koting, S.; Karami, H.; Mousavi, S.-F.; Farzin, S.; Ahmed, A.N.; Zawawi, B.; et al. Toward Bridging Future Irrigation Deficits Utilizing the Shark Algorithm Integrated with a Climate Change Model. Appl. Sci. 2019, 9, 3960. [Google Scholar] [CrossRef]
- Ehteram, M.; Binti Koting, S.; Afan, H.A.; Mohd, N.S.; Malek, M.A.; Ahmed, A.N.; El-shafie, A.H.; Onn, C.C.; Lai, S.H.; El-Shafie, A. New Evolutionary Algorithm for Optimizing Hydropower Generation Considering Multireservoir Systems. Appl. Sci. 2019, 9, 2280. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, P.; She, Q.; Lin, G. Research on Air Pollutant Concentration Prediction Method Based on Self-Adaptive Neuro-Fuzzy Weighted Extreme Learning Machine. Environ. Pollut. 2018. [Google Scholar] [CrossRef]
- Ehteram, M.; Singh, V.P.; Ferdowsi, A.; Mousavi, S.F.; Farzin, S.; Karami, H.; Mohd, N.S.; Afan, H.A.; Lai, S.H.; Kisi, O.; et al. An Improved Model Based on the Support Vector Machine and Cuckoo Algorithm for Simulating Reference Evapotranspiration. PLoS ONE 2019, 14. [Google Scholar] [CrossRef] [PubMed]
- Karami, H.; Ehteram, M.; Mousavi, S.-F.; Farzin, S.; Kisi, O.; El-Shafie, A. Optimization of Energy Management and Conversion in the Water Systems Based on Evolutionary Algorithms. Neural Comput. Appl. 2018, 31, 5951–5964. [Google Scholar] [CrossRef]
- Zhang, R.; Wu, P. The Investigation of Shape Factors in Determining Scour Depth at Culvert Outlets. ISH J. Hydraul. Eng. 2019, 1–7. [Google Scholar] [CrossRef]
- Das, B.S.; Devi, K.; Khatua, K.K. Prediction of Discharge in Converging and Diverging Compound Channel by Gene Expression Programming. ISH J. Hydraul. Eng. 2019, 1–11. [Google Scholar] [CrossRef]
- Roushangar, K.; Foroudi Khowr, A.; Saneie, M. Experimental Study and Artificial Intelligence-Based Modeling of Discharge Coefficient of Converging Ogee Spillways. ISH J. Hydraul. Eng. 2019, 1–8. [Google Scholar] [CrossRef]
- Kaveh, A.; Dadras, A.; Montazeran, A.H. Chaotic Enhanced Colliding Bodies Algorithms for Size Optimization of Truss Structures. Acta Mech. 2018, 229, 2883–2907. [Google Scholar] [CrossRef]
- Panda, A.; Pani, S. Determining Approximate Solutions of Nonlinear Ordinary Differential Equations Using Orthogonal Colliding Bodies Optimization. Neural Process. Lett. 2017, 48, 219–243. [Google Scholar] [CrossRef]
- Kaveh, A.; Sabeti, S. Structural Optimization of Jacket Supporting Structures for Offshore Wind Turbines Using Colliding Bodies Optimization Algorithm. Struct. Des. Tall Spec. Build. 2018, 27, e1494. [Google Scholar] [CrossRef]
- Kaveh, A.; Rezaei, M.; Shiravand, M.R. Optimal Design of Nonlinear Large-Scale Suspendome Using Cascade Optimization. Int. J. Space Struct. 2017, 33, 3–18. [Google Scholar] [CrossRef]
- Ehteram, M.; Karami, H.; Mousavi, S.F.; Farzin, S.; Celeste, A.B.; Shafie, A.-E. Reservoir Operation by a New Evolutionary Algorithm: Kidney Algorithm. Water Resour. Manag. 2018, 32, 4681–4706. [Google Scholar] [CrossRef]
- Ehteram, M.; Singh, V.P.; Karami, H.; Hosseini, K.; Dianatikhah, M.; Hossain, M.; Ming Fai, C.; El-Shafie, A. Irrigation Management Based on Reservoir Operation with an Improved Weed Algorithm. Water 2018, 10, 1267. [Google Scholar] [CrossRef]
- Cheng, L.; Yeow, K.; Zang, Z.; Li, F. 3D Scour below Pipelines under Waves and Combined Waves and Currents. Coast. Eng. 2014, 83, 137–149. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Saberi-Movahed, F. GMDH-GEP to Predict Free Span Expansion Rates below Pipelines under Waves. Mar. Georesour. Geotechnol. 2018, 37, 375–392. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
| Parameters | Range |
|---|---|
| H (m) (input) | 0.13–0.17 |
| T (s) (input) | 1.5–2.0 |
| Uw (m/s) (input) | 0.29–0.45 |
| em (mm) (input) | 5–20 |
| V*H (mm/s) (output) | 1.27–5.162 |
| V*L (mm/s) (output) | 1.19–4.527 |
| V*R (mm/s) (output) | 1.11–4.49 |
| V*v (mm/s) (output) | 0.592–2.405 |
| (input) | 0.18–0.30 |
| KC (input) | 8.7–18 |
| e/B (input) | 0.10–0.40 |
| (rad) (input) | 0.0–0.70 |
| a | ||||
| Parameter | Population Size | Inertia Weight | Individual Coefficient | Social Coefficient |
| Level 1 | 100, S/N:0.87 | 0.2, S/N:0.21 | 1.6, S/N:0.32 | 1.6, S/N:0.30 |
| Level 2 | 200, S/N:0.76 | 0.40, S/N:0.15 | 1.8, S/N:0.54 | 1.8, S/N:0.41 |
| Level 3 | 300 S/N:0.82 | 0.60, S/N:0.42 | 2.0, S/N:0.30 | 2.0, S/N:0.24 |
| Level 4 | 400, S/N:0.87 | 0.80, S/N:0.55 | 2.2, S/N:0.45 | 2.2, S/N:0.32 |
| b | ||||
| Parameter | Population Size | |||
| Level 1 | 100, S/N:0.84 | |||
| Level 2 | 200, S/N:0.96 | |||
| Level 3 | 300 S/N:0.83 | |||
| Level 4 | 400, S/N:0.87 | |||
| c | ||||
| WA, population size: 100, the maximum number of iterations: 200 | ||||
| Model | MAE (mm/s) | PBIAS | NSE |
|---|---|---|---|
| Train | |||
| MLP-CBO (VH*) | 0.345 | 0.12 | 0.95 |
| MLP-WA (VH*) | 0.389 | 0.17 | 0.93 |
| MLP-PSO (VH*) | 0.393 | 0.22 | 0.92 |
| Test | |||
| MLP-CBO (VH*) | 0.367 | 0.14 | 0.92 |
| MLP-WA (VH*) | 0.379 | 0.19 | 0.91 |
| MLP-PSO (VH*) | 0.391 | 0.23 | 0.90 |
| Train | |||
| MLP-CBO (VV*) | 0.412 | 0.18 | 0.91 |
| MLP-WA (VV*) | 0.422 | 0.22 | 0.89 |
| MLP-PSO (VV*) | 0.434 | 0.25 | 0.87 |
| Test | |||
| MLP-CBO (VV*) | 0.416 | 0.20 | 0.90 |
| MLP-WA (VV*) | 0.432 | 0.29 | 0.88 |
| MLP-PSO (VV*) | 0.449 | 0.32 | 0.86 |
| Train | |||
| MLP-CBO (VR*) | 0.512 | 0.27 | 0.89 |
| MLP-WA (VR*) | 0.522 | 0.32 | 0.87 |
| MLP-PSO (VR*) | 0.523 | 0.34 | 0.85 |
| Test | |||
| MLP-CBO (VR*) | 0.534 | 0.29 | 0.87 |
| MLP-WA (VR*) | 0.541 | 0.35 | 0.86 |
| MLP-PSO (VR*) | 0.555 | 0.37 | 0.85 |
| Train | |||
| MLP-CBO (VL*) | 0.612 | 0.31 | 0.86 |
| MLP-WA (VL*) | 0.621 | 0.39 | 0.84 |
| MLP-PSO (VL*) | 0.629 | 0.42 | 0.83 |
| Test | |||
| MLP-CBO (VL*) | 0.714 | 0.33 | 0.85 |
| MLP-WA (VL*) | 0.738 | 0.42 | 0.82 |
| MLP-PSO (VL*) | 0.742 | 0.45 | 0.80 |
| MODEL | MAE (MM/S) | PBIAS | NSE |
|---|---|---|---|
| EQUATION (28) | 1.59 | 0.55 | 0.87 |
| EQUATION (29) | 1.34 | 0.52 | 0.86 |
| EQUATION (30) | 1.37 | 0.56 | 0.85 |
| EQUATION (31) | 1.42 | 0.55 | 0.81 |
| EQUATION (32) | 1.45 | 0.54 | 0.80 |
| MLP-CBO (VH*) | 0.367 | 0.14 | 0.90 |
| MLP-WA (VH*) | 0.391 | 0.23 | 0.89 |
| MLP-PSO (VH*) | 0.399 | 0.25 | 0.87 |
| MLP-CBO (VL*) | 0.721 | 0.42 | 0.89 |
| MLP-WA (VL*) | 0.745 | 0.45 | 0.87 |
| MLP-PSO (VL*) | 0.814 | 0.49 | 0.86 |
| MLP-CBO (VR*) | 0.621 | 0.32 | 0.85 |
| MLP-WA (VR*) | 0.634 | 0.36 | 0.82 |
| MLP-PSO (VR*) | 0.642 | 0.38 | 0.80 |
| MLP-CBO (VV*) | 0.521 | 0.23 | 0.88 |
| MLP-WA (VV*) | 0.555 | 0.25 | 0.89 |
| MLP-PSO (VV*) | 0.591 | 0.27 | 0.89 |
| Performance Rating | RSR Value |
|---|---|
| Very Good | 0.00 ≤ RSR ≤ 0.5 |
| Good | 0.500 ≤ RSR ≤ 0.600 |
| Satisfactory | 0.600 ≤ RSR ≤ 0.700 |
| Unsatisfactory | RSR > 0.7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ehteram, M.; Ahmed, A.N.; Ling, L.; Fai, C.M.; Latif, S.D.; Afan, H.A.; Banadkooki, F.B.; El-Shafie, A. Pipeline Scour Rates Prediction-Based Model Utilizing a Multilayer Perceptron-Colliding Body Algorithm. Water 2020, 12, 902. https://doi.org/10.3390/w12030902
Ehteram M, Ahmed AN, Ling L, Fai CM, Latif SD, Afan HA, Banadkooki FB, El-Shafie A. Pipeline Scour Rates Prediction-Based Model Utilizing a Multilayer Perceptron-Colliding Body Algorithm. Water. 2020; 12(3):902. https://doi.org/10.3390/w12030902
Chicago/Turabian StyleEhteram, Mohammad, Ali Najah Ahmed, Lloyd Ling, Chow Ming Fai, Sarmad Dashti Latif, Haitham Abdulmohsin Afan, Fatemeh Barzegari Banadkooki, and Ahmed El-Shafie. 2020. "Pipeline Scour Rates Prediction-Based Model Utilizing a Multilayer Perceptron-Colliding Body Algorithm" Water 12, no. 3: 902. https://doi.org/10.3390/w12030902
APA StyleEhteram, M., Ahmed, A. N., Ling, L., Fai, C. M., Latif, S. D., Afan, H. A., Banadkooki, F. B., & El-Shafie, A. (2020). Pipeline Scour Rates Prediction-Based Model Utilizing a Multilayer Perceptron-Colliding Body Algorithm. Water, 12(3), 902. https://doi.org/10.3390/w12030902










