Calibration of a Distributed Hydrological Model in a Data-Scarce Basin Based on GLEAM Datasets
Abstract
:1. Introduction
2. Materials and Methods
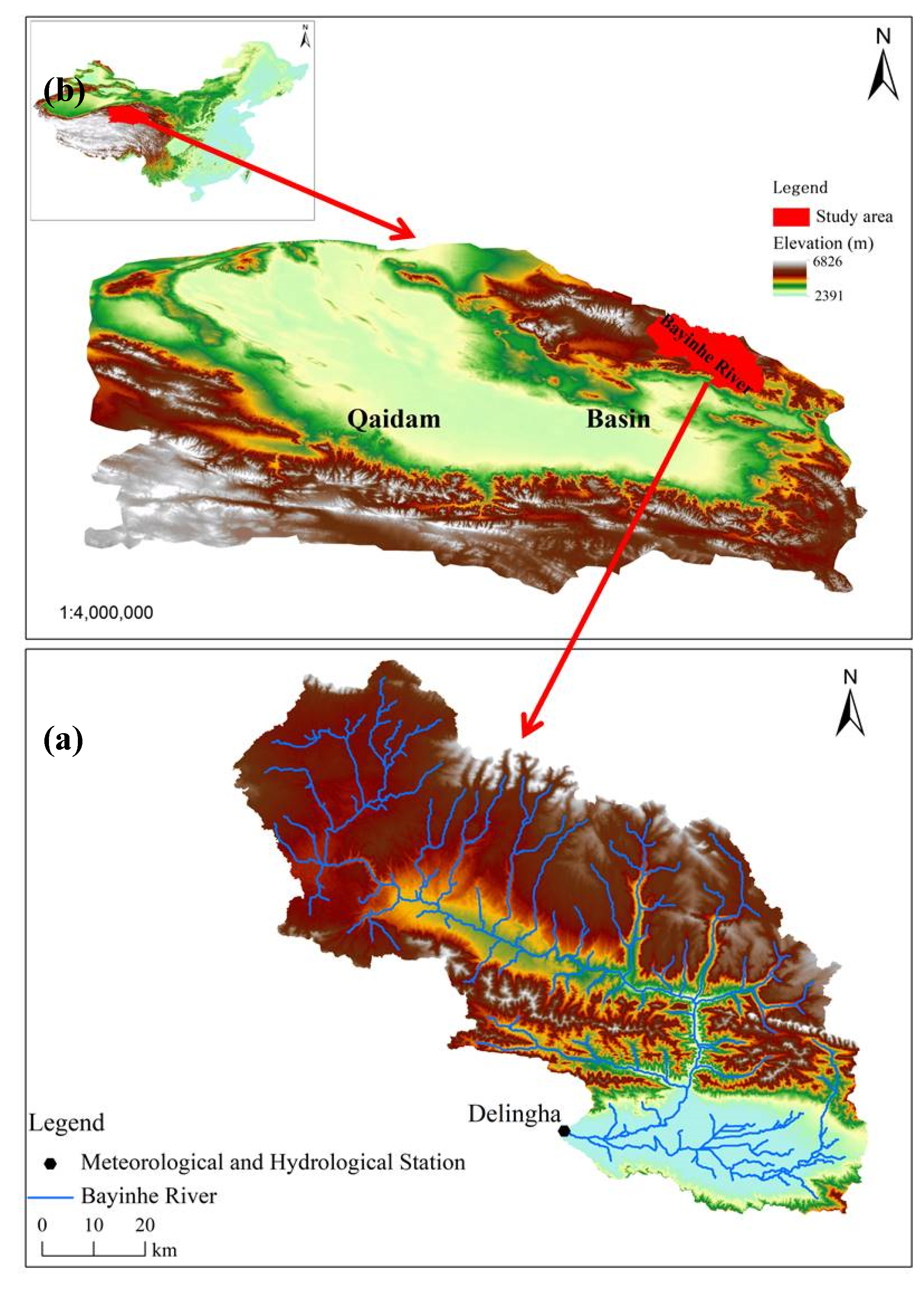
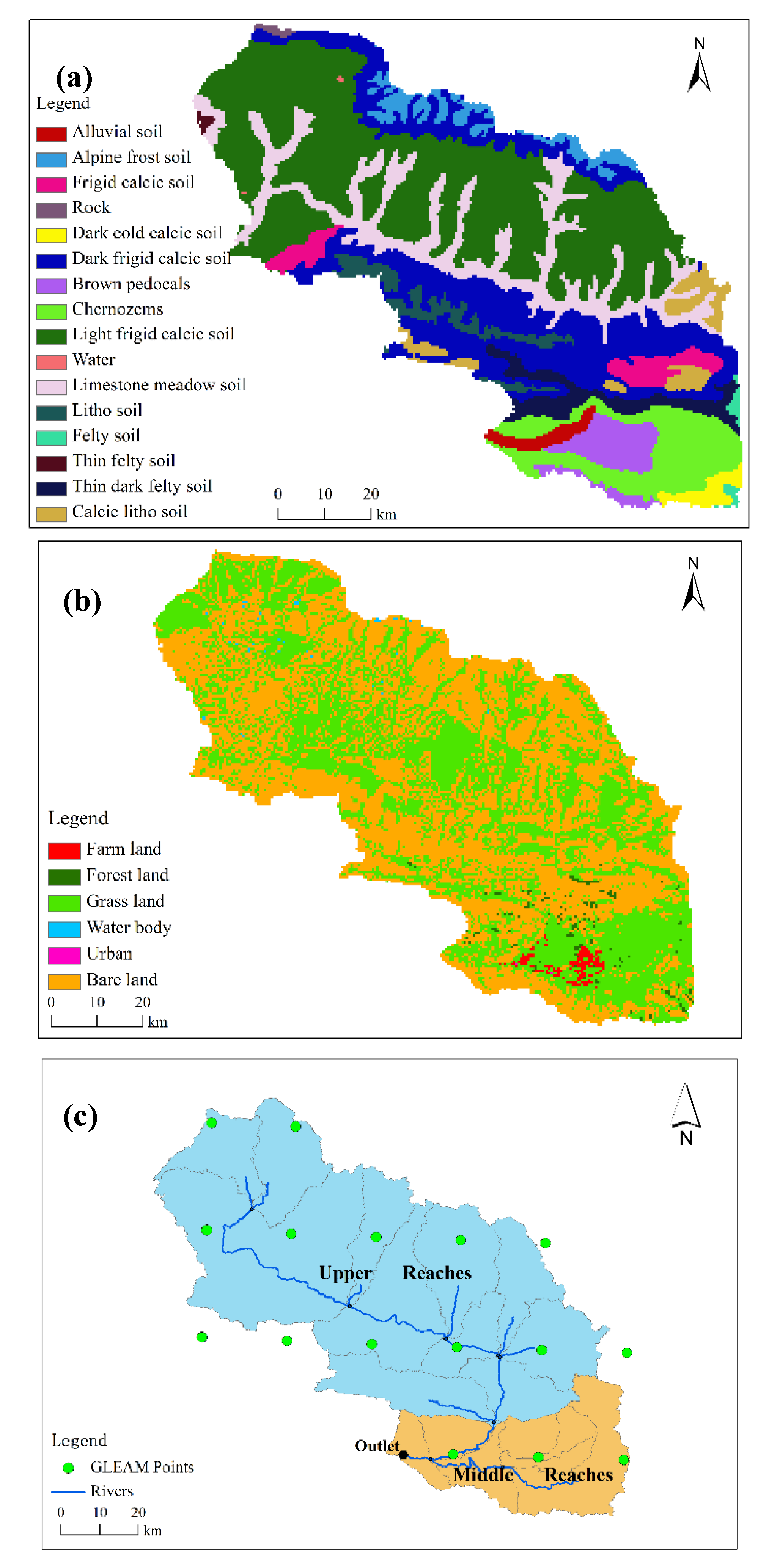
2.1. Study Area
2.2. Data Preparation
2.2.1. Basic Data of the SWAT Model
2.2.2. Data for Model Calibration
2.3. SWAT Model
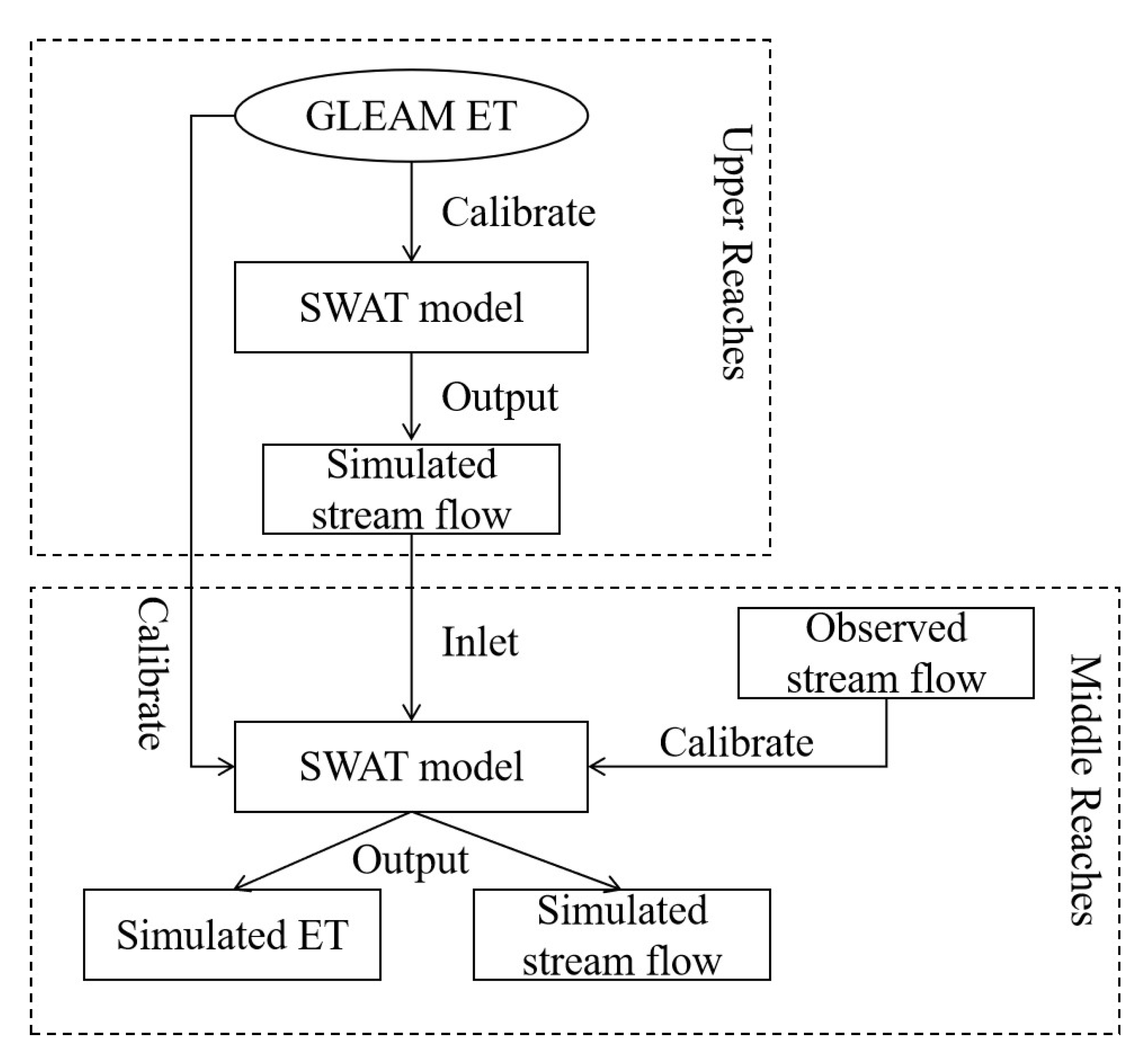
2.4. SWAT Model Calibration Strategy
2.5. Parameters Sensitivity
2.6. Indicators for Evaluating the SWAT Model Simulation Result
3. Results
3.1. Parameters Sensitivity
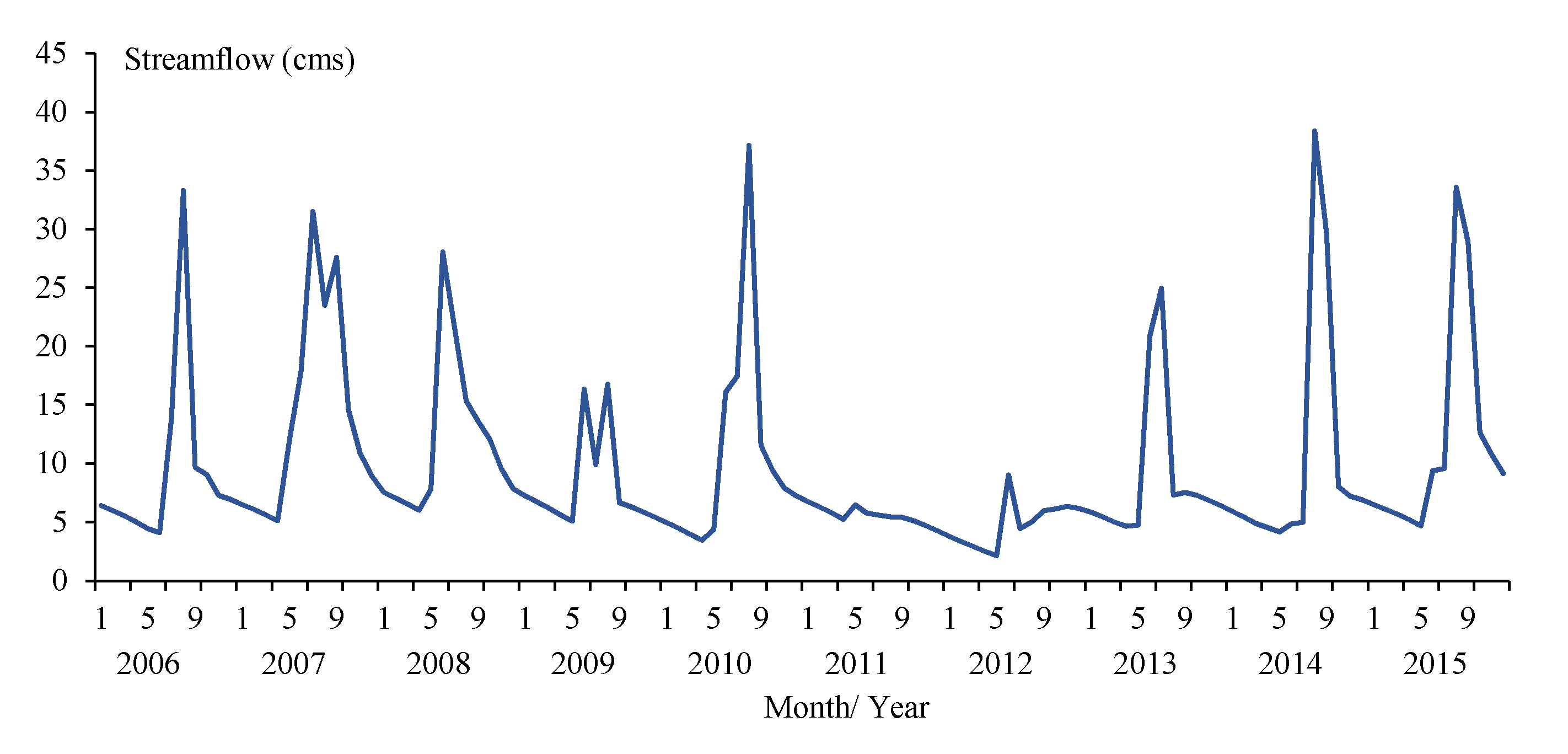
3.2. Non-Calibrated SWAT
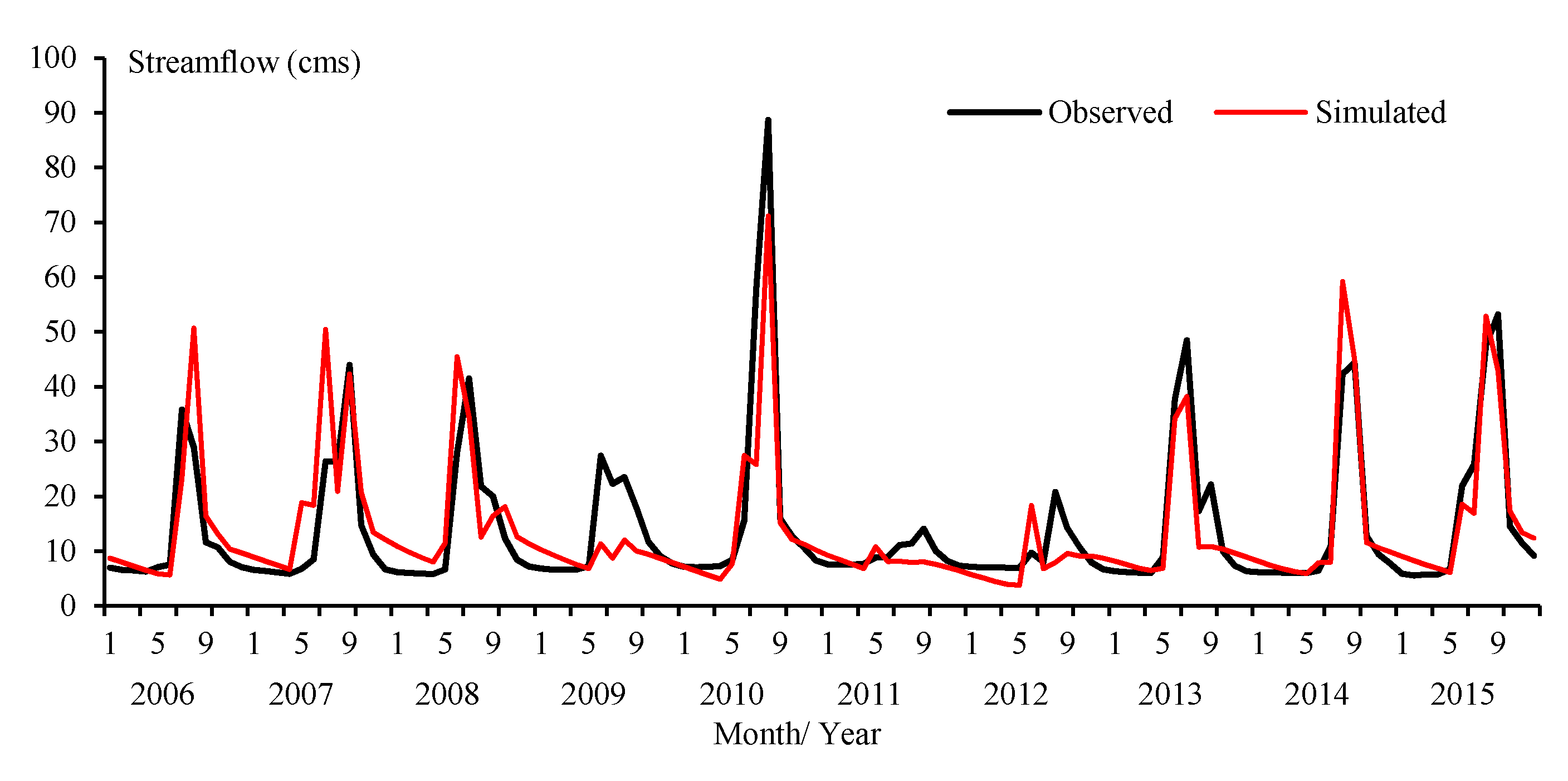
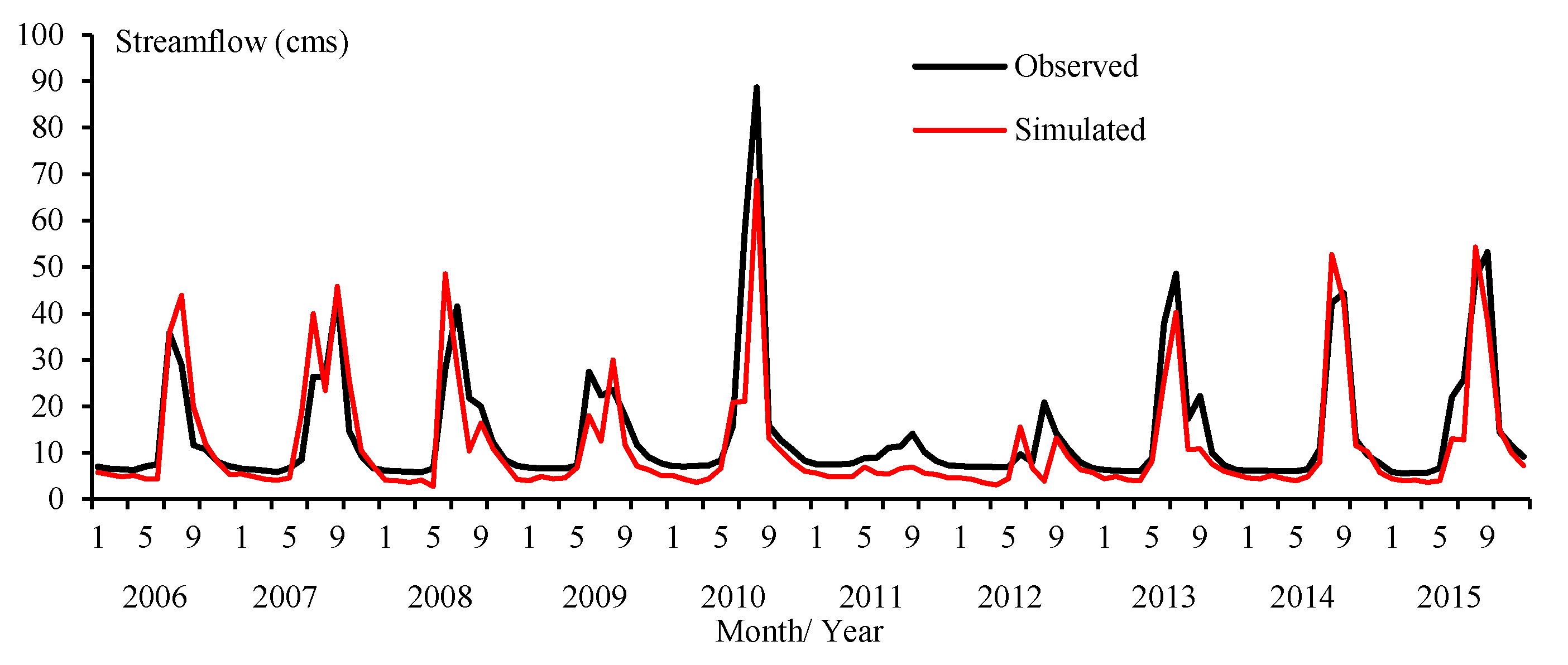
3.3. SWAT1 Performance
3.4. SWAT2U Performance
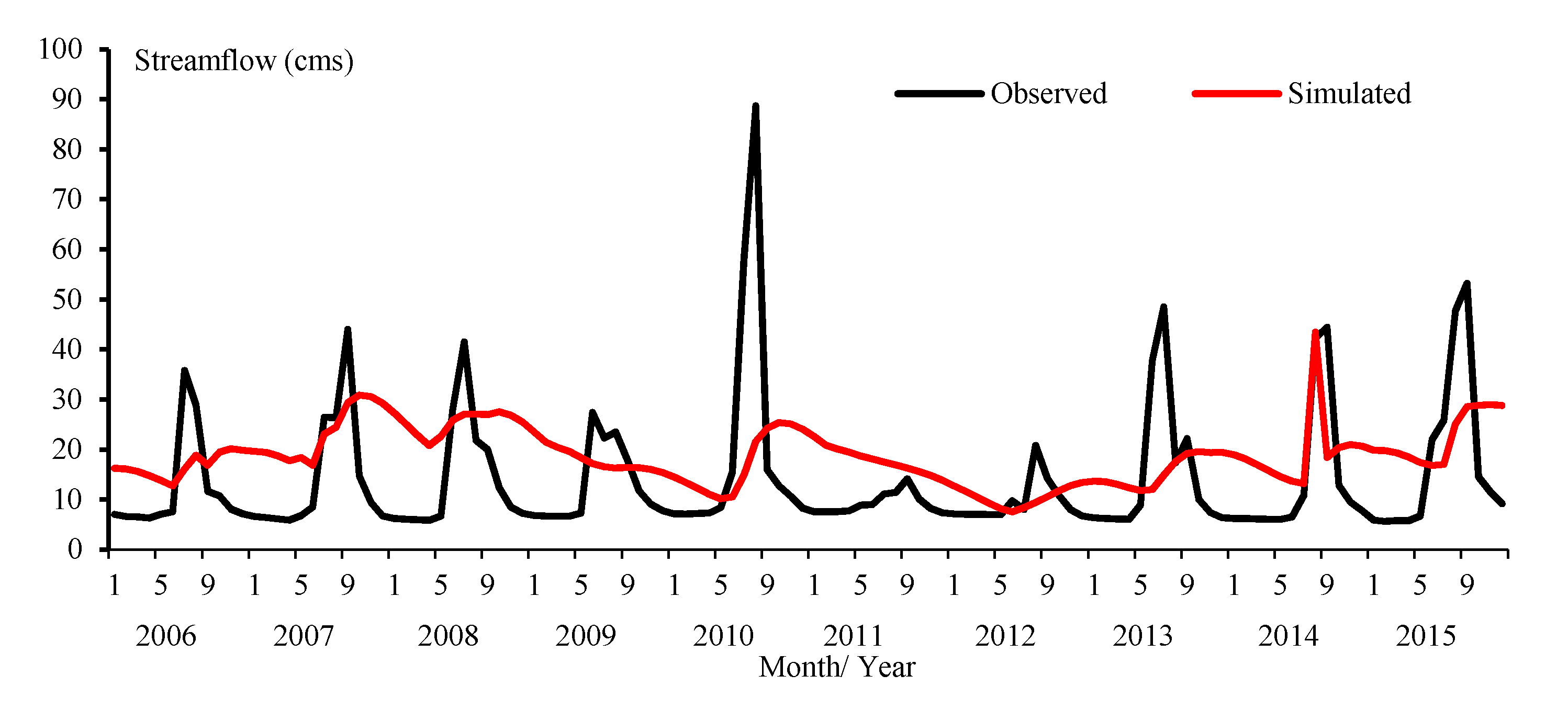
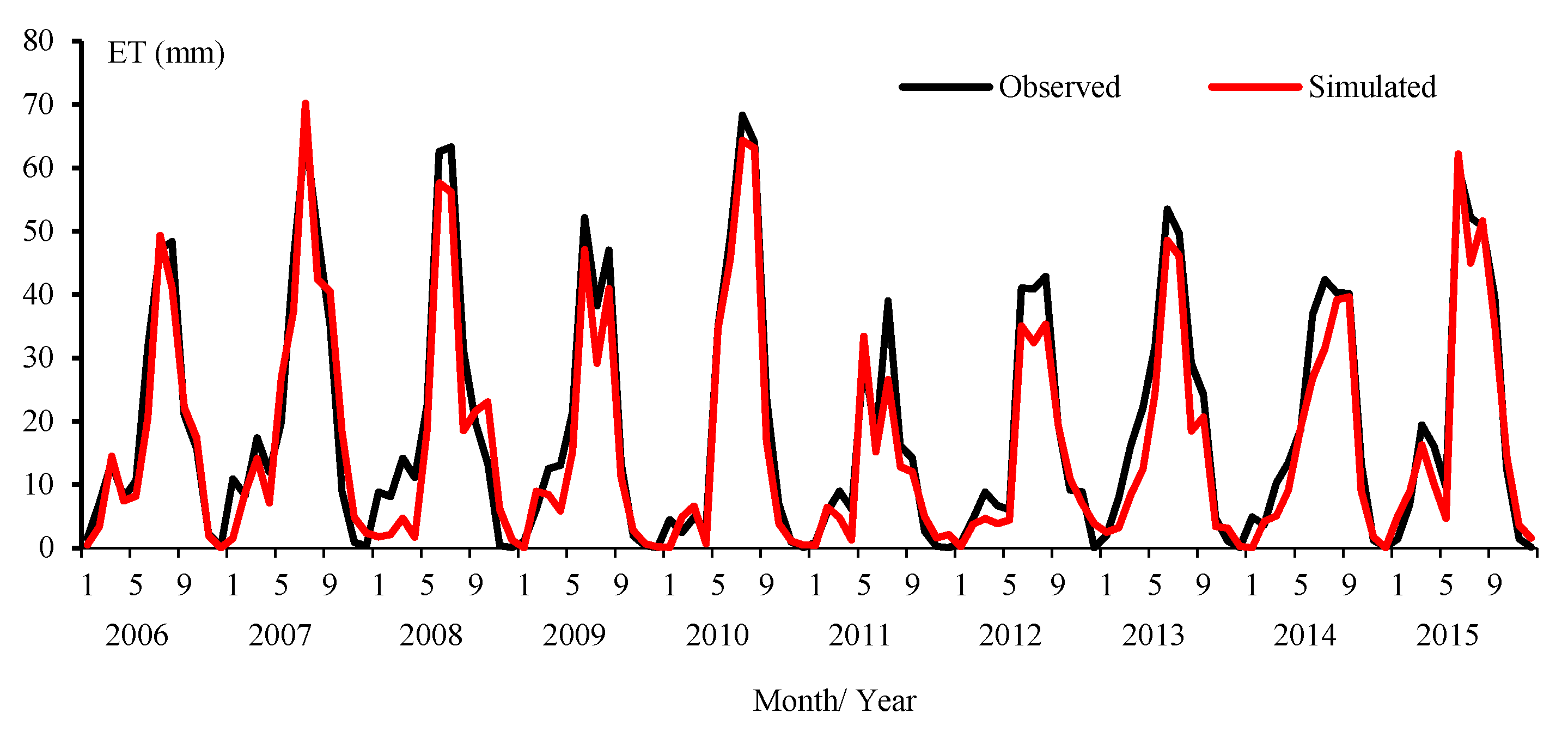
3.5. SWAT2M Performance
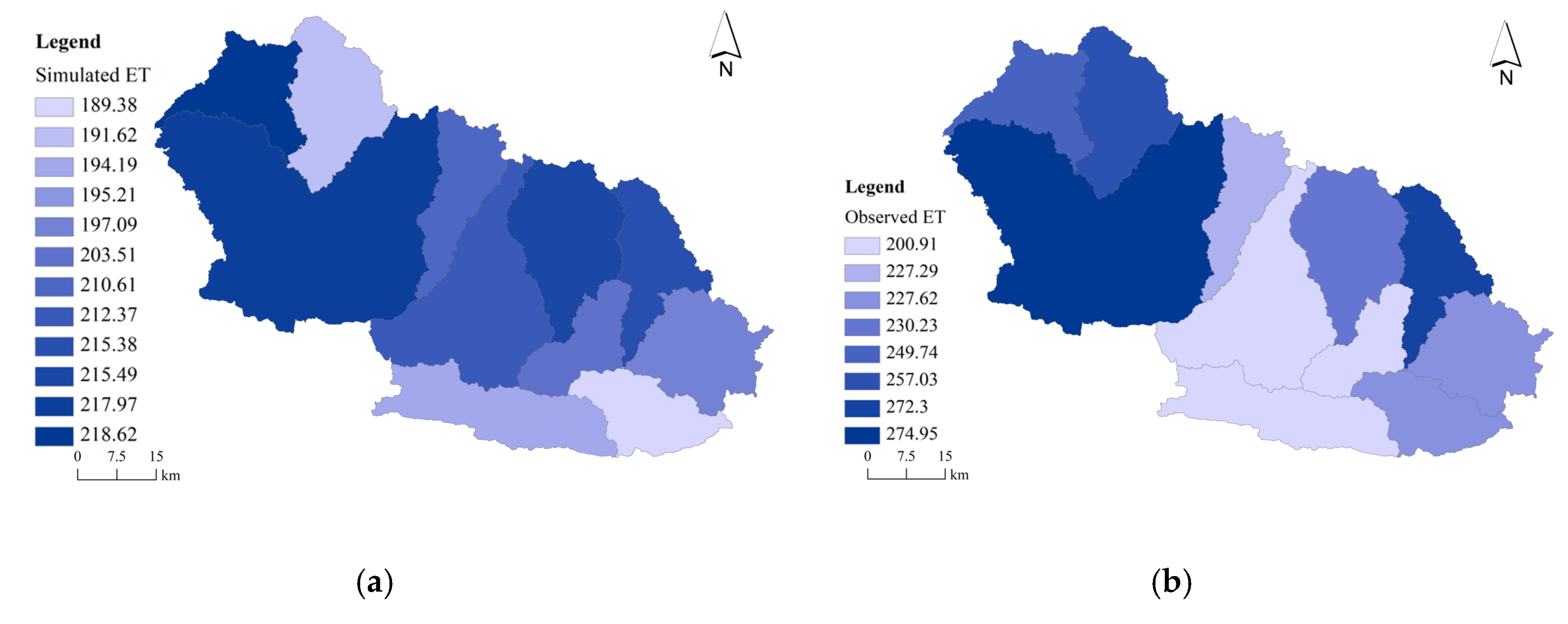
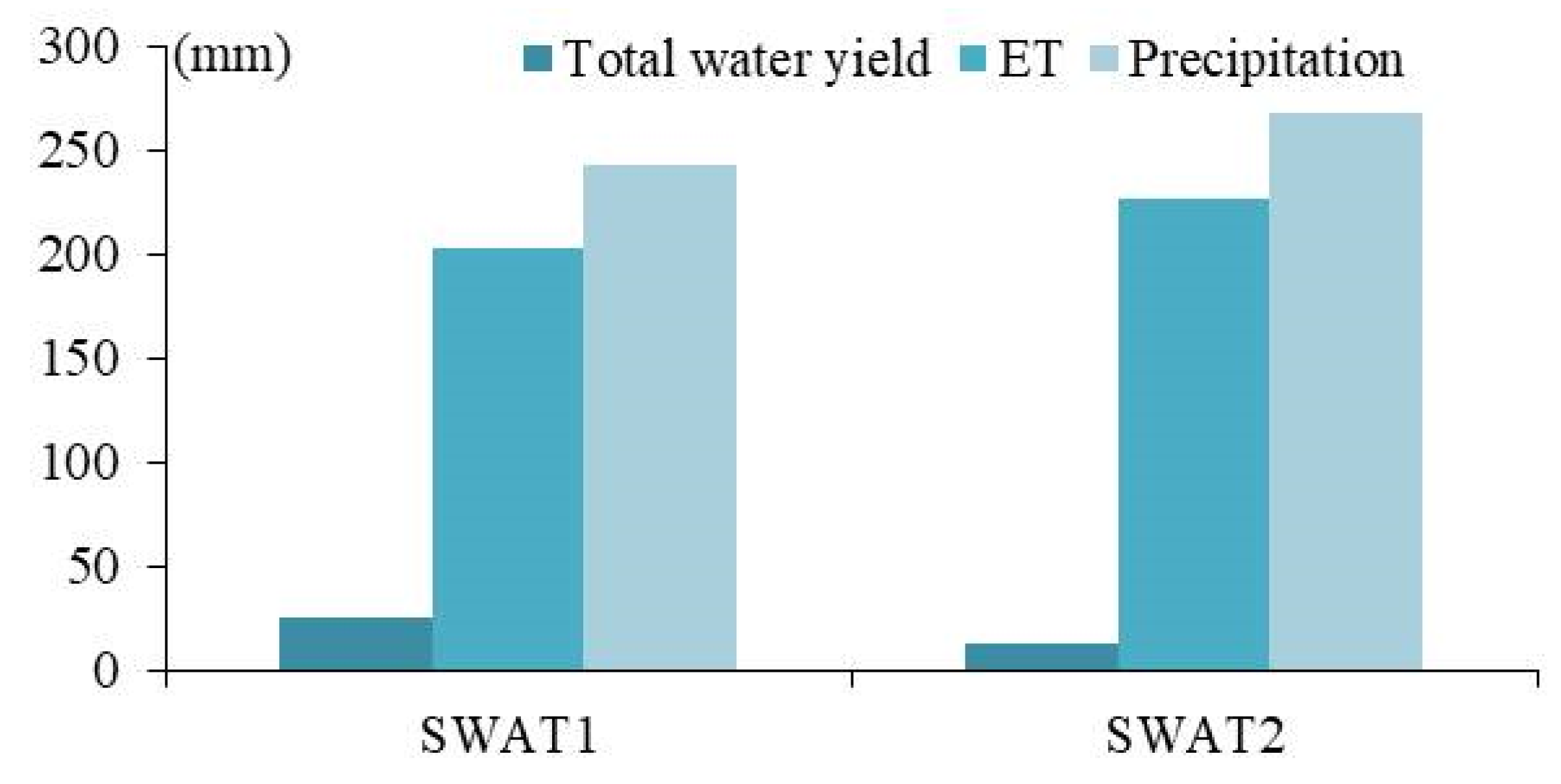
3.6. Water Balance
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data Availability
References
- Rodriguez, F.; Hervé, A.; Morena, F. A distributed hydrological model for urbanized areas-Model development and application to case studies. J. Hydrol. 2008, 351, 268–287. [Google Scholar] [CrossRef]
- Roshan, S.; Yasuto, T.; Kaoru, T. Input data resolution analysis for distributed hydrological modeling. J. Hydrol. 2006, 319, 36–50. [Google Scholar]
- Jin, X.; Zhang, L.; Gu, J.; Zhao, C.; Tian, J.; He, C. Modelling the impacts of spatial heterogeneity in soil hydraulic properties on hydrological process in the upper reach of the Heihe River in the Qilian Mountains, Northwest China. Hydrol. Process. 2015, 29, 3318–3327. [Google Scholar] [CrossRef]
- Wang, Y.; Brubaker, K. Implementing a nonlinear groundwater module in the soil and water assessment tool (SWAT). Hydrol. Process. 2014, 28, 3388–3403. [Google Scholar] [CrossRef]
- Pohlert, T.; Breuer, L.; Huisman, J.A.; Frede, H.G. Assessing the model performance of an integrated hydrological and biogeochemical model for discharge and nitrate load predictions. HESS 2007, 11, 997–1011. [Google Scholar] [CrossRef] [Green Version]
- Noori, N.; Kalin, L. Coupling SWAT and ANN models for enhanced daily streamflow prediction. J. Hydrol. 2016, 533, 141–151. [Google Scholar] [CrossRef]
- Jin, X.; He, C.; Zhang, L.; Zhang, B. A Modified Groundwater Module in SWAT for Improved Streamflow Simulation in a Large, Arid Endorheic River Watershed in Northwest China. Chin. Geogr. Sci. 2018, 28, 49–62. [Google Scholar] [CrossRef] [Green Version]
- Hartwich, J.; Schmidt, M.; Bölscher, J.; Reinhardt-Imjela, C.; Murach, D.; Schulte, A. Hydrological modelling of changes in the water balance due to the impact of woody biomass production in the North German Plain. Environ. Earth Sci. 2016, 75, 1071. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Kannan, N. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1345–1352. [Google Scholar] [CrossRef]
- Santosh, G.; Kolladi, Y.; Surya, T. Influence of Scale on SWAT Model Calibration for Streamflow in a River Basin in the Humid Tropics. Water Resour. Manag. 2010, 24, 4567–4578. [Google Scholar]
- Yesuf, H.M.; Melesse, A.M.; Zeleke, G.; Alamirew, T. Streamflow prediction uncertainty analysis and verification of SWAT model in a tropical watershed. Environ. Earth Sci. 2016, 75, 806. [Google Scholar] [CrossRef]
- Fisher, J.B.; Tu, K.P.; Baldocchi, D.D. Global estimates of the land–atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 FLUXNET sites. Remote Sens. Environ. 2008, 112, 901–919. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Miralles, D.G.; Holmes, T.R.H.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A.; Dolman, A.J. Global land-surface evaporation estimated from satellite-based observations. HESS 2010, 7, 8479–8519. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Xia, J.; Liang, S.; Feng, J.; Fisher, J.B.; Li, X.; Li, X.; Liu, S.; Ma, Z.; Miyata, A.; et al. Comparison of satellite-based evapotranspiration models over terrestrial ecosystems in China. Remote Sens. Environ. 2014, 140, 279–293. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Droogers, P. Calibration of a distributed hydrological model based on satellite evapotranspiration. J. Hydrol. 2008, 349, 411–424. [Google Scholar] [CrossRef]
- Rientjes, T.H.M.; Muthuwatta, L.P.; Bos, M.J.; Bhatti, H.A. Multi-variable calibration of a semi-distributed hydrological model using streamflow data and satellite-based evapotranspiration. J. Hydrol. 2013, 505, 276–290. [Google Scholar] [CrossRef]
- Parajuli, P.B.; Jayakody, P.; Ouyang, Y. Evaluation of Using Remote Sensing Evapotranspiration Data in SWAT. Water Resour. Manag. 2017, 32, 985–996. [Google Scholar] [CrossRef]
- Yang, X.; Wang, G.; Pan, X.; Zhang, Y. Spatio-temporal variability of terrestrial evapotranspiration in China from 1980 to 2011 based on GLEAM data. Trans. Chin. Soc. Agric. Eng. 2015, 31, 132–141, (in Chinese with English Abstract). [Google Scholar]
- Zhang, L.; Nan, Z.; Xu, Y.; Li, S. Hydrological Impacts of Land Use Change and Climate Variability in the Headwater Region of the Heihe River Basin, Northwest China. PLoS ONE 2016, 11, 1–25. [Google Scholar] [CrossRef]
- Jin, X.; Jin, Y.X.; Mao, X.F. Ecological risk assessment of cities on the Tibetan Plateau based on land use/land cover changes—Case study of Delingha City. Ecol. Indic. 2019, 101, 185–191. [Google Scholar] [CrossRef]
- Stannard, D.I. Comparison of Penman-Monteith, Shuttleworth-Wallace, and Modified Priestley-Taylor Evapotranspiration Models for wildland vegetation in semiarid rangeland. Water Resour. 1993, 29, 1379–1392. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Li, Z.; Xu, Z.; Shao, Q.; Yang, J. Parameter estimation and uncertainty analysis of SWAT model in upper reaches of the Heihe River basin. Hydrol. Process. 2009, 23, 2744–2753. [Google Scholar] [CrossRef]
- Yang, L.; Feng, Q.; Yin, Z.; Wen, X.; Si, J.; Li, C.; Deo, R.C. Identifying separate impacts of climate and land use/cover change on hydrological processes in upper stream of Heihe River, Northwest China. Hydrol. Process. 2017, 31, 1100–1113. [Google Scholar] [CrossRef]
| Variables | Datasets | Datasets Description |
|---|---|---|
| Solar radiation | ERA-interim | European Centre for Medium-Range Weather Forecasts (ECMWF) Interim Re-Analysis data |
| Air temperature | ERA-interim | European Centre for Medium-Range Weather Forecasts (ECMWF) Interim Re-Analysis data |
| Precipitation | MSWEP v2.2 | Multi-Source Weighted-Ensemble Precipitation version 2.2 |
| Snow water equivalent | GLOBSNOW L3A v2 & NSIDC v01 | GLOBSNOW version 2 and the National Snow and Ice Data Center version 01 |
| Vegetation optical thickness | LPRM | Land Parameter Retrieval Model |
| Surface soil water | ESA-CCI v4.3 | European Space Agency’s Climate Change Initiative version 4.3 |
| SWAT1 | SWAT2U | SWAT2M | ||||||
|---|---|---|---|---|---|---|---|---|
| Sensitivity Parameters | t-Stat | p-value | Sensitivity Parameters | t-Stat | p-value | Sensitivity Parameters | t-Stat | p-value |
| CN2 | −27.09 | 0.00 | CN2 | −29.16 | 0.00 | CN2 | 35.31 | 0.00 |
| CH_K2 | 7.89 | 0.00 | SOL_BD | −7.83 | 0.00 | SOL_BD | 17.82 | 0.00 |
| SOL_BD | −6.00 | 0.00 | SOL_K | −3.45 | 0.00 | SLSUBBSN | −15.89 | 0.00 |
| CH_N2 | 5.01 | 0.00 | ESCO | 2.86 | 0.00 | SOL_K | 13.47 | 0.00 |
| SOL_K | −3.87 | 0.00 | SLSUBBSN | 2.31 | 0.02 | HRU_SLP | 4.03 | 0.00 |
| SOL_AWC | −2.48 | 0.01 | GWQMN | −1.82 | 0.07 | ALPHA_BF | −3.88 | 0.00 |
| GW_REVAP | 1.96 | 0.05 | SMFMN | 1.19 | 0.23 | SOL_AWC | 2.97 | 0.00 |
| GWQMN | −1.75 | 0.08 | SNOCOVMN | −1.17 | 0.24 | ESCO | 2.61 | 0.01 |
| SLSUBBSN | 1.65 | 0.10 | SNO50COV | −0.96 | 0.34 | GW_REVAP | 2.07 | 0.04 |
| SMFMN | 1.07 | 0.19 | CH_N2 | −0.83 | 0.39 | GWQMN | 1.89 | 0.07 |
| Sub-Basin | Indicators | ||
|---|---|---|---|
| R2 | NSE | PBIAS | |
| 1 | 0.92 | 0.89 | 12.5 |
| 2 | 0.92 | 0.84 | 15.4 |
| 3 | 0.91 | 0.86 | 10.7 |
| 4 | 0.95 | 0.95 | 7.3 |
| 5 | 0.95 | 0.90 | −5.7 |
| 6 | 0.94 | 0.94 | 6.4 |
| 7 | 0.95 | 0.93 | −1.3 |
| 8 | 0.91 | 0.86 | 10.9 |
| 9 | 0.90 | 0.86 | 14.2 |
| 10 | 0.92 | 0.89 | 13.4 |
| 11 | 0.95 | 0.94 | 3.3 |
| 12 | 0.92 | 0.89 | 16.8 |
| SWAT2M Outputs | Location | Indicators | ||
|---|---|---|---|---|
| R2 | NSE | PBIAS | ||
| Streamflow | outlet | 0.78 | 0.75 | 16.5 |
| ET | Sub-basin 1 | 0.92 | 0.90 | 7.4 |
| ET | Sub-basin 2 | 0.92 | 0.88 | 6.2 |
| ET | Sub-basin 3 | 0.91 | 0.78 | −10.6 |
| ET | Sub-basin 4 | 0.93 | 0.90 | 12.4 |
| ET | Sub-basin 5 | 0.92 | 0.91 | 6.9 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, X.; Jin, Y. Calibration of a Distributed Hydrological Model in a Data-Scarce Basin Based on GLEAM Datasets. Water 2020, 12, 897. https://doi.org/10.3390/w12030897
Jin X, Jin Y. Calibration of a Distributed Hydrological Model in a Data-Scarce Basin Based on GLEAM Datasets. Water. 2020; 12(3):897. https://doi.org/10.3390/w12030897
Chicago/Turabian StyleJin, Xin, and Yanxiang Jin. 2020. "Calibration of a Distributed Hydrological Model in a Data-Scarce Basin Based on GLEAM Datasets" Water 12, no. 3: 897. https://doi.org/10.3390/w12030897
APA StyleJin, X., & Jin, Y. (2020). Calibration of a Distributed Hydrological Model in a Data-Scarce Basin Based on GLEAM Datasets. Water, 12(3), 897. https://doi.org/10.3390/w12030897




