Evaluation of Flood Prediction Capability of the WRF-Hydro Model Based on Multiple Forcing Scenarios
Abstract
1. Introduction
2. Data and Method
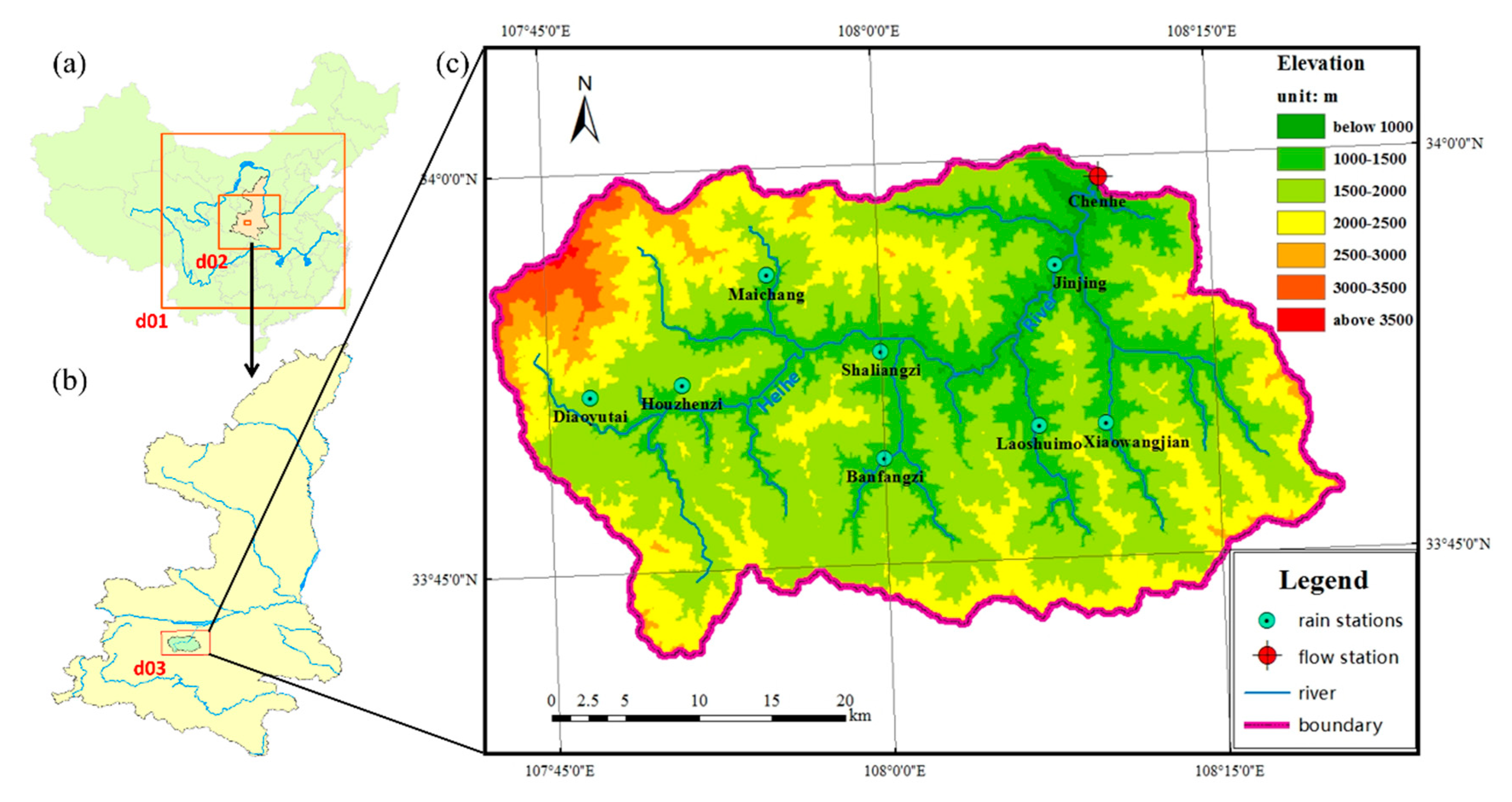
2.1. Study Catchment and Gauge Data
2.2. GLDAS
2.3. The WRF Model
2.4. The WRF-Hydro Model
2.4.1. A Brief Description
2.4.2. Data and Model Settings
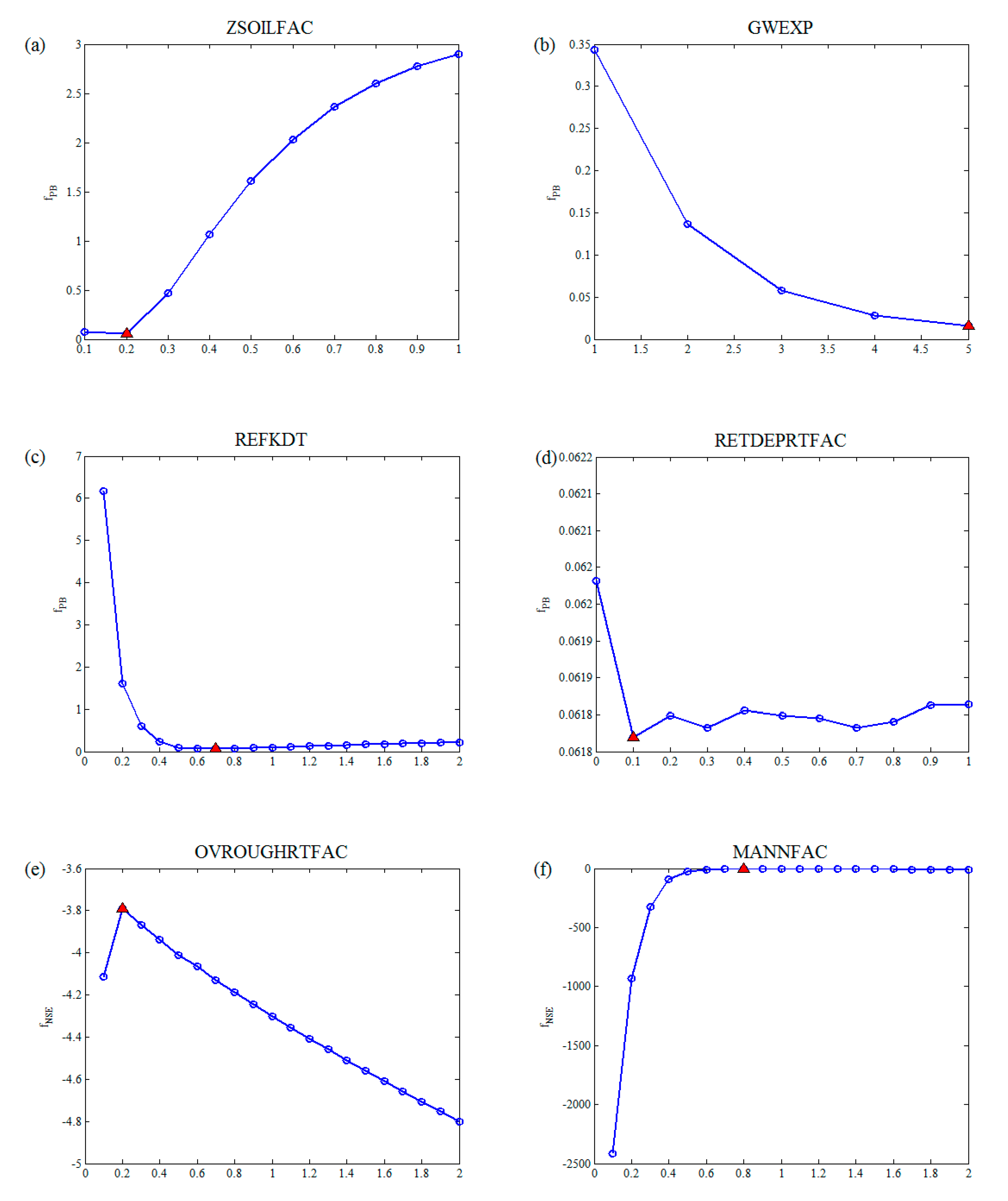
2.4.3. Calibration of Uncoupled WRF-Hydro Model
2.5. The Xinanjiang Model
2.6. Forcing Scenarios Design
2.7. Evaluation Metrics
3. Results and Discussion
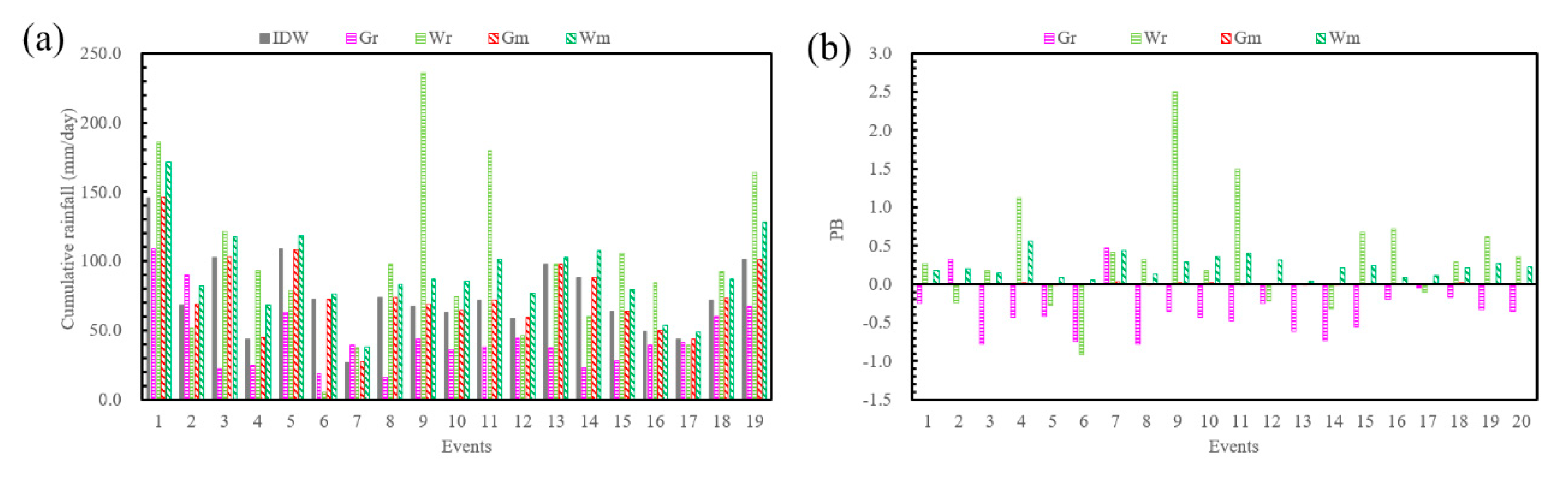
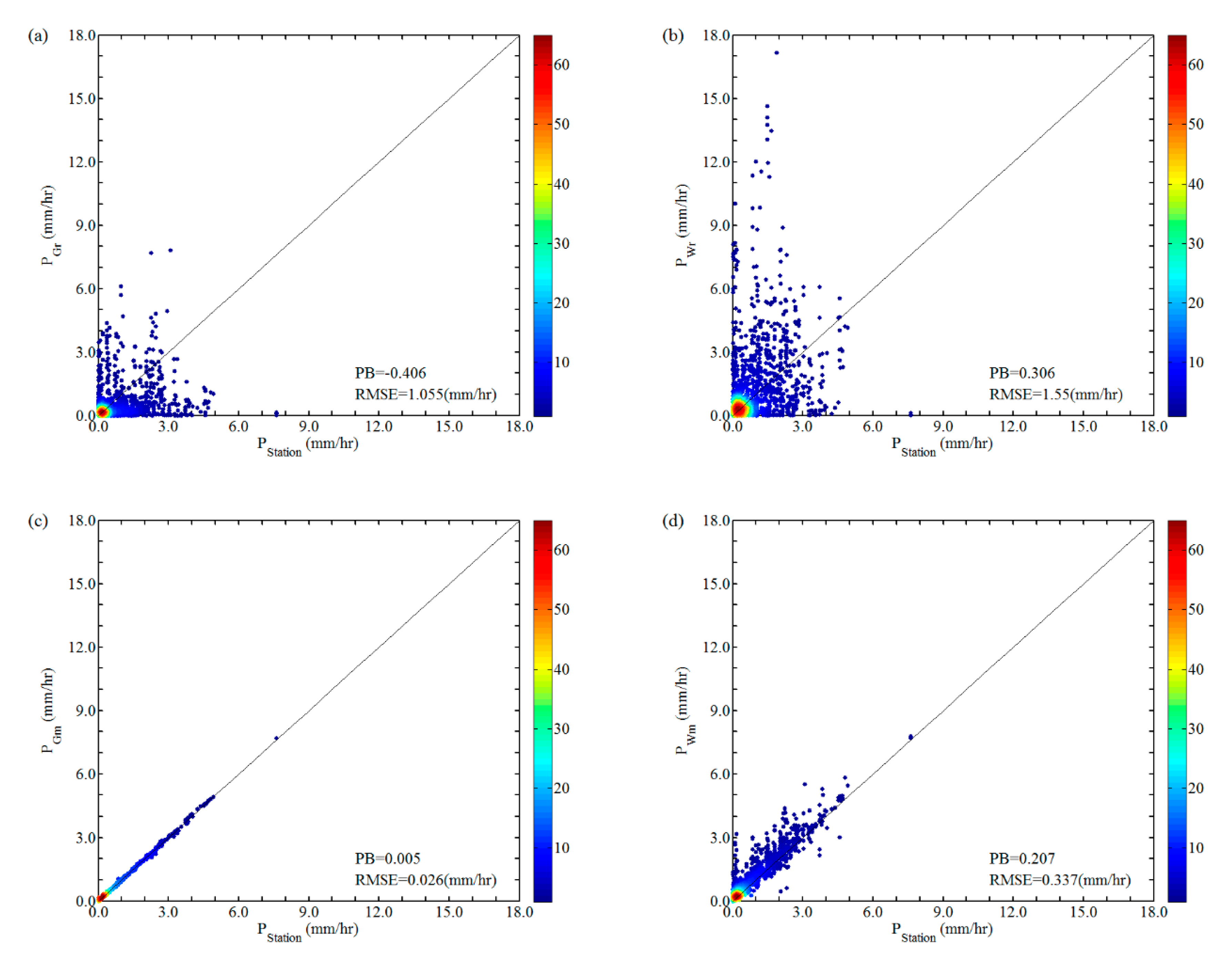
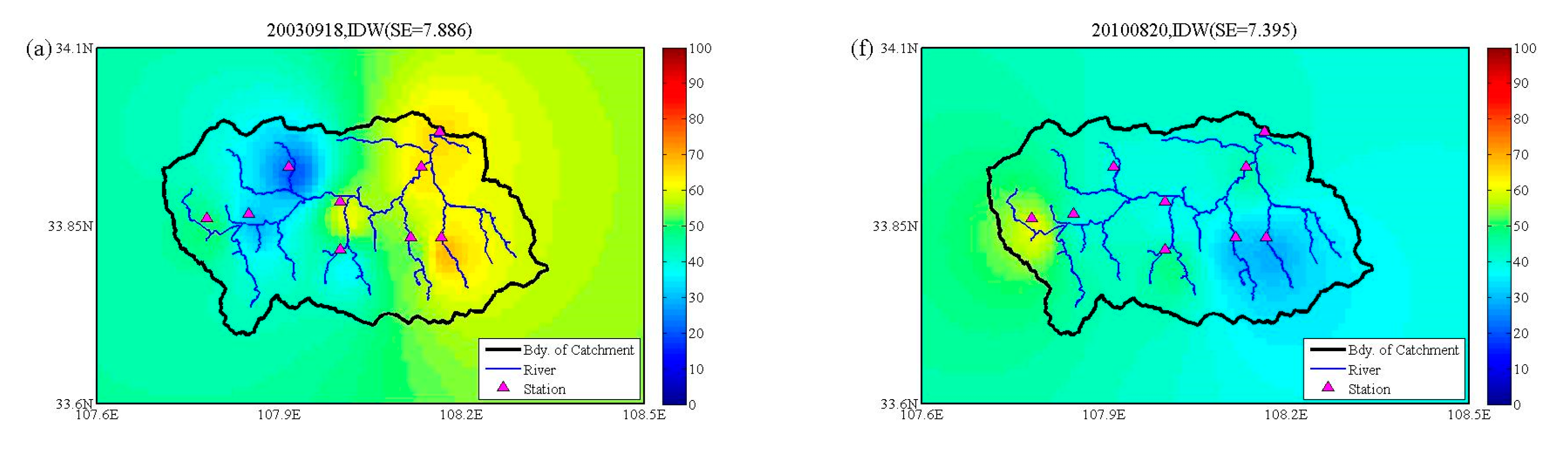
3.1. Evaluation of Five Rainfall Products
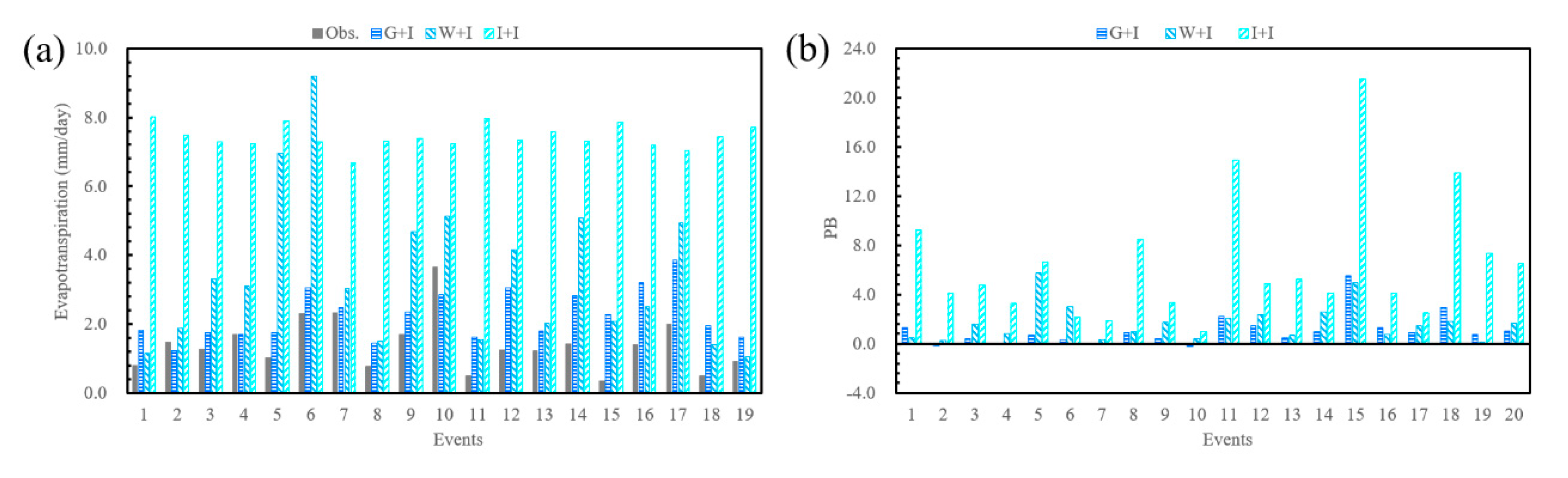
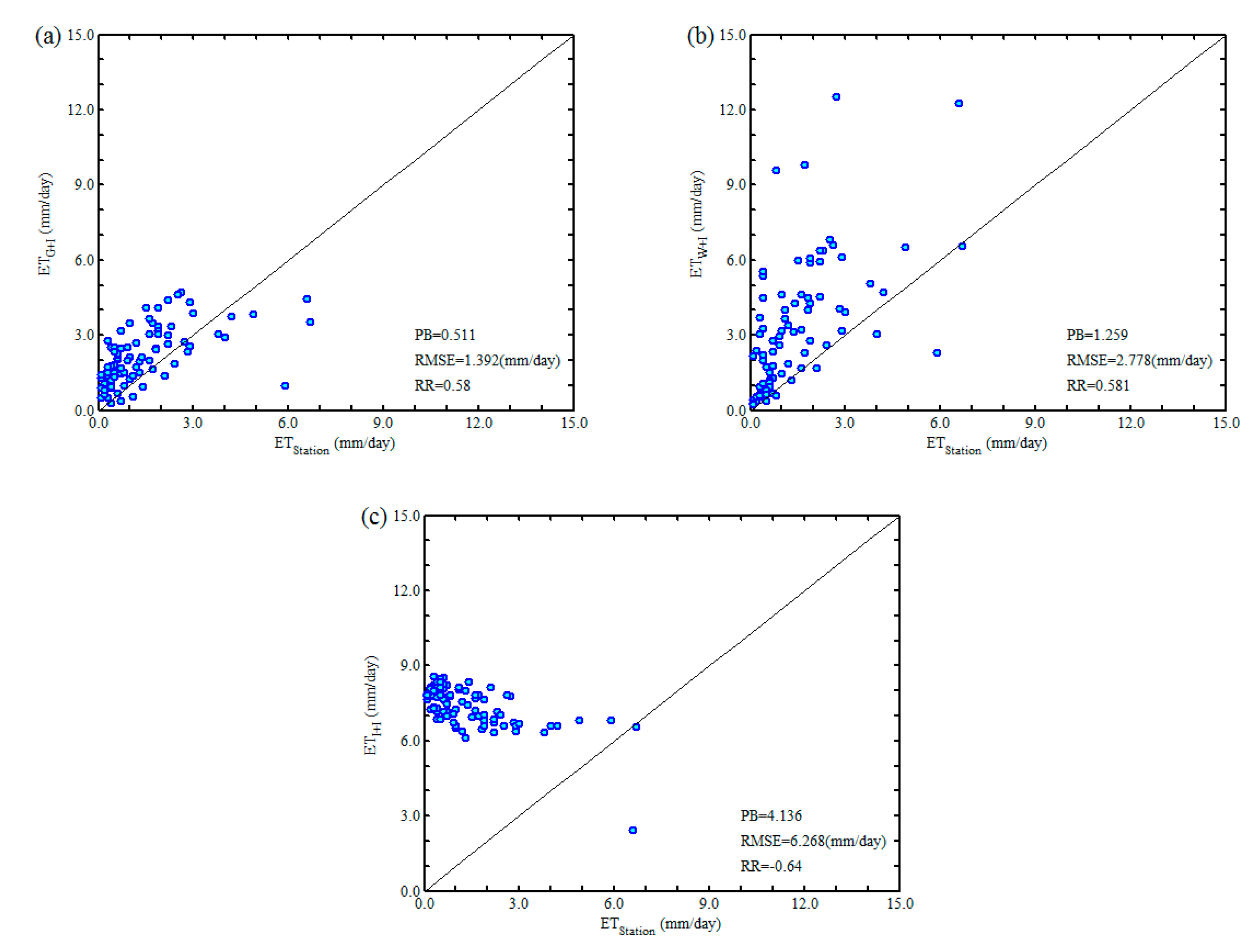
3.2. Evaluation of Daily WRF-Hydro-Derived ET in Three Scenarios
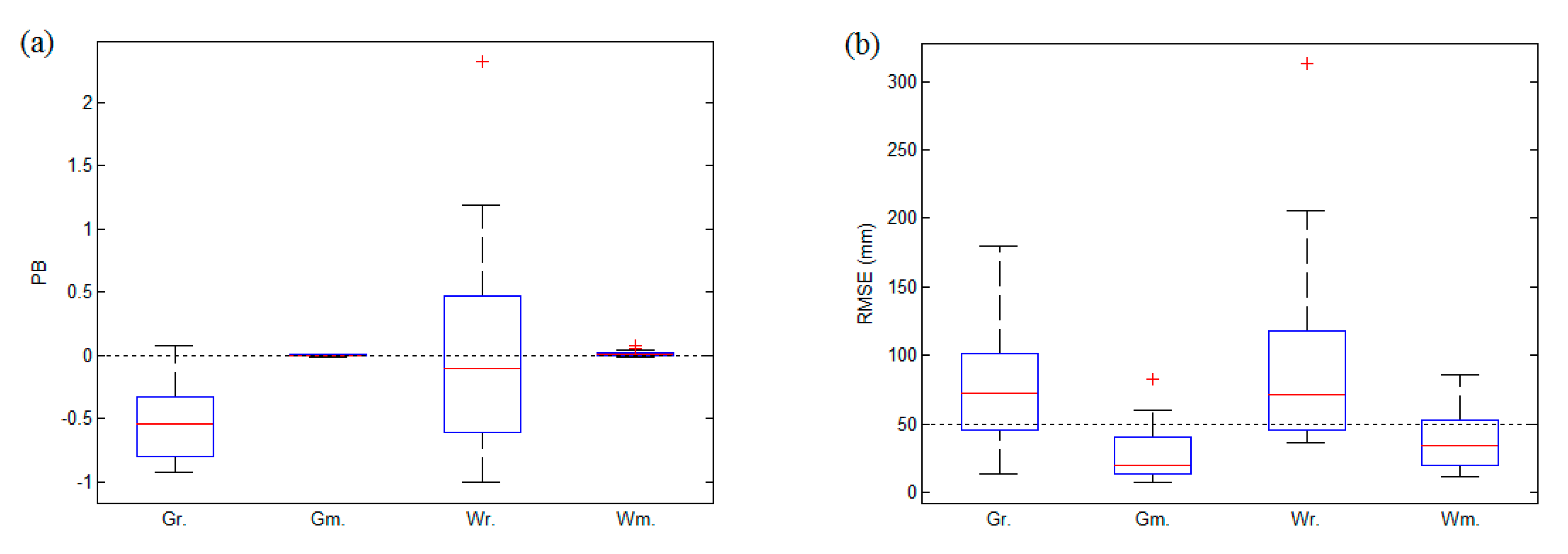
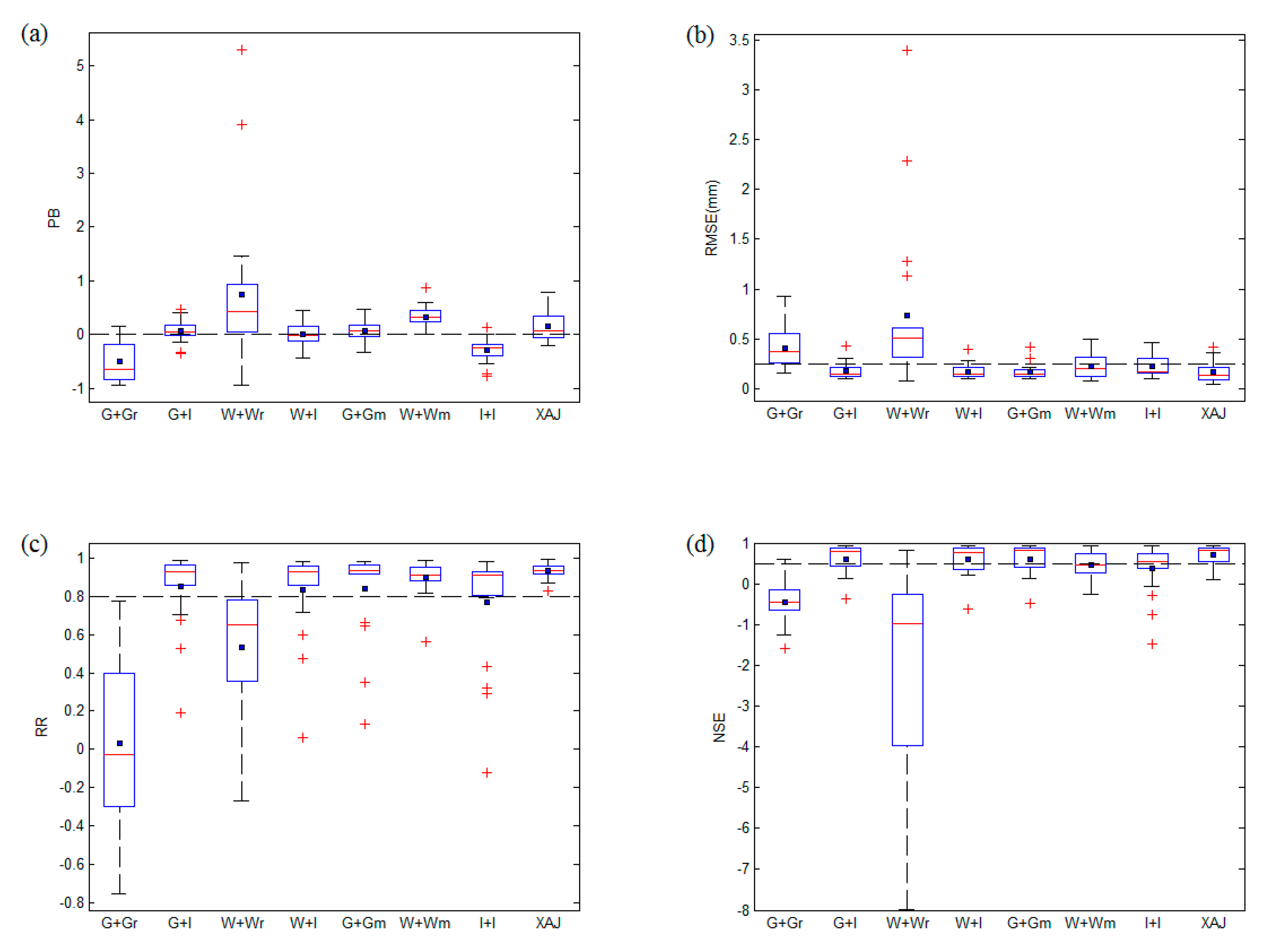
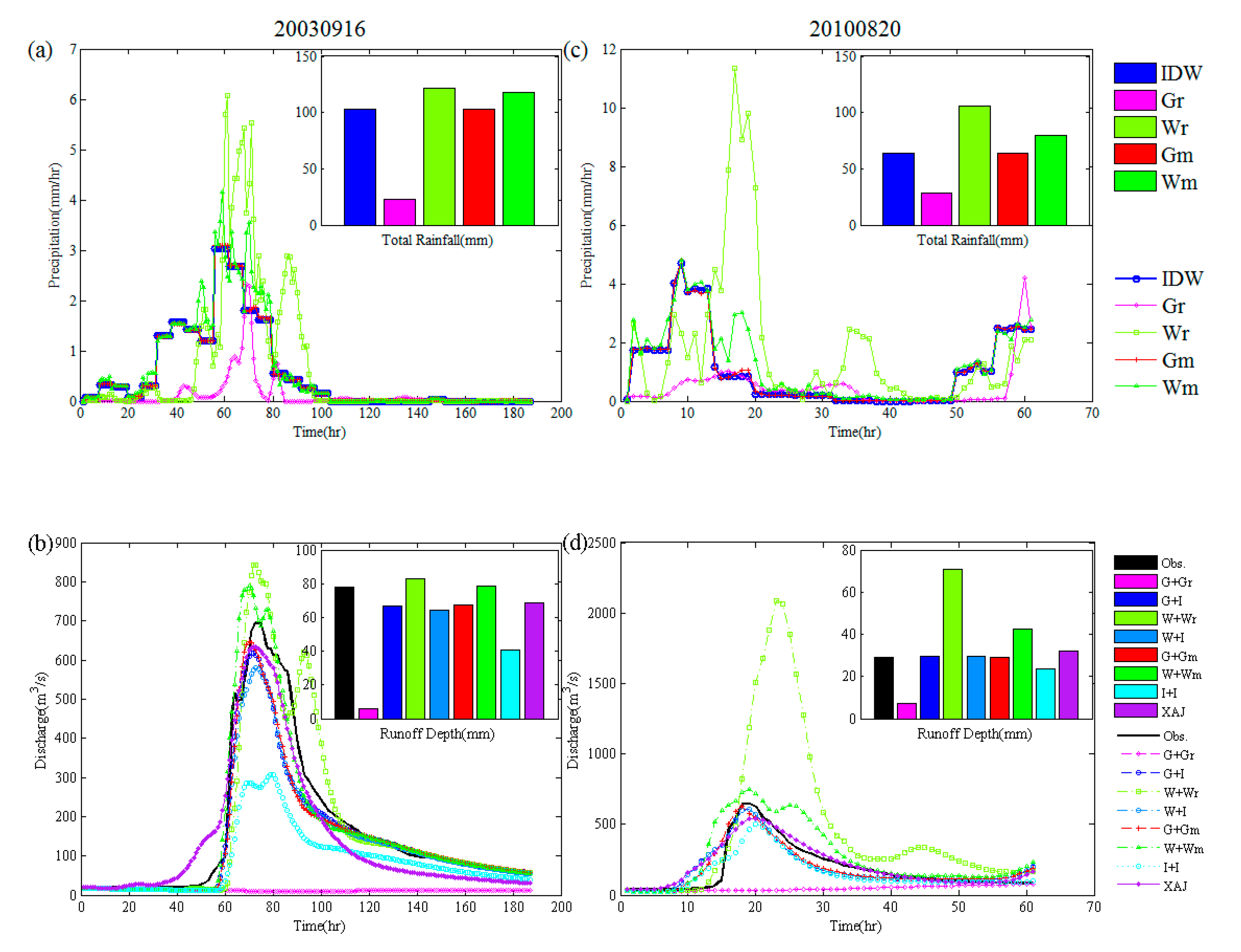
3.3. Evaluation of Streamflow for the Eight Scenarios
3.3.1. Comparison of the Scenarios Using the WRF-Hydro Model
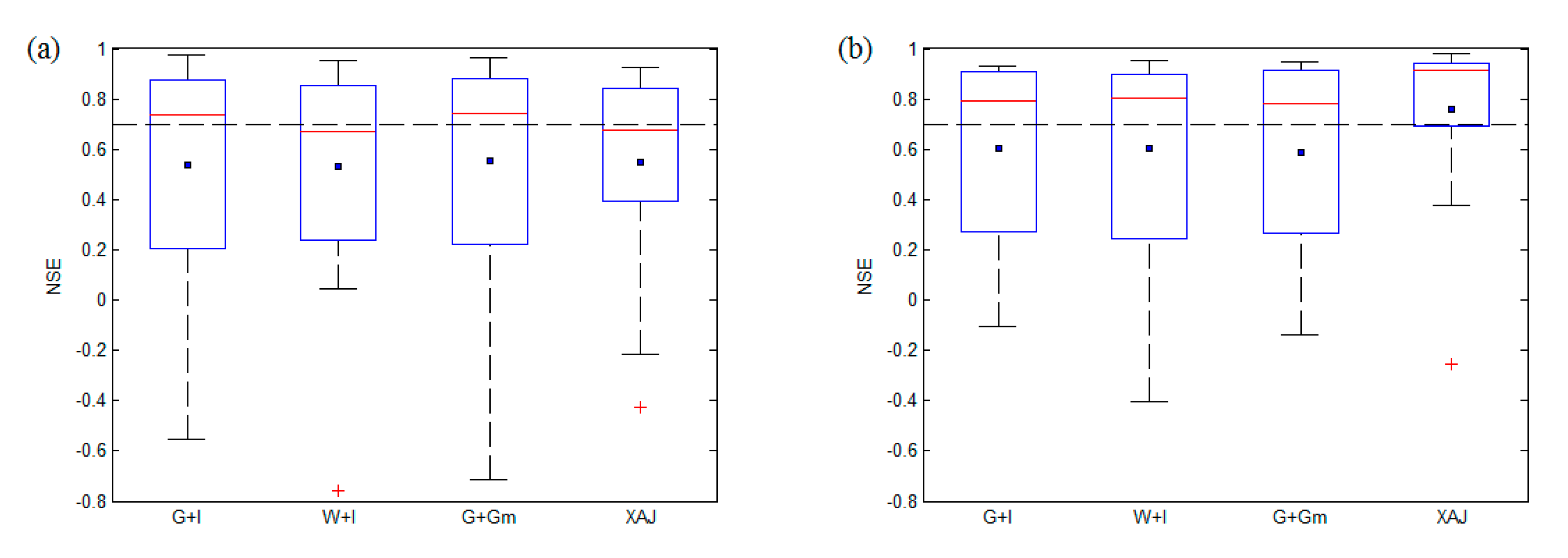
3.3.2. Comparison of the WRF-Hydro and Xinanjiang Model
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jonkman, S.N. Global Perspectives on Loss of Human Life Caused by Floods. Nat. Hazards 2005, 34, 151–175. [Google Scholar] [CrossRef]
- Ronco, P.; Gallina, V.; Torresan, S.; Zabeo, A.; Semenzin, E.; Critto, A.; Marcomini, A. The KULTURisk Regional Risk Assessment methodology for water-related natural hazards—Part 1: Physical–environmental assessment. Hydrol. Earth Syst. Sci. 2014, 18, 5399–5414. [Google Scholar] [CrossRef]
- He, B.S.; Huang, X.L.; Ma, M.H.; Chang, Q.R.; Tu, Y.; Li, Q.; Zhang, K.; Hong, Y. Analysis of flash flood disaster characteristics in China from 2011 to 2015. Nat. Hazards 2018, 90, 407–420. [Google Scholar] [CrossRef]
- Sun, Q.; Hu, J.; Zhang, L.; Ding, X.L. Towards Slow-Moving Landslide Monitoring by Integrating Multi-Sensor InSAR Time Series Datasets: The Zhouqu Case Study, China. Remote Sens. 2016, 8, 908. [Google Scholar] [CrossRef]
- Zhang, K.; Xue, X.W.; Hong, Y.; Gourley, J.J.; Lu, N.; Wan, Z.M.; Hong, Z.; Wooten, R. iCRESTRIGRS: A coupled modeling system for cascading flood-landslide disaster forecasting. Hydrol. Earth Syst. Sci. 2016, 20, 5035–5048. [Google Scholar] [CrossRef]
- Chao, L.J.; Zhang, K.; Li, Z.J.; Wang, J.F.; Yao, C.; Li, Q.L. Applicability assessment of the CASCade Two Dimensional SEDiment (CASC2D-SED) distributed hydrological model for flood forecasting across four typical medium and small watersheds in China(Article). J. Flood Risk Manag. 2019, 12, e12518. [Google Scholar] [CrossRef]
- Liu, Z.; Todini, E. Towards a comprehensive physically-based rainfall-runoff model. Hydrol. Earth Syst. Sci. 2002, 6, 859–881. [Google Scholar] [CrossRef]
- Todini, E. Rainfall-runoff modeling—Past, present and future. J. Hydrol. 1988, 100, 341–352. [Google Scholar] [CrossRef]
- Yao, C.; Li, Z.J.; Yu, Z.B.; Zhang, K. A priori parameter estimates for a distributed, grid-based Xinanjiang model using geographically based information. J. Hydrol. 2012, 468, 47–62. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Rozalis, S.; Morin, E.; Yair, Y.; Price, C. Flash flood prediction using an uncalibrated hydrological model and radar rainfall data in a Mediterranean watershed under changing hydrological conditions. J. Hydrol. 2010, 394, 245–255. [Google Scholar] [CrossRef]
- Wigmosta, M.S.; Lettenmaier, D.P.; Vail, L.W. A distributed hydrology-vegetation model for complex terrain. Water Resour. Res. 1994, 30, 1665–1679. [Google Scholar] [CrossRef]
- Anderson, M.L.; Chen, Z.-Q.; Kavvas, M.L.; Feldman, A. Coupling HEC-HMS with Atmospheric Models for Prediction of Watershed Runoff. J. Hydrol. Eng. 2002, 7, 312–318. [Google Scholar] [CrossRef]
- Yu, Z.B.; Lakhtakia, M.N.; Yarnal, B.; White, R.A.; Miller, D.A.; Frakes, B.; Barron, E.J.; Duffy, C.; Schwartz, F.W. Simulating the river-basin response to atmospheric forcing by linking a mesoscale meteorological model and hydrologic model system. J. Hydrol. 1999, 218, 72–91. [Google Scholar] [CrossRef]
- Harald, K.; Christiane, S. High resolution distributed atmospheric-hydrological modelling for Alpine catchments. J. Hydrol. 2005, 314, 105–124. [Google Scholar]
- Lin, C.A.; Wen, L.; Lu, G.H.; Wu, Z.Y.; Zhang, J.Y.; Yang, Y.; Zhu, Y.F.; Tong, L.Y. Atmospheric-hydrological modeling of severe precipitation and floods in the Huaihe River Basin, China. J. Hydrol. 2006, 330, 249–259. [Google Scholar] [CrossRef]
- Gochis, D.J.; Barlage, M.; Dugger, A.; FitzGerald, K.; Karsten, L.; McAllister, M.; McCreight, J.; Mills, J.; RafieeiNasab, A.; Read, L.; et al. The WRF-Hydro Modeling System Technical Description (Version 5.0); Center for Atmospheric Research (NCAR): Boulder, CO USA, 2018; Available online: https://ral.ucar.edu/sites/default/files/public/WRFHydroV5TechnicalDescription.pdf (accessed on 13 April 2018).
- Naabil, E.; Lamptey, B.L.; Arnault, J.; Olufayo, A.; Kunstmann, H. Water resources management using the WRF-Hydro modelling system: Case-study of the Tono dam in West Africa. J. Hydrol. Reg. Stud. 2017, 12, 196–209. [Google Scholar] [CrossRef]
- Xiang, T.X.; Vivoni, E.R.; Gochis, D.J.; Mascaro, G. On the diurnal cycle of surface energy fluxes in the North American monsoon region using the WRF-Hydro modeling system. J. Geophys. Res.-Atmos. 2017, 122, 9024–9049. [Google Scholar] [CrossRef]
- Gao, Y.H.; Li, K.; Chen, F.; Jiang, Y.S.; Lu, C.G. Assessing and improving Noah-MP land model simulations for the central Tibetan Plateau. J. Geophys. Res.-Atmos. 2015, 120, 9258–9278. [Google Scholar] [CrossRef]
- Li, W.K.; Guo, W.D.; Xue, Y.K.; Fu, C.B.; Qiu, B. Sensitivity of a regional climate model to land surface parameterization schemes for East Asian summer monsoon simulation. Clim. Dyn. 2016, 47, 2293–2308. [Google Scholar] [CrossRef]
- Salamanca, F.; Zhang, Y.; Barlage, M.; Chen, F.; Mahalov, A.; Miao, S. Evaluation of the WRF-Urban Modeling System Coupled to Noah and Noah-MP Land Surface Models Over a Semiarid Urban Environment. J. Geophys. Res.-Atmos. 2018, 123, 2387–2408. [Google Scholar] [CrossRef]
- Gochis, D.J.; Chen, F. Hydrological Enhancements to the Community Noah Land Surface Model: Technical Description; Center for Atmospheric Research (NCAR): Boulder, CO, USA, 2003; Available online: http://nldr.library.ucar.edu/repository/assets/technotes/TECH-NOTE-000-000-000-516.pdf (accessed on 13 April 2018).
- Yucel, I.; Onen, A.; Yilmaz, K.K.; Gochis, D.J. Calibration and evaluation of a flood forecasting system: Utility of numerical weather prediction model, data assimilation and satellite-based rainfall. J. Hydrol. 2015, 523, 49–66. [Google Scholar] [CrossRef]
- Senatore, A.; Mendicino, G.; Gochis, D.J.; Yu, W.; Yates, D.N.; Kunstmann, H. Fully coupled atmosphere-hydrology simulations for the central Mediterranean: Impact of enhanced hydrological parameterization for short and long time scales. J. Adv. Model. Earth Syst. 2015, 7, 1693–1715. [Google Scholar] [CrossRef]
- Kerandi, N.; Arnault, J.; Laux, P.; Wagner, S.; Kitheka, J.; Kunstmann, H. Joint atmospheric-terrestrial water balances for East Africa: A WRF-Hydro case study for the upper Tana River basin. Theor. Appl. Climatol. 2017, 131, 1337–1355. [Google Scholar] [CrossRef]
- Somos-Valenzuela, M.A.; Palmer, R.N. Use of WRF-Hydro over the Northeast of the US to Estimate Water Budget Tendencies in Small Watersheds. Water 2018, 10, 1709. [Google Scholar] [CrossRef]
- Xue, Z.G.; Gochis, D.J.; Yu, W.; Keim, B.D.; Rohli, R.V.; Zang, Z.C.; Sampson, K.; Dugger, A.; Sathiaraj, D.; Ge, Q. Modeling Hydroclimatic Change in Southwest Louisiana Rivers. Water 2018, 10, 596. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The global land data assimilation system. Bull. Amer. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Adhikari, A.; Maitra, A. Multi-technique observations on precipitation and other related phenomena during cyclone Aila at a tropical location. Int. J. Remote Sens. 2013, 34, 1965–1980. [Google Scholar] [CrossRef]
- Chao, L.J.; Zhang, K.; Li, Z.J.; Zhu, Y.L.; Wang, J.F.; Yu, Z.B. Geographically weighted regression based methods for merging satellite and gauge precipitation. J. Hydrol. 2018, 558, 275–289. [Google Scholar] [CrossRef]
- Yao, C.; Zhang, K.; Yu, Z.B.; Li, Z.J.; Li, Q.L. Improving the flood prediction capability of the Xinanjiang model in ungauged nested catchments by coupling it with the geomorphologic instantaneous unit hydrograph. J. Hydrol. 2014, 517, 1035–1048. [Google Scholar] [CrossRef]
- Dasari, H.P.; Salgado, R. Numerical modelling of heavy rainfall event over Madeira Island in Portugal: Sensitivity to different micro physical processes. Meteorol. Appl. 2015, 22, 113–127. [Google Scholar] [CrossRef]
- Hong, S.Y.; Lee, J.W. Assessment of the WRF model in reproducing a flash-flood heavy rainfall event over Korea. Atmos. Res. 2009, 93, 818–831. [Google Scholar] [CrossRef]
- Monteiro, C.; Ramirez-Rosado, I.J.; Fernandez-Jimenez, L.A. Short-term forecasting model for electric power production of small-hydro power plants. Renew. Energy 2013, 50, 387–394. [Google Scholar] [CrossRef]
- Caldwell, P.; Chin, H.-N.S.; Bader, D.C.; Bala, G. Evaluation of a WRF dynamical downscaling simulation over California. Clim. Chang. 2009, 95, 499–521. [Google Scholar] [CrossRef]
- Syed, T.H.; Famiglietti, J.S.; Rodell, M.; Chen, J.L.; Wilson, C.R. Analysis of terrestrial water storage changes from GRACE and GLDAS. Water Resour. Res. 2008, 44, 472–486. [Google Scholar] [CrossRef]
- Hill, D.J. Assimilation of weather radar and binary ubiquitous sensor measurements for quantitative precipitation estimation. J. Hydroinform. 2015, 17, 598–613. [Google Scholar] [CrossRef]
- Ma, Y.Z.; Yang, Y.; Han, Z.Y.; Tang, G.Q.; Maguire, L.; Chu, Z.G.; Hong, Y. Comprehensive evaluation of Ensemble Multi-Satellite Precipitation Dataset using the Dynamic Bayesian Model Averaging scheme over the Tibetan plateau. J. Hydrol. 2018, 556, 634–644. [Google Scholar] [CrossRef]
- Shen, Y.; Xiong, A.Y.; Wang, Y.; Xie, P.P. Performance of high-resolution satellite precipitation products over China. J. Geophys. Res.-Atmos. 2010, 115, 1–17. [Google Scholar] [CrossRef]
- Shen, Y.; Zhao, P.; Pan, Y.; Yu, J.J. A high spatiotemporal gauge-satellite merged precipitation analysis over China. J. Geophys. Res.-Atmos. 2014, 119, 3063–3075. [Google Scholar] [CrossRef]
- Cadet, D.L.; Diehl, B.C. Interannual Variability of Surface Fields over the Indian Ocean during Recent Decades. Mon. Weather Rev. 1984, 112, 1921–1935. [Google Scholar] [CrossRef][Green Version]
- Kim, K.-J.; Choi, J.-H.; Yoo, C.-S. Synthesis of Radar Measurements and Ground Measurements using the Successive Correction Method(SCM). J. Korea Water Resour. Assoc. 2008, 41, 681–692. [Google Scholar] [CrossRef]
- Uboldi, F.; Buzzi, A. Successive-correction methods applied to mesoscale meteorological analysis. Il Nuovo Cimento C 1994, 17, 745–761. [Google Scholar] [CrossRef]
- Yaremchuk, M.; Nechaev, D.; Panteleev, G. A Method of Successive Corrections of the Control Subspace in the Reduced-Order Variational Data Assimilation. Mon. Weather Rev. 2009, 137, 2966–2978. [Google Scholar] [CrossRef]
- Beaudoing, H.; Rodell, M. GLDAS Noah Land Surface Model L4 3 hourly 0.25 × 0.25 degree V2.1; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2016. [Google Scholar]
- Chen, F.; Mitchell, K.; Schaake, J.; Xue, Y.; Pan, H.-L.; Koren, V.; Duan, Q.Y.; Ek, M.; Betts, A. Modeling of land surface evaporation by four schemes and comparison with FIFE observations. J. Geophys. Res. 1996, 101, 7251–7268. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an Advanced Land Surface-Hydrology Model with the Penn State-NCAR MM5 Modeling System. Part I: Model Implementation and Sensitivity. Mon. Weather Rev. 2001, 129, 569. [Google Scholar] [CrossRef]
- Wang, F.X.; Wang, L.; Koike, T.; Zhou, H.C.; Yang, K.; Wang, A.H.; Li, W.L. Evaluation and application of a fine-resolution global data set in a semiarid mesoscale river basin with a distributed biosphere hydrological model. J. Geophys. Res.-Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Wang, W.; Cui, W.; Wang, A.J.; Chen, X. Evaluation of GLDAS-1 and GLDAS-2 Forcing Data and Noah Model Simulations over China at the Monthly Scale. J. Hydrometeorol. 2016, 17, 2815–2833. [Google Scholar] [CrossRef]
- Mastyło, M. Bilinear interpolation theorems and applications. J. Funct. Anal. 2013, 265, 185–207. [Google Scholar] [CrossRef]
- Zaitchik, B.F.; Rodell, M.; Olivera, F. Evaluation of the Global Land Data Assimilation System using global river discharge data and a source-to-sink routing scheme. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Yao, C.; Ye, J.Y.; He, Z.X.; Bastola, S.; Zhang, K.; Li, Z.J. Evaluation of flood prediction capability of the distributed Grid-Xinanjiang model driven by weather research and forecasting precipitation. J. Flood Risk Manag. 2019, 12, e12544. [Google Scholar] [CrossRef]
- Hong, S.Y.; DUDHIA, J.; CHEN, S.H. A Revised Approach to Ice Microphysical Processes for the Bulk Parameterization of Clouds and Precipitation. Mon. Weather Rev. 2004, 132, 103–120. [Google Scholar] [CrossRef]
- Kain, J.S.; Fritsch, J.M. The role of the convective “trigger function” in numerical forecasts of mesoscale convective systems. Meteorol. Atmos. Phys. 1992, 49, 93–106. [Google Scholar] [CrossRef]
- Hong, S.Y.; Pan, H.L. Nonlocal Boundary Layer Vertical Diffusion in a Medium-Range Forecast Model. Mon. Weather Rev. 1996, 124, 2322–2339. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Williams, R.T. Lambert and Mercator map projections in geology and geophysics. Comput. Geosci. 1995, 21, 353–364. [Google Scholar] [CrossRef]
- Julien, P.Y.; Saghafian, B.; Ogden, F.L. Raster-based hydrologic modeling of spatially-varied surface runoff. J. Am. Water Resour. Assoc. 1995, 31, 523–536. [Google Scholar] [CrossRef]
- Downer, C.W.; Ogden, F.L.; Martin, W.D.; Harmon, R.S. Theory, Development, and Applicability of the Surface Water Hydrologic Model CASC2D. Hydrol. Process. 2002, 16, 255–276. [Google Scholar] [CrossRef]
- Zimmerman, D.; Pavlik, C.; Ruggles, A.; Armstrong, M.P. An Experimental Comparison of Ordinary and Universal Kriging and Inverse Distance Weighting. Math. Geol. 1999, 31, 375–390. [Google Scholar] [CrossRef]
- Bardossy, A.; Huang, Y.; Wagener, T. Simultaneous calibration of hydrological models in geographical space. Hydrol. Earth Syst. Sci. 2016, 20, 2913–2928. [Google Scholar] [CrossRef]
- Zhao, R.J. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar]
- Li, H.Y.; Zhang, Y.Q.; Vaze, J.; Wang, B. Separating effects of vegetation change and climate variability using hydrological modelling and sensitivity-based approaches. J. Hydrol. 2011, 420, 403–418. [Google Scholar] [CrossRef]
- Huang, P.N.; Li, Z.J.; Chen, J.; Li, Q.L.; Yao, C. Event-based hydrological modeling for detecting dominant hydrological process and suitable model strategy for semi-arid catchments. J. Hydrol. 2016, 542, 292–303. [Google Scholar] [CrossRef]
- Zeng, Q.; Chen, H.; Xu, C.Y.; Jie, M.X.; Chen, J.; Guo, S.L.; Liu, J. The effect of rain gauge density and distribution on runoff simulation using a lumped hydrological modelling approach (Article). J. Hydrol. 2018, 563, 106–122. [Google Scholar] [CrossRef]
- Zhang, D.R.; Zhang, L.R.; Guan, Y.Q.; Chen, X.; Chen, X.F. Sensitivity analysis of Xinanjiang rainfall–runoff model parameters: A case study in Lianghui, Zhejiang province, China. Hydrol. Res. 2012, 43, 123–134. [Google Scholar] [CrossRef]
- Huo, W.B.; Li, Z.J.; Wang, J.F.; Yao, C.; Zhang, K.; Huang, Y.C. Multiple hydrological models comparison and an improved Bayesian model averaging approach for ensemble prediction over semi-humid regions. Stoch. Environ. Res. Risk Assess. 2019, 33, 217–238. [Google Scholar] [CrossRef]
- Arnault, J.; Rummler, T.; Baur, F.; Lerch, S.; Wagner, S.; Fersch, B.; Zhang, Z.; Kerandi, N.; Keil, C.; Kunstmann, H. Precipitation sensitivity to the uncertainty of terrestrial water flow in WRF-Hydro: An ensemble analysis for central Europe(Article). J. Hydrometeorol. 2018, 19, 1007–1025. [Google Scholar] [CrossRef]
- Ryu, Y.; Lim, Y.-J.; Ji, H.-S.; Park, H.-H.; Chang, E.-C.; Kim, B.-J. Applying a coupled hydrometeorological simulation system to flash flood forecasting over the Korean Peninsula. Asia-Pac. J. Atmos. Sci. 2017, 53, 421–430. [Google Scholar] [CrossRef]
- Silver, M.; Karnieli, A.; Ginat, H.; Meiri, E.; Fredj, E. An innovative method for determining hydrological calibration parameters for the WRF-Hydro model in arid regions(Article). Environ. Modell. Softw. 2017, 91, 47–69. [Google Scholar] [CrossRef]
- Arnault, J.; Wagner, S.; Rummler; Fersch, B.; Bliefernicht, J.; Andresen, S.; Kunstmann, H. Role of Runoff–Infiltration Partitioning and Resolved Overland Flow on Land–Atmosphere Feedbacks: A Case Study with the WRF-Hydro Coupled Modeling System for West Africa. J. Hydrometeorol. 2016, 17, 1489–1516. [Google Scholar] [CrossRef]
- Cressman, G.P. An operational objective analysis system. Mon. Weather Rev. 1959, 87, 367–374. [Google Scholar] [CrossRef]


| Year | Spin-Up Period | ID | Events | Start | End |
|---|---|---|---|---|---|
| 2003 | 1 June 2003, 0:00– 27 August, 18:00 | 1 | 030827 | 27 August, 18:00 | 4 September, 0:00 |
| 2 | 030902 | 2 September, 18:00 | 9 September, 12:00 | ||
| 3 | 030916 | 16 September, 6:00 | 24 September, 0:00 | ||
| 2004 | 1 June 2004, 0:00– 1 September, 6:00 | 4 | 040901 | 1 September, 6:00 | 9 September, 0:00 |
| 2005 | 1 June 2005, 0:00– 29 June, 18:00 | 5 | 050629 | 29 June, 18:00 | 4 July, 12:00 |
| 6 | 050716 | 16 July, 18:00 | 19 July, 18:00 | ||
| 2006 | 1 June 2006, 0:00– 2 September, 18:00 | 7 | 060902 | 2 September, 18:00 | 7 September, 18:00 |
| 8 | 060925 | 25 September, 12:00 | 3 October, 0:00 | ||
| 2007 | 1 June 2007, 0:00– 3 July, 18:00 | 9 | 070703 | 3 July, 18:00 | 7 July, 18:00 |
| 10 | 070808 | 8 August, 6:00 | 13 August, 0:00 | ||
| 2008 | 1 June 2008, 0:00– 20 July, 6:00 | 11 | 080720 | 20 July, 6:00 | 23 July, 12:00 |
| 2009 | 1 June 2009, 0:00– 17 August 18:00 | 12 | 090817 | 17 August, 18:00 | 24 August, 0:00 |
| 13 | 090910 | 10 September, 18:00 | 16 September, 18:00 | ||
| 2010 | 1 June 2010, 0:00– 21 July, 18:00 | 14 | 100721 | 21 July, 18:00 | 29 July, 6:00 |
| 15 | 100820 | 20 August, 12:00 | 23 August, 0:00 | ||
| 16 | 100822 | 22 August, 18:00 | 26 August, 18:00 | ||
| 2011 | 1 June 2011, 0:00– 3 August, 18:00 | 17 | 110803 | 3 August, 18:00 | 7 August, 18:00 |
| 18 | 110909 | 9 September, 0:00 | 15 September, 0:00 | ||
| 19 | 110916 | 16 September, 0:00 | 21 September, 0:00 |
| Category | Parameterization Selected | References |
|---|---|---|
| Microphysical processes | WGM 3-class simple ice model | [54] |
| Cumulus option | Kain-Fritsch scheme | [55] |
| Planetary boundary layer | Yonsei University scheme | [56] |
| Radiation scheme | RRTM, Dudhia | [57] |
| Land surface model | Noah LSM | [47] |
| Projection | Lambert | [58] |
| Category | Parameterization Selected | References |
|---|---|---|
| NWP model | WRF model | [36] |
| Land surface model | Noah LSM | [48] |
| Subsurface flow (i.e., Interflow) | Distributed hydrology soil and vegetation model | [12] |
| Overland flow | D8 method | [60] |
| Baseflow | Exponential storage-discharge function | [17] |
| Channel routing | Diffusive wave | [59] |
| Name | Meaning | Relevant Variables |
|---|---|---|
| ZSOILFAC | Scaling factor on subsurface layer depth | Soil moisture |
| GWEXP | The bucket model exponent of baseflow | Drainage of groundwater |
| REFKDT | Referring soil permeability | Infiltration and permeation rates |
| RETDEPRTFAC | Multiplier on maximum retention depth | Retention depth capacity |
| OVROUGHRTFAC | Multiplier on Manning’s roughness for overland flow | Overland runoff |
| MANNFAC | Multiplier on Manning’s roughness for channel | Streamflow |
| Parameter | ZSOILFAC | GWEXP | REFKDT | RETDEPRTFAC | OVROUGHRTFAC | MANNFAC |
|---|---|---|---|---|---|---|
| Lower | 0.1 | 1.0 | 0.1 | 0.0 | 0.1 | 0.1 |
| Upper | 1.0 | 5.0 | 2.0 | 1.0 | 2.0 | 2.0 |
| Increment | 0.1 | 1.0 | 0.1 | 0.1 | 0.1 | 0.1 |
| Parameter | Value | Meaning | Function |
|---|---|---|---|
| K | 0.5 | The ratio of potential evapotranspiration to pan evaporation | Controlling the simulated water volume |
| WM | 160 mm | Tension water storage capacity | |
| SM | 14 mm | Gravity water storage capacity | Controlling the simulated hydrograph shape |
| CS | 0.08 | The recession coefficient of runoff in channel network |
| Number | Scenario 2 | Model | Input Meteorological Forcings | |
|---|---|---|---|---|
| Rainfall | The Remaining Forcings | |||
| 1 | G + Gr 3 | WRF-Hydro | GLDAS-derived rainfall | GLDAS |
| 2 | G + I | IDW product | GLDAS | |
| 3 | W + Wr 4 | WRF-derived rainfall | WRF | |
| 4 | W + I | IDW product | WRF | |
| 5 | G + Gm | GLDAS-merged rainfall | GLDAS | |
| 6 | W + Wm | WRF-merged rainfall | WRF | |
| 7 | I + I | IDW product | Ideal forcings 5 | |
| 8 | XAJ | Xinanjiang | Rain gauge data and pan evaporation | |
| Variable Name | Description | Prescribed Value or Range | Timing |
|---|---|---|---|
| SWDOWN | Incoming shortwave radiation | 0–900 W/m2 | Diurnal cycle |
| LWDOWN | Incoming longwave radiation | 375–425 W/m2 | Diurnal cycle |
| Q2D | specific humidity | 0.01 kg/kg | Constant |
| T2D | Air temperature | 287–293 K | Diurnal cycle |
| PSFC | Surface pressure | 100,000 Pa | Constant |
| U2D | Near-surface wind speed in the u-component | 1.0 m/s | Constant |
| V2D | Near-surface wind speed in the v-component | 1.0 m/s | Constant |
| G + Gr | G + I | W + Wr | W + I | G + Gm | W + Wm | I + I | XAJ | |
|---|---|---|---|---|---|---|---|---|
| PB | −0.510 | 0.063 | 0.752 | 0.009 | 0.063 | 0.331 | −0.291 | 0.147 |
| RMSE (mm/h) | 0.41 | 0.18 | 0.74 | 0.18 | 0.17 | 0.23 | 0.23 | 0.17 |
| RR | 0.031 | 0.852 | 0.533 | 0.837 | 0.844 | 0.899 | 0.770 | 0.934 |
| NSE | -0.47 | 0.61 | −15.36 | 0.61 | 0.61 | 0.46 | 0.37 | 0.71 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, M.; Li, Z.; Yao, C.; Liu, Z.; Wang, J.; Hou, A.; Zhang, K.; Huo, W.; Liu, M. Evaluation of Flood Prediction Capability of the WRF-Hydro Model Based on Multiple Forcing Scenarios. Water 2020, 12, 874. https://doi.org/10.3390/w12030874
Sun M, Li Z, Yao C, Liu Z, Wang J, Hou A, Zhang K, Huo W, Liu M. Evaluation of Flood Prediction Capability of the WRF-Hydro Model Based on Multiple Forcing Scenarios. Water. 2020; 12(3):874. https://doi.org/10.3390/w12030874
Chicago/Turabian StyleSun, Mingkun, Zhijia Li, Cheng Yao, Zhiyu Liu, Jingfeng Wang, Aizhong Hou, Ke Zhang, Wenbo Huo, and Moyang Liu. 2020. "Evaluation of Flood Prediction Capability of the WRF-Hydro Model Based on Multiple Forcing Scenarios" Water 12, no. 3: 874. https://doi.org/10.3390/w12030874
APA StyleSun, M., Li, Z., Yao, C., Liu, Z., Wang, J., Hou, A., Zhang, K., Huo, W., & Liu, M. (2020). Evaluation of Flood Prediction Capability of the WRF-Hydro Model Based on Multiple Forcing Scenarios. Water, 12(3), 874. https://doi.org/10.3390/w12030874





