Hydraulic Properties of a Cultivated Soil in Temperate Continental Climate Determined by Mini Disk Infiltrometer
Abstract
1. Introduction
- (i)
- Does the MDI provide K(h) and Ks information comparable with HI?
- (ii)
- Does the MDI reflect the differences in topsoil properties caused by contrasting soil tillage operations (conventional tillage CT, reduced tillage RT, and no-tillage NT)?
- (iii)
- Is the MDI able to characterize and quantify the macropore contribution to the total water flux?
- (iv)
- How the data analysis method affects the resulting K(h) and Ks values with respect to different sources of van Genuchten [36] hydraulic parameters?
2. Materials and Methods
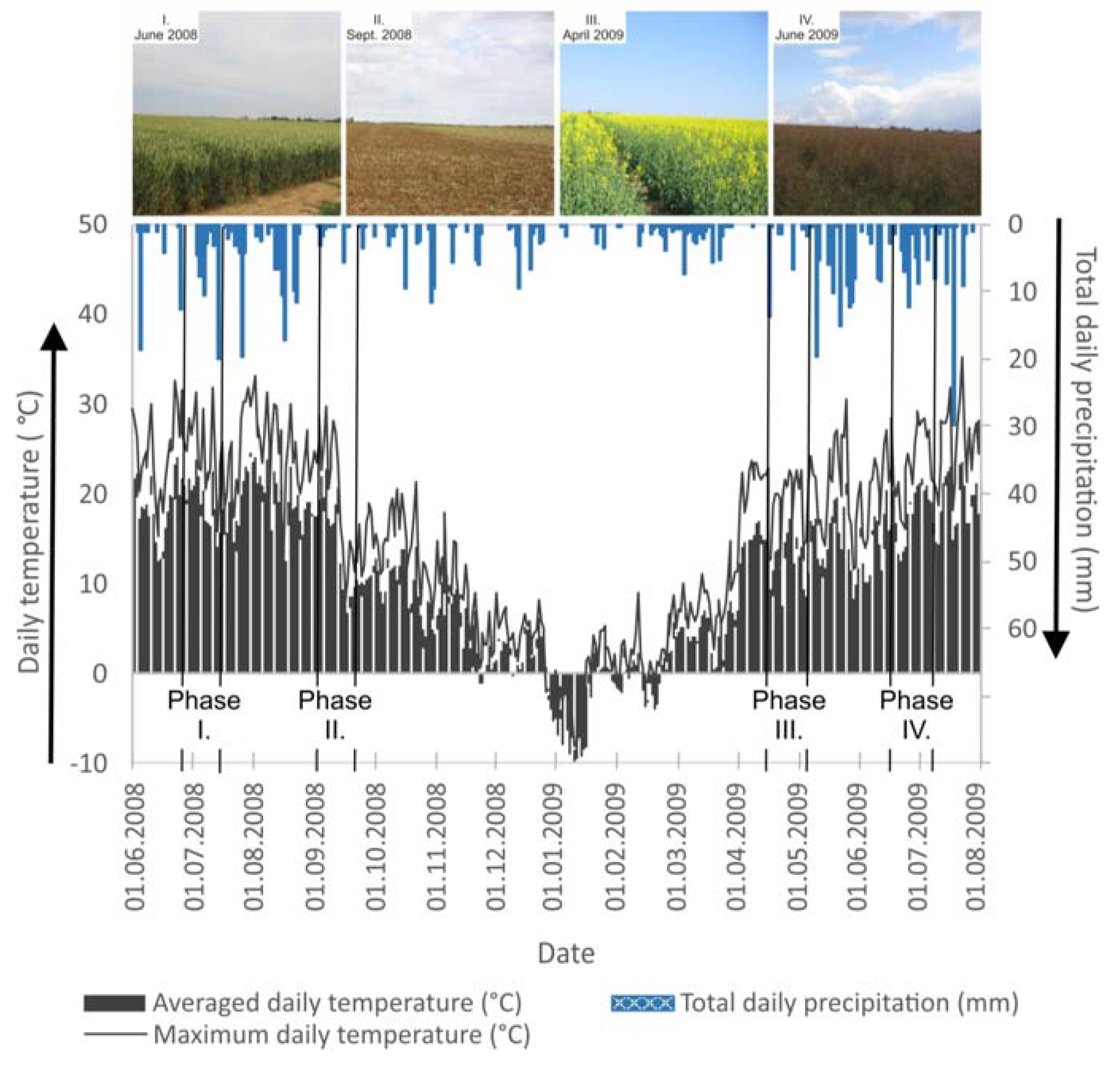
2.1. Study Area Description
2.2. Devices a Data Analyses Used for Hydraulic Conductivity Determination
2.2.1. Mini Disk Infiltrometer (METER Group, Inc. USA)
2.2.2. Hood Infiltrometer (Umwelt-Geräte-Technik, GmbH., Germany)
2.3. Evaluation of Soil Water Conductive Pore System
2.4. Statistical Evaluation
3. Results and Discussion
3.1. Basic Soil Characteristics
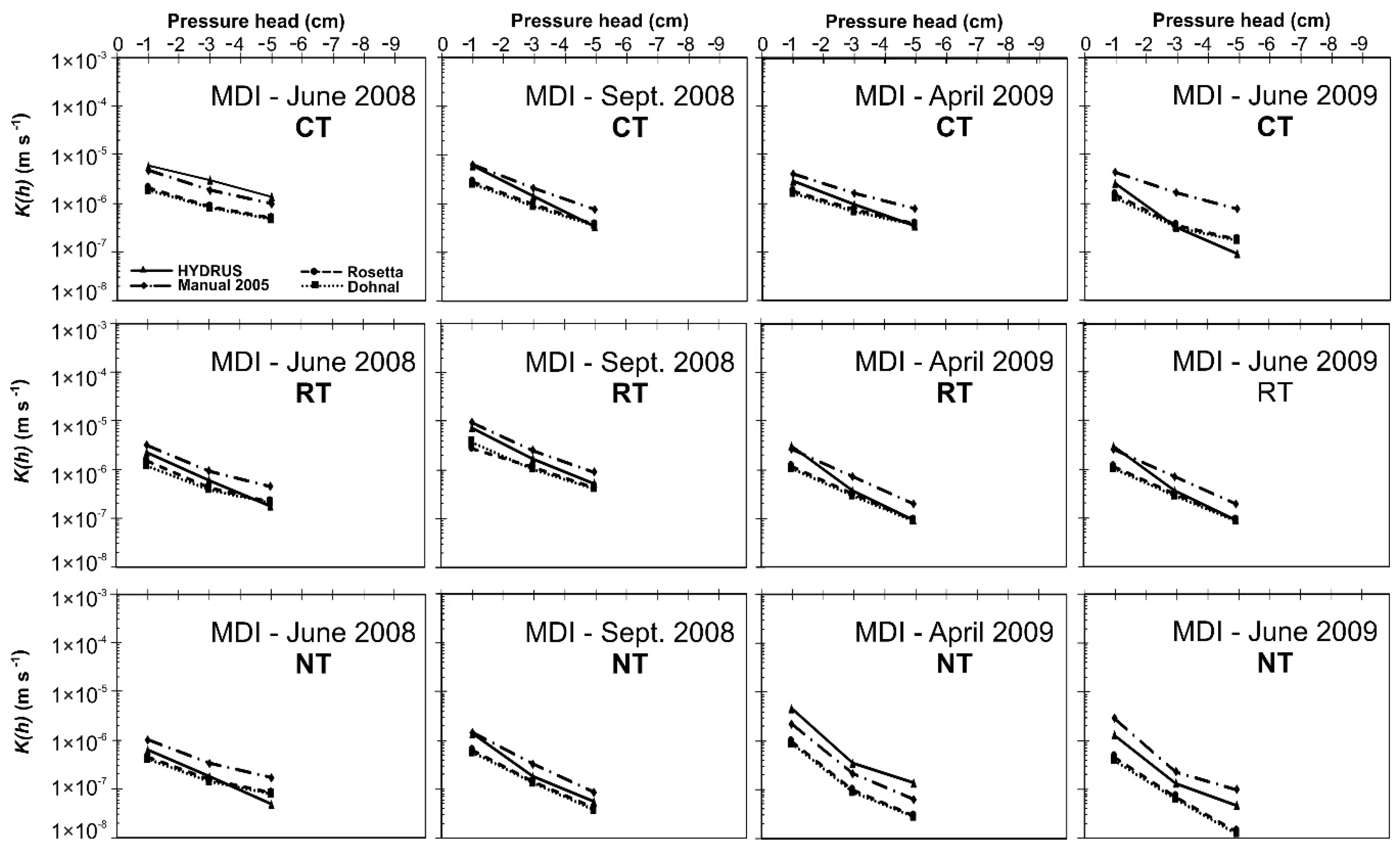
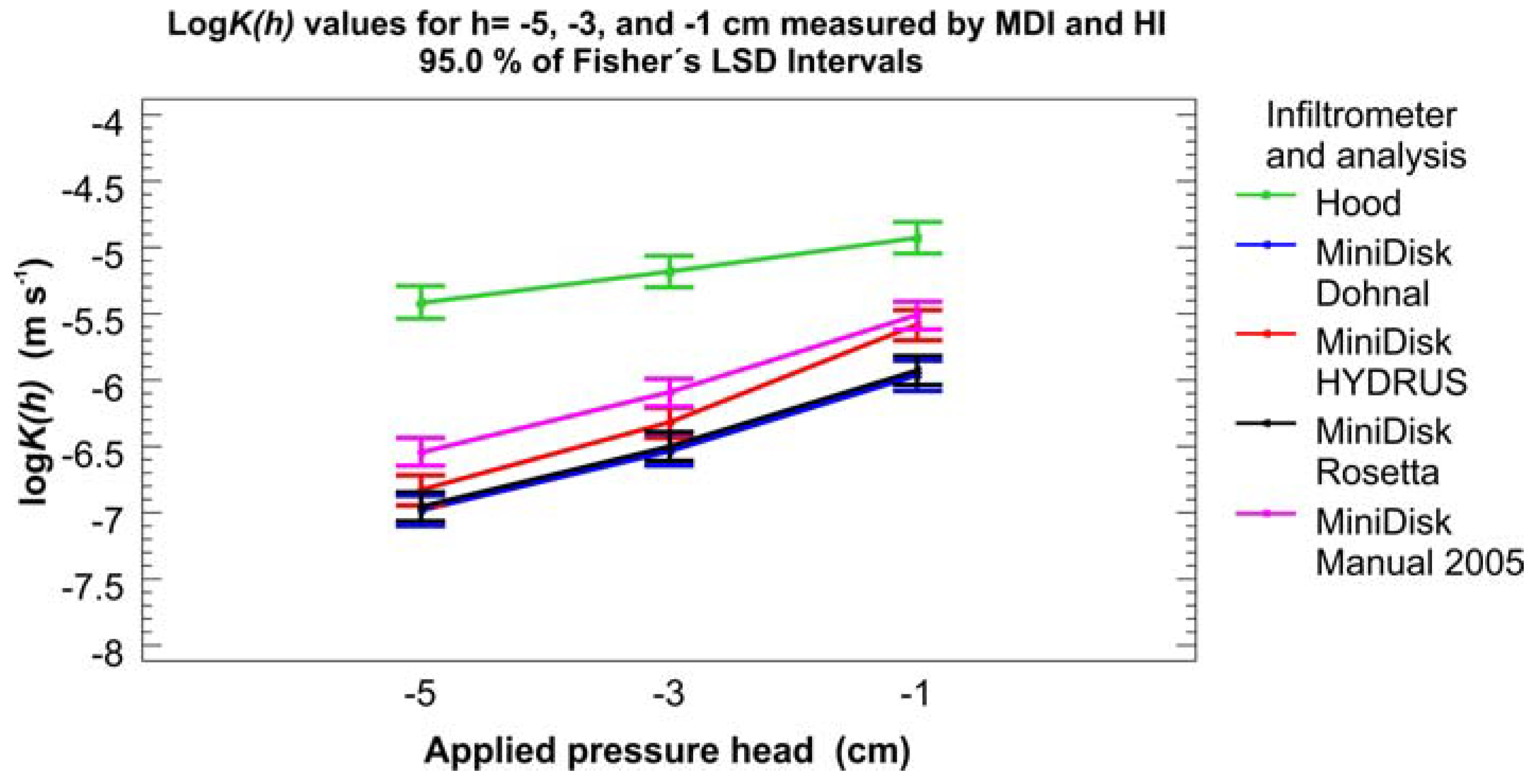
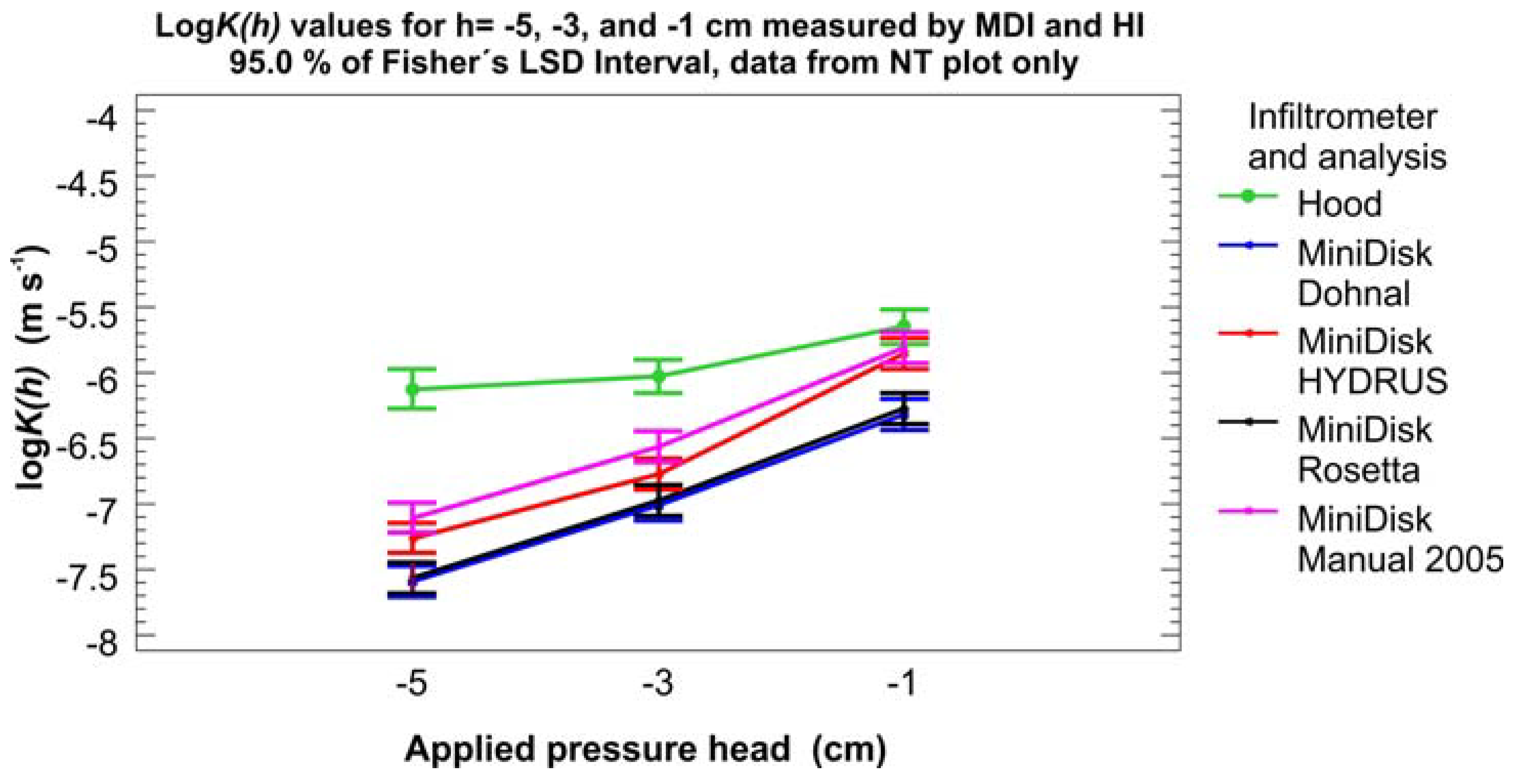
3.2. Unsaturated Hydraulic Conductivity K(h)
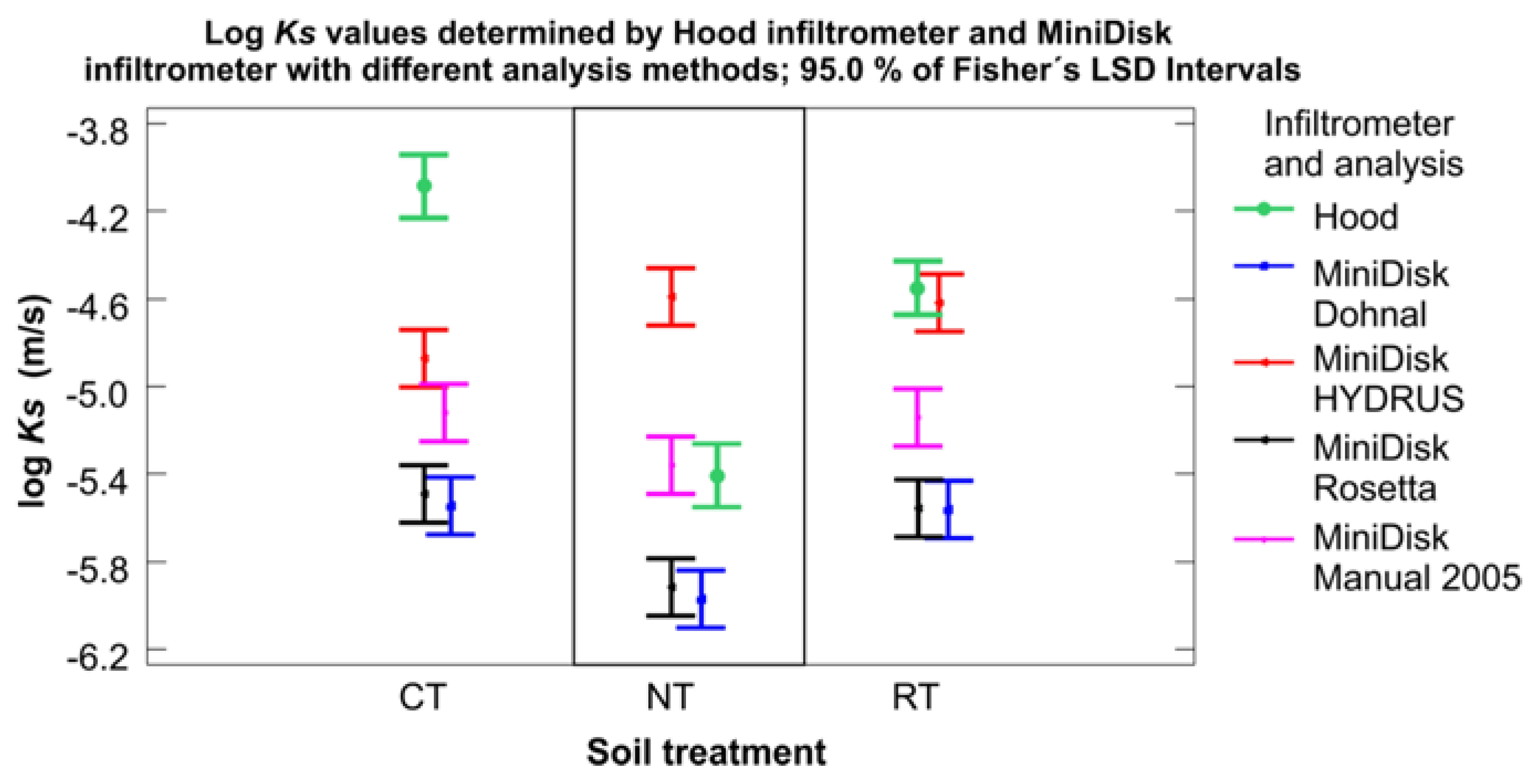
3.3. Saturated Hydraulic Conductivity Ks
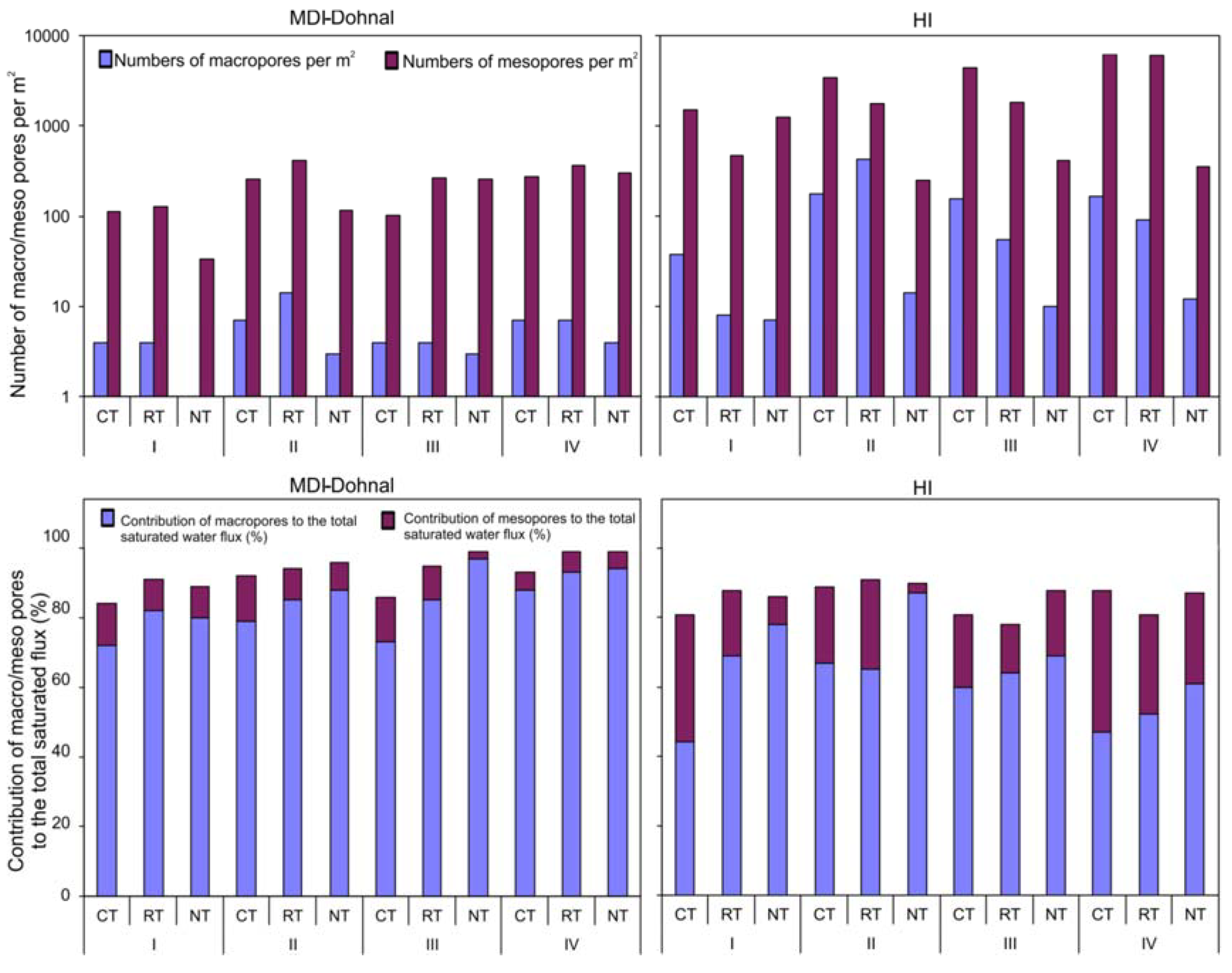
3.4. Mesopore and Macropore Contributions to the Total Saturated Flux
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shouse, P.J.; Mohanty, B.P. Scaling of near-saturated hydraulic conductivity measured using disc infiltrometers. Water Resour. Res. 1998, 34, 1195–1205. [Google Scholar] [CrossRef]
- Buczko, U.; Bens, O.; Hüttl, R.F. Tillage effects on hydraulic properties and macroporosity in silty and sandy soils. Soil Sci. Soc. Am. J. 2006, 70, 1998–2007. [Google Scholar] [CrossRef]
- Kumar, S.; Sekhar, M.; Reddy, D.V.; Mohan Kumar, M.S. Estimation of soil hydraulic properties and their uncertainty: Comparison between laboratory and field experiment. Hydrol. Process. 2010, 24, 3426–3435. [Google Scholar] [CrossRef]
- Standard Test Method for Infiltration Rate of Soils in Field Using Double-Ring Infiltrometer; ASTM D3385–03; ASTM International: West Conshohocken, PA, USA, 2003. [CrossRef]
- Standard Test Methods for Measurement of Hydraulic Conductivity of Unsaturated Soils; ASTM D7664–10e1; ASTM International: West Conshohocken, PA, USA, 2010. [CrossRef]
- Geotechnický Průzkum a Zkoušení—Laboratorní Zkoušky Zemin—Část 11: Stanovení Propustnosti; ČSN EN ISO 17892–11 (721007); Český Normalizační Institut: Prague, Czech Republic, 2019.
- Reynolds, W.D.; Topp, G.C. Soil Water Analyses. In Soil Sampling and Methods of Analysis, 2nd ed.; Carter, M.R., Gregorich, E.G., Eds.; CRC Press: Boca Raton, FL, USA, 2007; pp. 918–936. [Google Scholar]
- Casey, F.X.M.; Derby, N.E. Improved design for an automated tension infiltrometer. Soil Sci. Soc. Am. J. 2002, 66, 64–67. [Google Scholar] [CrossRef]
- Madsen, M.; Chandler, D. Automation and use of mini disk infiltrometers. Soil. Sci. Soc. Am. J. 2007, 71, 1469–1472. [Google Scholar] [CrossRef]
- Rodný, M.; Rodný, P.; Šurda, P.; Matula, S.; Miháliková, M.; Chala, A. Automation of mini disk infiltrometer based on particle tracking principle. Acta Hydrol. Slovaca 2013, 14, 460–465. [Google Scholar]
- Šurda, P.; Rodný, M.; Nagy, V.; Matula, S.; Miháliková, M.; Chala, A. Spatial variability of the hydraulic conductivity of the soil with biological soil crust in the horizontal and vertical direction. Acta Hydrol. Slovaca 2013, 14, 466–472. [Google Scholar]
- Kameníčková, I.; Larišová, L.; Stoklásková, A. The impact of different tillage treatments on hydraulic conductivity of loamy soil. Acta Universitatis Agriculturae Silviculturae Mendelianae Brunensis 2012, 5, 109–114. [Google Scholar] [CrossRef]
- Angulo-Jaramillo, R.; Vandervaere, J.-P.; Roulier, S.; Thony, J.-L.; Gaudet, J.-P.; Vauclin, M. Field measurement of soil surface hydraulic properties by disc and ring infiltrometers. A review and recent developments. Soil Till. Res. 2000, 55, 1–29. [Google Scholar] [CrossRef]
- Wooding, R.A. Steady infiltration from a shallow circular pond. Water Resour. Res. 1968, 4, 1259–1273. [Google Scholar] [CrossRef]
- White, I.; Sully, M.J. Macroscopic and microscopic capillary length and time scales from field infiltration. Water. Resour. Res. 1987, 23, 1514–1522. [Google Scholar] [CrossRef]
- Reynolds, W.D.; Elrick, D.E. Determination of hydraulic conductivity using a tension infiltrometer. Soil Sci. Soc. Am. J. 1991, 55, 633–639. [Google Scholar] [CrossRef]
- Ventrella, D.; Losavio, N.; Vonella, A.V.; Leij, F.J. Estimating hydraulic conductivity of a fine-textured soil using tension infiltrometry. Geoderma 2005, 124, 267–277. [Google Scholar] [CrossRef]
- Lazarovitch, N.; Ben-Gal, A.; Šimůnek, J.; Shani, U. Uniqueness of soil hydraulic parameters determined by a combined Wooding inverse approach. Soil Sci. Soc. Am. J. 2007, 71, 860–865. [Google Scholar] [CrossRef]
- Šimůnek, J.; Angulo-Jaramillo, R.; Shaap, M.G.; Vandervaere, J.P.; van Genuchten, M.T. Using an inverse method to estimate the hydraulic properties of crusted soils from tension-disc infiltrometer data. Geoderma 1998, 86, 61–81. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T. Estimating unsaturated soil hydraulic properties from tension disc infiltrometer data by numerical inversion. Water Resour. Res. 1996, 32, 2683–2696. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T. Estimating unsaturated soil hydraulic properties from multiple tension disc infiltrometer data. Soil Sci. 1997, 162, 383–398. [Google Scholar] [CrossRef]
- Strudley, M.W.; Green, T.R.; Ascough Ii, J.C. Tillage effects on soil hydraulic properties in space and time: State of the science. Soil Till. Res. 2008, 99, 4–48. [Google Scholar] [CrossRef]
- Rasiah, V.; Kay, B.D. Runoff and soil loss as influenced by selected stability parameters and cropping and tillage practices. Geoderma 1995, 68, 321–329. [Google Scholar] [CrossRef]
- Price, K.; Jackson, C.R.; Parker, A.J. Variation of surficial soil hydraulic properties across land uses in the southern Blue Ridge mountains, North Carolina, USA. J. Hydrol. 2010, 383, 256–268. [Google Scholar] [CrossRef]
- Friedrich, T. Engineering for conservation agriculture—Trends, concepts and challenges in a global perspective. In Proceedings of the International Soil Tillage Research Organisation Conference, Brisbane, Australia, 13–18 July 2003. [Google Scholar]
- Çelik, İ.; Günal, H.; Acar, M.; Acir, N.; Bereket Barut, Z.; Budak, M. Strategic tillage may sustain the benefits of long-term no-till in a Vertisol under Mediterranean climate. Soil Till. Res. 2019, 185, 17–28. [Google Scholar] [CrossRef]
- Sauer, T.; Clothier, B.E.; Daniel, T.C. Surface measurements of the hydraulic properties of a tilled and untilled soil. Soil Till. Res. 1990, 15, 359–369. [Google Scholar] [CrossRef]
- Ankeny, M.D.; Kaspar, T.C.; Horton, R. Characterization of tillage and traffic effects on unconfined infiltration measurement. Soil Sci. Soc. Am. J. 1990, 54, 810–837. [Google Scholar] [CrossRef]
- Cameira, M.R.; Fernando, R.M.; Pereira, L.S. Soil macropore dynamics affected by tillage and irrigation for a silty loam alluvial soil in southern Portugal. Soil Till. Res. 2003, 70, 131–140. [Google Scholar] [CrossRef]
- Moret, D.; Arrúe, J.L. Characterizing soil water-conducting macro and mesoporosity as influenced by tillage using tension infiltrometry. Soil Sci. Soc. Am. J. 2007, 71, 500–506. [Google Scholar] [CrossRef]
- Cassel, D.K. Spatial and temporal variability of soil physical properties following tillage of Norfolk loamy sand. Soil Sci. Soc. Am. J. 1983, 47, 196–201. [Google Scholar] [CrossRef]
- Mapa, R.B.; Green, R.E.; Santo, L. Temporal variability of soil hydraulic-properties with wetting and drying subsequent to tillage. Soil Sci. Soc. Am. J. 1986, 50, 1133–1138. [Google Scholar] [CrossRef]
- Rousseva, S.S.; Ahuja, L.R.; Heathman, G.C. Use of a surface gamma-neutron gauge for in-situ measurement of changes in bulk density of the tilled zone. Soil Till. Res. 1988, 12, 235–251. [Google Scholar] [CrossRef]
- Moret, D.; Arrúe, J.L. Dynamics of soil hydraulic properties during fallow as affected by tillage. Soil Till. Res. 2007, 96, 103–113. [Google Scholar]
- Kreiselmeier, J.; Chandrasekhar, P.; Weninger, T.; Schwen, A.; Julich, S.; Feger, K.-H.; Schwärzel, K. Temporal variations of the hydraulic conductivity characteristic under conventional and conservation tillage. Geoderma 2020, 362, 114127. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Soil Survey Staff. Keys to Soil Taxonomy, 12th ed.; USDA-Natural Resources Conservation Service: Washington, DC, USA, 2014; p. 360.
- IUSS Working Group WRB. World Reference Base for Soil Resources 2014, update 2015. In International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; World Soil Resources Reports No. 106; FAO: Rome, Italy, 2015; p. 192. [Google Scholar]
- Geotechnický Průzkum a Zkoušení—Laboratorní Zkoušky Zemin—Část 4: Stanovení Zrnitosti; ČSN EN ISO 17892–4 (721007); Český Normalizační Institut: Prague, Czech Republic, 2017.
- Walkley, A.; Black, I.A. An examination of the Degtjareff method for determining organic carbon in soils: Effect of variations in digestions and of inorganic soil constituents. Soil Sci. 1934, 63, 251–263. [Google Scholar] [CrossRef]
- Mühlbachová, G.; Kusá, H.; Růžek, P. Soil characteristics and crop yields under different tillage techniques. Plant Soil Environ. 2015, 61, 566–572. [Google Scholar] [CrossRef]
- Agrometeorological database. Available online: https://www.vurv.cz/meteo/ (accessed on 14 December 2018).
- Decagon Devices; METER Group. Mini Disk Infiltrometer—User’s Manual, 3rd version; Decagon Devices, Inc.: Pullman, WA, USA, 2005; p. 18. [Google Scholar]
- Decagon Devices; METER Group. Mini Disk Infiltrometer—User’s Manual; Version: September 10/2014; Decagon Devices, Inc.: Pullman, WA, USA, 2014; p. 21. [Google Scholar]
- Zhang, R. Infiltration models for the disk infiltrometer. Soil Sci. Soc. Am. J. 1997, 61, 1597–1603. [Google Scholar] [CrossRef]
- Philip, J.R. The theory of infiltration: 4. Sorptivity and algebraic infiltration equations. Soil Sci. 1957, 84, 257–264. [Google Scholar] [CrossRef]
- Rawls, W.J.; Brakensiek, D.L.; Saxton, K.E. Estimation of soil water properties. Trans. ASAE 1982, 25, 1316–1320. [Google Scholar] [CrossRef]
- Dohnal, M.; Dušek, J.; Vogel, T. Improving hydraulic conductivity estimates from Minidisk infiltrometer measurements for soils with wide pore-size distributions. Soil Sci. Soc. Am. J. 2010, 74, 804–811. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J.; van Genuchten, M.T. ROSETTA: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- Šimůnek, J.; Šejna, M.; van Genuchten, M.T. The HYDRUS-2D software package for simulating the two-dimensional movement of water, heat, and multiple solutes in variably-saturated media. In Version 2.0. USA Salinity Laboratory; Agricultural Research Service, USA Department of Agriculture: Riverside, CA, USA, 1999. [Google Scholar]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Clausnitzer, V.; Hopmans, J.W. Non-linear parameter estimation: LM_OPT. General-purpose optimization code based on the Levenberg-Marquart algorithm. In Land, Air and Water Resources; Paper No. 100032; University of California: Davis, CA, USA, 1995. [Google Scholar]
- Clausnitzer, V.; Hopmans, J.W.; Starr, J.L. Parameter uncertainty analysis of common infiltration models. Soil Sci. Soc. Am. J. 1998, 60, 1477–1487. [Google Scholar] [CrossRef]
- Umwelt-Geräte-Technik. Operating Instructions for Hood Infiltrometer IL-2700; Umwelt Geräte Technik GmbH: Münchenberg, Germany, 2005; p. 32. [Google Scholar]
- Thomas, G.W.; Philips, R.E. Consequences of water movement in macropores. J. Environ. Qual. 1979, 8, 149–156. [Google Scholar] [CrossRef]
- Luxmoore, R.J. Micro-, meso-, and macroporosity of soil. Soil Sci. Soc. Am. J. 1981, 45, 671–672. [Google Scholar] [CrossRef]
- Watson, K.W.; Luxmore, R.J. Estimating macroporosity in a forest watershed by the use of a tension infiltrometer. Soil Sci. Soc. Am. J. 1986, 50, 578–582. [Google Scholar] [CrossRef]
- Matula, S.; Miháliková, M.; Lufinková, J.; Báťková, K. The role of the initial soil water content in the determination of unsaturated soil hydraulic conductivity using a tension infiltrometer. Plant. Soil Environ. 2015, 61, 515–521. [Google Scholar] [CrossRef]
- Radinja, M.; Vidmar, I.; Atanasova, N.; Mikoš, M.; Šraj, M. Determination of spatial and temporal variability of soil hydraulic conductivity for urban runoff modelling. Water 2019, 11, 941. [Google Scholar] [CrossRef]
- Zhou, X.; Lin, H.S.; White, E.A. Surface soil hydraulic properties in four soil series under different land uses and their temporal changes. Catena 2008, 73, 180–188. [Google Scholar] [CrossRef]
- Schwärzel, K.; Punzel, J. Hood infiltrometer—A new type of tension infiltrometer. Soil Sci. Soc. Am. J. 2007, 71, 1438–1447. [Google Scholar] [CrossRef]
- Bagarello, V.; Iovino, M.; Tusa, G. Effect of contact material on tension infiltrometer measurements. Trans. ASAE 2001, 44, 911–916. [Google Scholar] [CrossRef]
- Reynolds, W.D.; Zebchuk, W.D. Use of contact material in tension infiltrometer measurements. Soil Technol. 1996, 9, 141–159. [Google Scholar] [CrossRef]
- Ramos, T.B.; Goncalves, M.C.; Martins, J.C.; van Genuchten, M.T.; Piers, F.P. Estimation of soil hydraulic properties from numerical inversion of tension disk infiltrometer data. Vadose Zone J. 2006, 5, 684–696. [Google Scholar] [CrossRef]
- Schwen, A.; Hernandez-Ramirez, G.; Lawrence-Smith, E.J.; Sinton, S.M.; Carrick, S.; Clothier, B.E.; Buchan, G.D.; Loiskandl, W. Hydraulic properties and the water-conducting porosity as affected by subsurface compaction using tension infiltrometers. Soil Sci. Soc. Am. J. 2011, 75, 822–831. [Google Scholar] [CrossRef]
- Matula, S.; Kozáková, H. A simple pressure infiltrometer for determination of soil hydraulic properties by in situ infiltration measurements. Plant. Prod. Rostlinná Výroba 1997, 43, 405–413. [Google Scholar]
- Hopmans, J.; Simunek, J. Review of inverse estimation of soil hydraulic properties. In Characterization and Measurement of the Hydraulic Properties of Unsaturated Porous Media; van Genuchten, M.T., Leij, F.J., Eds.; University of California: Riverside, CA, USA, 1999; pp. 643–659. [Google Scholar]
- Zou, Z.Y.; Young, M.H.; Li, Z.; Wierenga, P.J. Estimation of depth averaged unsaturated soil hydraulic properties from infiltration experiments. J. Hydrol. 2001, 242, 26–42. [Google Scholar] [CrossRef]
- Kosugi, K. Lognormal distribution model for unsaturated soil hydraulic properties. Water Resour. Res. 1996, 32, 2697–2703. [Google Scholar] [CrossRef]
- Durner, W. Hydraulic conductivity estimation for soils with heterogeneous pore structure. Water Resour. Res. 1994, 30, 211–223. [Google Scholar] [CrossRef]
- Fatehnia, M.; Tawfiq, K.; Abichou, T. Comparison of the methods of hydraulic conductivity estimation from mini disk infiltrometer. Electron. J. Geotech. Eng. 2014, 19, 1047–1063. [Google Scholar]
- Lai, J.; Luo, Y.; Ren, L. Buffer index effects on hydraulic conductivity measurements using numerical simulations of double-ring infiltration. Soil Sci. Soc. Am. J. 2010, 74, 1526–1536. [Google Scholar] [CrossRef]
- Picciafuoco, T.; Morbidelli, R.; Flammini, A.; Saltalippi, C.; Corradini, C.; Strauss, P.; Blöschl, G. On the estimation of spatially representative plot scale saturated hydraulic conductivity in an agricultural setting. J. Hydrol. 2019, 570, 106–117. [Google Scholar] [CrossRef]
- Ahmed, F.; Gulliver, J.S.; Nieber, J.L. Field infiltration measurements in grassed roadside drainage ditches: Spatial and temporal variability. J. Hydrol. 2015, 530, 604–611. [Google Scholar] [CrossRef]
- Rienzner, M.; Gandolfi, C. Investigation of spatial and temporal variability of saturated soil hydraulic conductivity at the field-scale. Soil Till. Res. 2014, 135, 28–40. [Google Scholar] [CrossRef]
- Reynolds, W.D.; Bowman, B.T.; Brunke, R.R.; Drury, C.F.; Tan, C.S. Comparison of tension infiltrometer, pressure infiltrometer, and soil core estimates of saturated hydraulic conductivity. Soil Sci. Soc. Am. J. 2000, 64, 478–484. [Google Scholar] [CrossRef]
- Nestingen, R.; Asleson, B.; Gulliver, J.S.; Hozalski, R.; Nieber, J.L. Laboratory comparison of field infiltrometers. J. Sustain. Water Built Environ. 2018, 4, 04018005. [Google Scholar] [CrossRef]
- Olson, N.C.; Gulliver, J.S.; Nieber, J.L.; Kayhanian, M. Remediation to improve infiltration into compact soils. J. Environ. Manag. 2013, 117, 85–95. [Google Scholar] [CrossRef]
- Morbidelli, R.; Saltalippi, C.; Flammini, A.; Cifrodelli, M.; Picciafuoco, T.; Corradini, C.; Govindaraju, R.S. In situ measurements of soil saturated hydraulic conductivity: Assessment of reliability through rainfall–runoff experiments. Hydrol. Process. 2017, 31, 3084–3094. [Google Scholar] [CrossRef]
- Ghosh, B.; Pekkat, S.; Kumar Yamsani, S. Evaluation of infiltrometers and permeameters for measuring hydraulic conductivity. Adv. Civil. Eng. Mat. 2019, 8, 308–321. [Google Scholar] [CrossRef]
- Angulo-Jaramillo, R.; Moreno, F.; Clothier, B.E.; Thony, J.L.; Vachaud, G.; Fernandez-Boy, E.; Cayuela, J.A. Seasonal variation of hydraulic properties of soils measured using a tension disk infiltrometer. Soil Sci. Soc. Am. J. 1997, 61, 27–32. [Google Scholar] [CrossRef]
- Ankeny, M.D.; Kaspar, K.C.; Horton, R. Design for an automated tension infiltrometer. Soil Sci. Soc. Am. J. 1988, 52, 893–896. [Google Scholar] [CrossRef]
- Klipa, V.; Sacha, J.; Snehota, M.; Dohnal, M.; Zumr, D.; Tacheci, P. Automated multi-point mini-disk infiltrometer measurements of unsaturated hydraulic conductivity. In Proceedings of the EGU General Assembly Conference Abstracts, EGU2014–7230, Vienna, Austria, 27 April–2 May 2014; Volume 16. [Google Scholar]


| Manual 2005 | Manual 2014 | Dohnal et al. [48] | ||||
| α = 0.01 | n = 1.23 | α = 0.01 | n = 1.23 | α = 0.01 | n = 1.23 | |
| Pressure head | Parameter A | Parameter A | Parameter A | |||
| −5 cm | 10.1 | 9.90 | 22.5 | |||
| −3 cm | 9.1 | 8.95 | 21.9 | |||
| −1 cm | 8.3 | 8.09 | 21.3 | |||
| Rosetta for CT | Rosetta for RT | Rosetta for NT | ||||
| α = 0.0087 | n = 1.4998 | α = 0.0083 | n = 1.5089 | α = 0.0083 | n = 1.5129 | |
| Pressure head | Parameter A | Parameter A | Parameter A | |||
| −5 cm | 20.1 | 21.1 | 21.2 | |||
| −3 cm | 19.1 | 20.1 | 20.2 | |||
| −1 cm | 18.1 | 19.1 | 19.3 | |||
| Soil Treatment | Exp. Phase | Time Indication | Dry Bulk Density (g cm−3) | Particle Density (g cm−3) | Total Porosity (%) | Organic Matter Content Cox (%) |
|---|---|---|---|---|---|---|
| RT | I. | June 2008 | 1.27 a | 2.61 a | 51.37 a | 2.44 b |
| II. | Sept. 2008 | 1.16 b | 2.63 a | 55.75 a | 2.50 b | |
| III. | April 2009 | 1.21 a | 2.64 a | 54.03 a | 2.58 b | |
| IV. | June 2009 | 1.26 a | 2.64 a | 52.19 a | 2.58 b | |
| NT | I. | June 2008 | 1.31 a | 2.64 a | 48.46 b | 3.01 c |
| II. | Sept. 2008 | 1.33 a | 2.64 a | 49.60 b | 2.67 c | |
| III. | April 2009 | 1.29 a | 2.60 a | 48.39 b | 2.96 c | |
| IV. | June 2009 | 1.36 a | 2.62 a | 47.98 b | 3.23 c | |
| CT | I. | June 2008 | 1.26 a | 2.60 a | 51.55 a | 1.81 a |
| II. | Sept. 2008 | 1.13 b | 2.61 a | 56.54 a | 1.82 a | |
| III. | April 2009 | 1.27 a | 2.62 a | 52.8 1a | 1.93 a | |
| IV. | June 2009 | 1.28 b | 2.61 a | 51.12 a | 1.83 a | |
| Max | 1.37 | 2.64 | 57.54 | 3.24 | ||
| Min | 1.13 | 2.6 | 46.98 | 1.74 | ||
| Standard deviation | 0.064 | 0.012 | 3.107 | 0.464 | ||
| Coefficient of variation (%) | 5.0 | 0.5 | 6.0 | 19.1 | ||
| Exp. Phase | Treatment | θinitial (cm3 cm−3) | θifinal (cm3 cm−3) | α (cm−1) | n (-) | R2 |
|---|---|---|---|---|---|---|
| I. | CT | 0.125 | 0.338 | 0.1397 | 2.1004 | 0.9986 |
| NT | 0.157 | 0.340 | 0.2052 | 1.8914 | 0.9950 | |
| RT | 0.139 | 0.342 | 0.1999 | 1.8178 | 0.9983 | |
| II. | CT | 0.187 | 0.323 | 0.2190 | 1.8829 | 0.9985 |
| NT | 0.222 | 0.347 | 0.6050 | 1.2315 | 0.9963 | |
| RT | 0.188 | 0.339 | 0.2512 | 1.5753 | 0.9983 | |
| III. | CT | 0.158 | 0.321 | 0.1627 | 1.5842 | 0.9987 |
| NT | 0.195 | 0.323 | 1.0524 | 1.4240 | 0.9928 | |
| RT | 0.155 | 0.338 | 0.5248 | 1.3931 | 0.9967 | |
| IV. | CT | 0.234 | 0.385 | 0.5129 | 1.2259 | 0.9982 |
| NT | 0.319 | 0.381 | 0.6256 | 1.1253 | 0.9926 | |
| RT | 0.290 | 0.406 | 0.5060 | 1.1780 | 0.9962 |
| Source | Sum of Squares 1 | Df 2 | Mean Square 3 | Var. Comp. 4 | Percent 5 |
|---|---|---|---|---|---|
| TOTAL (CORRECTED) | 329.176 | 485 | |||
| Infiltrometer type & Analysis | 111.561 | 4 | 27.890 | 0.2032 | 27.65 |
| Tension | 81.515 | 10 | 8.151 | 0.1714 | 23.33 |
| Treatment | 77.508 | 30 | 2.584 | 0.2115 | 28.78 |
| Experimental phase | 38.808 | 132 | 0.294 | 0.0847 | 11.53 |
| ERROR | 19.784 | 309 | 0.064 | 0.0640 | 8.71 |
| Criteria | MDI | HI | Rationale |
|---|---|---|---|
| Portability | Very high | Very low | MDI with its total length of 32.7 cm and tube diameter of 3.1 cm belongs among the smallest devices enabling measurements in distant areas with limited or no source of water. |
| Amount of water for infiltration | Very low | Very high | Only 95 mL can be infiltrated, and the device cannot be refilled without removal from the infiltration surface (which is possible with HI). |
| Size of the infiltration area | Low | Medium | MDI offers only 16 cm2 of infiltration area, but thanks to its small dimensions and weight, a freshly tilled soil can sustain its weight. |
| Time requirement for in-situ installation | Low | High | MDI can be ready to use relatively quickly; however, a special care needs to be paid to the infiltration surface preparation. |
| Need of contact material | Moderate | Very low | Use of contact material, its type, thickness and suitability has been widely discussed (e.g., [62,63]). |
| Suitability for K(h) determination | High | Very high | MDI has a limited range of pressure head settings (−0.5 to −7 cm), HI is limited by the soil bubbling point (approx. −10 cm for our tested soil), Soil Measurement Systems (USA) offer tension infiltrometers operating at pressure heads up to −30 cm, Ankeny et al. [82] presented an automated tension infiltrometer operating at pressure heads up to –50 cm. |
| Suitability for Ks determination | Low | Very high | MDI does not allow infiltration at pressure head 0 cm, the Ks value can only be estimated, e.g., by extrapolation based on the K(h) values or by inverse parametrization of the infiltration data. |
| Sensitivity to measurement influence by initial soil moisture content | High | Very low | MDI was proved to determine different infiltration rates for the same applied pressure head at the same soil with different initial soil moisture content (e.g., [9,58,59]). |
| Affordability due to cost of the device | Very high | Low | MDI is a relatively low-cost device, when automated some additional costs are required. Interesting automated settings of 6 MDI running simultaneously at two applied pressure heads was presented by Klipa et al. [83]. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Báťková, K.; Miháliková, M.; Matula, S. Hydraulic Properties of a Cultivated Soil in Temperate Continental Climate Determined by Mini Disk Infiltrometer. Water 2020, 12, 843. https://doi.org/10.3390/w12030843
Báťková K, Miháliková M, Matula S. Hydraulic Properties of a Cultivated Soil in Temperate Continental Climate Determined by Mini Disk Infiltrometer. Water. 2020; 12(3):843. https://doi.org/10.3390/w12030843
Chicago/Turabian StyleBáťková, Kamila, Markéta Miháliková, and Svatopluk Matula. 2020. "Hydraulic Properties of a Cultivated Soil in Temperate Continental Climate Determined by Mini Disk Infiltrometer" Water 12, no. 3: 843. https://doi.org/10.3390/w12030843
APA StyleBáťková, K., Miháliková, M., & Matula, S. (2020). Hydraulic Properties of a Cultivated Soil in Temperate Continental Climate Determined by Mini Disk Infiltrometer. Water, 12(3), 843. https://doi.org/10.3390/w12030843






