1. Introduction
A large number of hydropower stations have been built around the world, and engineering problems that occur in reservoirs have been discussed widely. The land-level changes due to reservoir impoundment have been discussed by numerous researchers [
1,
2,
3,
4]. However, river valley contractions (RVCs) are rarely reported, which can directly affect the safety and the operability of a dam [
5]. RVCs may occur both upstream and downstream of a reservoir and increase due to the impoundment or operational stage of a hydropower station and continue to grow for several years.
A specific case of RVCs occurred in the Zeuzier arch dam, located in Switzerland. These RVCs were first observed after the hydropower station safely operated for 21 years. The RVCs of the Zeuzier Dam ultimately reached approximately 75 mm, which resulted in up to 15 mm wide cracks forming on the downstream face of the dam [
6]. The RVCs at the Zeuzier Dam were confirmed to be caused by the settlements of rock masses, which is induced by the groundwater flows out of the rock masses and into the 400 m deep tunnel nearby [
7]. Besides the Zeuzier Dam, RVCs also appear in other hydropower stations. The RVCs that occurred in the Jinping-I Dam during the impoundment stage (approximately 10 mm) were supposedly induced by the shrinkage of the yield surface of the reservoir slope [
8]. During the excavation period of the AlpTransit Gotthard railway tunnel, valley contractions or expansions up to 14 mm were detected at a deformation monitored site known as Val Termine, and seasonal variations of the water table were proven to be the reason for this deformation [
5].
Drastic RVCs have been observed in the Xiluodu hydropower station since the reservoir impoundment, and the largest RVCs recorded have now exceeded 93 mm (26 April 2019). Moreover, the RVCs are continuously growing, which poses a threat to the safety of the dam. There have been some studies on RVCs of the Xiluodu Dam. The reservoir level and temperature were determined by Liang et al. [
9] to have little relation to RVCs; Liang et al. analyzed the correlation between the contract process and some impact factors, such as the reservoir level and temperature, using a stepwise regression model. Zhuang et al. [
10] simulated the RVCs with an analytical model and determined that the RVCs are highly correlated with changes to the reservoir level. Two-parameter exponential functions were used to fit the RVC data from 20 December 2012 to 19 May 2017. Then, the development of the RVCs were predicted, and the growth rate was determined to be less than 0.001 mm/d by August 2022 [
11]. Some studies view RVCs as local phenomena of landslides [
12]. Although landslides can decrease river width, no cracks on slope surfaces have been found at the Xiluodu reservoir, and no sliding surface inside the slope has been observed based on all the plumb-line monitoring data.
RVCs directly threaten the safety of the Xiluodu Dam, so it is particularly important to predict RVC development. However, the main factors that influence RVCs of the Xiluodu hydropower station have not been confirmed; there is currently no theory that can explain RVCs completely, nor can any deformation, statistical, or numerical method simulate RVC phenomena accurately.
The HST (hydrostatic–seasonal–time) model is widely used to analyze and predict the behavior of arch dams [
13]. The HST model is a statistical technique for analyzing and modelling the relationship between the variables and deformation of dams and has proven to be an effective method for the safety analysis of concrete dams [
14]. However, reports on statistical prediction models related to the RVCs of reservoirs, to the authors’ best knowledge, are rare and incomplete. Referring to the HST model, a groundwater hydrostatic seasonal (GHS) model was proposed for studying and predicting the development of RVCs. Unlike the HST model, which approximates the hydrostatic effect as a polynomial function of the reservoir level
h, and the irreversible effect of time as exponential, hyperbolic, or polynomial, in the GHS model, the hydrostatic effect is represented by an increase in the hydraulic head of a confined aquifer. The average increase in the hydraulic head is calculated through a groundwater analytical flow model [
15], which can reflect the hydraulic hysteresis effect more accurately than the polynomial function.
In this research, we first provide the background of the Xiluodu hydropower station. The RVCs phenomena that occurred in the Xiluodu reservoir is introduced, and the deformation mechanism is discussed. Secondly, an analytical solution for the hydraulic response of the confined aquifer to fluctuations of reservoir level was produced. Finally, a GHS model was proposed based on a groundwater analytical flow model and the model was applied to interpret the RVCs of the Xiluodu hydropower station.
2. Background of the Engineering
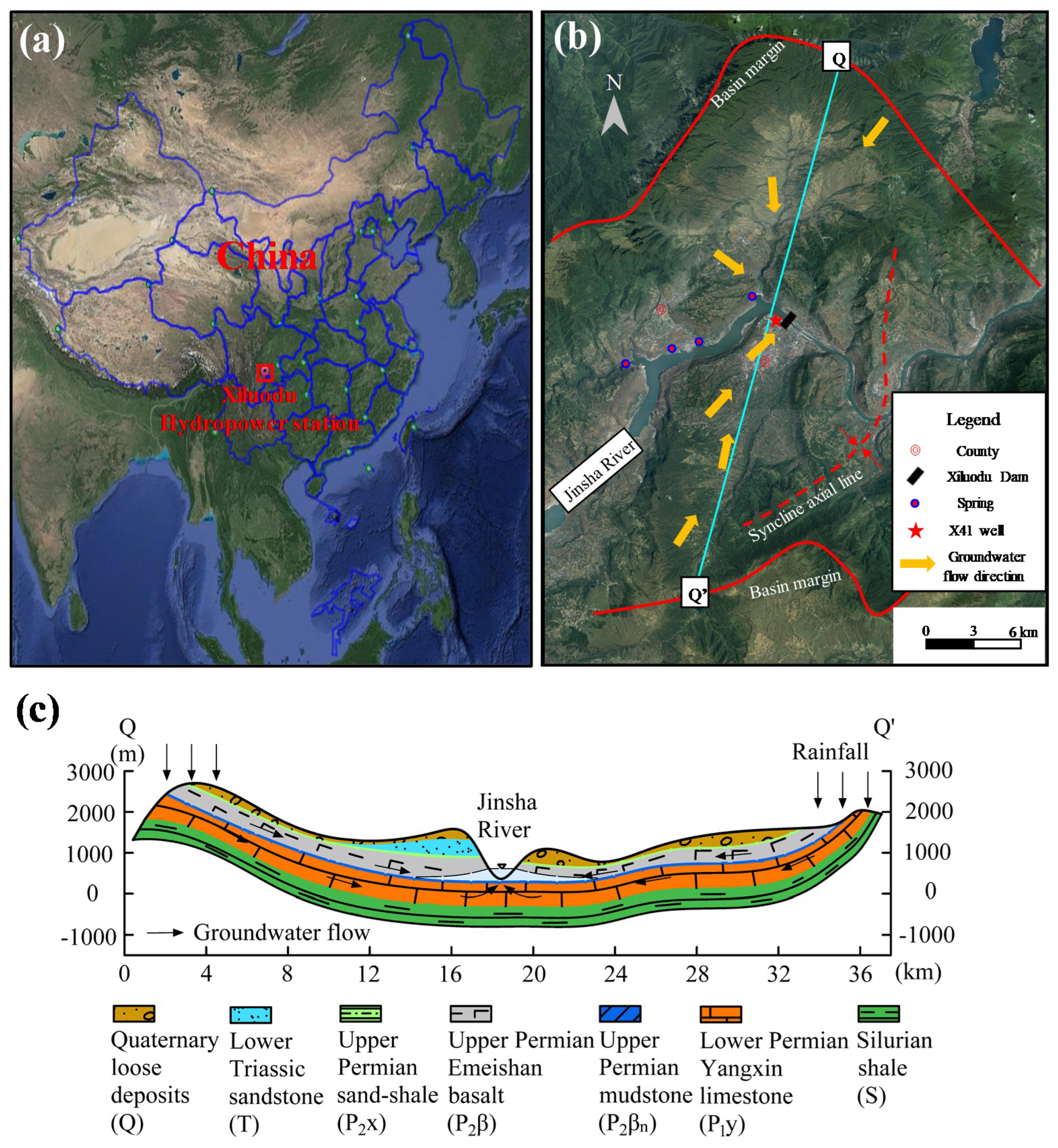
The Xiluodu arch dam is located in the Yongsheng synclinal basin in Yunnan province, China. It is a double-curved arch dam, with a height of 285.5 m and a 610 m crest elevation. The Yongsheng basin is 35 km long in the northeast and 25 km in the northwest, with an area of 750 km
2, as shown in
Figure 1b. The basin is a wide, gentle, and relatively complete tectonic synclinal basin, which has not been cut by regional faults. In this basin, the direction of the synclinal axial line is northeast, and the dip angle of the northwest wing is 10°–15°, while the southeast wing is 20°–35°.
The stratum of the Yongsheng synclinal basin includes three aquitard formations, namely Silurian shale (S), Upper Permian mudstone (P
2β
n), and Upper Permian sand-shale (P
2x), as well as three aquifer formations, namely Lower Permian Yangxin limestone (P
1y), Upper Permian Emeishan basalt (P
2β), and Quaternary loose deposits (Q). The aquitard and aquifer formations are adjacent to each other from the bottom to the top, and the contact surface of each formation features disconformity. Because the burial depth of the Silurian shale (S) is more than 500 m, the effect of this layer on the hydropower station was not considered in this paper. With a total thickness of 500 m, the Lower Permian Yangxin limestone formation is continuously buried, except for some of the formation exposed on the edge of the basin and part of the upstream channel. From upstream to downstream, the burial depth of the limestone formation increases gradually to about 90 m beneath the dam foundation. The thickness of the Upper Permian mudstone (P
2β
n) is generally 2 m (not more than 5 m), and its burial depth is 79–163 m near the dam. The Upper Permian Emeishan basalt formation is widely distributed over the Yongsheng synclinal basin, and its rock is dense and hard. The Upper Permian sand-shale (P
2x), which is continuously distributed in the region, forms the non-permeable bottom of the top pore aquifer (the Quaternary loose deposits) and plays an impermeable boundary role in groundwater movement. The geological conditions of the Xiluodu Dam area and the Q–Q’ cross-section of the Yongsheng synclinal basin are shown in
Figure 1.
The groundwater evolution in the dam area depends on the hydrogeological conditions of the Yongsheng synclinal basin, which is an independent hydrogeological unit [
16]. The Jinsha River crosses the Yongsheng synclinal basin, which is the base level of erosion and the drainage area of groundwater and surface water. In this basin, the Lower Permian Yangxin limestone formation forms a confined aquifer with two aquitards: the Silurian shale (S) on the bottom and the Upper Permian mudstone (P
2β
n) on the top. Above the Upper Permian mudstone, there is a basalt unconfined aquifer. Between the limestone confined aquifer and the basalt unconfined aquifer, there is a hydraulic head difference of 2 m near the riverbed. Hydrogeological investigations revealed some characteristics of the limestone confined aquifer, such as a large circulation depth, a long cycle route, and high salinity and temperature. The limestone confined aquifer receives rainfall recharge in outcropping regions at elevations about 2000 m. The limestone confined aquifer discharges at the bottom of the Jinsha River and numerous small overflow springs along the valley floor (at a 370 m to 400 m elevation above sea level;
Figure 1b). The basalt unconfined aquifer is recharged by rainfall at the edge of the basin and is discharged by springs in the Jinsha River. Due to the retardation of the Upper Permian sand-shale (P
2x) above the Upper Permian Emeishan basalt formation, the rainfall has difficulty infiltrating into the basalt layer, so the phreatic surface in the basalt layer is minimal.
Figure 1b,c illustrate regional groundwater flow in the Yongsheng basin.
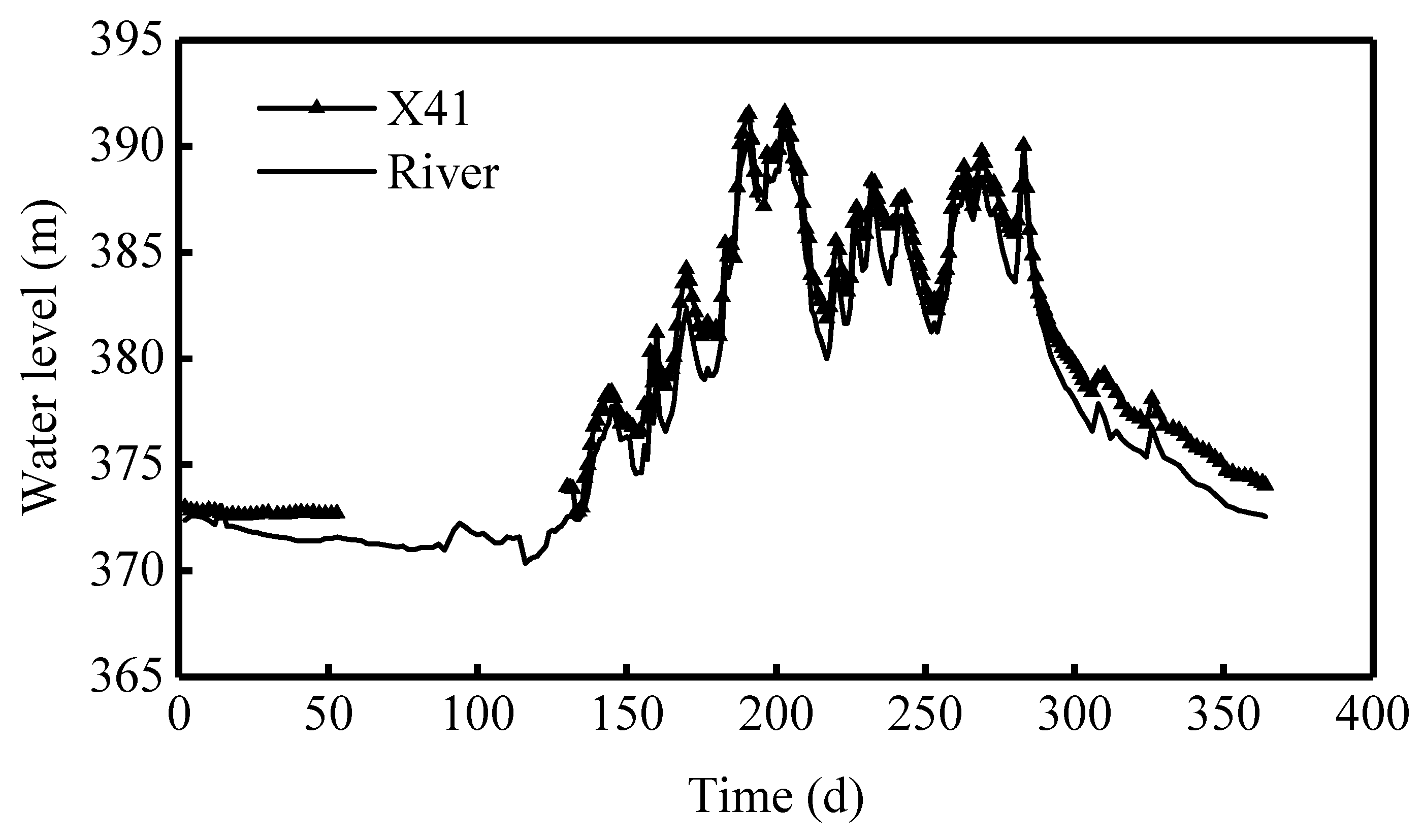
A hydrogeological survey revealed the close relationship between surface and groundwater. Before the construction of the hydropower project, many wells were used to monitor the groundwater level in the basin. Well X41 is located on the right bank of the river, 142 m from the river. The confined aquifer hydraulic head began to be monitored on 2 January 1995 (
Figure 2). The fluctuation of the hydraulic head in well X41 shows that the confined aquifer has good synchronization with the rise and fall of the river water level (
Figure 2). The synchronization of the well and river water level indicates that the limestone confined aquifer has large hydraulic diffusivity, and the storage space of the limestone rock mass is limited.
3. RVCs of the Xiluodu Dam
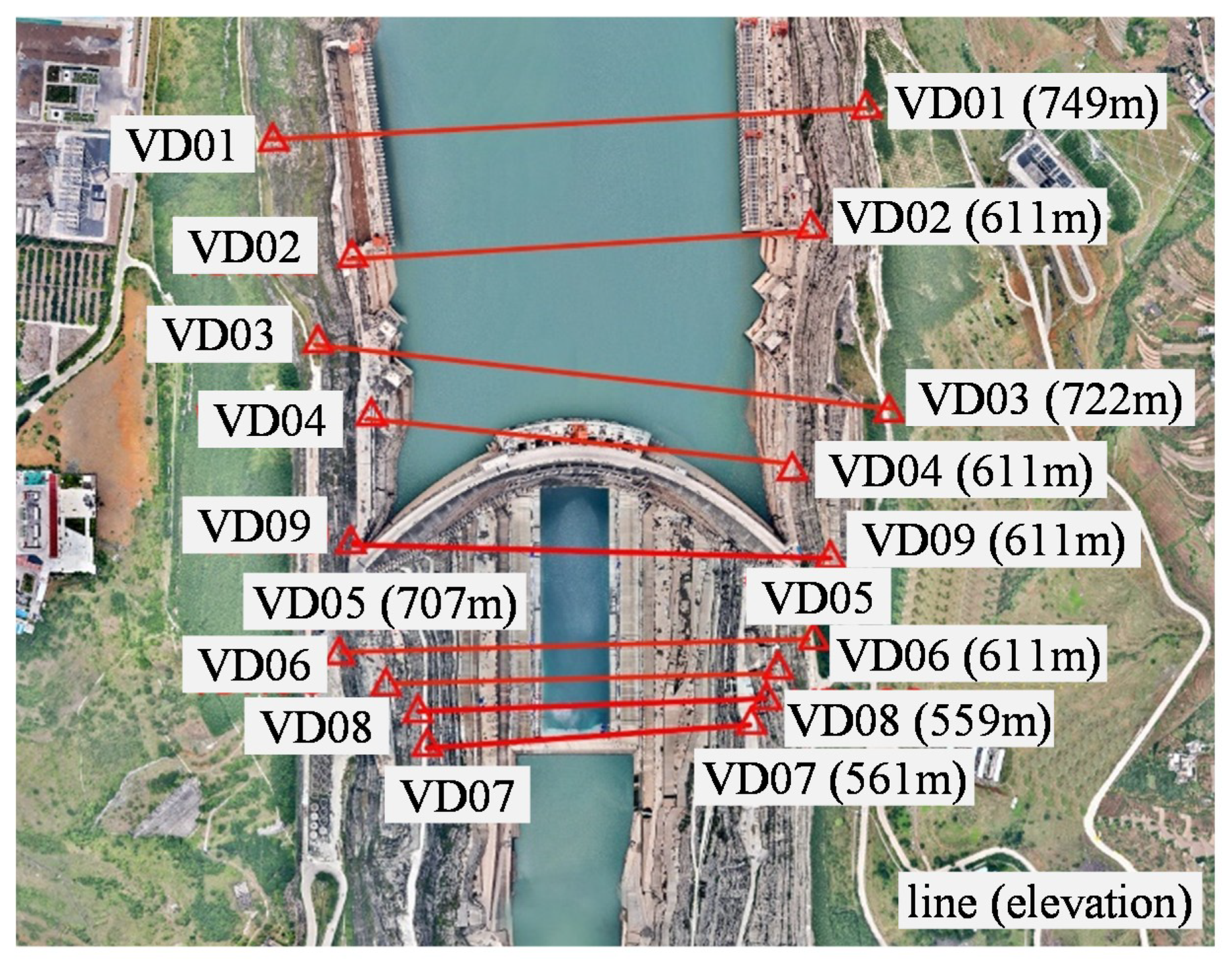
Before the construction of the Xiluodu Dam, the river level fluctuated between 370 m and 400 m in a single year. The water impoundment of the reservoir began in November 2012; then, the water level increased from 403.5 m and reached a normal water level of 600 m for the first time on 29 September 2014. During normal operation of the hydropower station, the reservoir level ranged from 550 m to 600 m, giving a maximum fluctuation of 50 m. Nine valley deformation monitoring lines were situated at the Xiluodu hydropower station to measure changes in valley width. Four of the lines are located upstream of the reservoir (namely, VD01, VD02, VD03, and VD04), while the other four are located downstream (namely, VD05, VD06, VD07, and VD08). Further, one is located at the top of the dam crest (VD09). The layout of each monitoring line is shown in
Figure 3.
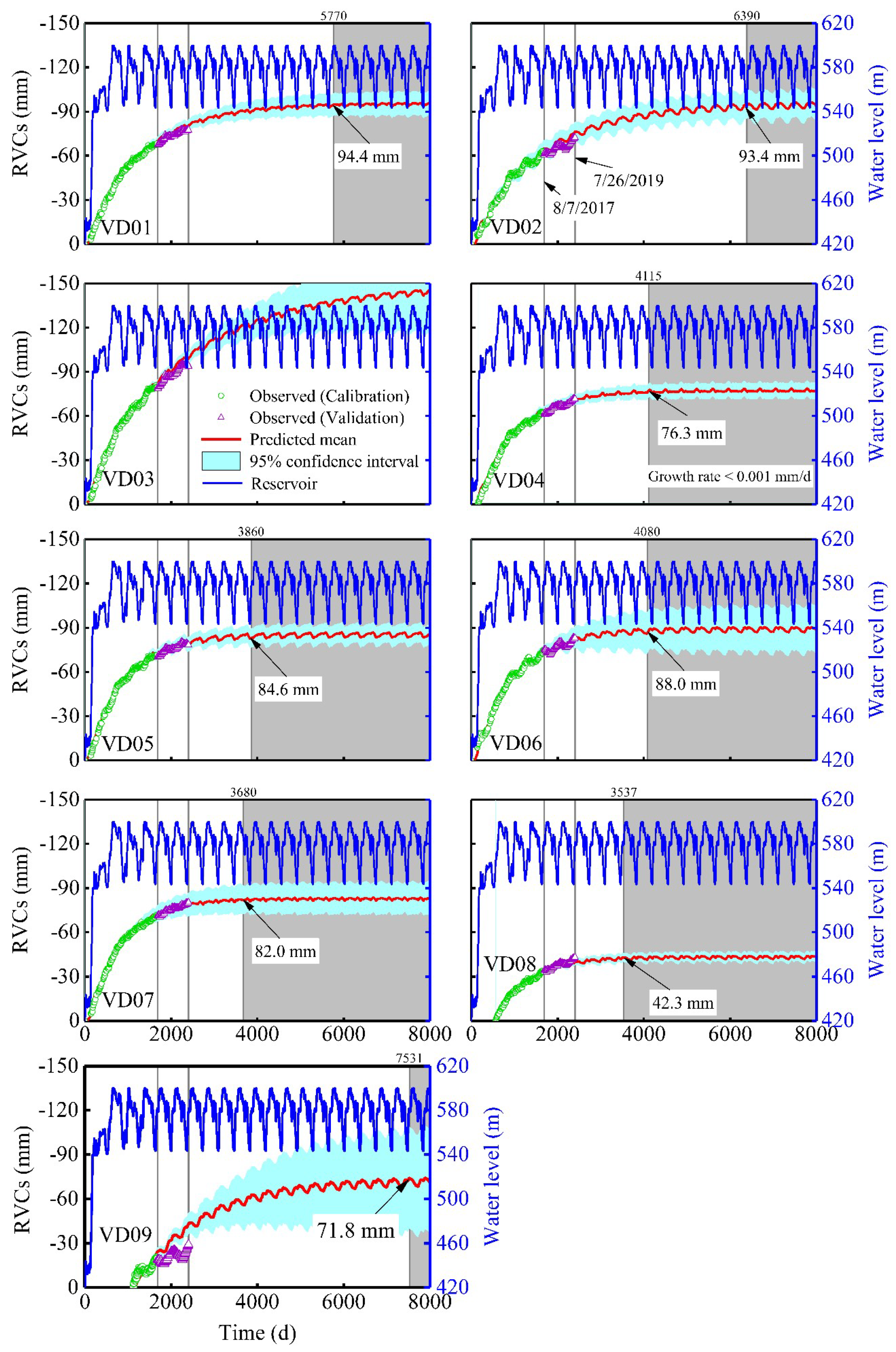
Most valley deformation monitoring lines began in December 2012, except for VD09, VD08, and VD04, which began in January 2016, July 2014, and May 2013, respectively. The VD08 monitoring line is arranged inside the drainage tunnel at a 561 m elevation (about 150 m deep into the rock mass). Observations of all nine monitoring lines reveal that the RVCs occurred in a large area upstream and downstream of the reservoir (
Figure 4), and their cumulative deformation is −22.47 mm to about −93.47 mm (26 April 2019). The (+) signs indicate the expansion of the river valley and (−) indicates the contraction of the river valley. The two main characteristics of the RVCs are summarized as follows: (1) the amount of the RVCs is very large; and (2) the amount of RVCs is approximately equal for different monitoring sites and different monitoring elevations.
Since the impoundment, the Xiluodu reservoir has experienced five complete periods of water storage and release. The RVCs of the Xiluodu reservoir grow continually. There are many studies on the mechanisms of the RVCs [
11,
17,
18]. However, none of these studies can explain the contraction phenomenon completely. We infer that the RVCs are induced by the reservoir impoundment based on the development of RVCs and the hydrogeological conditions of the Xiluodu reservoir. During the period of reservoir impoundment, the hydraulic head increased and the effective stress decreased in the limestone confined aquifer, leading to the expansion of the limestone formation. Under the special tectonic structures of the Yongsheng basin, the formations at the two river banks inclined toward the Jinsha River (
Figure 1c), and the expansion lead to the bank slope riverward deformation. Three conditions enhance the RVCs of the Xiluodu reservoir: The confined aquifer buried in the basin forms an expansion formation. The sharp increase in the hydraulic head of the confined aquifer after impoundment led to a sharp expansion of the limestone formation. The close hydraulic relationship between the surface water and groundwater led to a rapid rise of the hydraulic head in the confined aquifer. It can thus be concluded that the hydrogeological conditions at Xiluodu were particularly amenable to the RVCs phenomena.
Overall, the impoundment of the reservoir is the main factor that triggered the RVCs. In the forthcoming subsections, we will build a model to calculate the hydraulic head changes of the Yangxin limestone confined aquifer.
4. Hydraulic Response of the Confined Aquifer
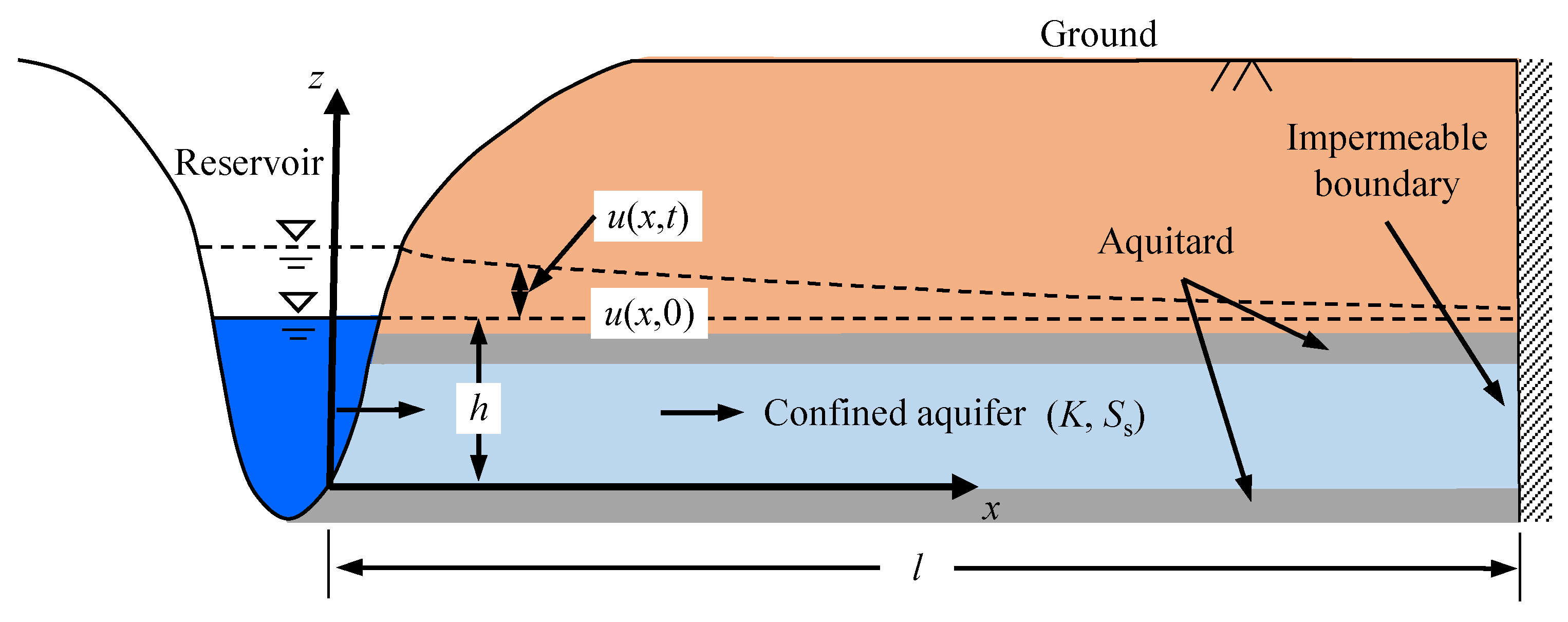
Long-term well data reveal that the groundwater level has a significant correlation with the river level. A one-dimensional confined aquifer model was established to describe the progress of the hydraulic transfer between the Jinsha River and the bank slope. Unlike the traditional model, which approximates river level changes as instantaneous changes that then remain constant or experience periodic fluctuations, we use a piecewise linear function to describe the river-level changes accurately. As shown in
Figure 1c, the limestone formation rises sharply at the edge of the basin, and the other boundary condition of the model can be set as the impermeable boundary. The hydraulic response of the one-dimensional limestone confined aquifer to the change in the reservoir water level is shown in
Figure 5.
In order to build the model, we make several simplifying assumptions: (1) We consider the confined aquifer to be homogeneous, isotropic, and with a uniform thickness, as well as with a horizontal extension length l; (2) we consider the aquifer as slightly compressible and bounded by the impermeable layer below and above; (3) we consider the hydraulic properties of the confined aquifer to be constant over time; (4) one boundary of the confined aquifer is impermeable, and the other boundary is the dynamic river water level; and (5) under natural conditions, the hydraulic head of the confined aquifer is equal to the river water level.
One dimensional, horizontal groundwater flow in a confined aquifer can be described as
subject to the following initial and boundary conditions:
where
u(
x,
t) represents the variation of the hydraulic head in the confined aquifer at
x and time
t in the
ith time period;
a =
K/
Ss is the hydraulic diffusivity;
K is the hydraulic conductivity;
Ss is the specific storage;
βi is the change rate of reservoir water level in the
ith time period;
ti is the
ith time node; and
t0 = 0. Zhuang et al. [
19] have provided an analytical solution to the boundary value problem, as shown in Equations (1) to (4), by using the method of separating variables:
where
Since different hydraulic responses occur at different locations in the aquifer, we consider the average hydraulic response of the aquifer. The hydraulic head
u was integrated and then divided by the horizontal extension length
l [
20]. The analytical solution of the average hydraulic response of the confined aquifer is shown below:
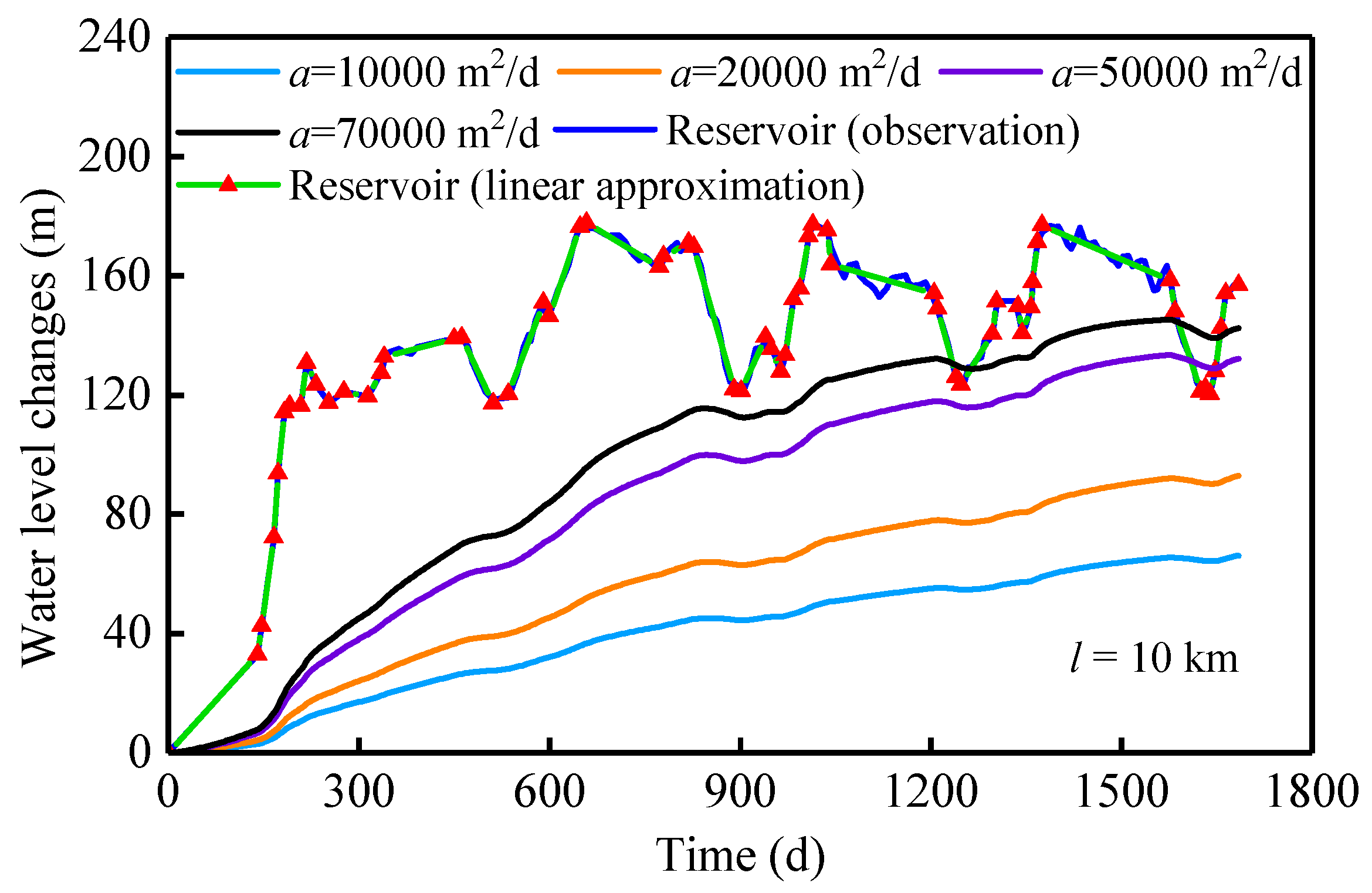
Based on Equation (7), the increase in the confined aquifer hydraulic head can be calculated easily. Taking 20 November 2012 as the initial time and 31 July 2017 as the end time of the research period, the fluctuating water level of the Xiluodu reservoir was fitted with 59 consecutive linear segments, as shown in
Figure 6. Assuming that the extended length of the confined aquifer is 10 km, the hydraulic diffusivity is 10,000, 20,000, 50,000, and 70,000 m
2/d, respectively, and the average increase in the hydraulic head of the confined aquifer can be calculated using Equation (7), as shown in
Figure 6. The calculation results reveal that (1) the average hydraulic head increases with time in the confined aquifer; (2) hydraulic diffusivity has an influence on the increased rate of the average hydraulic head. With a large hydraulic diffusivity, the average hydraulic head increases rapidly and enters a relatively stable stage quickly; and (3) a change in the reservoir water level determines the change of the hydraulic head of the confined aquifer. The average increase in the hydraulic head will approximate the mean value of the reservoir water level increase.
7. Discussion
Some regression models have been established to interpret the RVCs of the Xiluodu hydropower station [
10,
11,
21]. Liang [
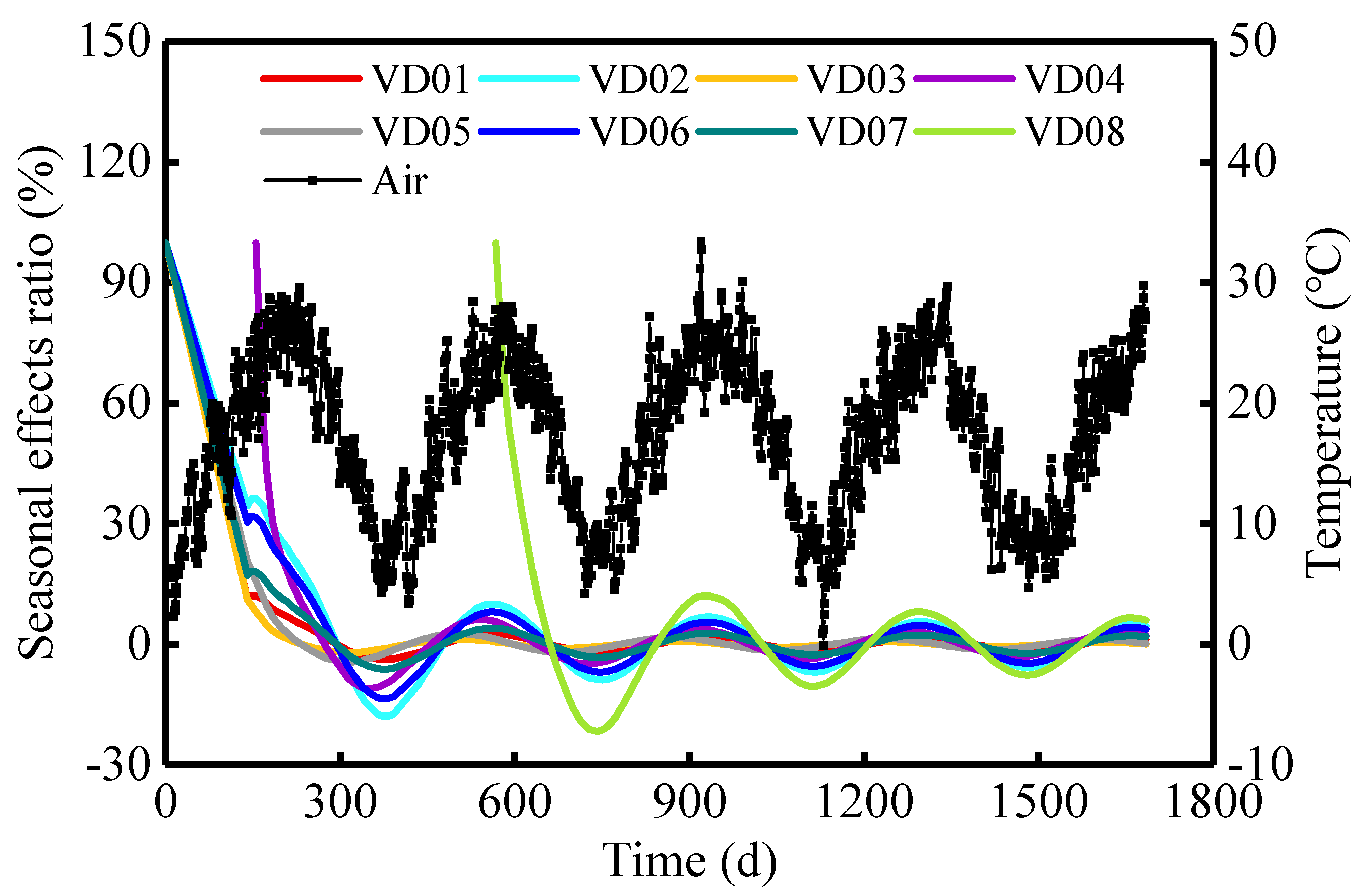
21], for example, added the hydraulic hysteresis effects to the HST model and studied the RVCs. He pointed out that it is necessary to consider the hydraulic hysteresis effect in the regression model. Liang supposed that the reservoir water level and temperature have little relationship with the RVCs. However, Liang used the reservoir water level at three specific time points (30, 60, and 90 days before calculation time) to reflect the hydraulic hysteresis effects, which is a very rough calculation. We proposed a GHS model and interpreted the RVCs. In the GHS model, the hydrostatic effect is calculated using a groundwater analytical flow model, which can accurately reflect the hydraulic hysteresis effects.
Our calculation results demonstrate that the increase in the hydraulic head of confined aquifer is the main cause of the RVCs, and that seasonal effects gave rise to less than 10% of the RVCs. These findings extend those of Liang, confirming that the reservoir water level affects the hydraulic head of the confined aquifer through hydraulic transfer, and the increase in the hydraulic head induced the RVCs. In addition, the proposed GHS model describes the RVCs with the aquifer parameters, which can be used to calculate the hydraulic diffusivity of the confined aquifer. This study indicates that the RVCs may occur in a wider range both sides of the river than the monitoring results, and the hydraulic transfer is the key factor affecting the RVCs. Our results reveal the main causes of the RVCs and predict its final amount, which provides a reference for engineering measures to protect the safety of the dam. However, some limitations are worth noting. Although our GHS model can simulate RVCs, the groundwater analytical flow model is simple, and it deviates from the real one. Future work should, therefore, adopt a more accurate groundwater analytical flow model. The physical mechanism of the RVCs caused by the increase in the hydraulic head of the confined aquifer needs to be further studied.
8. Conclusions
RVCs (river valley contractions) are rare phenomena that directly threaten the safety of the Xiluodu Dam, so it is particularly important to predict RVCs development. However, the main factors influencing the RVCs of the Xiluodu hydropower station have not been confirmed, nor can any theories completely explain RVC phenomena. Likewise, no statistical or numerical methods can simulate RVC phenomena accurately.
In this paper, we have presented a statistical study of the RVCs of the Xiluodu hydropower station. A novel model has been introduced to analyze the RVC phenomena. We found that the reservoir water level is closely related to RVCs. We infer that the RVCs of the Xiluodu Dam were developed through the expansion of the limestone confined aquifer. The main reason for this limestone expansion is the decrease in effective stress following the hydraulic head increase after the impoundment of the reservoir. Under specific syncline basin geological conditions, the expansion of the limestone formation induced the RVC phenomena. It can be concluded that the hydrogeological conditions at the Xiluodu Dam are particularly prone to RVC phenomena. The study of RVCs shows that the proposed GHS model can accurately reproduce the RVC process and predict its development. Therefore, the proposed GHS model can be applied to analyze the RVC phenomena that occur in similar reservoirs.